Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Sep 4;54(19):12307–12315. doi: 10.1021/acs.est.0c02982

Solving the Nonalignment of Methods and Approaches Used in Microplastic Research to Consistently Characterize Risk

Albert A Koelmans 1,*, Paula E Redondo-Hasselerharm 1, Nur Hazimah Mohamed Nor 1, Merel Kooi 1
PMCID: PMC7547870  PMID: 32885967

Abstract

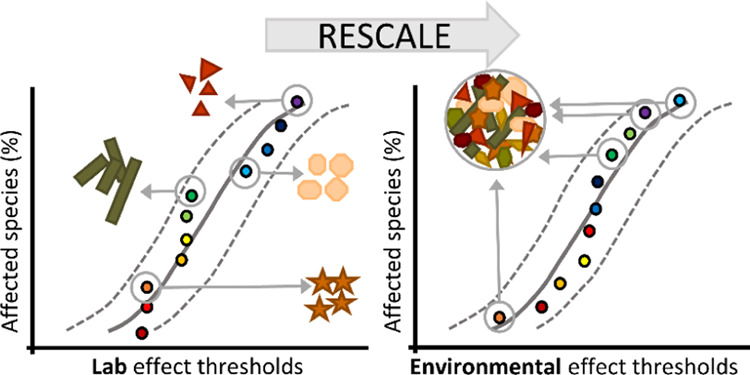
graphic file with name es0c02982_0005.jpg

The lack of standard approaches in microplastic research limits progress in the abatement of plastic pollution. Here, we propose and test rescaling methods that are able to improve the alignment of methods used in microplastic research. We describe a method to correct for the differences in size ranges as used by studies reporting microplastic concentrations and demonstrate how this reduces the variation in aqueous-phase concentrations caused by method differences. We provide a method to interchange between number, volume, and mass concentrations using probability density functions that represent environmental microplastic. Finally, we use this method to correct for the incompatibility of data as used in current species sensitivity distributions (SSDs), caused by differences in the microplastic types used in effect studies and those in nature. We derived threshold effect concentrations from such a corrected SSD for freshwater species. Comparison of the rescaled exposure concentrations and threshold effect concentrations reveals that the latter would be exceeded for 1.5% of the known surface water exposure concentrations worldwide. Altogether, this toolset allows us to correct for the diversity of microplastic, to address it in a common language, and to assess its risks as one environmental material.

Introduction

The literature portrays environmental microplastic as a diverse and complex material.1−5 This diversity follows from the fact that microplastic originates from many different types of products,2,3 and from how the material is defined: all plastic particles smaller than 5 mm.2,6−9 Because of the unspecific nature of this definition, microplastics (MPs) constitute a heterogeneous mixture of particles represented by a range of polymers, sizes, and shapes, and associated with all kinds of chemicals.2,3,10 Microplastics interact with natural particles and with organisms under a wide range of environmental conditions, which are even more diverse in space and time.11,12 This explains the challenges in assessing the risks these particles pose to the environment and to human health. It has even been argued to not consider “microplastic” as one contaminant, but instead focus on its components and address specific (classes of) microplastic for a range of types, sizes, and shapes.5

Assessing whether microplastic particles are a risk for human health and the environment is considered one of today’s major challenges in the environmental sciences.2 A consistent risk assessment for microplastic particles requires alignment of exposure and effect data. This means that whatever metric or unit is used to characterize exposure also is used for the effect assessment.1,13 For instance, ideally, one would measure exposure via all possible pathways for the entire size range that makes up microplastic, i.e., from 1 μm to 5 mm, according to an environmentally realistic size distribution. For the effect assessment, one would need to test particle effects for the same size distribution and boundaries, such that exposure and effect threshold data are aligned, and can be used in the risk characterization in a meaningful way.1

Unfortunately, the microplastic community is still far away from this situation. First, the literature uses different definitions of microplastics, with differences especially relating to the size ranges included in the definition.3,14 Second, methods to detect microplastic numbers or mass concentrations have different size detection limits.15 Since particles with smaller sizes typically occur at much higher number concentrations,4,16 methods that use finer sieve or filter mesh sizes and/or accurate spectroscopic methods would hence be able to capture most of these particles and yield orders of magnitude higher concentrations.15 Sieves or nets used for sampling often have either, e.g., 20, 100, 300, or 333 μm as the smallest size limit, whereas detection methods such as visual inspection, attenuated total reflection Fourier transform infrared (ATR-FTIR), focal-plane-array FTIR (FPA-FTIR), or Raman typically are associated with lower size detection limits of either 1000, 300, 20, or 1 μm, respectively.17 At the other end of the scale, sampling volume determines the detection limit for large particles, where larger particles with a low frequency of occurrence are simply missed when the volume is too small.15,18 Therefore, the aforementioned differences in methods have resulted in data incomparability. Third, conversion from number to mass concentrations (or vice versa) is usually done assuming microplastic particles to have a certain fixed shape (e.g., spherical) with the density of a discrete polymer.19,20 This, however, is not correct, because microplastic particles have a wide range of shapes and densities. More accurate conversions can be done by taking actual shape and density distributions into account. Fourth, there is nonalignment of microplastic particles used in effect tests. Tests often use particles of one size, or very limited size range, one polymer type, or one shape category, whereas other tests use particles with a wider range of properties.2 This renders these studies incomparable. Nevertheless, several recent publications have compared effect thresholds obtained for such highly different microplastic particle types in species sensitivity distributions (SSDs).19−24 A key feature for a meaningful SSD is that the threshold effect concentrations relate to the same stressor, which is not the case for these SSDs because the individual data points relate to very different particle types. This renders the hazard data obtained from these SSDs fundamentally flawed. Fifth, the exposure data do not align with the effect threshold data. This follows logically from the first two reasons. Exposure calculated from environmental concentration data automatically relates to environmental microplastic, a diverse mixture of sizes, polymer types, and shapes. This does not match with the types and sizes of microplastic particles used in effect tests, as mentioned. To have exposure and effect test data aligned such that a meaningful risk characterization can be done, the effect assessment should also be done with environmentally realistic, that is, diverse microplastic.1,4

One logical and ongoing strategy to deal with these issues is harmonization of methods, and when all is harmonized, use these methods to collect all necessary data to do risk assessments of sufficient quality. This, however, will take very long. There are several ongoing harmonization processes,9,25−27 but even they differ and there seems to be a lack of harmonization of these efforts in itself. This means that there is an urgent need for pragmatic workarounds to allow for the translation of all of these different types of data into one common currency, such that risk assessment for microplastic becomes feasible.

Here, we propose and test rescaling methods that are able to substantially reduce the nonalignment of methods used in microplastic research. First, we provide a simple method to correct for differences in size ranges targeted by studies reporting microplastic concentrations. This results in conversion of data obtained for any size range to default size ranges, like, for instance, 1 μm–5 mm, 20 μm–5 mm, or 1 μm–1 mm for microplastic.1−7 We apply the method to previously published concentration data to test the hypothesis that their variation decreases due to rescaling. Second, we provide a method to convert number to volume and mass concentration (or vice versa) taking the full heterogeneity of environmental microplastic into account. Third, we provide a method to correct for differences in the particle sizes, shapes, and densities in ecotoxicological particle effect studies. We apply the method to a traditionally constructed and flawed microplastic SSD for freshwater species to obtain a more meaningful SSD and hazardous microplastic threshold effect concentration (HC5). Finally, the latter microplastic threshold effect concentrations (HC5) for 1–5000 μm of microplastic are evaluated against the aforementioned rescaled 1–5000 μm microplastic concentrations for surface waters, to illustrate how a consistent characterization of risk can be done.

Methods

Aligning Data Sets That Target Different Size Ranges

The literature uses different size ranges to define microplastic, here referred to as default microplastic size ranges. An often-used pragmatic range is between approximately 20 and 5000 μm, where 20 μm relates to the practical detection limit of common FTIR spectroscopic methods. A formally more correct default range would include all particles between 1 and 5000 μm, with 1 μm being the size below which the material would be referred to as nanoplastic. Recently, it was proposed to use a range between 1 and 1000 μm as default; however, this range is only rarely used in the literature.3 We argue, however, that these differences are trivial because number concentration measured within each of these ranges can be translated into any other range as soon as the particle size distribution is known.28 Kooi and Koelmans4 demonstrated that microplastic size distributions typically follow a power law according to

graphic file with name es0c02982_m001.jpg 1

in which y and x are the relative abundance and size (i.e., length), respectively, and α and b are the fitting parameters. 4 This means that the number of particles found within any size range can be translated into the number expected for any other size range, by using a correction factor (CF) that scales the integral of eq 1 for the measured size range, against the integral of eq 1 for the default range.

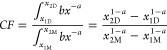graphic file with name es0c02982_m002.jpg 2

Here, subscripts 1 and 2 relate to the minimum and maximum values of the range (μm), and D and M denote default and measured ranges, respectively. For example, if a number concentration measured for a range from 30 to 2000 μm needs to be rescaled to the default definition range from 1 to 5000 μm, then the values for x1D, x2D, x1M, and x2M would be 1, 5000, 30, and 2000, respectively. With these boundary values and α = 1.6 (see below), the CF would be 8.32 (eq 2). If, for instance, a measured number concentration for the range from 30 to 2000 μm is 100 #/L, the extrapolated number concentration for the default definition range from 1 to 5000 μm would be 8.32 × 100 = 832 #/L. The parameter α may vary a bit among data sets and therefore can be best obtained by fitting the log-transformed version of eq 1 to the measured size distribution. When, however, no data on the distribution is available, then a default value for α of 1.6 is recommended, which is an average value based on 14 environmental microplastic size distributions.4 For the proof-of-principle calculations in the present paper, the value of α = 1.6 was used.

Using eq 2 (with α = 1.6),4 standard correction factors were calculated to translate size ranges commonly reported (e.g., 333–5000, 300–5000, 100–5000, 20–1000, 20–5000 μm) to the ranges suggested as preferred definitions of microplastic in the literature (1–5000, 20–5000, 1–1000 μm).2,3,14

Furthermore, as a case study, data on surface water number concentrations reported by Koelmans et al.15 were rescaled. These data were compiled from a large number of studies targeting different size ranges, with studies able to detect small, i.e. <100 μm particles reporting much higher number concentrations. Here, our hypothesis was that rescaling would result in a lower variation in the number concentrations.

Aligning Number and Mass Concentration Data for Microplastic

Currently, conversions of number to volume and mass concentration (or vice versa) based on the assumption of spherical shape are often inaccurate because the particles have a wide range of shapes and densities. More accurate conversions can be done by taking the actual shapes and densities into account. For instance, Kooi and Koelmans4 defined generic environmental microplastic via probability density functions for size (1 to 5000 μm), shape, and density. Shape was quantified by considering length/width/height (L/W/H) ratio distributions for common microplastic shape categories (e.g., spheres, fragments, films, fibers) and their relative abundances in the environment. These were then combined into overall L/W and L/H distributions (Figure 1). Subsequently, the latter distributions were further simplified into one Corey shape factor (CSF) distribution (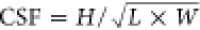Inline graphic).29,30L/W/H or CSF distributions can be used to translate number to volume and mass concentrations, as follows: First, Monte Carlo (MC) simulations are used to create a large number (n) of imaginary particles “i”, by randomly sampling their length from the length distribution (eq 1), and their L/W and L/H ratios from these known L/W/H distributions (Figure 1), keeping L/H ≥ L/W. Subsequently, the volume of an ellipsoid, as the best “one shape fits all” approximation for all possible microplastic particles, was calculated using

graphic file with name es0c02982_m004.jpg 3

Depending on L, W, and H, an ellipsoid can take the shape of an extremely elongated fiber, a thin film, a fragment, a microbead (oblate spheroid), or a sphere. The volume of the ellipsoid VEL,i for imaginary particle i can then be calculated from the sampled length (Li) distribution and the sampled L/W and L/H distributions.4 If desired, eq 3 can be further simplified by assuming that the length to width ratio equates to the width to height ratio (L/W = W/H),31,32 and by writing it as a function of CSF by implementing the CSF equation

graphic file with name es0c02982_m005.jpg 4

The simplified ellipsoid volume (VEL,iS) can thus be calculated from the lengths (Li) and CSFi values sampled from their respective distributions.4 Again, for 0 < CSF < 1, this results in ellipsoids that can be extremely elongated when CSF approaches zero, to the complete opposite: spherical shape when CSF = 1. For CSF = 1, eq 4 reduces to the volume equation for a sphere (with L = 2r). The resulting VEL,i or VEL,i (eqs 3 or 4) is then converted into particle mass MPS,i using a density selected from the density distribution.4VPS,i values and MPS,i values from all iterations are summed. This results in total volume and total mass for the total number of simulated particles, from which number–volume–mass conversion factors can be calculated. The factors will be more accurate if the number of simulated particles i (i.e., the number of MC iterations, n) is high enough to capture the variation in the probability density functions. Here, we used n = 105 in the MC simulations.

Figure 1.

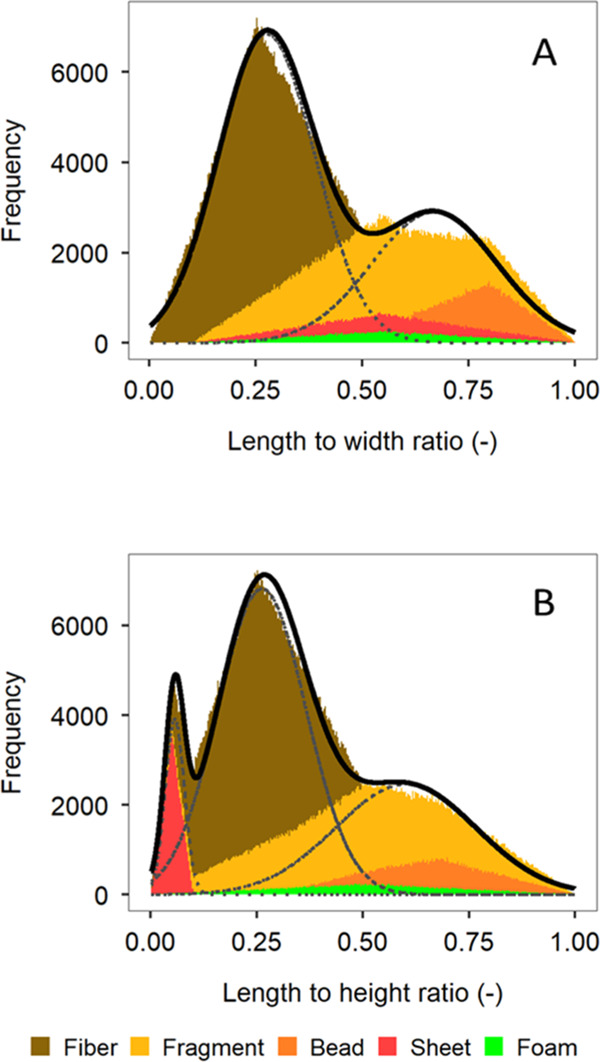
Figure 1

Open in a new tab

Length to width (panel A) and length to height (panel B) ratios for polydisperse microplastic, obtained from Monte Carlo simulations for the main microplastic shape categories, and their relative abundance in the environment4 for n = 1 × 106 iterations, with fitted bi- and trimodal distributions. The main difference is an extra peak for sheets at a low L/H ratio.

Aligning Threshold Effect Data Used in Species Sensitivity Distributions for Microplastic

Currently published SSDs need two corrections to make them consistent with environmental MP exposure concentrations: one aligning threshold effect concentrations among studies that use different types of MP and one aligning these threshold effect concentrations with actual MP exposure concentrations found in the environment.

Aligning Threshold Effect Concentrations Obtained from Microplastic Effect Studies Using Different and Nonrealistic Particle Types

Microplastic effect tests use different types of microplastic particles, widely varying in sizes, shapes, and densities, which makes the data incomparable and limits their use in, for instance, SSDs or risk characterizations.1,20 Furthermore, the types of particles used in effect tests are usually less diverse compared to those found in the environment. Here, we provide a calculation method to correct for this nonalignment. The approach is based on a method to convert published threshold effect concentrations into volume equivalent threshold effect concentrations for environmental microplastic, in combination with the method to convert number concentrations into volume and mass concentrations for environmental microplastic as described above.

Recent reports have identified that the most demonstrated and consistently reported effect mechanisms across both marine and freshwater taxa are inhibition of food assimilation and/or decreased nutritional value of food (“food dilution”), and internal physical damage due to microplastic ingestion.33−35 Ingestion of the low-caloric particles inevitably leads to loss of energy intake, causing growth inhibition and eventual mortality.2,12,19,34 If the effect mechanism is based on food dilution only, then the actual volume of ingested MP is of primary relevance, rather than the number or size of the MP particles. This implies that a reported threshold effect (number) concentration from an effect test with ingestible monodisperse MP (ECX,mono, with X being the affected fraction of the population) can be converted into a threshold effect concentration for an ingestible size range of particles from an environmentally realistic polydisperse MP suspension (ECX,poly), as long as the total volume of what is ingested remains the same. Information on polydispersity can be obtained either from experimental data or from MC simulations where the ingestible polydisperse distribution is based on selected parts of distributions that are parameterized using environmental data within the ingestible size range, e.g., from Kooi and Koelmans.4 The volume preservation equation is

graphic file with name es0c02982_m006.jpg 5

in which ECX,mono is the reported threshold effect number concentration (#/L), Vmono is the average volume per particle as used in the reported monodisperse MP effect test, ECX,poly is the volume equivalent threshold effect concentration of the ingestible size range of polydisperse MP particles (#/L), and Vpoly is the average volume per particle that is ingestible by the species under consideration. The latter Vpoly can be calculated as the ratio of the total volume of all bioavailable, i.e., ingestible (polydisperse) particles and the number of ingestible particles (kingestible) needed to make that volume:

graphic file with name es0c02982_m007.jpg 6

This can be generated with an MC simulation of particle volumes based on the aforementioned approach (previous section, eqs 3 or 4), however with k representing the number of ingestible particles. The volume equivalent effect threshold concentration corrected for the bioavailable fraction of environmental microplastic is then

graphic file with name es0c02982_m008.jpg 7

This threshold concentration is also referred to as the environmentally relevant threshold effect number concentration. An example calculation is provided in the Supporting Information.

Aligning Environmentally Relevant Threshold Effect Concentrations and the Actual Environmental Microplastic Exposure Concentration

The threshold effect concentration for environmentally relevant polydisperse microplastic ECX,poly (eqs 5 and 7) resembles the effect concentration while accounting for the full diversity of ingestible environmental microplastic in terms of size, shape, and density. However, this ECX,poly relates to ingestible particles and still is only a fraction of the total concentration of environmental microplastic that aquatic species are exposed to. Quantification of this species-specific fraction makes it possible to convert all ECX,poly threshold effect concentrations into threshold concentrations of “total” environmental microplastic (ECX,env). For example, in the present paper, n = 105 imaginary particles were created using Monte Carlo simulations. From these particles, a selection was made based on the species-specific ingestibility as described above (Table S1 and Table S2), resulting in the ingestible subset of particles, based on size constraints. The resulting number of selected particles is then expressed as a fraction (favailable) of the total number generated by the Monte Carlo simulations. Threshold concentrations of total environmental microplastic (ECX,env) were then calculated as

graphic file with name es0c02982_m009.jpg 8

Construction of Species Sensitivity Distributions

A traditional freshwater species sensitivity distribution (SSD) for microplastic was constructed by combining data from the SSDs published by Adam et al.22 and Besseling et al.20,36 These SSDs included data for nanoplastic and marine species, respectively, data that would be irrelevant for a microplastic SSD for freshwater species and thus were omitted. The remaining freshwater MP data were updated with effect threshold data from studies published in 2018 and 2019 (Table S2). To obtain an SSD consistent with the concept defined in the previous section (eqs 3–8), only invertebrate species for which ingestion was demonstrated37 (Table S1) and food dilution was suggested as the effect mechanism35 were retained, leading to 54 data points for 11 species (Table S2). Following Adam et al.,22 reported dose descriptors like EC50, EC10, and lowest observed effect concentration (LOEC) were converted into chronic no observed effect concentration (NOEC) values using an assessment factor (AF) to convert acute into chronic values (AFtime) and an AF to convert dose descriptors into NOECs (AFdescriptor), according to ECHA guidelines.38 Reported NOEC values, however, were considered too uncertain22 and were therefore omitted. To construct our new rescaled SSD for each of the species, an ingestible MP size range was defined based on literature data (Tables S1 and S2). Particle width (W) was taken as the relevant MP size dimension for ingestion, assuming that elongated particles can be ingested along their longest dimension (L). For instance, fibers often are found to be ingested, even though the size of the mouth is less than the fiber length.39 Using the US-EPA’s species sensitivity distribution generator,20 two SSDs were constructed: one using the original untransformed effect threshold data as reported (ECX,mono) and one using effect threshold concentrations rescaled according to eq 8 (ECX,env). By converting the original as well as the rescaled number concentration data into mass (eq 3), SSDs for mass concentration were obtained as well. Mass conversion of the original number concentration data was based on reported particles’ size and density. Rescaled data number to mass conversion was based on the polymer density distribution for polydisperse environmental MP as reported by Kooi and Koelmans.4

Results and Discussion

Aligning Data Sets That Target Different Size Ranges

The calculated correction factors can be used as standard factors to translate commonly used ranges into the default microplastic size ranges of either 1–5000, 1–1000, or 20–5000 μm (Table 1). For instance, microplastic number concentrations obtained with standard 333 μm trawling nets would require multiplying by a factor of 40.4 to obtain an estimate of the full 1–5000 μm microplastic size range. If one adopts a 20–5000 μm range for default microplastic, the correction factor would be 6.49. Table 1 also illustrates the sensitivity of the correction factor to some of the different approaches used in microplastic research. For instance, it makes only a 1% (40.37/39.97) difference normalizing to 1–5000 μm versus normalizing to 1–1000 μm. This is caused by the fact that sizes between 1000 and 5000 μm have very low contribution to the overall number concentration that reaches all the way down to 1 μm. This marginal difference in number concentrations, which are the units most frequently used in the literature, may reduce the urgency of revisiting the current habit of using 5 mm as the upper boundary in the definition of microplastic.3

Table 1. Correction Factors (CF) to Convert Number Concentrations Observed for Five Common Size Ranges (Measured Range) to Full Microplastic Size Ranges (1–5000, 1–1000, 20–5000 μm).

  measured range
CF to default size range of 333–5000 μm 300–5000 μm 100–5000 μm 20–1000 μm 20–5000 μm
1–5000 μm 40.37 37.36 17.42 6.63 6.22
1–1000 μm 39.97 36.99 17.25 6.57 6.16
20–5000 μm 6.49 6.00 2.80 1.07 1
Open in a new tab

We further explored the sensitivity of the correction factor with respect to variability in the value of the exponent α (eq 1). It appears that this sensitivity is quite large; a 10% increase or decrease in the default value of 1.6 results in a factor of two increase or decrease in the value of the correction factor needed to convert number concentration data from 333–5000 to 1–5000 μm (Figure S1). This sensitivity is much lower when the correction concerns a smaller difference in the size range. For instance, the 20–5000/333–5000 correction factor would change only by a factor of 1.4. Consequently, it is recommended to always correct a data set with a calibration of eq 1 that is based on that same data set. If this is not possible, for instance, when it concerns generic corrections, the generic value of α = 1.6 still is the best value available.

Aligning Microplastic Concentrations in Surface Waters

Microplastic number concentration data in water samples from either groundwater, surface water, wastewater, or drinking water show an enormous range.15 This can be attributed to many factors such as differences in water types, geographical locations, analytical methods, and target size ranges. Because of the latter, we expect that rescaling the different size ranges to one identical range would reduce the range of variation in the data. To test this hypothesis, surface water microplastic number concentration data from our previous review15 was rescaled to a standard microplastic range of 1–5000 μm using eq 2 with the minimum and maximum size boundaries as reported in the original studies,15 and α = 1.6. A convenient way to compare the rescaled number concentrations with the original values is via their cumulative frequency distributions (Figure 2). The comparison shows that the original data span 7.5 orders of magnitude (from 10–5 to 200 #/L), whereas the rescaled data span six orders of magnitude (from 10–3 to 800 #/L). Rescaling thus leads to a narrower frequency distribution. The difference in concentration is a factor of 100 at the lowest concentrations (10–5 versus 10–3), whereas it is only a factor of 4 (200 versus 800 #/L) at the highest concentrations (Figure 2). Low concentrations often were measured with methods that have a high size detection limit, for which thus a higher rescaling factor is used. In contrast, the high concentrations often were obtained with methods able to detect the smallest particle sizes, which therefore were already closer to the 1 to 5000 μm size range defined for environmental microplastic.

Figure 2.

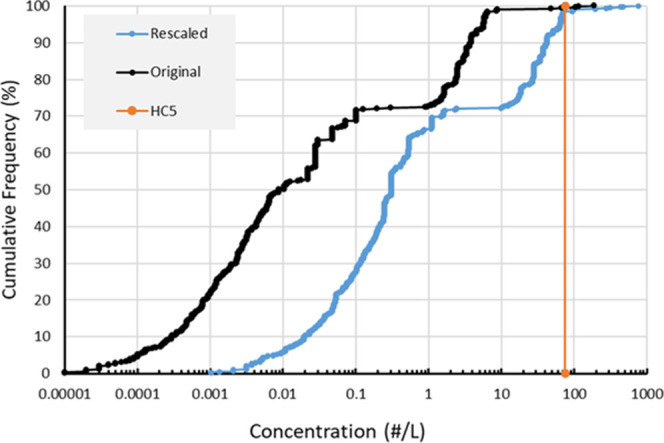
Figure 2

Open in a new tab

Cumulative frequency distribution of original global microplastic concentrations in surface freshwater taken from (15) (black curve), the same data consistently rescaled to 1–5000 μm, (blue curve), compared to the concentration (ECX,env; eq 8) protecting 95% of species obtained from threshold effect concentrations corrected for bioavailability and polydispersity as defined by probability density distributions for environmental microplastic (HC5, vertical orange line, obtained from the SSD in Figure 3B).

Instead of this visual approach, the variation in the data also can be explored using interquartile ranges. There were 634 surface water concentration values in the original data set (see Koelmans et al.15), which had an interquartile range of 6.16 #/L, whereas the corrected data set had a higher interquartile range of 16.7 #/L. Thus, the correction leads to a higher number concentration (Figure 2). To quantify the relative variation in the data, we calculated the ratio of the quartile for 75 and 25% of the data (IQR75%/IQR25%). For the original data, this IQR75%/IQR25% ratio is 2200, whereas for the rescaled data set, this ratio is only 223, thus an order of magnitude lower. Rescaling thus indeed helps to substantially reduce the artifactual variation as expected. When rescaled to a standard microplastic range of 20–5000 μm, the IQR75%/IQR25% ratio still is 10 times smaller than that for the original data, showing that the improvement is not very sensitive to the definition of the microplastic size range. The remaining IQR75%/IQR25% variability, i.e., 223, can be seen as a better estimate of the actual variability of microplastic concentrations in and across surface waters. Although it remains a correction method based on extrapolation, rescaling has demonstrated the ability to reduce the artifact of different size ranges used when comparing number concentration data across studies.

Rescaling Species Sensitivity Distributions for Environmental Microplastic

Equations 3–8 were used to rescale and align the threshold effect concentrations of a traditional SSD (Figure 3A). This SSD uses effect concentrations for ingestible microplastics, which were thus 100% bioavailable in the laboratory tests. However, in nature, a much wider environmental microplastic continuum is present, part of which is not bioavailable for organisms that ingest microplastic, for instance, because it would have a size larger than the organisms’ mouth opening.40 The traditional SSD (Figure 3A) further used the threshold effect number concentrations from the literature as reported, neglecting that two identical number concentrations do not mean the same thing if they relate to microplastic particles of different sizes, shapes, and densities, which in fact are different stressors. The effect threshold concentrations reported so far are thus incomparable.19−24 Therefore, our rescaling concerned two corrections. First, all reported threshold effect number concentrations from effect tests largely performed with monodisperse MP suspensions were converted into “environmentally realistic” threshold effect number concentrations for the ingestible size range of particles, with the size distributions of these particles matching those of the ingestible polydisperse environmental microplastic, and assuming preservation of ingested volume (eq 5). Second, the bio-unavailable fraction of environmental microplastic was corrected. Threshold effect concentrations were calculated so they relate to the fraction of environmental microplastic that is ingestible by the species based on size and density. To this end, ingestible size ranges were defined for each of the species, based on literature data (Tables S1 and S2). The ratio of species size and maximum ingestible MP size is 50.5 ± 14.9 (n = 8) on average, which agrees well with the range of 40 to 50 recently reported for small invertebrate species.41 Autotrophic phytoplankton and macrophyte species were not supposed to ingest microplastic particles, in which case the bio-unavailable fraction of environmental microplastic was assumed to be negligible. From the MC simulations, it appeared that the ingestible percentages ranged from 93 (Ceriodaphnia dubia) to 99% (Haworthiopsis attenuata) based on particle numbers (Figure S2A), and from 0.0054 to 1.7% based on mass (Figure S2B). The difference in these percentages is explained by high numbers of small particles calculated to be ingestible, which, however, represent very little mass. Microplastic is thus highly bioavailable when expressed in number concentrations, yet marginally bioavailable when expressed in mass concentrations. As for density, all polymer types are sometimes reported at the water surface, in the water column, or in sediments.4 Therefore, for the current implementation, we assigned all polymer densities to be available for all species.

Figure 3.

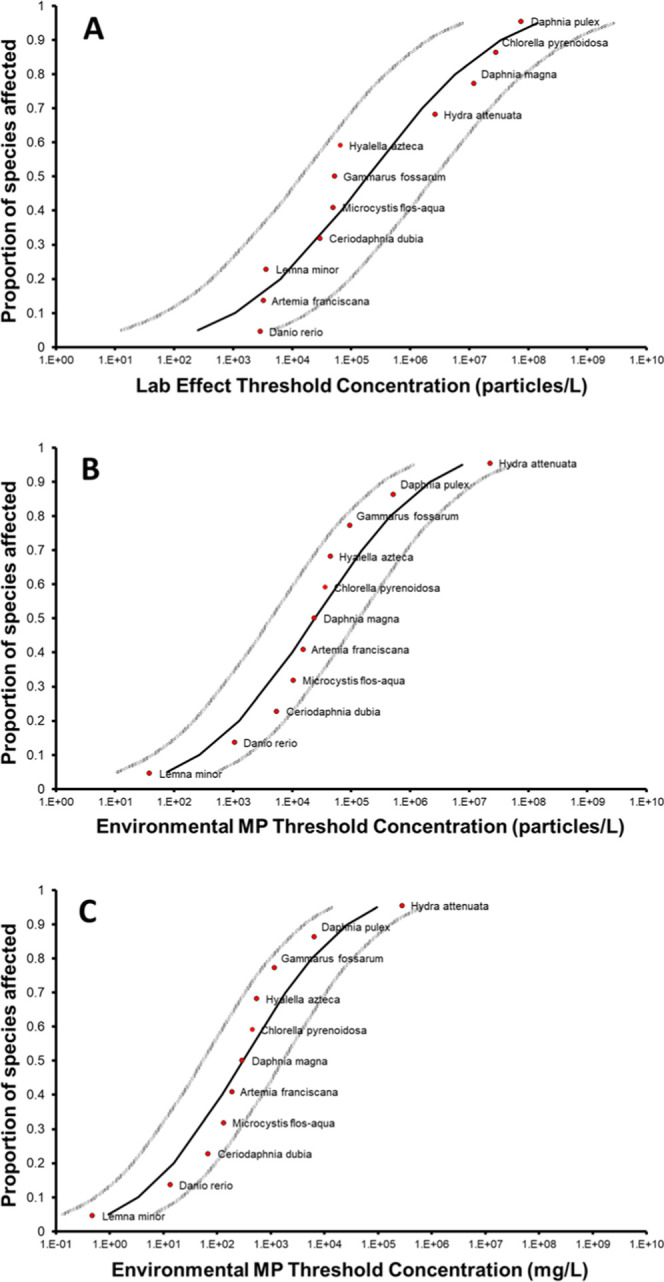
Figure 3

Open in a new tab

Species sensitivity distributions for microplastic based on laboratory data for different types of particles (panel A, R2 = 0.896, HC5 = 251 #/L), and based on the same data after corrections for bioavailability and polydispersity at the threshold effect concentration resulting in (ECX,env) x-axis values in particles/L (panel B, R2 = 0.940, HC5 = 75.6 #/L) or mg/L (panel C, R2 = 0.940, HC5 = 0.94 mg/L). Gray curves relate to 95% confidence intervals.

As a result of these corrections, the recalculated x-axis values now consistently relate to the environmental microplastic concentrations (ECX,env) needed to provide a bioavailable fraction with a volume equal to the ingested volume at the threshold effect concentration in the laboratory tests (Figure 3B). Consequently, the order of the species in the SSD changes because differences in bioavailability and ingestibility are now taken into account. Furthermore, the hazardous concentration for 5% of the species (HC5) changes from 251 #/L (Figure 3A) to an ingestible volume as well as a bioavailability-corrected effect threshold of 75.6 #/L (Figure 3B, R2 = 0.940, 95% confidence interval: 11–521 #/L). Here, it is emphasized that the two HC5 values 251 and 75.6 #/L cannot be compared directly because they relate to different things. In Figure 3A, each x-axis value relates to a concentration of another stressor (i.e., microplastic particles of different sizes, shapes, densities), which means that the HC5 value is fundamentally flawed and largely meaningless. In Figure 3B, x-axis values all relate to the same variable: the concentration of “1–5000 μm polydisperse environmental MP”. In this example, they are defined by the probability distributions provided by Kooi and Koelmans.4 The effect threshold of 75.6 #/L can thus be compared with exposure concentrations as long as these are also measured or rescaled to cover the same size range of 1–5000 μm, e.g., like those calculated in the previous section.

The MC simulations provided an accurate number to mass conversion, as for each individual simulated particle, size, shape, and density were sampled from their respective probability density functions, from which particle weight was calculated. This yields estimates of the characteristics of a single, average environmentally relevant microplastic particle: a weight of 12.5 μg, a volume of 0.011 mm3, and a density of 1.141 g cm3. For the ingestible particles, these simulations were used to construct a mass concentration-based SSD with an effect HC5 threshold of 0.95 mg/L (Figure 3C, R2 = 0.940, 95% confidence interval: 0.14–6.5 mg/L). Note that this concentration equates to the product of the number-based threshold (75.6 #/L) and the average weight of an individual particle (12.5 μg).

Risk Characterization Using Rescaled Exposure and Effect Threshold Data

Risk assessment implies a comparison of predicted environmental concentration (PEC) with species sensitivity, often expressed as predicted no effect concentration (PNEC).1,2 Risk is indicated when the PEC/PNEC ratio is larger than 1.1 Previous assessments for microplastic suffered from the fact that PEC and PNEC data were incomparable. For instance, exposure data were often reported for particles larger than 100 or 300 μm, whereas laboratory tests usually used much smaller particles, e.g., <20 μm.2 The aforementioned correction methods allow for a more consistent PEC/PNEC comparison for 1–5000 μm microplastic, that is, with all data recalculated to match an environmentally relevant size distribution for this size range, and with correction for those parts of the microplastic size, shape, and density continuum that are not available for species. The latter depends on species traits (Table S1). Here, we used the cumulative frequency distribution of 1–5000 μm global microplastic concentrations in surface freshwater (Figure 2).15 They can be compared to the concentration protecting 95% of species (HC5) obtained from threshold effect concentrations also rescaled for bioavailable fraction, size, shape, and density as defined by probability density distributions for environmental microplastic in water (Figure 2, vertical line). The comparison shows that based on these available data, risk would be indicated for only a very small percentage (1.5%) of the locations in the data set. For the ten locations at the right-hand side of the risk threshold, PEC/PNEC ranges from 1 to 10, with an average of 3.7. This quantitative assessment supports the conclusions of two recent reports stating that at present, risks of microplastic are not widespread, but could occur at (rare) hotspot locations.2,6 The comparison is still surrounded by uncertainty as can be seen from the rather high uncertainty interval for the SSD (Figure 3B), which ranges from 11 to 521 #/L for the HC5. In other words, if we take the lower limit of the 95% confidence interval, i.e., 11 #/L, risk would be indicated for 28% of the locations. Conversely, we can say risk is really unlikely for 72% of the locations in the data set. Obviously, these percentages are not representative for “all locations in the world,” given that the data set we used15 is not necessarily representative.

Implications and Prospects

Because microplastic is perceived as a diverse and complex mixture, researchers have suggested focusing on its components.5 Although this may seem reasonable at first sight, the question is whether this strategy of complexifying microplastic is the best way forward. This view may lead to fragmentation and delay of research effort. After all, testing all of the possible combinations of particles that make up environmental microplastic with all possible endpoints in biota is a daunting, if not, impossible task. From an ecological or human health point of view, assessing the risk of all of the components of microplastics is insufficient. For exposure, the bioavailable fraction of the whole plastic continuum is relevant, whereas that bioavailable fraction in itself is a continuum across all biota present in the biosphere. Therefore, innovative concepts and tools need to be developed to understand the joint behavior and risks of the plastic continuum within the biological continuum. We propose that by using such tools, the complexity of microplastic can be reduced to the extent required to assess their risk. To some extent, this is similar to the previous development of quantitative structure–activity relationships (QSARs)42,43 to understand the toxicity of wide ranges of different organic chemicals.

A rescaling methodology to increase the comparability of concentration data obtained with different measurement methods as well as a methodology to align exposure and effect data to get a consistent characterization of risk have been presented. The essence of these methodologies is that the measured diversity of environmental microplastic is captured via continuous probability density functions, which subsequently allow for quantitative rescaling and corrections while fully preserving this diversity. This is not necessarily limited to microplastics because the same concepts are applicable to macroplastics and nanoplastics as well. Providing, explaining, and testing the method was the primary aim of this paper, not necessarily providing the final answers with respect to concentrations and risks of microplastic in the environment. After all, the data used in the present paper may be the best available but still need to be renewed and expanded for several reasons. For instance, the most recent chemometric procedures to analyze microplastic spectroscopic data are able to provide particle number, size, shape, polymer type, and therefore weight, in one go.32,44 This will inevitably lead to more accurate data and possibly refined and different parameterizations of the probability density functions. It is thus recommended to use automated analysis and always report and interpret analytical data also in the form of such functions. This will make it possible to assess how accurate parametrizations for average microplastic are, and whether they need to become compartment specific. A second reason is that the concentration data for surface waters used in the present analysis (Figures 2 and 3) partly relate to less reliable methodologies.15 We expect future studies to deploy higher levels of quality assurance during sampling, laboratory handling, and detection of microplastics, which will thus also affect the outcomes of the example calculations provided here. A third reason relates to SSDs, which already have been qualified as sophisticated,45 high-level risk assessments,6 and have been used to inform the risk assessment for microplastic particles as done by several international expert groups.2,6,24 However, they have conceptual flaws as explained and they still have limited data. A new SSD based on best available data for freshwater species was provided here. The SSD focuses on food dilution by low-caloric plastic particles as the effect mechanism. Other mechanisms may also play a role but data for these are still insufficient to build SSDs on.35 Generating new experimental data to build new SSDs was beyond the scope of the present study. However, higher quality and uniformity in future microplastic effects tests are expected.35,46

The applicability of our methodologies goes beyond the aforementioned examples. For instance, imagine an effect mechanism where membrane translocation of <3 μm particles47−49 is followed by distribution in the body tissues and subsequent inflammation responses, which could be relevant for human health as well as for ecological risks.2 In such a case, exposure would benefit from the method provided to align concentration data, whereas alignment of effect threshold data still would benefit substantially from the representation of environmental microplastic via probability density functions.4 The relevant particle size fractions were now quantified by sampling from the MP parameter space for particles that fit in an organism’s mouth opening, which after all is an important prerequisite for food dilution. However, for translocation, followed by inflammation, one should sample the 10 nm to 3 μm size fraction, while further only selecting particles with an aspect ratio considered to be relevant for the specific inflammatory response.

In conclusion, the presented toolkit would be useful for any type of microplastic exposure and effect studies, from ecological to human health, and would lead to more meaningful risk assessments in the future.

Acknowledgments

A.A.K., M.K., and P.E.R.H. acknowledge financial support from the NWO-TT project “Technologies for the Risk Assessment of Microplastics” (TRAMP).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.est.0c02982.

  • Detailed explanation and example calculation for ECX,poly and the effect concentration for environmental microplastic ECX,env; ingestible size ranges (Table S1); original and rescaled effect threshold concentrations as used in Figures 3A,B, respectively (Table S2); sensitivity analysis for exponent α (Figure S1); and bioavailable fractions of number concentrations and mass concentrations for 11 studied species (Figure S2) (PDF)

The authors declare no competing financial interest.

Supplementary Material

es0c02982_si_001.pdf (155.5KB, pdf)

References

  1. Koelmans A. A.; Besseling E.; Foekema E.; Kooi M.; Mintenig S.; Ossendorp B. C.; Redondo-Hasselerharm P. E.; Verschoor A.; van Wezel A. P.; Scheffer M. Risks of Plastic Debris: Unravelling fact, opinion, perception and belief. Environ. Sci. Technol. 2017, 51, 11513–11519. 10.1021/acs.est.7b02219. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. SAPEA, Science Advice for Policy by European Academies. A Scientific Perspective on Microplastics in Nature and Society. SAPEA: Berlin, 2019. [Google Scholar]
  3. Hartmann N. B.; Hüffer T.; Thompson R. C.; Hassellöv M.; Verschoor A.; Daugaard A. E.; Rist S.; Karlsson T.; Brennholt N.; Cole M.; Herrling M. P.; Hess M. C.; Ivleva N. P.; Lusher A. L.; Wagner M. Are We Speaking the Same Language? Recommendations for a Definition and Categorization Framework for Plastic Debris. Environ. Sci. Technol. 2019, 53, 1039–1047. 10.1021/acs.est.8b05297. [DOI] [PubMed] [Google Scholar]
  4. Kooi M.; Koelmans A. A. Simplifying microplastic via continuous probability distributions for size, shape and density. Environ. Sci. Technol. Lett. 2019, 6, 551–557. 10.1021/acs.estlett.9b00379. [DOI] [Google Scholar]
  5. Rochman C. M.; Brookson C.; Bikker J.; Djuric N.; Earn A.; Bucci K.; Athey S.; Huntington A.; McIlwraith H.; Munno K.; De Frond H.; Kolomijeca A.; Erdle L.; Grbic J.; Bayoumi M.; Borrelle S. B.; Wu T.; Santoro S.; Werbowski L. M.; Zhu X.; Giles R. K.; Hamilton B. M.; Thaysen C.; Kaura A.; Klasios N.; Ead L.; Kim J.; Sherlock C.; Ho A.; Hung C. Rethinking microplastics as a diverse contaminant suite. Environ. Toxicol. Chem. 2019, 38, 703–711. 10.1002/etc.4371. [DOI] [PubMed] [Google Scholar]
  6. Kershaw P. J.; Carney Almroth B.; Villarrubia-Gómez P.; Koelmans A. A.; Gouin T.. Proceedings of the GESAMP International Workshop on assessing the risks associated with plastics and microplastics in the marine environment 2020, Vol. 103, p 68.
  7. Thompson R. C.; Moore C. J.; vom Saal F. S.; Swan S. H. Plastics, the environment and human health: current consensus and future trends. Philos. Trans. R. Soc., B 2009, 364, 2153–2166. 10.1098/rstb.2009.0053. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Proceedings of the International Research Workshop on the Occurrence, Effects and Fate of Micro-plastic Marine Debris. Sept 9-11, 2008. NOAA TechnicalMemorandum NOS-OR&R-30 Arthur C.; Baker J.; Bamford H., Eds.; 2009.
  9. Bessa F.; Frias J.; Kögel T.; Lusher A.; Andrade J. M.; Antunes J.; Sobral P.; Pagter E.; Nash R.; O’Connor I.; Pedrotti M. L.; Kerros M. E.; León V.; Tirelli V.; Suaria G.; Lopes C.; Raimundo J.; Caetano M.; Gago J.; Viñas L.; Carretero O.; Magnusson K.; Granberg M.; Dris R.; Fischer M.; Scholz-Böttcher B.; Muniategui S.; Grueiro G.; Fernández V.; Palazzo L.; de Lucia A.; Camedda A.; Avio G. C.; Gorbi S.; Pittura L.; Regoli F.; Gerdts G.. Harmonized Protocol for Monitoring Microplastics in Biota, JPI-Oceans BASEMAN, 2019.
  10. Hazardous Chemicals Associated with Plastics in the Marine Environment; Takada H.; Karapanagioti H. K., Eds.; Springer International Publishing: Switzerland, 2016. [Google Scholar]
  11. Redondo-Hasselerharm P. E.; Gort G.; Peeters E. T. H. M.; Koelmans A. A. Nano- and microplastics affect the composition of freshwater benthic communities in the long term. Sci. Adv. 2020, 6, eaay4054 10.1126/sciadv.aay4054. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Kögel T.; Bjorøy Ø.; Toto B.; Bienfait A. M.; Sanden M. Micro- and nanoplastic toxicity on aquatic life: Determining factors. Sci. Total Environ. 2020, 709, 136050 10.1016/j.scitotenv.2019.136050. [DOI] [PubMed] [Google Scholar]
  13. Gouin T.; Becker R. A.; Collot A. G.; Davis J. W.; Howard B.; Inawaka K.; Lampi M.; Ramon B. S.; Shi J.; Hopp P. W. Toward the Development and Application of an Environmental Risk Assessment Framework for Microplastic. Environ.Toxicol. Chem. 2019, 38, 2087–2100. 10.1002/etc.4529. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Wagner M.; Scherer C.; Alvarez-Muñoz D.; Brennholt N.; Bourrain X.; Buchinger S.; Fries E.; Grosbois C.; Klasmeier J.; Marti T.; Rodriguez-Mozaz S.; Urbatzka R.; Vethaak A. D.; Winther-Nielsen M.; Reifferscheid G. Microplastics in freshwater ecosystems: what we know and what we need to know. Environ. Sci. Eur. 2014, 26, 12 10.1186/s12302-014-0012-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Koelmans A. A.; Mohamed Nor N. H.; Hermsen E.; Kooi M.; Mintenig S. M.; De France J. Microplastics in Freshwaters and Drinking Water: Critical Review and Assessment of Data Quality. Water Res. 2019, 155, 410–422. 10.1016/j.watres.2019.02.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Lenz R.; Enders K.; Nielsen T. G. Microplastic exposure studies should be environmentally realistic. Proc. Natl. Acad. Sci. U.S.A. 2016, 113, E4121–E4122. 10.1073/pnas.1606615113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Mintenig S. M.; Bäuerlein P. S.; Koelmans A. A.; Dekker S. C.; van Wezel A. P. Closing the gap between small and smaller: Towards a framework to analyse nano- and microplastics in aqueous environmental samples. Environ. Sci.: Nano 2018, 5, 1640–1649. 10.1039/C8EN00186C. [DOI] [Google Scholar]
  18. Karlsson T. M.; Kärrman A.; Rotander A.; Hassellöv M. Comparison between manta trawl and in situ pump filtration methods, and guidance for visual identification of microplastics in surface waters. Environ. Sci. Pollut. Res. 2020, 27, 5559–5571. 10.1007/s11356-019-07274-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Everaert G.; Van Cauwenberghe L.; De Rijcke M.; Koelmans A. A.; Mees J.; Vandegehuchte M.; Janssen C. R. Risk assessment of microplastics in the ocean: modelling approach and first conclusions. Environ. Pollut. 2018, 242, 1930–1938. 10.1016/j.envpol.2018.07.069. [DOI] [PubMed] [Google Scholar]
  20. Besseling E.; Redondo-Hasselerharm P. E.; Foekema E. M.; Koelmans A. A. Quantifying Ecological Risks of Aquatic Micro- and Nanoplastic. Crit. Rev. Environ. Sci. Technol. 2019, 49, 32–80. 10.1080/10643389.2018.1531688. [DOI] [Google Scholar]
  21. Burns E. E.; Boxall A. B. A. Microplastics in the Aquatic Environment: Evidence for or against Adverse Impacts and Major Knowledge Gaps. Environ. Toxicol. Chem. 2018, 37, 2776–2796. 10.1002/etc.4268. [DOI] [PubMed] [Google Scholar]
  22. Adam V.; Yang T.; Nowack B. Toward an Ecotoxicological Risk Assessment of Microplastics: Comparison of Available Hazard and Exposure Data in Freshwaters. Environ. Toxicol. Chem. 2019, 38, 436–47. 10.1002/etc.4323. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Zhang X.; Leng Y.; Liu X.; Huang K.; Wang J. Microplastics’ pollution and risk assessment in an urban river: A case study in the Yongjiang River, Nanning City, South China. Exposure Health 2020, 12, 141–151. 10.1007/s12403-018-00296-3. [DOI] [Google Scholar]
  24. Skåre J. U.; Alexander J.; Have M.; Jakubowicz I.; Knutsen H. K.; Lusher A. L.; Ogonowski M.; Rakkestad K. E.; Skaar I.; Tvedt Sverdrup L. E.; Wagner M.; Agdestein A.; Bodin J.; Elvevoll E.; Hemre G. I.; Hessen D. O.; Hofshagen M.; Husøy T.; Krogdahl Å.; Nilsen A. M.; Rafoss T.; Skjerdal T.; Strand T. A.; Vandvik V.; Wasteson Y.. Microplastics; Occurrence, Levels and Implications for Environment and Human Health Related to Food. Opinion of the Steering Committee of the Norwegian Scientific Committee for Food and Environment; Norwegian Scientific Commitee for Food and Environment (VKM): 2019. [Google Scholar]
  25. Rochman C. M.; Regan F.; Thompson R. C. On the harmonization of methods for measuring the occurrence, fate and effects of microplastics. Anal. Methods 2017, 9, 1324–1325. 10.1039/C7AY90014G. [DOI] [Google Scholar]
  26. Michida Y.; Chavanich S.; Cózar Cabañas A.; Hagmann P.; Hinata H.; Isobe A.; Kershaw P.; Kozlovskii N.; Li D.; Lusher A. L.; Martí E.; Mason S. A.; Mu J.; Saito H.; Shim W. J.; Syakti A. D.; Takada H.; Thompson R. C.; Tokai T.; Uchida K.; Vasilenko K.; Wang J.. Guidelines for Harmonizing Ocean Surface Microplastic Monitoring Methods, Version 1.1; Ministry of the Environment: Japan. https://www.env.go.jp/en/water/marine_litter/method.html, 2019.
  27. Guidelines or the Monitoring and Assessment of Plastic Litter and Microplastics in the Ocean; Kershaw P. J.; Turra A.; Galgani F., Eds.; GESAMP Joint Group of Experts on the Scientific Aspects of Marine Environmental Protection: 2019; p 130. [Google Scholar]
  28. Roch S.; Walter T.; Ittner L. D.; Friedrich C.; Brinker A. A systematic study of the microplastic burden in freshwater fishes of south-western Germany - Are we searching at the right scale?. Sci. Total Environ. 2019, 689, 1001–1011. 10.1016/j.scitotenv.2019.06.404. [DOI] [PubMed] [Google Scholar]
  29. Waldschläger K.; Schüttrumpf H. Effects of Particle Properties on the Settling and Rise Velocities of Microplastics in Freshwater under Laboratory Conditions. Environ. Sci. Technol. 2019, 53, 1958–1966. 10.1021/acs.est.8b06794. [DOI] [PubMed] [Google Scholar]
  30. McNown J. S.; Malaika J. Effect of particle shape on settling velocity at low Reynolds numbers. Trans., Am. Geophys. Union. 1950, 31, 74–82. 10.1029/TR031i001p00074. [DOI] [Google Scholar]
  31. Simon M.; van Last N.; Vollertsen J. Quantification of microplastic mass and removal rates at wastewater treatment plants applying Focal Plane Array (FPA)-based Fourier Transform Infrared (FT-IR) imaging. Water Res. 2018, 142, 1–9. 10.1016/j.watres.2018.05.019. [DOI] [PubMed] [Google Scholar]
  32. Mintenig S. M.; Kooi M.; Erich M. W.; Primpke S.; Redondo-Hasselerharm P. E.; Dekker S. C.; Koelmans A. A.; van Wezel A. P. A systems approach to understand microplastic occurrences in Dutch riverine surface waters. Water Res. 2020, 176, 115723 10.1016/j.watres.2020.115723. [DOI] [PubMed] [Google Scholar]
  33. Wright S. L.; Rowe D.; Thompson R. C.; Galloway T. S. Microplastic ingestion decreases energy reserves in marine worms. Curr. Biol. 2013, 23, R1031–R1033. 10.1016/j.cub.2013.10.068. [DOI] [PubMed] [Google Scholar]
  34. Foley C. J.; Feiner Z. S.; Malinich T. D.; Höök T. O. A meta-analysis of the effects of exposure to microplastics on fish and aquatic invertebrates. Sci. Total Environ. 2018, 631–632, 550–559. 10.1016/j.scitotenv.2018.03.046. [DOI] [PubMed] [Google Scholar]
  35. De Ruijter V. N.; Redondo-Hasselerharm P. E.; Gouin T.; Koelmans A. A. Quality criteria for microplastic effect studies in the context of risk assessment: A critical review. Environ. Sci.Technol. 2020, 10.1021/acs.est.0c03057. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Besseling E.; Redondo-Hasselerharm P. E.; Foekema E. M.; Koelmans A. A. 2019. Correction to ‘Quantifying ecological risks of aquatic micro- and nanoplastic’. Crit. Rev. Environ. Sci. Technol. 2019, 49, 32–80. 10.1080/10643389.2019.1595472. [DOI] [Google Scholar]
  37. Gouin T. Towards improved understanding of the ingestion and trophic transfer of microplastic particles - Critical review and implications for future research. Environ. Toxicol. Chem. 2020, 39, 1119–1137. 10.1002/etc.4718. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. ECHA . Characterization of Dose [Concentration]-Response for Environment. In Guidance on Information Requirements and Chemical Safety Assessment.; European Chemicals Agency, 2008; Chapter R.8. [Google Scholar]
  39. Ziajahromi S.; Kumar A.; Neale P. A.; Leusch F. D. L. Impact of microplastic beads and fibers on waterflea (Ceriodaphnia Dubia) survival, growth, and reproduction: Implications of single and mixture exposures. Environ. Sci. Technol. 2017, 51, 13397–13406. 10.1021/acs.est.7b03574. [DOI] [PubMed] [Google Scholar]
  40. Sørensen L.; Rogers E.; Altin D.; Salaberria J.; Booth A. M. Sorption of PAHs to microplastic and their bioavailability and toxicity to marine copepods under co-exposure conditions. Environ. Pollut. 2020, 258, 113844 10.1016/j.envpol.2019.113844. [DOI] [PubMed] [Google Scholar]
  41. Jâms I. B.; Windsor F. M.; Poudevigne-Durance T.; Ormerod S. J.; Durance I. Estimating the size distribution of plastics ingested by animals. Nat. Commun. 2020, 11, 1594 10.1038/s41467-020-15406-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Verma J.; Khedkar V. M.; Coutinho E. C. 3D-QSAR in drug design--a review. Curr. Top. Med. Chem. 2010, 10, 95–115. 10.2174/156802610790232260. [DOI] [PubMed] [Google Scholar]
  43. Cherkasov A.; Muratov E. N.; Fourches D.; Varnek A.; Baskin I. I.; Cronin M.; Dearden J.; Gramatica P.; Martin Y. C.; Todeschini R.; Consonni V.; Kuz’min V. E.; Cramer R.; Benigni R.; Yang C.; Rathman J.; Terfloth L.; Gasteiger J.; Richard A.; Tropsha A. QSAR modeling: where have you been? Where are you going to?. J. Med. Chem. 2014, 57, 4977–5010. 10.1021/jm4004285. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Primpke S.; Lorenz C.; Rascher-Friesenhausen R.; Gerdts G. An automated approach for microplastics analysis using focal plane array (FPA) FTIR microscopy and image analysis. Anal. Methods 2017, 9, 1499–1511. 10.1039/C6AY02476A. [DOI] [Google Scholar]
  45. ECHA; Annex XV Restriction Report– Microplastic, 2019. https://echa.europa.eu/documents/10162/12414bc7-6bb2-17e7-c9ec-652a20fa43fc.
  46. Connors K. A.; Dyer S. D.; Belanger S. E. Advancing the quality of environmental microplastic research. Environ. Toxicol. Chem. 2017, 36, 1697–1703. 10.1002/etc.3829. [DOI] [PubMed] [Google Scholar]
  47. Doyle-McCullough M.; Smyth S. H.; Moyes S. M.; Carr K. E. Factors influencing intestinal microparticle uptake in vivo. Int. J. Pharm. 2007, 335, 79–89. 10.1016/j.ijpharm.2006.10.043. [DOI] [PubMed] [Google Scholar]
  48. Carr K. E.; Smyth S. H.; McCullough M. T.; Morris J. F.; Moyes S. M. Morphological aspects of interactions between microparticles and mammalian cells: Intestinal uptake and onward movement. Prog. Histochem. Cytochem. 2012, 46, 185–252. 10.1016/j.proghi.2011.11.001. [DOI] [PubMed] [Google Scholar]
  49. Presence of microplastics and nanoplastics in food, with particular focus on seafood. EFSA J. 2016, 14, e04501 10.2903/j.efsa.2016.4501. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

es0c02982_si_001.pdf (155.5KB, pdf)

Articles from Environmental Science & Technology are provided here courtesy of American Chemical Society

RESOURCES