Multi-site harmonization of diffusion MRI data in a registration framework

Abstract

Diffusion MRI (dMRI) data acquired on different scanners varies significantly in its content throughout the brain even if the acquisition parameters are nearly identical. Thus, proper harmonization of such data sets is necessary to increase the sample size and thereby the statistical power of neuroimaging studies. In this paper, we present a novel approach to harmonize dMRI data (the raw signal, instead of dMRI derived measures such as fractional anisotropy) using rotation invariant spherical harmonic (RISH) features embedded within a multi-modal image registration framework. All dMRI data sets from all sites are registered to a common template and voxel-wise differences in RISH features between sites at a group level are used to harmonize the signal in a subject-specific manner. We validate our method on diffusion data acquired from seven different sites (two GE, three Philips, and two Siemens scanners) on a group of age-matched healthy subjects. We demonstrate the efficacy of our method by statistically comparing diffusion measures such as fractional anisotropy, mean diffusivity and generalized fractional anisotropy across these sites before and after data harmonization. Validation was also done on a group oftest subjects, which were not used to “learn” the harmonization parameters. We also show results using TBSS before and after harmonization for independent validation of the proposed methodology. Using synthetic data, we show that any abnormality in diffusion measures due to disease is preserved during the harmonization process. Our experimental results demonstrate that, for nearly identical acquisition protocol across sites, scanner-specific differences in the signal can be removed using the proposed method in a model independent manner.

Introduction

Diffusion MRI (dMRI) data is widely used to study several brain disorders, such as Alzheimer’s disease, schizophrenia etc. Several multi-center studies have acquired dMRI data at different sites. However, the inter-scanner variability poses a potential problem for joint analysis of these data sets (Matsui 2014; Magnotta et al. 2012; Dariya et al. 2016). This inter-site variability in the measurements can come from several sources, such as the number of head coils used (16, 20 or 32 channel head coil), sensitivity of the coils, the imaging gradient non-linearity, the magnetic field inhomogeneity, the differences in the algorithms used to reconstruct the data, and other scanner related factors (Kochunov et al. 2014). These factors lead to non-linear changes in the data as well as in the estimated diffusion measures such as fractional anisotropy (FA). Thus, aggregating data sets from different sites is challenging due to the inherent differences in the acquired images from different scanners (Giannelli et al. 2014). Although the inter-site variability can be minimized by acquiring data using similar type of scanners (same vendor and version) with similar pulse sequence parameters (Cannon et al. 2014), many recent studies have shown that there still exist large differences between diffusion measurements from different sites (Kochunov et al. 2014; Mirzaalian et al. 2015, 2016). Specifically, the inter-site variability in FA and mean diffusivity (MD) is not uniform over the entire brain, but is tissue specific as well as region specific (Mirzaalian et al. 2015; Mirzaalian et al. 2016). Thus, harmonizing dMRI data across sites is imperative for joint analysis of the data.

There are three major categories of methods that have addressed the issue of dMRI data pooling (not necessarily harmonization). The first category of methods use Meta Analysis (Salimi-Khorshidi et al. 2009; Jahanshad et al. 2013; Kochunov et al. 2014), which involves combining z-scores of a given diffusion measure (say FA) from all sites to determine group differences. However, the subject population at each site may not be sufficient to capture the variance of the entire population, a critical requirement to ensure proper pooling and analysis of the z-scores (which depends on the variance and not just the mean). The second category of methods use Statistical Covariates to account for site-specific differences (Forsyth and Cannon 2014; Venkatraman et al. 2015). For example, the method of Kochunov et al. (2014) uses z-scores from each site and then regresses-out site specific differences using statistical covariates. In general, a linear model is used to account for these site-specific differences, which may not be accurate enough if one wants to analyze fiber tracts that travel between distant brain regions, as regional variations are not taken into account in this framework. Finally, both of the methodologies mentioned above correct for scanner differences at the last stage of the analysis using specific dMRI measures based on a certain model of diffusion.

Recently, we proposed a third category of method (Mirzaalian et al. 2015, 2016), which harmonized the dMRI data in a model independent manner. We harmonized the raw dMRI signal appropriately in different brain regions and tissue types. In this work, we further build on this methodology, but significantly simplify it and address some of its limitations as discussed below.

Our contribution

In this paper, we provide an extension of our previous work (Mirzaalian et al. 2015, 2016) and address some of its limitations by using a registration-based framework. The main contributions of this work are: i) The current work has no dependence or requirement of an a-priori computed Freesurfer (or any other) segmentation to obtain correspondence between different brain regions across subjects. In fact, this was one of the challenges of our earlier work, where a separate mechanism was devised to correct all errors in the Freesurfer segmentation, which were quite common. For example, several voxels at the boundary between white and gray would be easily misclassified by Freesurfer once it was transformed to the diffusion MRI space of each subject due to limited resolution. This correction was done separately for each site and had to be tuned for each region. These limitations don’t exist in the current work; ii) In our earlier work, a single group level difference between sites for each SH order was computed for each region separately, which was then uniformly used to update all voxels in that particular region. In comparison, the proposed framework is voxel-wise and thus allows to update the differences at a voxel level, albeit in a smooth manner. This can be clearly seen in Fig. 2, where both voxel wise and region-wise differences in RISH features are displayed for all the sites; iii) In our earlier work, two levels of mapping were required: 1. Region-wise, 2. Voxel-wise. In the current framework, this is simplified and only a voxel-wise mapping is directly computed. iv). Using synthetic data, we also show that the proposed method is robust and preserves the changes in diffusion measures due to subtle pathology.

Fig. 2.

Regionwise (R) and voxelwise (V) RISH features for different SH orders and sites

Thus, the proposed method is a much more simplified version of our earlier work and is quite easy to use and implement, without the requirement for any kind of parameter tuning or dependence on Freesurfer or any other kind of segmentation algorithm. The code will be publicly available soon. Please contact the senior author on this paper for further details.

Method

Figure 1 shows an outline of our dMRI data harmonization procedure. Details about each of the steps in this procedure are given in the following sections.

Fig. 1.

Outline of the proposed method for inter-site dMRI data harmonization. The reference and the target sites are shown in green and red, respectively. Given the RISH features, we start by performing multi-modal registration between all data sets. Next, we compute voxel-wise population average of the RISH features for each site and also the group differences (Δ) between the sites. By unwarping the computed differences to a given subject in a target site, we map the SH coefficients, which are then used to harmonize the dMRI signal

Multi-modal image registration

Any dMRI signal (at a single b-value) can be represented accurately in a basis of spherical harmonics. Rotation invariant features derived from this representation can be used to harmonize the diffusion signal as these features do not depend on the orientation of the white matter fibers or gray matter tissue, but only on the frequency content. Thus, the signal can be modified by changing the rotation invariant spherical harmonic (RISH) features, without changing the underlying fiber orientation (and hence the connectivity) of each subject. Consequently, we use the RISH features to harmonize dMRI data.

We start by computing a set of RISH features at each voxel from the dMRI signal S = [s₁...s_G]^T along G unique gradient directions. This signal can be compactly represented in a basis of spherical harmonics (SH) with coefficients C_ij given by: S ≈ Σ_i Σ_j C_ijY_ij, where Y_ij are the SH basis functions of order i and degree j. Several RISH features $\mathcal{F}$ at each voxel can be computed as follows (Mirzaalian et al. 2015; Descoteaux et al. 2007)¹:

$$\mathcal{F}=[{\Vert C_o\Vert }^2{\Vert C_2\Vert }^2\dots {\Vert C_8\Vert }^2]\text{where:}{\Vert C_i\Vert }^2=\sum _{j=1}^{2i+1}{\left(C_{ij}\right)}^2.$$ (1)

These RISH feature images are then used within a registration framework with data from all subjects across all sites to create a single template. There are 5 RISH features for SH of up to order 8; each RISH feature can be represented as a scalar image (see Fig. 2). Thus, for each subject we have 5 image volumes (RISH feature images), which we term as multi-modal images as they capture different aspects (frequency) of the diffusion signal. Our multi-modal template (consisting of the 5 RISH feature images) is computed using the ANTs algorithm (Avants et al. 2014) (i.e., vector-image registration of RISH feature images).

In the template space, given the registered RISH images, we approximate the expected value of the voxel-wise RISH features as the sample mean over the N_t subjects for the t^th site using:

$${\mathbb{E}}_t([{\Vert C_i\Vert }^2])\approx \sum _{n=1}^{N_t}\left[{\Vert C_i^n\Vert }^2\right]/N_t,$$

where ${\Vert C_i^n\Vert }^2$ is the RISH feature of order i for the n^th subject. Unlike the method of Mirzaalian et al. (2015) and Mirzaalian et al. (2016), where two separate mappings are computed, one at the ROI level and another one at the voxel level, in this work, we only compute one mapping at each voxel to harmonize the signal. In Fig. 2, we show examples of voxel-wise (using the registered images) and region-wise (using Freesurfer label maps) RISH features for different SH orders and different sites. As can be seen in these figures, the RISH features vary significantly across the brain as well as in different tissue types (white matter, neocortical, subcortical). Comparing the amount of energy of the signal at different orders in Fig. 2, it can be seen that the energy at order 8 is 500 times smaller than the one at order 0. Therefore, using SH order of up to 8 in our pipeline, we capture 99.9 % of the energy of the signal. This is also consistent with all works that have used spherical harmonics, where they have also truncated the SH basis at order 6 or 8, (Descoteaux et al. 2007; Özarslan et al. 2006; Tournier et al. 2007).

Mapping voxel-wise RISH features between sites

As part of the diffeomorphic registration procedure to compute a template, we also obtain the deformation field that maps each voxel location ν to Π_n(ν), where Π_n is a diffeomorphism for subject n. Further, the voxelwise expected value of each of the RISH features for the target and reference site $\left\{{\mathbb{E}}_r,{\mathbb{E}}_t\right\}$ are also computed in the template space. Using a procedure analogous to the one used in Mirzaalian et al. (2015, 2016), harmonization is achieved by scaling each of the SH coefficients based on the difference between the group means of the two sites (for matched set of subjects). This ensures that only the shape of the signal changes, but not its orientation (a critical requirement to preserve subject-specific anatomical connectivity). This was also numerically verified in Mirzaalian et al. (2015), where it was shown that this scaling procedure does not change the orientation of the underlying fiber orientation distribution function (fODF).

Given the computed $\left\{{\mathbb{E}}_r,{\mathbb{E}}_t\right\}$, we harmonize the signal by scaling the SH coefficients of the signal at ν′ by:

$$\pi \left(C_{ij}\left(v^{\prime }\right)\right)=\sqrt{\frac{{\Vert C_i\left(v^{\prime }\right)\Vert }^2+{\mathbb{E}}_r(v)-{\mathbb{E}}_k(v)}{{\Vert C_i\left(v^{\prime }\right)\Vert }^2}}{C}_{ij}\left(v^{\prime }\right)$$ (2)

where $v^{\prime }={\mathrm{\Pi }}_n^{-1}(v)$. The final harmonized diffusion signal at ν′ is then computed using:

$$\widehat{S}\left(v^{\prime }\right)=\sum _i\sum _j\pi \left(C_{ij}\left(v^{\prime }\right)\right)Y_{ij}.$$ (3)

We applied this procedure to harmonize data from several sites as described in the next section.

Experiments and results

Diffusion MRI data was acquired at seven different sites (two GE, three Philips, and two Siemens scanners) on a group of matched healthy subjects. All the healthy subjects were matched for age and handedness to the best possible extent. Demographic and scanner details are given in Table 1. All data sets had a spatial resolution of 2 mm isotropic voxel size and a b-value of 1000 s/mm². Since the subjects were matched across all the sites, at a statistical group level, we do not expect to see statistical biological differences. Therefore, it is reasonable to hypothesize that the differences in the RISH features and standard diffusion measures are only due to scanner related inconsistencies. To validate our hypothesis, we used a paired t-test to compute p-values of RISH features and standard diffusion measures (such as MD, FA, and generalized fractional anisotropy (GFA)) between an arbitrarily chosen reference site and all of the other (target) sites. Tables 2, 3 and 4 show that prior to harmonization, significant statistical differences exist between sites in Freesurfer defined ROIs for all diffusion measures. However, using the proposed multi-modal registration based harmonization procedure, all statistical site differences in each of the Freesurfer ROIs are removed. For the sake of comparison, we included the results from our earlier work (Mirzaalian et al. 2016) on the same set of subjects, but using the Freesurfer ROI based method in the appendix section (see Table 7). As can be seen, our results are comparable to those presented in Mirzaalian et al. (2016).

Table 1.

Scanner details and demographic information for each site (M - Male, F - Female, R - right handed, L - left handed)

Site#	Manufacturer	Field strength	Model	Software version	# of channels	# of subjects	# of directions	Age	Handedness	Gender
1	Philips	3T	Achieva	2.6.3	8	20	64	35±11	20R 0L	10F, 10M
2	Philips	3T	Achieva	2.6.3	8	20	64	35±12	17R 3L	14F, 6M
3	Philips	3T	Achieva	2.6.3	8	7	64	36±12	7R 0L	4F, 3M
4	GE	3T	MR750	20xM4	8	6	86	37±10	6R 0L	1F, 5M
5	GE	3T	MR750	M4	8	16	86	37±9	14R 2L	12F, 4M
6	Siemens	3T	Tim Trio	vb17	12	24	87	35±12	23R 1L	6F, 18M
Ref.	Siemens	3T	Tim Trio	VB15	12	23	87	36±11	20R 3L	13F, 10M

Table 2.

P-values in Freesurfer defined regions for MD before and after data harmonization

	Site#1		Site#2		Site#3		Site#4		Site#5		Site#6
	Before	After	Before	After	Before	After	Before	After	Before	After	Before	After
lFrontal	2.6e-04	0.56	4.0e-02	0.66	1.9e-04	0.81	3.2e-04	0.74	2.4e-08	0.70	0.17	0.97
lParietal	1.7e-09	0.62	2.3e-09	0.58	1.7e-06	0.98	1.5e-04	0.80	9.6e-09	0.62	3.6e-03	0.97
lTemporal	8.5e-11	0.60	1.7e-11	0.50	8.0e-07	0.83	8.5e-05	0.53	2.2e-08	0.66	1.9e-03	0.95
lOccipital	1.7e-05	0.61	2.1e-07	0.57	1.6e-03	0.71	0.21	0.88	1.1e-03	0.91	0.11	0.85
lCentrumSemiovale	1.5e-15	0.21	4.8e-14	0.20	3.5e-10	0.40	3.3e-07	0.44	1.8e-10	0.80	7.2e-05	0.80
lCerebellum	3.6e-06	0.37	4.9e-09	0.48	4.9e-05	0.65	5.3e-03	0.89	0.17	0.42	0.77	0.76
rFrontal	4.4e-05	0.62	2.1e-03	0.72	9.5e-05	0.74	1.1e-04	0.76	2.0e-09	0.83	5.1e-02	0.92
rParietal	1.1e-05	0.63	7.7e-06	0.60	2.0e-05	0.99	9.4e-03	0.93	8.8e-05	0.92	0.15	0.88
rTemporal	3.1e-06	0.82	3.5e-07	0.77	9.8e-05	0.92	1.9e-02	0.94	4.7e-05	0.83	2.1e-02	0.82
rOccipital	7.3e-03	0.75	4.5e-04	0.68	2.5e-03	0.97	0.76	0.77	0.87	0.36	0.67	0.80
rCentrumSemiovale	1.8e-12	0.72	2.5e-11	0.52	2.1e-08	0.96	1.0e-05	0.75	2.7e-09	0.84	1.3e-05	0.88
rCerebellum	9.7e-02	0.98	3.8e-05	0.70	0.28	0.91	0.16	0.73	0.11	0.15	0.84	0.98
BrainStem	1.3e-18	0.084	6.1e-21	0.078	8.9e-12	0.079	8.0e-07	0.34	9.9e-05	0.81	2.5e-04	0.68
Corpus	1.7e-09	0.67	3.7e-06	0.55	2.0e-06	0.89	1.3e-03	0.67	2.3e-06	0.81	0.34	0.89

Table 3.

p-values for FA before and after harmonization in Freesurfer ROIs

	Site#1		Site#2		Site#3		Site#4		Site#5		Site#6
	Before	After	Before	After	Before	After	Before	After	Before	After	Before	After
lFrontal	6.4e-07	0.85	6.3e-06	0.83	2.5e-04	0.98	0.28	0.50	5.8e-03	0.72	0.28	0.99
lParietal	1.7e-08	0.71	1.6e-08	0.72	2.9e-05	0.82	0.15	0.64	1.2e-04	0.90	2.1e-02	0.80
lTemporal	4.0e-08	0.89	9.4e-09	0.81	3.6e-04	0.66	0.23	0.40	2.5e-03	0.54	9.3e-02	0.77
lOccipital	3.9e-07	0.72	5.7e-08	0.72	2.3e-04	0.64	0.83	0.39	4.4e-02	0.87	0.25	0.88
lCentrumSemiovale	1.9e-12	0.92	2.2e-11	0.91	1.8e-07	0.85	2.4e-03	0.57	5.1e-06	0.94	7.1e-03	0.90
lCerebellum	3.5e-10	0.74	1.1e-11	0.56	9.9e-10	0.56	0.65	0.85	0.69	0.53	0.15	0.63
rFrontal	1.2e-07	0.77	3.6e-06	0.70	1.3e-04	0.98	0.20	0.64	4.3e-03	0.91	0.15	0.93
rParietal	7.3e-09	0.64	3.6e-08	0.76	9.5e-06	0.93	0.45	0.48	1.3e-03	0.94	4.9e-02	0.81
rTemporal	7.6e-08	0.82	6.7e-08	0.69	1.2e-04	0.88	0.54	0.47	2.0e-02	0.90	0.11	0.96
rOccipital	2.9e-05	0.88	3.0e-06	0.81	4.1e-05	0.97	0.83	0.34	0.59	0.97	0.64	0.84
rCentrumSemiovale	3.3e-11	0.57	2.6e-10	0.60	2.6e-07	0.78	4.0e-03	0.80	8.9e-06	0.72	1.0e-03	0.83
rCerebellum	5.8e-07	0.46	2.8e-10	0.45	3.1e-05	0.48	0.78	0.99	0.39	0.35	0.53	0.83
BrainStem	1.4e-11	0.48	1.7e-14	0.67	7.6e-10	0.64	0.10	0.41	0.29	0.77	3.8e-04	0.75
Corpus	8.6e-07	0.35	2.0e-04	0.44	5.9e-04	0.78	0.90	0.84	6.9e-02	0.99	0.79	0.74

Table 4.

P-values in Freesurfer defined regions for GFA before and after data harmonization

	Site#1		Site#2		Site#3		Site#4		Site#5		Site#6
	Before	After	Before	After	Before	After	Before	After	Before	After	Before	After
lFrontal	2.8e-09	0.56	1.6e-10	0.72	9.6e-04	0.76	6.9e-04	0.81	4.7e-03	0.81	0.27	0.40
lParietal	4.1e-06	0.46	4.3e-06	0.49	2.7e-03	0.73	2.1e-03	0.85	0.11	0.70	0.49	0.27
lTemporal	6.3e-06	0.89	1.6e-06	0.97	2.5e-02	0.76	2.0e-03	0.74	5.0e-02	0.68	0.068	0.70
lOccipital	2.4e-07	0.72	1.7e-05	0.45	1.4e-03	0.80	3.0e-03	0.90	0.15	0.56	0.39	0.27
lCentrumSemiovale	2.8e-04	0.44	6.6e-05	0.36	0.20	0.79	1.8e-05	0.90	5.0e-03	0.80	0.053	0.42
lCerebellum	2.6e-08	0.90	7.0e-08	0.89	1.6e-06	0.76	5.8e-03	0.78	0.19	0.85	0.23	0.60
rFrontal	7.5e-09	0.71	8.3e-10	0.66	8.8e-04	0.83	6.6e-04	0.96	3.3e-04	0.73	0.14	0.35
rParietal	2.7e-09	0.55	0.80	0.48	5.3e-05	0.84	1.4e-02	0.69	0.85	0.87	0.90	0.30
rTemporal	6.3e-10	0.86	5.5e-11	0.99	7.7e-05	0.92	7.5e-02	0.73	0.39	0.83	0.27	0.58
rOccipital	2.8e-10	0.49	1.8e-09	0.69	1.1e-06	0.71	0.10	0.70	0.63	0.69	0.75	0.28
rCentrumSemiovale	8.3e-07	0.63	2.9e-06	0.30	1.1e-02	0.91	8.5e-04	0.85	5.0e-03	0.81	0.079	0.47
rCerebellum	1.8e-13	0.67	7.2e-12	0.60	2.8e-07	0.83	0.13	0.89	0.17	0.62	0.23	0.61
BrainStem	0.21	0.52	0.12	0.86	7.7e-02	0.41	9.7e-06	0.43	1.7e-05	0.80	0.02	0.29
Corpus	6.4e-05	0.68	5.8e-05	0.51	0.39	0.79	1.8e-05	0.91	4.3e-03	0.86	0.11	0.38

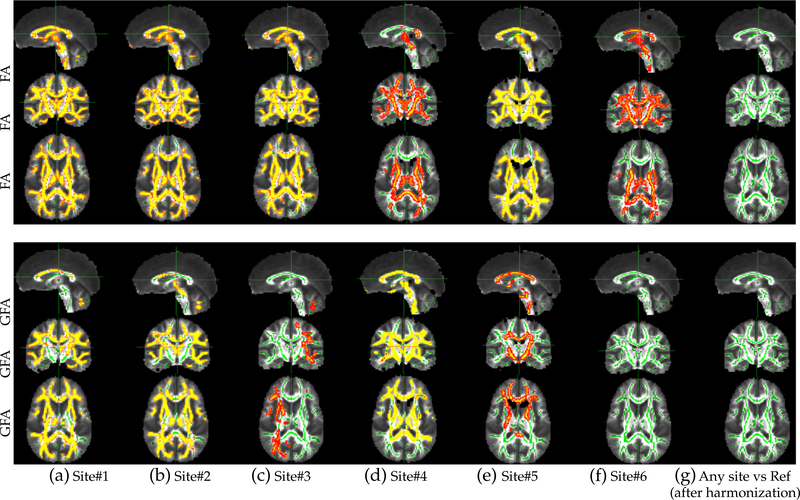
To ensure our method is unbiased and robust, we used an independent voxel-wise method to test the robustness of our harmonization procedure. We used tract-based spatial statistics (TBSS) (Smitha et al. 2006) to demonstrate that scanner related differences in FA and GFA, which existed prior to data harmonization are practically removed by using the proposed harmonization procedure; see Fig. 3. An interesting point to note is that, significant FA differences in the centrum-semiovale region exist prior to harmonization between the two Siemens scanners (Site#6), but not in GFA indicating that FA is a poor metric to use in crossing fiber regions. However, all differences in FA and GFA are removed after harmonization.

Fig. 3.

TBSS results using FA and GFA for different target sites before (a-f) and (g) after harmonization. The yellow-red colormap displays p-values less than 0.05

Validation on unseen subjects

In the above experiments, all subjects were used to obtain the site differences $\left\{{\mathbb{E}}_r-{\mathbb{E}}_t\right\}$ in RISH features, which were then used for harmonization. To test the validity of our approach on a set of new subjects, we created two distinct data sets, one for training and one for testing from two different sites. We used 70 % of the subjects in the reference and the target sites (Site#1) to learn the harmonization parameters using (2) and computed the p-values before and after harmonization for rest of the 30 % of the subjects, which were excluded from the training stage. Note that, in this experiment, the data in the training/testing groups at the two sites were age-matched. Computed p-values are reported in Table 5, which are very similar to results shown in Tables 2–4. Thus, the proposed method could be used in a true data harmonization scenario, at least when the acquisition protocol is similar across sites. Note that, our numerical results in Tables 2–5 are comparable to those in our earlier work (Tables 7 and 8 in Appendix).

Table 5.

P-values before and after harmonization for MD, FA, GFA for different sites and ROIs using test data excluded from training

	MD		FA		GFA
	Before	After	Before	After	Before	After
lFrontal	8.3e-03	0.84	3.4e-05	0.35	3.4e-07	0.20
lParietal	1.2e-06	0.77	6.4e-07	0.22	3.6e-05	0.12
lTemporal	9.3e-08	0.97	1.8e-06	0.53	4.3e-04	0.48
lOccipital	2.4e-03	0.67	6.3e-05	0.20	4.9e-05	0.31
lCentrumSemiovale	1.0e-10	0.48	7.5e-09	0.73	6.6e-03	0.30
lCerebellum	1.0e-04	0.45	5.5e-08	0.69	3.7e-06	0.96
rFrontal	3.3e-03	0.73	1.5e-05	0.18	4.3e-07	0.14
rParietal	1.1e-03	0.73	3.3e-07	0.21	1.2e-08	0.20
rTemporal	3.9e-04	0.73	1.5e-06	0.25	2.9e-08	0.57
rOccipital	9.5e-02	0.69	8.0e-04	0.45	3.5e-08	0.55
rCentrumSemiovale	1.9e-08	0.68	1.5e-07	0.25	8.5e-05	0.53
rCerebellum	0.26	0.87	7.5e-05	0.31	2.3e-10	0.69
BrainStem	2.7e-13	0.08	2.5e-09	0.17	9.7e-01	0.53
Corpus	1.6e-06	0.49	9.9e-05	0.83	2.1e-03	0.39

Validation on a traveling subject

Using the learnt parameters in our pipeline, we harmonized the images of a traveling subject for which there existed data acquired on six different sites (all sites except site #3). The computed region-wise p-values for {MD, FA, GFA} between voxels from each Freesurfer ROI before and after data harmonization are reported in Table 6, which are all above 0.05 after harmonization, indicating that scanner specific differences were removed in this traveling subject. We should point out that statistically, significant differences in FA, MD and GFA existed prior to harmonization in this traveling subject as seen in Table 6.

Table 6.

P-values in Freesurfer defined regions for MD (top), FA (middle), and GFA (bottom) before and after data harmonization for the traveling subject

	MD		FA		GFA
	Before	After	Before	After	Before	After
Site#1
lFrontal	1.1e-01	6.5e-01	2.1e-01	5.2e-01	1.8e-01	8.6e-01
lParietal	4.0e-04	4.7e-01	2.7e-01	1.0e-01	4.8e-01	1.6e-01
lTemporal	7.1e-02	5.4e-01	3.7e-02	0.8e-01	6.7e-02	0.6e-01
lOccipital	3.1e-01	0.5e-01	1.1e-01	3.6e-01	1.9e-01	3.9e-01
lCentrumS.	4.6e-02	1.0e-01	2.8e-02	2.8e-01	4.3e-01	0.9e-01
rFrontal	2.2e-01	3.0e-01	1.4e-01	5.4e-01	9.2e-02	9.1e-01
rParietal	3.4e-01	0.6e-01	2.5e-01	6.3e-01	1.9e-01	0.7e-01
rTemporal	3.3e-01	4.4e-01	4.7e-03	1.7e-01	6.3e-03	2.2e-01
rOccipital	5.1e-01	9.3e-01	2.6e-01	6.3e-01	2.4e-01	3.6e-01
rCentrumS.	7.7e-01	2.9e-01	6.3e-01	1.3e-01	6.5e-01	7.4e-01
rCereb.	2.3e-01	3.1e-01	1.3e-01	1.1e-01	8.3e-01	2.8e-01
BrainStem	8.1e-01	1.0e-01	7.9e-01	6.9e-01	2.2e-02	3.1e-01
Corpus	1.7e-01	0.9e-01	9.9e-02	5.8e-01	8.3e-02	2.3e-01
Site#2
lFrontal	3.4e-02	1.9e-01	2.3e-01	3.4e-01	2.9e-01	5.8e-01
lTemporal	1.2e-02	0.6e-01	3.3e-02	1.5e-01	2.3e-01	1.6e-01
lOccipital	2.1e-02	3.3e-01	4.6e-02	2.1e-01	2.8e-01	3.6e-01
lCentrumS.	3.2e-05	1.9e-01	1.2e-02	1.5e-01	6.0e-01	0.7e-01
lCereb.	6.9e-03	6.4e-02	2.3e-02	1.7e-01	3.2e-01	2.9e-01
rFrontal	1.1e-02	1.0e-01	1.8e-01	2.5e-01	2.5e-01	4.3e-01
rParietal	8.7e-05	0.8e-01	5.7e-02	2.0e-01	1.1e-01	1.9e-01
rTemporal	1.3e-01	0.9e-01	1.7e-03	4.8e-01	4.4e-03	1.3e-01
rOccipital	1.6e-02	2.3e-01	3.9e-02	4.7e-01	5.9e-02	2.7e-01
rCentrumS.	1.8e-01	1.3e-01	7.1e-01	5.7e-01	7.8e-01	6.1e-01
rCereb.	2.0e-01	2.1e-01	5.9e-01	2.6e-01	4.9e-01	1.2e-01
BrainStem	9.4e-01	6.5e-01	4.4e-02	1.2e-01	9.9e-01	2.0e-01
Corpus	5.6e-03	9.0e-02	1.5e-02	3.4e-01	2.5e-02	3.7e-01
Site#4
lFrontal	9.6e-04	1.8e-01	5.8e-01	3.7e-01	7.2e-01	1.2e-01
lParietal	1.8e-03	5.5e-01	3.9e-01	2.7e-01	7.2e-01	7.1e-01
lTemporal	1.8e-02	7.3e-01	1.9e-01	8.1e-01	8.9e-01	2.5e-01
lOccipital	3.5e-01	3.4e-01	7.7e-01	4.8e-01	8.6e-01	2.6e-01
lCentrumS.	4.4e-01	0.8e-01	3.7e-01	7.7e-01	3.3e-01	3.9e-01
rFrontal	2.6e-03	0.9e-01	7.7e-01	3.6e-01	6.3e-01	3.4e-01
rParietal	1.6e-01	0.7e-01	6.9e-01	6.6e-01	7.3e-01	1.9e-01
rOccipital	8.8e-01	1.3e-01	8.9e-01	0.9e-01	9.0e-01	0.9e-01
rCentrumS.	8.1e-01	6.7e-01	7.5e-01	5.3e-01	9.7e-01	1.7e-01
rCereb.	7.3e-03	3.1e-01	1.7e-01	0.8e-01	8.1e-01	1.6e-01
BrainStem	2.3e-01	1.4e-01	7.3e-02	0.7e-01	7.8e-01	0.7e-01
Corpus	2.8e-01	8.3e-01	9.7e-01	4.3e-01	5.2e-01	1.2e-01
Site#5
lFrontal	2.6e-04	2.7e-01	3.9e-01	5.5e-01	8.7e-01	6.5e-01
lParietal	1.0e-02	5.2e-01	2.0e-01	1.7e-01	5.5e-01	3.1e-01
lTemporal	2.6e-02	6.0e-01	7.6e-02	2.5e-01	4.4e-01	4.8e-01
lOccipital	1.3e-01	4.1e-01	4.2e-01	1.7e-01	6.9e-01	1.8e-01
lCentrumS.	2.4e-04	3.6e-01	3.8e-03	1.0e-01	6.3e-01	1.4e-01
lCereb.	4.0e-02	1.0e-01	1.2e-01	4.8e-01	9.9e-01	5.8e-01
rFrontal	4.3e-04	4.7e-01	6.7e-01	5.4e-01	6.2e-01	4.5e-01
rParietal	6.4e-02	0.6e-01	5.6e-01	6.9e-01	7.1e-01	7.9e-01
rOccipital	7.7e-01	2.0e-01	9.9e-01	5.9e-01	8.0e-01	0.8e-01
rCentrumS.	9.5e-01	1.0e-01	7.8e-01	7.9e-01	9.5e-01	4.2e-01
rCereb.	4.6e-01	3.5e-01	8.7e-01	4.5e-01	4.8e-01	3.2e-01
BrainStem	9.8e-02	3.2e-01	2.6e-01	1.4e-01	9.8e-01	5.3e-01
Corpus	1.3e-01	2.5e-01	4.5e-01	2.4e-01	9.6e-01	3.7e-01
Site#6
lFrontal	3.9e-01	1.2e-01	8.5e-01	6.7e-01	9.4e-01	8.3e-01
lParietal	2.0e-01	1.3e-01	9.8e-01	1.3e-01	9.5e-01	7.0e-01
lTemporal	9.0e-01	8.3e-02	9.1e-01	3.2e-01	7.7e-01	1.0e-01
lOccipital	7.2e-01	9.4e-01	2.8e-01	2.0e-01	3.5e-01	8.1e-01
lCentrumS.	9.3e-01	3.9e-01	6.5e-01	3.2e-01	5.5e-01	0.9e-01
lCereb.	4.3e-01	5.1e-01	4.0e-01	0.9e-01	8.6e-01	1.4e-01
rFrontal	8.2e-01	3.0e-01	7.7e-01	8.4e-01	8.1e-01	5.1e-01
rParietal	7.8e-01	1.6e-01	7.9e-01	5.7e-01	8.0e-01	6.4e-01
rTemporal	3.8e-01	2.0e-01	7.5e-01	5.6e-02	4.4e-01	3.6e-01
rOccipital	6.8e-01	1.9e-01	5.3e-01	3.5e-01	5.0e-01	2.7e-01
rCentrumS.	9.4e-01	2.4e-01	6.7e-01	0.6e-01	8.1e-01	5.3e-01
rCereb.	8.8e-01	4.8e-01	4.6e-01	0.7e-01	2.8e-01	2.3e-01
BrainStem	7.0e-01	4.2e-01	1.3e-01	3.5e-01	8.9e-02	3.9e-01
Corpus	9.2e-01	7.4e-01	9.5e-01	2.1e-01	9.3e-01	8.4e-01

Synthetic validation in the presence of pathology

To demonstrate the robustness of the harmonization procedure in the presence of pathology, we did some synthetic experiments. We generated three synthetic images labeled as {S^r, S^t,1, S^t,2}, where i) S^r is a control subject at the reference site; ii) S^t,1 is a control subject at the target site; and iii) S^t,2 is a synthetically generated subject with pathology in white matter at the target site. To generate S^t,1, we first introduced a simple warping (rotation) to S^r and added some bias to the second order RISH features of S^r; the bias was added to voxels within a mask denoted by Mask1 (Fig. 4). This is similar to a data set where the data acquired at the target and reference site are different, as is typically the case for in-vivo data. In particular, the FA in the simulated white matter region for S^r was 0.79, for S^t,1 was 0.82, while for S^t,2 it was 0.79 (lower FA due to pathology). Various levels of rician noise (standard deviation of noise ranging from 0 to 0.2) was added to test the effect of noise on the harmonization procedure.

Fig. 4.

The procedure to evaluate the effect of harmonization in the presence of pathology. Synthetic images {S^r, S^t,1, S^t,2} are generated and feature differences of the diseased and control subjects at the target site before (i.e. S^t,1 vs S^t,2) and after harmonization (i.e. ${\widehat{S}}^{t,1}$ vs ${\widehat{S}}^{t,2}$) are reported in Fig. 5, which indicate that our method would preserve the differences during harmonization of the data

The data, S^t,2 was generated by adding some bias to the second order RISH features of S^t,1 within voxels given by another mask, Mask2; in fact, we assumed that the voxels within Mask2 were affected by disease. The second order RISH features of {S^r, S^t,1, S^t,2} and the masks are shown in Fig. 4. We first registered S^t,1 to S^r to learn the spatial mapping (for different noise levels) followed by computing the region-wise mean of the RISH features, which were used to obtain the harmonized images $\{{\widehat{S}}^{t,1},{\widehat{S}}^{t,2}\}$, respectively.

In Fig. 5, for the voxels within Mask2 with different levels of rician noise, we report the differences between: i) S^t,1 and S^t,2; and ii) ${\widehat{S}}^{t,1}$ and ${\widehat{S}}^{t,2}$ for each of the following measures: C₂², FA, and GFA. Our goal is to demonstrate that the differences in FA and GFA due to disease are preserved during the harmonization procedure, i.e., $S^{t,1}-S^{t,2}\approx {\widehat{S}}^{t,1}-{\widehat{S}}^{t,2}$. From the plots in Fig. 5 with 100 different realizations for each noise level, we see that subtle differences in diffusion measures are preserved during the harmonization procedure. Thus, this method could potentially be used to harmonize dMRI data, by first “learning” the harmonization parameters from a group of matched control subjects followed by applying the same parameters to the “diseased” cases.

Fig. 5.

Difference of ∥C₂∥², FA, and GFA between: i) S^t,2 and S^t,2; (original data) and ii) ${\widehat{S}}^{t,2}$ and ${\widehat{S}}^{t,2}$ (harmonized data) for different levels of rician noise. It can be seen that the differences computed between the normal and patient cases at the target site are preserved after data harmonization

Conclusion and limitations

In this work, we proposed a registration based framework to harmonize the raw dMRI signal from different sites in a subject-dependent manner, by removing scanner specific differences from the signal.

In our earlier region-wise harmonization method, we required both the DWI images and a structural (T1weighted) image of the subjects; the structural images were used to perform the region-wise segmentation task. Then, the label maps were registered to the DWI space to obtain inter-subject correspondences. Further, we automatically (albeit with some parameter tuning) had to sub-segment large regions into smaller regions to be able to properly harmonize the data. However, our new registration framework is free of: i) requirement of a structural image; ii) segmentation of the structural image; iii) registration between the structural and the DWI images; and iv) correction of Freesurfer segmentation errors. This significantly simplifies the entire processing pipeline while maintaining the accuracy of the method.

Using synthetic experiments, we demonstrated that, once the signal is harmonized using data from healthy subjects, it can then be used to map another cohort of diseased subjects without altering the signal due to disease or pathology. The proposed method is model independent and directly maps the signal to the reference site. We also validated our approach on a group of new subjects not used to “learn” the mapping transformation, demonstrating the robustness of the proposed approach on new unseen data sets. Thus, the method can be of great use to aggregate data from multiple sites for joint analysis of a large sample of data.

An ideal scenario in which the proposed method could be used is when a few traveling human phantoms are available from all sites, scanned within a very short period of time. In this case, the scanner specific differences can be obtained from these traveling subjects and subsequently used for data harmonization. A similar scheme, albeit using only the dMRI derived scalar measures of FA and MD obtained from a limited single tensor model was used in Pohl et al. (2016). In contrast, our method will allow to harmonize the acquired dMRI data without any modeling assumptions.

Nevertheless, a comprehensive in-vivo validation study needs to be done to ensure that the dMRI signal due to disease is preserved during the harmonization procedure (we only did synthetic validation, which shows encouraging results). Further, the effect of using this procedure in the case of extreme pathologies such as brain tumors needs to be evaluated. The proposed method cannot be used for DSI data sets, however, it can be used to separately harmonize each b-value shell for multi-shell diffusion data.

Appendix

Table 7.

P-values before and after harmonization for MD, FA, GFA for different sites and ROIs applying the harmonization method at Mirzaalian et al. (2015)

	Site#1		Site#2		Site#3		Site#4		Site#5		Site#6
	Before	After	Before	After	Before	After	Before	After	Before	After	Before	After
lFrontal	7.7e-02	1	9.9e-02	1	8.0e-03	1	2.9e-02	1	8.5e-05	1	1.7e-01	1
lParietal	2.6e-11	1	2.7e-10	1	8.4e-07	1	1.2e-03	1	1.1e-09	1	2.2e-02	1
lTemporal	6.8e-04	1	1.2e-01	1	2.6e-03	1	7.1e-04	1	7.8e-05	1	1.3e-02	1
lOccipital	2.6e-07	1	1.9e-09	1	7.2e-03	1	1.0e-01	1	6.5e-04	1	2.2e-01	1
lCentrumSemiovale	5.9e-16	1	4.2e-14	1	1.9e-09	1	9.2e-06	1	4.2e-13	1	6.0e-06	1
lCerebellum	2.3e-09	1	3.9e-15	1	2.6e-05	1	9.5e-05	1	2.2e-05	1	3.4e-03	1
rFrontal	1.8e-05	1	1.3e-03	1	5.8e-03	1	1.6e-02	1	3.9e-05	1	1.7e-01	1
rParietal	3.8e-10	1	2.9e-09	1	4.7e-06	1	6.1e-02	1	2.3e-06	1	2.1e-01	1
rTemporal	6.4e-04	1	8.5e-03	1	4.4e-02	1	3.4e-02	1	4.4e-05	1	8.9e-02	1
rOccipital	1.5e-03	1	3.2e-02	1	6.6e-02	1	2.6e-01	1	6.2e-01	1	6.4e-01	1
rCentrumSemiovale	5.6e-15	1	9.9e-14	1	1.3e-08	1	1.5e-05	1	9.4e-15	1	1.3e-07	1
rCerebellum	1.4e-04	1	5.7e-10	1	8.4e-04	1	4.9e-02	1	8.8e-01	1	2.1e-03	1
Corpus callosum	9.0e-14	1	1.3e-09	1	4.7e-07	1	3.8e-02	1	4.1e-09	1	1.7e-01	1
	FA
lFrontal	2.9e-02	4.2e-01	5.0e-02	4.3e-01	1.1e-02	6.3e-01	5.8e-01	6.7e-01	7.8e-02	5.2e-01	2.3e-01	6.1e-01
lParietal	4.3e-10	2.5e-01	7.5e-10	2.1e-01	2.6e-05	4.7e-01	8.0e-02	6.8e-01	9.5e-06	2.3e-01	2.9e-02	5.4e-01
lTemporal	2.5e-05	3.5e-01	5.1e-05	3.7e-01	2.8e-02	5.8e-01	3.8e-01	7.4e-01	7.0e-02	4.6e-01	4.8e-01	6.1e-01
lOccipital	1.5e-02	2.9e-01	3.3e-02	3.7e-01	6.3e-02	6.1e-01	2.0e-01	7.1e-01	5.7e-01	2.8e-01	5.9e-01	5.7e-01
lCentrumSemiovale	1.1e-12	1.3e-01	8.9e-11	2.3e-01	1.0e-08	3.9e-01	2.9e-03	5.1e-01	1.6e-07	2.8e-01	7.1e-03	3.4e-01
lCerebellum	9.6e-06	9.5e-02	7.6e-07	6.3e-02	2.0e-07	7.8e-02	2.4e-01	4.2e-01	8.2e-01	4.1e-01	6.2e-01	2.3e-01
rFrontal	5.3e-04	3.9e-01	3.8e-03	5.0e-01	1.3e-02	5.8e-01	3.5e-01	6.5e-01	6.1e-02	4.8e-01	1.7e-01	6.5e-01
rParietal	1.6e-08	2.5e-01	6.4e-08	3.3e-01	3.3e-05	5.2e-01	2.4e-01	7.7e-01	2.7e-04	3.4e-01	2.5e-01	5.8e-01
rTemporal	2.5e-05	3.4e-01	3.3e-05	4.0e-01	9.5e-03	5.7e-01	5.2e-01	7.0e-01	1.3e-01	5.1e-01	4.2e-01	6.3e-01
rOccipital	3.1e-04	4.0e-01	1.1e-05	3.0e-01	1.5e-04	3.6e-01	5.8e-01	7.9e-01	3.9e-01	3.9e-01	9.2e-01	8.2e-01
rCentrumSemiovale	1.1e-11	1.0e-01	7.3e-10	1.1e-01	2.3e-07	4.0e-01	3.9e-02	5.8e-01	9.0e-07	2.4e-01	1.7e-02	2.9e-01
rCerebellum	1.8e-06	1.1e-01	3.4e-10	2.5e-01	4.2e-06	1.1e-01	1.7e-01	4.2e-01	4.5e-02	9.4e-01	8.8e-01	3.7e-01
Corpus callosum	7.4e-13	1.0e-01	4.5e-10	2.0e-01	4.2e-05	5.6e-01	2.5e-01	5.1e-01	8.5e-04	8.6e-01	1.3e-01	8.1e-01
	GFA
lFrontal	5.8e-02	5.6e-01	5.0e-02	5.3e-01	1.0e-01	7.2e-01	9.1e-02	6.4e-01	2.1e-01	5.9e-01	4.0e-01	6.8e-01
lParietal	6.3e-03	3.9e-01	3.3e-03	3.7e-01	8.0e-02	5.1e-01	2.6e-01	6.1e-01	4.4e-01	2.2e-01	3.2e-01	4.3e-01
lTemporal	1.6e-02	3.5e-01	1.1e-01	3.8e-01	3.4e-01	5.8e-01	1.9e-01	7.8e-01	5.0e-01	5.4e-01	1.5e-01	6.7e-01
lOccipital	3.1e-01	5.4e-01	6.4e-01	4.2e-01	3.2e-01	7.4e-01	1.2e-01	7.4e-01	2.1e-01	4.5e-01	4.9e-01	6.7e-01
lCentrumSemiovale	1.2e-05	1.7e-01	7.9e-06	2.2e-01	2.1e-04	3.3e-01	2.8e-01	6.4e-01	6.3e-01	5.1e-01	2.7e-01	4.6e-01
lCerebellum	6.7e-03	1.9e-01	1.7e-03	1.3e-01	2.9e-06	1.9e-01	4.4e-01	6.3e-01	2.8e-02	5.6e-01	4.9e-02	4.8e-01
rFrontal	1.9e-03	5.5e-01	2.7e-04	6.2e-01	8.4e-02	6.4e-01	8.5e-02	6.7e-01	1.1e-01	5.7e-01	2.9e-01	7.6e-01
rParietal	1.1e-03	4.3e-01	6.8e-04	4.9e-01	8.0e-02	5.3e-01	4.2e-01	7.1e-01	2.1e-01	3.3e-01	3.7e-01	6.5e-01
rTemporal	8.1e-04	3.0e-01	1.1e-05	3.8e-01	3.3e-02	4.7e-01	1.6e-01	6.7e-01	9.3e-02	3.8e-01	2.1e-01	7.1e-01
rOccipital	2.7e-04	4.6e-01	9.2e-06	4.0e-01	8.4e-04	4.5e-01	5.7e-01	7.6e-01	3.5e-01	4.2e-01	8.2e-01	8.6e-01
rCentrumSemiovale	5.2e-06	1.7e-01	3.6e-05	1.6e-01	6.6e-04	3.6e-01	1.1e-01	7.1e-01	5.2e-02	4.5e-01	3.1e-02	4.9e-01
rCerebellum	3.2e-07	1.6e-01	7.4e-09	4.6e-02	1.3e-05	2.2e-01	6.3e-01	5.7e-01	1.4e-01	8.0e-01	1.8e-02	6.3e-01
Corpus callosum	2.7e-05	8.1e-01	5.8e-04	8.2e-01	1.8e-01	6.6e-01	2.0e-01	2.5e-01	5.4e-01	5.3e-01	4.3e-01	7.0e-01

Table 8.

P-values before and after harmonization for MD, FA, GFA for different sites and ROIs using test data excluded from training applying the harmonization method at Mirzaalian et al. (2015)

	MD		FA		GFA
	Before	After	Before	After	Before	After
lFrontal	8.3e-03	0.84	3.4e-05	0.35	3.4e-07	0.20
lParietal	1.2e-06	0.77	6.4e-07	0.22	3.6e-05	0.12
lTemporal	9.3e-08	0.97	1.8e-06	0.53	4.3e-04	0.48
lOccipital	2.4e-03	0.67	6.3e-05	0.20	4.9e-05	0.31
lCentrumSemiovale	1.0e-10	0.48	7.5e-09	0.73	6.6e-03	0.30
lCerebellum	1.0e-04	0.45	5.5e-08	0.69	3.7e-06	0.96
rFrontal	3.3e-03	0.73	1.5e-05	0.18	4.3e-07	0.14
rParietal	1.1e-03	0.73	3.3e-07	0.21	1.2e-08	0.20
rTemporal	3.9e-04	0.73	1.5e-06	0.25	2.9e-08	0.57
rOccipital	9.5e-02	0.69	8.0e-04	0.45	3.5e-08	0.55
rCentrumSemiovale	1.9e-08	0.68	1.5e-07	0.25	8.5e-05	0.53
rCerebellum	0.26	0.87	7.5e-05	0.31	2.3e-10	0.69
BrainStem	2.7e-13	0.08	2.5e-09	0.17	9.7e-01	0.53
Corpus	1.6e-06	0.49	9.9e-05	0.83	2.1e-03	0.39