Abstract
Protein-protein interactions regulate almost all cellular functions and rely on a fine tune of surface amino acids properties involved on both molecular partners. The disruption of a molecular association can be caused even by a single residue mutation, often leading to a pathological modification of a biochemical pathway. Therefore the evaluation of the effects of amino acid substitutions on binding, and the ad hoc design of protein-protein interfaces, is one of the biggest challenges in computational biology. Here, we present a novel strategy for computational mutation and optimization of protein-protein interfaces. Modeling the interaction surface properties using the Zernike polynomials, we describe the shape and electrostatics of binding sites with an ordered set of descriptors, making possible the evaluation of complementarity between interacting surfaces. With a Monte Carlo approach, we obtain protein mutants with controlled molecular complementarities. Applying this strategy to the relevant case of the interaction between Ferritin and Transferrin Receptor, we obtain a set of Ferritin mutants with increased or decreased complementarity. The extensive molecular dynamics validation of the method results confirms its efficacy, showing that this strategy represents a very promising approach in designing correct molecular interfaces.
Keywords: Computational molecular design, Protein-protein interactions, Complementarity optimization, Ferritin
1. Introduction
The majority of the cellular functions are mediated by processes that occur when two molecules recognize each other and bind [1], [2]. In particular, protein-protein non-covalent associations play an essential role in several aspects, such as biocatalysis, organism immunity or cell regulatory network construction [3], [4].
Since the complex network of energetic couplings occurring between interacting atoms ensures the stability of the molecular complex, residues involved in protein interfaces undergo additional evolutionary pressure, and therefore they are more conserved than other surface residues [5], [6]. Indeed the substitution of an amino acid residue can modify the protein structure, stability, binding affinity and function, thus potentially leading to an altered activity of the whole complex, often pathogenic [7], [8].
Because protein-protein interactions are involved in a plethora of cellular processes and consist of fine tuning of chemico-physical properties at the interfaces, in the last years many computational methods have been developed for predicting the effects of mutations on binding, relying on a wide range of techniques spanning from all-atom molecular dynamics to multiple features machine learning approaches [9], [10], [11], [12], [13]. An accurate in silico evaluation of mutations that strengthen or weaken a specific protein-protein interaction would represent a key guide in the identification of hot sites to target, preventing time and effort consuming experimental protocols. Indeed, methods for affinity optimization of interacting proteins, and even for the design of new binder molecules, have been developed [14], [15], [16], [17]. These computational methods aim at redesigning protein sequences to selectively modify the characteristics of the binding sites [18], [19]: the applications of such approaches can be extremely interesting, from antibody design to the optimization of inhibitors against pathogens [20], [21], [22], [23].
A fundamental step for devising an effective computational design of molecular interfaces is the formulation of an accurate scoring function for evaluating protein-protein complexes. This is a classic field in structural computational biology [24], and in the past years numerous scoring functions have been developed. They are generally based on combinations of several factors, such as energetical evaluation, solvation effects, statistical and knowledge-based potential, geometrical features or empirical consideration [25], [26], [27], [28], [29].
In this scenario, the Zernike polynomials represent a very promising strategy for rapid and effective evaluation of binding complementarity between molecular partners [30], [31], [32], [33]. Indeed, once a protein region of a molecule is selected, its shape and its electrostatic potential can be represented as functions and then expanded on the basis of the Zernike polynomials [34], [35], obtaining an ordered set of numerical descriptors invariant under rotation and translation.
The 3D Zernike description is widely applicable and it has been recently adopted for the characterization of protein-protein interfaces, where the authors use a machine learning approach to detect similarities between the interface region of proteins in terms of shape and physico-chemical similarity of local surface patch [36].
However, here we exploit the possibility of evaluating the shape and electrostatics complementarity between 2 molecular regions, to design protein mutants with increased binding compatibility: after representing both the binding sites in this compact formalism, the complementarity between them can be easily assessed comparing the corresponding Zernike descriptors through a distance metrics [30], [33].
Thanks to the compactness of such an approach in evaluating the complementarity between two large biomolecules, we can accurately scan a very large set of possible mutations and assess their effects in terms of molecular complementarity. Here we present a Monte Carlo (MC) approach for the optimization of the binding interface between two proteins. More in details, once the residues composing the binding site are identified, we perform extensive computational mutagenesis – substituting in each step an interacting residue with a random one – and we evaluate the mutants complementarity comparing their Zernike descriptors, accepting or rejecting the mutation according to MC cost function. This procedure can produce mutants characterized by an increased or decreased complementarity with respect to the wild type, simply inverting the sign of the cost function. Combining the compactness of Zernike evaluation of complementarity with the MC clever exploration of the possible mutants, we devised an automated computational protocol to identify the set of residue substitutions that confer the desired properties to the protein-protein interface.
To test the method we focus on the case of the complex between human transferrin receptor 1 (CD71 or hTfR1) and the Human heavy-chain Ferritin (H-Ft), whose structural details have been recently published [37].
The interaction between these two molecules is significant both in physiological and pathological conditions [38], [39]. Ferritin/CD71 complex contributes to the maintenance of cellular iron homeostasis. Ferritin works as molecular storage of iron within the cell, thus preventing its oxidative damage. The transmembrane glycoprotein CD71 regulates and mediates iron import to the cell in the form of a complex with plasma iron-binding proteins, such as ferritin or transferrin, in response to variation of intracellular iron concentration. Beyond the importance of this system in regulating iron metabolism, H-Ft/CD71 interaction is largely exploited in nanotechnology and medicine as drug delivery tools, selective for cancer cells [40], [41].
Indeed, many metastatic cancers overexpress up to a hundred times more CD71 than healthy cells because of their uncontrolled proliferation rate that requires increasing iron uptake [42], [43]. On the other hand, the hollow-cage like architecture of Ferritin can be easily assembled/disassembled by pH variation in the 24 subunits that compose it, thus providing a simple mechanism for encapsulating small molecules. Therefore, numerous Ft/CD71-based strategies have been developed for anticancer treatment, being the receptor a selective route of access to tumor cells for the internalization of engineered Fts, either chemically conjugated or filled up with cytotoxic drugs.
In this context, obtaining Ferritin mutants with increased or decreased complementarity would provide a powerful tool to fine tune the therapeutic/diagnostic cargo transport and delivery from engineered Fts to cancer cells. The physiological nanomolar affinity that controls Ft and CD71 binding might be alternatively modulated depending on cancer types and stage and the cellular context to minimize detrimental effects on healthy cells. As an example, H-Ft with optimized binding properties to CD71 would increase the Ft-nanocages uptake by damaged cells, reducing the dose of Ft-encapsulated agent injected and side effects.
In addition, CD71 is also the cell entry carrier for several human-affecting viruses [44], [45], [46], [47] and for Plasmodium vivax [48], the most common malaria parasite. Since these pathogens mostly share the ferritin epitope on CD71 [49], the optimization of the H-Ft-CD71 interface can enable the development of alternative ferritin-like therapeutic ligands capable of blocking the common epitopes on CD71with anti-viral or anti-parasite activity.
Applying our MC approach to the H-Ft binding site, we propose both a set of 10 independent mutants that maximize the Zernike complementarity (H-C-mut) and 10 mutants that minimize the complementarity (L-C-mut).
To accurately test the reliability of proposed mutants, the analysis of the dynamical behavior of the designed molecular complexes is necessary. Since in the last years molecular dynamics simulations have been widely applied to investigate dynamically the binding properties of protein-protein associations [50], [51], [52], [53], we simulated the molecular complex between CD71 and both the ferritin wild type and mutated variants, thus performing 21 extensive independent simulations and studying the interface properties of the various molecular complexes. Both an interface stability analysis and an energetic investigation of all molecular dynamics simulation underline a higher binding propensity of H-C-mut with respect to the L-C-mut.
This general and fast procedure allows an effective sampling of the very large space of possible protein mutations, obtaining protein mutants with the desired binding molecular complementarity. The strategy presented here can therefore represent an important step in the elusive task of the computational design of optimal proteins interface.
2. Results and discussion
2.1. Complementarity evaluation
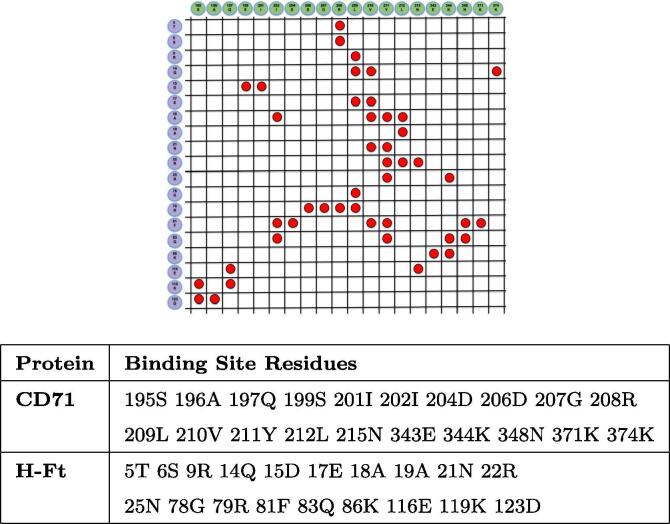
The structural details of the interaction between H-Ft and CD71 have been recently discovered with Cryo-EM technique and deposited in Protein Data Bank (PDB id:6H5I) [37]. Dealing with the experimental structure, we define the molecules binding sites as the set of residues whose atoms are closer than 5 Å to a molecular partner atom (Fig. 1).
Fig. 1.
H-Ft and CD71 residues composing the binding sites and their contacts. In the top figure, a contact between a ferritin residue (blue) and a receptor residue (green) is established if the minimum distance between their atoms is lower than 5 Å, and the corresponding square is labeled with a red circle. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Once the molecular surface and the electrostatic surface potential for both the structures have been computed, we selected only the surface points generated by the binding site residues, labeled with their value of electrostatic potential. Through the voxelization procedure, we built the 3D functions representing the geometrical shape and the electrostatic potential of the binding site. Adopting the Zernike expansion the geometrical and electrostatic properties of a molecular interface are summarized in an ordered set of numbers, independently from the region size or orientation. Indeed the patch representing functions were expanded in the Zernike polynomials basis, and the coefficients of this expansion retain the information about the form of the expanded function (See Methods for a more detailed treatment). Since the functions represent the interface properties, the Zernike coefficients are descriptive about them.
In this manner, it is possible to characterize the binding regions with such a compact formalism that we can establish a complementarity metrics simply using a distance between the descriptors of the interacting surfaces. On one hand, since the shape of two interacting surfaces is very similar, their shape Zernike descriptors exhibit a low distance. On the other hand, the positive electrostatic potential of one interface side has to match the negative potential of the other side – and vice versa – so as we can define the complementarity as the mean cross distance between positive and negative electrostatic descriptors. It is worth noting that when the complementarity is high, the distance between two surfaces is low (See Methods).
Once we evaluated the shape and electrostatic complementarity between wild type H-Ft and CD71 residues, we performed computational mutagenesis on human ferritin. We randomly selected and mutated a single residue to obtain a new interaction site characterized by different shapes and electrostatic properties.
At this stage we recomputed the Zernike descriptors of the mutated H-Ft binding sites, evaluating the new complementarity observed with the receptor. In particular, we define the shape and electrostatics complementarity balance as
| (1) |
| (2) |
where and are the shape distances between the interacting surfaces when wild type or mutated interface are considered, and similarly the electrostatic potential distances are and . These distances are formally defined in Method Section.
Since the complementarity is high when D is low, if the mutation produces a higher complementary surface while if the mutation is deleterious.
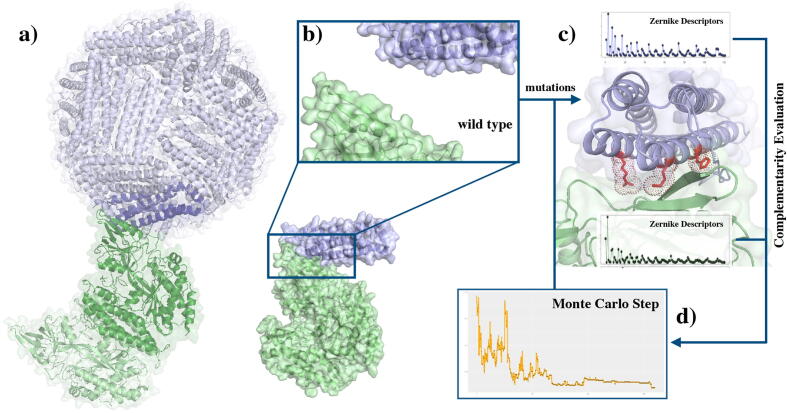
The complete procedure we adopted for the complementarity evaluation is schematically illustrated in Fig. 2.
Fig. 2.
Scheme of the Zernike complementarity evaluation upon mutation on the Ferritin Binding site. a) The experimental complex between wild type H-Ft (blue) and CD71 (green). b) The local binding surfaces (whose residues are shown in Fig. 1) are extracted from the whole protein. c) After the computational mutagenesis with a random residue, the new Ferritin binding site surface is described in Zernike formalism. The complementarity between the CD71 binding region and the mutated surface can be therefore compared with the wild type one. d) The molecular complementarity as a function of the number of Mo.nte Carlo steps. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
2.2. Monte Carlo procedure
To effectively sample the huge space of possible mutants, we iterate the procedure described in the previous section performing a MC exploration. The scope is the selection, with a limited number of residues different from wild type ferritin, of mutants that are characterized by an increased complementarity, in terms of both shape and electrostatics. In each step the mutation is accepted according to the following cost function:
| (3) |
where and are fixed parameters (See Methods for the values). M is the number of the mutations with respect to the wild type H-Ft, and the purpose is to keep M low to achieve a final mutant not too different from the wild type.
It is worth noting that the additive formulation of the cost function allows a separate and independent evaluation of each of the factors, ensuring the applicability of the protocol to a wide range of molecular interfaces and choosing in each case the aspect that is better to optimize.
In particular, each mutation is accepted with the probability [54]:
| (4) |
where is the temperature factor, that is progressively decreased to freeze the system in an energy minimum performing a simulated annealing process [55].
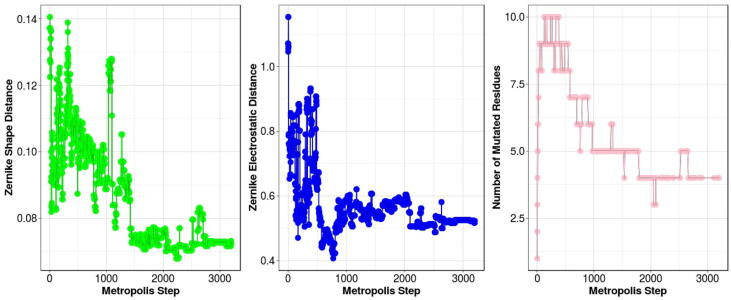
In Fig. 3 we report an example of the results obtained for such MC exploration. As illustrated, during the mutants evaluation the Zernike complementarity (distance), both shape and electrostatic case, basically increases (decreases) its value, meaning that this procedure correctly identifies mutants with improved compatibility with their molecular partner. The number of mutations is kept low, limiting the possibility that the introduced mutations affect the overall fold of the protein.
Fig. 3.
Monte Carlo Simulation Results. Left) The Complementarity between CD71 and H-Ft binding sites in terms of shape Zernike descriptors, as a function of the number of Monte Carlo steps. Center) The Complementarity between CD71 and H-Ft binding sites in terms of electrostatics Zernike descriptors, as a function of the number of Monte Carlo steps. Right) The number of mutated residues in H-Ft binding site, as a function of the number of Monte Carlo steps.
A completely analogous protocol could be applied for minimizing the complementarity, simply reversing the sign in the Eq. (3), thus creating mutants with lower binding efficiencies than the wild-type.
We performed 10 independent MC simulations to select H-C-mut and 10 independent simulations to obtain L-C-mut. We report the results in Table 1 and a more detailed analysis of the results can be found in Supplementary Materials (Supplementary Table 1).
Table 1.
High and low complementarity mutants. In each row the mutations regarding a single mutant are reported. The M represent the number of residue mutations with respect to the wild type.
 |
Interestingly, even if each MC simulation ran independently from the others, the set of H-C and the set of L-C mutants proposed are consistent with each other. Indeed, following the chemico-physical properties of the interacting residues of the CD71 apical domain, mostly composed by basic amino acids (Fig. 4, left), the H-C-mut display preferentially negatively charged and shorter side-chains with respect to the wild type: as a result, the interpenetration between the contacting regions is optimized, in compliance with the surface steric hindrance, favoring the formation of novel and/or alternative contacts (Fig. 4, upper panels). Conversely, the L-C-mut show predominantly positively charged residues and longer side-chains, hindering the H-Ft/CD71 interactions by combining charge repulsion forces to steric clashes (Fig. 4, lower panels) (See Supplementary Table 2 for a chemico-psyical analysis of the obtained mutants).
Fig. 4.
Ferritin mutants proposed after MC simulations. Top figure: Effects of H-C and L-C mutations. On the left, green ribbon representation of one CD71 monomer (pdbpdb1cxcx8 [56]). Apical domain residues involved in the interaction with H-Ft are shown as surface model colored by electrostatic (Coulomb) potential (5 kcal in red to +5 kcal in blue). On the right, examples of how one of the proposed H-C-mut (mut A, R9D/Q14N/R79G/K86H, upper panel) and one L-C-mut (mut H, D15R/A18R/E116K/D123R, lower panel) might change the interaction with CD71. H-Ft is in blue and CD71 is in green ribbon representation (pbd 6h5i, [37]. Mutations, introduced by simply mutating the corresponding H-Ft wild type residues by COOT [57] are represented in yellow sticks, while the related wild type amino acids are in white. Residues involved in interactions are represented as sticks and labelled. Black boxes label mutations. Secondary structural elements are labelled. In both panels, arrows represent all possible H-Ft mut/CD71 contacts: dashed and dotted arrows indicate electrostatic and hydrophobic interactions, respectively. Blue arrows are contacts maintained by mutants; green arrows represent contacts that mut A might form (upper panels); red arrows indicate repulsive interactions and clashes that mut H might cause (lower panels). We show the effect of H-C-mut A mutations (upper panels) and the effect of L-C-mut H mutations. (lower panels). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
In addition, it is of interest to notice that multiple mutations in a single mutant do not work as isolated perturbations, but cooperate to guarantee the desired effect. We examined in some detail the case of H-C-mut A and the case of L-C H (see Fig. 4). In the first one, the substitution of long and positively charged arginines with glycine in position 79 and aspartate in position 9 can cause several effect: i) might provide room for R208 of CD71 that could rearrange establishing electrostatic interaction with D9; ii) might favor a closer positioning of L209 of CD71 to the N-terminus of H-Ft contacting Y12; iii) could allow R43 from the flank monomer of H-Ft to establish electrostatic interaction with the backbone carbonyl of G207 and of N206 of CD71. Moreover Q14N mutation also promotes protein-protein interaction thanks to the one unit reduced steric hindrance of the side chain, yet preserving the electrostatic contact with K374 of CD71. Similarly, K86H maintains electrostatic interaction with E343, but its aromatic nature might also allow the formation of a -cation interaction with K344. Conversely, in the case of L-C-mut H all substitutions aim at extending the arm of the side chains of residues at positions 15, 18, 116 and 123 mostly involved in electrostatic contacts with the receptor thus hindering protein-protein binding by charge repulsion effects (such as, the contact between A18R and K374 on CD71) and steric clashes with CD71 (as in the case of A18R that clashes the strand of CD71 and D123R that bumps the loop of CD71). Moreover, some mutations help others to keep the distance from the receptor: for example, the contact that D123R might form with the -carbonyl group of Q197 of CD71 would strengthen the charge repulsion effect of E116K since it forces the amide unit of Q197 to be oriented with the -amino group exposed to the positive charge of K at position 116. In conclusion, the substantial homogeneity in the results of independent simulations, considering H-C and L-C mutants separately, testifies that this procedure falls in a stable energy minimum, proving the method reliability.
2.3. Computational test of proposed mutants
The Ferritin mutants obtained with the MC protocols, both for the H-C-mut and L-C-mut case, have been computationally tested via extensive molecular dynamics simulations. Indeed, we simulated the different binding behavior between CD71 and the mutants in comparison with the wild type complex to probe the efficacy of our results.
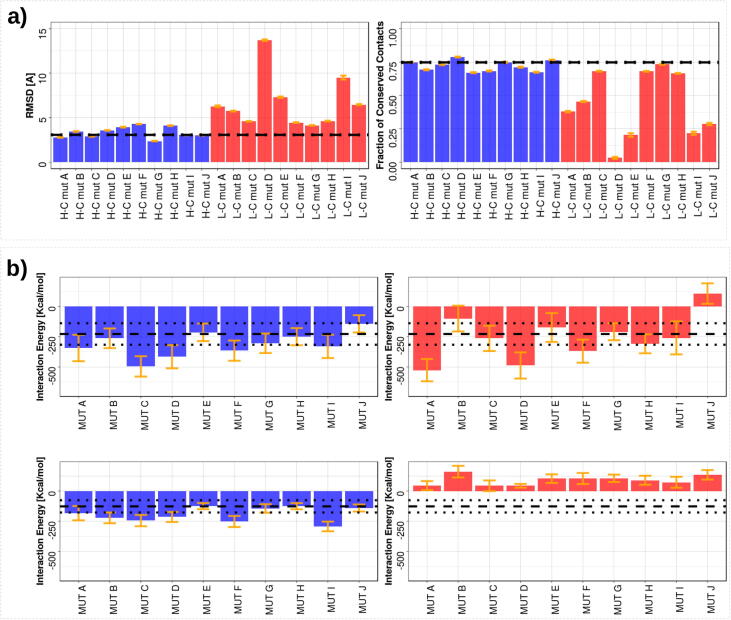
We report the analysis of molecular dynamics simulation in Fig. 5. As it emerges from these analyses, the stability of the binding is high when H-C-mut are considered, while the simulations of CD71 in complex with L-C-mut exhibit a remarkable unsteadiness.
Fig. 5.
Molecular dynamics simulation of the CD71/H-Ft complex. The results in blue and in red are for high and low complementarity mutants, respectively. The mean values presented here are obtained disregarding the initial 25 ns of equilibration. a) The stability analysis of the complexes. In the left panel the mean value of RMSD, with respect to the initial conformation. In the right panel the mean percentage of residue-residue interface contacts conserved with respect to the initial conformation. The black dotted lines represent the mean values observed when the wild type interface is simulated. b) The energetic analysis of the interfaces. The values reported here are averaged on all the MD equilibrium frames. In the top row, we report the mean energy of non-covalent interactions (Coulomb and van der Waals terms) between all the atoms of the CD71 and H-Ft. In the bottom row, we focus on the mean energy exchanged at the interface, i.e., considering only the atoms belonging to residues defined in Fig. 1. The orange line represents one standard deviation interval centered on the mean. The black dotted lines represent the mean and standard deviation of the. wild type case. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
In particular, for each MD simulation, we report the Root Mean Square Deviation (RMSD) with respect to the initial configuration and the percentage of contact conserved along with the simulation, where contact between 2 residues exists if any 2 atoms of these residues are closer than 5 A. The bindings between H-C-mut and CD-71 are stable, since the values of RMSD and conserved contacts observed are very similar to the wild type case. Conversely, the simulation of the complexes with L-C-mut typically has very high values of RMSD, and very few contacts (if any) are conserved along with dynamics.
Also, we perform an analysis of the energetic interactions occurring between ferritin and receptor, to explain the different behavior of the mutant species. Indeed, we calculated for each frame the non-covalent energies (Coulomb and Van der Walls terms) exchanged through the molecular interface between any atoms of the 2 molecules. We adopted the same formalism as we did in [58], [59].
In Fig. 5, we show the mean energies of the interactions between the two molecules.
As it emerges from RMSD and conserved contacts analysis, since the undergone mutations make L-C-mut unsuitable for binding CD71 interaction site, in MD they move to find a different and more favourable conformation (see Supplementary Fig. 2 for a more detailed analysis). Even if in most cases the interaction energies between all ferritin and receptor residues are comparable, as expected H-C-mut interact with CD71 having, on average, more favorable energy than their counterparts.
Importantly, if the analysis is focused only on the binding site (residues identified in Fig. 1), the difference becomes even clearer. The H-C-mut are all characterized by favorable energies, at least of the same order than the wild type complex, while all the L-C-mut exhibit unfavorable energies. This result confirms that in L-C-mut the original binding site is completely disrupted, and it is not able anymore to bind CD71, while H-C-mut energetically conserve (and in some cases improve) their compatibility with CD71 interaction site.
All these results highlight the reliability of the MC protocol because the ferritin H-C-mut are designed to bind the CD71 binding site (with an increased complementarity with respect to the wild type), while the Ferritin L-C-mut are designed to minimize the possibility of interaction with the CD71 epitope.
3. Discussions
The importance of protein-protein interactions can hardly be overestimated since they are involved in the majority of the cellular biochemical pathway. The right physiological form of binding between proteins is guaranteed by a large set of concomitant factors (such as pH, cofactors, enzymes, …), but surely it is necessary to have a favorable energetic interaction between the interface residues. For these reasons, one of the most challenging tasks in computational biology is the design of specific protein-protein interactions with desired properties.
In a typical protein-protein interaction dozens of different residues are involved, on both sides of the interface, and the network of their interactions can not be easily analyzed. This notwithstanding, in many cases even the substitution of a single amino acid is enough to disrupt an association, and therefore many pathological conditions are associated with a single mutation in a binding region [60].
Dealing with all this complexity, in the last decades, much effort has been addressed in the development of computational methods for the prediction of mutation effects in a protein-protein interface and, more ambitiously, for the design of protein mutants able to improve (or to decrease) the affinity with its molecular partner.
Unfortunately, the protein-protein interfaces are composed by many residues, each of which can in principle undergo a mutation in one of the 19 different ones: it becomes evident that the space of possible protein mutants is very large and the development of an efficient method to explore a large number of possibilities is essential. For this reason, experimental blind site-directed mutagenesis may require a significant amount of effort and time to scan.
Here we proposed a general and completely automated method, based on the geometric and electrostatic complementarity and a MC approach, for the identification of protein mutants that optimize the compatibility with the molecular partner. Thanks to the speed of computational mutagenesis and Zernike characterization, we could explore a large portion of the possible mutants space, reaching an optimal solution in terms of shape and electrostatic complementarity (and with a limited number of mutations with respect to the wild type).
We applied this protocol to the relevant case of the interaction between Ferritin and Transferrin Receptor, obtaining Ferritin mutants characterized selectively by increased or decreased complementarity with Transferrin Receptor. These results might have important bioengineering implications in developing alternative ferritin-based agents.
Simulating these complexes in molecular dynamics we demonstrate that high complementarity mutants exhibit higher partner compatibility than their lower complementarity counterparts.
The method demonstrated capability in testing a very large set of possible mutations, identifying the correct set of mutations able to increase or decrease the molecular complementarity in a limited amount of time, represent a new and very promising strategy for the computational design of protein-protein interfaces. The possible applications of such an approach are numerous, from antibody design to the optimization of inhibitors against pathogens.
4. Materials and methods
4.1. Surface construction
Starting from the experimental structure, the computational mutagenesis has been performed using the SCWRL4 software [61].
In each step, atomic charges and radii were assigned using PDB2PQR [62]. Solvent Accessible Surface and Electrostatic surface potential are computed using Bluues software (with flags -srf and -srfpot) [63]. Bluues uses a generalized Born (GB) models in order to obtain the surface potential. We adopted Standard parameters: inner dielectric constant 1.0, outer dielectric constant 78.54, temperature 298.15 K, ionic strength 0.150 M. The surface points generated by each residue were associated with the mean electrostatic potential of the examined residue. For protein structure manipulation we used ‘geometry’ [64] and ‘Bio3D’ [65] packages available in R.
4.2. The Zernike expansion
Once the molecular surface is built, through the voxelization procedure, the surface shape and electrostatic characterization can be represented as 3D functions [66]. In particular, the set of selected molecular surface points was scaled to the unit sphere and placed into a 3D grid of dimension . Voxelization was performed differently for shape and electrostatics. In shape voxelization, each voxel was set to 1 if the center of the voxel was closer than 1.7 to any surface point, 0 otherwise. In electrostatic voxelization, each voxel is labeled with the mean electrostatic value of the points inside it. In this way we built the 3D functions associating the x,y,z value to the 1-0 shape representation or to the mean electrostatic potentials. The Zernike descriptors are obtained by expanding the functions in the Zernike Polynomials basis, summarizing the functions as an ordered set of Zernike descriptors.
In order to quantitatively describe a molecular surface region, we use the Zernike polynomials expansion and the related moments. Moment-based representations are a class of mathematical descriptors, originally utilized for 2D pattern recognition and then extended to 3D [67], [34], [35].
A function representing a surface property , defined in the unit sphere, can be written as:
| (5) |
where the are the 3D Zernike polynomials, and the coefficients are the Zernike moments.
The Zernike polynomials are defined as:
| (6) |
where the Y functions are spherical harmonics of corresponding indices depending on angular coordinates while R, depending only on the radius r, is given by:
| (7) |
where N is a normalization factor.
The accuracy of the description is modulated selecting the order N at which the sum over n is truncated. In this work, we use N = 20, corresponding to 121 coefficients for each function.
Indeed, the 3D Zernike Moments of a function are defined as:
| (8) |
where is the polynomial complex conjugate.
In order to obtain the descriptors, invariant under translation and rotation, we compute the norm (the sum over the index m) of the Zernike Moments. The 3D Zernike Descriptors (3DZD) are defined as:
| (9) |
A more complete description of the Zernike formalism can be found here [68], [69]. The calculation of the Zernike descriptors is made using the python code described in Ref. [70].
4.3. Complementarity metrics of Zernike descriptors
We used the manhattan distance for the comparisons between Zernike descriptors.
If T and V are 2 vectors of 121 components, the manhattan distance between them is:
| (10) |
Given 2 protein regions, A and B, when we analyze the complementarity between their Zernike descriptors we have:
| (11) |
| (12) |
where are, respectively, the shape, the electrostatic positive potential, and the electrostatic negative potential Zernike descriptors.
As said, the shape of 2 fitting surfaces is similar and therefore the distance between the Zernike descriptors should be small. On the other hand, in order to achieve a high electrostatic complementarity, the Zernike descriptors describing the positive potential of one patch have to be similar to the negative potential ones of the interacting patch (and vice versa).
High complementarity is achieved when the distance between the corresponding descriptors are small.
4.4. Monte Carlo details
As described in Monte Carlo Procedure section, we perform 2 different Monte Carlo simulation types, one to increase and one to decrease the complementarity.
When we deal with the complementarity increase, the potential energy function is:
| (13) |
where and . M is the number of the mutations with respect to the wild type. The subscripts new and old refer to the new and the last accepted mutation respectively. Each mutation is accepted with the probability:
| (14) |
where is the temperature factor. values start from 75 and go to 600 with a jump of 75: each of 8 value is maintained for 400 steps for a total of 3200 steps.
When we deal with complementairty loss, the potential form is:
| (15) |
and the acceptation probability is Eq. (14).
4.5. Molecular simulation
Starting from the cryo-EM structure (PDB id:6h5i), we simulate the wild type complex between H-Ft and CD71, and then CD71 in complex with both 10 high complementarity and 10 low complementarity mutants. For each of 21 complexes we minimized using the steepest descent algorithm. We thus perform sequentially a NVT and a NPT 100 ps long equilibration dynamics. Lastly we run 100-ns long simulation using gromacs [71] with CHARMM force field [72]. We adopted the Verlet cut-off scheme and the particle-mesh Ewald algorithm. Each simulation has been carried out with the interacting chain, i.e., one chain for CD71 and the unit H-Ft dimer.
4.6. Software availability
The main software, performing the complete protocol for surface optimization is available upon request. An amino acid substitution with the relative Zernike calculation requires tens of second: the time needed for the complete protocol application depends on the system size and on the selected number of steps.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
CRediT authorship contribution statement
Lorenzo Di Rienzo: Conceptualization, Methodology, Software, Investigation. Edoardo Milanetti: Conceptualization, Methodology, Software. Claudia Testi: Conceptualization, Investigation. Linda Celeste Montemiglio: Conceptualization, Investigation. Paola Baiocco: Conceptualization. Alberto Boffi: Conceptualization. Giancarlo Ruocco: Conceptualization, Methodology, Supervision.
Footnotes
Supplementary data associated with this article can be found, in the online version, athttps://doi.org/10.1016/j.csbj.2020.09.020.
Supplementary data
The following are the Supplementary data to this article:
References
- 1.Jones S., Thornton J.M. Principles of protein-protein interactions. Proc Natl Acad Sci. 1996;93(1):13–20. doi: 10.1073/pnas.93.1.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gromiha M.M., Yugandhar K., Jemimah S. Protein–protein interactions: scoring schemes and binding affinity. Curr Opin Struct Biol. 2017;44:31–38. doi: 10.1016/j.sbi.2016.10.016. [DOI] [PubMed] [Google Scholar]
- 3.Gavin A.-C., Bösche M., Krause R., Grandi P., Marzioch M., Bauer A., Schultz J., Rick J.M., Michon A.-M., Cruciat C.-M. Functional organization of the yeast proteome by systematic analysis of protein complexes. Nature. 2002;415(6868):141–147. doi: 10.1038/415141a. [DOI] [PubMed] [Google Scholar]
- 4.Han J.-D.J., Bertin N., Hao T., Goldberg D.S., Berriz G.F., Zhang L.V., Dupuy D., Walhout A.J., Cusick M.E., Roth F.P. Evidence for dynamically organized modularity in the yeast protein–protein interaction network. Nature. 2004;430(6995):88–93. doi: 10.1038/nature02555. [DOI] [PubMed] [Google Scholar]
- 5.Chelliah V., Chen L., Blundell T.L., Lovell S.C. Distinguishing structural and functional restraints in evolution in order to identify interaction sites. J Mol Biol. 2004;342(5):1487–1504. doi: 10.1016/j.jmb.2004.08.022. [DOI] [PubMed] [Google Scholar]
- 6.Innis C.A., Shi J., Blundell T.L. Evolutionary trace analysis of tgf-β) and related growth factors: implications for site-directed mutagenesis. Protein Eng. 2000;13(12):839–847. doi: 10.1093/protein/13.12.839. [DOI] [PubMed] [Google Scholar]
- 7.Forbes S.A., Beare D., Gunasekaran P., Leung K., Bindal N., Boutselakis H., Ding M., Bamford S., Cole C., Ward S. Cosmic: exploring the world’s knowledge of somatic mutations in human cancer. Nucl Acids Res. 2015;43(D1):D805–D811. doi: 10.1093/nar/gku1075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Landrum M.J., Lee J.M., Benson M., Brown G., Chao C., Chitipiralla S., Gu B., Hart J., Hoffman D., Hoover J. Clinvar: public archive of interpretations of clinically relevant variants. Nucl Acids Res. 2016;44(D1):D862–D868. doi: 10.1093/nar/gkv1222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Moretti R., Fleishman S.J., Agius R., Torchala M., Bates P.A., Kastritis P.L., Rodrigues J.P., Trellet M., Bonvin A.M., Cui M. Community-wide evaluation of methods for predicting the effect of mutations on protein–protein interactions. Proteins: Struct Funct Bioinf. 2013;81(11):1980–1987. doi: 10.1002/prot.24356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Brender J.R., Zhang Y. Predicting the effect of mutations on protein-protein binding interactions through structure-based interface profiles. PLoS Comput Biol. 2015;11(10) doi: 10.1371/journal.pcbi.1004494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Vangone A., Bonvin A.M. Contacts-based prediction of binding affinity in protein–protein complexes. elife. 2015;4 doi: 10.7554/eLife.07454. e07454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dehouck Y., Kwasigroch J.M., Rooman M., Gilis D. Beatmusic: prediction of changes in protein–protein binding affinity on mutations. Nucl Acids Res. 2013;41(W1):W333–W339. doi: 10.1093/nar/gkt450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kamisetty H., Ghosh B., Langmead C.J., Bailey-Kellogg C. Learning sequence determinants of protein: protein interaction specificity with sparse graphical models. J Comput Biol. 2015;22(6):474–486. doi: 10.1089/cmb.2014.0289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fleishman S.J., Whitehead T.A., Ekiert D.C., Dreyfus C., Corn J.E., Strauch E.-M., Wilson I.A., Baker D. Computational design of proteins targeting the conserved stem region of influenza hemagglutinin. Science. 2011;332(6031):816–821. doi: 10.1126/science.1202617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jiang L., Althoff E.A., Clemente F.R., Doyle L., Röthlisberger D., Zanghellini A., Gallaher J.L., Betker J.L., Tanaka F., Barbas C.F. De novo computational design of retro-aldol enzymes. Science. 2008;319(5868):1387–1391. doi: 10.1126/science.1152692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Obarska-Kosinska A., Iacoangeli A., Lepore R., Tramontano A. Pepcomposer: computational design of peptides binding to a given protein surface. Nucl Acids Res. 2016;44(W1):W522–W528. doi: 10.1093/nar/gkw366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Liu Y., Kuhlman B. Rosettadesign server for protein design. Nucl Acids Res. 2006;34(suppl 2):W235–W238. doi: 10.1093/nar/gkl163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kastritis P.L., Bonvin A.M. On the binding affinity of macromolecular interactions: daring to ask why proteins interact. J R Soc Interface. 2013;10(79):20120835. doi: 10.1098/rsif.2012.0835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Schreiber G., Fleishman S.J. Computational design of protein–protein interactions. Curr Opin Struct Biol. 2013;23(6):903–910. doi: 10.1016/j.sbi.2013.08.003. [DOI] [PubMed] [Google Scholar]
- 20.Kuroda D., Shirai H., Jacobson M.P., Nakamura H. Computer-aided antibody design. Protein Eng Design Select. 2012;25(10):507–522. doi: 10.1093/protein/gzs024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Whitehead T.A., Chevalier A., Song Y., Dreyfus C., Fleishman S.J., De Mattos C., Myers C.A., Kamisetty H., Blair P., Wilson I.A. Optimization of affinity, specificity and function of designed influenza inhibitors using deep sequencing. Nat Biotechnol. 2012;30(6):543. doi: 10.1038/nbt.2214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Azoitei M.L., Ban Y.-E.A., Julien J.-P., Bryson S., Schroeter A., Kalyuzhniy O., Porter J.R., Adachi Y., Baker D., Pai E.F. Computational design of high-affinity epitope scaffolds by backbone grafting of a linear epitope. J Mol Biol. 2012;415(1):175–192. doi: 10.1016/j.jmb.2011.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Choi Y., Furlon J.M., Amos R.B., Griswold K.E., Bailey-Kellogg C. Disruppi: structure-based computational redesign algorithm for protein binding disruption. Bioinformatics. 2018;34(13):i245–i253. doi: 10.1093/bioinformatics/bty274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kuntz I.D., Blaney J.M., Oatley S.J., Langridge R., Ferrin T.E. A geometric approach to macromolecule-ligand interactions. J Mol Biol. 1982;161(2):269–288. doi: 10.1016/0022-2836(82)90153-x. [DOI] [PubMed] [Google Scholar]
- 25.Kozakov D., Hall D.R., Xia B., Porter K.A., Padhorny D., Yueh C., Beglov D., Vajda S. The cluspro web server for protein–protein docking. Nat Protoc. 2017;12(2):255. doi: 10.1038/nprot.2016.169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Moreira I.S., Martins J.M., Coimbra J.T., Ramos M.J., Fernandes P.A. A new scoring function for protein–protein docking that identifies native structures with unprecedented accuracy. Phys Chem Chem Phys. 2015;17(4):2378–2387. doi: 10.1039/c4cp04688a. [DOI] [PubMed] [Google Scholar]
- 27.Krüger D.M., Garzón J.I., Chacón P., Gohlke H. Drugscore ppi knowledge-based potentials used as scoring and objective function in protein-protein docking. PloS One. 2014;9(2) doi: 10.1371/journal.pone.0089466. e89466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Schneidman-Duhovny D., Inbar Y., Nussinov R., Wolfson H.J. Patchdock and symmdock: servers for rigid and symmetric docking. Nucl Acids Res. 2005;33(suppl 2):W363–W367. doi: 10.1093/nar/gki481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mezei M. Rescore protein–protein docked ensembles with an interface contact statistics. Proteins: Struct Funct Bioinf. 2017;85(2):235–241. doi: 10.1002/prot.25209. [DOI] [PubMed] [Google Scholar]
- 30.Venkatraman V., Yang Y.D., Sael L., Kihara D. Protein-protein docking using region-based 3d zernike descriptors. BMC Bioinf. 2009;10(1):407. doi: 10.1186/1471-2105-10-407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kihara D., Sael L., Chikhi R., Esquivel-Rodriguez J. Molecular surface representation using 3d zernike descriptors for protein shape comparison and docking. Curr Protein Peptide Sci. 2011;12(6):520–530. doi: 10.2174/138920311796957612. [DOI] [PubMed] [Google Scholar]
- 32.Alba J., Rienzo L.D., Milanetti E., Acuto O., D’Abramo M. Molecular dynamics simulations reveal canonical conformations in different pmhc/tcr interactions. Cells. 2020;9(4):942. doi: 10.3390/cells9040942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Di Rienzo L, Milanetti E, Alba J, D’Abramo M. Quantitative characterization of binding pockets and binding complementarity by means of zernike descriptors. J Chem Inf Model. [DOI] [PMC free article] [PubMed]
- 34.Canterakis N. 3d zernike moments and zernike affine invariants for 3d image analysis and recognition. In In 11th Scandinavian Conf. on Image Analysis, Citeseer; 1999.
- 35.Novotni M., Klein R. Shape retrieval using 3d zernike descriptors. Computer-Aided Design. 2004;36(11):1047–1062. [Google Scholar]
- 36.Daberdaku S., Ferrari C. Exploring the potential of 3d zernike descriptors and svm for protein–protein interface prediction. BMC Bioinf. 2018;19(1):35. doi: 10.1186/s12859-018-2043-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Montemiglio L.C., Testi C., Ceci P., Falvo E., Pitea M., Savino C., Arcovito A., Peruzzi G., Baiocco P., Mancia F. Cryo-em structure of the human ferritin–transferrin receptor 1 complex. Nat Commun. 2019;10(1):1–8. doi: 10.1038/s41467-019-09098-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Greene C.J., Attwood K., Sharma N.J., Gross K.W., Smith G.J., Xu B., Kauffman E.C. Transferrin receptor 1 upregulation in primary tumor and downregulation in benign kidney is associated with progression and mortality in renal cell carcinoma patients. Oncotarget. 2017;8(63) doi: 10.18632/oncotarget.22323. 107052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Rosager A.M., Sørensen M.D., Dahlrot R.H., Hansen S., Schonberg D.L., Rich J.N., Lathia J.D., Kristensen B.W. Transferrin receptor-1 and ferritin heavy and light chains in astrocytic brain tumors: Expression and prognostic value. PLoS One. 2017;12(8) doi: 10.1371/journal.pone.0182954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Truffi M., Fiandra L., Sorrentino L., Monieri M., Corsi F., Mazzucchelli S. Ferritin nanocages: a biological platform for drug delivery, imaging and theranostics in cancer. Pharmacol Res. 2016;107:57–65. doi: 10.1016/j.phrs.2016.03.002. [DOI] [PubMed] [Google Scholar]
- 41.Calisti L., Trabuco M.C., Boffi A., Testi C., Montemiglio L.C., des Georges A., Benni I., Ilari A., Taciak B., Białasek M. Engineered ferritin for lanthanide binding. PloS one. 2018;13(8) doi: 10.1371/journal.pone.0201859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Daniels-Wells TR, Penichet ML. Transferrin receptor 1: a target for antibody-mediated cancer therapy; 2016. [DOI] [PubMed]
- 43.Falvo E., Tremante E., Arcovito A., Papi M., Elad N., Boffi A., Morea V., Conti G., Toffoli G., Fracasso G. Improved doxorubicin encapsulation and pharmacokinetics of ferritin–fusion protein nanocarriers bearing proline, serine, and alanine elements. Biomacromolecules. 2016;17(2):514–522. doi: 10.1021/acs.biomac.5b01446. [DOI] [PubMed] [Google Scholar]
- 44.Abraham J., Corbett K.D., Farzan M., Choe H., Harrison S.C. Structural basis for receptor recognition by new world hemorrhagic fever arenaviruses. Nat Struct Mol Biol. 2010;17(4):438. doi: 10.1038/nsmb.1772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Radoshitzky S.R., Abraham J., Spiropoulou C.F., Kuhn J.H., Nguyen D., Li W., Nagel J., Schmidt P.J., Nunberg J.H., Andrews N.C. Transferrin receptor 1 is a cellular receptor for new world haemorrhagic fever arenaviruses. Nature. 2007;446(7131):92–96. doi: 10.1038/nature05539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Martin D.N., Uprichard S.L. Identification of transferrin receptor 1 as a hepatitis c virus entry factor. Proc Natl Acad Sci. 2013;110(26):10777–10782. doi: 10.1073/pnas.1301764110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Radoshitzky S.R., Longobardi L.E., Kuhn J.H., Retterer C., Dong L., Clester J.C., Kota K., Carra J., Bavari S. Machupo virus glycoprotein determinants for human transferrin receptor 1 binding and cell entry. PloS one. 2011;6(7) doi: 10.1371/journal.pone.0021398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Gruszczyk J., Huang R.K., Chan L.-J., Menant S., Hong C., Murphy J.M., Mok Y.-F., Griffin M.D., Pearson R.D., Wong W. Cryo-em structure of an essential plasmodium vivax invasion complex. Nature. 2018;559(7712):135–139. doi: 10.1038/s41586-018-0249-1. [DOI] [PubMed] [Google Scholar]
- 49.Testi C., Boffi A., Montemiglio L.C. Structural analysis of the transferrin receptor multifaceted ligand (s) interface. Biophys Chem. 2019;254 doi: 10.1016/j.bpc.2019.106242. 106242. [DOI] [PubMed] [Google Scholar]
- 50.Deng Y., Roux B. Computations of standard binding free energies with molecular dynamics simulations. J Phys Chem B. 2009;113(8):2234–2246. doi: 10.1021/jp807701h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Hou T., Wang J., Li Y., Wang W. Assessing the performance of the mm/pbsa and mm/gbsa methods. 1. the accuracy of binding free energy calculations based on molecular dynamics simulations. J Chem Inf Model. 2011;51(1):69–82. doi: 10.1021/ci100275a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Proctor E.A., Yin S., Tropsha A., Dokholyan N.V. Discrete molecular dynamics distinguishes nativelike binding poses from decoys in difficult targets. Biophys J. 2012;102(1):144–151. doi: 10.1016/j.bpj.2011.11.4008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Mermelstein D.J., Lin C., Nelson G., Kretsch R., McCammon J.A., Walker R.C. Fast and flexible gpu accelerated binding free energy calculations within the amber molecular dynamics package. J Comput Chem. 2018;39(19):1354–1358. doi: 10.1002/jcc.25187. [DOI] [PubMed] [Google Scholar]
- 54.Metropolis N., Rosenbluth A.W., Rosenbluth M.N., Teller A.H., Teller E. Equation of state calculations by fast computing machines. J Chem Phys. 1953;21(6):1087–1092. [Google Scholar]
- 55.Kirkpatrick S., Gelatt C.D., Vecchi M.P. Optimization by simulated annealing. Science. 1983;220(4598):671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- 56.Lawrence C.M., Ray S., Babyonyshev M., Galluser R., Borhani D.W., Harrison S.C. Crystal structure of the ectodomain of human transferrin receptor. Science. 1999;286(5440):779–782. doi: 10.1126/science.286.5440.779. [DOI] [PubMed] [Google Scholar]
- 57.Emsley P., Cowtan K. Coot: model-building tools for molecular graphics. Acta Crystallogr Sect D. 2004;60(12):2126–2132. doi: 10.1107/S0907444904019158. [DOI] [PubMed] [Google Scholar]
- 58.Miotto M., Olimpieri P.P., Di Rienzo L., Ambrosetti F., Corsi P., Lepore R., Tartaglia G.G., Milanetti E. Insights on protein thermal stability: a graph representation of molecular interactions. Bioinformatics. 2019;35(15):2569–2577. doi: 10.1093/bioinformatics/bty1011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Miotto M., Di Rienzo L., Corsi P., Ruocco G., Raimondo D., Milanetti E. Simulated epidemics in 3d protein structures to detect functional properties. J Chem Inf Model. 2020;60(3):1884–1891. doi: 10.1021/acs.jcim.9b01027. [DOI] [PubMed] [Google Scholar]
- 60.Jubb H.C., Pandurangan A.P., Turner M.A., Ochoa-Montaño B., Blundell T.L., Ascher D.B. Mutations at protein-protein interfaces: small changes over big surfaces have large impacts on human health. Prog Biophys Mol Biol. 2017;128:3–13. doi: 10.1016/j.pbiomolbio.2016.10.002. [DOI] [PubMed] [Google Scholar]
- 61.Krivov G.G., Shapovalov M.V., Dunbrack R.L., Jr Improved prediction of protein side-chain conformations with scwrl4. Proteins: Struct Funct Bioinf. 2009;77(4):778–795. doi: 10.1002/prot.22488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Dolinsky T.J., Nielsen J.E., McCammon J.A., Baker N.A. Pdb2pqr: an automated pipeline for the setup of poisson–boltzmann electrostatics calculations. Nucl Acids Res. 2004;32(suppl 2):W665–W667. doi: 10.1093/nar/gkh381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Fogolari F., Corazza A., Yarra V., Jalaru A., Viglino P., Esposito G. Bluues: a program for the analysis of the electrostatic properties of proteins based on generalized born radii. BMC Bioinf. 2012;13(4):S18. doi: 10.1186/1471-2105-13-S4-S18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Habel K, Grasman R, Gramacy RB, Mozharovskyi P, Sterratt DC. geometry: mesh generation and surface tessellation, r package version 0.4.1; 2019.https://CRAN.R-project.org/package=geometry.
- 65.Grant B.J., Rodrigues A.P., ElSawy K.M., McCammon J.A., Caves L.S. Bio3d: an r package for the comparative analysis of protein structures. Bioinformatics. 2006;22(21):2695–2696. doi: 10.1093/bioinformatics/btl461. [DOI] [PubMed] [Google Scholar]
- 66.Di Rienzo L., Milanetti E., Lepore R., Olimpieri P.P., Tramontano A. Superposition-free comparison and clustering of antibody binding sites: implications for the prediction of the nature of their antigen. Scientific Rep. 2017;7(1):1–10. doi: 10.1038/srep45053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Hu M.-K. Visual pattern recognition by moment invariants. IRE Trans Inf Theory. 1962;8(2):179–187. [Google Scholar]
- 68.Sit A., Mitchell J.C., Phillips G.N., Wright S.J. An extension of 3d zernike moments for shape description and retrieval of maps defined in rectangular solids. Comput Math Biophys. 2013;1:75–89. [Google Scholar]
- 69.Venkatraman V., Sael L., Kihara D. Potential for protein surface shape analysis using spherical harmonics and 3d zernike descriptors. Cell Biochem Biophys. 2009;54(1–3):23–32. doi: 10.1007/s12013-009-9051-x. [DOI] [PubMed] [Google Scholar]
- 70.Grandison S., Roberts C., Morris R.J. The application of 3d zernike moments for the description of ”model-free” molecular structure, functional motion, and structural reliability. J Comput Biol. 2009;16(3):487–500. doi: 10.1089/cmb.2008.0083. [DOI] [PubMed] [Google Scholar]
- 71.Abraham M.J., Murtola T., Schulz R., Páll S., Smith J.C., Hess B., Lindahl E. Gromacs: high performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX. 2015;1:19–25. [Google Scholar]
- 72.Bjelkmar P., Larsson P., Cuendet M.A., Hess B., Lindahl E. Implementation of the charmm force field in gromacs: analysis of protein stability effects from correction maps, virtual interaction sites, and water models. J Chem Theory Comput. 2010;6(2):459–466. doi: 10.1021/ct900549r. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.