Development and validation of QSPR models for corrosion inhibition of carbon steel by some pyridazine derivatives in acidic medium

Abstract

Statistical modeling of the corrosion inhibition process by twenty-one pyridazine derivatives for mild steel in acidic medium was investigated by the quantitative structure property relationship (QSPR) approach. This modeling was established by the correlation between the corrosion inhibition efficiency (IE %) and a number of the electronic and structural properties of these inhibitors such as: the E_HOMO (highest occupied molecular orbital energy), the E_LUMO (lowest unoccupied molecular orbital energy), the energy gap (E_L-H), the dipole moment (μ), the hardness (η), the softness (σ), the absolute electronegativity (χ), the ionization potential (IP), the electron affinity (EA), the fraction of electrons transferred (ΔN), the electrophilicity index ω the molecular volume (V_m), the logarithm of the partition coefficient (Log P), and the molecular mass (M), in addition to the inhibitor concentration (C_i). The structure electronic properties was calculated by the use of the density functional theory method (DFT), at B3LYP/6-31G (d, p) level of theory and the analysis of dimensionality and redundancy as well as the test of collinearity between descriptors are carried out using principal component analysis (PCA). Whereas, the correlation between EI % and molecular structure is performed through the development of tree mathematical models, based-QSPR approaches: the partial least squares regression (PLS), the principal component regression (PCR) and the artificial neural networks (ANN). Indeed, the statistical quantitative results revealed that PCR and ANN were the most relevant and predictive models in comparison with the PLS model. This pertinence was demonstrated by using leave one-out cross-validation as an efficient method for testing the internal stability and predictive capability of said models with a high cross-validated determination coefficient R²_cv= 0.92 and predicted determination coefficient R²_pred= 0.92 and R²_pred= 0.90 for PCR and ANN respectively; in addition to an extrapolation test set as an external validation with a significant external coefficient of determination: R²_test= 0.94 and R²_test= 0.92, for the two correspondingly models.

Materials chemistry, Theoretical chemistry, Corrosion inhibition; DFT calculations; Principal components analysis; Partial least squares regression; Principal component regression; Artificial neural networks; Cross validation

1. Introduction

The corrosion of the metal compounds and alloys as well as the deterioration of its characteristics is a major industrial problem. It is considered a worrying source of pollution for the environment; especially, in carbon steel industry, where acids are being used to pickling, descaling and cleaning. Therefore, scientists are encouraged to look for solutions to protect these materials and reduce their environmental impact [1, 2, 3, 4, 5, 6, 7]. For this reason, the use of corrosion inhibitors to control the metal dissolution and to limit the corrosion rate is one of the common techniques [8, 9, 10, 11, 12, 13, 14]. Indeed, the use of corrosion inhibitors differs according to the nature of the corrosive environment. For example, in acidic mediums, organic molecules remain the most common class of inhibitors to remedy this problem. The action and effectiveness of these compounds depends, to a large extent, on their structural and electronic properties. They generally have chemical structures containing multiple, double and triple bonds, as well as heteroatoms such as nitrogen, oxygen, sulphur or phosphorus embedded in aromatic rings, which give them better adsorption on the surface of the material, and therefore high reactivity [15, 16, 17, 18]. In this optic, previous studies suggest that pyridazine derivatives are considered as a potential class of corrosion inhibitors in electrolytic media, and especially, in acidic solutions [19, 20, 21, 22, 23]. In fact, the choice of this class of molecules for inhibiting corrosion applications is reported by several authors, such as, Chetouani et al. [24], Bouklah et al. [25], Bentiss et al. [26], Zerga et al. [27], Khadiri et al. [28], Mashuga et al. [29] and El-Hajjaji et al. [30]. Experimentally, these organic derivatives can provide electrons to the metal surface to form coordinate covalent bonds and can also accept free electrons from the metal surface by using their lower unoccupied orbital, which facilitates their adsorption onto the metallic surface. This adsorption allows the blocking of active sites by reducing the steel dissolution rate along with the discharge of proton, which increases the coverage ratio, reflected by an elevation of inhibition effect of these compounds [27,29,31, 32, 33, 34, 35, 36, 37].

Parallel to the experimental study, the quantum chemical approaches have proven to be very useful in determining the molecular structure as well as elucidating the electronic structure and the characteristics of the reactive sites [38,39] in order to explain the mechanism of reactivity for corrosion inhibition process, and to understand the relationship between the corrosion inhibition efficiency and a number of molecular indices of these inhibitors [40,41]. On the other hand, quantitative structure-property relationship (QSPR) [42,43] has been widely used recently, to provide quantitative analysis of corrosion inhibition process, as attempts to find consistent relationship between the variations in the values of molecular properties and the inhibitor activity for a series of compounds. Thereby, the application of this approach in corrosion inhibition research, especially, in acidic media, was reported by several authors: F.B. Growcock et al. [45,54], P.G. Abdul-Ahad et al. [46], P. Dupin et al. [47] and I. Lukovits et al. [48,49].

The use of this mathematical technique can supply useful qualitative and quantitative information, for a better understanding of this corrosion inhibition phenomenon. The objective of the present work is to attempt an established a quantitative structure-activity/property relationship between the corrosion inhibition efficiency (IE %) and a number of molecular indices such as E_HOMO, E_LUMO, E_L-H, μ, η, σ, χ, IP, EA, ΔN, ω, V_m, Log P, and (M), in addition to the inhibitor concentration (C_i), computed, in aqueous phases by the means of the DFT at B3LYP methods with 6-31G (d, p) basis set, for twenty one (n = 21) pyridazine derivatives denoted hereafter, P1 to P21, illustrated in Figure 1, already studied experimentally as mild steel corrosion inhibitors in 1.0 M HCl for a various range of inhibitor concentration with distinguishable efficiencies [27,29,31, 32, 33, 34, 35, 36, 37]. This statistical investigation is evaluated by a comparative study between three mathematical regression models: the partial least squares regression (PLS), the principal component regression (PCR) and the artificial neural networks (ANN); in order to deeply understand the corrosion inhibition mechanism and to determine the relevant molecular indices influencing the variation of the inhibition efficiency for the studied compounds. As well as, the exploitation of the established equations makes it furthermore possible to estimate the inhibition properties of other similar compounds, in the absence of experimental data, and consequently to orient the organic partner to their synthesis due to the predicted promising character.

Figure 1.

2D un-optimized molecular structures of the studied pyridazine derivatives.

2. Materials and methods

2.1. Experimental data

In the present study, twenty-one pyridazine derivatives were selected in order to establish a quantitative structure property relationship (QSPR) between their inhibitive potential and their molecular structure. This work is considered as a complementary statistical study and a second part of several searches already published for the proposed pyridazine compounds differently substituted and studied as mild steel corrosion inhibitors in 1.0 M HCl at different concentration with distinguishable efficiencies [27,29,31, 32, 33, 34, 35, 36, 37]. The studied compounds names and their corresponding experimental corrosion inhibition efficiencies are summarized in Table 1.

Table 1.

Names and experimental corrosion inhibition efficiency values (IE_exp%) of the studied compounds at different concentrations.

Inhibitor	IUPAC name	Ci/M	IEexp%	Reference
P1	6-methyl-4,5-dihydro-2H-pyridazine-3-one	0.5. 10−3	17.70	[31]
P2	6-phenyl-2H-pyridazine-3-one	0.5. 10−3	25.60	[31]
P3	6-phenyl-2H-pyridazine-3-thione	0.5. 10−3	98.50	[31]
P4	3-Chloro-6-(1H-pyrazol-1-yl) pyridazine	2.8. 10−3	69.05	[32]
P5	1-(6-Chloro pyridazin-3-yl) piperidin-4-ol	2.3. 10−3	82.42	[32]
P6	3-Chloro-6-(3,5-dimethyl-1H-pyrazol-1-yl) pyridazine	2.2. 10−3	83.04	[32]
P7	Ethyl (6-methyl-3-oxopyridazin-2-yl) acetate	1.10–3	81.10	[33]
P8	Ethyl[4-(2-chlorobenzyl)-3-methyl-6-thioxopyridazin-1(6H)-yl] acetate	1.10–3	97.00	[27,34]
P9	Ethyl[4-(2-chlorobenzyl)-3-methyl-6-oxopyridazin-1(6H)-yl] acetate	1.10–3	91.00	[27,34]
P10	5-(2-chlorobenzyl)-2-(2-hydroxyethyle)-6-methylpyridazin-3(2H)-one	1.10–3	87.00	[27,34]
P11	5-(2-chlorobenzyl)-2-(2-hydroxyethyle)-6-methylpyridazin-3(2H)-thione	1.10–3	93.00	[27,34]
P12	5-benzyl-6-methyl pyridazine-3-thione	1.10–4	90.00	[35]
P13	5-benzyl-6-methyl pyridazine-3-one	1.10–4	65.00	[35]
P14	stet 5-benzyl-6-methylpyridazin-3-yl thioethanoic	1.10–4	87.00	[36]
P15	(5-benzyl-6-methyl–3-Oxopyridazin-3-yl)Ethonoate d'ethyle	1.10–4	69.00	[36]
P16	(5-benzyl-6-methylpyridazin-3-yl)Thioethonoate d'ethyle	1.10–4	83.00	[36]
P17	2-(6-chloropyridazin-3-yl)-2-phenylacetonitrile	2.2. 10−3	95.84	[29]
P18	3-(6-chloro-3-pyridazinyl)-1H-indole	2.2. 10−3	95.67	[29]
P19	4-(6-chloropyridazin-3-yl) benzoic acid	2.1. 10−3	72.64	[29]
P20	3-(6-chloropyridazin-3-yl) benzoic acid	2.1. 10−3	85.20	[29]
P21	1,4-bis(2-pyridyl)-5H-pyridazino[4,5-b] indole	1.10–4	90.20	[37]

2.2. Methodology

2.2.1. Computational methods

In terms of the structure and the molecular properties, the geometry of the corrosion inhibitors affects directly the characteristics and the nature of the interface inhibitor/metal and plays a major role in the mechanism of adsorption of the molecule on the metal surface. In this context, the 3D molecular structures were generated by the Gauss View 03 software, and the quantum chemical calculations were performed with complete geometry optimizations using the density functional theory (DFT) with the Beck's three parameter exchange functional along with the Lee-Yang-Parr non local correlation functional (B3LYP) at 6-31G (d, p) basis set [50, 51, 52], by the exploitation of the options of the Gaussian-03 software [53]; in attempt to determine the pertinent theoretical parameters, and to identify the inhibition properties of the undertaken derivatives. On the other hand, ChemSketch program, version 12.0 [54] was also employed to calculate the others molecular descriptors, which are selected to correlate the inhibition activity to their chemical structures of the under investigated compounds.

2.2.2. Statistical analysis

The statistical study was carried out on twenty-one pyridazine derivatives in order to establish a quantitative relationship structure-property between the corrosion inhibition efficiency (IE %) and the intrinsic electronic and structural properties of these compounds [45,55,56].

The proposed approach for this study is to perform a principal components analysis (PCA), which allows us to check redundancy and collinearity between the descriptors studied and to conduct a comparative statistical study between three proposed mathematical models: the partial least squares regression (PLS), the principal component regression (PCR) and the artificial neural networks (ANN); in order to correlate the anticorrosion activity to the molecular structure.

After their calculations, and by using XLSTAT software, version 2014 [57], the selected descriptors were used to establish statistical models that relate the inhibitive activity of compounds to their chemical structures such as electronic and structural molecular indices; by separating the data set into a training set, which are used to establish the three QSPR models and a test set which are exploited to assess the performance of these obtained models.

2.2.3. Validation

To evaluate the quality of explicability and the degree of prediction of each QSAR/QSPR model, validation tests must be carried out. In this context, internal and external validations are necessary. Internal validation is based, on the one hand, on several statistical parameters, such as: the determination coefficient R², the adjusted determination coefficient R²_adj, the predicted determination coefficient R²_pred, the predicted residual sum of squares PRESS, the standard deviation SD and the significance level p-value; on the other hand, it is justified by the means of the leave one out (LOO) cross validation method, using the cross-validated coefficient of determination R²_cv as an indicator to evaluate the pertinence of this procedure. The R²_cv is expressed as [58, 59, 60]:

$$R_{CV}^2=1-\frac{\sum _{i=1}^n{(I{E}_{\exp }-I{E}_{cal})}^2}{\sum _{i=1}^n{(I{E}_{\exp }-I\overline{E})}^2}$$ (1)

where $I{E}_{\exp }$ and $I{E}_{cal}$ are the experimental and calculated values for the dependent variables, respectively, and $I\overline{E}$ is the average experimental value.

On the other hand, the external validation was verified by earmarking 20 % of the sample as a test set, using external coefficient of determination R²_ext, which is determined as follows [58, 59, 60]:

$$R_{ext}^2=1-\frac{\sum _{i=1}^n{(I{E}_{cal(test)}-I{E}_{\exp (test)})}^2}{\sum _{i=1}^n{(I{E}_{\exp (test)}-I{\overline{E}}_{\exp (training)})}^2}$$ (2)

where $I{E}_{cal(test)}$ and $I{E}_{\exp (test)}$ are the calculated and experimental values for the test set, respectively; and $I{\overline{E}}_{\exp (training)}$ is the average experimental value for the training set of the dependent variables.

3. Results and discussion

3.1. Quantum calculation

3.1.1. Molecular geometry

The molecular geometries of the investigated compounds are determined by optimizing all structural parameters in aqueous phases, using the Density Functional Theory (DFT) at B3LYP/6-31G (d, p) level of theory [50, 51, 52]. The obtained geometries were qualified by the minimum energy of the molecular structures, which is proved by the absence of imaginary frequencies and by the comparison of the bond lengths and the pertinent dihedral angel values with the referential values. The final optimized geometries are listed in Figure 2.

Figure 2.

Optimized geometries obtained by B3LYP/6-31G (d, p) of the studied molecules.

3.1.2. Calculations of molecular descriptors

Because of the dependence of this corrosion inhibition phenomenon on various factors, the experimental study alone cannot explain the metal/solution interface behavior; which implies a coupling of this study with a quantum and/or statistical study such as a quantitative structure property relationship (QSPR). In this context, the QSPR approach focuses essentially on the correlation of the intrinsic properties of each molecule with its inhibitory potential. To this end, many models have been developed by several researchers in order to be able to link the inhibition efficiency of molecules to some of their properties. So, the inhibition efficiency can be predicted from molecular descriptors and elucidate the mechanism of inhibition. Thus, according to the literature, the most relevant descriptors that can influence the adsorption of the molecular inhibitors onto the metallic surface and their inhibition efficiencies are mainly the electronic, structural and lipophilic index. The pertinent descriptors considered in this work were: the highest occupied molecular orbital energy (E_HOMO), the lowest unoccupied molecular orbital energy (E_LUMO), the energy gap (E_L-H), the dipole moment (μ), the hardness (η), the softness (σ), the absolute electronegativity (χ), the ionization potential (IP), the electron affinity (EA), the fraction of electrons transferred (ΔN), the electrophilicity index (ω), the molecular volume (V_m), the logarithm of the partition coefficient (Log P), and the molecular mass (M), in addition to the inhibitor concentration (C_i). The obtained values of the used descriptors are illustrated in Table2.

Table 2.

The values of Molecular descriptor calculated at B3LYP/6-31G∗∗ in aqueous phase with the IE_exp% for different concentrations.

Compound	Ci/M	IEexp %	EHOMO(eV)	ELUMO(eV)	EL-H(eV)	μ (D)	IP (eV)	EA (eV)	χ (eV)	Ƞ (eV)	σ (eV−1)	ΔN	ω (eV)	Log P	M g.mol−1	Vmcm3.mol−1
P1	0.5 10−3	17.70	-6.727	-0.949	5.77	4.090	6.727	0.949	3.840	2.89	0.345	0.547	2.55	0.770	110.113	89.90
P2	0.5 10−3	25.60	-6.511	-2.274	4.24	4.130	6.511	2.274	4.390	2.19	0.456	0.615	4.400	0.980	172.183	143.10
P3	0.5 10−3	98.50	-6.013	-2.496	3.51	5.310	6.013	2.496	4.250	1.76	0.568	0.780	5.131	1.590	188.248	154.50
P4	2.8 10−3	69.05	-7.088	-2.271	4.817	6.317	7.088	2.271	4.679	2.409	0.415	0.481	4.545	0.860	180.594	122.30
P5	2.3 10−3	82.42	-6.253	-1.808	4.445	6.203	6.253	1.808	4.031	2.222	0.450	0.668	3.656	0.420	213.664	157.00
P6	2.2 10−3	83.04	-5.691	-1.967	3.724	5.733	5.691	1.967	3.829	1.862	0.537	0.851	3.936	0.570	222.674	169.00
P7	1.0 10−3	81.10	-6.228	-1.577	4.711	2.433	6.228	1.577	3.902	2.325	0.430	0.666	3.274	0.380	196.207	163.70
P8	1.0 10−3	97.00	-6.068	-2.095	3.973	8.399	6.068	2.095	4.081	1.986	0.503	0.736	4.192	3.140	336.836	268.70
P9	1.0 10−3	91.00	-6.476	-1.714	4.572	5.787	6.476	1.714	4.095	2.381	0.419	0.610	3.521	2.530	320.770	257.20
P10	1.0 10−3	87.00	-6.558	-1.742	4.816	6.438	6.558	1.742	4.150	2.408	0.415	0.592	3.576	1.280	278.734	219.50
P11	1.0 10−3	93.00	-6.068	-2.095	3.973	6.550	6.558	2.095	4.326	2.231	0.448	0.599	4.194	1.880	294.799	230.90
P12	1.0 10−4	90.00	-6.038	-1.985	4.053	8.900	6.038	1.985	4.011	2.026	0.493	0.737	3.970	2.150	216.302	185.90
P13	1.0 10−4	65.00	-6.392	-1.523	4.869	5.438	6.392	1.523	3.957	2.869	0.348	0.530	2.728	1.540	200.236	174.50
P14	1.0 10−4	87.00	-6.392	-1.360	5.032	2.976	6.392	1.360	3.876	2.516	0.397	0.620	2.985	2.280	274.338	209.30
P15	1.0 10−4	69.00	-6.446	-1.632	4.814	4.519	6.446	1.632	4.039	2.407	0.415	0.615	3.388	1.940	286.325	247.90
P16	1.0 10−4	83.00	-6.392	-1.360	5.032	2.525	6.392	1.360	3.876	2.516	0.397	0.620	2.985	2.810	302.391	250.50
P17	2.2 10−3	95.84	-7.380	-2.460	4.920	7.050	7.380	2.460	4.920	2.46	0.390	0.422	4.920	1.180	229.665	177.80
P18	2.2 10−3	95.67	-5.920	-1.820	4.100	6.880	5.920	1.820	3.870	2.05	0.487	0.763	3.652	1.910	229.665	165.50
P19	2.1 10−3	72.64	-7.190	-2.550	5.360	2.870	7.190	2.550	4.870	2.68	0.373	0.397	4.424	1.760	234.638	165.60
P20	2.1 10−3	85.20	-7.090	-2.220	4.870	6.230	7.090	2.220	4.660	2.44	0.409	0.479	4.449	1.840	234.638	165.60
P21	1.0 10−4	90.20	-7.631	-1.910	5.721	6.356	7.631	1.910	4.770	2.860	0.349	0.389	3.977	3.267	323.350	239.40

3.2. QSPR study

3.2.1. Principal component analysis

Principal component analysis (PCA) [61] is a statistical qualitative analysis procedure. This descriptive method can be used to reduce the dimensionality of large data set, by transforming a large set of variables into a smaller one that are uncorrelated. These new variables are called “main components”, or main axes. It allows the practitioner to reduce the number of variables and make the information less redundant [62].

Accordingly, in this work, the principal component analysis (PCA) was performed to the fourteen descriptors with the molecular concentration of the twenty-one molecules. The fifteen principal obtained components are presented in Figure 3.

Figure 3.

The principal components and their variances.

The contributions of the descriptors to the principal components F₁, F₂ and F₃ were summarized in Table 3. According to these results, the descriptors E_HOMO, E_L-H, IP, ƞ, σ and ΔN have the most significant contributions to F₁, while the descriptors, E_LUMO, EA, χ, and ω have the most significant contributions to F₂, whereas the descriptors Log P, M, V_m and C_i have the most significant contributions to F₃. On the contrary, the descriptor μ represents a low contribution to the three principal components; with a slight contribution value to F2.

Table 3.

Descriptor contributions to the first three principal components F₁, F₂ and F₃.

Descriptor	F1		F2		F3
	Correlation	Contribution	Correlation	Contribution	Correlation	Contribution
		%		%		%
Ci/M	0.0998	0.1711	-0.4971	5.5329	-0.4409	6.0253
EHOMO/eV	0.8526	12.4849	0.4827	5.2167	0.0058	0.0010
ELUMO/eV	-0.2350	0.9487	0.9364	19.6318	0.1284	0.5112
EL-H/eV	-0.9591	15.7973	0.1617	0.5854	0.0269	0.0224
μ/D	0.3296	1.8659	-0.4534	4.6026	0.2460	1.8754
IP/eV	-0.8431	12.2079	-0.5141	5.9179	0.0294	0.0268
EA/eV	0.2350	0.9487	-0.9364	19.6318	-0.1284	0.5112
Χ/eV	-0.4476	3.4407	-0.8859	17.5709	-0.0530	0.0870
ƞ/eV	-0.9578	15.7567	0.1968	0.8670	0.0602	0.1123
σ/eV−1	0.9662	16.0331	-0.1679	0.6313	-0.0736	0.1681
ΔN	0.9149	14.3753	0.3799	3.2306	-0.0170	0.0090
ω/eV	0.4053	2.8212	-0.7382	12.2001	-0.1616	0.8093
Log P	-0.0928	0.1478	-0.1628	0.5934	0.8744	23.7032
M/g.mol−1	0.0269	0.0124	-0.1627	0.5928	0.9449	27.6791
Vm/cm3.mol−1	0.0825	0.1168	-0.0147	0.0048	0.9589	28.5038

According to the projection of the variables in the plane of the three first principal components F1, F2 and F3 and based on their percentage contribution in the two correlation circles illustrate in Figure 4, these axes account for as much of the variability in the data as possible. They represent respectively, (36.39 %; 27.92 % and 20.16 %) of the total variance and the total information is estimated to a percentage of 84.47 %, were enough to describe the information represented by the data set.

Figure 4.

Correlation circles between the principle compounds F₁–F₂ (a) and F₁–F₃ (b).

The principal component analysis (PCA) was also performed to detect and identify the correlation between the different variables. This correlation was presented in Table 4.

Table 4.

The correlation matrix (Pearson (n)) between different descriptors.

Variable	Ci	EHOMO	ELUMO	EL-H	μ	IP	EA	Χ	ƞ	σ	ΔN	ω	Log P	M	Vm	IEexp %
Ci	1.000
EHOMO	-0.147	1.000
ELUMO	-0.481	0.231	1.000
EL-H	-0.143	-0.766	0.401	1.000
μ	0.221	0.046	-0.389	-0.402	1.000
IP	0.144	-0.978	-0.260	0.726	-0.017	1.000
EA	0.481	-0.231	-1.000	-0.401	0.389	0.260	1.000
Χ	0.374	-0.745	-0.746	0.273	0.210	0.837	0.746	1.000
ƞ	-0.224	-0.700	0.415	0.939	-0.350	0.693	-0.415	0.242	1.000
σ	0.164	0.720	-0.392	-0.936	0.343	-0.719	0.392	-0.273	-0.984	1.000
ΔN	-0.085	0.943	0.146	-0.794	0.122	-0.963	-0.146	-0.747	-0.815	0.841	1.000
ω	0.215	-0.036	-0.742	-0.498	0.276	0.049	0.802	0.487	-0.539	0.572	0.103	1.000
Log P	-0.429	-0.158	-0.032	0.093	0.285	0.175	0.032	0.138	0.116	-0.093	-0.143	0.020	1.000
M	-0.202	-0.042	-0.044	-0.026	0.234	0.089	0.044	0.086	-0.019	-0.019	-0.053	-0.086	0.779	1.000
Vm	-0.386	0.078	0.065	-0.074	0.182	-0.035	-0.065	-0.061	-0.041	0.006	0.045	-0.136	0.756	0.963	1.000
IEexp %	0.183	0.163	-0.313	-0.379	0.380	-0.135	0.313	0.085	-0.408	0.374	0.213	0.320	0.391	0.619	0.550	1.000

The correlation coefficients in the obtained matrix provide the information about the high or low interrelationship between the used descriptors. Generally, to decrease the redundancy existing in the used data matrix, the descriptors that are highly correlated (R ≥ 0.75), were excluded [63, 64, 65]. Accordingly, a perfectly negative correlation was observed between E_LUMO and EA (R = -1) and a strongly negative correlations was noticed between E_HOMO and IP (R = - 0.98); E_L-H and σ (R = - 0.94); IP and ΔN (R = - 0.96); σ and ƞ (R = - 0.98); E_L-H and E_HOMO (R = - 0.76); ΔN and E_L-H (R = - 0.79) and ΔN and ƞ (R = - 0.82). On the other hand, a positive collinearity was also observed between M and Log P (R = 0.78); V_m and M (R = 0.96); V_m and Log P (R = 0.76); ΔN and E_HOMO (R = 0.94); ƞ and E_L-H (R = 0.93); X and IP (R = 0.84); ΔN and σ (R = 0.84) and ω and EA (R = 0.80) which implies that these variables are redundant.

From the descriptive analysis of the PCA, it appeared that there are strong collinearities between the descriptors, i.e., some explanatory variables are linear combinations of the others. In this frame, and in view of this perfect collinearity, the matrix (X'X)⁻¹ is not invertible. Therefore, the least squares estimator is not determinable. Accordingly, the research of a linear (MLR) or polynomial (MPR) regression model is not possible for the prediction of anticorrosion activity IE % from the structure of the molecules studied, due to the loss of a large part of the useful information for the construction of the desired model. which prompted us to evaluate other statistical models, such as: the partial least squares regression (PLS), the principal component regression (PCR) and the artificial neural networks (ANN).

3.2.2. Partial least squares regression (PLS)

Partial least squares regression (PLS) was proposed to predict quantitatively the inhibitive activity of the studied compounds.

The PLS model is expressed in the following Eq. (3):

$$I{E}_{cal}\%=a_0+a_1{C}_i+a_2{E}_{HOMO}+a_3{E}_{LUMO}+a_4{E}_{L-H}+a_5\mu +a_6\text{IP}+a_7\text{EA}+a_8\text{Χ}+a_9\eta +a_{10}\text{σ}+a_{11}\Delta \text{N}+a_{12}\text{ω}+a_{13}\text{LogP}+a_{14}\text{M}+a_{15}{V}_m$$ (3)

where a₀ is a constant of regression; a₁, a₂, a₃, a₄, a₅, a₆, a₇, a₈, a₉, a₁₀, a₁₁, a₁₂, a₁₃, a₁₄ and a₁₅ represent the regression coefficients and E_HOMO, E_LUMO, E_L-H, μ, IP, EA, χ, $\eta$, $\sigma$, $\Delta N$, $\omega$, Log P, M and $V_m$ represent the variables; C_i denotes the inhibitor concentration.

The expression of the established PLS model, accompanied with the values of the statistical parameters, is represented by the following Eq. (4):

$$I{E}_{cal}\%=46.335+402.642C_i+1.4722E_{HOMO}-5.652E_{LUMO}-3.687E_{L-H}+0.949\mu -1.302\text{IP}+5.652\text{EA}+1.981\text{Χ}-7.162\eta +33.496\text{σ}+8.158\Delta \text{N}+1.687\text{ω}+2.042\text{LogP}+0.047\text{M}+0.058V_m$$ (4)

N = 17; R²= 0.89; R²_adj= 0.88; SD = 4.75; PRESS = 475.32; R²_pred= 0.84

The values of the analysis of variance table (ANOVA) for the obtained PLS equation are provided in Table 5.

Table 5.

ANOVA for PLS model.

Source	DF	SS	MS	p-value
Regression	1	2627.552	2627.552	<0.001
Residual error	15	338.576	22.571
Total	16	2966.128

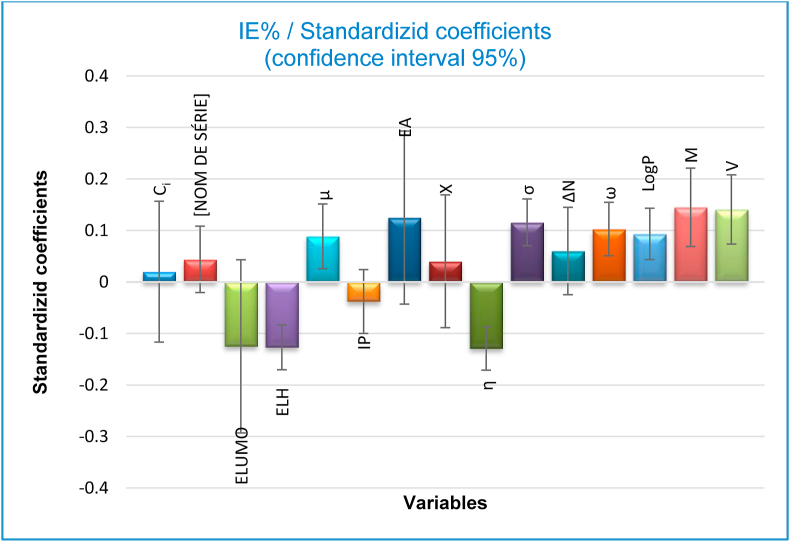
according to the descriptors mentioned in the partial least squares regression Eq. (4), the significance of each individual descriptor vs. the standardized regression coefficients is presented in Figure 5.

Figure 5.

Standardized coefficients versus variables in the proposed PLS model.

It can be seen from Figure 5, that the significance of anticorrosion activity based on molecular structure differs from one descriptor to another. However, because the descriptors in final PLS model have not the same units, these standardized coefficients are estimates with no real scale, which implies that these normalized coefficients cannot be employed to determine the real relative importance and significance of each descriptor in the regression analysis. Therefore, their usefulness is limited to the determination of the positive or negative effect of the molecular indices on the anti-corrosion property under investigation.

Returning to the statistical parameters, and from the values of the determination coefficient (R2 = 0.89), the adjusted determination coefficient (R2adj = 0.88) and the standard deviation (SD = 4.75), it appears that PLS does not have a great robustness in predicting the values of the inhibition efficiency. This insufficiency appeared very clearly in Figure 6, when representing the predictive values versus the experimental values of IE % where the residual error is very important.

Figure 6.

Correlation of experimental vs. calculated IE % efficiencies obtained by the PLS model.

The unsatisfactory statistical results of the PLS model prompted us to evaluate other statistical models, such as: the Principal components regression PCR and the artificial neural networks ANNs models.

3.2.3. Principal components regression (PCR)

To increase the quality of the prediction and degree of the correlation between the corrosion inhibition efficiency and the molecular structure, the selected descriptors were exploited to evaluate a principal components regression PCR, where the general expression of its equation is the identical to that of the PLS regression.

The obtained PCR equation accompanied with the statistical parameters calculated by the means of the following ANOVA table is expressed in Eq. (5) as:

$$I{E}_{cal}\%=572.153-16605C_i-52.204E_{HOMO}-94.370E_{LUMO}-46.037E_{L-H}-0.646\mu +135.513\text{IP}+94.370\text{EA}-249.553\text{Χ}-154.287\eta -1958\text{σ}+621.626\text{ΔN}+6.563\text{ω}-3.028\text{LogP}+0.897\text{M}-1.013V_m$$ (5)

N = 17; R²= 0.97; R²_adj= 0.97; SD = 3.33; PRESS = 475.32; R²_pred= 0.92

The values of the analysis of variance table are summarized in ANOVA Table 6:

Table 6.

ANOVA for PCR model.

Source	DF	SS	MS	p-value
Regression	1	5587.965	5587.965	<0.001
Residual error	15	166.053	11.070
Total	16	5754.019

By the inspection of statistical results, it appeared that the principal components regression (PCR) has a good quality and best prediction of the inhibition efficiency compared with the partial least squares regression (PLS), with it is characterized by a fairly considerable values of determination coefficient (R² = 0.97) and adjusted determination coefficient (R²_adj = 0.97) and a low value of the standard deviation: SD = 3.33.

The obtained values of the inhibition efficiency predicted by the PCR are fitted with the experimental IE % in the Figure 7.

Figure 7.

Correlation of experimental vs. Calculated IE % obtained by the PCR model.

Despite the good quality of significance and prediction of the PCR model, we have proposed artificial neural networks (ANN) as a multiple non-linear model and a suitable concept for better modeling the inhibition efficiency with the molecular structure for studied inhibitors.

3.2.4. Artificial neural networks (ANN)

In order to increase the degree of prediction the inhibition activity of the studied compounds based on the molecular structures, an artificial neural networks (ANN) was tested [66, 67, 68]. Is one of the commonly used methods in the machine learning field. It is a non-linear mathematical approach, which can be investigated to model in a complicated way the inhibitor structures with corrosion inhibition efficiency. Generally, this process involves using three layers: one input layer, which are represents by the number of the selected descriptors. One hidden layer, where the number of nodes in which is an important factor determining network performance. Previous studies have proposed a parameter ρ, leading to the determination of the number of hidden neurons, which has a major role in determining the best network architecture. ρ is defined as a ratio between the number of data in the training set and the sum of the number of connections. It should have a value between 1 and 3 [69,70]. Accordingly, to determine the relevant descriptors that will be used for a non-linear ANN regression, considering the correlations and mathematical relationships between these different indices, several attempts have been made. Indeed, the best non-linear combination obtained is of the type: (7-2-1), where the number of weights is 17 and ρ = 1, which is considered an acceptable value to build the appropriate ANN. In addition, one output layer [71], represents the prediction results. Thereby, the ANN configuration is illustrated in Figure 8.

Figure 8.

The architecture of the selected artificial neural networks (ANN).

By the use of Matlab software, version 9.0 [72], the obtained predicted inhibition efficiency IE_cal % accompanied with the residual error (RE.-ANN) values are listed in Table 8. In addition, the correlation between IE_exp % and IE_cal % accompanied with the statistical parameters is illustrated in Figure 9.

N = 17; R² = 0.95; SD = 4.19; PRESS = 475.32; R²_pred= 0.90

Table 8.

E_cal% vs. E_exp% obtained by PLS, PCR, ANN and CV models, proposed for DFT-B3LYP/6-31G∗∗ along with the residual error (RE).

Inhibitor	Ci/M	IEexp%	IEcal% Training set			IEcal%	Residual Error (RE)
			PLS	PCR	ANN	CV	RE.-PLS	RE.-PCR	RE.-ANN
P1	0.5. 10−3	17.70	40.49	19.87	23.56	21.48	-22.79	-2.17	-5.86
P3	0.5. 10−3	98.50	91.20	98.11	87.86	86.82	7.30	0.39	10.64
P4	2.8. 10−3	69.05	76.70	71.13	73.43	66.00	-7.65	-2.08	-4.38
P5	2.3. 10−3	82.42	78.79	81.03	78.23	75.19	3.63	1.39	4.19
P6	2.2. 10−3	83.04	84.82	87.36	86.59	89.59	-1.78	-4.32	-3.55
P7	1.10–3	81.10	68.33	73.89	77.21	76.78	12.77	7.21	3.89
P8	1.10–3	97.00	90.19	97.40	93.97	94.83	6.81	-0.40	3.03
P9	1.10–3	91.00	88.23	92.59	87.74	87.10	2.77	-1.59	3.26
P11	1.10–3	93.00	95.41	93.00	90.41	88.51	-2.41	0.00	2.59
P12	1.10–4	90.00	93.76	90.73	95.40	97.52	-3.76	-0.73	-5.40
P13	1.10–4	65.00	63.79	64.15	62.98	63.49	1.21	0.85	2.02
P14	1.10–4	87.00	84.26	92.83	93.57	95.00	2.74	-5.83	-6.57
P17	2.2. 10−3	95.84	89.79	98.49	96.84	96.04	6.05	-2.65	-1.00
P18	2.2. 10−3	95.67	88.99	90.75	91.00	92.64	6.68	4.92	4.67
P19	2.1. 10−3	72.64	77.09	73.68	73.49	75.69	-4.45	-1.04	-0.85
P20	2.1. 10−3	85.20	82.01	82.85	83.04	83.00	3.19	2.35	2.16
P21	1.10–4	90.20	88.30	86.53	87.95	86.31	1.90	3.67	2.25

RE.-PLS: Residual error between E_exp % and E_cal % obtained by using PLS.

RE.-PCR: Residual error between E_exp % and E_cal % obtained by using PCR.

RE.-ANN: Residual error between E_exp % and E_cal % obtained by using ANN.

Figure 9.

Correlation of experimental vs. calculated IE % efficiencies obtained by the ANN model.

The values of the analysis of variance table are summarized in ANOVA Table 7:

Table 7.

ANOVA for ANN model.

Source	DF	SS	MS	p-value
Regression	1	4643.236	4643.236	<0.001
Residual error	15	263.145	17.543
Total	16	4906.381

The obtained values of the inhibition efficiency predicted by the ANN are fitted with the experimental IE % in the Figure 9.

The analysis of the fitting parameters shows that the ANN models bring globally a significant amount of information, which means that the inhibition efficiency is directly related to the selected molecular descriptors, and which implies that the good quality and best prediction of this model, demonstrated by the high determination coefficient R² = 0.95 and the very low value of the standard deviation SD = 4.19.

The comparison between the experimental and calculated efficiency values is exemplified in Figure 10.

Figure 10.

Comparison diagram of IE % values obtained with PLS, PCR and ANN models.

A comparative analysis between the histograms illustrated in Figure 10 and the values of the residual errors (RE) arranged in Table 8 reveals that the PCR and ANN models explain the inhibition efficiency with a high level of significance when compared to PLS model. This relevance is demonstrated by the best concordance and the lowest values of (RE-PCR) and (RE-ANN) visualized between the IE_exp % and IE_cal %. The explanatory power of these two models is also highlighted by the statistical parameters such as R², R²_adj, R²_pred and SD.

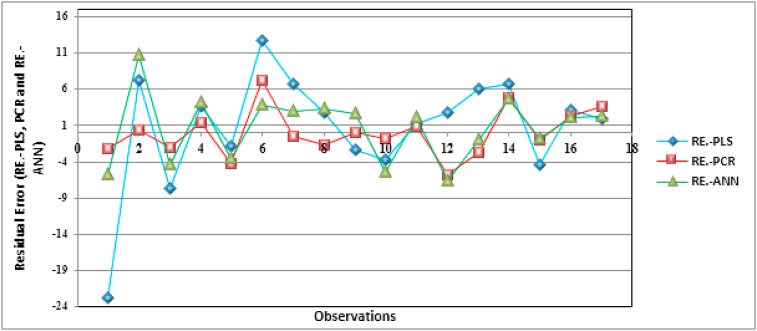
Moreover, it is very important to check for the presence of systematic errors that contravene the basic assumptions of the regression model. If there is a high systematic error in the model, then this model should be discarded [73] and performing any internal or external validation tests is of no use on this model. In this order, the residual error (RE) versus each observation of the training set was listed in Figure 11.

Figure 11.

The residual error (RE) between the experimental and the predicted IE % calculated with PLS, PCR and ANN models.

According to the Figure 11, the random distribution of the residuals shows that they are independent of each other, which implies that the residual errors follow a normal law with a homogeneity of their variance and a nullity of their expectations, and justifies the validity of such statistical models.

3.2.5. Internal and external validation models

3.2.5.1. Cross Validation (CV)

The most common technique used to determine the stability of the predictive model is to test the influence of each sample on the final model. Indeed, a Leave One Out (LOO) cross validation technique is used [74]. For a simple of N observations, this process consists to exclude each time an individual from the training test and to start the calculation. The excluded individual is considered as a test set regarding the rest [75,76]. In fact, this operation is repeated N times, and exploited to predict the IE % for all items in the studied sample.

Accordingly, in this work and by the means of Matlab software version 9.0 [72], this process is repeated 17 consecutive executions in order to predict the values of all the training set compounds. Indeed, the CV results are reported in Table 8 and the correlation between the experimental and the cross-validation predicted values of IE % coupled with the statistical characteristics are displayed in Figure 12.

N = 17; R²_cv = 0.92; SD = 5.26; p-value < 0.0001.

Figure 12.

Correlation of experimental vs. calculated IE % efficiencies obtained by the LOO cross validation.

As can be seen from the lowest value of the standard deviation SD = 5.26; that the mean square error between the observed and the predicted efficiency values is minimum. This are reflected by the highly significant cross-validated coefficient of determination (R²_cv = 0.92); which indicates a significant accordance between the results of the PLS, PCR and ANN as a QSPR models and the results of CV as an internal validation model and justifies that these proposed models, especially, possess a significantly statistical quality.

3.2.5.2. External validation

To assess the quality of the prediction and the degree of performance of the final extrapolation models, the external test of validation was carried out. For this purpose, and according to the above analyses and discussions, the dataset was divided into two samples: N = 17 compounds as a training set which is investigated to developing the QSPR models and k = 4 compounds as a test set which is exploited for an external validation. Following this sequential order, the external validation results are collected in Table 9.

Table 9.

Predicted vs. observed inhibition efficiency along with the residual error (RE) obtained by the external validation (test set).

Inhibitor	Ci/M	IEexp%	IEcal% Test set			Residual Error (RE)
			PLS	PCR	ANN	RE.-PLS (test)	RE.-PCR (test)	RE.-ANN(test)
P2	0.5. 10−3	25.60	65.56	34.04	29.87	-39.96	-8.44	-4.27
P10	1.10–3	87.00	79.78	81.61	75.35	7.22	5.39	11.65
P15	1.10–4	69.00	77.83	77.08	74.48	-8.83	-8.08	-5.48
P16	1.10–4	83.00	72.72	75.46	72.74	10.28	7.54	10.26

The exploitation of the Table 9 allows to extract the statistical parameters related to the external validation which are listed in Table 10.

Table 10.

Statistical parameters derived from the external validation of statistical models.

Parameter	Statistical model
	PLS	PCR	ANN
n	4	4	4
R2ext	0.71	0.94	0.92
p-value	< 0.001	<0.001	< 0.001

As a confirmation with the above analyses and discussions, for the PLS, PCR and ANN models and as they indicate their values of the external coefficient of determination R²_ext: 0.71, 0.94 and 0.92 respectively, they are superior of 0.5 as a critical value [58, 59, 60]. Which implies that the proposed principal component regression and artificial neural networks models have a highest predictive power. Their extrapolation can be successfully used for the prediction of the corrosion inhibition efficiency of other compounds that are not included in the establishment of these QSPR models.

According to all the obtained statistical results, the degree of robustness and the quality of prediction of the developed models are compared in Table 11.

Table 11.

Comparison of the statistical parameters of PLS, PCR and ANN models.

Parameter	Statistical model
	PLS	PCR	ANN
N	17	17	17
R2	0.89	0.97	0.95
R2adj	0.88	0.97	0.95
R2pred	0.84	0.92	0.90
SD	4.75	3.33	4.19
R2ext	0.71	0.94	0.92
Fobs	116.408	504.774	264.677
p-value	<0.001	<0.001	<0.001

The overall analysis of the statistical results of PLS, PCR and ANN from the Table 11 shows that PCR and ANN are the most predictive models for estimating the anticorrosion activity of the inhibitors selected in this work, compared to the PLS model. This robustness in prediction is justified by the best statistical parameters associated to these two models, especially, the predicted determination coefficient, where R²_pred = 0.92 and R²_pred = 0.90 for PCR and ANN respectively. Furthermore, an extensive comparison of the current results with those of similar studies reported in the literature by I. Lukovits et al. [77], E. S. H. El Ashry et al. [78], H. El Sayed et al. [79], F. Bentiss et al. [80,81], El H. El Assiri et al. [1,2], M. R. Fissa et al. [82], A. Aouidate et al. [83], A. Ghaleb et al. [84], P. Toropova et al. [85], shows that that the arsenal of quantum chemistry can be used to establish correlations between molecular structure and activity using the Quantitative Structure Activity/Property Relationship (QSAR/QSPR) approach, by developing mathematical models to predict inhibition efficiency and to select compounds with desired properties. This statistical technique based on the correlation between the inhibition properties of molecules and their molecular structures can also provide useful qualitative and quantitative information for a better understanding of the corrosion inhibition process.

The exploitation of the established equations also makes it possible to estimate the inhibition properties of other similar compounds in the absence of the data and consequently, guide the organic partner to their synthesis through the promising character predicted.

4. Conclusion

From the above analyses and discussions, the following main conclusions can be drawn:

• -Twenty-one pyridazine derivatives have been theoretically and statistically investigated as corrosion inhibitors for carbon steel in 1.0 M HCl solution.
• -The calculation of the molecular descriptors by the means of DFT quantum method allows to correlate the corrosion inhibition efficiency IE % to the molecular structure using the QSPR approach.
• -A qualitative analysis with the principal component analysis (PCA) allowed us to examine redundancy and collinearity between the proposed descriptors.
• -The established regressions show that the anticorrosion activity of the molecules studied can be explained in terms of the electronic and structural properties of such inhibitors.
• -The inspection of the quantitative analyses results demonstrates that PCR and ANN are the most robust models to predict the inhibition efficiency of the selected compounds in comparison with PLS model. Indeed, the relevance of these models is reflected by the means of the internal validation including the leave one out cross-validation and by the external validation using a test set as an extrapolation of these proposed models.
• -PCR and ANN results can be suggested to predict the corrosion inhibition efficiency of new pyridazine compounds, and to encourage the collaboration between experimenters, theorists and industrialists. As well as to assist the organic chemist in the synthesis of promising molecules as corrosion inhibitors.

Declarations

Author contribution statement

El Hassan El Assiri, Majid Driouch, Jamila Lazrak: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Zakariae Bensouda, Ali Elhaloui: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.

Mouhcine Sfaira, Taoufiq Saffaj, Mustapha Taleb: Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.