Diverse Cell Stimulation Kinetics Identify Predictive Signal Transduction Models

Summary

Computationally understanding the molecular mechanisms that give rise to cell signaling responses upon different environmental, chemical, and genetic perturbations is a long-standing challenge that requires models that fit and predict quantitative responses for new biological conditions. Overcoming this challenge depends not only on good models and detailed experimental data but also on the rigorous integration of both. We propose a quantitative framework to perturb and model generic signaling networks using multiple and diverse changing environments (hereafter “kinetic stimulations”) resulting in distinct pathway activation dynamics. We demonstrate that utilizing multiple diverse kinetic stimulations better constrains model parameters and enables predictions of signaling dynamics that would be impossible using traditional dose-response or individual kinetic stimulations. To demonstrate our approach, we use experimentally identified models to predict signaling dynamics in normal, mutated, and drug-treated conditions upon multitudes of kinetic stimulations and quantify which proteins and reaction rates are most sensitive to which extracellular stimulations.

Graphical Abstract

Highlights

• •Diverse kinetic cell stimulations result in distinct signaling response dynamics
• •Diverse kinetics compared with step stimulations better constrain model parameters
• •Diverse kinetic stimulations improve predictions of WT and mutant pathway responses
• •Diverse kinetic stimulations compared with steps discriminate competing signaling models

Bioinformatics; Complex System Biology; Systems Biology

Introduction

One of the longest standing challenges of modeling in systems biology has been to make accurate quantitative predictions for cell signaling responses over time, upon genetic mutations, when subjected to variable drug concentrations, and under time-varying changes of environment (Fujita et al., 2010; Handly et al., 2016; Rowland et al., 2011; Sorre et al., 2014; Lim and Bruce Mayer, 2017). Examples of environmental perturbations that change over time that cells experience (defined as “kinetic stimulations”) include changes in levels of hormones (Kubota et al., 2012; Steiner et al., 1982), growth factors (Fujita et al., 2010; Sorre et al., 2014), morphogens (Briscoe and Small, 2015; Huang et al., 2017), cytokines (Oyler-Yaniv et al., 2017), or extracellular stressors such as oxidative stress (Goulev et al., 2017) or osmolarity (Granados et al., 2017; Mitchell et al., 2015; Young et al., 2013). These environmental changes can modulate signaling dynamics in pathways in both healthy and disease tissue (Akhurst and Hata, 2012; Cildir et al., 2016; Hanahan and Weinberg, 2000; Hata and Chen, 2016; Hotamisligil and Davis, 2016). Therefore, understanding and predicting signal transduction network behavior will be a critical step to identify unknown regulatory mechanisms, to distinguish between proteins and reaction rates that are sensitive to kinetic stimulations, and to detect and treat abnormal regulation that occurs in a large number of human diseases.

A key obstacle that prevents predictive modeling of cell signaling is the gross mismatch between the preponderance of biological complexity and the sparsity of quantitative experimental data (Handly et al., 2016; Janes and Lauffenburger, 2013; Vanhaelen et al., 2017). As a consequence, most current models of signal transduction pathways suffer from lack of dynamic richness in the data resulting in either too simple (Adler and Alon, 2018; Csete and Doyle, 2002; Muzzey et al., 2009) or too complex (Groβ et al., 2019; Klipp et al., 2005; Romers et al., 2020) models with limited predictive power (Handly et al., 2016; Janes and Lauffenburger, 2013). To address the disparity between biological complexity and lack of richness in experimental data, one paradigm has been to devise experiments with higher content (e.g., sequencing or multiplexed single-cell imaging) or higher throughput (e.g., flow cytometry or parallelized microfluidics) in hope that large amounts of data will eventually fill the gap between mechanistic and predictive understanding (Efremova et al., 2020; Labib and Kelley, 2020). These approaches have been helpful to quantify RNA or protein abundances or phosphorylation states of many proteins using the minimal number of time points to better constrain complex models (Kinney et al., 2019). Another approach has been to fit computational models to experiments at steady state in different environments (Hao and O'Shea, 2012), to dose-response curves measured with sudden step-like perturbations (Shaw et al., 2019), to repetitive pulsatile perturbations of different frequencies (Albeck et al., 2013; Ashall et al., 2009; Hersen et al., 2008; Mettetal et al., 2008; Mitchell et al., 2015; Rahi et al., 2017; Wang et al., 2012; Zhang et al., 2019), or to individual spatial gradients (Huang et al., 2017) or design optimal experiments that constrain parameters for a specific perturbation profile (Apgar et al., 2008; Bandara et al., 2009; Casey et al., 2006; Faller et al., 2003; Hagen et al., 2013). In addition, pioneering studies have further demonstrated that individual and different kinetic stimulations can dramatically affect intracellular signaling dynamics to create distinct cell phenotypes (Fujita et al., 2010; Granados et al., 2017; Kubota et al., 2012; Muzzey et al., 2009; Shimizu et al., 2010; Sorre et al., 2014; Thiemicke et al., 2019; Twohig et al., 2019; Wang et al., 2012; Young et al., 2013). However, from these previous studies, it is not understood how parameter uncertainty, model predictions, and model identification quantitatively depend on the amount and type of experimental data.

Here we systematically explore how multiple, kinetically distinct inputs can activate signaling pathways to achieve diverse signaling responses, and we show that this diversity of input-output relationships is key to the identification of predictive models for complex biological pathways (Figure 1). To demonstrate the feasibility of this task, we infer several models from single-cell time-lapse microscopy data for cell signaling in the conserved High Osmolarity Glycerol (HOG/p38) pathway, a prototypical mitogen-activated protein kinase (MAPK) pathway in the yeast Saccharomyces cerevisiae that is important for stress adaptation and cell survival (Figure 1A) (Cuadrado and Nebreda, 2010; Saito and Posas, 2012; Thiemicke et al., 2019). This eukaryotic model system includes the most relevant features of signaling networks, including a terminal signaling protein (Hog1) and a branched protein network that comprises membrane sensors, phosphorelays, kinases, phosphatases, autoregulation, and feedback and feedforward loops that are found in the majority of signaling pathways (Lim and Bruce Mayer, 2017). With this system, it has been previously demonstrated experimentally that changing the extracellular osmolyte concentrations over time results in distinct Hog1 activation dynamics as pathway response output (Figures 1B and 1C) (Ferrigno et al., 1998; Hersen et al., 2008; Mettetal et al., 2008; Mitchell et al., 2015; Thiemicke et al., 2019). Because of these attributes that are common in many signal transduction pathways in eukaryotic cells, we now seek to explore what general implications the diversity of multiple input-to-output dynamics can have on the possibility to identify predictive signaling models and the regulatory mechanisms that are sensitive to kinetic environmental perturbations.

Figure 1.

Kinetic Stimulation of Signaling Pathways Is Required to Identify Predictive Models and Phenotypes

(A) Different extracellular kinetic stimulations (left) activate a signaling pathway (middle) and result in distinct dynamic kinase signaling and nuclear localization (right).

(B) MAPK Hog1 nuclear localization dynamics upon step increases in NaCl to different final concentrations.

(C) Hog1 dynamics upon step, linear, or quadratic increases from 0 to 0.4 M NaCl. Lines are means, and shaded areas are the standard deviation of multiple biological replicates (Transparent Methods).

(D–F) (D) Schematic overview of model identification based on models' predictions utilizing kinetic cell stimulations. (E) Schematic overview of signaling models of different complexity where pathways are modeled with ordinary differential equations (ODE) (Figure S1; Transparent Methods). The middle model is defined as the “true model” to simulate synthetic data for pathway response (defined as the activation of node x₄). Different models were fitted to the same data to identify parameters. (F) These models were then used to make predictions for pathway activation, depicted as black solid line, upon a different kinetic input, which resulted in different responses for different models (colored lines).

(G) Diverse kinetic perturbations corresponding to step (t⁰), root ($\sqrt{t}$), linear (t¹), quadratic (t²), quint (t⁵), and heptic (t⁷) changes over time (left) are applied to the true model (middle) resulting in synthetic signaling activation dynamics (right). In synthetic signaling data, lines are means and shaded areas are the standard deviation of simulated replicates (Transparent Methods).

(H) Diverse kinetic inputs reaching different final concentrations plus four alternating stimulations result in 58 distinct simulated datasets for each model. These datasets are used to train models and test their predictions. The alternating stimulations include a staircase input, two pulsatile inputs, and a sinusoidal oscillatory input (Figures S3E–S3H).

See also Figures S1–S3 and Table S1.

Results

Parametrizing Signaling Models with Experimental Data Enables Predictions of Pathway Responses upon Kinetic Stimulations

As the HOG model pathway combines universal signaling network features as outlined earlier, it serves as a blueprint to build predictive signaling models of varying complexity (Figures 1A–1E). Previous published models have limitations in that they are too simple and lack molecular detail (Hersen et al., 2008; Muzzey et al., 2009) or that they are too complex having too many parameters to estimate (Klipp et al., 2005). Furthermore, other models are too specific, and their complexity is difficult to adapt when seeking to identify predictive models from finite amounts of experimental data (Granados et al., 2017; Schaber et al., 2012; Zi et al., 2010). To circumvent the challenge of variable complexity, we specify a class of expandable network topologies outlined in Figures 1E and S1K. In this class, model nodes are defined based on branching points in the Hog1 pathway starting from the Hog1 kinase, and complexity of the pathway can be increased by separating nodes into sub-nodes (Figure 1E, left to right) (Transparent Methods). For example, the representative model in Figure 1E (middle) resembles a simplified branched signaling pathway consisting of four nodes, including one activating and one repressing sensor protein, constant basal regulators, and a negative feedback loop from the terminal kinase to an upstream signaling branch (Figures S1A). In the context of the HOG pathway, the node x₁ represents the SLN1 branch including the proteins Sln1, Ypd1, Ssk1, and Ssk2/Ssk22. The SLN1 branch utilizes a two-component phosphorelay mechanism to transmit its signal, with b₁ representing the constant deactivation of the SLN1 branch (Hohmann et al., 2007; Maeda et al., 1994). The node x₂ describes the SHO1 branch of the HOG pathway that utilizes protein kinases to relay its information. The SHO1 branch consists of the proteins Sho1, Msb2, Hkr1, Opy2, Cdc42, Ste20/Cla4, Ste11, and Ste50, with b₂ modeling the basal deactivation of the SHO1 branch (Tatebayashi et al., 2015). The SHO1 branch is also regulated by the Hog1 kinase through a feedback loop (Hao et al., 2007; O'Rourke and Herskowitz, 1998; Westfall and Thorner, 2006). The node x₃ represents an MAPKK such as Pbs2 that integrates information flow from two branches and has basal regulation (b₃) through phosphatases such as Ptc1/2/3. Last, x₄ represents a terminal kinase such as Hog1 that is activated by Pbs2. Hog1 is deactivated through phosphatases Ptc1/2/3 and Ptp2/3 (Mattison and Ota, 2000; Warmka et al., 2001; Young et al., 2002). Deactivation of Hog1 via constitutively active phosphatases is modeled as the act of basal deactivator b₄ on x₄.

We parametrized these representative biologically inspired models (Transparent Methods) by fitting them to experimental Hog1 nuclear localization data (Figures 1B and S1K–S1M). Using experimentally constrained parameters for each model, we predicted Hog1 signaling dynamics upon different kinetic stimulation profiles and evaluated each model's ability to predict independent experimental Hog1 dynamics. The model (Figure 1E, middle) and the parameter set (Table S1) resulting in the smallest prediction error was defined as the “true model” and the “true parameters,” respectively. From this model, we simulate synthetic signaling data upon diverse kinetic stimulations for the remainder of this study. Using a known model for this task, rather than additional experiments, allows us to systematically and quantitatively establish how diverse kinetic stimulations impact model identifiability and predictive power in a controlled setting where ground truth knowledge is available to check performance.

Diverse Kinetic Cell Stimulations Result in Distinct Pathway Activation Dynamics

With a specified “true model,” we can now rigorously explore diverse kinetic inputs to pathway dynamics (Figure 1G). We simulated 54 synthetic datasets (Figures 1H, and S2) under a wide range of physiologically feasible and mutually independent kinetic stimulation profiles (see Transparent Methods) such that each of the 54 profiles stimulates the pathway to express a unique temporal behavior. Our simulated data (Figures 2 and S2) qualitatively and quantitatively capture the main characteristics of measured dynamics for Hog and other signaling pathways, including modulation of activation level, diversity of signaling dynamics, delayed onset of activation, variable time to reach maximum activation, perfect adaptation, and measurement error observed in experiments (Figures 1B and 1C). Each signaling dataset covers the same duration and sampling range and has the same amount of data. However, different datasets may constrain model parameters to different extents that, in turn, could lead to predictions of different accuracy. To compare the performance of kinetic stimulations, we also simulated signaling activation dynamics upon staircase, pulsatile, and sinusoidal stimulation inputs (Figures 1H, datasets 55–58, and S3).

Figure 2.

Models Trained Using Same Kinetic-Type Inputs Fail to Predict Pathway Response to Other Kinetics

(A–F) Models trained using step inputs fail to predict pathway response to kinetic stimulations. Gray lines show synthetic pathway activation dynamics over time at different kinetic inputs as indicated inside each panel: step (t⁰, A), root ($\sqrt{t}$, B), linear (t¹, C), quadratic (t², D), quint (t⁵, E), and heptic (t⁷, F) input kinetics over time each to increasing final concentrations of 0.10, 0.20, 0.30, and 0.50 M. (A) Model fit simultaneously to steps of 0.2 and 0.3 M data are shown in red. (A–F) Predictions under all other conditions are shown in blue. Predictions in (E) and (F) of all four concentrations overlap. Thick lines and shaded areas show median and interquartile range out of 10 independent fits and their corresponding predictions, respectively. As shown as an inset in (A), the first, second, and third quartiles are used to plot shaded error bars where the thick line and upper and lower shaded areas represent Q2, (Q3-Q2), and (Q2-Q1), respectively. This convention is used throughout the article.

(G–L) Similar to (A–F), models trained using quadratic inputs fail to predict pathway response to other kinetics.

See also Figure S2.

Lack of Kinetic Stimulation Diversity Limits Model Prediction Power

To explore what effects different stimulations have on model predictive power, we fit the true model to many independent sets of simulated data with experimentally realistic noise (Transparent Methods). The results of model fit simultaneously for two steps of 0.2 and 0.3 M NaCl is shown in Figure 2A (red). After confirming that these fits had converged to maximize the likelihood of observing the training data (Figures S1G–S1J; Transparent Methods), we then predicted the remaining 54 datasets for steps as well as all other kinetics (blue) (Figure 2). Comparison of the fits and predictions to the corresponding training and testing data shows that the quality of predictions is nearly as good as fits for the same type of kinetics (Figures 2A and 2J, blue), but predictions become worse for different types of kinetics (Figures 2B–2F, 2G–2I, 2K, and 2L). This raises the question if the lack of predictability is due to the lack of data or due to limited kinetic diversity in the training data.

To address the possibility of having too little data, we fit the model to six-step (t⁰) data simultaneously (Figure 3A, red), and we predicted the signaling dynamics upon all remaining kinetic stimulations (48 datasets). We compared model predictions of signaling dynamics for linear kinetic stimulations (t¹) or nonlinear kinetic stimulations (t⁹) of different final concentrations to their corresponding synthetic data (Figure 3A, blue or green, respectively, compared to gray). After convergence, each set of model fits resulted in poor predictions for all datasets except for testing data collected using the same kinetic type as the training data. This observation was the same for subsequent training datasets with homogeneous input types (Figures S3A–S3C). Comparing how model predictability depends on the amount of training data of the same type illustrates that simply collecting more data of the same type does not automatically result in improved predictability (Figures 3B and S3A–S3C, right). Rather, the specific kinetics upon which the cells are stimulated may be of greater importance.

Figure 3.

Kinetic Stimulation Improves Model Predictions

(A) Simultaneous fits (red) to six simulated step input response of different concentrations (gray) and subsequent model predictions of signaling dynamics upon different concentrations of linear input stimulations (predictions1 in blue, testdata1 in gray) or different concentrations of nonlinear inputs of the shape t⁹ (predictions3 in green, testdata3 in gray).

(B) Box plots of fit and prediction errors when an increasing number of step inputs is used to train the model.

(C) Simultaneous fit (red) to six different kinetic input stimulations of the same final concentration (gray) and model predictions for different concentrations of linear input stimulations (predictions1 in blue, testdata1 in gray) or different concentrations of nonlinear input stimulations of the shape t⁹ (predictions3 in green, testdata3 in gray). In (A and C), thick lines and shaded areas in gray show the mean and the standard deviation of synthetic data. Thick lines and shaded areas in red, blue, and green show median and interquartile range of 10 independent fits and their corresponding predictions, respectively.

(D) Box plots of fit and prediction errors when an increasing number of diverse kinetics (t⁰ t⁷) is used to train the model. For (B and D), squares and error bars show median and first and third quartiles, respectively. Horizontal dotted black line denotes the standard deviation of the simulated data. Fit or prediction errors (FE or PE1-PE4) are the mean absolute difference of the fit or predictions and their corresponding synthetic data over time (Transparent Methods). Fit error (FE) statistics are drawn from n_train datasets over 10 independent fits (10 × n_train errors) where n_train = 1,2, …6 is the number of datasets used to train the model. Similarly, PE1, PE2, and PE3 are drawn from prediction errors of testdata1 (36-n_train datasets over 10 independent fits), testdata2 (12 datasets over 10 independent fits), and testdata3 (6 datasets over 10 independent fits), respectively (Figure 1H).

(E–G) (E) Upon a sinusoidal oscillatory stimulation input (Figure S3H), model predictions (examples of P4 in purple) compared with testdata4 (gray) under (F) six steps versus (G) six diverse kinetics training.

(H) Full boxplots of fit (FE) and predictions errors (PE1, PE2, PE3, and PE4) compared with standard deviation of the synthetic data (horizontal dashed line) when six datasets of each kinetics (or equivalent) are used to train the model. Quantifications are from 10 independent fits for each condition. PE4 is prediction errors quantified from alternating stimulations that consist of staircase, pulsatile1, pulsatile2, and sinusoidal oscillatory inputs (Figures S3E–S3H). When either of the alternating stimulations is used as training data, PE4 is quantified over the other three alternating stimulations.

See also Figure S3 and Video S1.

Diversified Kinetic Stimulations Better Constrain Model Parameters and Improve Model Predictions

To address the importance of kinetic diversity in training data, we fit signaling dynamics for different kinetic stimulations (t⁰−t⁷) of a given final concentration (Figure 3C, red), and we predicted the signaling dynamics for the remaining kinetic stimulations (Figure 3C, blue and green). Comparing model predictions of signaling dynamics for linear kinetic stimulations (t¹) or nonlinear kinetic stimulations (t⁹) of several different final concentrations with their corresponding synthetic data (Figures 3C and S3D, blue or green, respectively, compared with gray) indicates that all the predictions are substantially improved and are nearly as good as the fits, whereas the amount of training data is still the same as in Figure 3A. Quantitatively comparing how model predictability depends on the amount of different types of training data illustrates that kinetically diverse training data substantially improve predictability under all test kinetics (Figure 3D, blue, yellow, or green quantified from testdata1, testdata2, or testdata3).

Our results indicate that a minimum of five diverse training datasets are sufficient to achieve average prediction errors within 75% of the standard deviation of data, and six diverse datasets result in average prediction errors within 51% of the standard deviation of the data. For a more stringent evaluation of generality and extensibility, we then challenged the various trained models with entirely different sets of novel alternating stimulations including staircase, pulsatile, or complex sinusoidal oscillatory inputs (testdata4) (Figures 3E–3G and S3E–S3H). After training using six steps (Figures 3A and S3I), six t⁵ kinetics (Figure S3J), or six diverse kinetics (Figures 3C and S3K), we compared model predictions with their corresponding simulated data for four alternative stimulations (S3E–S3K, purple compared with gray). Finally, we fit each of the 11 different training datasets and predict the remaining data (Figure 3H). Each of the 11 different training datasets contains the same amount of data and fits equally well to its respective training data, but training using diverse kinetics led to far better predictions in comparison to any of the other sets of perturbations (Figure 3H). A comprehensive comparison of model predictions with all testdata under each of the 11 different training conditions is given in Video S1. A detailed analysis demonstrates that when using training data restricted to a single type, prediction errors increase as test data deviate away from kinetically similar training data (Figures 4A and S4A–S4I).

Figure 4.

Kinetically Diverse Stimulations Constrain Model Parameters Substantially Better than Homogeneous Kinetic Types

(A) Comprehensive quantification of prediction errors of each kinetic stimulation type when five datasets of any given type is used to train the model (lighter colors denote smaller errors).

(B) Comparison of prediction errors (Predictions3) under increasing amounts of training data of the same kinetic type (e.g., step, linear, quadratic) or diverse kinetic types (0.3 and 0.7 M). Horizontal dotted black line denotes the standard deviation of the simulated data.

(C–E) Verification of FIM using MLEs. Under each of six step versus six diverse 0.7 M kinetics training, total model uncertainty is estimated by determinant of (C) FIM⁻¹, (D) covariance matrix of MLEs, and (E) covariance matrix of Bayesian posterior. Analyses in (C–E) are all performed with four free model parameters (λ11, λ13, λ15, λ21) (see Transparent Methods and Figures S4J and S4K).

(F) Parameter uncertainty of the model estimated as inverse of determinant of FIM (i.e., D-Optimality) when the model is fit to all six of each dataset.

(G) Ellipses are representative 95% confidence intervals for a representative pair of parameters estimated from FIM⁻¹. Colors correspond to the five different sets of experiments considered in (F).

(H) FIM optimal experimental design by minimizing the determinant of inverse FIM determines D-Optimal experiments for increasing number of datasets (n = 1,2, …6) among all possible combinations (36 choose n) (purple) compared with steps (black) or diverse 0.7 M (blue).

(I) Comparison of prediction errors (Predictions1, Predictions2, and Predictions3) under increasing amounts of training data of the steps, diverse 0.7 M, and D-Optimal experiments. Results are from three independent model fits and their corresponding predictions. Horizontal dotted black line denotes average standard deviation of the simulated data.

(J–L) Bayesian analysis to quantify model parameters posterior and predictions under different kinetics. Under (J) six steps, (K) six diverse 0.7 M, and (L) six D-Optimal training kinetics, model fits (red) and predictions (green) for 100 parameters sets sampled from Bayesian posterior are compared with their corresponding training and test data (gray). Results are from multiple independent chains (steps 3, diverse 3, and D-Optimal 7 chains) (see Transparent Methods). The values for the determinant of covariance of posterior (average over all independent chains), average fit errors (<FE>), and average prediction errors (<PE>) are given for each condition. The <FE> and <PE > quantifications are from 100 samples from posteriors of each independent chain. FE are from six training datasets; PE are from the remaining 52 test datasets (Figure 1H).

See also Figure S4.

Video S1. Diversified Kinetic Stimulations Disproportionately Improve Model Predictions, Related to Figures 3 and S3

Model fits (red) simultaneously to six data (or equivalent amount of data) of each kinetic (gray) and model predictions of the other kinetics (blue, yellow, green, and purple) are compared with their corresponding test data (gray); Training data are as follows:

Frame 1: six steps (t⁰, A), 6 × 50 min training data,

Frame 2: six roots ($\sqrt{t}$, B), 6 × 50 min training data,

Frame 3: six linears (t¹, C), 6 × 50 min training data,

Frame 4: six quadratics (t², D), 6 × 50 min training data,

Frame 5: six quints (t⁵, E), 6 × 50 min training data,

Frame 6: six heptics (t⁷, F), 6 × 50 min training data,

Frame 7: staircase (J), 1 × 300 min training data,

Frame 8: Paulsatile1 (K), 1 × 300 min training data

Frame 9: Paulsatile2 (L), 1 × 300 min training data

Frame 10: Oscillatory (M), 1 × 300 min training data,

Frame 11: six diverse kinetics (one each of t⁰, $\sqrt{t}$, t¹, t², t⁵, t⁷), 6 × 50 min training data,

Frame 12: repeat of Frame 11 except the YScale in (N) is linear in Frame 12.

Each condition is from 10 independent fits. Shaded plots (red, blue, yellow, green, purple) present 10, 50, and 90 percentiles out of 10 independent fits and their corresponding predictions over time. (N) Full boxplots of fit (FE) and predictions errors (PE1, PE2, PE3, and PE4) compared with standard deviation of the synthetic data (black dotted line) at each frame. Fit error (FE) statistics are drawn from n_train datasets over 10 independent fits (10 × n_train errors) where n_train = 6 in Frames 1–6 and Frame 11, whereas n_train = 1 in Frames 7–10 is the number of datasets used to train the model. Similarly, PE1, PE2, and PE3 are drawn from prediction errors of testdata1 (30 datasets over 10 independent fits), testdata2 (12 datasets over 10 independent fits), and testdata3 (6 datasets over 10 independent fits), respectively (Figure 1H). PE4 is prediction errors quantified from alternating stimulations that consist of staircase, pulsatile1, pulsatile2, and sinusoidal oscillatory inputs (Figures S3E–S3H). When either of the alternating stimulations is used as training data (Frames 7–10), PE4 is quantified over the other three alternative stimulations.

To better understand why multiple diverse kinetic stimulations result in better predictions and reduced predictions uncertainties, we next sought to analyze the effects of different training inputs on prediction errors (Figures 4B and S3A–S3D). By comparing predictions for an increasing number of training data, we find that prediction errors decrease with increase in the amount of training data regardless of the training data type, but the prediction improvement is much faster when using diverse training data (Figure 4B). We applied both frequentist and Bayesian analyses to explore how variability in parameters and predictions arises from different experimental settings. For the frequentist analysis, we developed a Fisher Information Matrix (FIM) analysis framework to directly estimate the expected uncertainties of maximum likelihood estimations (MLE) when performing multiple independent replicas of the same experiment designs (Apgar et al., 2010; Fox and Munsky, 2019; Hagen et al., 2013; Komorowski et al., 2011) (Transparent Methods). We verified the FIM computation by performing MLE parameter searches for 1,000 simulated datasets per experiment design (Transparent Methods), and we found that 95% confidence intervals of MLE pairwise parameters match their 95% confidence intervals predicted by the FIM analysis (Figures 4C, 4D, S4J, and S4K). The verified FIM analysis shows that MLE estimates will have the least uncertainty when trained with diverse kinetic profiles when compared with homogeneous profiles (compare ellipses in Figures S4K and S4J, respectively). This improvement is explained by the fact that different kinetic profiles constrain different combinations of parameters resulting in different parameters uncertainties (Figures 4F and S4L–S4O), as shown for a specific pair of parameters (λ₁₁,λ₁₂) that defines the regulation of the terminal kinase through the activity of phosphatases (Figure 4G). Next, we employed a complementary Bayesian analysis to quantify the posterior uncertainty of parameters given a single set of training data (see Transparent Methods). In agreement with the frequentist analysis, we found that posteriors for homogeneous inputs were much broader than those found for the diverse input signals (Figure 4E).

Because the frequentist FIM analysis requires no data generation or fitting, it is many orders of magnitude more computationally efficient than the Bayesian analysis. Using the verified FIM to estimate the expected uncertainty for a given combination of input kinetics, we could next explore all possible combinations (36 choose n) for up to n kinetic inputs (2,391,495 total). Through this exhaustive search, we found that the D-Optimal (i.e., the set of experiments expected to minimize the determinant of FIM⁻¹) combination of n = 6 kinetic inputs was a diverse combination composed of inputs of two steps to 0.5 and 0.7 M (t⁰), one root to 0.7 M ($\surd t$), one quadratic to 0.5 M (t²), and two heptics to 0.5 and 0.7 M (t⁷). This optimal experiment further reduces total parameter uncertainty compared with steps or the original diverse kinetics (Figure 4H). Comparing the determinants of covariance of the posterior (Det(cov)) for all parameters using the Bayesian approach, we find that the posterior for the FIM D-Optimal inputs was tighter when compared with diverse and homogeneous step input signals (compare Det(cov) in Figures 4J–4L).

We next applied these frequentist and Bayesian perspectives to ask how parameter uncertainty affects prediction accuracy. To answer this question from the frequentist perspective (i.e., how sensitive are predictions to the spread of MLE-based estimations corresponding to different replicas of the same experiment), we sampled parameter sets from a multivariate distribution centered at the true parameters and distributed with a covariance matrix equal to the inverse FIM. To answer this question from the Bayesian perspective (i.e., how sensitive are predictions to parameter uncertainty after constraining to a single replica experiment), we used Monte Carlo to sample parameter sets from the posterior distribution (see Transparent Methods). In both cases, we found that predictions based upon models fit to the diverse data as well as the FIM D-Optimal design provided much tighter and more accurate estimates of behaviors in unseen testing conditions (Figures 4I–4L). Our results indicate that six-step training datasets achieve an average prediction error within 143% of the standard deviation of data. In comparison, six diverse and six D-Optimal datasets result in average prediction errors within 79% and 87% of the standard deviation of the data (compare <PE>/std in Figures 4J–4L). We find that with the optimally designed experiments, a combination of three diverse experiments (comprised of one step (t⁰), one quadratic (t²), and one heptic (t⁷) input), constrain the parameters sufficiently well to make predictions within 70% of the standard deviation of the data (Figure 4I). For clarity, results in Figure 4I are obtained using the frequentist approach while those in Figures 4J–4L are obtained using the Bayesian approach.

These results indicate that signaling models built based on one type of kinetic stimulations may be predictive under different intensities of that same kinetic input, but they are likely to fail to predict pathway responses upon other types of kinetic stimulations. This is important to consider because most computational models to date are often parametrized with measurements performed under constant stimulation profiles (Hao and O'Shea, 2012; Shaw et al., 2019). We find that training the model simultaneously with diverse kinetics constrains parameters better and improves predictions substantially.

Diverse Kinetic Stimulations Improve Identification of Model Structures

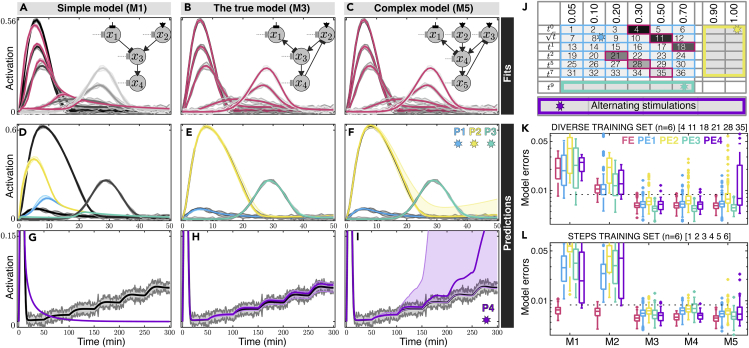
Next, we examined how kinetically different cell stimulations affect model structure identifiability (e.g., the number and mechanisms of interacting signaling proteins), and we sought to elucidate the contribution of specific signaling proteins to overall dynamic signaling responses. Figures 5 and S5 show fits (red) and predictions (blue, yellow, green, and purple) of five models with varying complexity to six different signaling response dynamics. This analysis is performed using datasets that are simulated from model M3. Simpler models were built by removing one or two regulatory elements from M3 to form M2 or M1, respectively, to simulate two mutants of the true model where the corresponding kinase activities are removed resulting in loss of feedback regulations (Figures S5A–S5C). A more complex model was built by adding two extra regulation elements to the true model, which could represent unknown regulatory elements yet to be discovered such as feedbacks from the terminal kinase to the upstream kinases (Figure S5D, model M4) (Suzuki et al., 2020). Finally, another complex model is generated by adding an entirely new signaling branch consisting of a third sensor node and introducing three additional regulatory elements to the true model that could correspond to SHO1 sub-branches in the HOG pathway (Figure S5E, model M5) (Tatebayashi et al., 2015). As expected, the simplest model cannot fit all data simultaneously (Figures 5A, S5A, and S5B, red), whereas the true model and the more complex models both fit well to the simulated data (Figures 5B, 5C, and S5C–S5E, red). In each case, multiple MLEs were performed and models were then used to make four sets of predictions (Figures 5D–5I, blue, green, yellow, purple) (see Transparent Methods). As expected, the simple model does not predict well (Figures 5D and 5G), whereas the medium and complex model predictions are consistent with the true responses, but with an increasing level of prediction uncertainties (Figures 5E, 5F, 5H, and 5I).

Figure 5.

Kinetically Diverse Stimulation Profiles Enable Unprecedented Model Predictions

(A–I) Predictions enable identification of the true model among models of increasing complexities. (A–C) Three models with increasing complexity from left to right (M1 in A, M3 in B, and M5 in C) each are trained with six diverse kinetics datasets that are simulated from M3 (see Transparent Methods). Model fits are shown in red and compared with training data in gray. (D–I) Model predictions (examples of Predictions1 in blue, Predictions2 in yellow, Predictions3 in green, and Predictions4 in purple) are compared with their corresponding test data (gray) indicated with stars in the table of train/test data in (J). Thick lines and shaded areas in gray show the means and the standard deviations of synthetic data, respectively. Thick lines and shaded areas in red, blue, yellow, green, and purple show 10, 50, and 90 percentiles out of independent MLE fits of each model and their corresponding predictions over time.

(J) An overview of sets of training and testing data that are used for fits and predictions. Red, blue, yellow, green, and purple squares indicate the datasets used in (K), and stars indicate predictions that are presented in (D–I). (K) Quantification (boxplots) of fit and prediction errors for five models of increasing complexity after training each model with six diverse kinetics (see Transparent Methods and Figure S5 for model definitions and further analysis). Horizontal dotted black line denotes the standard deviation of the simulated data. Fit errors (FE) statistics are drawn from six train datasets over multiple independent trainings. Similarly, PE1, PE2, PE3, and PE4 are drawn from prediction errors of testdata1 (30 datasets, blue in J), testdata2 (12 datasets, yellow in J), testdata3 (6 datasets, green in J), and testdata4 (4 datasets, purple in J with stimulation profiles given in Figures S3E–S3H), respectively, each collected over multiple independent fits. Predictions for M4 and M5 are all specifically collected from MLEs that have objective of at least as low as that of converged M3 MLEs.

(L) Quantification of fit and prediction errors for five models of increasing complexity after training each model with six step kinetics. See also Figure S5.

We next performed systematic cross-validation of fits to specific input-output responses and prediction validation analyses using other datasets to explore how identification of a predictive model structure (e.g., selecting among models M1 to M5) depends on the specific types of training and validation data (Figures 5J–5L, S5F, and S5G). In all cases, as the model complexity increases from M1 to M5, the fits to training data improve monotonically (Figures 5K and 5L, S5F, and S5G, red), but the validation errors should reach a minimum when using the model structure that is most predictive given the available data (Figures 5K and 5L, S5F, and S5G, non-red markers). When training data consist of steps, simpler models (M1 and M2) fit well to the simulated data, therefore it is not possible to distinguish the true model using only steps data (Figure 5L). By quantifying predictions of each model upon all kinetic inputs (Figure 5J), it is possible on average to identify the true model (M3), but the certainty of structure identification depends heavily on the type of validation data (compare different colors in Figure 5L). In comparison, similar to diverse training data (Figure 5K), when using optimal experiments suggested by the FIM analysis, the over-simplified models fit less well to training data (Figures S5F and S5G), and validation data allowed for more certain selection of the true model. These results demonstrate that different kinetic cell stimulations can improve predictability in the process of complex model structure identification.

Diverse Kinetic Stimulations Improve Predictions of Mutant Responses

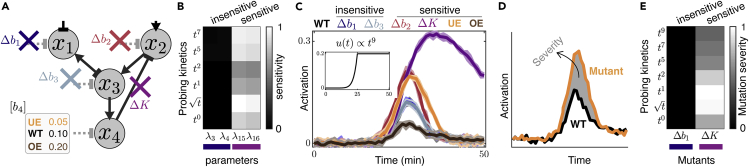
Finally, we examined how diverse kinetic stimulations affect predictive performance for other in silico biologically realistic mutations to specific signaling proteins in signal transduction pathways (Figures 6A and S6) (Hohmann et al., 2007; Mattison and Ota, 2000; O'Rourke and Herskowitz, 1998; Westfall and Thorner, 2006; Young et al., 2002). Sensitivity analysis of the wild-type (WT) model that was trained with diverse kinetics allowed us to categorize model parameters into two main groups of insensitive (sensitivity = 0) and sensitive (sensitivity = 1) parameters that we then use to predict putative mutations (Figures 6A, 6B, and S6). To determine whether diverse kinetic cell stimulations can identify biological mechanisms, we computationally introduced six mutations in our true model (Transparent Methods). These include three knockout mutants that remove basal deactivators on x₁ (Δb₁, blue cross), x₂ (Δb₂, red cross), or x₃ (Δb₃, teal cross). Mutants Δb₁ and Δb₂ can be interpreted as removing the constitutive deactivation of SLN1 or SHO1 branches, respectively, which could change the half-life of their active states. Mutant Δb₃ could represent regulation of Pbs2 through deletion of Ptc1/2/3 phosphatases. The node x₄ can be mutated by removing kinase activity of x₄ (ΔK, purple cross, e.g., kinase dead or kinase activity inhibited) and can be regulated through overexpression (b₄, OE, orange), and underexpression (b₄, UE, brown) of the basal deactivator on x₄ such as the Ptp2/3 phosphatases (Figure 6A).

Figure 6.

Kinetically Diverse Stimulations Elucidate Dynamic Effects of Mutants

Training the WT true model (M3 in Figure 5B) on its signaling dynamics upon diverse kinetics (red in Figure 5J) reveals insights into the response of several mutated models under all tested kinetic inputs. (A) The six mutants of the WT model correspond to deletions of basal regulators (e.g., phosphatases) on x₁ (Δb₁, blue), x₂ (Δb₂, red), or x₃ (Δb₃, teal); removal of the kinase activity (e.g., kinase dead or inhibited MAPK) of x₄ (ΔK, purple); and under- or overexpressing b₄ (e.g. phosphatase) that regulates x₄ (UE in orange and OE in brown). (B) Sensitivity analysis of WT model with respect to model parameters around their best value from the fits predicts insensitive (e.g., λ₃ and λ₄ corresponding to Δb₁) and sensitive (λ₁₅ and λ₁₆ corresponding to ΔK) mutants (see Figure S6). (C) Comparing the activation dynamics of mutants (simulated using ${\text{Λ}}^0$ in Table S1) with WT under a representative kinetic input (t⁹ to 0.2 M, inset). Thick line and shaded area (colors) show the mean and the standard deviation of synthetic data for the corresponding strains. (D) Mutation severity, defined as the difference in activation dynamics of a mutant from that of the WT (Transparent Methods). (E) Mutation severity is shown for two representative mutant strains, Δb₁ (insensitive) and ΔK (sensitive) over all kinetic types summed over all their final concentrations. See also Figure S6.

We simulated corresponding synthetic pathway activations from all six mutants upon all 54 kinetic stimulations (Transparent Methods). Pathway activations upon a representative kinetic stimulation input of t⁹ are shown for all six mutants compared with the WT in Figure 6C. To quantify the differences in signaling dynamics between normal and mutant cells, we define severity as the difference in the activation dynamics of a mutant compared with that of the WT (Figure 6D and Transparent Methods). We observed that pathway activation in some mutant strains shows no difference from WT under all kinetic inputs (Δb₁ and Δb₃, mutation “severity” = 0), whereas other mutants with non-zero severity (Δb₂, ΔK, UE, and OE) are different from WT (Figure 6C). Comparing the sensitivity with respect to specific parameters in the model (Figure 6B) with the severity of the corresponding mutants' effect on signaling dynamics (Figure 6E) highlights that sensitive parameters are indicators of how much specific mutations will affect signaling under different kinetics of specific types (Figure S6). Furthermore, constraining the parameters of WT model on its synthetic data under diverse kinetic stimulations enabled us to accurately predict the activation responses of all the six mutants over time under all 54 kinetic inputs tested (Figures 7 and S7). These results are quantitatively summarized in Figure 7E, showing that the prediction errors for simulated mutations are comparable to prediction errors of non-mutated WT cells.

Figure 7.

Kinetically Diverse Stimulations Enable to Predict Mutants' Response Dynamics

Training the WT true model on its signaling dynamics upon diverse kinetics enables predictions for the response of mutants upon all tested kinetic inputs.

(A) A mutant where the kinase activity of x₄ is eliminated (e.g., kinase dead or inhibited MAPK, purple cross) leads to a loss of feedback regulation from x₄ on x₂.

(B) Extracellular stimulation of the models results in elongated response adaptation in ΔK mutant compared with WT.

(C and D) Example pathway activation predictions (predictions3 in green) are compared with their corresponding synthetic data for WT (C, gray) and ΔK (D, purple) under representative t⁹ kinetic inputs.

(E) Prediction errors (PE1, PE2, PE3) are quantified over all 54 kinetics (Figure 1H) for each of the six mutants (Figure 6A) compared with WT. These predictions are made using parameters constrained from five independent fits of WT model tarined on its signaling dynamics upon six diverse kinetics in Figure 5J.

See also Figure S7.

Discussion

Our experimental and simulation results demonstrate that different kinetic cell stimulations of a pathway give rise to distinct signaling activation dynamics (Figure 1). When compared with the same amount of any type of homogeneous kinetics, kinetically diverse cell stimulations perform much better to constrain complex model parameter sets and result in substantially reduced predictions errors (Figures 3 and 4). The FIM analysis approach provides a rigorous and clear mathematical interpretation of this effect. Specifically, the eigenvector of the FIM corresponding to the greatest eigenvalue indicates the parameter combination that is most likely to be accurately identified using a given kinetic stimulation (Figure S4O). By comparing eigenvectors corresponding to large FIM eigenvalues, it is easy to see which kinetic type may be most effective to constrain specific parameters of a complex regulatory network. Similarly, by examining eigenvectors corresponding to small FIM eigenvalues, it becomes apparent which parameter combinations cannot be precisely identified using a specific kinetic input. By choosing diverse and complementary input kinetics, such that the full parameter space is spanned by high-eigenvalue FIM eigenvectors from one or multiple kinetic inputs, it becomes possible to constrain the entire parameter set (Figures 4F, 4G, and S4L–S4O).

Better constrained parameters make it easier to identify predictive models of signal transduction (Figures 5 and S5). This also enables improved predictions of pathway activation dynamics for protein mutant strains upon kinetic stimulations (Figures 6, S6, and S7). To illustrate these predictions, we revisited the HOG pathway as an example (Figure 6). We predicted that mutations that alter the SLN1 branch (b₁) will not impact Hog1 signaling dynamics, which is consistent with previously published observation that changes in Ypd1 do not alter Hog1 signaling (Mukherji, 2010). Next we focused on the node x₂ that describes the SHO1 branch in which mutating b₂ could result in an increase or decrease in Hog1 signaling. We predicted that Δb₂ results in increased Hog1 signaling amplitude. In addition, the SHO1 branch can be altered in its activity by the feedback regulation from Hog1 kinase. In our model, we predicted that removing Hog1 kinase activity or inhibiting Hog1 kinase activity (ΔK) results in increased and prolonged Hog1 activation, which is consistent with previous published experimental work on small molecule inhibition of Hog1 activity (Muzzey et al., 2009; Westfall and Thorner, 2006). Next, we focused on the node x₃, which represents Pbs2. Our model predicted that deletions of individual phosphatases such as Ptc1/2/3 would not alter Hog1 signaling dynamics through changed Pbs2 activity (Δb₃) (Mapes and Ota, 2004; Warmka et al., 2001). Last, x₄ represents the terminal kinase Hog1 that can be deactivated through phosphatases Ptc1/2/3 and Ptp2/3 (b₄) (Martín et al., 2005; Murakami et al., 2008; Warmka et al., 2001; Young et al., 2002). The model predicted that changing the value of b₄ through over- or underexpression has a strong impact on Hog1 signaling intensity. The experimental observations of the effect of above-mentioned mutants on the HOG pathway dynamics under step profiles qualitatively aligns with our simulated data for all mutants validating our modeling approach for mutants (Figure 6) (O'Rourke and Herskowitz, 1998; Saito and Posas, 2012; Tatebayashi et al., 2015; Warmka et al., 2001). Using simulated data, we verified our mutant findings by quantitatively comparing predictions from each mutant to their corresponding synthetic data (Figure 7).

These results demonstrate that kinetic cell stimulations are ideally suited to discover novel regulatory interactions, reveal key functional proteins, identify predictive and biologically meaningful models, and help to gain novel insights to cell function or dysfunction. The potential for generality of kinetic stimulations is supported by emerging studies in many pathways and in different cell types. Examples are differential cellular responses upon step, pulsatile, or linear stimulations of EGF (Akt pathway, PC12 cells, Fujita et al., 2010), TGF-β (TGF-β pathways, myoblast progenitor C2C12 cell line, Sorre et al., 2014), cytokines IL-6 (STAT1/3, lymphocytes, Twohig et al., 2019) and TNF (NF-κB signaling, HeLa/neuroblastoma cells, Ashall et al., 2009; Mokashi et al., 2019), insulin (Akt/S6K pathway, rat hepatoma Fao cells, Kubota et al., 2012), H2O2 (Yap1 signaling, yeast cells (Goulev et al., 2017), or diacetyl in tetramisole hydrochloride (C. elegans AWA neurons, Rahi et al., 2017). We believe that implementing diverse kinetic stimulations may provide new opportunities in constraining complex model parameters in situations where experimental design methods based on instantaneous changes in the environment such as steps or pulses of varying heights or frequencies have not provided great success (Billings, 2013; Isermann and Münchhof, 2011). Given the complexity of signal transduction networks (Akhurst and Hata, 2012; Cildir et al., 2016; Hanahan and Weinberg, 2000; Hata and Chen, 2016; Hotamisligil and Davis, 2016) and their limited response bandwidths (Hersen et al., 2008), steps or pulsatile stimulations of even varying intensities or frequencies may not provide enough kinetics to efficiently probe the rich dynamics underlying these networks (Billings, 2013; Isermann and Münchhof, 2011). Our approach on the other hand is widely applicable to many biological pathways that respond to a kinetic cell stimulation with a dynamic signaling response, and our approach may have far-reaching implications for predicting pathway response upon specific mutations or drugs (Akhurst and Hata, 2012; Cildir et al., 2016; Hanahan and Weinberg, 2000; Handly et al., 2016; Hata and Chen, 2016; Hotamisligil and Davis, 2016; Janes and Lauffenburger, 2013; Rowland et al., 2011; Vanhaelen et al., 2017; Lim and Bruce Mayer, 2017). Being able to predict the pathway activation dynamics upon mutations or upon environmental changes may help design better drug treatment regimes. In addition, these results could benefit our understanding of human biology, particularly in areas such as optogenetics, gene regulatory networks, or synthetic biology, where predictive understanding of the system behavior with respect to extracellular kinetics or intercellular genetic perturbations is of immense interest (Aoki et al., 2019; Bashor et al., 2019; Gardner, 2013; Harrigan et al., 2018).

Limitations of the Study

The basic requirement for applying this framework to other systems is (1) that different environmental gradients can be generated, (2) that the pathway response changes over time, (3) that the pathway response time is homogeneous from cell to cell, and (4) that the central limit theorem is fulfilled in single cells.

Resource Availability

Lead Contact

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Gregor Neuert (gregor.neuert@vanderbilt.edu).

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

The datasets and code generated during this study are available at https://github.com/neuertlab/Jashnsaz_iScience_2020. The published article includes all datasets generated and analyzed during this study.

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Published: October 23, 2020