Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Sep 7;6(10):5620–5631. doi: 10.1021/acsbiomaterials.0c00975

Tissue Rheology as a Possible Complementary Procedure to Advance Histological Diagnosis of Colon Cancer

Piotr Deptuła †, Dawid Łysik ‡, Katarzyna Pogoda §, Mateusz Cieśluk †, Andrzej Namiot ⊥, Joanna Mystkowska ‡, Grzegorz Król ∥, Stanisław Głuszek ¶,∇, Paul A Janmey ○,◆, Robert Bucki †,*
PMCID: PMC7549092  PMID: 33062848

Abstract

graphic file with name ab0c00975_0008.jpg

In recent years, rheological measurements of cells and tissues at physiological and pathological stages have become an essential method to determine how forces and changes in mechanical properties contribute to disease development and progression, but there is no standardization of this procedure so far. In this study, we evaluate the potential of nanoscale atomic force microscopy (AFM) and macroscopic shear rheometry to assess the mechanical properties of healthy and cancerous human colon tissues. The direct comparison of tissue mechanical behavior under uniaxial and shear deformation shows that cancerous tissues not only are stiffer compared to healthy tissue but also respond differently when shear and compressive stresses are applied. These results suggest that rheological parameters can be useful measures of colon cancer mechanopathology. Additionally, we extend the list of biological materials exhibiting compressional stiffening and shear weakening effects to human colon tumors. These mechanical responses might be promising mechanomarkers and become part of the new procedures in colon cancer diagnosis. Enrichment of histopathological grading with rheological assessment of tissue mechanical properties will potentially allow more accurate colon cancer diagnosis and improve prognosis.

Keywords: tissue rheology, colon cancer, mechanomarkers, mechanobiology, histopathology

1. Introduction

Colorectal carcinomas are one of the most common types of cancers diagnosed in patients worldwide, and they are a leading cause of death in both Europe and the United States.1−3 Although over the past decade, the incidence and mortality of colorectal cancer have decreased, 20–25% of patients with colon cancer have metastases at the time of diagnosis and a large percentage (up to 60%) of the others will develop metastases later. Most of those cases of metastasis are fatal.1,4,5 More than 90% of colorectal carcinomas are adenocarcinomas originating from epithelial cells of the colorectal mucosa.6 Smaller fractions of colorectal carcinomas include neuroendocrine, squamous cell, adenosquamous, and spindle cell tumors.6 Histopathology of colon cancers includes accurate assessment of their origin and pathological stage as well as analysis of surgical tissue margins.6 For colorectal carcinomas, histopathology is the clinical standard technique and an important final confirmation of diagnosis, which will determine the patients’ therapy, treatment options, and potential outcomes.6,7 Because of tissue handling steps required for histopathological grading, limitations resulting from the tissue shape, sample size, and orientation make this analysis time-consuming and might give misleading and inconsistent results.6−8 Despite significant advances in cancer diagnostic methods, new early detection techniques that speed up the time of diagnosis, especially for patients at the early stage of the disease, are needed. In recent years, more attention is paid not only to morphological and molecular screening of the tissue samples but also to their mechanical properties, in order to fully understand the physiological and pathological processes at the cell and tissue level.9−17

All physiological processes and their malfunction during disease development require structural changes that manifest at different organization levels in organs, tissues, single cells, and cellular organelles. All of these structures have specific mechanical properties that can be characterized by rheological parameters. However, relating structural elements to mechanical properties is especially complex within biological samples and depends on the internal cell rearrangements and cellular interactions with molecules that compose the extracellular matrix (ECM) of stroma (e.g., fibrous proteins, proteoglycans, hyaluronic acid, chemokines, growth factors). Most of the factors that determine tissue/cell rheology cannot presently be assessed during the histological evaluation, even if they tightly connect to the health status of the organism,9 and these properties are important in maintaining proper functionality of the organ.10,11,18 Very often, tissues increase their stiffness during the pathological development and progression of cancer,19−22 and some types of tumors can even be detected by physical palpation.23 Cancerous tissues are characterized by an abnormal altered stroma that facilitates cancer development by providing nutritional support and imposing a barrier for host defense mechanisms.24 The tumor stroma consists of fibroblasts, immune cells, vasculature, fibrillar proteins, and an ECM composed mainly of collagen I, fibronectin, and elastin as well as hyaluronan and other glycosaminoglycans.24,25 Abnormal changes in stroma include an increase in ECM stiffness and an accumulation of stress gradients inside the tumor mass.24,26 Abnormal mechanical stresses can increase the invasive and metastatic potential and migration of cancer cells and tissue development.27−29 Mechanical effects are likely to be especially important in colon cancer because human colon cancer-derived cell lines show strong responses to substrate stiffness and can initiate metastasis-related phenotypes in a stiffness-dependent manner.30,31

To analyze the mechanical properties of soft biological samples, various techniques, such as atomic force microscopy (AFM), shear rheometry, micropipette aspiration, optical stretching, and magnetic twisting cytometry, have been developed.11 Atomic force microscopes and shear rheometers, which can quantify the mechanical properties of soft tissues, are promising tools in terms of cancer diagnosis and assessment of anticancer treatment effectiveness. AFM offers the capability of surface imaging at the nanoscale and nanomechanical characterization by indentation of soft biological materials such as cells and tissues under physiological conditions.11,13,14,20,32,33 Not only is AFM a useful tool to assess the mechanics of biological samples, but also there are attempts to apply it for routine cancer diagnosis.13,34 It is also possible to characterize healthy and diseased tissues in vivo using noninvasive techniques such as shear wave elastography (SWE) and magnetic resonance elastography (MRE).35−38 Elastography is an imaging technique that infers stiffness by examining a tissue’s response to externally applied mechanical excitation. Excitation leads to the tissue deformation, which can be measured.39 Despite their undeniable advantages, these methods have drawbacks due to the complex structure of the tissues and the location of the organs away from the source of excitation and because the results strongly depend on the excitation frequency, which is often greater than the time scale to which cells respond.35−37 A combination of ex vivo rheometric analysis with in vivo measurements by elastography has the potential to increase reliability and clinical utility of mechanical measurements. Recently, the idea of employing shear rheometers to evaluate the mechanical state of cells and tissues in the clinical routine has gained interest,14,22,40 but there is a need to develop and describe useful biomarker(s), or more precisely mechanomarker(s), that will be a measurement outcome and could support current diagnosis. Moreover, when it comes to clinical oncology, such mechanomarker(s) must be well characterized and repeatedly predict the relevant stage of the disease. The aim of this study was to assess the potential of atomic force microscopy and shear rheometry to measure mechanical properties of fresh human colon tissues and to verify if there are clear mechanical indicators of the cancer state that could support histopathological scoring and strengthen cancer diagnosis and/or classification.

2. Experimental Section

2.1. Materials and Methods

2.1.1. Tissue Samples

Mechanical properties of fresh human healthy and cancer colon tissues were tested by atomic force microscopy and shear rheometry. Biopsy specimens were obtained from four patients diagnosed with colorectal carcinomas at the Clinical Department of General Oncological and Endocrinological Surgery, Regional Hospital, Kielce, Poland. The collection of tissue samples was performed in accordance with an IRB (no 18/2019 approved by the Bioethics Committee of the Faculty of Medicine and Health Sciences, Jan Kochanowski University, Kielce, Poland). All tissue samples were stored in Dulbecco’s Modified Eagle Medium (DMEM; Sigma-Aldrich, St. Louis, MO) and measured within 5 h postsurgery. The patient population included both males and females. A sample of cancerous and healthy tissue (a margin) was collected from each patient. Healthy tissue was dissected in order to reach the tumor tissue. All diseased tissue samples were collected from patients with Stage III cancer, where the tumor had grown to a specific size. We confirmed the cancer stage using standard histological procedures. No cancer metastases were found in the patients. Healthy tissues without physical interaction with the tumor were harvested from a location in the colon 10 cm away from the tumor mass. Tissue samples were harvested from the descending and sigmoid colon.

2.1.2. Rheological Characterization

In the first step of our investigations, small, millimeter-scale samples obtained from the biopsy of human tumors as well as healthy colon tissues were measured with a NanoWizard 4 BioScience JPK Instruments atomic force microscope (AFM) working in the force spectroscopy mode. Force indentation curves were collected using a silicon nitride cantilever with a nominal spring constant of 0.62 N/m and measured spring constant in the range of 0.4–0.6 N/m using the thermal tune method, with a 4.5 μm diameter polystyrene bead attached. The cantilevers were manufactured by Novascan Technologies, Inc. (Figure 1A).

Figure 1.

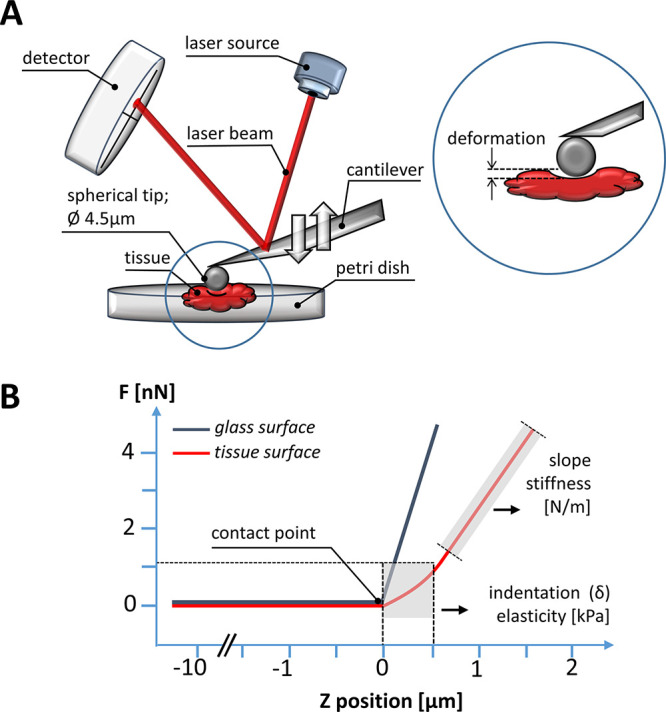
Figure 1

Open in a new tab

AFM experimental setup: (A) The main AFM components are a cantilever with a spherical tip (4.5 μm in diameter bead), a laser source, a photosensitive photodiode, and a piezoelectric scanner that can accurately apply compressive force to soft tissues at the nanoscale. The application of the compressive force measured as a function of the sample’s position in the Z-direction gives rise to so-called force vs distance curves (B). The difference between the cantilever deflection on a stiff glass or hard plastic surface (blue curve) and the soft, sample (red curve) describes the deformation of the tissue sample under the load, which allows the determination of the sample’s modulus of elasticity (Young’s modulus).

The bead–tissue contact area during the tests ranged from 7 to 32 μm2, depending on the depth of indentation. AFM experiments were made maximally 5 h after biopsy, and tissues were kept in culture medium during the experiments at 37 °C. Tissues were glued using cyanoacrylate glue onto a Petri dish and immersed in DMEM for measurements. To account for cantilever bending, force curves were first recorded on a rigid plastic substrate, and then, the rigid surface was replaced by the compliant tissue sample. Indentations were carried out in multiple places on the tissue surface. Up to 15 maps consisting of 8 × 8 points corresponding to a scan area of 10 × 10 μm were made for each sample. Indentations were carried out in multiple places on the tissue surface, in the central zone of each tumor sample. The difference between the cantilever deflection on a rigid surface and the compliant tissue sample describes the deformation of the tissue under the bead load (Figure 1B). When the force used for deformation is plotted against the depth of indentation that this force induced, so-called force-versus-indentation curves can be obtained. To determine the elastic modulus (i.e., the Young’s modulus), we fitted the curves to the Hertz contact model for a sphere using following formula:

2.1.2. 1

where E* is the apparent Young’s modulus:

2.1.2. 2

If Esample ≪ Etip (as is true for living cells), then 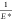Inline graphic can be simplified:

2.1.2. 3

Esample is the Young’s modulus of the tissue, and μsample is the Poisson ratio of the sample, related to the compressibility of the material10,41 and assumed to be 0.5 for an incompressible material, as is true for tissues. Histograms of the distributions of Young’s modulus values for each sample were prepared, and the mean values for all healthy and cancer tissues along with standard deviations were calculated.

Macroscopic rheometry, using a HAAKE Rheostress 6000 rheometer (Thermo Fisher Scientific, Waltham, MA, USA) fitted with a 20 mm diameter parallel plate system, was used to measure the viscoelasticity of tissue samples. The height of the tissue slices ranged from 3 to 5 mm in the uncompressed state. Healthy and colon cancer tissues were cut into disk-shaped samples using a 20 mm diameter steel punch. To avoid tissue slippage during the measurements, samples were placed on sand paper (P800) gaskets inside Petri dishes, and dishes were glued to the rheometer bottom plate (Figure 2A). Experiments were also made maximally 5 h after biopsy, and tissues were kept at 37 °C during the experiment. During the test, a sample hood was used to prevent heat loss and water evaporation from the tissue. The tests were carried out in the deformation control system, where the deflection of the upper measuring plate by the angle φ is converted into shear deformation:

2.1.2. 4

where r is the radius of the plate and h is the gap height between the rheometer’s plates.

Figure 2.

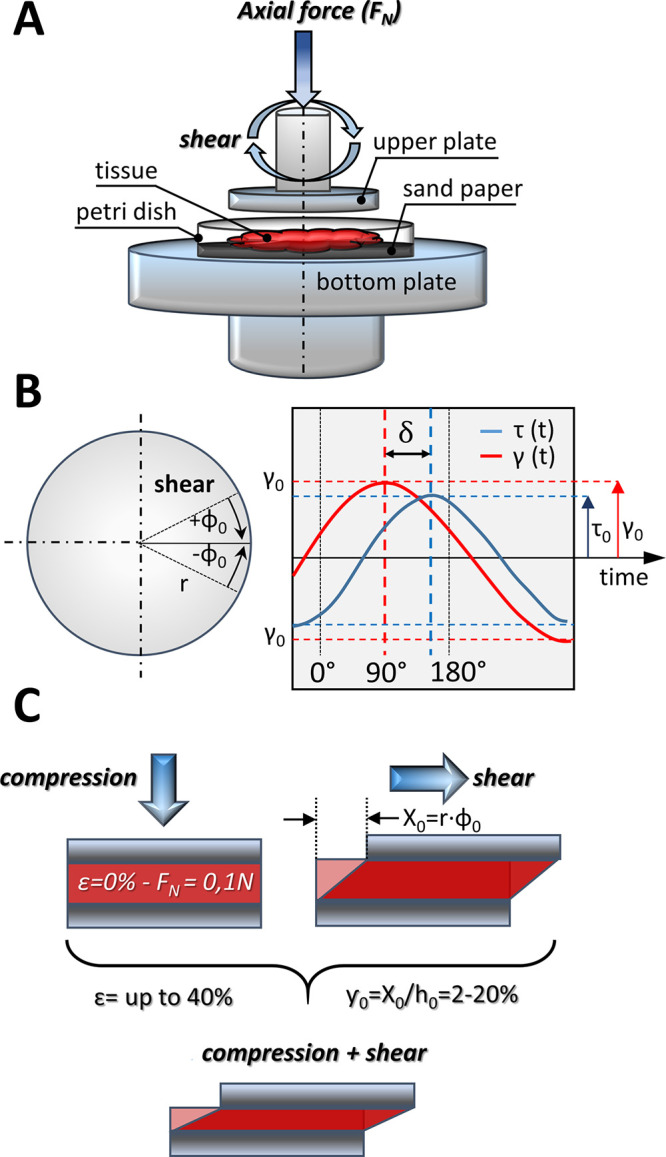
Figure 2

Open in a new tab

Rheological experimental setup: (A) human colon samples were cut to a diameter of 20 mm and placed on sand paper. Tension and compression were caused by applying force in a direction perpendicular to the tissue samples. Sample stress as a function of axial deformation and time, storage modulus and loss modulus as a function of axial strain, and axial stress and shear strain as well as changes of phase shift as a function of shear strain were measured; (B) viscoelastic behavior of the sample (as a sinusoidal function versus time with phase shift between them); (C) stresses applied to the sample: shear forces (in combination with tissue compression, axial stress) were applied by rotating the upper plate in a direction parallel to the sample.

The measured torque M corresponds to the stresses τ in the sample:

2.1.2. 5

In dynamic tests, the course of strain over time can be presented as

2.1.2. 6

where γ0 is the amplitude and ω = 2πf is the angular frequency (in our studies f = 1 Hz).

Viscoelastic tissues exhibit mechanical behavior somewhere between that of a purely viscous and a purely elastic material; therefore, there is a phase lag in the measured stress in relation to the applied shear strain. The shear stress as a function of time equals:

2.1.2. 7

where δ is the phase lag between stress and strain.

The complex modulus of viscoelasticity G* is the ratio of stress and strain:

2.1.2. 8

and the modulus of elasticity and viscosity can be calculated from

2.1.2. 9
2.1.2. 10

where G′ is known as the modulus of elasticity or storage modulus and G″ is known as the viscous or loss modulus.

The moduli are related to the phase lag angle δ by the relation Inline graphic. For an ideally elastic material, δ = 0°, and for an ideally viscous material, δ = 90° (Figure 2).

Two kinds of rheological tests were performed. The first consisted of oscillating shear deformation of the tissue with 2% constant shear amplitude (and constant frequency of 1 Hz) and simultaneous application of uniaxial strain, which was applied by changing the distance between the parallel plates, i.e., gap height, by lowering (compression) or lifting (extension) the upper plate in the range of 0–40% of the sample initial height with a 10% increment. During these tests, the course of normal stress (determined by dividing the recorded normal force FN by the surface area of the upper rheometer plate in contact with the tissue) and shear stress as a function of time was determined. The second test consisted of oscillating shear deformation of the sample with variable amplitude ranging from 2% to 20% at a frequency (f) of 1 Hz. At the same time, the tissue was subjected to constant compression in the range of 0–40%. In this way, the G′ and G″ moduli were obtained as a function of shear deformation in compressed and uncompressed states that mimic the range of deformations expected to occur in vivo. For example, gastric volume after a meal can change by a factor of 60 by unfolding and stretching of the gastric wall by as much as ∼160%.42

2.1.3. Histopathological Evaluation

Healthy and cancer tissues were subjected to histopathological scoring to illustrate mucosa and submucosa architecture. Intestines were fixed in 10% neutral-buffered formalin for 12 h, dehydrated in an automatic tissue processor (LEICA, TP1020), and embedded using a paraffin dispenser (Bio Optica DP500). Tissue orientation was chosen such that positions where AFM indentation was performed were visible on the microscopic slide, and the entire thickness of the examined tissue could be assessed. The paraffin blocks were cut on a microtome (Leica RM2125 RTS) for 1 to 2 μm thick sections, dewaxed, irrigated, and stained with hematoxylin and eosin (Diapath, Italy) using a dyeing machine (Bio Optica AUS124). Microscope slides were than evaluated using an OLYMPUS BX53 microscope.

2.1.4. Statistical Analysis

The significance of differences was determined using the two-tailed Student’s t test. Statistical analyses were performed using OriginPro 9.65 (OriginLab Corporation, Northampton, MA, USA). p < 0.05 was considered to be statistically significant. Results are the average from all force curves for each patient sample (Figure 3F). Overall average values of Young’s modulus are presented as mean ± SD, where the mean is the average value for the patient from all curves and SD is standard deviation.

Figure 3.

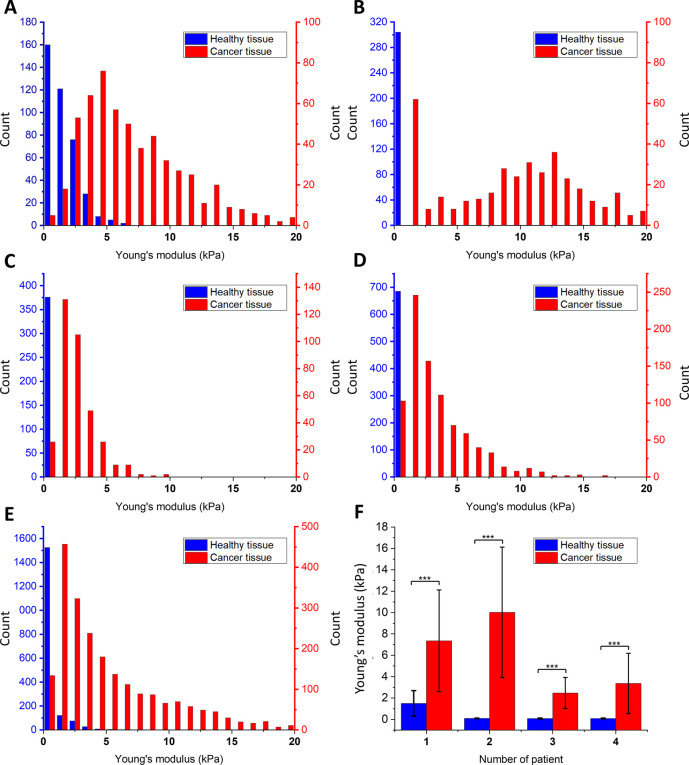
Figure 3

Open in a new tab

Young’s modulus values obtained for healthy and cancer tissues using AFM indentation: (A–D) The Young’s modulus distributions for healthy and cancer tissue for each patient. The blue column represents healthy tissues, and the red column represents cancer tissues: (A) patient no. 1; (B) patient no. 2; (C) patient no. 3; (D) patient no. 4; (E) Young’s modulus distribution for healthy and cancer tissue for all patients with fitted probability density function of the log-normal distribution; (F) average Young’s modulus values for each patient demonstrating the significantly smaller deformability of cancerous tissues compared to healthy ones.

3. Results and Discussion

For many human diseases including cancers, histopathology, along with genetic and molecular tests, is the standard procedure confirming diagnosis and directing therapy that translates into a patient’s treatment plan. Any additional method(s) supporting this procedure might be helpful to obtain more accurate diagnosis. Histopathology is performed using fixed tissues subjected to specific staining that allow the determination of the morphology of cells and changes in the tissue architecture, and using immunohistochemistry, the presence of specific markers is determined. However, information for the characterization of tissue mechanical properties is lost when the tissue is fixed after taking the sample. All biological structures at the organization level starting from cell organelles through whole cells, tissues, and organs have specific mechanical properties that can be characterized by rheological parameters, like elasticity or viscosity, and that affect their functions. Dysfunction of physiological processes during disease development usually generates changes in these structures that translate into changes of cell and tissue mechanical properties.10,11,18 However, these mechanical properties cannot be accurately determined when histopathology of fixed or frozen material is performed.

Cancer development is usually associated with a genetic mutation causing pathological alterations of the cell cycle and invasive motility. For most cancers, changes in tissue stroma are also important. In many cases, tissues stiffen during cancer progression.19,20,22,26 Quick and precise measurements of stiffness and other rheological parameters characterizing tissue mechanics, so-called mechanomarkers, might provide a new means to describe tissue pathology. In recent years, the development of AFM has provided a new method for nanoscale characterization of a wide spectrum of biomaterials, including human tissues,11,13−15,40,43 and stiffness is the key parameter to be determined. Solid material stiffness is generally defined as the resistance to deformation caused by the mechanical force after applying tension, compression, or shear to the material.11 Stiffness can be quantified by the corresponding modulus, such as Young’s modulus (elastic modulus), which is a quantity that measures a material’s resistance to being deformed elastically when uniaxial stress is applied.11,44 The elastic modulus of a material is defined as the slope of its stress–strain curve in the elastic deformation region.44 Basic laws of mechanics can be applied to study the physicochemical properties of biological materials, such as human healthy and diseased tissues.21,45 In the course of this study, we assessed the potential of atomic force microscopy and shear rheometry to determine the rheological properties of healthy tissue margins and diseased colon tissues to test the hypothesis that rheological data might be used to complement the histopathological description of colon cancer tissue. In our work, we have used colloidal AFM tips as nanoscale indenters together with Hertz contact mechanics to determine tissues stiffness with high resolution.

3.1. AFM Measurements

AFM testing consisted of the series of loading–unloading cycles over the tissue’s surface with a constant force of 1 nN. Figure 3 shows relative values of the Young’s modulus distributions for 4 patients, where healthy and cancer tissues were compared.

We observed that the values of Young’s moduli for healthy and diseased tissues using the AFM method are significantly different and much greater for cancer tissue than for healthy tissue. These results agree with previous reports11,13,14,34 that cancer development and progression are associated with changes in mechano-cellular phenotype and manifested by changes in tissue stiffness with cancer tissue being stiffer than the healthy tissue of its origin.

Figure 3A–D shows distributions of the Young’s modulus values for each sample. Young’s modulus values of cancer samples are shifted to higher values, and a significant difference between healthy and diseased tissues stiffness can be seen. The summary histogram presented in Figure 3E shows the overall results obtained for all samples. The mean Young’s modulus value and the calculated standard deviation for healthy tissue is 0.44 ± 0.3 kPa, whereas for cancer tissue, it is 5.80 ± 3.8 kPa (Figure 3F). Only one of the healthy tissue samples showed higher stiffness in comparison to the other healthy samples (patient 1), but still, it is significantly softer than cancerous tissues (Figure 3A). This may mean that the process of fibrosis or neoplastic change could have started earlier than visible changes in the morphology of tissue cells, especially when histopathological examination did not confirm the presence of neoplastic changes. Previous studies clearly indicate that deviations in the stiffness and complex mechanics of cancerous tissues are closely related to alterations in the extracellular matrix, which provides structural support for cells allowing their proliferation, motility, and survival.46 The distributions of Young’s modulus values are similar to previously reported data for the stiffness of human breast cancer tissues that support an attempt to provide an approach for nanomechanical profiling of breast cancer.34 Stiffness profiles observed in our study for healthy colon tissue, characterized by a single sharp peak, differ from the broad distribution of Young’s modulus in colon cancer, indicative of tissue mechanical heterogeneity in disease. The high heterogeneity of cancer tissue architecture is reflected in the shape of the histograms presented in Figure 3, which are much wider for samples from cancerous than normal tissues. This difference is also manifested in the error bars (standard deviations) of the averaged values presented in Figure 3F. The increase in tissue stiffness may be associated with extracellular matrix protein alignment or overexpression, especially of different types of collagens, increased matrix fibrosis, cross-linking, and vascularization during cancer progression.18,26,47 Despite many possible sources of ECM alterations, their overall contribution to the tissue mechanical properties is significant, and we propose to use stiffness as a new mechanomarker of colon pathology.

On the other hand, we cannot disregard the challenge posed by the accurate measurement of tissue stiffness that has recently been expressed.48 It is reasonable to propose that tissue stiffening is not a simple process that is proportional to the extent of cancer progression because of the nonlinear mechanical nature of tissues and the compression stiffening that can arise as pressure gradients develop in solid tumors. Furthermore, tissue sections from solid tumors are complex nonlinear materials that can exhibit molecular, cellular, and architectural alterations, manifested by various mechanical properties with microranges. When measuring the stiffness map using an atomic force microscope in a traditional way, we do not know the exact place where the AFM’s tip contacts the tissue, thus lacking information about the correlation between the stiffness and local tissue morphology. The small contact area and relatively low indentation caused by the AFM tip results in small deformations where only individual cells or their parts undergo compression. Overall, the AFM strategy, as a procedure of colon cancer diagnosis, should include a large number of measurements performed at different locations in order to get a useful mechanical profile of the examined tissue. As argued clearly in a previous report,48 there is currently no possibility to base the entire colon cancer diagnosis on AFM studies. Therefore, progress in AFM technology will be required to develop a method that will offer an accurate test to examine the extraction of tissue samples collected during biopsy or surgical procedures. Rheology tests can serve as an additional step to expand histopathological procedures, especially when facing disputable cases and when microscopic based diagnosis is unclear. Overall, there is significant potential for AFM as a device for identification and early cancer grading and classification.11,13,48

3.2. Shear Rheometry

In general, rheological properties of tissues, especially soft ones, might be determined with higher accuracy using shear rheometry.14,22,40 In our study, more detailed mechanical properties of colon cancer tissues subjected to different compression levels are described. One of the biggest advantage of using shear rheometry is that it allows the determination of the mechanical properties of a larger fragment of the 3D tissue and gives average mechanical parameters for the entire tissue volume, not just for the thin surface layer of the cells and extracellular matrix that is in contact with the AFM probe. The large size of the biopsy specimens allows for more thorough tissue rheological characterization in a strain-controlled shear rheometer. Figures 4–6 show the change in axial stress as a function of axial strain and time, storage modulus (G′) and loss modulus (G″) as a function of axial strain, and axial stress and shear strain as well as changes of phase shift as a function of shear strain. Our first observation using strain rheometry showed, similarly to the AFM results, that cancer tissues are clearly stiffer than normal ones, which can be seen as an increase in storage modulus G′ of cancer tissues compared to G′ of normal tissues (G′ for healthy tissue, 1.52 kPa, and G′ for cancer tissue, 9.60 kPa, for 40% tissue compression). Differences of storage and loss modulus values between healthy and cancer tissue were clearly evident and confirm our AFM data and previous studies.11,13,14,34 Therefore, we postulate that G′ similarly to Young’s modulus can be proposed as a promising mechanomarker of colon cancer.

Figure 4.

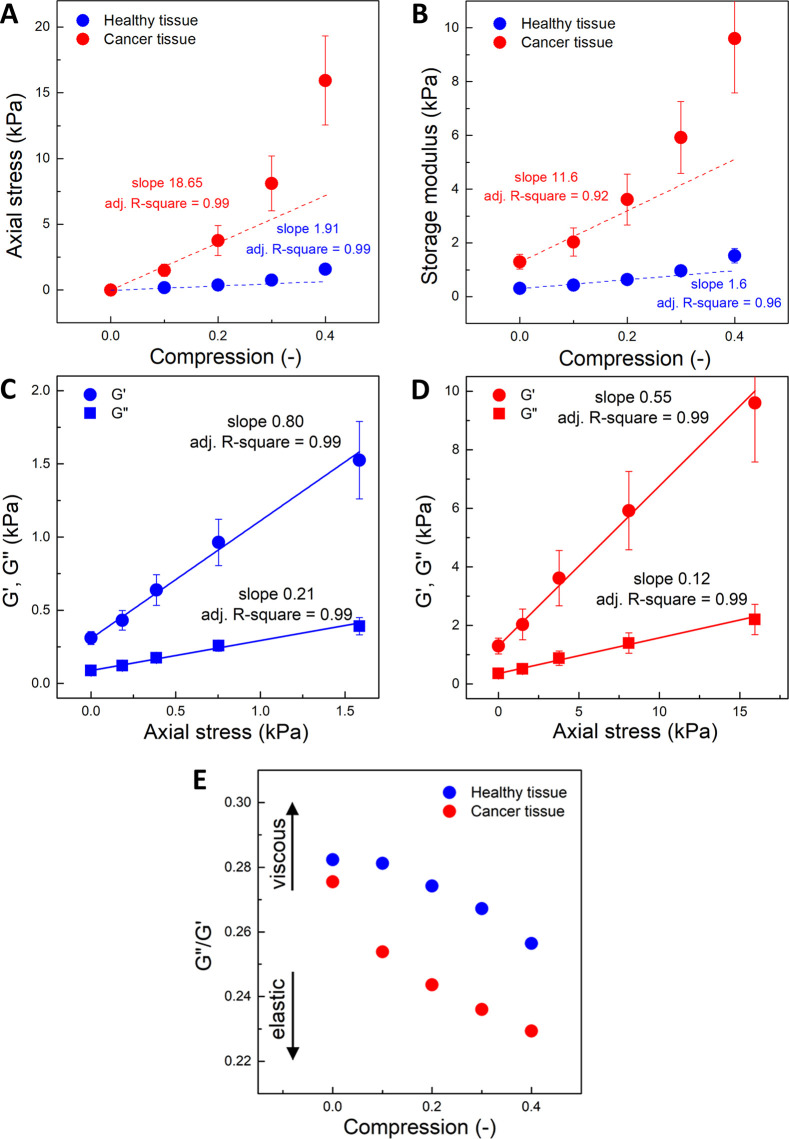
Figure 4

Open in a new tab

Rheological properties of the healthy and cancer tissues: (A) stress (normal force/sample surface) as a function of axial strain; (B) G′ as a function of axial strain (compression); (C, D) G′ and G″ as a function of axial stress. Average values for all samples. Blue, healthy tissue; red, cancer tissue. (E) G″/G′ as a function of axial stress. For both healthy and cancer samples, the compression stiffening effect is visible, but cancer tissues have significantly higher storage modulus and stiffen to a greater extent when compressive force is applied. Cancer tissue in compression reacts by increasing elasticity more prominently compared to healthy tissue. At increasing compression, samples become more elastic and less dissipative, especially cancer tissues.

Figure 6.

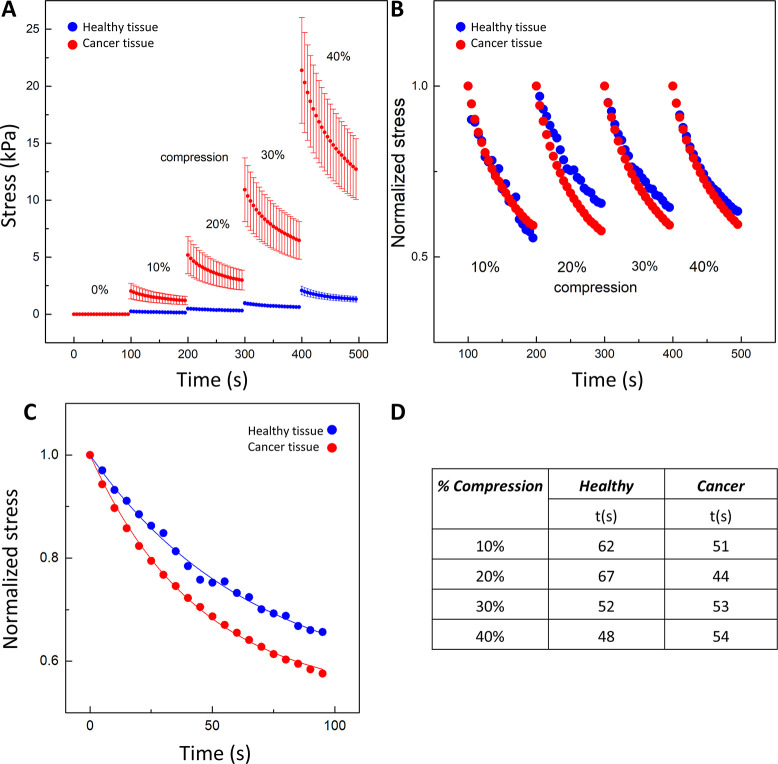
Figure 6

Open in a new tab

Axial stress exerted by the tissues at different levels of uniaxial compression, from 0 up to 40% with 10% increments. The amount of stress for healthy (blue) and cancer (red) tissues was calculated by dividing the normal force (FN) registered by the force transducer by the sample surface area in contact with the rheometer plate. (A) Stress–relaxation for cancer and healthy tissues; (B) stress–relaxation normalized to the initial stress just before each compression step; (C) stress–relaxation course for cancer tissue in 20% compression with a two-component stress–relaxation model: σ(t) = 1 – σ∞(1 + e–t/τ), where σ(t) is the reduced relaxation function and σ∞ and τ are the fitting constants for the equilibrium modulus and relaxation time constant, respectively; (D) exponential decay time (t) for cancer and healthy tissues at different levels of compression.56

Figure 4 shows cancer and healthy tissues’ mechanical response under different levels of compression. Figure 4A shows how the axial stress increases in compression, and Figure 4B shows parallel results for the shear storage modulus G′. Figure 4C,D compares the shear storage and loss moduli (G′, G″) for normal and cancer tissues, respectively, and Figure 4E shows how the ratio of the two moduli changes in compression.

For the normal sample, the stress–strain relationship is linear and the apparent Young’s modulus, calculated from the slope, is 1.9 kPa, consistent with the value obtained by AFM. For the cancerous tissue, the stress–strain plot is clearly nonlinear and the local slope increases with increasing strain, a feature that is characteristic of other fibrotic diseased tissues.22 Although it is possible to create a regression line with the coefficient of determination (R2) similar for both healthy and cancer tissues, the stress values at 40% compression for cancer tissue clearly stand out from the rest. From the initial slope at strains below 20%, where the tissue response is approximately linear, the calculated Young’s modulus for cancer tissues is 18.6 kPa, again consistent with the values measured by AFM, although somewhat higher, which likely reflects the higher strains of the macroscopic measurement and the dominance of the stiffest regions of the sample in the macroscopic response. The order of magnitude difference between Young’s modulus for normal and diseased tissues is similar for both means of measurement. The mechanical response of cancer tissues to compressive stress is more pronounced when compared to the healthy margin tissue, and it increases with the increasing level of tissue compression. This observation confirms the values of G′ as a function of axial deformation. Additionally, a higher storage modulus for cancer tissue and its increase with compression were observed. This is also in agreement with results previously published.14,22,41,49 Tissue strengthening during compression was described previously40 as a compression stiffening effect.

Although plots of axial stress and G′ vs axial strain are nonlinear for cancer samples, plots of G′ and G″ vs axial stress are linear for both normal and cancer samples. Storage (G″) and loss (G″) moduli as functions of axial stress are shown in Figure 4C,D. Although both G′ and G″ rise with increasing axial stress, the slopes of these plots are different. At increasing compression, the human colon samples become more elastic and less dissipative, as the ratio G″/G′ decreases, as seen by the smaller slope for G″ than for G′ and also in Figure 4E. This feature is more evident in cancer tissues.

The observed changes in mechanical response of cancer tissues under axial and tangential forces might allow for the identification of specific mechanomarkers and, in particular, stiffness, as quantified by a uniaxial or shear elastic modulus, might be a new mechanomarker of colon cancers and potentially other colon pathology. On the basis of our results, we confirm that tissue shear dissipation might also be a new effective marker of cancer distinct from the changes in magnitude of the elastic modulus. Recent studies of brain tumors using magnetic resonance elastography suggest the potential of a dissipative feature of tissue rheology as a new marker in tissue pathology.14,50−52

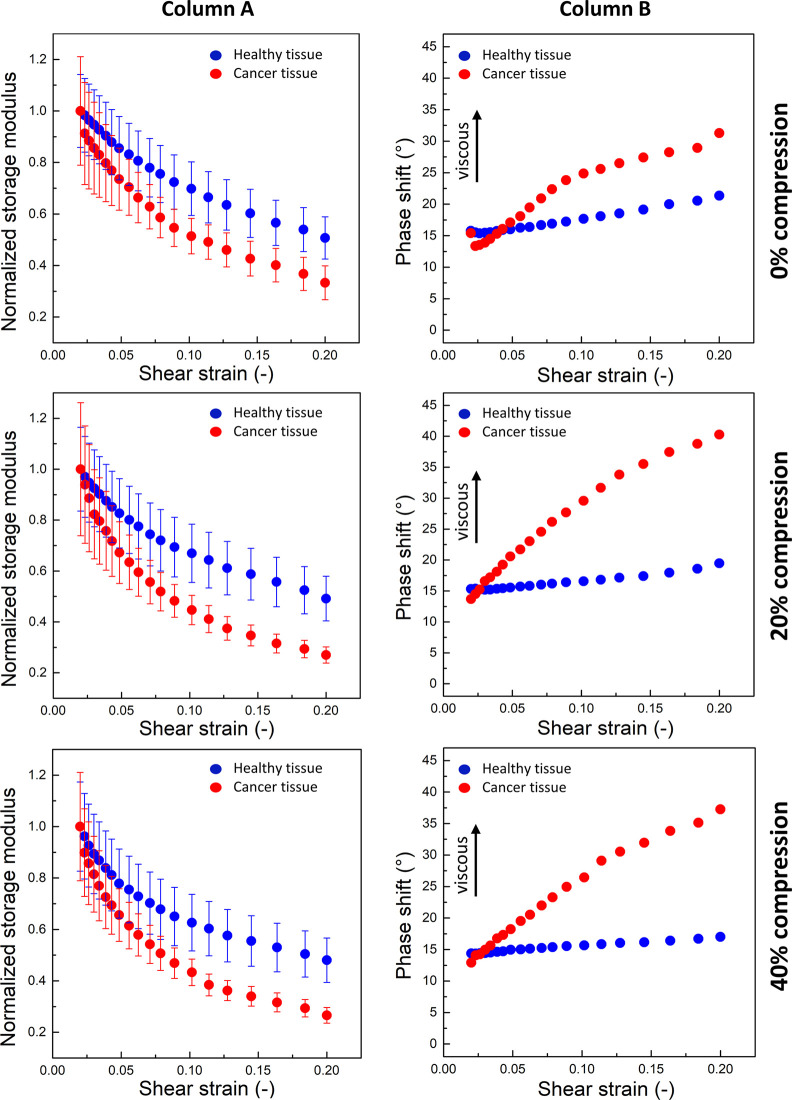
In contrast to the increase in G′ with increasing uniaxial strain, neither G′ nor G″ increase with increasing shear strain. Figure 5 Column A shows plots of normalized G′ as a function of increasing shear strain. G′ decreases with increasing shear strain for all tissues. Similar shear weakening of liver tissue has been observed in an earlier study.22 The colon tissues were subjected to oscillating shear strain in the range of 2–20% in the uncompressed state and at 20% and 40% uniaxial compression. If the tissue is modeled as a composite of a fibrous extracellular matrix and cells within the matrix mesh, the shear modulus is determined by the resistance of the matrix fibers, the cells, and the interface between them. Reference (53) shows how volume conserving cells restrict the possible movements of matrix fibers and eliminate some of the mechanisms by which fibrous networks stiffen in shear. At the same time, the contacts between the cell and the matrix are a combination of stable and dynamic bonds. At large strains, some of these bonds detach, and this effect leads to softening. However, if the strain is not so large as to damage the tissue, the stable bonds remain and, then, the shear strain is removed; the sample can recover its initial state, and the dynamic bonds can reform in the relaxed state.

Figure 5.

Figure 5

Open in a new tab

Rheological properties of healthy and cancer tissues under shear strain: Column A, the normalized storage modulus (G′) as a function of shear strain for different degrees of axial compression (0%, 20%, and 40%). The decrease of G′ with increasing shear strain depicts strain weakening and is greater for cancer tissues (red dots). Column B, the phase shift angle as a function of shear strain for different degrees of axial compression. Cancerous tissues became significantly more dissipative at increased shear strain (Column B). G′ was normalized to the minimum shear strain value.

Shear strain softening of the tissue samples occurs both with and without superimposed uniaxial compression. The strongest effect of shear strain softening was visible for cancer tissue. These results agree with reports of the mechanical behavior of other tissues under different levels of shear strain.22 Stiffening under axial compression and a decrease of G′ with increasing shear strain is not a universal feature of soft materials and is not observed for purified extracellular matrices such as fibrin gel and collagen gel,49,54 which exhibit strain-stiffening in shear and softening in compression.55 The pronounced shear strain softening of cancerous tissue even in the uncompressed state can also be considered as a possible mechanomarker of colon pathology. The phase shift angle δ between the oscillation curves is related to the ratio G″/G′ and is a measure of viscous dissipation within the material. For a phase shift angle equal to 0°, the material exhibits ideal elastic behavior, while for 90°, ideal viscous flow is observed. Figure 5 Column B shows δ as a function of shear strain for uncompressed as well as 20% and 40% uniaxially compressed tissue samples. While healthy tissues did not change their dissipative response significantly with increased shear strain, cancerous tissues became significantly more dissipative at increased shear strain. In the range of 2–20% shear stress, the phase shift angle for healthy tissue ranges from 15° (for small strains) to 20° (this decreases with increasing compression), which indicates a relatively elastic response. In the case of cancerous tissue, this angle increases from 12.5° for small deformations up to 41° with 20% shear strain. This change indicates that tumor tissue becomes more viscous with increasing shear deformation, and this observation suggests that the phase shift angle δ can be considered as a new mechanomarker.

When the normal force registered by the force transducer is measured, the compressive stress exerted by the tissue during compression can be calculated. Figure 6 shows compressive stress as a function of time when shear strain was set to 2% over the whole course of an experiment in which tissues were rapidly compressed at 10% increments. The compressive stress in cancer tissues (red dots) is much higher than in healthy tissues (blue dots) at every level of compression. For 10% compression, the maximum stress in healthy tissue is 252 Pa and in cancer tissue, 2030 Pa, while at 40% compression, the maximum compressive stress is ∼2 kPa in healthy tissues and ∼21 kPa in cancer tissues. Both tissues relax with time. A similar phenomenon was seen in ref (22) for healthy and fibrotic rat liver tissues. The forces exerted in compression are much higher for rat cancer tissues, but a larger relaxation of the stress has not been observed.

Figure 6C shows that the stress caused by subsequent lowering of the upper rheometer plate, after reaching the maximal value, decreases in a nonlinear way over time. Individual relaxation curves were fitted to a simple stress–relaxation model σ(t) = 1 – σ∞(1 + e–t/τ), where σ(t) is the reduced relaxation function and σ∞ and τ are the fitting constants for the equilibrium modulus and relaxation time constant, respectively.56 In compression, healthy tissues relax slightly more slowly at modest levels of compression (Figure 6D). These observations of compressive stress–relaxation over time do not provide a clear discrimination between normal and cancerous tissues.

The response of tissues under compressive, tensile, and shear force have recently been modeled by systems based on biopolymers in which cell-like inclusions are embedded.53 Understanding the rheological properties of tissue models can help us to identify mechanisms by which tissue stiffness is altered in disease and to assess how these changes lead to cellular dysfunction. The work53 of van Oosten et al. presents multiple experimental setups with a combination of nonlinear polymer networks with and without small elastic particles that mimic cells inside the tissue, and interestingly, this approach shows that the mechanical behavior of native tissues cannot be reproduced by biopolymer networks or by particle systems alone.53 This study shows that tissue rheology arises closely from an interaction between the polymer network and volume-conserving cells within the network. This is especially consequential for tumor promotion, which is associated with uncontrolled multiplication of mutated cells, their migratory and invasive potential in response to external loads, pressure gradients, and changes in ECM mechanoarchitecture.57,58 While mechanical testing of such complex 3D systems is possible with AFM and is sufficient to distinguish between healthy and diseased tissue, bulk rheometer testing seems to be a faster and simpler method for rheological testing that could support histopathology or even intraoperative decisions. Although there are other possibilities to assess tissue neoplastic conditions, such as measurements of the density of the samples,59 which are in addition to standard histopathological methods, rheological properties of cancerous tissues and comparing them to healthy tissues will provide a broader and more accurate view of tissue changes in cancer progression. The rheological examination of tissues removed during surgery is possible, and with miniaturization of this technique, it might be possible even if a small tissue volume is obtained.56 This work provides evidence that rheological examination of tissues may be a part of new procedures to describe tissue pathology.

3.3. Histopathological Evaluation

All the samples measured by AFM and rheometry underwent histopathological evaluation. Figure 7 shows representative images of stained healthy colon tissues.

Figure 7.

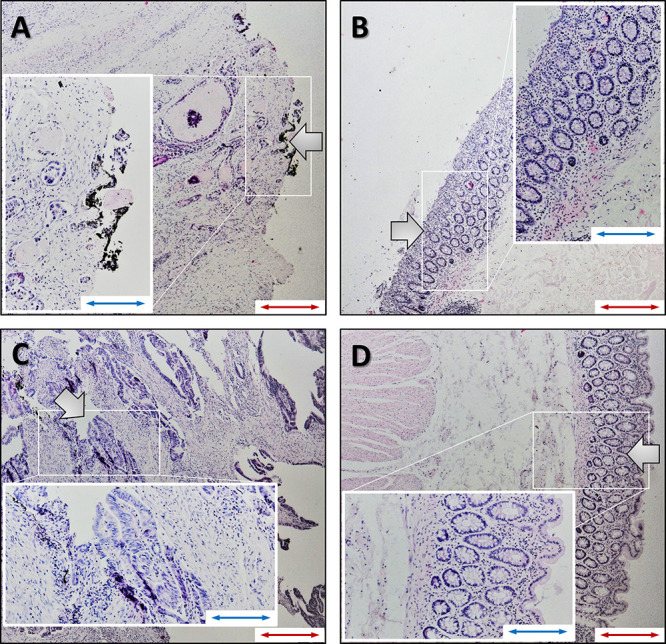
Figure 7

Open in a new tab

Representative images of stained colon tissues: (A, C) tumor tissues; (B, D) healthy colon tissues. (A, B) Sample sections from AFM; (C, D) Sections from a sample measured in the rheometer. The morphology of healthy colon tissue shows surface epithelium, mucosa with colon crypts, goblet cells, lamina propria, and muscularis mucosa and submucosa. The crypts open to the surface epithelium in this cross section, and some of the crypts appear partially or below the surface. A section of cancer tissue from AFM (A) shows the infiltration of adenocarcinoma with necrosis in the submucosa together with the desmoplastic reaction and microinflammation. A section of cancer tissue from the rheometer (C) shows the infiltration of adenocarcinoma with a fibrous inflammation reaction. The tissue is damaged due to the destructive nature of the rheometer tests at large strains (red scale bar, 100 μm; blue scale bar, 200 μm). Large arrows indicate the places from which the data was collected.

These images confirm that the tissue samples have normal morphology with the mucosal submucosa layer and the muscularis. Histopathological evaluation confirmed neoplastic changes in all colon cancer tissues, with typical changes such as cancer cell infiltration, desmoplastic reactions, and inflammation. The heterogeneity of cancer tissue structure, as observed in histopathological images, manifests strongly in the AFM measurements, where local mechanical properties of the tissue surface can be measured, whereas bulk rheology measurements using strain rheometry reflects averaged properties of the whole tissue sample.

4. Conclusions

The analysis of data collected using atomic force microscopy and shear rheometry revealed that colon cancer tissues have different mechanical properties compared to the healthy margin of the tissue. Significantly higher Young’s and shear modulus values for the cancer samples were observed. This difference was more pronounced after separating the Young’s modulus, shear storage, and loss modulus values. Overall, more pronounced compression stiffening of colon cancer tissue samples was observed. A combination of histopathological and mechanical tests directed to assess different mechanomarkers might place tissue rheology as a complementary procedure in the advanced diagnosis of colon cancer.

Acknowledgments

This work was financially supported by the National Science Center, Poland, under Grant UMO-2018/30/M/NZ6/00502 (to R.B.), by Medical University of Bialystok SUB/1/DN/19/001/1162 (to R.B.), and by the program of the Minister of Science and Higher Education under the name “Regional Initiative of Excellence in 2019-2022”, project number 024/RID/2018/19, financing amount: 11.999.000,00 PLN. Part of the study was conducted with the use of equipment purchased by the Medical University of Bialystok as part of the RPOWP 2007-2013 funding, Priority I, Axis 1.1, contract No. UDA-RPPD.01.01.00-20-001/15-00 dated 26.06.2015. Additional support was provided by grant EB017753 from the US National Institutes of Health.

The authors declare no competing financial interest.

References

  1. Tsitskari M.; Filippiadis D.; Kostantos C.; Palialexis K.; Zavridis P.; Kelekis N.; Brountzos E. The role of interventional oncology in the treatment of colorectal cancer liver metastases. Ann. Gastroenterol 2019, 32 (2), 147–155. 10.20524/aog.2019.0338. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Ferlay J.; Steliarova-Foucher E.; Lortet-Tieulent J.; Rosso S.; Coebergh J. W.; Comber H.; Forman D.; Bray F. Cancer incidence and mortality patterns in Europe: estimates for 40 countries in 2012. Eur. J. Cancer 2013, 49 (6), 1374–403. 10.1016/j.ejca.2012.12.027. [DOI] [PubMed] [Google Scholar]
  3. Siegel R.; Ward E.; Brawley O.; Jemal A. Cancer statistics, 2011: the impact of eliminating socioeconomic and racial disparities on premature cancer deaths. Ca-Cancer J. Clin. 2011, 61 (4), 212–36. 10.3322/caac.20121. [DOI] [PubMed] [Google Scholar]
  4. Torre L. A.; Bray F.; Siegel R. L.; Ferlay J.; Lortet-Tieulent J.; Jemal A. Global cancer statistics, 2012. Ca-Cancer J. Clin. 2015, 65 (2), 87–108. 10.3322/caac.21262. [DOI] [PubMed] [Google Scholar]
  5. Rees M.; Tekkis P. P.; Welsh F. K.; O’Rourke T.; John T. G. Evaluation of long-term survival after hepatic resection for metastatic colorectal cancer: a multifactorial model of 929 patients. Ann. Surg. 2008, 247 (1), 125–35. 10.1097/SLA.0b013e31815aa2c2. [DOI] [PubMed] [Google Scholar]
  6. Fleming M.; Ravula S.; Tatishchev S. F.; Wang H. L. Colorectal carcinoma: Pathologic aspects. J. Gastrointest. Oncol. 2012, 3 (3), 153–173. 10.3978/j.issn.2078-6891.2012.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Histopathology is ripe for automation. Nat. Biomed Eng. 2017, 1 (12), 925. 10.1038/s41551-017-0179-5. [DOI] [PubMed] [Google Scholar]
  8. Erben U.; Loddenkemper C.; Doerfel K.; Spieckermann S.; Haller D.; Heimesaat M. M.; Zeitz M.; Siegmund B.; Kuhl A. A. A guide to histomorphological evaluation of intestinal inflammation in mouse models. Int. J. Clin Exp Pathol 2014, 7 (8), 4557–4576. [PMC free article] [PubMed] [Google Scholar]
  9. Janmey P. A.; Winer J. P.; Murray M. E.; Wen Q. The hard life of soft cells. Cell Motil. Cytoskeleton 2009, 66 (8), 597–605. 10.1002/cm.20382. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Pogoda K.; Jaczewska J.; Wiltowska-Zuber J.; Klymenko O.; Zuber K.; Fornal M.; Lekka M. Depth-sensing analysis of cytoskeleton organization based on AFM data. Eur. Biophys. J. 2012, 41 (1), 79–87. 10.1007/s00249-011-0761-9. [DOI] [PubMed] [Google Scholar]
  11. Stylianou A.; Lekka M.; Stylianopoulos T. AFM assessing of nanomechanical fingerprints for cancer early diagnosis and classification: from single cell to tissue level. Nanoscale 2018, 10 (45), 20930–20945. 10.1039/C8NR06146G. [DOI] [PubMed] [Google Scholar]
  12. Weihs D.; Mason T. G.; Teitell M. A. Bio-microrheology: a frontier in microrheology. Biophys. J. 2006, 91 (11), 4296–305. 10.1529/biophysj.106.081109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Zemla J.; Danilkiewicz J.; Orzechowska B.; Pabijan J.; Seweryn S.; Lekka M. Atomic force microscopy as a tool for assessing the cellular elasticity and adhesiveness to identify cancer cells and tissues. Semin. Cell Dev. Biol. 2018, 73, 115–124. 10.1016/j.semcdb.2017.06.029. [DOI] [PubMed] [Google Scholar]
  14. Pogoda K.; Janmey P. A. Glial tissue mechanics and mechanosensing by glial cells. Front. Cell. Neurosci. 2018, 12, 25. 10.3389/fncel.2018.00025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Hayashi K.; Iwata M. Stiffness of cancer cells measured with an AFM indentation method. J. Mech Behav Biomed Mater. 2015, 49, 105–11. 10.1016/j.jmbbm.2015.04.030. [DOI] [PubMed] [Google Scholar]
  16. Wyss H. M.; Henderson J. M.; Byfield F. J.; Bruggeman L. A.; Ding Y.; Huang C.; Suh J. H.; Franke T.; Mele E.; Pollak M. R.; Miner J. H.; Janmey P. A.; Weitz D. A.; Miller R. T. Biophysical properties of normal and diseased renal glomeruli. Am. J. Physiol Cell Physiol 2011, 300 (3), C397–405. 10.1152/ajpcell.00438.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Solon J.; Levental I.; Sengupta K.; Georges P. C.; Janmey P. A. Fibroblast adaptation and stiffness matching to soft elastic substrates. Biophys. J. 2007, 93 (12), 4453–61. 10.1529/biophysj.106.101386. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Baker E. L.; Bonnecaze R. T.; Zaman M. H. Extracellular matrix stiffness and architecture govern intracellular rheology in cancer. Biophys. J. 2009, 97 (4), 1013–21. 10.1016/j.bpj.2009.05.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Chin L.; Xia Y.; Discher D. E.; Janmey P. A. Mechanotransduction in cancer. Curr. Opin. Chem. Eng. 2016, 11, 77–84. 10.1016/j.coche.2016.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Minelli E.; Ciasca G.; Sassun T. E.; Antonelli M.; Palmieri V.; Papi M.; Maulucci G.; Santoro A.; Giangaspero F.; Delfini R.; et al. A fully-automated neural network analysis of AFM force-distance curves for cancer tissue diagnosis. Appl. Phys. Lett. 2017, 111 (14), 143701. 10.1063/1.4996300. [DOI] [Google Scholar]
  21. Akhtar R.; Sherratt M. J.; Cruickshank J. K.; Derby B. Characterizing the elastic properties of tissues. Mater. Today (Oxford, U. K.) 2011, 14 (3), 96–105. 10.1016/S1369-7021(11)70059-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Perepelyuk M.; Chin L.; Cao X.; van Oosten A.; Shenoy V. B.; Janmey P. A.; Wells R. G. Normal and Fibrotic Rat Livers Demonstrate Shear Strain Softening and Compression Stiffening: A Model for Soft Tissue Mechanics. PLoS One 2016, 11 (1), e0146588 10.1371/journal.pone.0146588. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Kufe D., Ed. Holland-Frei Cancer Medicine, 6th ed.; BC Decker: Hamilton, ON, 2003. [Google Scholar]
  24. Kalli M.; Stylianopoulos T. Defining the Role of Solid Stress and Matrix Stiffness in Cancer Cell Proliferation and Metastasis. Front. Oncol. 2018, 8, 55. 10.3389/fonc.2018.00055. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Baneyx G.; Vogel V. Self-assembly of fibronectin into fibrillar networks underneath dipalmitoyl phosphatidylcholine monolayers: role of lipid matrix and tensile forces. Proc. Natl. Acad. Sci. U. S. A. 1999, 96 (22), 12518–23. 10.1073/pnas.96.22.12518. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Lampi M. C.; Reinhart-King C. A. Targeting extracellular matrix stiffness to attenuate disease: From molecular mechanisms to clinical trials. Sci. Transl. Med. 2018, 10 (422), eaao0475. 10.1126/scitranslmed.aao0475. [DOI] [PubMed] [Google Scholar]
  27. Broders-Bondon F.; Nguyen Ho-Bouldoires T. H.; Fernandez-Sanchez M. E.; Farge E. Mechanotransduction in tumor progression: The dark side of the force. J. Cell Biol. 2018, 217 (5), 1571–1587. 10.1083/jcb.201701039. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Northey J. J.; Przybyla L.; Weaver V. M. Tissue Force Programs Cell Fate and Tumor Aggression. Cancer Discovery 2017, 7 (11), 1224–1237. 10.1158/2159-8290.CD-16-0733. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Kumar S.; Weaver V. M. Mechanics, malignancy, and metastasis: the force journey of a tumor cell. Cancer Metastasis Rev. 2009, 28 (1–2), 113–27. 10.1007/s10555-008-9173-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Krndija D.; Schmid H.; Eismann J.; Lother U.; Adler G.; Oswald F.; Seufferlein T.; Von Wichert G. Substrate stiffness and the receptor-type tyrosine-protein phosphatase alpha regulate spreading of colon cancer cells through cytoskeletal contractility. Oncogene 2010, 29 (18), 2724. 10.1038/onc.2010.25. [DOI] [PubMed] [Google Scholar]
  31. Tang X.; Kuhlenschmidt T. B.; Li Q.; Ali S.; Lezmi S.; Chen H.; Pires-Alves M.; Laegreid W. W.; Saif T. A.; Kuhlenschmidt M. S. A mechanically-induced colon cancer cell population shows increased metastatic potential. Mol. Cancer 2014, 13, 131. 10.1186/1476-4598-13-131. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Ding Y.; Xu G. K.; Wang G. F. On the determination of elastic moduli of cells by AFM based indentation. Sci. Rep. 2017, 7, 45575. 10.1038/srep45575. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Pachenari M.; Seyedpour S. M.; Janmaleki M.; Babazadeh Shayan S.; Taranejoo S.; Hosseinkhani H. Mechanical properties of cancer cytoskeleton depend on actin filaments to microtubules content: investigating different grades of colon cancer cell lines. J. Biomech 2014, 47 (2), 373–9. 10.1016/j.jbiomech.2013.11.020. [DOI] [PubMed] [Google Scholar]
  34. Plodinec M.; Loparic M.; Monnier C. A.; Obermann E. C.; Zanetti-Dallenbach R.; Oertle P.; Hyotyla J. T.; Aebi U.; Bentires-Alj M.; Lim R. Y.; Schoenenberger C. A. The nanomechanical signature of breast cancer. Nat. Nanotechnol. 2012, 7 (11), 757–65. 10.1038/nnano.2012.167. [DOI] [PubMed] [Google Scholar]
  35. Costa J.; Ahluwalia A. Advances and Current Challenges in Intestinal in vitro Model Engineering: A Digest. Front. Bioeng. Biotechnol. 2019, 7, 144. 10.3389/fbioe.2019.00144. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Mariappan Y. K.; Glaser K. J.; Ehman R. L. Magnetic resonance elastography: a review. Clin Anat 2010, 23 (5), 497–511. 10.1002/ca.21006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Ozturk A.; Grajo J. R.; Dhyani M.; Anthony B. W.; Samir A. E. Principles of ultrasound elastography. Abdom Radiol (NY) 2018, 43 (4), 773–785. 10.1007/s00261-018-1475-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Johnson C. L.; Telzer E. H. Magnetic resonance elastography for examining developmental changes in the mechanical properties of the brain. Dev Cogn Neurosci 2018, 33, 176–181. 10.1016/j.dcn.2017.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Fovargue D.; Nordsletten D.; Sinkus R. Stiffness reconstruction methods for MR elastography. NMR Biomed. 2018, 31 (10), e3935 10.1002/nbm.3935. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Engstrom T. A.; Pogoda K.; Cruz K.; Janmey P. A.; Schwarz J. M. Compression stiffening in biological tissues: On the possibility of classic elasticity origins. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 2019, 99 (5–1), 052413. 10.1103/PhysRevE.99.052413. [DOI] [PubMed] [Google Scholar]
  41. Pogoda K.; Chin L.; Georges P. C.; Byfield F. J.; Bucki R.; Kim R.; Weaver M.; Wells R. G.; Marcinkiewicz C.; Janmey P. A. Compression stiffening of brain and its effect on mechanosensing by glioma cells. New J. Phys. 2014, 16 (7), 075002. 10.1088/1367-2630/16/7/075002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Brandstaeter S.; Fuchs S. L.; Aydin R. C.; Cyron C. J. Mechanics of the stomach: A review of an emerging field of biomechanics. GAMM-Mitteilungen 2019, 42 (3), e201900001 10.1002/gamm.201900001. [DOI] [Google Scholar]
  43. Bilston L. E. Soft tissue rheology and its implications for elastography: Challenges and opportunities. NMR Biomed. 2018, 31 (10), e3832 10.1002/nbm.3832. [DOI] [PubMed] [Google Scholar]
  44. McKee C. T.; Last J. A.; Russell P.; Murphy C. J. Indentation versus tensile measurements of Young’s modulus for soft biological tissues. Tissue Eng., Part B 2011, 17 (3), 155–64. 10.1089/ten.teb.2010.0520. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Zhang M.; Zheng Y. P.; Mak A. F. Estimating the effective Young’s modulus of soft tissues from indentation tests--nonlinear finite element analysis of effects of friction and large deformation. Med. Eng. Phys. 1997, 19 (6), 512–7. 10.1016/S1350-4533(97)00017-9. [DOI] [PubMed] [Google Scholar]
  46. Malandrino A.; Mak M.; Kamm R. D.; Moeendarbary E. Complex mechanics of the heterogeneous extracellular matrix in cancer. Extreme Mech Lett. 2018, 21, 25–34. 10.1016/j.eml.2018.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Brauchle E.; Kasper J.; Daum R.; Schierbaum N.; Falch C.; Kirschniak A.; Schaffer T. E.; Schenke-Layland K. Biomechanical and biomolecular characterization of extracellular matrix structures in human colon carcinomas. Matrix Biol. 2018, 68–69, 180–193. 10.1016/j.matbio.2018.03.016. [DOI] [PubMed] [Google Scholar]
  48. Lekka M. Atomic force microscopy: A tip for diagnosing cancer. Nat. Nanotechnol. 2012, 7 (11), 691–2. 10.1038/nnano.2012.196. [DOI] [PubMed] [Google Scholar]
  49. Van Oosten A. S.; Vahabi M.; Licup A. J.; Sharma A.; Galie P. A.; MacKintosh F. C.; Janmey P. A. Uncoupling shear and uniaxial elastic moduli of semiflexible biopolymer networks: compression-softening and stretch-stiffening. Sci. Rep. 2016, 6, 19270. 10.1038/srep19270. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Yin Z.; Romano A. J.; Manduca A.; Ehman R. L.; Huston J. 3rd Stiffness and Beyond: What MR Elastography Can Tell Us About Brain Structure and Function Under Physiologic and Pathologic Conditions. Top Magn Reson Imaging 2018, 27 (5), 305–318. 10.1097/RMR.0000000000000178. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Zhang J.; Green M. A.; Sinkus R.; Bilston L. E. Viscoelastic properties of human cerebellum using magnetic resonance elastography. J. Biomech 2011, 44 (10), 1909–13. 10.1016/j.jbiomech.2011.04.034. [DOI] [PubMed] [Google Scholar]
  52. Pepin K. M.; McGee K. P.; Arani A.; Lake D. S.; Glaser K. J.; Manduca A.; Parney I. F.; Ehman R. L.; Huston J. 3rd MR Elastography Analysis of Glioma Stiffness and IDH1-Mutation Status. AJNR Am. J. Neuroradiol 2018, 39 (1), 31–36. 10.3174/ajnr.A5415. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. van Oosten A. S. G.; Chen X.; Chin L.; Cruz K.; Patteson A. E.; Pogoda K.; Shenoy V. B.; Janmey P. A. Emergence of tissue-like mechanics from fibrous networks confined by close-packed cells. Nature 2019, 573 (7772), 96–101. 10.1038/s41586-019-1516-5. [DOI] [PubMed] [Google Scholar]
  54. Storm C.; Pastore J. J.; MacKintosh F. C.; Lubensky T. C.; Janmey P. A. Nonlinear elasticity in biological gels. Nature 2005, 435 (7039), 191–4. 10.1038/nature03521. [DOI] [PubMed] [Google Scholar]
  55. Vahabi M.; Sharma A.; Licup A. J.; Van Oosten A. S.; Galie P. A.; Janmey P. A.; MacKintosh F. C. Elasticity of fibrous networks under uniaxial prestress. Soft Matter 2016, 12 (22), 5050–5060. 10.1039/C6SM00606J. [DOI] [PubMed] [Google Scholar]
  56. Levental I.; Levental K. R.; Klein E. A.; Assoian R.; Miller R. T.; Wells R. G.; Janmey P. A. A simple indentation device for measuring micrometer-scale tissue stiffness. J. Phys.: Condens. Matter 2010, 22 (19), 194120. 10.1088/0953-8984/22/19/194120. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Sonnenschein C.; Soto A. M. Theories of carcinogenesis: an emerging perspective. Semin. Cancer Biol. 2008, 18 (5), 372–7. 10.1016/j.semcancer.2008.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Lopez-Lazaro M. A new view of carcinogenesis and an alternative approach to cancer therapy. Mol. Med. 2010, 16 (3–4), 144–53. 10.2119/molmed.2009.00162. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Chen J.-H.; Chan S.; Zhang Y.; Li S.; Chang R.-F.; Su M.-Y. Evaluation of breast stiffness measured by ultrasound and breast density measured by MRI using a prone-supine deformation model. Biomarker research 2019, 7 (1), 20. 10.1186/s40364-019-0171-1. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from ACS Biomaterials Science & Engineering are provided here courtesy of American Chemical Society

RESOURCES