Characterization of cell fate probabilities in single-cell data with Palantir

Abstract

Single-cell RNA sequencing (scRNA-seq) studies of differentiating systems have raised fundamental questions regarding the discrete versus continuous nature of both differentiation and cell fate. Here we present Palantir, an algorithm that models trajectories of differentiating cells—treating cell fate as a probabilistic process—and leverages entropy to measure cell plasticity along the trajectory. Palantir generates a high-resolution pseudotime ordering of cells and, for each cell state, assigns a probability of differentiating into each terminal state. We apply our algorithm to human bone marrow scRNA-seq data and detect important landmarks of hematopoietic differentiation. Palantir’s resolution enables the identification of key transcription factors that drive lineage fate choice and closely track when cells lose plasticity. We show that Palantir outperforms existing algorithms in identifying cell lineages and recapitulating gene expression trends during differentiation generalizable to diverse tissue types and well-suited to resolve less-studied differentiating systems.

Introduction

Differentiation is among the most fundamental processes in biology. In the traditional view, cells transition from a less- to a more-differentiated state via a series of discrete, well-defined stages. Single-cell studies^1-6 have, however, demonstrated that during differentiation, cell states reside along largely continuous spaces . Despite this evolution in thinking, cell fate decisions continue to be largely conceptualized as a series of discrete bifurcations along development, leading to terminal cell states^{7, 8}.

Epigenetic studies, however, support a probabilistic view of cell fate choice. Epigenomic measurements such as DNase-seq and ATAC-seq suggest potential mechanisms for a continuous process by indicating that progressive enhancer restriction, coupled with pre-establishment of lineage-specifying enhancers in precursor cells, can serve as a vehicle for driving differentiation^{5, 9, 10}. Indeed, in human bone marrow, we observe a lack of well-defined bifurcation points when scRNA-seq profiles are projected along the strongest axes of variation (Fig. 1a). Even at the level of individual genes, we find a broad representation of gene ratios rather than bimodal expression states (Fig. 1a). These observations raise fundamental questions about whether cell fates, like cell state transitions, are continuous and when and how cell fate choices are made.

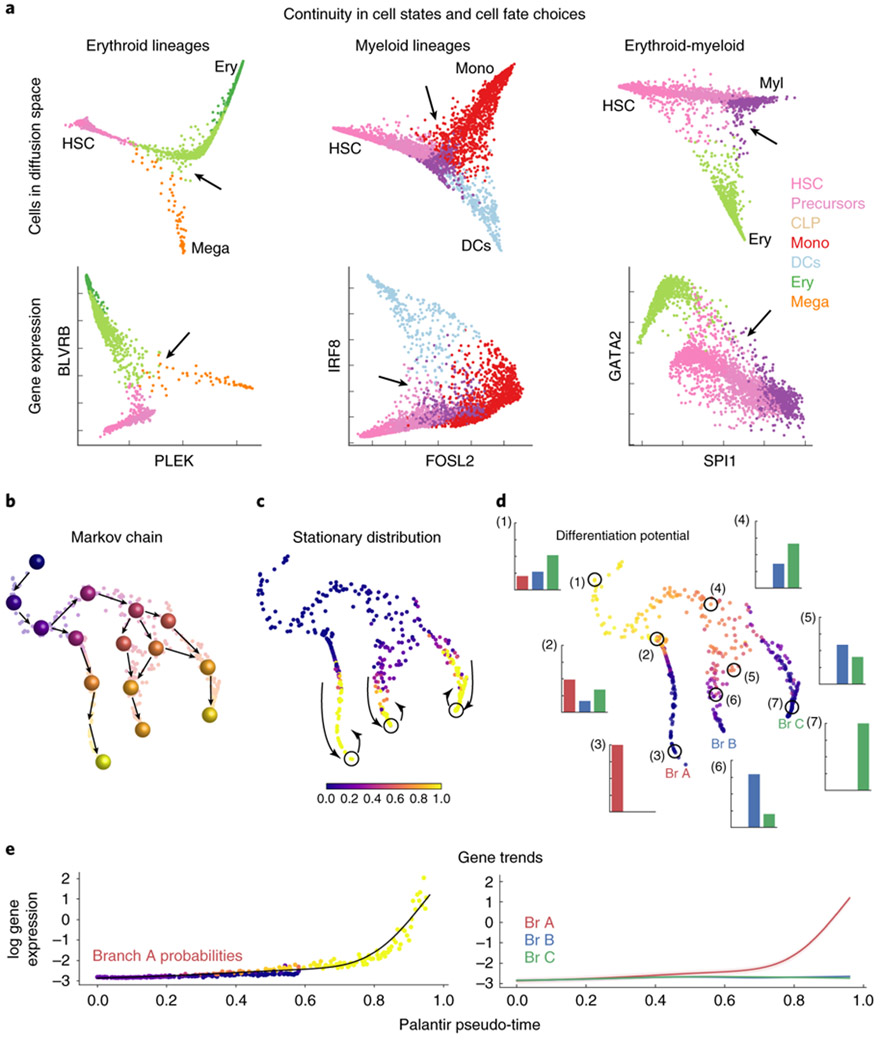
Figure 1.

Palantir characterizes cell fate choices in a continuous model of differentiation. (a) Top: Projection of CD34+ human bone marrow cells along diffusion components. Bottom: Expression of gene pairs involved in lineage decisions for cells in the corresponding top panel. Cells colored by Phenograph cluster (Supplementary Fig. 4a); arrows highlight continuity in cell fate choices as a pervasive lack of well-defined branch points in decision-making regions. Plots show comparison of 3170, 4224 and 3510 cells respectively(b-d) Palantir phenotypic manifold for a subsampled dataset of CD34+ human hematopoiesis. Each dot represents a cell embedded into diffusion space based on the first 3 components and visualized using tSNE. (b) Cartoon of Markov chain construction over the manifold. Cells colored by pseudo-time. (c) Cells colored by the stationary distribution of the Markov chain in (b), demonstrating outliers (yellow) in the mature states. Outliers that are also boundary states (circles) are selected as terminal states. (d) Cells colored by differentiation potential. Highlighted examples (circles) show relationship between pseudo-time, differentiation potential and branch probabilities (histogram with bars colored by terminal state or branch, Br). High differentiation potential (1) decreases gradually as cells move towards commitment (2-3). Modeling cell fate choices as probabilities provides a representation of their continuity (4-7). (e) Expression of a branch A–specific gene along pseudo-time. Left: Each dot represents a cell colored by its probability of reaching terminus A. Black line, gene expression trend for this data. Right. Expression trends for the 3 lineages. The unified framework of pseudo-time and branch probabilities enable gene expression dynamics to be characterized across a common axis.

To investigate these questions, we developed Palantir, an algorithm that leverages scRNA-seq data to model the landscape of differentiation and characterize continuity in both cell state and fate choice. As differentiation is asynchronous, sequencing a population of differentiating cells yields a snapshot representing a range of cell states. Based on scRNA-seq data from a single sample and the selection of a representative early cell, Palantir generates a pseudo-time ordering of cells and, for each cell state, assigns a probability for differentiating into each terminal state. We applied Palantir to characterize human hematopoietic differentiation using scRNA-seq profiles of ~25,000 cells enriched for CD34, a marker for hematopoietic stem and progenitor cells¹¹. Palantir identified established terminal states and ordered cells along a pseudo-time that recapitulated known marker trends in development. Notably, Palantir identified points along the trajectory where the differentiation potential drastically shifts. These shifts mark key events in hematopoiesis. Palantir thus provides a quantitative approach to characterizing a continuous model of cell fate choice.

Results

Development as a Markov Process

Differentiation proceeds through cell divisions, where daughter cells are generally very similar to their mother cells. Thus, the population is established by incremental divergences, driven by regulatory mechanisms that create paths through the space of possible cell states (phenotypes). Regulation constrains cell states to a low-dimensional manifold of possible phenotypes¹². Nearest-neighbor graphs, where each node represents a particular cell state and edges connect most similar cells, have been widely used to model this manifold^{1-3, 13}.

A single bone marrow sample contains the full spectrum of cell states in hematopoiesis and importantly the frequencies of each cell state. We leverage cell state frequencies to inform our model of possible differentiation paths in the neighbor graph and their likelihoods. Critically, paths along the graph represent likely trajectories of cells in the population rather than the path of a particular cell, and each cell state (graph node) is associated with a probability distribution for reaching the terminal states. We assert that cells traverse the manifold in small steps which can be modeled using a Markov chain to represent cell fate choices in a probabilistic manner, based on two key assumptions. Firstly, as in all pseudo-time inference algorithms^{1, 3, 7, 8}, we assume unidirectional progression from a less to a more differentiated state. We posit that it is a reasonable first order approximation for healthy differentiation, but note that it fails in aberrant systems such as cancer, which require additional information (e.g. mutations) to determine directionality. Second, we assume that for any node, the probability of traversing to any neighbor is independent of its history, i.e. the path taken to reach that state. Note that for a particular cell, the cell’s developmental history is likely to be encoded in its epigenetic profile and will likely impact cell fate choices. However, nodes are abstract cell states representing multiple histories and potential trajectories rather than the path of an individual cell. Accounting for all past paths into this cell state, we can compute population-level probabilities for future states, based on the structure and connectivity of nodes in the graph manifold.

The Palantir Algorithm

Given scRNA-seq data from a sample of differentiating cells and the expression profile of a user-defined ‘early’ cell, Palantir orders cells along a pseudo-time, characterizes terminal differentiated states, and assigns each cell a probability distribution representing the cell’s branch probability for reaching each terminal state (Supplementary Note 1).

First, we represent the phenotypic manifold using a nearest-neighbor graph (Supplementary Fig. 1a, Supplementary Note 1). We use diffusion maps¹⁴ to focus on developmental trends and avoid spurious edges resulting from the sparsity and noise in scRNA-seq. Projecting the data onto the top diffusion components effectively focuses edges in directions with high cell density and reweighs similarity along these directions (Supplementary Fig. 1a). Diffusion maps have been previously used to study single-cell data^{2, 3} and are particularly adept at capturing differentiation trajectories^{3, 15}. Unlike other tools, Palantir uses multiple DCs when computing the pseudo-time ordering of cells, since we observe that a single DC can only approximate trajectories leading to a subset of fates (Supplementary Fig. 2). Shortest paths from a user-defined early cell initiate pseudo-time, which is then iteratively refined by identifying the shortest distances from waypoints—sets of cells sampled to span the differentiation landscape (Supplementary Fig. 1b-c)^{1, 2}. The computed pseudo-time does not represent a trajectory, but rather assigns each cell a relative distance from an initial cell, regardless of its lineage or terminal fates.

We use the neighbor graph and pseudo-time to construct a Markov chain that models differentiation as a stochastic process, where a cell reaches one or more terminal states through a series of steps in the manifold (Fig. 1b). Pseudo-time provides directionality that is used to orient edges in the neighbor graph in a manner consistent with the ordering (Supplementary Fig. 1d-e). For each directed edge, we assign a transition probability of reaching a neighboring cell in one step. The probability of reaching a more distant cell is computed over multiple steps and will be high if many paths connect them, i.e., there is a high density of observed intermediary cell states (Supplementary Fig. 1f and Supplementary Note 1). Thus, while each single step is stochastic, over longer distances, the manifold graph structure implicitly encodes developmental trajectories.

The Markov chain is also used to infer terminal states from the data. Palantir identifies terminal states as boundary cells (extrema of diffusion components) that are outliers in the stationary distribution, i.e., the states into which the random walks converge (Fig. 1c). Once the terminal states are identified, we convert them to absorbing states with no outgoing edges. In an absorbing Markov chain, a random walk from any state will continue until it reaches a terminal absorbing state. For each cell, Palantir then integrates all possible random walks from the cell to each possible terminal state to yield a vector of branch probabilities (Supplementary Fig. 1f,g). We define a cell’s differentiation potential to be the entropy over the branch probabilities, providing a novel quantitative metric for cell plasticity (Fig. 1d, Supplementary Fig. 1h).

Palantir assigns each cell both a pseudo-time (relative distance from the start) and branch probabilities to all terminal states. Thus, Palantir’s pseudo-time provides a unified ordering that enables precise alignment, characterization and comparison of gene expression dynamics along all lineages, without having to select cells in subsets of lineages (Supplementary Note 1). From this ordering, we compute gene expression trends using generalized additive models (GAMs), weighing each cell’s contribution based on branch probabilities (Fig. 1e, Supplementary Fig. 3, Supplementary Note 2). GAMs are particularly suitable for deriving a robust estimate of non-linear trends and estimating the standard error of prediction¹⁶.

Landscape of early human hematopoiesis

Hematopoiesis is a well-studied biological process with established markers to facilitate the identification of lineages¹¹, and many pseudo-time algorithms have been developed using it as a model system^{2, 7, 17}. While scRNA-seq has been extensively used to study hematopoiesis in mouse^{6, 18}, we chose to investigate early human hematopoiesis, since single-cell studies are particularly empowering in a system where perturbations are not possible. Hematopoiesis has classically been characterized as a series of bifurcations leading to mature, terminal cell states¹¹, but single-cell profiling of sorted populations suggests a continuous process of fate assignment^{4, 5}. Fundamental questions remain about how cell fate choice is determined at the earliest stages of human hematopoiesis and the degree of plasticity in early progenitors. To investigate these cell fate choices, we generated approximately 25,000 single-cell transcriptomes of bead-purified CD34+ cells from three human bone marrow donors using 10X Chromium (Methods).

We first clustered the scRNA-seq profiles using PhenoGraph¹³ (Supplementary Fig. 4a). We identified the full complement of hematopoietic cells, including hematopoietic stem and progenitors (HSPCs), as well as cells committed to lymphoid, erythroid, monocytic, classical and plasmacytoid dendritic cell (cDCs & pDCs respectively) lineages and megakaryocytes (Fig. 2a,b)^{19, 20} (Supplementary Fig. 4b,c). HSPCs comprised ~63% of the total sorted cells. Lineage-committed cells were also detected because of imperfect CD34 purification (~90% pure) and the temporal lag in surface protein levels compared to mRNA.

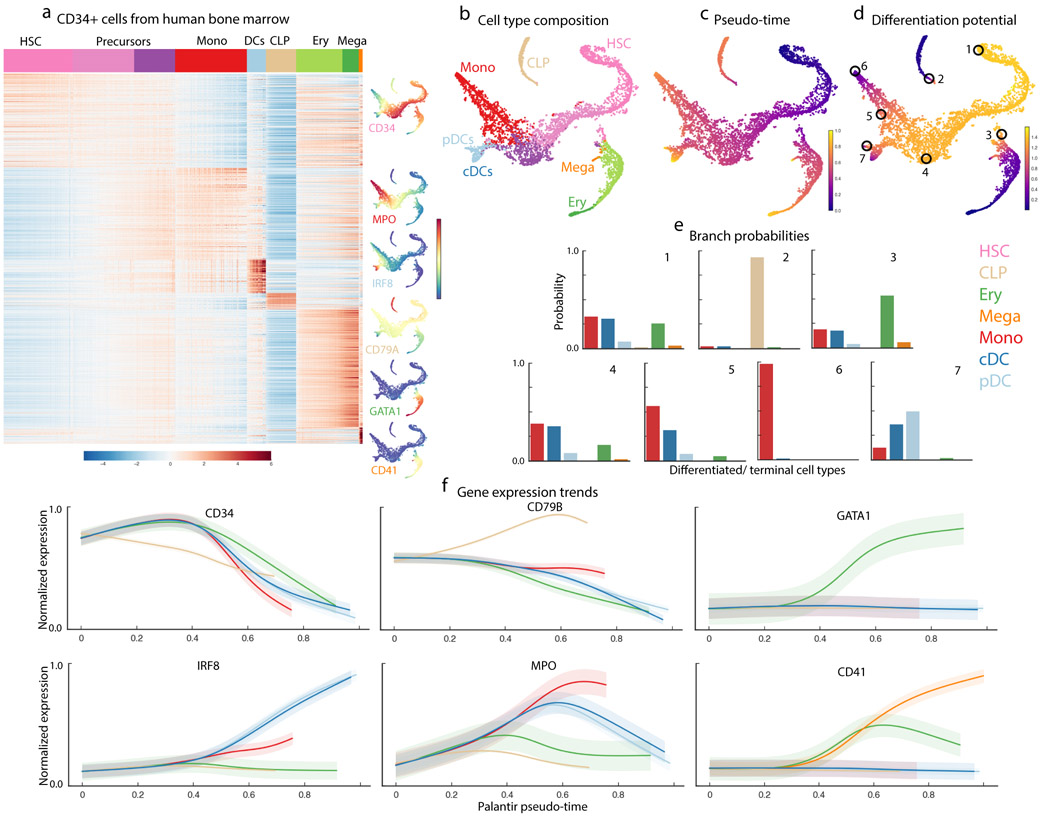
Figure 2.

Differentiation landscape of early human hematopoiesis. Data shown for CD34+ human bone marrow cells, replicate 1. (a) MAGIC imputed expression of genes (rows) differentially expressed between PhenoGraph¹³ clusters (based on MAST⁵¹). Cells (columns) are ordered by cluster; top row represents annotated cluster labels, with color coding scheme used in all figures. tSNE maps show cells colored by imputed expression of characteristic cell lineage markers. (b-d) tSNE maps of full scRNA-seq dataset generated using one HSC as a start cell. 5780 cells are shown on the tSNE maps.(b) Cells colored by cluster labels in (a), annotated by correlation with bulk sorted populations. (c) Cells colored by Palantir pseudo-time. (d) Cells colored by Palantir differentiation potential. (e) Branch probabilities of example cells circled in (d), highlighting early cells (1), lymphoid and erythroid lineages (2,3) and monocyte and DC lineages (4-7). Bars are colored by cell type as in (a). (f) Gene expression trends for characteristic lineage genes, plotted as in Supplementary Fig. 3.

Palantir recapitulates expected hematopoiesis trends

We applied Palantir to the hematopoiesis data, selecting a CD34 high cell as the start cell (Methods), and analyzed each of the three replicates separately to evaluate robustness. The algorithm correctly identified all expected cell types, including monocytes, erythroid cells, megakaryocytes, lymphoid progenitors and the two DC populations as terminal states (Fig. 2b,c). The trajectory identified by Palantir follows the expected progression from HSCs to differentiated cell types (Fig. 2c) and cells at the beginning of the trajectory have the potential to reach any terminal state, with a gradual loss of plasticity as they commit towards a particular lineage (Fig. 2d,e).

To evaluate the trajectories, we computed the expression trends of key markers (Fig. 2f). As expected, CD34 shows a decreasing trend as cells commit in all lineages¹¹ whereas lineage-specific factors such as CD79A, GATA1 and IRF8 are selectively upregulated in the lymphoid, erythroid and DC lineages, respectively. MPO shows an initial upward trend across all lineages, which is subsequently maintained only in the monocyte lineage (Fig. 2f). Finally, CD41 expression is consistent with its role as a marker of early erythroid and megakaryocytic precursors, exhibiting continued upregulation in the megakaryocytic lineages²¹.

We next evaluated Palantir’s robustness and reproducibility. Our experiments demonstrate that both pseudo-time and differentiation potential (DP) are robust to a wide range of parameters, including the number of neighbors for graph construction, number of diffusion components and different sampling of waypoints and sub-sampling of cells (Supplementary Figs. 5-8, Methods). Pseudo-time and DP are highly correlated between independent applications of Palantir to datasets from different bone marrow donors (Supplementary Figs. 9-11), and gene expression trends are also reproducible across the biological replicates (Supplementary Fig. 11). These findings collectively show that Palantir results are reproducible and suggest that they correctly characterize gene expression dynamics in early hematopoiesis.

A hierarchical, continuous model of hematopoietic fate choice

A number of single-cell studies^{4, 6} have hypothesized that hematopoietic decision-making is a continuous process, but that it lacks hierarchy. However, these studies were based on sorted populations and might have missed intermediate cell stages; more importantly, the relative proportions of different cell types were not retained. On the other hand, lineage-tracing studies of murine hematopoiesis²² support a hierarchical developmental model with stepwise losses in potential as stem cells differentiate into specific cell types.

By comparing the change in differentiation potential (DP) across lineages, we can use Palantir to query human hematopoiesis, where genetic perturbation studies are impossible. DP decreases along any given lineage, as cells lose their ability to commit to other lineages (Supplementary Fig. 12a-d). Tracking branch probabilities (BPs) and DP along pseudo-time enables us to determine when and in what manner these probabilities change for each terminal fate. Our results suggest continuity in early hematopoietic lineage commitment: DP remains consistently high throughout early hematopoiesis, with gradual losses as cells differentiate towards specific lineages (Fig. 3a, Supplementary Fig. 12e).

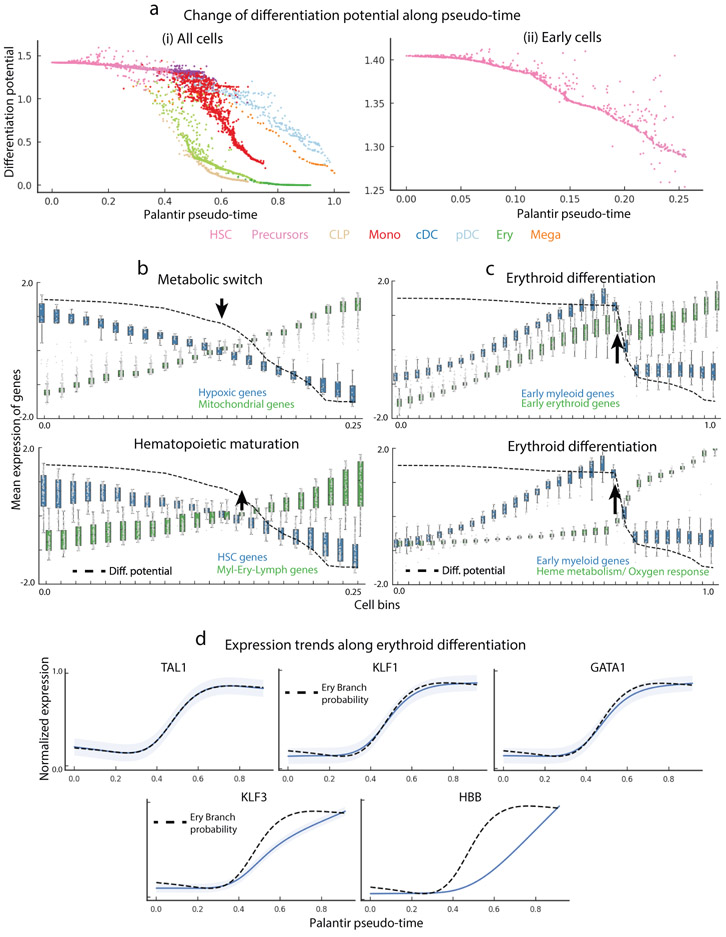
Figure 3.

Palantir differentiation potential identifies landmarks of hematopoietic differentiation. Data shown for CD34+ human bone marrow cells, replicate 1. (a) Differentiation potential along pseudo-time for all cells (left) or early cells (right) decreases as cells commit to lineages. Each dot represents a cell colored by cell type as in Fig. 2b and at bottom. (b) Mean expression of hypoxic and mitochondrial genes (top) and stem cell and mature lineage-specifying genes (bottom) in equal-sized bins along Palantir pseudo-time. Box plots show the mean expression and 1.5 std. Dotted black line, DP; arrow, point of maximal DP change, corresponding to crossover points in gene expression. (c) Mean expression of early myeloid and early erythroid genes (top), and early myeloid genes and genes involved in functional specification of erythroid function (bottom). Dotted black line, DP; arrow, point of maximal DP change, corresponding to point of higher erythroid gene expression. d) Gene expression trends (blue) of key erythroid TFs TAL1, KLF1 and GATA1 are the most correlated with erythroid branch probability (dotted black line). Gene expression of downstream regulators KLF3 and HBB is also shown. Shaded region represents 1 s.d.

Importantly, we note that the rate of change in DP varies greatly along pseudo-time and across lineages (Fig. 3a, Supplementary Fig. 12e, Methods). If lineage commitment was non-hierarchical, we would expect DP for different lineages to simultaneously drop downward at a particular point along pseudo-time. Instead, we observe a sequential commitment to the lymphoid, erythroid/megakaryocytic and finally, myeloid lineages (Fig. 3a, Supplementary Fig. 12e), supporting a hierarchical mode of lineage commitment. These results suggest that differentiation in early human hematopoiesis is hierarchical.

DP identifies hematopoietic differentiation landmarks

Differentiation potential represents a quantitative measure of a cell’s potential to differentiate into different lineages and can detect when cell fate specification changes. We observe points along pseudo-time where substantial changes in DP occur and posit that these changes reflect key molecular and cellular events driving differentiation. Most of these changes coincide with commitment to different lineages (Fig. 3a left panel, Supplementary Fig. 12), except for a substantial decrease in DP in early differentiation (Fig. 3a, early cells) not associated with commitment towards any specific lineage.

To gain insight into this drop in DP, we characterized gene expression trends in the vicinity of this event. We clustered genes along pseudo-time, assuming that genes involved in coherent biological processes share similar expression dynamics, and used gene ontology enrichment to annotate the resulting clusters (Supplementary Note 3). The strongest trends involved upregulation of aerobic and mitochondrial respiration, and downregulation of hypoxic genes (Fig 3b, Supplementary Fig. 13b). These data suggest a decrease in DP at the earliest stages of hematopoiesis corresponds with a change in metabolic state, occurring before cells begin to commit towards lineages (Fig. 3b).

Studies have shown that hematopoietic stem cell (HSC) differentiation requires an exit from the slow-cycling, quiescent long-term HSC (LT-HSC) state to a metabolically active short-term HSC (ST-HSC) state, a process known as the metabolic switch²³. The range of cell types into which a cell can differentiate is thought to remain unaltered during this transition. Consistent with these studies, we show that the change in DP correlates with the metabolic switch reproducibly and independently in each of the three replicate samples (Fig. 3b, Supplementary Fig. 14). DP change is also correlated with expression dynamics of THY1(CD90), a well characterized marker of transition between LT-HSCs to ST-HSCs (Supplementary Fig. 13c)²⁴. Moreover, change in DP is also accompanied by increased expression of early myeloid-erythroid-lymphoid genes compared to HSC genes (Fig. 3b, Supplementary Fig. 14). These results demonstrate that DP, as computed by Palantir strictly from the data, can identify key differentiation events such as metabolic switch even when these are unrelated to specific cell fate choices.

Differentiation potential during erythroid commitment

We next characterized DP changes during lineage commitment using erythropoiesis as a case study. Erythrocytes are derived from megakaryocyte-erythroid precursor cells (MEPs)²⁵. Upon erythroid commitment, we observe a sharp decrease in DP (Fig. 3a). To identify processes concordant with this decrease, we repeated the pseudo-temporal trend-based gene set analysis as before (Supplementary Fig. 13d). Gene expression trends in cells undergoing erythroid lineage commitment (increasing BP toward erythroid fate) are associated with continued upregulation of early erythroid genes and a downregulation of early myeloid genes (Fig. 3c). As expected for maturing red blood cells, decrease in DP also coincides with upregulation of heme metabolism and oxygen response genes (Fig. 3c).

We reasoned that the transcription factors (TFs) most closely correlated with erythroid BP are likely to be key regulators of erythroid commitment. Hence, we systematically correlated all TFs with erythroid BP and found the most correlated TFs to be TAL1, KLF1 and GATA1 (Pearson correlation > 0.99) (Fig. 3d, Supplementary Fig. 13e (Cluster 0)). Each has been shown to play a central role in erythropoiesis: TAL1 enhances erythroid potential²⁶; KLF1 regulates early erythroid precursor genes and suppresses the megakaryocyte lineage²⁷; and loss of GATA1 leads to complete loss of erythropoiesis²⁸. Thus, we find remarkable correspondence between erythroid BP, computed based on all genes with no prior knowledge, and expression trends of known key regulators of erythropoiesis.

The high resolution ordering of Palantir allows us to characterize the order and timing of events during erythropoiesis. We find that upregulation of KLF1 is followed by upregulation of KLF3, a known target of KLF1 that stabilizes the erythroid program (Fig. 3d, Supplementary Fig. 13e (Cluster 6))²⁹, and globin genes such as HBB are upregulated in the final wave conferring functional identity to red blood cells (Fig. 3d, Supplementary Fig. 13e (Cluster 8)). These results strongly suggest that erythroid specification occurs in stages of coordinated gene upregulation.

Transcriptional regulation of erythroid commitment

Given the strong correspondence between key erythroid TF expression and erythroid BP, we next sought to use Palantir to identify factors that influence lineage fate choices. We reasoned that such TFs should be expressed prior to the lineage decision; they should be upregulated during early specification and correlate with increasing lineage probability; and they should be downregulated in alternate lineages.

Upon a systematic evaluation of all TFs expressed in the erythroid lineage (Supplementary Note 4), we identified GATA2, LYL1 and MXD4 as best satisfying our criteria of high expression in precursor cells and strong correlation with erythroid commitment (Supplementary Fig. 15a,b). GATA2 shows the highest expression and correlation (Supplementary Fig. 15b). The interplay between GATA1, GATA2 and PU.1 (SPI1) has been proposed to drive the myeloid-versus-erythroid lineage decision³⁰ with mutual antagonization between PU.1 and GATA1 driving myeloid and erythroid lineage commitments respectively^{30, 31}. More recently, GATA2 rather than GATA1 has been proposed to be the agonist of PU.1^{32, 33}, consistent with Palantir identification of GATA2 as a potential driver of erythroid commitment.

Previous studies have shown that expression ratios between competing TF pairs can be critical determinants of lineage specification^{31, 34}. While average GATA2 levels remain relatively constant during early hematopoiesis (Supplementary Fig. 15c), we observe that a decrease in the ratio of PU.1 to GATA2 precedes the drop in DP (Supplementary Fig. 15d), suggesting that gene expression programs conferring erythroid fate are initiated as the balance of expression tilts towards GATA2 dominance. Indeed, the ratio of PU.1 to GATA2 is correlated with DP change along the erythroid lineage (Fig. 4c).

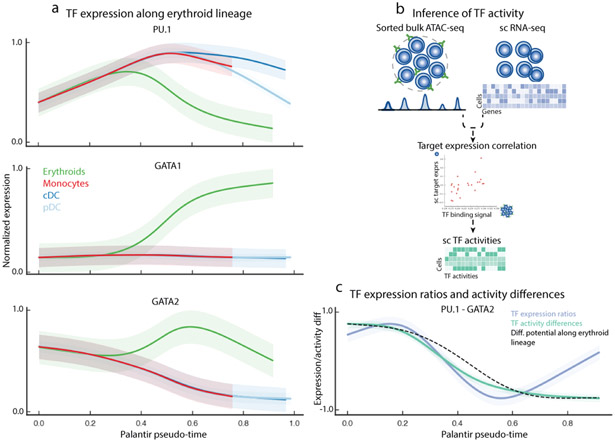
Figure 4.

Transcriptional regulation of erythroid differentiation. Data shown are for CD34+ human bone marrow cells, replicate 1 5708 cells). (a) Gene expression trends for PU.1, GATA1 and GATA2 in the myeloid and erythroid lineages. Trends are colored based on lineage, as in Fig. 2b. Shaded region represents 1 s.d. (b) Single-cell TF activity inference using scRNA-seq data and ATAC-seq data from bulk sorted populations. ATAC-seq data is used to identify cell-type-specific TF targets, and TF activity in each cell is inferred by measuring the correlation between predicted TF sequence affinity of the targets with their expression. (c) PU.1 / GATA2 expression ratio and PU.1 - GATA2 TF activity difference (colored trends) strongly correlate with DP (black) change along erythroid lineage. Shaded regions represent 1 s.d.

To explore this further, we characterized the behavior of PU.1 and GATA2 target genes along the erythroid lineage. Measuring the concordant behavior of multiple target genes not only mitigates individual gene measurement noise, but also provides a functional readout of TF activity. We leveraged published bulk ATAC-seq data¹⁰ from sorted erythroid and GMP cells for GATA2 and PU.1 targets, respectively, to determine TF activities at the single-cell level (Fig. 4b, Supplementary Fig. 15e, Supplementary Note 5). In line with the expression ratios, the change in PU.1 and GATA activity difference precedes the change in DP (Supplementary Fig. 15d) and is also strongly correlated with the decrease in DP along the erythroid lineage (Fig. 4c, Supplementary Fig. 15f-g). Together, these results provide in vivo evidence that GATA2, rather than GATA1, functions as a mutual agonist of PU.1 to achieve erythroid specification during human hematopoiesis.

Analysis of mouse hematopoiesis and colon differentiation

Palantir is ideally suited for our CD34+ human hematopoiesis dataset, which is heavily enriched for multipotent precursors and provides sufficient early cells for fine resolution mapping of lineage fate decisions. To test Palantir on more challenging data with a paucity of early cells and potential bias induced by cell sorting, we selected a mouse hematopoiesis dataset that profiled Lin⁻c-Kit⁺Sca-1⁺ cells using MARS-seq2 ⁶. This study sorted cells for different myeloid and erythroid precursor populations, but excluded the most multipotent stem cells, creating a challenge to correctly resolve branching probabilities.

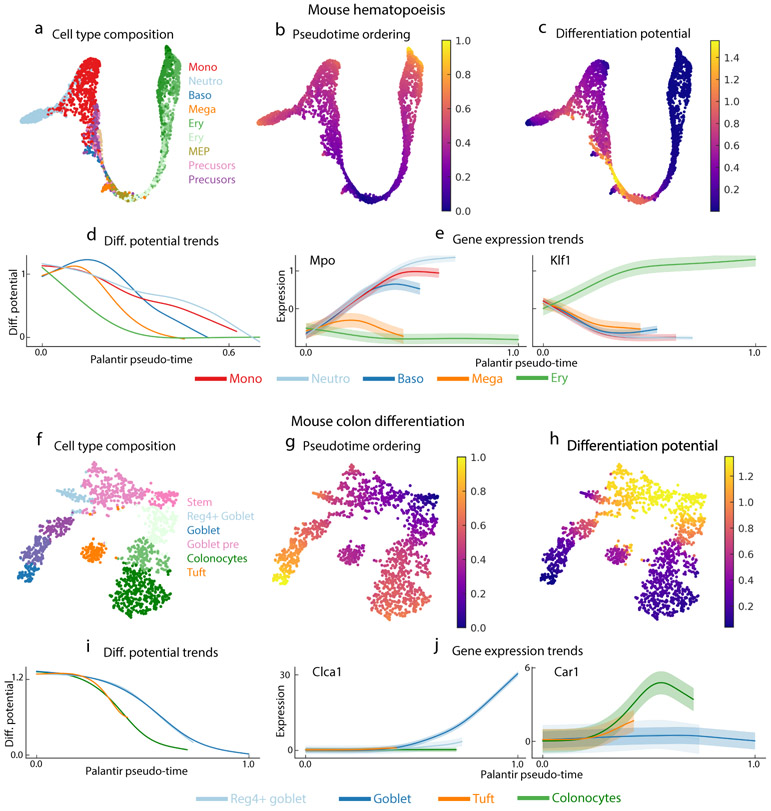
Even with a paucity of early cells (Fig. 5a), Palantir was able to correctly identify terminal states and estimate pseudo-time and DP characterizing mouse hematopoiesis (Fig. 5b,c, Supplementary Fig. 16a, Methods). The small number of multipotent cells does appear to affect accuracy and resolution in early hematopoiesis, as the peak DP is not located at the start of the pseudo-time trajectory (Fig. 5d). Despite these limitations, we observe a clear hierarchical structure in lineage specification, consistent with recent lineage tracing experiments²². The hierarchical structure is similar to human hematopoiesis, with commitment to erythroid lineage followed by specification of the different myeloid lineages (Fig. 5d). In further support of the Palantir model, the expression of key erythroid and myeloid genes Mpo and Klf1 are consistent with their roles in their respective lineages (Fig. 5e)²⁷ and their patterns in human hematopoiesis (Fig. 2f, 3d).

Figure 5.

Palantir generalizes to mouse hematopoiesis and colon differentiation datasets. (a) tSNE map of mouse hematopoiesis data generated by scRNA-seq of sorted precursor populations⁶ lacking a well-defined stem cell population. Cell are colored by clusters generated in ref ⁶. 2700 cells are shown on the tSNE maps. (b,c) Palantir pseudo-time (b) and differentiation potential (c), generated after selecting an early cell for initiation. (d) DP trends along pseudo-time, highlighting the hierarchical nature of murine hematopoiesis (commitment towards erythroid lineage followed by commitment towards the myeloid lineages). Trends are colored by clusters as in Fig. 5a. (e) Expression trends of myeloid factor Mpo and erythroid factor Klf1 recapitulate expected behavior and are consistent with their dynamics in human hematopoiesis. (f) tSNE map of scRNA-seq dataset of epithelial enriched cells from the mouse colon³⁵. Cells are colored by Phenograph cluster. 1811 cells are shown on the tSNE maps. (g,h) Palantir pseudo-time (g) and DP (h) generated using an Lgr5+ stem cell as the start cell and manually setting the tuft cells as one of the terminal states. (i) DP trends recapitulate known hierarchy of lineage specification (colonocytes followed by goblet cell populations). Trends colored by cluster as in Fig. 5f. (j) Expression trends of Clca1 and Car1 across lineages.

To test whether Palantir generalizes beyond hematopoietic datasets, we applied it to a mouse colon differentiation dataset generated using the InDrop platform³⁵. Lgr5+ stem cells were shown to differentiate to colonocytes, tuft cells, goblet cells and Reg4+ goblet cells (Fig. 5f). Palantir automatically identified the two goblet populations and colonocytes as terminal states but failed to identify Tuft cells as a terminal state since this population is not completely mature and is situated closer to Lgr5+ cells (Fig. 5f,g). By manually setting Tuft cells as one of the terminal states, Palantir correctly identified the pseudo-time ordering, hierarchical relationships and order of lineage commitment in mouse colon differentiation (Fig. 5g-i, Supplementary Fig 16b)³⁶. Palantir also recovers expected gene expression trends: Clca1 is specifically upregulated in goblet cells; Car1 first increases and then drops slightly in colonocytes; Muc2 shows strongest induction in Reg4+ goblet cells and Lgr5 is downregulated across all lineages (Fig. 5j, Supplementary Fig. 16c) ³⁵. BP changes and expression trends along lineages other than Tuft were not significantly altered when Tuft cells were not set as a terminal state (Correlation: 0.98; Supplementary Fig. 16d), demonstrating that Palantir is robust to missing populations and mislabeled cells.

Comparison with trajectory inference algorithms

While significant advances have been made for resolving the ordering of cells, state-of-the-art pseudo-time algorithms continue to model differentiation as a series of discrete, deterministic bifurcations, predominantly approximated by clustering the data^{7, 8}. We compared Palantir to leading and widely used pseudo-time algorithms such as Monocle2¹⁷, Partition Based Graph Abstraction⁷, DPT³, Slingshot⁸ and FateID³⁷.

We evaluated the algorithms based on their ability to identify lineages and recover known gene expression trends in human hematopoiesis, a well-studied system with scientific consensus on ground truth benchmarks (Supplementary Figs. 17-22, Supplementary Note 6). In particular, we assessed their ability to identify low frequency lineages such as megakaryocytes, cDCs and pDCs and recover the expression trends of key genes such as CD34¹¹, MPO³⁸, CD79B³⁹, GATA1²⁸, CSF1R⁴⁰ and CD41²¹. We also compared the nature of the outputs generated and the amount of prior biological knowledge needed as input to each algorithm. Palantir requires the least amount of a priori biological information (start cell) and provides both pseudo-time and cell fate probabilities as output (Supplementary Fig. 17a). However, PAGA is the only algorithm that allows a general topological structure.

Palantir outperforms the other algorithms (Supplementary Fig. 17b) by distinguishing the two DC populations, identifying megakaryocytic cells as separate from the erythroid lineage (Fig. 2e, Supplementary Fig. 6) and accurately recovering the expression dynamics of key lineage genes (Fig. 2f) (See Supplementary Note 6 for details of the evaluations). Monocle 2¹⁷ and FateID³⁷ (using RaceID clustering) fail to generate a coherent map of hematopoiesis (Supplementary Figs. 18 and 21), PAGA⁴¹ and DPT³ identify the major lineages, but are unable to identify rarer lineages and lose resolution in gene expression trends (Supplementary Fig. 19). Slingshot⁸ identifies the major lineages but not rare populations, resulting in incorrect gene dynamics (Supplementary Fig. 20), and it does not provide a unified framework for comparing expression trends across lineages⁸. FateID³⁷ using Palantir’s preprocessing and clustering is still largely incorrect for most cell fate probabilities and critically, includes all early cells in the CLP lineage, leading to mischaracterized expression dynamics (Supplementary Fig. 21). Finally, while individual diffusion components have been used to model differentiation trajectories^{15, 42}, in the CD34+ human bone marrow data they can only be used to infer ordering in CLP and monocyte lineages (Supplementary Fig. 22). Notably, none of the algorithms discussed above explicitly model and quantify the plasticity and branch probabilities along the differentiation landscape. Taken together, only Palantir could accurately associate expression changes in key transcription factors with changes in commitment to the lineages these regulate.

Discussion

Unlike existing algorithms, Palantir generates a probabilistic model of cell fate choice as a continuous process. Palantir is robust to parameters, reproducible across replicates, and generalizes to diverse datasets. Palantir’s high-resolution mapping of cells along differentiation trajectories allowed us to characterize the order and timing of regulatory factors that drive lineage choices in hematopoiesis. Our findings clarified that differentiation potential drops gradually during the progression from stem to differentiated cells and is hierarchical, such that cells are predisposed sequentially towards lymphoid, erythroid and finally myeloid lineages (potential drops gradually within each lineage).

The key to Palantir’s high resolution in pseudo-time is the use of multiple diffusion components and neighbor graphs to measure distances between cells in this embedded space (Supplementary Fig. 23a-c). This enables Markov chain construction, which is central to both terminal state identification and modeling continuities in lineage choices. Palantir outperforms other pseudo-time algorithms, which largely treat lineage choices as discrete bifurcations, in recovering biologically consistent gene expression trends and lineage relationships. Enrichment of stem and precursor cells from bone marrow was necessary to characterize lineage choices in early human hematopoiesis at high resolution. However, Palantir can robustly recover expression trends in datasets for which precursors are not enriched.

We anticipate that Palantir will be a valuable discovery tool for many less characterized systems, including those profiled by the Human Cell Atlas Project⁴³. A key requisite is the presence of the full range of differentiating cells, made possible by the asynchronous nature of differentiation in tissues such as bone marrow, colon and olfactory epithelium^{8, 18, 35}. We note that this is not a feature of embryogenesis, which is typically studied using time course experiments^{42, 44}. Time course data require explicit modeling of connectivity between time points and corrections for confounding by batch effects.

The most important assumption made by pseudo-time algorithms, including Palantir, is that differentiation is unidirectional and proceeds towards functionally mature cells. While this is reasonable for healthy differentiation, the assumption is violated in systems such as tissue regeneration⁴⁵ and cancer⁴⁶. If cells dedifferentiate or trans-differentiate to earlier transcriptional states, scRNA-seq data alone will be insufficient to distinguish these populations and their differentiation paths. In-vivo lineage tracing technologies can provide ground truth for lineage relationships^{47, 48} but require genetic modification, and hence are unsuitable to study cancer progression, metastasis and healthy development in human tissues. As an alternative, mutations occur rapidly in most cancers and can provide a source of directionality and lineage information in human systems. Recent studies⁴⁹ have demonstrated that somatic mutations occur at a rate that enables lineage tracing even in healthy human tissues. The ability to simultaneously profile the transcriptome and DNA⁵⁰ has great potential to elucidate disease initiation and progression by extending Palantir to incorporate lineage information to model cell fate decisions.

scRNA-seq of CD34+ human bone marrow cells

Cryopreserved bone marrow stem/progenitor CD34+ cells from healthy donors were purchased from AllCells, LLC. (Cat. No. ABM022F) and stored in vapor phase nitrogen until use. Typical for scRNA-seq, a vial was removed from the storage and immediately thawed at 37°C in a water bath for 2-3 minutes. Next, vial content (1ml) was transferred to a 50ml conical tube. In order to prevent osmotic lysis and ensure gradual loss of cryoprotectant, 1ml of warm media (IMDM with 10% FBS supplement) was added dropwise, while gently shaking the tube. Then the cell suspension was serially diluted 5 times with 1:1 volume additions of complete growth media with 2 minutes wait between additions. Final ~32ml volume of cell suspension was pelleted at 300rcf for 5 minutes. After removing supernatant, cells were washed twice in ice cold 1X PBS with 0.04% (wt/vol) BSA supplement to remove traces of media. Cell concentration and viability was determined with Countess II automatic cell counter employing trypan blue staining method.

Single cell RNA sequencing was performed with 10X genomics system using Chromium Single Cell 3` Library and Gel Bead Kit V2 (Cat. No. 120234). Briefly, 8700 cells (viability 90-97%) were loaded per reaction, targeting recovery of 5000 cells with 3.9% multiplet rate. After reverse transcription reaction emulsions were broken, barcoded cDNA was purified with DynaBeads, followed by 12 cycles of PCR amplification. The resulting amplified cDNA was sufficient to construct NGS libraries, which were sequenced on Illumina HiSeq 2500 system (HiSeq SBS V4 chemistry kit).

Single cell RNA-seq data processing

Data preprocessing

Data derived from each replicate was processed independently. Single cell RNA-seq data was preprocessed using the SEQC pipeline ¹⁹ using hg38 human genome and the default SEQC parameters for 10X to obtain the molecule count matrix. The SEQC pipeline aligns the reads to the genome; corrects barcode and UMI errors; resolves multi-mapping reads and generates a molecule count matrix ¹⁹. SEQC also performs a number of filtering steps: (a) Identification of true cells from cumulative distribution of molecule counts per barcode, (b) removal of apoptotic cells identified at cells with >20% of molecules derived from the mitochondria and (c) removal of low complexity cells identified as cells where the detected molecules are aligned to a small subset of genes ¹⁹. In addition, cells with less than 1000 molecules detected were filtered out. Finally, genes that were detected in at least 10 cells were retained for downstream analysis. The retained cells have a median molecule count of ~3200 and median gene count of ~1800 indicating the high quality of the data (Supplementary Fig. 24).

The filtered count matrix was normalized by dividing the counts of each cell by the total molecule counts detected in that particular cell. The normalized matrix was multiplied by the median of total molecules across cells to avoid numerical issues ⁵². Normalized data was log transformed with a pseudocount of 0.1.

Cell cycle correction

Expression of cell cycle genes can confound the ordering of cells in a differentiation trajectory. and hence we applied f-scLVM ^{53, 54} to factor out the cell-cycle effect across all cells. Normalized and log transformed data was used as input to f-scLVM correction with default parameters. The following gene ontology annotations were used to annotate the cell cycle effect: GO:0000279 M phase, GO:0006260 DNA replication, GO:0007059 chromosome segregation, GO:0000087 M phase of mitotic cell cycle, GO:0048285 organelle fission.

Following cell cycle correction, PCA was performed keeping the top 300 components and diffusion maps were computed using the PCs as input ¹⁴. See section “Adaptive anisotropic kernel” under the Palantir algorithm description for details on constructing the diffusion maps.

Annotation of cell types and filtering of mature populations

Gene expression profiles from sorted bulk hematopoietic populations were used to annotate the cell types ^{19, 20}. Cell cycle corrected data was clustered with Phenograph ¹³ using default parameters and the top 300 principle components as inputs. Cluster centroids were determined for each cluster and the expression of each gene was standardized. Bulk expression data was downloaded from the Dmap portal (http://portals.broadinstitute.org/dmap/home) and expression of each cell type was standardized. For each cluster, average correlation across bulk replicates was computed for each cell type and the cell type with the highest correlation was used to annotate the cluster (Supplementary Fig. 4c). Note, the inferred cell types are used only for interpretation and not used by Palantir.

To limit the data to cell types undergoing differentiation in the bone marrow, clusters that were annotated as T-cells and mature granulocytes were filtered out. T cells were filtered out, since these migrate from the periphery and do not differentiate in the bone marrow. Mature granulocytes were filtered out since no coherent precursor population was identified in the data.

tSNE visualization

tSNE maps ⁵⁵ were generated using diffusion components scaled by the Eigenvalues as inputs rather than principal components of the data and perplexity set to 150. The scaling of Eigenvectors ensures less sensitivity to outliers in the data and is performed as follow:

$$e_{i\_scaled}=\frac{{\lambda }_l}{1-{\lambda }_l}{e}_i$$ (1)

This scaling is equivalent to estimating diffusion distances from 1, 2. … ∞ steps. See section “Measuring distances between cells in the phenotypic manifold” under the Palantir algorithm description for details on scaling and its impact on the representation. The number of components were chosen based on the Eigen gap of the Eigenvalue decomposition of the diffusion operator. The set of diffusion components is the same set used for running Palantir. Using diffusion components as inputs led to maps more representative of differentiation when compared to the maps generated on principal components or force directed graphs (Supplementary Fig. 25). We found that force directed graphs represent the distinct mature populations better and provide less resolution in the regions of manifold where lineage decisions are being made. An example of generating tSNE maps using diffusion components is available here: http://nbviewer.jupyter.org/github/dpeerlab/Palantir/blob/master/notebooks/Palantir_sample_notebook.ipynb

Differential expression of genes

Differentially expressed genes between clusters were determined using MAST ⁵¹. MAST was run using default parameters with normalized counts (without log transform) as the input. Genes with FDR corrected p-value < 1e-2 and absolute log fold change > 1.25 were considered significantly different.

Subsampled data used for figure 1

A dataset was generated using the human CD34+ hematopoiesis dataset by waypoint sampling of cells from erythroid and myeloid lineages (clusters 0, 1, 2, 3, 4, 6, 7, 8 - Supplementary Fig. 4a). tSNE map was generated as described in “Single cell RNA-seq data preprocessing” and the projection of stem cells was manually adjusted for cleaner visualization.

Application of Palantir to CD34+ cells

Palantir was applied to each replicate separately using 1200 waypoints and one of the CD34+ cells as the start cell. The parameter k was set to 10% of the total number of cells in the data. The results however are stable to the choice of k (Supplementary Fig. 6). The number of diffusion components were chosen based on the Eigen gap of the Eigenvector decomposition of the diffusion operator. The results are stable to choice of the number of diffusion components and the choice of waypoints (Supplementary Fig. 7).

Robustness of Palantir results to parameters

Palantir has the following parameters or variables: (a) k, number of neighbors for constructing the nearest neighbor graph, (b) Waypoint sampling (random waypoints selected) and (c) Number of diffusion components, which by default is determined based on the Eigen gap. We systematically evaluated the robustness of Palantir using data from replicate 1 of the CD34+ bone marrow data (Supplementary Figs. 5-8). The same start cell was used across all runs. Palantir was run with different parameters and the robustness of the results was measured using the following criteria:

1. Pearson correlation of pseudo-time, differentiation potential and branch probabilities for the different branches between a given pair of Palantir runs.

2. Pearson correlation of pseudo-time, differentiation potential and branch probabilities for a subset of cells sampled from the middle of the differentiation process (Supplementary Fig. 4, Cluster 1). CLP lineage was excluded from this analysis since cells of Cluster 1 have differentiated away from this lineage.

Robustness to waypoint sampling

Robustness to waypoint sampling was tested by fixing k and the number of diffusion components (Supplementary Figs. 5). The correlation of pseudo-time, differentiation potential and branch probabilities for all branches, for all cells are shown in Supplementary Fig. 5a-b. All the correlations comparing between runs are > 0.98. A subset of cells sampled from the middle of the differentiation process is shown in Supplementary Fig. 5c with the corresponding pseudo-time, differentiation potential and branch probability correlations shown in Supplementary Fig. 5c-d. Pseudo-time ordering correlations are all > 0.97, differentiation potential correlations range between 0.85 – 0.95 with 75% of correlations > 0.9 (Supplementary Fig. 5c). Branch probability correlations range between 0.85 – 0.95 with 90% of correlations > 0.9 (Supplementary Fig. 5d)

Robustness to k, the number of neighbors for kNN graph construction

Robustness to k was tested by fixing the number of diffusion components, waypoints and terminal states (Supplementary Fig. 6). The correlation of pseudo-time, differentiation potential and branch probabilities for all branches for all cells are shown in Supplementary Fig. 6a-b. All the correlations comparing between runs are > 0.97. A subset of cells sampled from the middle of the differentiation process is shown in Supplementary Fig. 6c with the corresponding pseudo-time, differentiation potential and branch probability correlations shown in Supplementary Fig. 6c-d. Pseudo-time ordering correlations are all > 0.97, differentiation potential correlations are all > 0.9 (Supplementary Fig. 6c). Branch probability correlations range are > 0.94 except for pDC branch with k = 25 where the correlations are lower because of insufficient connectivity of the graph. (Supplementary Fig. 6d).

Robustness to number of diffusion components

Robustness to number of diffusion components was tested by using fixing k, waypoints and terminal states (Supplementary Fig. 7). The correlation of pseudo-time, differentiation potential and branch probabilities for all branches for all cells are shown in Supplementary Fig. 7a-b. Pseudo-time ordering and differentiation potential correlation are all > 0.96 (Supplementary Fig. 7a). Branch probabilities correlations are > 0.94 (Supplementary Fig. 7b). A subset of cells sampled from the middle of the differentiation process is shown in Supplementary Fig. 7c with the corresponding pseudo-time, differentiation potential and branch probability correlations shown in Supplementary Fig. 7c-d. Pseudo-time ordering correlations are all > 0.97, differentiation potential correlations range between 0.84 – 0.99 with 75% of correlations > 0.9 (Supplementary Fig. 7c). Branch probability correlations are all > 0.94 Supplementary Fig. 7d).

Robustness to sub-sampling of cells

In order to test the robustness of Palantir to sub-sampling of the cells, cells from the different lineages were subsampled at different rates (25%, 50% and 75%) from each of the following clusters individually (Supplementary Fig. 2): (a) 3, 6 – Mono, (b) 5 – CLP and (c) 2, 8 – Erythroid lineage (Supplementary Fig. 8). The robustness was measured using pearson correlation between pseudo-time, differentiation potential and branch probabilities with and without sub-sampling (Supplementary Fig. 8). All correlations are > 0.94.

Comparison of Palantir results across replicates

Palantir results, specifically pseudo-time and differentiation potential, from one replicate are projected onto cells from a second replicate using mutually nearest neighbors (Supplementary Fig. 10). The projected results are then correlated with Palantir results derived de novo from the second replicate to measure reproducibility of Palantir results across the replicates.

Let N₁ and N₂ be the number of the cells in replicate 1 and 2 respectively. As a first step, the count matrices of both replicates are combined to create a unified molecule count matrix using genes detected in both replicates. This matrix is normalized as described in “Single cell RNA-seq analysis: Data preprocessing” and log transformed with a pseudo count of 0.1, followed by PCA. Principal component space of the combined count matrix is used to determine the k-nearest replicate 1 neighbors of replicate 2. This neighborhood graph can be represented by an adjacency matrix D²¹ ∈ R^N₂×N₁where $D_{ij}^{21}$ is the distance between cell i of replicate 2 and cell j of replicate 1 if i and j are neighbors. Similarly let D¹² ∈ R^N₁×N₂represent the adjacency matrix of replicate 2 neighbors of replicate 1.

Mutually nearest neighbors between the two replicates is computed as below

$$MN{N}^2=D^{21}\odot D^{{12}^T}$$ (2)

where MNN ∈ R^N₂×N₁ and ⊙ is the Hadamard product or element-wise multiplication operator.

The distances of the MNN adjacency matrix is converted to an affinity matrix using Equation (12) (Supplementary Note 1).

$$W_{ij}=exp(-MN{N}_{ij}^2)∕\sum _{k=1:N_2}exp(-MN{N}_{ik}^2)$$ (3)

Palantir results of replicate 1 are projected on to the cells of replicate 2 using the weights computed in Equation (27) (Supplementary Note 1). The projected results are thus a weighted average of the mutually nearest neighbors of each cell.

Let τ_Rep1 and τ_Rep2 be the de novo psuedo-time ordering of replicates 1 and 2 respectively. The projected pseudo-time is computed as follows

$${\tau }_{Rep2\_projected}=W\ast {\tau }_{Rep1}$$ (4)

Pearson correlation between τ_{Rep2_projected}and τ_Rep2 gives a measure of reproducibility of Palantir pseudo-time. Similarly, the projected differentiation potential is computed as follow

$$E_{Rep2\_projected}=W\ast E_{Rep1}$$ (5)

Similar to the pseudo-time, Pearson correlation between E_{Rep2_projected}and E_Rep2gives a measure of reproducibility of the differentiation potential.

Additional datasets

Mouse hematopoiesis dataset

Mouse hematopoiesis dataset ⁶ was downloaded and preprocessed using the procedure outlined in scanpy (https://github.com/theislab/paga/blob/master/blood/paul15/paul15.ipynb). A cluster of cells annotated as DCs were projected as a clear outlier along a diffusion component without a well-defined differentiation path (likely due to insufficient cell sampling) and therefore were excluded from the analysis. PCA was performed on the preprocessed data and components that explain 85% of the variance were used for generating diffusion maps as described in “The Palantir algorithm”. Eigen gap suggested use of 7 diffusion components, but 13 components were used instead to ensure inclusion of all cell types. Note that the frequencies of some of the populations such as basophils is extremely low necessitating the inclusion of additional components.

Palantir was run using one of the cells annotated as MEPs since these are the most primitive cells present in the data. Palantir automatically determined the different terminal states and determined pseudo-time ordering, differentiation potential and branch probabilities. Differentiation potential trends and gene expression trends were generated as described in “Gene expression trends” section.

Mouse colon data

Raw counts for the mouse colon dataset ³⁵ was downloaded from GEO (GSE102698 - https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE102698). Cells with low molecule count (<1000) and high mitochondrial molecule fraction (>0.2) were excluded from the analysis. Immune cells were also excluded since they are not relevant for differentiation. Data was normalized as described in “single cell data preprocessing”. Phenograph clustering of data revealed a cluster of cells with low molecule count distribution, which was excluded from the analysis. To maintain consistency with the analysis in the original publication, the data was not log transformed and was restricted to genes used by the authors. The gene list was downloaded from Flowrepository (http://flowrepository.org/id/FR-FCM-ZYAG).

As before, PCA was performed to reduce the data to 20 components (explaining 85% of the variance) and diffusion maps were computed using PCs as the input. Palantir was run using one of the Lgr5+ stem cells as the start. Palantir automatically identified colonocytes, goblet cells and Reg4+ goblet cells as the terminal states but failed to identify Tuft cells as one of the terminal states. Tuft cells are very similar in their expression profiles to the early cells and thus there was not sufficient variability for the small number of Tuft cells to be projected onto a distinct diffusion component (note, we believe greater cell numbers would have resolved this). The results in Fig. 5b were generated by manually setting Tuft cells as one of the terminal states.

Performance of competing methods on the CD34+ marrow data

We undertook a systematic evaluation of the performance of Palantir in comparison to widely-used trajectory inference algorithms such as Monocle2, Diffusion Pseudotime (DPT), Partition based Graph Abstraction (PAGA- based on DPT), Slingshot, FateID, and Monocle 2.

We first compared the algorithms by evaluating their setup: the prior biology knowledge required as input and the diversity of outputs provided by each algorithm using the following criteria:

1. Does the algorithm require the specification of start cell or start state?

2. Does the algorithm require the specification of number of branches or clustering / segmentation of the data a priori.

3. Are the terminal states automatically determined by the algorithm?

4. Does the algorithm generate a unified pseudo-time ordering of cells that enables the comparison of gene expression patterns across different lineages

5. Does the algorithm Identify continuities in cell fate specification by determining branch probabilities, fate biases or differentiation potential

6. Does the algorithm generalize to topological structures beyond a tree topology?

Supplementary Fig. 17a summarizes the characteristics of the different algorithms according to the criteria outline above:

1. All the algorithms require the specification of a start cell or a state to orient the pseudo-time ordering.

2. DPT, Slingshot and FateID all require the specification of either the number of branches and/or pre-determined clustering of the data, making them sensitive to the number of branches selected and the quality of the clustering, which is notoriously sensitive in the case of continuous differentiation data.

3. Palantir and Slingshot can automatically determine the terminal states. PAGA requires specification of the PAGA clusters that belong to a particular lineage; FateID and Monocle 2 require explicit specification of the terminal states. DPT requires the specification of number of branches.

4. Slingshot and FateID do not provide a unified pseudo-time ordering of cells and thus do not facilitate comparison of gene expression trends across lineages

5. Palantir and FateID both output a probability vector of cell fate choice continuities for each cell. Furthermore, Palantir also quantifies the differentiation potential of a cell by summarizing the cell fate choice branch probabilities.

6. PAGA is the only algorithm that determines the topological structure of the differentiation hierarchy without prior assumptions about the topology.

Thus, Palantir uses minimal a priori biological information to (a) automatically determine the different terminal states, (b) generate a unified pseudo-time ordering to compare gene expression trends across lineages and (c) identify continuous branch probabilities and differentiation potential for each cell.

We next used the CD34+ human bone marrow data (replicate 1) as a benchmark to compare the results of the different algorithms. Due to the varied nature of the different outputs, we evaluated the ability of the algorithm to determine known and well established features of human hematopoiesis such as (a) identification of the different lineages represented in the data, with emphasis on less frequent populations such as megakaryocytes, cDCs and pDCs, which are more subtle and challenging to infer (b) recovering known expression trends of key genes across multiple lineages. We choose well-studied canonical genes across the different lineages, whose expression dynamics are known and can thus serve as ground truth. The following canonical genes, representing a broad spectrum of gene expression dynamics, were chosen for this evaluation:

1. CD34. Marker of stem and precursor cells and known to be downregulated with differentiation in all cells¹¹.

2. MPO. Early marker for myeloid lineages with higher expression during monocyte lineage commitment³⁸.

3. CD79B. Marker for lymphoid lineage commitment³⁹.

4. GATA1. Marker for erythroid lineage commitment²⁸.

5. CSF1R. Known to be upregulated in cDCs and downregulated in pDCs following an initial upregulation⁴⁰.

6. CD41. Marker for megakaryocyte lineage commitment²¹.

Supplementary Fig. 17b shows the results of this comparison for the different algorithms. Palantir and DPT were able to identify the megakaryocyte lineages, whereas PAGA and Slingshot included these cells to be part of the erythroid lineage. Palantir was the only algorithm able to recover the distinction between the two DC lineages. Comparing the expression trends, all algorithms except Monocle 2 recovered the downregulation of CD34 across all lineages. Palantir recovers the known gene expression trends across all lineages (Fig. 2). While PAGA, DPT and Slingshot identify the trends in the larger lineages, PAGA (and DPT) suffer from a loss in resolution in gene expression trends and Slingshot does not provide a unified ordering of cells to compare gene expression trends across lineages. FateID with the default clustering using RaceID failed to identify any correct lineages and gene expression trends, whereas FateID with a preprocessing procedure and clustering followed in Palantir identifies correct expression trends in only the monocyte and CLP lineages. Monocle 2 could not recover the key hematopoietic lineages or expression trends from the CD34+ bone marrow data. See Supplementary Note 6 for a detailed description of the different algorithms and their performance.

Software availability

Palantir is available as a python module here: https://github.com/dpeerlab/Palantir/, A jupyter notebook detailing the workflow including data preprocessing, running Palantir along with a demonstration of various plots and visualizations is available at http://nbviewer.jupyter.org/github/dpeerlab/Palantir/blob/master/notebooks/Palantir_sample_notebook.ipynb

The code and data for this article, along with an accompanying computational environment, are available and executable online as a Code Ocean capsule: https://doi.org/10.24433/CO.6f3a9d2b-82d6-45bd-a583-5346a30e0c5d

Data availability

Raw and processed data is available through the Human Cell Atlas data portal at https://prod.data.humancellatlas.org/explore/projects/29f53b7e-071b-44b5-998a-0ae70d0229a4