Sample size requirements for the internal validation of psychiatric scales

Abstract

The ratio of subjects to variables (N/p), as a rule to calculate the sample size required in internal validity studies on measurement scales, has been recommended without any strict theoretical or empirical basis being provided. The purpose of the present study was to develop a tool to determine sample size for these studies in the field of psychiatry. First, a literature review was carried out to identify the distinctive features of psychiatric scales. Then, two simulation methods were developed to generate data according to: (1) the model for factor structure derived from the literature review and (2) a real dataset. This enabled the study of the quality of solutions obtained from principal component analysis or Exploratory Factor Analysis (EFA) on various sample sizes. Lastly, the influence of sample size on the precision of Cronbach's alpha coefficient was examined. The N/p ratio rule is not upheld by this study: short scales do not allow smaller sample size. As a rule of thumb, if one's aim is to reveal the factor structure, a minimum of 300 subjects is generally acceptable but should be increased when the number of factors within the scale is large, when EFA is used and when the number of items is small. Copyright © 2011 John Wiley & Sons, Ltd.

Introduction

One of the most critical methodological issues when designing a study and planning the statistical analysis, is the number of subjects to include. Generally, the sample size is based on the power of a statistical test of hypothesis. In descriptive studies, this approach cannot be used, and it is usually the range of the confidence interval of a given parameter which determines sample size. This is likely to be the case in internal validity studies of measurement scales in which, traditionally, two types of parameters are of interest: Cronbach's alpha coefficient (α) which assesses reliability, and factor analysis loadings which explore the dimensional structure of the scale. In practice, these loadings are estimated either by Principal Component Analysis (PCA) or by Exploratory Factor Analysis (EFA). A formula for the confidence interval of Cronbach's alpha coefficient was developed by Feldt in the 1960s (Fan and Thompson, 2001; Feldt, 1965). The sample size required for a desired precision of this coefficient can, therefore, be easily assessed. In fact, the difficulty in establishing a simple rule for sample size calculation in internal validity studies arises from the use of factor analysis.

Many recommendations regarding sample size in factor analysis have been made, but none are founded on a strict theoretical or empirical basis. The most widely used rule uses the ratio of the number of subjects (N) to the number of items (p), and this varies from three to 10 depending on authors (Cattell, 1978; Everitt, 1975; Gorsuch, 1983; Nunnaly, 1978). Other authors have suggested an absolute minimum sample size of 50 to 500 to enable factor analysis (Aleamoni, 1973; Comrey, 1978; Comrey and Lee, 1992; Loo, 1983). Given these various recommendations and their lack of documented explanation, some researchers have put them to the test by studying the consequences of using factor analysis on insufficient sample sizes. They all found that, in addition to N, two other parameters are important to obtain accurate and stable solutions: firstly the ratio of the number of variables to the number of factors (ratio p/M, which is an indicator of “factor overdetermination”, a concept defined by MacCallum et al. in 1999 as the degree to which each factor is clearly represented by a sufficient number of variables, at least three or four); and secondly the level of factor loadings (which reflects the level of communalities, the communality of a variable being the portion of the variance that a variable shares with the common factors). The lower the p/M ratio and the factor loading level, the larger the sample size required for a given accuracy and stability of solutions obtained from factor analysis (Guadagnoli and Velicer, 1988; Hogarty et al., 2005; MacCallum et al., 1999; Mundfrom et al., 2005; Velicer and Fava, 1998). All these studies have shown that sample size partly depends on the nature of the data: their “strength”. Strong data in factor analysis means uniformly high communalities without cross‐loadings, plus several variables loading strongly on each factor (Costello and Osborn, 2005; Fabrigar et al., 1999). The stronger the data, the smaller the sample size required. It does not therefore seem possible to recommend a general rule for sample size calculation that is valid in all the fields to which psychometric procedures apply.

However, in each field, there are distinctive features. In psychiatry, factor loading values are usually close to 0.6, the p/M ratio can vary from three to 20 or more, depending on scales, and the number of items is often different for each factor within a scale (Dawkins et al., 2006; Gabryelewicz et al., 2004; Iwata et al., 2000; Loza et al., 2003). Another characteristic observed in psychiatric scales is the shape of the scree plot. Unidimensionality is rare, and usually there is a first dimension representing a large part of the variance contained in the data (from 30 to 35%), and then there are one or more other dimensions explaining smaller and decreasing proportions of variance (from 15 to 5%) (Chapman et al., 2009; Sanchez‐Lopez and Dresch, 2008; Uslu et al., 2008; Villalta‐Gil et al., 2006). This factor structure can be explained by the presence of correlated factors or, likewise, by a two‐order factor model in which a second‐order factor explains the pattern of correlations among the first‐order factors.

The unresolved methodological issue about sample size in validation studies of measurement scales can lead to erroneous conclusions being drawn if the sample is too small. Conversely, the inclusion of too many subjects in a study wastes time and resources for researchers. The main purpose of this study is therefore to use the distinctive features encountered in psychiatric scales to develop a tool for the determination of the sample size required in internal validity studies on such scales in order to guarantee an acceptable level of precision for Cronbach's alpha coefficient and, above all, accuracy and stability of the factor solution. A secondary aim is to determine the influence of the choice of PCA or EFA on the sample size required and on the accuracy of the factor solution.

Material and methods

This study comprised three stages. The first consisted in a literature review to determine the shared characteristics of psychiatric scales. The second used simulations to study the influence of sample size on the stability and accuracy of the solutions obtained from PCA and EFA. These simulations were based, firstly, on artificial data generated according to the factor pattern observed in psychiatric scales from the literature review, and then on real data. Finally, the influence of sample size on the precision of Cronbach's alpha coefficient in the conditions encountered in psychiatry was studied.

Literature review

Ten psychiatric scales were selected taking account of the frequency of their use in clinical practice and their representativeness of different pathologies encountered in psychiatry:

• Positive and Negative Syndrome Scale (PANSS – 30 items)

• Brief Psychiatric Rating Scale (BPRS – 18 items)

• Beck Anxiety Inventory (BAI – 21 items)

• State–Trait Anxiety Inventory (STAI – 40 items)

• Hamilton Anxiety Rating Scale (HAMA – 14 items)

• Hamilton Rating Scale for Depression (HAMD – 17 items)

• Montgomery–Asberg Depression Rating Scale (MADRS – 10 items)

• Beck Depression Inventory (BDI – 21 items)

• Hospital Anxiety and Depression Scale (HADS – 14 items)

• General Health Questionnaire (GHQ – 12 items)

Articles including results of PCA or EFA concerning any of these 10 scales were sought in the Medline database using the following keywords: for each scale, the “name of the scale” and/or “its abbreviation”, the expressions “factor analysis” and/or “components analysis” and the article language “English” and/or “French”. A pre‐selection was carried out on the basis of the abstracts, and articles were then included if the following three criteria were met: the factor structure of one of the 10 scales was studied using PCA or EFA; eigenvalues or percentage of variance accounted for by each factor before rotation were specified; sample size was equal to or greater than 100.

In each article, the following data were collected: the method used for factor extraction (PCA or EFA), the rotation method used (orthogonal or oblique), the number of factors extracted, the eigenvalues or the percentage of variance accounted for by each factor before rotation, the number of items per factor and the values of the factor inter‐correlations. When the loading matrix was reproduced, the mean of the salient loadings was calculated by considering only the higher value in case of cross‐loadings. If several groups were studied, only the results from the largest group were considered. Likewise, if analyses were carried out on data collected at different times, only the results collected at the initial collection time were considered. All these data were recorded on the Microsoft®Office Excel 2007 spreadsheet program and descriptive statistical analyses for each of these variables were performed using R software 2.6.2 (R Development Core Team, 2008).

Simulation studies

Simulations based on artificial data

The simulation method developed here is based on the common factor model and is described in the Appendix. To summarize, certain important points should be noted. In this simulation model, two hypotheses are set. The first is the existence of a simple structure, i.e. each item loads on a single factor and all the non‐salient loadings are equal to zero. The second is that all salient loadings (λ) are equal. When a common factor model is used, responses have a normal distribution. To come closer to real‐life instruments, these responses were categorized into four‐class ordered variables as in a four‐point Likert response pattern. The response distribution was different for each item in the scale and non‐symmetrical so as to simulate floor and ceiling effects. Finally, parameters that can be controlled using this method are: the number of items (p), the number of factors (M), the number of items loading on each factor in the scale (p_m, m = 1 to M), the value of salient loadings (λ), the level of the factor inter‐correlations (cor(F_m,F_m'), m ≠ m′) and the sample size (N).

For M and p, we decided to study the values usually encountered in psychiatry, i.e. scales with two, three or four factors and a number of items varying between 10 and 45 (p = 10, 15, 20, 25, 30, 35, 40 or 45). The results from the literature review then enabled the determination of the value of λ and p_m. Levels of factor inter‐correlations were chosen amongst the values encountered in the literature review, and also in order to obtain the percentage of variance accounted for by each factor that was nearest to the mean of this percentage found in the review. Once all these parameter values were determined, two sets of 10,000 samples were generated for each sample size studied (N = 50, 100, 150, 200, 300, 500, 1000) and for each condition defined by M and p. Then, PCA was performed on one set and EFA on the other. These two methods of factor extraction were followed by a promax rotation which is an oblique rotation method as recommended when factors are correlated with each other (Costello and Osborn, 2005; Fabrigar et al., 1999; Floyd and Widaman, 1995). To determine the adequate sample size, three criteria were used as a threshold for good quality of the factor solution:

• standard deviation of the salient loadings obtained after rotation over the 10,000 simulations (σ_λ) below 0.05 (95% confidence interval of the salient loadings close to $\widehat{\lambda }\pm 0.1$)

• percentage of simulations in which all the items in the scale loaded on the right factor (i.e. that which is determined in the simulation model) after rotation (R_%) greater than 90%

• the mean of percentages of items loading on the wrong factor in the scale after rotation over the 10,000 simulations (W_%) below 1%

When EFA was performed, the percentage of simulations where Heywood cases occurred (i.e. loading estimates greater than 1.0, which occurs only with EFA) was also estimated. Finally, for either method (PCA and EFA), the mean of the salient loadings over the 10,000 simulations (μ_λ) was computed.

Simulations based on real data

To offer a complementary perspective, a simulation study was also conducted by the aid of an important real data set of 1009 patients consecutively hospitalized between January 1988 and July 2004 in the Eating Disorder Unit of the Clinique des Maladies Mentales et de l'Encéphale at Sainte‐Anne Hospital, Paris, France. Patient characteristics and procedures have been described previously in Fedorowicz et al. (2007). We focused on two instruments, the 13‐item version of the BDI (Beck et al., 1961) and the 21‐item version of the HAMD (Hamilton, 1960). For each of these scales, a parallel analysis was performed to determine the number of factors to extract. Next, two sets of 10,000 samples were repeatedly drawn from the entire sample (with replacement) for each sample size: 100, 200, 300, 400, 500, 600, 700 and 800. Then, PCA was performed on one set and EFA on the other, followed by a promax rotation in the case of a multidimensional instrument. The mean of the standard deviations of the loadings was then calculated over the 10,000 samples for each sample size.

These analyses were performed using R software 2.6.2. The function princomp was used for PCA and the loading matrix obtained was rotated using promax with a constant set at four (Costello and Osborn, 2005; Jackson, 1991). For EFA, the function factanal (with the argument rotation  =  promax, which uses the maximum likelihood estimation procedure, was chosen for two reasons: it finds the solution with the optimal statistical properties and it is likely the most widely used method (Revelle, 2008). Finally, the draw was performed using the function sample and parallel analysis using the function scree.plot from the psy package.

Precision of Cronbach's alpha coefficient

The most widely cited minimum value considered as acceptable for the Cronbach's alpha coefficient is 0.7 (Fedorowicz et al., 2007; Nunnaly, 1978; Peterson, 1994). We therefore chose to study the half‐width of the confidence interval of this coefficient for three expected values (α = 0.7, 0.8 and 0.9) in relation to p and N (same values as previously). Feldt's formula for this confidence interval was used with type I error rate set at 0.05 (Fan and Thompson, 2001; Feldt, 1965).

$$\text{Upper\hspace{0.17em}bound}\text{:}C{I}_{\mathit{upper}}=1-\left[\left(1-\alpha \right)\times {\mathfrak{I}}_{0.025,dd{l}_1,dd{l}_2}\right]$$

$$\text{Lower\hspace{0.17em}bound}\text{:}C{I}_{\mathit{lower}}=1-\left[\left(1-\alpha \right)\times {\mathfrak{I}}_{0.975,dd{l}_1,dd{l}_2}\right]$$

where ddl₁ = N − 1, ddl₂ = (N − 1) × (p − 1) and $\mathfrak{I}$ represents the values of the F‐distribution for percentiles 0.025 and 0.975 respectively.

Results

Psychiatric scale characteristics

The keywords used for the search in Medline database enabled the identification of 827 studies. Amongst these, 232 articles were pre‐selected on the basis of the abstracts, and a total of 56 articles met the inclusion criteria. Five of these articles showed results from factor analysis on two of the scales selected for this review, which finally increased the total to 61 references. Table 1 contains, for each scale, the total number of references included and the number of references extracting the same number of factors for each.

Table 1.

References included and numbers of references extracting the same number of factors for each scale

Scale	References	Total	Number of factors
			2	3	4	5	6	7
PANSS	(Bell et al., 1994; Fresan et al., 2005; Honey et al., 2003; Kay and Sevy, 1990; Lancon et al., 1999; Lee et al., 2003; Lindenmayer et al., 2004; Loza et al., 2003; Lykouras et al., 2000; Salokangas et al., 2002; Villalta‐Gil et al., 2006)	11	—	—	1	8	—	2
BPRS	(Adachi et al., 2000; Harvey et al., 1996; Lachar et al., 2001; Ventura et al., 2000)	4	—	—	2	1	1	—
BAI	(Beck, 1991; Chapman et al., 2009; Kabacoff et al., 1997; Steer et al., 1995; Steer et al., 1993)	5	4	—	1	—	—	—
STAI	(Iwata et al., 2000; Iwata et al., 1998; Kabacoff et al., 1997)	3	2	1	—	—	—	—
HAMA	(Beck, 1991; Serretti et al., 1999)	2	2	—	—	—	—	—
HAMD	(Grunebaum et al., 2005; Olden et al., 2009)	2	—	—	1	1	—	—
MADRS	(Gabryelewicz et al., 2004; Galinowski and Lehert, 1995; Lee et al., 2003; Parker et al., 2003; Serretti et al., 1999)	5	3	2	—	—	—	—
BDI	(Basker et al., 2007; Bonicatto et al., 1998; Bonilla et al., 2004; Gorenstein et al., 1999; Grunebaum et al., 2005; Helm and Boward, 2003; Jo et al., 2007; Killgore, 1999; Munoz et al., 2007; Powell, 2003; Salamero et al., 1994; Shek, 1990; Steer et al., 1989; Uslu et al., 2008; Wang et al., 2005)	15	9	2	3	—	—	1
HADS	(Dagnan et al., 2008; Dawkins et al., 2006; Friedman et al., 2001; Pallant and Bailey, 2005; Smith et al., 2002; Woolrich et al., 2006)	6	4	2	—	—	—	—
GHQ	(Castro‐Costa et al., 2008; Farrell, 1998; Hankins, 2008; Hu et al., 2007; Kilic et al., 1997; Lopez‐Castedo and Fernandez, 2005; Sanchez‐Lopez and Dresch, 2008; Werneke et al., 2000)	8	5	3	—	—	—	—
Total		61	29	10	8	10	1	3

In order to estimate a pattern of factor structure encountered in psychiatric scales, the descriptive statistical analyses were carried out over all the references without considering the number of factors found in the scales. The means of percentages of variance accounted for by each factor before rotation are shown in Table 2 for each scale and a box‐plot of these percentages over all the references is provided in Figure 1.

Table 2.

Percentage of variance accounted for by each factor and numbers of references used to estimate the means for each scale

Scale		Factors
		F 1	F 2	F 3	F 4	F 5	F 6	F 7
PANSS	Mean (Minimum–Maximum)	25.8 (14.5–41.2)	12.8 (8.7–18.6)	8.8 (6.1–13.4)	6.8 (3.9–11.1)	5.8 (3.6–9.3)	3.6 (3.6–3.7)	3.6 (3.6–3.7)
	Number of references	11	11	11	11	10	2	2
BPRS	Mean (Minimum–Maximum)	18.9 (12.8–23.3)	14.0 (9.3–17.2)	10.4 (8.7–11.7)	8.3 (6.7–10.0)	6.9 (6.1–7.8)	6.7 (—)
	Number of references	4	4	4	4	2	1
BAI	Mean (Minimum–Maximum)	37.6 (36.3–39.5)	7.2 (4.4–7.7)	6.2 (—)	5.2 (—)
	Number of references	5	5	1	1
STAI	Mean (Minimum–Maximum)	32.2 (29.8–34.3)	9.6 (7.4–11)	6.0 (—)
	Number of references	3	3	1
HAMA	Mean (Minimum–Maximum)	26.9 (20.4–33.5)	8.2 (6.4–10)
	Number of references	2	2
HAMD	Mean (Minimum–Maximum)	12.8 (12.6–13.0)	11.3 (11.2–11.4)	10.7 (10.4–11.0)	8.5 (7.3–9.8)	9.4 (—)
	Number of references	2	2	2	2	1
MADRS	Mean (Minimum–Maximum)	33.7 (25.1–41.1)	15.6 (10.4–26.9)	10.6 (10.2–1.0)
	Number of references	5	5	2
BDI	Mean (Minimum–Maximum)	29.4 (22.9–34.5)	8.8 (5.9–25.1)	6.8 (5.0–6.1)	5.4 (4.9–6.1)	6.0 (—)	5.5 (—)	4.9 (—)
	Number of references	15	15	6	4	1	1	1
HADS	Mean (Minimum–Maximum)	34.3 (23.6–41.4)	13.1 (11.4–16.4)	8.4 (8.1–8.6)
	Number of references	6	6	2
GHQ	Mean (Minimum–Maximum)	39.6 (30.3–50.9)	13.0 (8.5–25.9)	9.2 (8.6–9.8)
	Number of references	8	8	3
Total	Mean (Minimum–Maximum)	30.4 (12.6–50.8)	11.3 (4.4–26.9)	8.7 (5.0–13.4)	6.9 (3.9–11.1)	6.3 (3.6–9.4)	4.9 (3.6–6.7)	4.0 (3.6–4.9)
	Number of references	61	61	32	22	14	4	3

Figure 1.

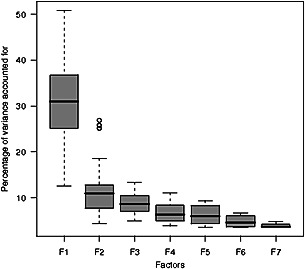
Box‐plot of the percentage of variance accounted for by each factor, according to the factor rank in the scale, in all the references.

The loadings matrix was present in 95.1% (58) of the references. The mean of the salient loadings was 0.626 with a median (med) of 0.636 and an interquartile range (IQR) of [0.587; 0.662]. This mean was 0.635 (med = 0.642, IQR = [0.601; 0.671]) when the method of factor extraction was PCA (80.3% – 49 – of the references) and 0.593 (med = 0.601, IQR = [0.545; 0.637]) in the case of EFA. The orthogonal rotation method was used in 63.9% (39) of the references and the values of factor inter‐correlations were reported in 34.4% (21) which represented 51 values (mean = 0.356, med = 0.33, IQR = [0.155; 0.535]). Concerning the p/M ratio, on average 7.1 items loaded on each factor in the scale (med = 6, IQR = [5; 10.5]) but this number varied depending on the number and the rank of the factors present within the scale as is shown in Table 3.

Table 3.

Mean of the percentages of items per factor (IQR, interquartile range)

Number of factors in the scale		Factors
		F 1	F 2	F 3	F 4	F 5	F 6	F 7
2	Mean	55.7 [50.0–59.2]	39.0 [33.3–42.9]
	IQR
3	Mean	43.2 [40.4–49.4]	34.8 [27.8–41.3]	20.2 [16.7–24.1]
	IQR
4	Mean	29.1 [27.0–33.0]	26.6 [22.9–32.2]	19.3 [16.3–20.6]	20.3 [14.8–23.7]
	IQR
5	Mean	22.6 [20.0–25.8]	20.1 [16.7–22.5]	15.7 [13.3–19.2]	16.7 [16.7–19.7]	15.1 [12.7–16.7]
	IQR
6	Mean	16.7 [—]	22.2 [—]	16.7 [—]	16.7 [—]	11.1 [—]	16.7 [—]
	IQR
7	Mean	24.1 [19.5–26.7]	22.4 [20.2–25.2]	12.5 [10.5–15.5]	15.2 [13.3–16.9]	12.1 [9.8–13.3]	6.5 [5.0–8.1]	7.1 [4.0–9.0]
	IQR

Sample size influence on the quality of solutions obtained using PCA or EFA

Results using artificial data

Choice of the parameter values for the simulation models: The determination of λ was based on the literature review so that λ was fixed at 0.6. Determination of the p_m values was based on the percentages shown in Table 3. For example, in the three‐factor model, the largest integer not greater than p × 0.45 was chosen as the value for p ₁, the largest integer not greater than p × 0.35 as the value for p ₂ and the remaining items loaded on the third factor. As regards the values of factor inter‐correlations, they were set at 0.45 in the two‐factor model, at 0.45 for cor(F ₁,F ₂) and 0.35 for the two other inter‐correlations in the three‐factor model and finally, in the four‐factor model, at 0.45 for cor(F ₁,F ₂), cor(F ₂,F ₄) and cor(F ₁,F ₄) and 0.35 for the three other inter‐correlations. Figure 2 shows the path diagram for the three‐factor simulation model with 10 items.

Figure 2.

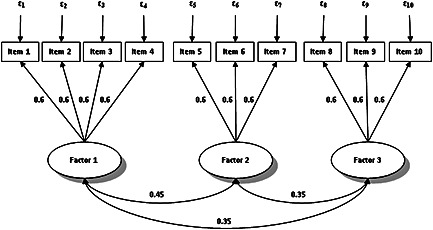
Path diagram for the three‐factor simulation model with 10 items.

Criteria of quality of the factor solutions: To reduce amounts of data presented in the results, only the details concerning the three criteria σ_λ, R_% and W_% in the case of a three‐factor scale are shown. Table 4 presents results when PCA was performed and Table 5 when it was EFA. All three criteria, σ_λ < 0.05, R_% > 90% and W_% < 1% were met when N = 500 if the scale contained less than 25 items, and when N = 300 if the scale contained 25 items or more in the case of PCA. When EFA was performed, N needed to be larger to reach the thresholds: 1000 if the scale contained less than 20 items, 500 if there were 25 items or more. For a two‐factor scale, on the whole, N could be smaller to meet the thresholds: 300 unless the scale contained less than 30 items and EFA was used, in which case N needed to be 500. In contrast, with both methods of factor analysis, a higher N value (500) was necessary when the scale contained four factors (and the criteria were not satisfied when N = 1000 in the case of EFA and p below 20). Concerning the percentage of simulations where Heywood cases occurred when EFA was performed, it was always under 2% whatever the number of factors in the scale with these values of N.

Table 4.

Values of the three criteria after PCA in the case of a three‐factor scale

Sample size		Number of items
		10	15	20	25	30	35	40	45
50	σλ	0.182	0.161	0.144	0.136	0.130	0.127	0.124	0.123
	R%	48.4	48.5	51.1	50.7	51.3	51.5	50.6	49.5
	W%	9.3	6.5	4.4	3.4	2.7	2.3	2.1	1.9
100	σλ	0.111	0.097	0.092	0.088	0.087	0.086	0.084	0.083
	R%	88.8	92.6	94.6	95.9	96.4	97.1	96.9	97.1
	W%	1.5	0.6	0.3	0.2	0.1	0.1	0.1	0.1
150	σλ	0.081	0.075	0.072	0.071	0.069	0.069	0.068	0.068
	R%	97.8	99.4	99.5	99.7	99.8	99.7	99.8	99.8
	W%	0.3	0.1	—	—	—	—	—	—
200	σλ	0.067	0.063	0.062	0.061	0.060	0.059	0.059	0.059
	R%	99.5	99.9	99.8	99.8	99.9	99.9	99.9	99.8
	W%	0.1	—	—	—	—	—	—	0.1
300	σλ	0.052	0.050	0.051	0.049	0.049	0.049	0.048	0.048
	R%	99.9	100.0	99.8	99.9	99.9	99.8	100.0	99.8
	W%	0.1	—	0.1	—	—	0.1	—	—
500	σλ	0.039	0.039	0.039	0.039	0.038	0.037	0.037	0.038
	R%	99.9	100.0	99.9	99.9	99.9	99.9	99.9	99.9
	W%	—	—	—	—	—	—	—	—
1000	σλ	0.029	0.027	0.027	0.027	0.027	0.027	0.026	0.026
	R%	99.9	100.0	100.0	99.9	100.0	99.9	100.0	100.0
	W%	0.1	—	—	—	—	—	—	—

Note : σ_λ, standard deviation of the salient loadings obtained after rotation over the 10,000 simulations; R_%, percentage of simulations in which all the items in the scale load on the right factor; W_%, mean of percentages of items loading on the wrong factor in the scale after rotation over the 10,000 simulations ; —, < 5 × 10^–2.

Table 5.

Values of the three criteria after EFA in the case of a three‐factor scale

Sample size		Number of items
		10	15	20	25	30	35	40	45
50	σλ	0.226	0.187	0.164	0.153	0.144	0.138	0.134	0.131
	R%	31.1	34.9	40.9	43.7	45.3	47.3	47.1	46.7
	W%	14.9	10.5	6.6	4.8	3.5	2.8	2.4	2.1
100	σλ	0.159	0.125	0.109	0.101	0.096	0.093	0.091	0.089
	R%	70.7	86.3	92.7	95.0	95.8	96.5	96.6	96.9
	W%	4.4	1.3	0.4	0.2	0.1	0.1	0.1	0.1
150	σλ	0.128	0.098	0.086	0.080	0.077	0.075	0.073	0.072
	R%	89.8	98.7	99.4	99.7	99.6	99.8	99.7	99.8
	W%	1.3	0.1	0.0	0.0	0.0	0.0	0.0	0.0
200	σλ	0.109	0.082	0.073	0.069	0.066	0.064	0.063	0.062
	R%	96.4	99.8	99.8	99.9	99.9	99.9	99.9	99.9
	W%	0.4	—	—	—	—	—	—	—
300	σλ	0.086	0.065	0.059	0.056	0.054	0.052	0.051	0.051
	R%	99.6	99.9	99.9	99.9	99.9	99.9	100.0	99.9
	W%	—	—	—	—	—	—	—	—
500	σλ	0.063	0.050	0.045	0.043	0.041	0.040	0.039	0.040
	R%	99.9	99.9	100.0	99.9	100.0	99.9	100.0	99.8
	W%	—	—	—	—	—	—	—	0.1
1000	σλ	0.043	0.034	0.032	0.030	0.029	0.028	0.028	0.027
	R%	100.0	100.0	99.9	100.0	100.0	100.0	100.0	100.0
	W%	—	—	—	—	—	—	—	—

Note: σ_λ, standard deviation of the salient loadings obtained after rotation over the 10,000 simulations, R_%, percentage of simulations in which all the items of the scale load on the right factor ; W_%, mean of percentages of items loading on the wrong factor in the scale after rotation over the 10,000 simulations ; —, < 5 × 10^–2.

In order to narrow the sample size required to meet the criteria, we interpolated values from the curves representing σ_λ in relation to N for the two methods of factor extraction, and each value of p and M. The junction between these curves and the line corresponding to σ_λ = 0.05 allowed the determination of the sample sizes required with a precision of 50 subjects. Results are summarized in Table 6. Numbers reported in Table 6 were always overestimated and at these sample sizes, the two other criteria were always met.

Table 6.

Sample size required to meet the three criteria thresholds for quality of factor solutions

Method of factor extraction	Number of factors	Number of items
		10	15	20	25	30	35	40	45
PCA	2	300	300	300	300	300	300	250	250
	3	350	350	350	300	300	300	300	300
	4	400	400	350	350	350	350	350	350
EFA	2	500	400	350	300	300	300	300	300
	3	800	500	450	400	350	350	350	350
	4	—	—	600	500	450	400	400	400

Note : —, >1000.

Accuracy of factor solutions: Figure 3 shows the relationship between μ_λ and N for each value of p and each method of factor extraction in the case of a three‐factor scale. When PCA was used, the smaller the number of items, the greater the distance from the expected value (λ = 0.6) μ_λ. There was little influence of N. Conversely, in the case of EFA, sample size had rather more influence and, whatever the number of items, all the curves tended towards the expected value as N increased. The shape of these curves was the same when there were two or four factors within the scale, but the overestimation of the value of the salient loadings was all the greater when M was greater in the case of PCA. Likewise, the sample size required to tend towards the expected value was also much greater when M was greater in the case of EFA.

Figure 3.

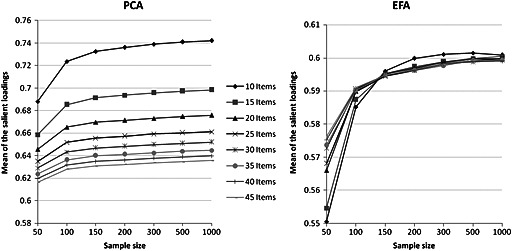
Mean of the values of the salient loadings after rotation on the 10,000 simulations in relation to sample size. Example of a three‐factor scale.

Standard deviation of the loadings using real data

Due to missing data, analyses were performed on 960 (95.1%) subjects for the BDI and 817 (81.0%) subjects for the HAMD. Parallel analysis suggested extracting one factor for the BDI and three factors for the HAMD. Figure 4 shows the mean of the standard deviations of the loadings over the 10,000 samples in relation to sample size in the case of PCA or EFA followed by a promax rotation for each scale. For the BDI, this mean was lower than 0.05 when the sample size was equal to or greater than 100 in the case of PCA. When EFA was used, the sample size needed to be larger, i.e. around 250, to obtain a mean lower than 0.05. In the case of the HAMD, even with 800 subjects the mean of the standard deviations of the loadings was higher than 0.05.

Figure 4.

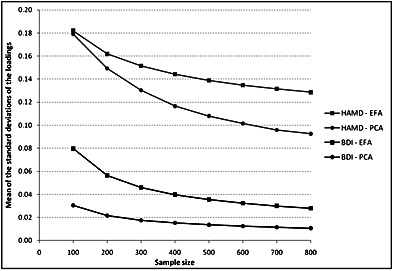
Mean of the standard deviations of the loadings over the 10,000 samples in relation to sample size in the case of Principal Component Analysis (PCA) or Exploratory Factor Analysis (EFA) followed by a promax rotation for the Beck Depression Inventory (BDI) and the Hamilton Depression Rating Scale (HAMD).

These rather unsatisfactory results found in the case of the HAMD, especially when EFA was performed, needed to be further investigated. We hypothesized that high standard deviations resulted from the possible presence of several underlying factor structures. To test this hypothesis, normal mixture modeling (function Mclust from the mclust package of the R software 2.6.2) was performed on the distribution of each salient loading of the HAMD for a sample size equal to 400 (10,000 samplings). The hypothesis of a unique component was systematically rejected and the number of components which optimized the Bayesian Information Criterion (BIC), ranged from two to six with a mode equal to three (the simulation program ruled out the possibility of an artificial phenomenon of label switching).

Influence of sample size on the precision of Cronbach's alpha coefficient

The half‐width of the 95% confidence interval of Cronbach's alpha coefficient in relation to N for the three expected values (α = 0.7, 0.8 and 0.9) is shown in Figure 5. Only the two extreme values for the number of items (p = 10 and 45) are represented because, as can be seen from Figure 5, there was little influence of p on the precision of Cronbach's alpha coefficient in the conditions studied here. A half‐width of 0.05 was reached when N = 300 for α = 0.7, 150 for α = 0.8 and only 50 for α = 0.9.

Figure 5.

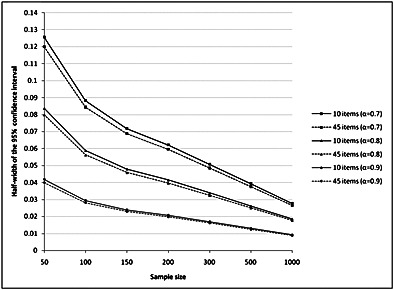
Half‐width of the 95% confidence interval of Cronbach's alpha coefficient for three expected values (α) in relation to the sample size and the number of items.

Discussion

These simulation studies, approaching as closely as possible the conditions usually met in practice during an internal validity study on a psychiatric scale, provide an answer to researchers facing the unavoidable issue of sample size in this field. When the factor structure underlying the instrument is clear, Table 6 gives the estimates for the numbers of subjects required to obtain stable and accurate solution in factor analysis in various usual conditions, defined by the number of items and the number of factors present within a psychiatric scale. These estimates can then be adapted to the results set out in Figure 5 according to the desired precision of the Cronbach's alpha coefficient.

As shown by the simulation study using artificial data, a sample size of 300 is generally required, but it needs to be increased in three cases: when the number of factors within the scale is large, when EFA is chosen as the method for factor extraction and when the number of items is small. One of the most important results of this study is this last point. Indeed, it shows how the use of the N/p ratio rule can be deleterious, particularly for scales with a small number of items. This is consistent with the conclusions drawn by other recent simulation studies on sample size in factor analysis. These studies did not however provide a simple answer to the sample size issue because of the wide ranges of the parameter values (λ, p, M) studied (Guadagnoli and Velicer, 1988; Hogarty et al., 2005; MacCallum et al., 1999; Mundfrom et al., 2005; Velicer and Fava, 1998). Another important result concerns the choice between the two different methods of factor extraction. Criticisms have been voiced in the literature against the use of the PCA. The common factor model rests on the assumption of the existence of latent variables that explain the inter‐item correlations observed. It is often remarked that PCA is not fully compatible with this assumption (Costello and Osborn, 2005; Fabrigar et al., 1999; Floyd and Widaman, 1995). Another criticism concerns the part of variance taken into account to estimate the loadings. In the common factor model, the shared variance of each item is partitioned from its unique variance and error variance whereas in PCA, this distinction is not made (Fabrigar et al., 1999; Ford et al., 1986; Widaman, 1993). Relationships between items are therefore overestimated and in the conditions occurring in psychiatry, loading estimates obtained by PCA are all the more overestimated when p is small and M large; and when N is large, this bias does not diminish (Figure 3). The use of EFA is therefore recommended in this field to obtain factor solutions with a lesser bias.

Considering the difficulty in recommending a general rule for sample size calculation valid in all the fields to which psychometric procedures apply, the literature review made it possible to determine an “average” pattern of factor structure characteristic of psychiatric scales. While a review is not as accurate as a formal meta‐analysis, it suggested that, in psychiatry, a particular factor structure is generally observed. Factors are correlated, salient loadings are close to 0.6 and there is a rather good factor overdetermination with an average p/M ratio greater than seven. The simulation of the categorical data was then performed on the basis of these characteristics and took into account different levels of floor and ceiling effects for each item. This was not the case in the previous simulation studies exploring sample size in factor analysis (Guadagnoli and Velicer, 1988; Hogarty et al., 2005; MacCallum et al., 1999; Mundfrom et al., 2005; Velicer and Fava, 1998; Velicer et al., 1982). The conditions encountered in psychiatry were therefore nearly reproduced in the artificial data. This helped to obtain results appropriate to this field that can be easily used in practice.

Concerning the limitations of the present results, two assumptions were made that could have artificially increased the strength of the artificial data as compared to real psychiatric data. One of these assumptions concerns the equality of the salient loadings. The absence of any significant influence of this on the quality of the factor solutions has been highlighted in a simulation study conducted by Velicer and Fava in 1998. The other assumption relates to simple structure (absence of cross‐loadings and non‐salient loadings set at zero). The simulation study based on real data suggests that the sample sizes recommended here could be underestimated. This is not certain. Different factor solutions were observed after resampling from the real data set. The standard deviations of loadings were thus high because of the melded fluctuations due to sampling and to the mixture of factor solutions. The interpretation of these standard deviations is not straightforward and, obviously, future studies are needed to further explore this area. At this point, we can conclude that sample sizes presented in the Table 6 represent minimal values determined from an idealized situation in which the common factor model is true. In practice, the stability of a solution obtained from real data can require a larger sample size. Of course, the present results are based on an “average” psychiatric scale and can vary according to the properties of a given instrument. However, certain elements of knowledge concerning p and M could help to obtain a clearer idea. For example, determination of the internal validity of a five‐factor psychiatric scale requires at least 400 subjects if PCA is chosen as the method of factor extraction, and 450 in the case of EFA. Finally, we chose to study the influence of sample size on the precision of Cronbach's alpha coefficient, but recent developments suggest more appropriate methods for reliability estimation, such as those based on non‐linear structural equation modeling (Green and Yang, 2009) or estimation of the greatest lower bound (Sijtsma, 2009a). However, debate is still open concerning which method should be used (Sijtsma, 2009b) and the Cronbach's alpha coefficient is by far the most used in practice.

Conclusion

The rule of the N/p ratio, which has already been criticized in previous studies on required sample sizes for factor analysis, is not upheld by the results of this simulation study, and researchers should refrain from using it. The validation of short scales (i.e. with a small number of items) does not warrant smaller sample size. If one's aim is to reveal the factor structure, under the hypothesis that the underlying common factor model is true, a minimum of 300 subjects is generally acceptable in the conditions encountered in the field of psychiatry. This sample size needs, however, to be larger when the expected number of factors within the scale is large. Furthermore, this study shows that, to obtain more accurate solutions, researchers should choose EFA as the method for factor extraction.

Declaration of interest statement

The authors have no competing interests.

The common factor model postulates that each observed variable is a linear function of one or more common factors and one unique factor. Its fundamental equation can be written:

$$y_j={\lambda }_{j1}{F}_1+{\lambda }_{j2}{F}_2+\dots +{\lambda }_{\mathit{jm}}{F}_m+\dots +{\lambda }_{\mathit{jM}}{F}_M+{\epsilon }_j$$

where y_j is the vector of the N subjects' answers to the item j (j = 1 to p) and F_m the vector of the N subjects' non‐observable scores on the common factor m (m = 1 to M). Each item j loads on each common factor m with the factor loading λ_jm. The unique factor ε_j, for each item j is independent (⊥) from all the F_m and from the other ε_(j'≠j) (Brown, 2006). In our simulation model, two hypotheses are set out. The first is the existence of a simple structure, i.e. each item loads on a single factor and all the non‐salient loadings are equal to zero. The second is that all salient loadings (λ) are equal. Therefore, if the p ₁ first items load only onto the first factor F ₁, the p ₂ following items load onto F ₂, …, the p_m following onto F_m, …, and the p_m last items onto F_M, $({\sum }_{m=1}^M{p}_m=p)$, then all the answers to a p item scale can be modeled as:

$$\{\begin{array}{cc}\hfill \forall j\in [1,p_1],\hfill & \hfill y_j={\lambda }^{\prime }{F}_1+{\epsilon }_j\hfill \\ \hfill \forall j\in \left[\right(p_1+1),p_2]\hfill & \hfill y_j={\lambda }^{\prime }{F}_2+{\epsilon }_j\hfill \\ \hfill ⋮\hfill & \hfill \hfill \\ \hfill \forall j\in \left[\right(p_{(m-1)}+1),p_m],\hfill & \hfill y_j={\lambda }^{\prime }{F}_m+{\epsilon }_j\hfill \\ \hfill \hfill & \hfill ⋮\hfill \\ \hfill \forall j\in \left[\right(p_{(M-1)}+1),p_M],\hfill & \hfill y_j={\lambda }^{\prime }{F}_M+{\epsilon }_j\hfill \end{array}$$

where ∀ j ∈ [1, p], ε_j ~ N(0,1) and ε_j ⊥ ε_(j'≠j) and ∀ m ∈ [1, M], F_m ~ N(0,1) and F_m ⊥ ε_j

In this model, the coefficient λ′ is not directly equal to the salient loadings. Indeed, in order to preserve the variances of the y_j equal to unity, standardization is required using the factor $\frac{1}{\sqrt{1+{{\lambda }^{\prime }}^2}}$. Individual data can therefore be simulated in a matrix where each row represents the answers of one individual to all p items in the scale and each column represents the answers of the N individuals to one item. If i represents subjects (i = 1 to N), the answer of the subject i to the item j is:

$$\forall i\in [1,N],\forall m\in [1,M],\forall j\in \left[\right(p_{(m-1)}+1),p_m],y_{\mathit{ij}}=\frac{{\lambda }^{\prime }{F}_{\mathit{mi}}+{\epsilon }_{\mathit{ij}}}{\sqrt{1+{{\lambda }^{\prime }}^2}}$$

To introduce correlations between factors in this simulation model, each factor is modeled using a term specific to each factor (f_m ~ N(0,1)) and a term common to all factors (C ~ N(0,1)):

$$F_m=a_m{f}_m+b_{m}C$$

Thus, the proportions of each of these terms, a_m and b_m, make it possible to control for the factor inter‐correlation levels with solely the constraint that $a_m^2+b_m^2=1$ to preserve the variances of factors equal to unity. A last stage is necessary to obtain a non‐symmetrical distribution of categorical data, as for data encountered in a real internal validity study on a psychiatric scale, for example, answers to a four‐point Likert scale. The conversion of the y_ij into integral numbers from one to four is performed using three breakpoints in their distribution N(0,1). For each item j, these three breakpoints are (−1 + δ_j), (0 + δ_j), and (1 + δ_j) where δ_j is drawn from a uniform distribution between [−0.5, 0.5] to introduce asymmetry and thus simulate floor and ceiling effects. The data simulation was performed using R software 2.6.2.; vectors ε_j, f_m and C were generated using the function rnorm and δ_j using runif.