Tautomeric Equilibria of Nucleobases in the Hachimoji Expanded Genetic Alphabet

Abstract

Evolution has yielded biopolymers that are constructed from exactly four building blocks and are able to support Darwinian evolution. Synthetic biology aims to extend this alphabet, and we recently showed that 8-letter (hachimoji) DNA can support rule-based information encoding. One source of replicative error in non-natural DNA-like systems, however, is the occurrence of alternative tautomeric forms, which pair differently. Unfortunately, little is known about how structural modifications impact free-energy differences between tautomers of the non-natural nucleobases used in the hachimoji expanded genetic alphabet. Determining experimental tautomer ratios is technically difficult and so strategies for improving hachimoji DNA replication efficiency will benefit from accurate computational predictions of equilibrium tautomeric ratios. We now report that high-level quantum-chemical calculations in aqueous solution by the embedded cluster reference interaction site model (EC-RISM), benchmarked against free energy molecular simulations for solvation thermodynamics, provide useful quantitative information on the tautomer ratios of both Watson-Crick and hachimoji nucleobases. In agreement with previous computational studies, all four Watson-Crick nucleobases adopt essentially only one tautomer in water. This is not the case, however, for non-natural nucleobases and their analogs. For example, although the enols of isoguanine and a series of related purines are not populated in water, these heterocycles possess N1-H and N3-H keto tautomers that are similar in energy thereby adversely impacting accurate nucleobase pairing. These robust computational strategies offer a firm basis for improving experimental measurements of tautomeric ratios, which are currently limited to studying molecules that exist only as two tautomers in solution.

Graphical Abstract

INTRODUCTION

Creating artificial genetic information systems (AEGIS) capable of Darwinian evolution is a central theme in the emerging field of synthetic biology and, in particular, the sub-discipline of xenobiology.^1,2 To capture this capability, presumed to be archetypal of life universally, AEGIS biopolymers must be able to direct the synthesis of copies of themselves with a small number of imperfections, but where those imperfections can themselves be copied.³ In natural DNA, two rules of nucleobase complementarity are instrumental to this process: (i) size, in which large purines pair with small pyrimidines, and (ii) hydrogen bonding, in which donor groups interact with acceptors. These requirements are realized by non-covalent, Watson-Crick (WC) pairing of heterocyclic bases located in two anti-parallel strands.⁴

Some time ago, it was noted that nucleobases other than adenine, guanine 1, thymine and cytidine could meet these complementarity rules within the geometry of Watson-Crick base pairs but with expanded pairing rules.⁵ By rearranging hydrogen-bond donor and acceptor groups, up to eight “biologically absent” nucleobases can be imagined, which are potentially capable of forming up to four additional mutually exclusive base pairs that fit the appropriate geometry (Figure 1). For example, one of these orthogonal nucleobase pairs involves hydrogen bonding between isoguanine (isoG or hachimoji “B”) and isocytosine (isoC or hachimoji “S”),¹ which was first proposed as a component of an expanded genetic alphabet for RNA by Rich,⁶ and has been used in human diagnostics.⁷ The isoG heterocycle presents a purine “donor-donor-acceptor” hydrogen-bonding pattern (puDDA, proceeding from the major groove to the minor groove); isoC has the complementary pyrimidine “acceptor-acceptor-donor” (pyAAD) pattern (Figure 1).

Figure 1.

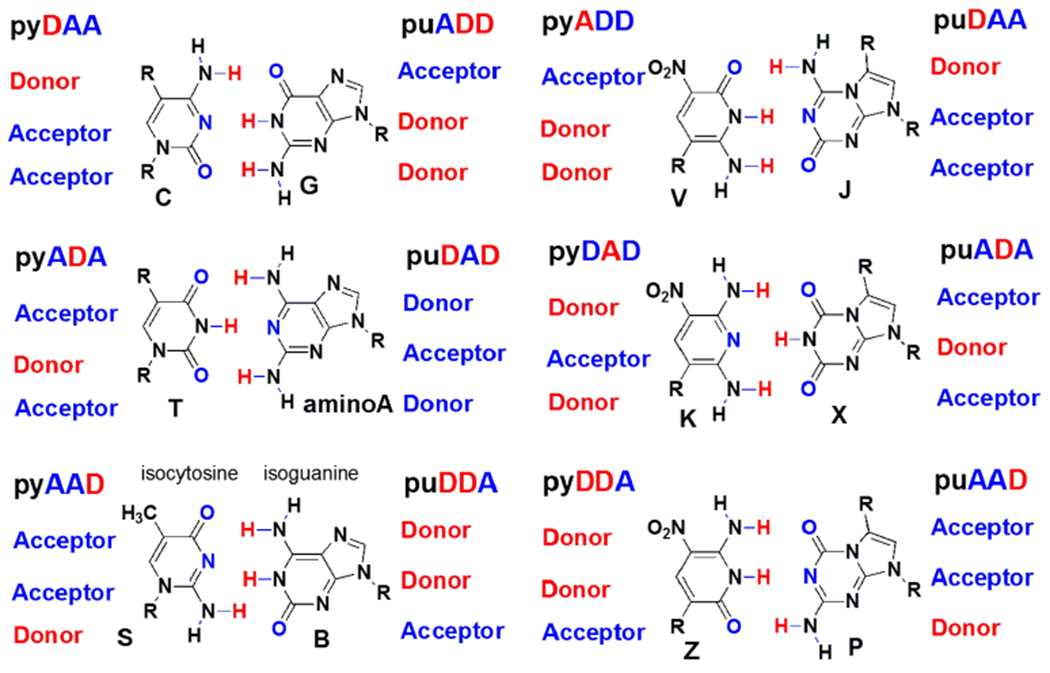
Up to twelve nucleobases (six orthogonal base pairs) can be accommodated within the general structure of Watson-Crick pairing. Large purines (pu) hydrogen bond to small pyrimidines (py) using different donor (D) and acceptor (A) groups.

The realization of these ideas in the synthesis and characterization of hachimoji DNA¹ immediately gives rise to the question of why natural DNA and RNA have not evolved to take advantage of these additional hydrogen-bonding patterns, thereby generating DNA and RNA molecules with increased information density? Amongst others,⁸ Szathmary offered an interesting answer.⁹ He noted that although adding nucleotides to DNA did indeed increase information density, it also increased opportunities for mispairing. Such mispairs included those arising from protonation and deprotonation of the nucleobases¹⁰ and the presence of tautomeric forms, which necessarily change the pattern of hydrogen bonding (Figure 2).¹¹ Because enzymes can recognize a change in charge more easily than one change in tautomeric form (which neither creates nor destroys a charge), the second mispairing mechanism has proven to be a more challenging problem for synthetic biology. Indeed, a fraction of natural mutational events may arise from the existence of minor tautomeric forms of natural nucleobases, in particular of guanine.¹²

Figure 2.

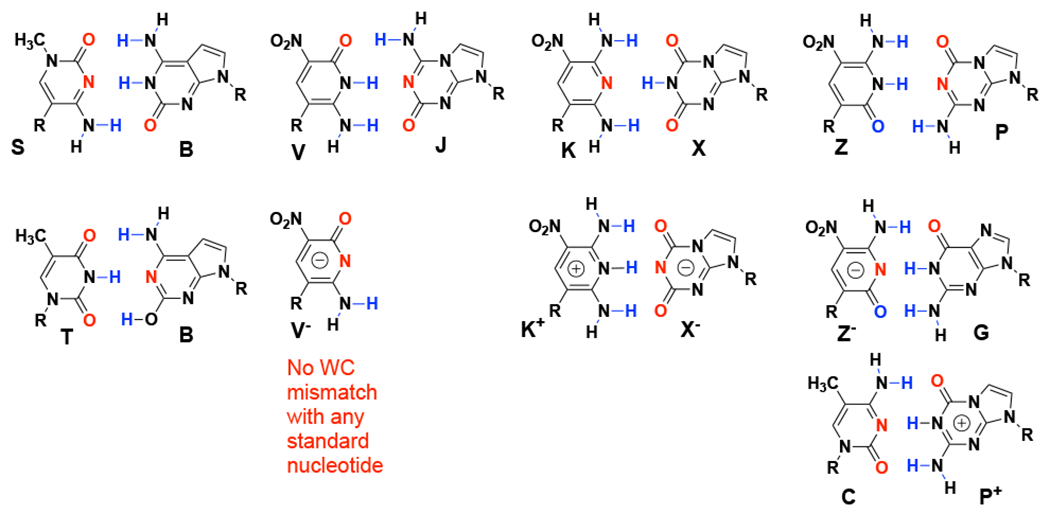
Base-pairing mismatches arising from alternate tautomers or charged forms of the “hachimoji” nucleobases (S:B, V:J, K:X and Z:P) used in the construction of an expanded genetic alphabet.¹

Clearly, the robustness of the hydrogen-bond pattern determines whether a nucleobase might be added to a genetic alphabet, for either academic or commercial use. Unfortunately, as we suggest in this study, existing experimental methods are hard-pressed to measure the tautomeric equilibrium for a heterocycle. Isoguanine 2 (Figure 3), one of the eight components of hachimoji DNA and RNA,¹ is an illustrative example because it can adopt an “enolic” tautomeric form¹³ that is significantly populated in water and duplex DNA.^14,15 Instead of the pu(DDA) pattern of isoG that is complementary to isoC, this enol tautomer presents a pu(DAD) hydrogen-bonding pattern that is complementary to thymine (Figure 3). By contrast, the most populated minor (enol) tautomer of guanosine has been estimated to comprise only 0.01% of its total concentration in water.¹² As a result, repeated PCR cycling results in loss of the isoG:isoC pair due to tautomer-associated mismatching.¹⁶

Figure 3.

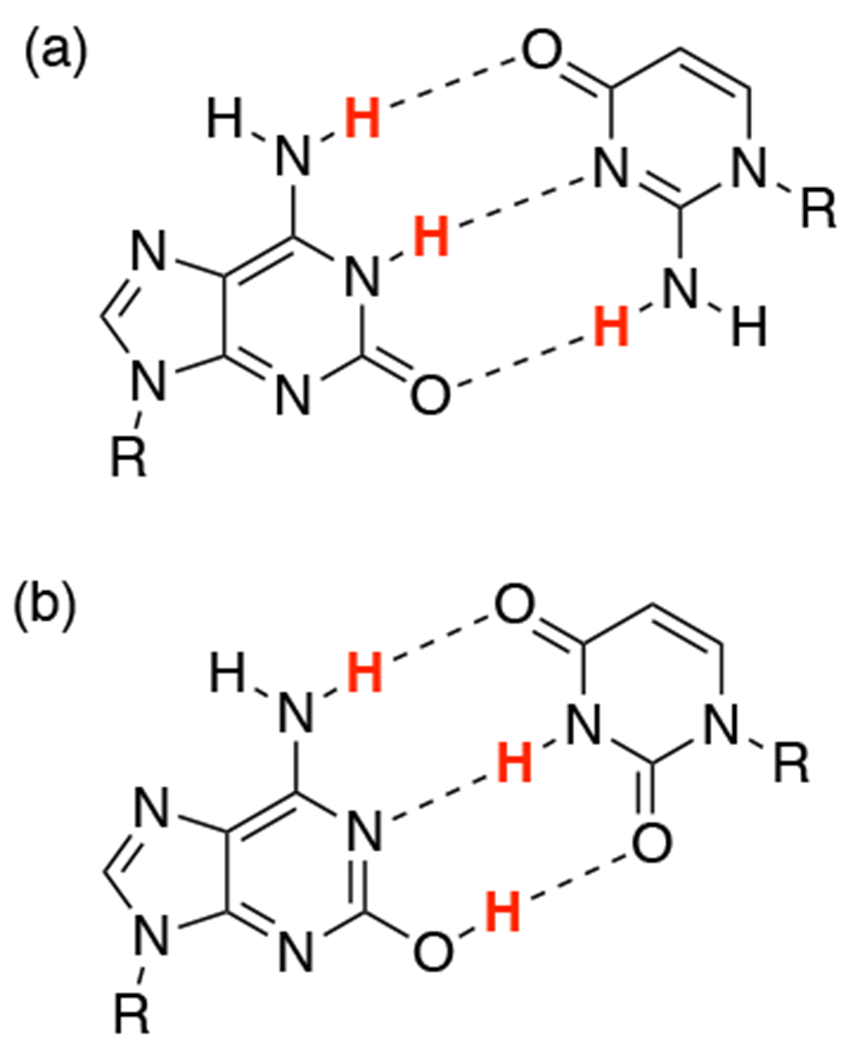
Non-natural nucleobase pairs and tautomer mismatches. (a) The isoG:isoC base pair and (b) the isoG:T base pair. R represents a deoxyribose substituent.

Using a “trial and error” strategy, several groups have sought to overcome this problem by (i) modifying the isoG structure,^14,17–19 (ii) seeking polymerases that exhibit higher levels of isoG:isoC fidelity,²⁰ or (iii) synthesizing thymidine analogues that cannot pair with the minor tautomeric form of isoG.²¹ Atom replacement to give modified structures, such as 7-deaza-isoG 3,¹⁷ 8-aza-7-deaza-isoG 4,⁸⁷ and 8-aza-isoG 5¹⁹ (Chart 1), does appear to decrease base-pairing ambiguity relative to that observed for isoG.^14,17,18 The introduction of sulfur in place of oxygen to give 2-thioisoguanine has also been found to improve its ability to base pair with isoC (hachimoji “S”) rather than to T.²² Systematically implementing an atom replacement strategy for other non-natural nucleobase analogs is greatly hindered, however, by the inability of current experimental strategies to adumbrate the tautomeric ratio of numerous analogs. Likewise, predictive theoretical calculations able to guide synthetic biologists are difficult because these must model the effect of polar environments on the relative free energies of tautomeric species.²³ It is therefore timely to ask what level of theory is really needed to guide any rational design of artificial genetic systems.

Chart 1.

Tautomers of heterocycles 1-5 for which free-energy calculations were performed. Structures in which N7 was protonated in preference to N9 were not considered because we were interested only in tautomeric forms that might be adopted in single-stranded DNA or RNA.

In an effort to address this question, we now report the use of high-level quantum-chemical (QC) calculations combined with the “embedded cluster reference interaction site model” (EC-RISM)²⁴ to determine the preferred tautomeric forms in water of the four Watson-Crick (1, 6-8) and four non-natural nucleobases (2, 9-11) that comprise hachimoji DNA.¹ Our EC-RISM calculations are calibrated for guanine 1 and the related non-natural analogs 2-5 (Chart 1) by independent free-energy molecular dynamics (FEMD)/Monte-Carlo (FEMC) simulations using different Lennard-Jones force fields, and comparisons with commonly used QC solvation methodologies. Given its success in matching the average values for heterocycles 1-5 (Chart 1), subsequent calculations of compute the tautomeric preferences of the remaining six nucleobases 6-11 in hachimoji DNA (Chart 2) were performed using EC-RISM. In addition to providing useful insights into the likely base pairing behavior of the non-natural nucleobases 2, 9, 10 and 11, our findings highlight the severe limitations of existing experimental methods for evaluating tautomer populations in water.

Chart 2.

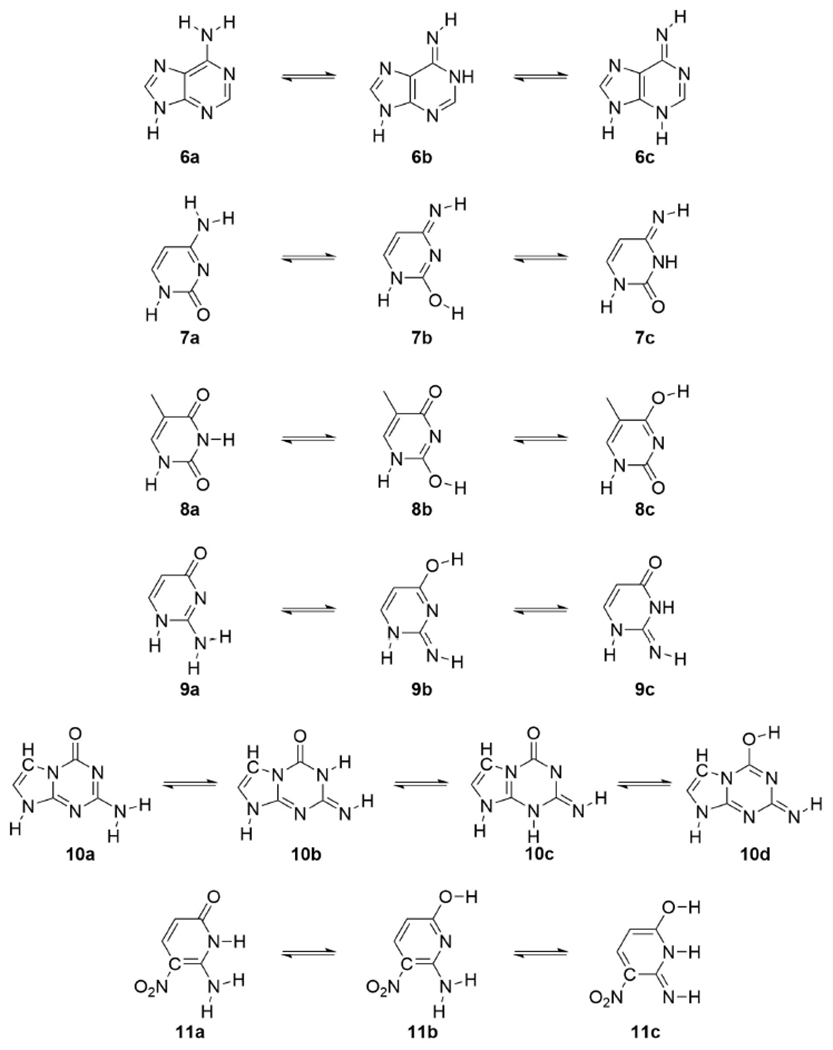
Tautomers of heterocycles 6-11 for which free-energy calculations were performed. Structures in which N7 was protonated in preference to N9 were not considered for reasons given above.

MATERIALS AND METHODS

Computational Models.

Traditionally, the problem of calculating relative free energies for tautomers in solution has been divided into two distinctly different parts; obtaining accurate electronic energies and adequately treating solvation effects. Methods for computing electronic energies for molecules in the gas phase calculations are well defined, permitting systematic improvements in the level of quantum chemical theory to obtain results that are chemically accurate.²⁵ Attacking the second part of the problem is less straightforward because no hierarchy of methods exists to compute solvation free energies with increasing accuracy,²⁶ even though an accurate, solvent-polarized wavefunction together with the corresponding excess chemical potential should, in principle, be all that is required to compute the relative energies of tautomers in solution.²⁷

A generalized thermodynamic cycle provides the framework for combining different levels of theory to calculate the free-energy difference between tautomers A and B (Figure 4). In using this model, we assume thermodynamic quantities to refer to a standard state of infinite dilution at 1 bar and to a temperature of 298.15 K. Our goal is to predict ΔG⁽¹⁾, which is possible if we have access to the chemical potentials (for simplicity denoted by G) of each tautomer (A and B) in solution. Obtaining ΔG⁽¹⁾ is then accomplished by computing the difference of the total energies of A and B in models containing a solvent polarized electronic and a solvation term:

$$\Delta G^{(1)}=G({\text{B}}_{\mathrm{sol}}^{\mathrm{QC}})-G({\text{A}}_{\mathrm{sol}}^{\mathrm{QC}})$$ (eq. 1)

Using this “direct” approach (eq. 1) for low-level theories using, for example, small basis sets and Hartree-Fock theory is not recommended when these are parameterized with respect to experimental solvation free energies at an identical level of theory for the tautomers in the gas phase. As a result, an “indirect” QC route that uses a more rigorous level of theory in the gas phase (ΔG⁽⁸⁾) is advantageous for obtaining the desired free energy difference (Figure 4). Thus, solvation free energies for each tautomer (ΔG^(2a) and ΔG^(3a)) are computed using a “low-level” QC method. This leads to the following expression from consideration of the extended thermodynamic cycle:

$$\Delta G^{(1)}=\Delta G_{\mathrm{low\; level}}^{(3\text{a})}+\Delta G_{\mathrm{low\; level}}^{(2a)}+\Delta G_{\mathrm{high\; level}}^{(8)}$$ (eq. 2)

Common solvation models such as the polarizable continuum model (PCM)^28–30 are typically parameterized for a low level of QC theory. Direct methods, such as EC-RISM,^24,27 are capable of including the effects of hydrogen bonding without adding explicit water molecules. Briefly, EC-RISM employs QC calculations coupled to a statistical, granular model of the water phase and yields self-consistent electronic and solvent structure around the solute by mapping the solvent charge distribution onto background point charges. In turn, these point charges polarize the electronic Hamiltonian and the resulting solute potential perturbs solute-solvent site distribution functions calculated from three-dimensional (3D) RISM integral equation theory. This theory provides approximate access to solute-solvent distribution functions at the same level of atomic detail as would be obtained using explicit-solvent MD simulations of the nucleobases in water. Here, a force-field description is employed for water and the dispersive-repulsive (Lennard-Jones) solute-solvent interactions,^24,31,32 while the electrostatic solute-solvent energies are derived from the interaction of “classical” water with the QC electrostatic potential of the solute. This preserves the anisotropic polar nature of water as a solvent, which acts on the solute electronic Hamiltonian via the solvent charge distribution resulting from solute-solvent pair distributions. As in the case of PCM calculations, a solvent-perturbed electronic energy is obtained to which the 3D RISM excess chemical potential is added to give the free energy for the electronically polarized solute species at the given optimized geometry in solution. The difference between tautomers computed by the direct method (eq. 1) then yields an estimate of the tautomerization free energy while the combination of EC-RISM-derived hydration free energies with high-level gas phase calculations represents the indirect route (eq. 2).

Figure 4.

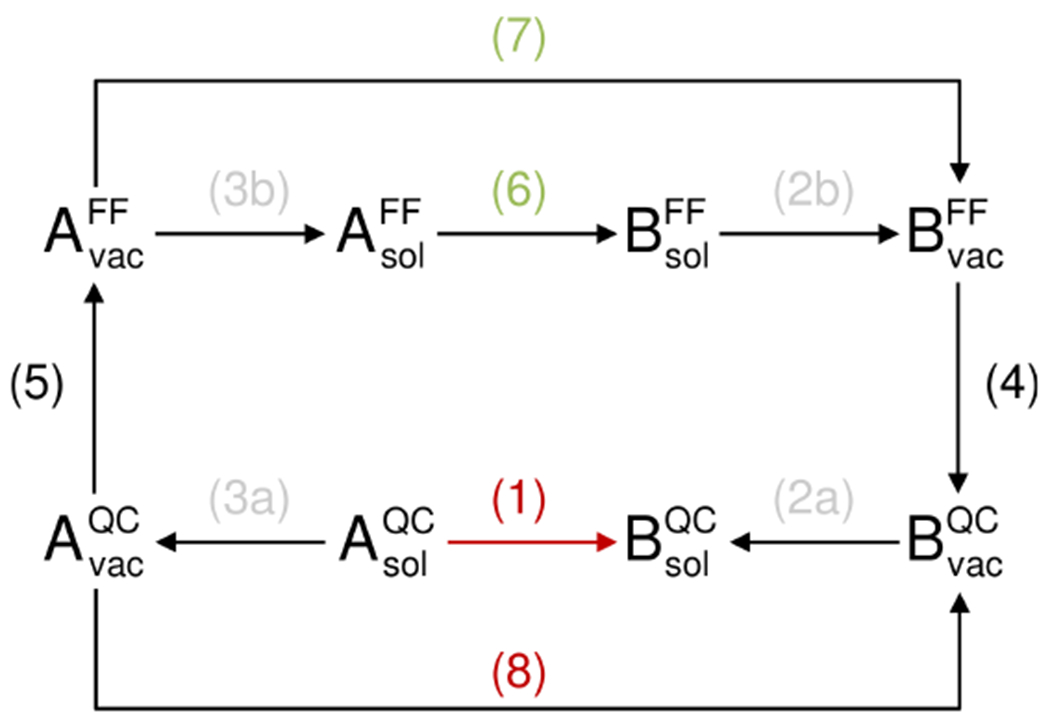
Generalized thermodynamic cycle covering both quantum chemical (QC) and force-field based (FF) calculations for determining the free energy difference between two tautomers A and B in solution (sol) and the gas phase (vac). See text for the meaning of reaction numbering.

Similarly, it is possible to combine high-level QC calculations with force field-based (FF) free energy (FE) calculations using either molecular dynamics (MD) simulations³³ or Monte-Carlo (MC) sampling.³⁴ By definition, the hypothetical “exact” FF and QC models are expected to reproduce the hydration free energies of both tautomers, leading to the expression

$$\Delta G^{(2\text{a})}+\Delta G^{(2\text{b})}=\Delta G^{(3\text{a})}+\Delta G^{(3\text{b})}=0$$ (eq. 3)

that is formally necessary to close the thermodynamic cycle composed of two different (QC and FF) Hamiltonians. Considering the “outer” and “inner” thermodynamic cycles (Figure 4) and taking eq. (3) into account leads to the following result:

$$\begin{gathered} \Delta G^{(1)}=\Delta G^{(6)}+\Delta G^{(5)}+\Delta G^{(4)} \\ =G({\text{B}}_{\mathrm{sol}}^{\mathrm{FF}})-G({\text{A}}_{\mathrm{sol}}^{\mathrm{FF}})+G({\text{A}}_{\mathrm{vac}}^{\mathrm{FF}})-G({\text{A}}_{\mathrm{vac}}^{\mathrm{QC}})+G({\text{B}}_{\mathrm{vac}}^{\mathrm{QC}})-G(B_{\mathrm{vac}}^{\mathrm{FF}}) \\ =\underset{\Delta G^{(6)}\mathrm{from\; FEMD/MC}(\mathrm{sol})}{\underbrace{[G({\text{B}}_{\mathrm{sol}}^{\mathrm{FF}})-G({\text{A}}_{\mathrm{sol}}^{\mathrm{FF}})]}}\underset{+\Delta G^{(8)}\mathrm{from\; QC}(\mathrm{vac})}{\underbrace{+[G({\text{B}}_{\mathrm{vac}}^{\mathrm{QC}})-G({\text{A}}_{\mathrm{vac}}^{\mathrm{QC}})]}}\underset{-\Delta G^{(7)}\mathrm{from\; FEMD/MC}(\mathrm{vac})}{\underbrace{-[G({\text{B}}_{\mathrm{vac}}^{\mathrm{FF}})-G({\text{A}}_{\mathrm{vac}}^{\mathrm{FF}})]}}. \end{gathered}$$ (eq. 4)

In this “indirect” FF calculation, the difference of A → B transformation free energies between solution (sol) and gas phase (vac) (ΔG⁽⁶⁾-ΔG⁽⁷⁾) is equivalent to a single topology approach in free-energy calculations employing either FEMD simulations or FEMC sampling. The analogous dual topology approach, equivalent to computing differences of hydration free energies, can be obtained by reordering terms:

$$\begin{gathered} \Delta G^{(1)}=[G({\text{B}}_{\mathrm{vac}}^{\mathrm{QC}})-G({\text{A}}_{\mathrm{vac}}^{\mathrm{QC}})]+[G({\text{B}}_{\mathrm{sol}}^{\mathrm{FF}})-G({\text{B}}_{\mathrm{vac}}^{\mathrm{FF}})-[G({\text{A}}_{\mathrm{sol}}^{\mathrm{FF}})-G({\text{A}}_{\mathrm{vac}}^{\mathrm{FF}})] \\ =\underset{\Delta G^{(8)}\mathrm{from\; QC}(\mathrm{vac})}{\underbrace{[G({\text{B}}_{\mathrm{vac}}^{\mathrm{QC}})-G({\text{A}}_{\mathrm{vac}}^{\mathrm{QC}})]}}\underset{-\Delta G^{(2\text{b})}\mathrm{from\; FEMD/MC}(\mathrm{vac/sol})}{\underbrace{+{\Delta }_{\mathrm{hyd}}G({\text{B}}^{\mathrm{FF}})}}\underset{-\Delta G^{(3\text{b})}\mathrm{from\; FEMD/MC}(\mathrm{vac/sol})}{\underbrace{-{\Delta }_{\mathrm{hyd}}G({\text{A}}^{\mathrm{FF}}).}} \end{gathered}$$ (eq. 5)

EC-RISM/PCM and gas phase quantum chemical calculations.

To calculate Gibbs free energies of hydration with EC-RISM we used the optimized methodological framework introduced within the SAMPL6 challenge (periodicity-corrected exact solute-solvent electrostatics) to predict aqueous acidity constants of small molecules.^31,32 The Gibbs energy for multiple conformations of tautomer A (in this case the set of rotameric states c) is given by the discrete partition function

$$G({\text{A}}_{\mathrm{sol}}^{\mathrm{QC}})=-RT\ln \sum _c\exp [-G_c({\text{A}}_{\mathrm{sol}}^{\mathrm{QC}})/RT]$$ (eq. 6)

where the superscript QC indicates QC derived energies, R is the molar gas constant and T is 298.15 K [these energies were used in eq. (1)]. The Gibbs energy per conformation is then computed from:

$$G_c({\text{A}}_{\mathrm{sol}}^{\mathrm{QC}})=E_c^{\mathrm{sol}}({\text{A}}_{\mathrm{sol}}^{\mathrm{QC}})+{\mu }_c^{\mathrm{ex},\mathrm{corr}}({\text{A}}_{\mathrm{sol}})$$ (eq. 7)

using the electronic energy of the conformation in solution E^sol and the corrected excess chemical potential μ^ex,corr, which comprises the usual RISM chemical potential augmented by a linearly scaled infinite dilution partial molar volume,³² which is itself adjusted to reproduce hydration free energies (MNSOL database).³⁵ A scaling parameter c_V = −0.10251 kcal mol⁻¹ Å⁻³ (needed to obtain RISM-derived solvent compressibility in the expression for the partial molar volume)²⁹ was used for all calculations reported here.

“Indirect” calculations using eq. (2) required hydration free energies to be computed for each tautomer. Gas-phase energies were again given by a discrete partition function over conformational states for both EC-RISM and PCM models:

$$E({\text{A}}_{\mathrm{vac}}^{\mathrm{QC}})=-RT\ln \sum _c\exp [-E_c({\text{A}}_{\mathrm{vac}}^{\mathrm{QC}})/RT]$$ (eq. 8)

to yield the following approximate expression for the (standard) Gibbs energy of hydration in the Ben-Naim reference state (i.e. assuming identical gas phase and solution phase concentrations):

$${\Delta }_{\mathrm{hyd}}G({\text{A}}^{\mathrm{QC}})=G({\text{A}}_{\mathrm{sol}}^{\mathrm{QC}})-E({\text{A}}_{\mathrm{vac}}^{\mathrm{QC}})$$ (eq. 9)

Entropic contributions from vibrational and rotational degrees of freedom were not explicitly included because they are implicit in the parameterization on experimental data. Completing the gas phase “leg” of the thermodynamic cycle, however, required the inclusion of thermal corrections (TC),³⁶ which were averaged over all rotameric states by forming the partition function:

$$G({\text{A}}_{\mathrm{vac}}^{\mathrm{QC}})=-RT\ln \sum _c\exp [-(E_c({\text{A}}_{\mathrm{vac}}^{\mathrm{QC}})+G_c^{\mathrm{TC}}({\text{A}}_{\mathrm{vac}}^{\mathrm{QC}}))/RT]$$ (eq. 10)

Gas-phase energy differences (ΔG⁽⁸⁾) used in eq. (2) were provided by CCSD(T) calculations whereas the hydration free energies (ΔG^(2a) and ΔG^(3a)) contained lower-level gas-phase energies that match the parameterization strategy of each solvation model. TC were approximated from the lower-level calculations at the B3LYP/6-31G(d,p) level,³⁷ given the computational cost of CCSD(T) frequency calculations. The resulting thermally corrected gas-phase reaction free energies (ΔG⁽⁸⁾) were also used in the thermodynamic cycles (eqs. 4 and 5) used for calculations that employ MD/MC-derived hydration free energies (ΔG^(2a) and ΔG^(3a)).

Initial structures were optimized by B3LYP/6-31G(d,p);³⁷ frequency calculations confirmed the structures as local minima and provided data for the TC corrections. These geometries were used for subsequent single-point gas-phase CCSD(T)/aug-cc-pVTZ calculations,³⁸ as implemented in Gaussian09.³⁹ Preliminary calculations with respect to the complete basis set limit indicated converged results, their deviation being on the order of 0.1 kcal mol⁻¹ compared to aug-cc-pVTZ³⁶ (close to the statistical error of MD and MC-derived free energies). For consistency with the AMBER force field,⁴⁰ atomic partial charges used in the MD/MC calculations were obtained from the HF/6-31G(d) wavefunction of MP2(full)/cc-pVDZ/PCM-optimized structures^30,41,42 by the RESP method.⁴³

Solution phase QC calculations used B3LYP/6-311+G(d,p)/PCM(IEF)-optimized tautomer structures, with the default values for water as implemented in Gaussian 09.^39,44 To obtain theory level-consistent structures, these were again re-optimized in vacuum using B3LYP/6-311+G(d,p) when calculating Gibbs free energies of hydration from eq. 9. EC-RISM calculations were performed on PCM-derived structures using settings reported for the SAMPL6 blind prediction challenge³¹ (140³ 3D RISM grids with 0.3 Å spacing, PSE-2 closure,⁴⁵ modified SPC/E water model, GAFF force field (version 1.5, identical Lennard-Jones parameters as in version 1.4)^46,47 with Lorentz-Berthelot mixing rules for Lennard-Jones interactions) on the MP2/6-311+G(d,p) level of theory in Gaussian 09.⁴⁴ The same structures were also used in MP2/6-311+G(d,p)/PCM calculations to compute PCM-based hydration free energies. To check the dependence of our results on the theory level, hydration free energies from the PCM solvation model were also estimated by the original B3LYP results directly obtained from the optimization runs.

EC-RISM calculations on the tautomer preferences of nucleobases 6-11 (Chart 2) followed similar procedures to those outlined above for nucleobases 1-5 (Chart 1) except that the ORCA software⁴⁸ was used, applying the R1-F12 approximation^49,50 and the slightly smaller cc-pVTZ basis set for the CCSD(T) gas-phase energy evaluations. The results of this procedure for heterocycles 1-5 deviate only slightly from those evaluated as described above (Table S6, Supporting Information).

Raw computational data for our calculations are listed elsewhere (Tables S1, S2, S5 and S6, Supporting Information) together with structural coordinates and all parameters used in these studies (Structures_and_FF_Parameters.xlsx).

Free-energy differences for tautomers from dual-topology Monte-Carlo sampling calculations.

Dual-topology³⁴ Monte-Carlo replica exchange thermodynamic integration (RETI)⁵¹ simulations were performed with ProtoMS.⁵² The interaction energy of a pair of solutes with their surroundings (e.g., with the solvent) was gradually turned on or off with the coupling parameter, λ. As a result, a gas-phase calculation is not required for these solvation free-energy calculations because there are no interactions of the solute with its surroundings in the gas phase. Parameter derivation, system set-up and analyses were performed according to literature protocols established previously,⁵³ using Antechamber from the Amber 18 software suite⁵⁴ and standard ProtoMS scripts.⁵² The quantum-chemically derived solute structures used for site charge calculations were solvated in TIP4P water⁵⁵ boxes that exceeded the solute dimensions by approximately 10 Å in either direction (approx. 518 water molecules). A 10 Å cutoff was used for GAFF non-bonded interactions (version 1.6),^46,47 which was “feathered” over the last 0.5 Å. NpT simulations were performed at 298.15 K and 1 atm, and sixteen windows were chosen along the λ coordinate (0, 0.067, 0.133, 0.200, 0.267, 0.333, 0.4, 0.467, 0.533, 0.6, 0.667, 0.733, 0.8, 0.867, 0.933, 1) to merge ligands [1-5]a smoothly into ligands [1-5]b or [1-5]c, respectively. Each λ window was equilibrated for 100M equilibration moves and data were then collected over 100M simulation moves. Each perturbation was repeated five times (independent runs with different random seeds) allowing an estimate of the standard error by averaging over the five runs (Table S3, Supporting Information). Standard ProtoMS values (protoms.py) were assigned to other simulation parameters.⁵²

Free-energy differences for tautomers from single-topology MD simulations.

Thermodynamic integration (TI) calculations were performed with GROMACS^56,57 and used data from five independent MD simulations. Partial atomic charges for all solute structures were identical to those used in the Monte-Carlo sampling studies with bonded interaction parameters being assigned from the OPLS-AA (all-atom) force-field using the LigParGen server.⁵⁸ Each tautomer was placed in a dodecahedral box (30 Å x 30 Å x 30 Å) containing approximately 850 TIP3P water molecules.⁵⁵ Long-range electrostatic interactions were calculated by particle-mesh Ewald⁵⁹ (1.2 Å grid spacing, 6th order) with short-range interactions being truncated at 12 Å. After energy minimization, all systems were equilibrated in the NVT (5 ns) and then in the NpT (25 ns) ensembles (298.15 K, 1 bar; Langevin/Parrinello-Rahman),⁶⁰ using a 1 fs time step, from which five snapshots were taken at five ns intervals. These structures were then used in independent TI calculations thereby allowing an estimate of the standard error by averaging over the five runs (Table S4, Supporting Information). Twenty-one windows were chosen along the λ coordinate (0, 0.005, 0.01, 0.02, 0.03, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.95, 0.97, 0.98, 0.99, 0.995, 1) in the TI runs, which were performed with soft-core scaling of solute-solvent interactions. Each simulation at a given λ window was run for 11 ns, without additional minimization, with a 1 fs time step; structures in the last 10 ns were used for averaging. Gas-phase TI runs were performed by a similar workflow under aperiodic conditions, turning off potential truncation and pressure coupling. Free-energy estimates were obtained using standard methods (alchemical.analysis.py)⁶¹ and cubic spline integration over the λ coordinate. BAR and MBAR analyses (data not shown)⁶² indicated that converged results had been obtained in these calculations.

RESULTS AND DISCUSSION

Tautomer free-energy calculations:

Five independent approaches were used to calculate tautomerization free energies in water for guanine 1, isoG 2, 7-deaza-isoguanine 3, 7-deaza-8-aza-isoguanine 4 and 8-aza-isoguanine 5 (Chart 1). In addition to direct EC-RISM calculations, we employed CCSD(T)²⁵ gas-phase energies together with hydration free energies obtained by PCM, EC-RISM and two types of simulations employing classical force fields (single-topology thermodynamic integration (TI) MD⁶³ and dual-topology MC replica exchange TI³⁴). The MD/MC calculations used the same set of partial charges for each of the tautomers, and OPLS^58,64/TIP3P⁵⁵ and GAFF⁴⁶/TIP4P⁵⁵ models for the non-bonded interactions and water molecules, respectively.

The keto 1a and enol 1b tautomers were found to differ by 0.1 kcal mol⁻¹ (298.15 K) at our highest level of theory due to the entropy contributions (Table 1), within the error of our computational method (± 1.0 kcal mol⁻¹)²³ and consistent with the results of prior work.⁶⁵ At 12 K the calculated gas-phase energy difference of 1a and 1b of guanine was zero, which agrees with the equilibrium constant of approximately 1.1 (0.03 ± 0.01 kcal mol⁻¹) for interconversion of keto 1a and enol 1b in an argon matrix as determined by infra-red spectroscopy.⁶⁶ The enol form of the four non-natural nucleobases 2-5 is preferred in the gas-phase (298.15 K), and there seems to be an energetic preference for the keto-tautomer of 2-5 in which N3 is protonated rather than N1 (Table 1). Our findings are again consistent with prior computational studies of tautomer preferences for isoG 2 and 8-aza-isoguanine 5 (Chart 1),^67–69 although the electronic origin of the increased gas-phase stability of N3-H keto-tautomers 2c-5c remains to be established.

Table 1.

Calculated standard reaction free energies ΔG (kcal mol⁻¹) and populations for selected tautomeric forms of guanine derivatives 1-5 Chart 1) relative to the N1-H keto tautomers [1-5]a, and solution phase dipole moments (D) obtained from converged EC-RISM calculations.

	CCSD(T)[a]	PCM/CCSD(T)[b]	EC-RISM[c]	EC-RISM/CCSD(T)[d]	FEMD/CCSD(T)[e]	FEMC/CCSD(T)[f]	Average ΔG (EC-RISM/FEMD/MC)	Previous ΔG calculations	Average population (EC-RISM/FEMD/MC)	Dipole moment
1a	0.00	0.00	0.00	0.00	0.0	0.0	0.0		> 0.9999	11.4
1b	−0.09	4.64	6.15	6.12	6.7	7.3	6.6 ± 0.2	5.7/5.1[g]	< 0.0001	5.1
1c	17.44	8.62	6.96	5.66	8.7	8.7	7.5 ± 0.6	−7.1/9.4[g]	< 10−5	21.1
2a[h]	0.00	0.00	0.00	0.00	0.0	0.0	0.0		0.80	10.6
2b	−7.76	−0.54	1.57	3.11	2.6	4.4	2.9 ± 0.5	1.4[i]/6.7/6.8[j]	0.01	4.3
2c	−1.00	−0.93	0.91	0.14	1.1	1.2	0.8 ± 0.2	0.6[i]/0.2[j]	0.19	12.4
3a	0.00	0.00	0.00	0.00	0.0	0.0	0.0		0.879	14.1
3b	−8.16	−0.10	1.87	4.30	4.1	5.3	3.9 ± 0.6		0.001	6.6
3c	−1.92	−0.72	0.50	0.52	2.3	1.5	1.2 ± 0.3		0.12	13.2
4a	0.00	0.00	0.00	0.00	0.0	0.0	0.0		0.96	14.1
4b	−8.59	0.49	2.32	4.36	7.8	6.9	5.3 ± 1.0		< 0.001	4.3
4c	−3.79	−1.15	0.30	0.35	4.3	2.4	1.8 ± 0.7		0.04	8.7
5a	0.00	0.00	0.00	0.00	0.0	0.0	0.0		0.97	10.3
5b	−6.97	1.37	1.38	4.59	5.9	6.9	4.7 ± 0.9	3.0/3.3[k]	< 0.001	2.1
5c	−1.58	0.58	0.44	2.08	2.4	3.1	2.0 ± 0.4	0.0[k]	0.03	7.1

^[a]CCSD(T)/aug-cc-pVTZ gas phase reaction free energy.

^[b]MP2/6-311+G(d,p)/PCM hydration free energy differences/CCSD(T)/aug-cc-pVTZ gas phase reaction free energy.

^[c]MP2/6-311+G(d,p)/EC-RISM.

^[d]MP2/6-311+G(d,p) hydration free energy differences/CCSD(T)/aug-cc-pVTZ gas phase reaction free energy.

^[e]TI MD (OPLS/TIP3P) and

^[f]MC (GAFF/TIP4P) hydration free energy differences using RESP charges and CCSD(T)/aug-cc-pVTZ gas phase reaction free energy.

^[g]CCSD(T)/aug-cc-PVDZ/SCRF with MD/COSMO solvation models, respectively (Ref. 65).

^[h]2 corresponds to hachimoji “B”.

^[i]MP4- and CCSD(T)-corrected MP2/aug-cc-pVTZ/SCRF with MD (Ref. 67).

^[j]QC/Poisson-Boltzmann (Ref. 68).

^[k]B3LYP/6-311(+)G(d,p)/PCM (Ref. 69). Solution phase dipole moments (in D) are obtained from converged EC-RISM calculations.

All EC-RISM and FEMD/FEMC methods yield the same energetic ordering of keto and enol forms of guanine and the nucleobase analogs in water (Table 1), allowing us to obtain a statistically significant discrimination of tautomer populations by averaging over the four calculated values of relative free energies. Importantly, the average free-energy difference for guanine 1 (6.6 ± 0.2 kcal mol⁻¹) is consistent with experimental (5.6 kcal mol⁻¹)¹³ and previous computational (5.7/5.1 kcal mol⁻¹)⁶⁵ estimates for the keto 1a:enol 1b equilibrium (Table 1). For these five heterocycles, however, PCM theory²⁸ seems to over-stabilize enol and N3-H keto forms in water, with the exception of guanine 1. Qualitative agreement of the relative abundance of N1-H and N3-H keto forms of the remaining purine analogs 2-5 is obtained with PCM, as judged by those calculated using the other four methods. Our calculations also suggest that the populations of the desired N1-H keto forms of 4 and 5 will be greater than that of isoG 2. Experimental verification of this prediction, however, remains to be reported.

In a more interesting finding, our EC-RISM and FEMD/MC calculations suggest that the N3-H tautomers (2c-5c), which have been rarely considered in previous experimental studies of isoG 2 and related purine analogs,^14,18–20 are only slightly less energetically favorable (0.8 - 2.0 kcal mol⁻¹) in water than the N1-H tautomers (2a-5a) (Table 1). We note that Switzer’s group, while considering the viability of a six-nucleotide genetic system (A, T, G, C, isoG, and isoC), also found computational evidence for an especially stable N3-H tautomer of isoG 2 , attributing this unusual stability to the large dipole moment of this structure.⁷⁰ Our computed dipole moments in water do not, however, show a clear distinction between isoG 2 and the other three isoguanine analogs 3-5 (Table 1). In contrast, all EC-RISM and MD/MC free energy calculations show that the N3-H tautomer of guanine 1c is greatly disfavored in water relative to the N1-H tautomer 1a. We therefore conclude that the population of the N3-H tautomer of guanine 1 in water is insignificant. Our conclusion, however, differs from that reached by Hobza et al., who reported that 1c was more stable in water than 1a by −7.1 kcal mol⁻¹ (Table 1) on the basis of MD simulations,⁶⁵ primarily because of the difference in hydration free energies of the N1-H (1a) and N3-H (1c) tautomers, which was calculated by these authors to be −24.8 kcal mol⁻¹. We would argue, however, that this value of −24.8 kcal mol⁻¹ is erroneous because the absolute EC-RISM solvation free energy of 1a is −27.9 kcal mol⁻¹ (Table S2, Supporting Information) leading to an estimate of −52.6 kcal mol⁻¹ for the solvation free energy of 1c. This very large solvation free energy lies well outside the value expected for neutral small molecules.³² On the other hand, using the COSMO continuum solvation model,⁷¹ Hobza et al. reported a calculated free energy difference of +9.4 kcal mol⁻¹ for 1c relative to 1a,⁶⁵ which is in better agreement with the results of our EC-RISM/FEMD/MC calculations (Table 1).

In light of these results, we decided use our EC-RISM methodologies to determine the tautomerization free energies in water for adenine 6, cytosine 7, thymidine 8, isoC 9 (hachimoji “S”), 2-amino-8-(1-beta-D-2’-deoxyribofuranosyl)imidazo [1,2-a]-1,3,5-triazin-[8H]-4-one 10 (hachimoji “P”) and 6-amino-3-(2’-deoxyribofuranosyl)-5-nitro-1H-pyridin-2-one 11 (hachimjoi “Z”). In agreement with experimental observation, and numerous other prior calculations,^23,72–74 the three Watson-Crick nucleobases populate only a single tautomer. This was also the case for 10, the structure of which was obtained after a substantial amount of chemical synthesis and experimentation.⁷⁵ We note, however, that the interesting, complementary nucleobase 11 is predicted to exist in the alternate tautomer 11c to extent of approximately 0.1%; an amount that can introduce mismatches in PCR amplification but is difficult to detect using current experimental methods.

Evidence for the existence of N3-H tautomers.

N3-H tautomers have been discussed in the context of unnatural DNA backbones and non-Watson-Crick geometries. For example, for an xNA analog containing hexose in place of ribose, Krishnamurthy and co-workers considered the N3-H tautomer 2c to be present in a “reverse Watson Crick” pairing between strands having opposite chirality, but noted that this was entirely hypothetical.⁷⁶ The N3-H tautomer 2c may also be present in duplexes formed from two antiparallel strands. Thus, Geyer et al. found experimentally that an isoG:G mismatch to be unexpectedly stable in such duplexes and interpreted this observation as possibly arising from a size complementary pair between isoG in its syn-conformation and G in its anti-conformation.⁷⁷ Given the energetic accessibility of 2c seen in the calculations reported here, such a mismatch might equally arise from a purine:purine pair between G and isoG with the latter nucleobase as either its N3-H or syn O2-H tautomer (Figure 5).^15,78

Figure 5.

Possible base-pairing interactions between isoG and G or 8H-imidazo-[1,2-a]-[1,3,5]-triazin-4-one (P) in duplex DNA (R = 2’-deoxyribose). (a) Proposal of Roberts et al.;70 (b) Involvement of the O2-H enol isoG tautomer proposed by Geyer et al.;77 (c) Interaction of the N1-H isoG tautomer with the non-natural purine analogue P as proposed by Seela et al.;80 (d) Model of isoG:G base pair in which size and hydrogen-bonding complementarity is maintained by employing the N1-H isoG tautomer in its syn conformation. The involvement of N3-H tautomer 2c in forming a purine:purine pair in duplex DNA has also been invoked elsewhere,⁷⁹ and an exceptionally strong pair involving 2-amino-8-(2-deoxy-D-erythro-pentofuranosyl)-8H-imidazo-[1,2-a]-[1,3,5]-triazin-4-one, which is hydrogen bond-complementary with isoG 2 in its N3-H tautomeric form, has been reported.⁸⁰

CONCLUSIONS

Building on a number of prior computational studies of non-natural nucleobases that might be components of expanded genetic alphabets,^68–70,81 we have demonstrated that QC/EC-RISM calculations provide a firm basis for determining tautomeric ratios of purine and pyrimidine analogs. As discussed by many other researchers, especially Orozco^67,72,74,81 and Hobza^23,65 among others, Watson-Crick nucleobases all exist in a tautomeric form that is remarkably stable relative to all other possibilities. In addition, guanine 1 (Table 1) and adenine 2 (Table 2) discriminate strongly (>99% population) between the Watson-Crick-capable (N1-H) and the alternative keto (N3-H) tautomers. In the case of guanine 1, our calculations suggest that the origin of this behavior is the large difference in the electronic energies of the two keto tautomers 1a and 1c for which the correspondingly large (negative) hydration free energy does not suffice to compensate even though the dipole moment of 1c is larger than any other computed for this set of tautomers (Table 1). This is not the case for the cognate tautomers of nucleobases 2-5. In addition, there appears to be room for improving the hachimoji nucleobases, which, with the exception of 10, can exist as mixtures of tautomers in water.

Table 2.

Calculated standard reaction free energies ΔG (kcal mol⁻¹) and populations from EC-RISM calculations for selected tautomeric forms of 6-11 relative to the tautomers [6-11]a.

	CCSD(T)[a]	EC-RISM[b]	EC-RISM/CCSD(T)[c]	Average ΔG (EC-RISM)	Average population (EC-RISM)
6a	0	0	0	0	> 0.9999
6b	11.65	8.83	8.34	8.6 ± 0.3	< 10−6
6c	28.25	16.71	13.25	15.0 ± 2.4	< 10−10
7a	0	0	0	0	> 0.9999
7b	15.68	19.67	19.44	19.6 ± 0.2	< 10−14
7c	1.04	6.54	6.72	6.6 ± 0.1	< 10−4
8a	0	0	0	0	> 0.9999
8b	16.50	12.19	11.30	11.8 ± 0.6	< 10−8
8c	11.81	8.92	8.67	8.8 ± 0.2	< 10−6
9a[d]	0	0	0	0	0.9999
9b	4.19	14.20	13.91	14.1 ± 0.2	< 10−10
9c	−3.12	5.57	5.02	5.3 ± 0.5	0.0001
10a[e]	0	0	0	0	> 0.9999
10b	8.03	10.76	10.47	10.6 ± 0.2	< 10−7
10c	27.12	17.68	16.20	16.9 ± 1.0	< 10−12
10d	28.88	26.02	24.93	25.5 ± 0.8	< 10−18
11a[f]	0	0	0	0	0.998
11b	−3.19	3.18	4.33	3.8 ± 0.8	0.002
11c	19.75	19.01	18.80	18.91 ± 0.2	< 10−13 ± < 10−14

^[a]CCSD(T)/cc-pVTZ gas phase reaction free energy using the RI and F12 corrections. The results using this level of theory for compounds 1-5 are within an error of 0.12 kcal mol⁻¹ compared to the CCSD(T)/aug-cc-pVTZ approach (Table 1).

^[b]MP2/6-311+G(d,p)/EC-RISM.

^[c]MP2/6-311+G(d,p) hydration free energy differences/CCSD(T)/cc-pVTZ gas phase reaction free energy.

^[d]9 corresponds to hachimoji “S”.

^[e]10 corresponds to hachimoji “P”.

^[f]11 corresponds to hachimoji “Z”.

Second, the consistency of our multiple, independent sets of EC-RISM and FEMD/MC calculations raises the question of why the N3-H tautomers 2c-5c do not seem to be considered in experimental measurements of purine-like heterocycles. We note that the unusual stability of the N3-H tautomer has also been remarked upon in prior computational studies of isoguanosine.^68–70 This discrepancy between theory and experiment seems rooted in the technical difficulty of assessing tautomeric ratios when three different species are present in rapid equilibrium in solution. Standard spectroscopy-based approaches generally assume the existence of only two rapidly interconverting tautomers due to limitations of the mathematical formalism used to obtain the keto-enol ratio.⁸² Hence, if multiple tautomers are present in solution with similar spectroscopic properties, significant challenges arise in using current experimental strategies to assess tautomeric ratios. Such challenges were undoubtedly encountered in recent experimental work in this area,^14,83 precluding any useful comparison of tautomer ratios obtained by theoretical methods and experiment in our opinion. For example, in studies of isoG 2 and its variants in solution, spectroscopic signatures that might have indicated the existence of a third tautomer would be small compared to approximations introduced when using methylated species as “fixed proton” analogues. Interestingly, the N3-H tautomer of isoG may be manifested in recent experimental observations concerning purine:purine mispairs in duplex DNA.⁸⁴

Given these technical limitations of existing experimental strategies for determining the tautomer ratios of purine-related, and perhaps other, heterocycles, we suggest that access to state-of-the-art computational strategies, such as those described here, will be essential to identify non-natural nucleobases needed for the design of expanded genetic alphabets that exploit altered patterns of hydrogen bonding rather than steric complementarity.^85–88