Abstract
Purpose
It is unclear how and to what extent various infection prevention and control (IPC) policies affect the spread of an epidemic during work resumption. In order to assess the impact of IPC policies, this research addresses the results of a policy simulation in Shanghai, China, which estimates the transmission dynamics of COVID-19 under various IPC policies and offers evidence-based outcomes of work resumption policies for the world.
Materials and Methods
This simulation research is based on a system dynamics (SD) model that integrates IPC work resumption policies implemented in Shanghai into the classical susceptible-exposed-infected-removed (SEIR) epidemiological model. Input data were obtained from official websites, the Baidu migration index and published literature. The SD model was validated by comparing results with real-world data.
Results
The simulations show that a non-quarantined and non-staged approach to work resumption (Policy 1) would bring a small secondary outbreak of COVID-19. The quarantined but non-staged approach (Policy 2) and the non-quarantined but staged approach (Policy 3) would not bring a secondary outbreak of COVID-19. However, they both would generate more newly confirmed cases than the staged and quarantined approach (Policy 4). Moreover, the 14-day quarantine policy alone appears to be more effective in reducing transmission risk than the staged work resumption policy alone. The combined staged and quarantined IPC policy led to the fewest confirmed cases caused by work resumption in Shanghai, and the spread of COVID-19 stopped (ie, the number of newly confirmed cases reduced to zero) at the earliest date.
Conclusion
Conservative IPC policies can prevent a second outbreak of COVID-19 during work resumption. The dynamic systems model designed in this study can serve as a tool to test various IPC work resumption policies, facilitating decision-making in responses to combating the COVID-19 pandemic.
Keywords: IPC policies, work resumption, COVID-19, system dynamics, SEIR
Introduction
The World Health Organization (WHO) characterized the COVID-19 outbreak as a pandemic in March 2020.1 Three months prior, a type of coronavirus with unknown origins was detected in Wuhan, China, with the potential of widespread contagion. Shanghai was said to be at high risk because it is a mega-city in China with a permanent residency of 24.28 million and a highly population density (approximately 2059 inhabitants per square kilometer). Moreover, Shanghai is also a vital transportation and trade hub in China, with massive flows of people and goods arriving and departing daily.2 An early forecast by Lancaster University published on January 24, the number of COVID-19 patients in Shanghai could reach 800,000, or about 3% of the population. Under this prediction, it would become one of the highest risk cities in China outside Wuhan, Hubei.3
Before the WHO’s declaration, Shanghai had already implemented strict policies of infection prevention and control (IPC), such as restricting resident movements, tracing close contacts, quarantining suspected and confirmed cases, and even banning travel.4 The first phase of IPC policies started on January 23, in concert with the lockdown of Wuhan. On that day, the cumulative number of confirmed cases in Shanghai had reached 20, a small fraction of the total of 830 confirmed cases nationwide. The centrality of Shanghai increased the risk of a fast-growing infected population. In reality, on February 8, the cumulative number of confirmed cases in Shanghai was 292, a severe jump, but much less than the initial forecasts.5 We believe that the integrated IPC policies were central to limiting the impact of the disease and dispelling worries that confirmed cases would increase beyond all capacity to manage.
The second phase of IPC policies in Shanghai started in early February 2020 when the local government made a schedule for reinstating economic production. The reopening would lead to an increase in the contact rate among people, and the risk of propagating the epidemic would increase accordingly. On the other hand, there would undoubtedly be a potential increase in imported cases when the migrants gradually began to return to Shanghai after the Spring Festival holidays.
Concerns were sparked over a second potential epidemic peak in Shanghai.6 Therefore, the Shanghai Municipal Government initiated a combined IPC policy for reintroducing work, which involved of staged resumption of work, combined with a quarantine. The second epidemic peak actually did not occur after the implementation of the combined IPC policy. It can be said that Shanghai provides a valuable experience for implementing work resumption under the epidemic.
However, it is unclear how and to what extent the combined IPC policy has affected the spread of the epidemic. Considering that the COVID-19 is still propagating worldwide and may return this autumn, it is very important to assess the impact of the IPC policies on the epidemic. In this study, we apply the System Dynamics method to construct a modified susceptible-exposed-infected-removed (SEIR) epidemiological model that incorporates the domestic migration data and the COVID-19 epidemiological data to predict the transmission dynamics of epidemics under various IPC polices. This study will produce a testbed for IPC policies and offer evidence-based experiences of work resumption for the world.
Materials and Methods
Data Sources
The COVID-19 epidemic data was obtained from publicly released data by the National Health Commission of the People’s Republic of China and the Shanghai Municipal Health Commission.7,8 The retrieved data was between January 10 and May 9, and included: (1) Daily counts of newly confirmed cases, fatalities, and recoveries; (2) Cumulative counts of confirmed cases, deaths, and recoveries; and (3) Daily counts of cases getting medical treatment in hospitals. From these data, it is possible to estimate rates of change needed to parameterize a dynamic model. The population flow in and out of Shanghai was obtained from the Baidu migration index and the Shanghai government official website.9,10 The China National Bureau of Statistics website provided population data for Shanghai.11
Methodology
We applied system dynamics techniques to codify a transmission model of COVID-19, building on classic differential equation-based SEIR epidemiological models.12,19 Our model considers Shanghai’s role as a migratory hub, as well as the IPC policies employed in vivo. Vensim® 8.09 was the software for the model building and policy simulation.
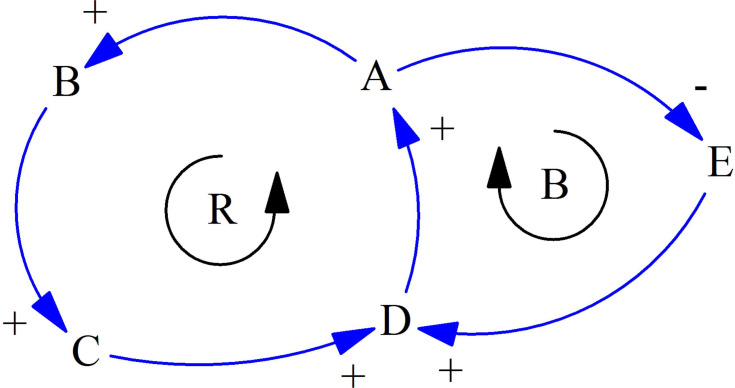
System Dynamics (SD) is a method that constructs models based on system structure, often represented by feedback loops and stock and flow diagrams.13 Feedback loops are a simplified representation of how key variables relate to each other. There are two fundamental kinds of feedback loops: reinforcing loops (as marked R in Figure 1) and balancing loops (as marked B in Figure 1). In a reinforcing loop, a small deviation in one variable will be amplified through the loop generating an exponential growth or exponential decay behavior, while in a balancing loop, a small deviation in one variable will be reduced over the loop leading to a behavior that approaches an equilibrium.14
Figure 1.
Feedback loops in system dynamics.
Abbreviations: NB, A link with a “+” means a positive relationship in which the effect changes in the same direction as the cause, while a link with a “−” means a negative relationship in which the effect changes in the opposite direction as the cause.
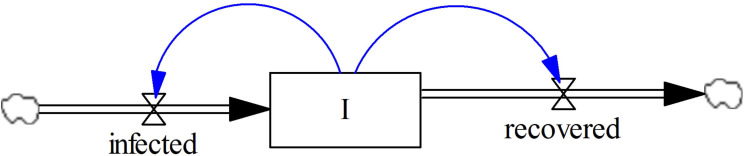
A stock and flow diagram is instrumental in system dynamics modeling, and captures the accumulation and dispersal processes. Stock variables illustrate the state of the system, eg, the infected population (the variable I within the box in Figure 2). The infected population increases as new individuals become infected and decreases as infected people die or recover. Stock variables change only through the accumulation of flow variables. Specifically, flow variables represent the rate of change of stock variables. For example, as more people become infected, the rate at which the size of the infected population grows will increase. Although stock variables change based on flow variables, stock variables often affect the flow variables at the same time (eg, a larger infected population leads to faster infection, which completes the feedback loop).
Figure 2.
Stock and flow structure in SD.
SD models are structure-based models that are useful for understanding a problem even when data is lacking. They are particularly helpful in analyzing complex problems, as when multiple feedback forces alter the time-based behavior (dynamics) of the system. These dynamics are often accompanied by changes in loop dominance over time, indicating emergent and unexpected outcomes. Through model simulation, it is possible to investigate how a system’s behavior evolves under various scenarios. It is also useful when real-world complexity surpasses the ability to create closed-form solutions. Thus, SD models can be used as a micro-environment to test the effectiveness of various policies.15
Much of the research in transmission dynamics applies the mathematics of differential equation (DE) or agent-based (AB) models,16 depending on the level of aggregation appropriate for the analysis.17 SD belongs to DE models, which simulate the model at an aggregated level, not considering that each individual behaves differently. On the other hand, agent-based simulation disaggregates the model to individual behaviors as it captures the heterogeneity in reality.18 However, AB models require much more data or a broad set of assumptions to mimic individual actions, which might not be available under the condition of a novel virus situation.16 Moreover, modelers always face the dilemma of whether to disaggregate the model to include more details or to keep the model simple and understand the inherent mechanism thoroughly. In this study, as we are investigating IPC policies from the Shanghai government, which apply with some consistency across individuals. Thus, we hope to gain insights without the delays associated with data collection or behavioral modeling at granular levels. SD can help us evaluate the effectiveness of various policies in a simple and clear way.
The System Dynamics of COVID-19
The Model Structure
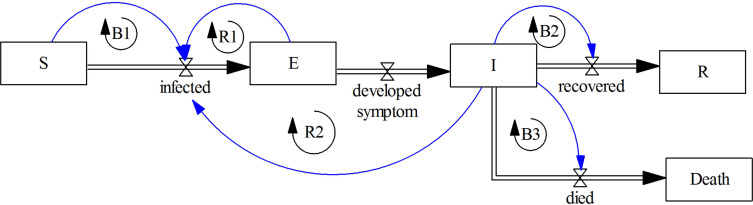
Much previous research has used SD to analyze the spread of infectious diseases,19 such as HIV/AIDs,20–22 Chlamydia,23,24 etc. Although the complexity of models varies according to the underlying research questions, most of the models rise from the classic compartment models based on the SIR or SEIR structures and feedback shown in Figure 3.19
Figure 3.
The fundamental feedback loops in SEIR model.
R1 and R2 represent reinforcing loops in which growth in the exposed or infected population leads to more infection in the susceptible population. B1 is the balancing loop that captures the population limits: when more people are exposed, fewer people remain in the susceptible group, which will lead to fewer people left to be exposed later. B2 and B3 are balancing loops reflecting the transition of infected people to either recovery or death. As the infected population grows, more will recover or die, leaving fewer people in the infected state.
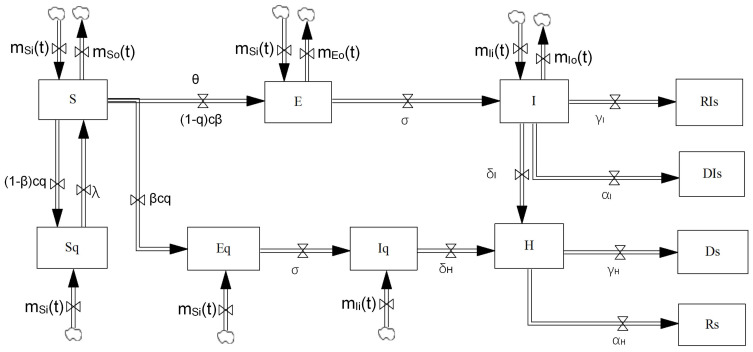
This fundamental model assumes that there are no other influences on the system, and therefore requires some adaptation to place it in the context of the real world. In this study, to investigate the effectiveness of IPC policies, we extended the SEIR epidemiological model in two ways: first, to include population flow in and out Shanghai, with the consideration that the inbound and outbound population could be Susceptible (S), Exposed (E), Infected (I) or Recovered (R); second, we included the interventions taken by Shanghai authorities, such as quarantining close contacts of confirmed patients, suspected cases and outsiders coming to Shanghai, isolating and treating confirmed cases. We also incorporated structure relevant to governmental interventions and further stratified the total population in Shanghai (N) to include (1) the quarantined susceptible (Sq), (2) the quarantined exposed (Eq), (3) the quarantined infectious (Iq), (4) the hospitalized (H), and (5) the migrating (m) population. Figure 4 shows this expanded and general conceptual model of the COVID-19 infection.
Figure 4.
The model of the COVID-19 infection.
The migrating group includes people entering and leaving Shanghai, mainly those who are traveling for the Lunar New Year holiday. Migrants have disease exposure risks, as some may have been exposed or infected before or during their travels. Emigrants [subscript o] consist of susceptible, exposed, and infectious individuals and leave Shanghai at a rate of mSo(t), mEo(t), and mIo(t), respectively. For immigrants, there also exists mSi(t), mEi(t), and mIi(t), with t serving as a time index. With a quarantine intervention in place, immigrants returning to Shanghai after their travels enter the quarantined population groups, Sq, Eq, and Iq, segregated from the general model population. Without a quarantine, immigrants mix in with the general population, S, E, and I.
While government agencies work to trace close contacts of suspected and confirmed patients, the process is imperfect. Only a proportion, q, of individuals exposed to the virus are identified and quarantined. The complement, 1-q, consists of individuals exposed to the virus who miss contact tracing. Let the transmission probability be β, and the contact rate be c. When these presumably exposed individuals are identified, they move to Eq at the rate βcq, while uninfected individuals in quarantine move from the general S population to Sq at the rate of (1-β)cq. At the end of the quarantine period, uninfected individuals in Sq return to the susceptible group S at a rate of λ.
Persons outside of quarantine move to the exposed group if exposed through contacts, or they stay in group S as exposure risk diminishes. If found to be exposed, they will move to group E at a rate of βc(1-q). If exposed individuals outside of quarantine show symptoms, they move to the group I at a rate of σ. Individuals with severe symptoms go to hospitals where they are isolated and get medical treatment at a rate of δI. Infected individuals who do not go to hospital move to the recovery group RIs or death group DIs at a rate of γI and αI, respectively, without hospital treatment. Medical resources and symptom severity influence the decision to admit symptomatic individuals to the hospital or the use of less intensive treatment.
Exposed individuals in Eq move to the group Iq at a rate of σ and get medical treatment in the hospital at a rate of δH. Then they move to the recovery group Rs or the death group Ds at a rate of γH and αH, respectively.
The exposed but not quarantined individuals in the group E can also transmit the disease to the susceptible S in a similar way as the infected group I, but with a lower proportion θ as an asymptomatic individual is less infectious than a symptomatic individual.25
Based on the above transmission dynamics, the SD model for the COVID-19 infection may be captured through the following differential equations:
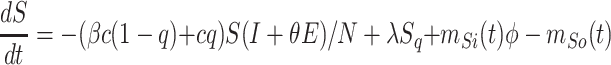 |
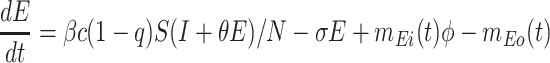 |
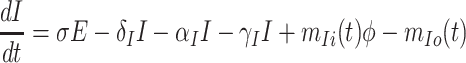 |
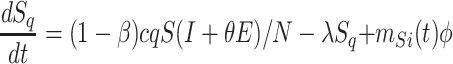 |
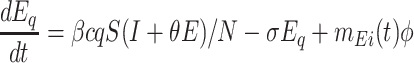 |
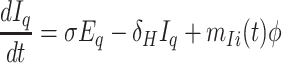 |
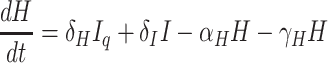 |
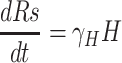 |
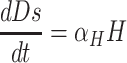 |
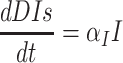 |
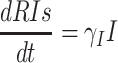 |
where Φ is a binary variable indicating whether the quarantining intervention is adopted.
Parameter Settings and Initial Values
The initial value for the contact rate c is 14.8, indicating a relatively high contact rate in Shanghai before the outbreak and quarantine programs.12 The contact rate c changes once isolation requirements are put in place, and is represented by a piecewise function. The mean incubation period of COVID-19 is 5.2 days, which implies a rate of exposed individuals to the infected class, σ, of 0.19/day.26 It takes 14 days before the quarantined uninfected contacts are released into the wider community, so the value of λ is 1/14, or 0.07.27 The transition rate of symptomatic infected individuals to the hospitalized group, δI, is 1/average waiting time, initialized as 0.12.28,29 The full set of parameters for the COVID-19 epidemiological model (Shanghai) is available in Table a1 in the Appendix.
The starting time of the model was set to January 10, 2020, when the National Health Commission of the People’s Republic of China publicly released the coronavirus pneumonia epidemic data for the first time.7 The first confirmed case in Shanghai had a travel history from Wuhan, arrived in Shanghai on January 12, and was reported as the first confirmed case on January 20. Accordingly, it is reasonable to assume no one had been infected by January 10, and all individuals in Shanghai were susceptible to COVID-19. The population of Shanghai by the end of 2019 is around 24.28 million,11 ie, S(0) equals 24.28 million and values of all the other groups are initialized to zero.
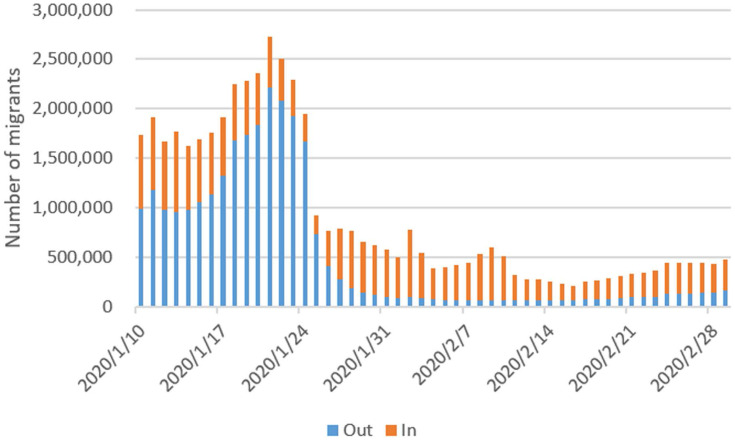
January 10 was also the first day of China’s annual Spring Festival travel rush (called Chunyun). In the following days, the overall trend of population migration in Shanghai went through two stages. In the first stage, from January 10 to January 23, the population leaving the city was much larger than the population returning, as some Shanghai residents were going back to their hometowns for family reunions. Some exposed and infected individuals entered Shanghai during that time, including people from Wuhan. After January 24, with the increased public awareness of the epidemic and Shanghai’s intensive prevention and control measures, population flow decreased dramatically. The February data shows the effects of the end of the holiday period and anticipation of work resumption, with a couple of returning peaks (Figure 5). By the middle of March, nearly all migrants had returned to Shanghai, and work and production had resumed in an orderly manner.
Figure 5.
Daily distribution of the migration group.
The model parameters were adjusted to reflect this seasonal effect. During the January 10–24th stage, the proportions of susceptible, exposed, and infectious migrants were estimated according to the respective proportions in the national population, except Shanghai. That is,
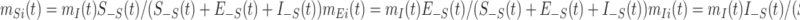 |
where S−S(t) (or E−S (t), or I−S (t)) is the number of susceptible (or exposed, or infectious) individuals outside Shanghai at time t.7,8 The population inflow, mI(t), was retrieved from the Baidu migration index and the Shanghai government official website.9,10 The initial value on January 10, mI(0), is 0.75 million.
In the second stage, after January 24, with the lockdown of Wuhan, the move-in ratio excludes both Shanghai and Wuhan.
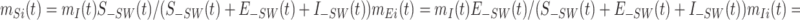 |
where S−SW(t) (or E−SW(t), or I−SW(t)) is the number of susceptible (or exposed, or infectious) individuals outside Shanghai and Wuhan at time t.7,8
The proportions of susceptible, exposed, and infectious individuals in Shanghai are adopted for the calculation of the outflows of susceptible, exposed, and infectious population. That is,
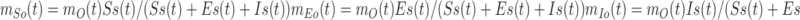 |
where SS(t) (or ES(t), or IS(t)) is the number of susceptible (or exposed, or infectious) individuals outside Shanghai at time t.8 The initial value of population outflow on January 10, mO(0), is 0.98 million.9,10
Model Validation
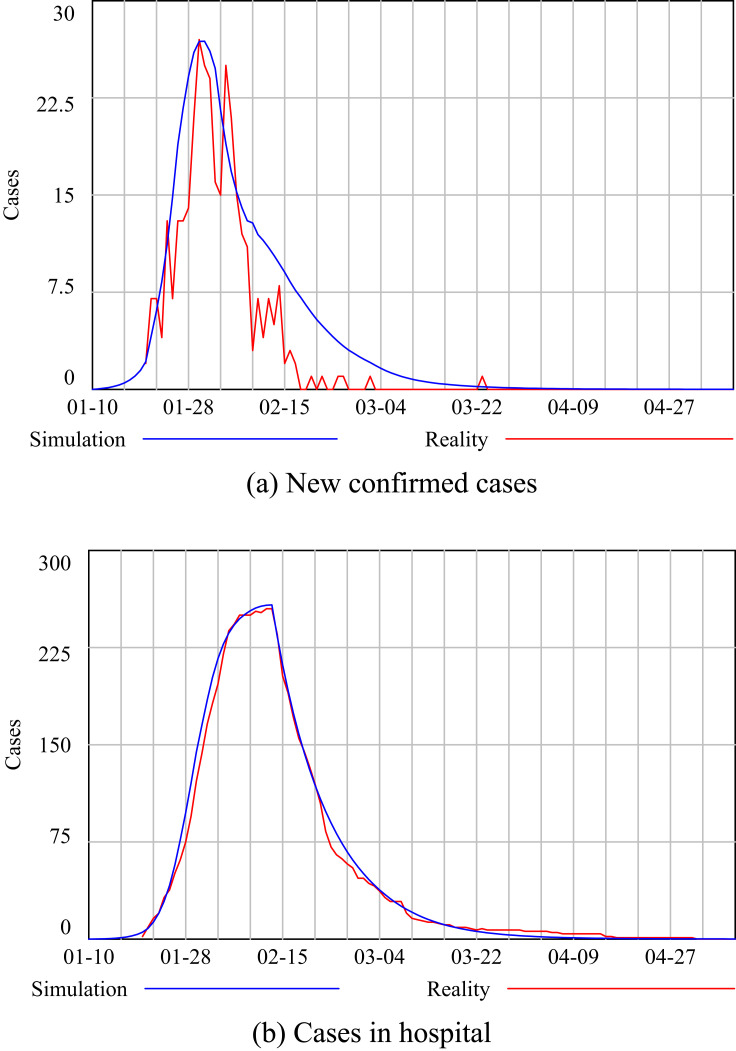
Vensim® 8.09 was adopted to construct the COVID-19 epidemiological model as parameterized for Shanghai. Extensive model verification and validation activities were undertaken, including white-box tests (scrutinizing the model structure and mathematical equations) and black-box tests (testing the behavior of the model), and comparing results with real-world data. Simulation results show that the newly confirmed cases and the count of confirmed cases in Shanghai hospitals are highly consistent with historical data released by the Shanghai Municipal Heath Commission, as shown in Figure 6. Table 1 compares the simulated peak value and peak date with historical data, and shows validation outcomes with RMSE and MAPE. Further validation outcomes are given in Figure a1 in the Appendix. Therefore, the validity of the COVID-19 epidemiological model (Shanghai) was confirmed, and the model is thus ready for running policy simulations.
Figure 6.
Simulation results and historical data from the government.
Table 1.
Comparing Simulated Results with Historical Data
| New Confirmed Cases | Cases in Hospital | |
|---|---|---|
| Simulated Peak Date | January 30 and 31 | February 13 |
| Historical Peak Date | January 30 | February 13 |
| Simulated Peak Value | 27 | 258 |
| Historical Peak Value | 27 | 255 |
| Difference of Peak Value | 0% | 1.2% |
| RMSE | 3.06 | 6.76 |
| MAPE | 32.28 | 32.23 |
Results: Policy Simulation
As part of its IPC response, the Shanghai Municipal Government initiated a strategy of staged resumption of work in which workers in the most critical industries were allowed to return to work first. Also, people who returned to the city were quarantined for 14 days before starting to work. It is unclear what the situation would have been like without either or both interventions. Moreover, the relative effectiveness of the staged resumption of work and the quarantine policy also needs investigation. Therefore, we tested four sets of policies using the COVID-19 model (Table 2).
Table 2.
Four Sets of Policies
| Measures | Non-Staged Work Resumption | Staged Work Resumption |
|---|---|---|
| No 14-day quarantine | Policy 1 | Policy 3 |
| 14-day quarantine | Policy 2 | Policy 4 (in vivo) |
Our analysis of the Baidu migration index from January 10 to January 24 showed that around 13.6 million people left Shanghai to celebrate the Spring Festival and were expecting to return to Shanghai for work resumption. Because the Shanghai government implemented staged work resumption, people came back to Shanghai more gradually than in a typical year. The estimated population flow in 2020 represents the policy of staged work resumption. To capture the possible migration effect in the absence of COVID-19, we used 2019 data for the same period (Chunyun period) after the Spring Festival.
Policy 1: Non-Quarantined and Non-Staged
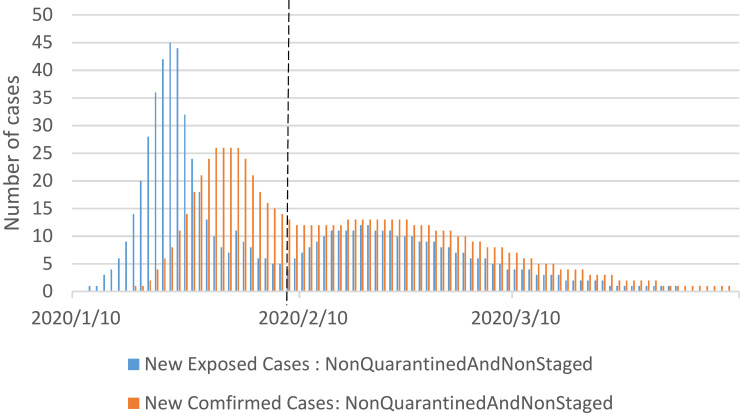
Our first policy test was the absence of either staged or quarantine policies for immigrants. Under this scenario, returnees would come back to Shanghai according to the pattern of 2019 and enter the S, E, and I directly (Φ=0). The contact rate increased immediately after work resumption.
There would be a second disease outbreak, as the number of newly exposed cases and new confirmed cases rose over time, as shown in Figure 7. Starting from February 7, the number of exposed cases increased until around February 20. The number of new confirmed cases increased several days later. The rate of newly identified cases would have a small secondary rise, reaching its second peak value of 13 cases per day between February 16th and 24th, and reducing to zero after April 8.
Figure 7.
Simulation results for the non-quarantined and non-staged policy.
Policy 2: Quarantined but Non-Staged
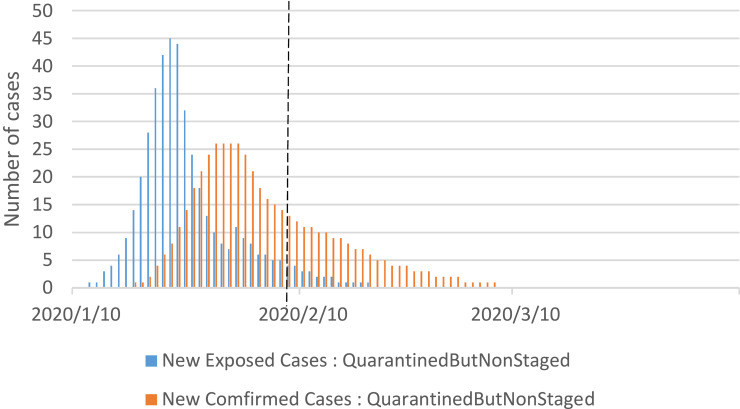
Our second policy test isolated the effect of a quarantine. Here, we applied the pattern of 2019 returns to work after the Spring Festival. With only a quarantine, returnees entered the Sq, Eq, and Iq groups, respectively (Φ=1). The contact rate increased immediately after the end of the quarantining period.
The simulation results in Figure 8 showed no further increase of either the number of newly exposed cases or the number of newly confirmed cases, compared to the situation before work resumption. Both the number of exposed cases and the number of newly confirmed cases decreased over time, and the number of exposed cases reached zero in late February, followed by the number of newly confirmed cases around March 7.
Figure 8.
Simulation results for the quarantined but non-staged policy.
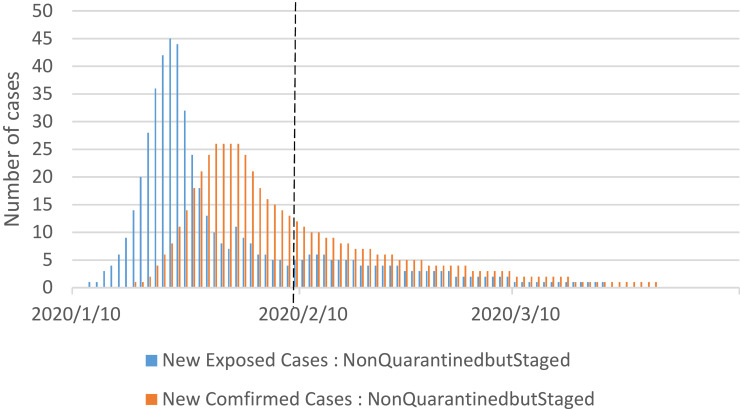
Policy 3: Non-Quarantined but Staged
If the IPC policy included staged work resumption without quarantining, returnees would come back to work based on the pattern observed in 2020 and would enter S, E, and I. The contact rate increased along with staged work resumption.
As shown in Figure 9, only an insignificant increase in the number of daily exposed cases occurred after February 8. But for the daily newly confirmed cases, there was no increasing trend. The number of newly confirmed cases reduced to zero after March 29.
Figure 9.
Simulation results for the non-quarantined but staged policy.
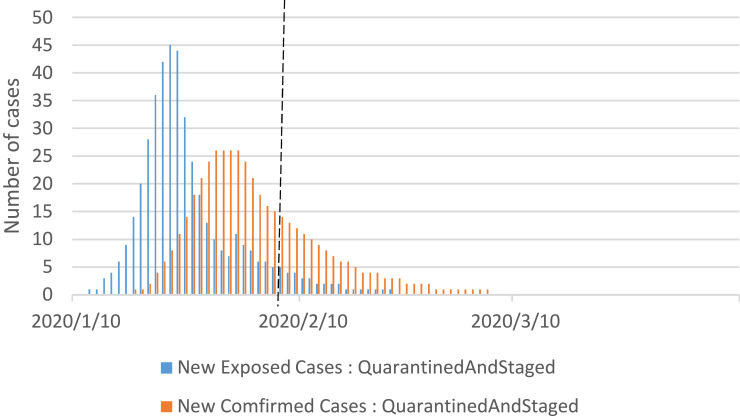
Policy 4: Quarantined and Staged
For staged work resumption, returnees would come back to work according to the pattern observed in 2020. With quarantine, returnees entered the quarantined population, that is, Sq, Eq, Iq (Φ=1). The contact rate increased along with staged work resumption after the quarantining period.
Simulation results in Figure 10 showed no increase in the number of daily new exposed cases and new confirmed cased under this policy. The number of new confirmed cases became zero after March 6.
Figure 10.
Simulation results for the quarantined and staged policy.
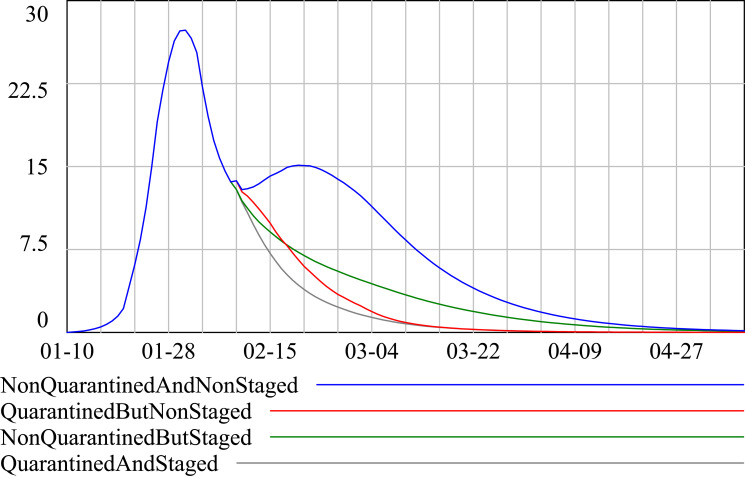
The relative effects of the four sets of work resumption policies on the COVID-19 in Shanghai are summarized in Figure 11. The simulations indicated that Shanghai would have suffered another COVID-19 outbreak if Policy 1 (non-quarantined and non-staged) had been adopted. The increase of newly confirmed cases is not much, peaking at 13 cases in several successive days. As shown in Table 3, the total number of newly-confirmed cases following work resumption would increase by 251% compared with the situation in Policy 4 (quarantined and staged). Moreover, the end of infection spread would be postponed to for almost a month, from March 6 to April 8.
Figure 11.
Daily new confirmed cases under different policies.
Table 3.
Comparing Simulation Results Under Different Policies
| Policy | The Date When Daily New Confirmed Reaches Zero | Percent of Increment of New Confirmed Cases After Work Resumption, Compared to Policy 4 |
|---|---|---|
| Policy 1 | April 8 | 251% |
| Policy 2 | March 7 | 26% |
| Policy 3 | March 29 | 76% |
Policy 2 (quarantined but non-staged) and Policy 3 (non-quarantined but staged) would not have resulted in a secondary outbreak of COVID-19 in Shanghai. The cumulative confirmed cases would still increase, 26% for Policy 2, and 76% for Policy 3, compared with the data from Policy 4. Policy 2 would reach zero new confirmed cases almost the same day as that of Policy 4, but Policy 3 witnessed the end of infections delayed to the end of March.
Discussion
The combination of quarantined and staged approach (Policy 4) is the policy currently adopted by the Shanghai government, which is the most conservative and safest policy from a disease control perspective. The quarantined but non-staged work resumption (Policy 2) and the non-quarantined but staged work resumption (Policy 3) would also not result in a secondary outbreak of COVID-19 in Shanghai. However, the non-quarantined and non-staged (Policy 1) would lead to a mild increase in newly confirmed cases according to the simulation results.
In conclusion, even Policy 1 would have not led to a severe, secondary outbreak of COVID-19 during work resumption in Shanghai. The low risk of a second outbreak can be explained by the fact that nearly all the exposed and infected cases and their close contacts had already been quarantined or isolated before the beginning of work resumption in Shanghai. Therefore, people who were allowed to move in and out of Shanghai were mostly virus free and thus limited the growths in the exposed and infected populations. This finding suggests that the first phase of the IPC policies implemented in Shanghai were very effective at controlling the spread of COVID-19 before the work resumption, and that the timing for work resumption was not too early.
Even though the risk of a second outbreak was low, the use of the most conservative policy was plausible, because COVID-19 is highly contagious and one infected person has the potential to infect tens of close contacts, especially in areas with a high population density. Examples include, “Patient 31” in Daegu church in Korea,30 the clustered infection in a public bath center of China,31 as well as the “super spreader” event in Chicago.32 Considering the possibility of high transmission risk in workplaces, the Shanghai Municipal Government adopted a policy of staged work resumption and quarantine for 14 days, which was the strictest policy (Policy 4) to protect the citizens of Shanghai. Enterprises manufacturing raw materials and products for IPC were the first to resume work, followed by food processing enterprises, ensuring stable supplies in the Shanghai market. Finally, the remaining workers unable to work from home were gradually allowed to return to their work places. To keep imported cases under control, the government overlaid a self-quarantining/centralized isolation policy on those who had returned to the workplace. Before returning to work, all immigrants arriving at Shanghai boarders were required to self-quarantine immediately at home for at least 14 days. If the individuals came from a place of high-risk level, they were made subject to medical observations in a designated, centralized hotel for 14 days.33
Conservative IPC work resumption policies can be very costly in the short run, including both social costs (individual stress, disruption of routines, etc.) and economic costs such as lost productivity, and the significant resources in dollars and labor required for policy implementation. However, the limited number of newly confirmed cases have allowed most economic activities to get back to normal since March. The economic growth returned to positive in Shanghai in the second quarter of 2020.34 Therefore, the painful choices made by the Shanghai Municipal Government seem to have been worthwhile. A detailed analysis of the costs and benefits of these IPC policies is beyond the scope of this paper. Such an analysis could provide additional insights and facilitate future decision-making.
By comparing Policy 2 with Policy 3, we can examine the relative effects of quarantine and staged work resumption IPC policies, respectively. It is noteworthy that a 14-day quarantine policy is more effective in reducing transmission risk than a staged work reduction alone, with the quarantine resulting in 50% fewer newly confirmed cases and reaching the “zero” timeline about 22 days earlier than the staged work resumption policy (Table 3). Given the emerging risk associated with imported cases from other countries, the 14-day quarantine policy has been playing a vital role in reducing transmission risk and keeping the disease under control in a mega-city like Shanghai and should therefore be continued. So far, a total of 279 imported cases from abroad have been identified through the centralized isolation period in Shanghai, while few cases from other areas in China were found after April.8 These pieces of evidence have further proven that a quarantine policy is of great importance for work resumption.
Furthermore, at the current stage of the pandemic, many countries around the world are facing a dilemma in decision-making: how to resume economic production while keeping the epidemic under control. It is a difficult balance. Internationally, we have already witnessed some examples of pre-mature economic reopening. As of June 23, 2020, four sunbelt states in the US, Arizona, California, Florida, and Texas, were confronting a significant resurgence of COVID-19 after reopening.35 According to a recent report published in Science,36 we might have to live with COVID-19 until 2025. It is thus extremely important for governments as well as academics to seek approaches and act wisely to make an appropriate balance between economic reopening and epidemic prevention, so as to minimize the adverse social and economic consequence of living with the virus.37,38 There has been very limited research in this field.39,40 At the same time, the dynamic systems model presented in this study can serve as an effective means of helping to test work resumption policies for countries around the world. Though simulation, it is possible to model the evolution of the pandemic under different IPC policy scenarios implemented at various places and provide policymakers with quantified, science-based real-time consequences of different IPC policies.
Finally, it is worth noting that most western countries have different political realities than is the case for Shanghai, in that the rates of compliance with certain policies may be lower there, even if compliance is mandatory. There are also differences in geographic setting, travel patterns and the like. Such unique geographic, social and political realities of each jurisdiction would not change the basic structure of our model. However, parameter settings and initial values should be adjusted to reflect these features. Further empirical studies are likely needed to determine appropriate parameter values when applying the model in other jurisdictions.
Conclusion
In this study, a dynamic systems model that captured the structure of coronavirus transmission in Shanghai was developed. Based on this model, simulations of four IPC policy alternatives were carried out for analysis and comparisons. The simulation results suggested that the policy of “Staged work resumption and quarantine” was the most effective in lowering the risk of a second COVID-19 outbreak caused by the resumption of work, and produced the fewest confirmed cases. A stand-alone 14-day quarantine policy is more effective in reducing transmission risk than a stand-alone staged work resumption policy.
The current situation of the wide-spread of COVID-19 in various countries shows that the challenge of work resumption faced by Shanghai is a global issue. And the dynamic systems model designed in this study can serve as an important tool for countries around the world to test various policies of work resumption, facilitating decision-making in enacting appropriate responses to combating the COVID-19 pandemic.
Acknowledgments
We wish to thank the members of the System Dynamics Chapter, Systems Engineering Society of China, who contributed their time, ideas, expertise, and experiences to this effort, including Guangle Yan and Linlin Wang. We thank David Whyte for proofreading portions of the manuscript, thank Luojia Dai for improving literature review, and thank Zhiling Dai and Lei Wang for verifying the obtained COVID-19 epidemic data. Special thanks are also extended to Dr. Eliot Rich, Associate Professor and Chair of Information Systems and Business Analytics, School of Business, University at Albany, who carefully reviewed this manuscript and improved presentation of the context.
Funding Statement
This work was supported by National Social Science Foundation of China (No. 18BGL235 and No. 20AZD059), National Natural Science Foundation of China (No. 20VYJ064 and No. 71432006), and Shanghai Jiao Tong University think tank leading research project (No. ZKYJ-2020014).
Disclosure
The authors report no potential conflicts of interest for this work.
References
- 1.Tedros AG WHO Director-General’s opening remarks at the media briefing on COVID-19; 2020. Available from: https://www.who.int/dg/speeches/detail/who-director-general-s-opening-remarks-at-the-media-briefing-on-covid-19—11-march-2020. Accessed April21, 2020..
- 2.Shanghai Statistics Bureau. Shanghai National Economic and Social Development Statistical Bulletin (2019); 2020. Available from: http://tjj.sh.gov.cn/tjgb/20200329/05f0f4abb2d448a69e4517f6a6448819.html. Accessed April21, 2020..
- 3.Read JM, Bridgen JR, Cummings DA, Ho A, Jewell CP Novel coronavirus 2019-nCoV: early estimation of epidemiological parameters and epidemic predictions. medRxiv; 2020. Available from: https://www.medrxiv.org/content/10.1101/2020.01.23.20018549v2. Accessed July21, 2020.. [DOI] [PMC free article] [PubMed]
- 4.Lu HZ, Ai JW, Shen YZ, et al. A descriptive study of the impact of disease control and prevention on the epidemic dynamics and clinical features of SARS-CoV-2 outbreak in Shanghai, lessons learned for metropolis epidemics prevention. medRxiv; 2020. Available from: https://www.medrxiv.org/content/10.1101/2020.02.19.20025031v1. Accessed July21, 2020..
- 5.ShanghaiEye. 6 More Coronavirus Cases Confirmed in Shanghai, Total Hits 292; 2020. Available from: https://www.shanghaieye.com.cn/6-more-coronavirus-cases-confirmed-in-shanghai-total-hits-292/. Accessed April10, 2020..
- 6.Rapoza K. All Eyes on Shanghai As A Million More People Returning To Work. Forbes; 2020. Available from: https://www.forbes.com/sites/kenrapoza/2020/02/26/all-eyes-on-shanghai-as-a-million-more-people-returning-to-work/#3af6b09c2d6a. Accessed April10, 2020..
- 7.National Health Commission of the People’s Republic of China. COVID-19 Bulletin (in Chinese); 2020. Available from: http://www.nhc.gov.cn/xcs/yqfkdt/gzbd_index.shtml. Accessed April10, 2020..
- 8.Shanghai Municipal Health Commission. COVID-19 Bulletin (in Chinese); 2020. Available from: http://wsjkw.sh.gov.cn/yqtb/index.html. Accessed August3, 2020..
- 9.Baidu. Mobile Population and Migration Data; 2020. Available from: http://qianxi.baidu.com/. Accessed April10, 2020..
- 10.Shanghai Municipal People’s Government. Return passenger flow rises slowly and traffic slightly congested (in Chinese); 2020. Available from: http://www.shanghai.gov.cn/nw2/nw2314/nw2315/nw4411/u21aw1427002.html. Accessed April10, 2020..
- 11.National Bureau of Statistics of China. Population (Sample Survey)(person); 2020. Available from: http://data.stats.gov.cn/english/easyquery.htm?cn=C01. Accessed April10, 2020..
- 12.Tang B, Wang X, Li Q, et al. Estimation of the Transmission Risk of the 2019-nCoV and Its Implication for Public Health Interventions. J Clin Med. 2020;9(2):462. doi: 10.3390/jcm9020462 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sterman JD. Business Dynamics: Systems Thinking and Modeling for a Complex World. New York: McGraw-Hill; 2000. [Google Scholar]
- 14.Fang Y, Lim K, Qian Y, et al. System dynamics modeling for information systems research theory development and practical application. MIS Quarterly. 2018;24(4):1303–1329. [Google Scholar]
- 15.Sterman JD. Learning from evidence in a complex world. Am J Public Health. 2006;96(3):505–514. doi: 10.2105/AJPH.2005.066043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Yang Z, Zeng Z, Wang K, et al. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J Thorac Dis. 2020;12(3):165–174. doi: 10.21037/jtd.2020.02.64 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Adam D. Special report: the simulations driving the world’s response to COVID-19. Nature. 2020;580(7803):7803. doi: 10.1038/d41586-020-01003-6 [DOI] [PubMed] [Google Scholar]
- 18.Rahmandad H, Stermn J. Heterogeneity and Network Structure in the Dynamics of Diffusion: comparing Agent-Based and Differential Equation Models. Manage Sci. 2008;54(5):998–1014. [Google Scholar]
- 19.Darabi N, Hosseinichimeh N. System dynamics modeling in health and medicine: a systematic literature review. Sys Dynam Rev. 2020;36(1):29–73. doi: 10.1002/sdr.1646 [DOI] [Google Scholar]
- 20.Roberts C, Dangerfield B. Modelling the Epidemiological Consequences of HIV Infection and AIDS: A Contribution from Operational Research. J Oper Res Soc. 1990;41(4):273–289. doi: 10.1057/jors.1990.49 [DOI] [Google Scholar]
- 21.Weeks MR, Li J, Lounsbury D, et al. Using Participatory System Dynamics Modeling to Examine the Local HIV Test and Treatment Care Continuum in Order to Reduce Community Viral Load. Am J Community Psychol. 2017;60(3–4):584–598. doi: 10.1002/ajcp.12204 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zou X, Xu Y, Chen W, et al. Strategies to control HIV and HCV in methadone maintenance treatment in Guangdong Province, China: a system dynamic modeling study. Subst Abuse Treat Prev Policy. 2018;13(1):1. doi: 10.1186/s13011-017-0140-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Viana J, Brailsford SC, Harindra V, Harper PR. Combining discrete-event simulation and system dynamics in a healthcare setting: A composite model for Chlamydia infection. Eur J Oper Res. 2014;237(1):196–206. doi: 10.1016/j.ejor.2014.02.052 [DOI] [Google Scholar]
- 24.Teng Y, Kong N, Tu W. Optimizing strategies for population-based chlamydia infection screening among young women: an age-structured system dynamics approach. BMC Public Health. 2015;15(1):639. doi: 10.1186/s12889-015-1975-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ferguson NM, Laydon D, Nedjati-Gilani G, et al. Impact of non-pharmaceutical interventions (NPIs) to reduce COVID19 mortality and healthcare demand.; 2020. Available from: https://spiral.imperial.ac.uk:8443/handle/10044/1/77482. Accessed April13, 2020..
- 26.Li Q, Guan X, Wu P, et al. Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus–Infected Pneumonia. N Engl J Med. 2020;382(13):1199–1207. doi: 10.1056/NEJMoa2001316 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Shanghai Municipal Health Commission. Returnees stay home for 14 days (in Chinese); 2020. Available from: http://wsjkw.sh.gov.cn/xwfb/20200204/db01b711b12040c4bbba663289ea00f7.html. Accessed March10, 2020.
- 28.Wu JT, Leung K, Leung GM. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020;395(10225):689–697. doi: 10.1016/S0140-6736(20)30260-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Shanghai Municipal Health Commission. Strengthening the management of the setting of specialized fever clinics (in Chinese); 2020. Available from: http://wsjkw.sh.gov.cn/yzgl3/20200421/d42a97b510784bfb9ff4636afd37ee02.html. Accessed April10, 2020.
- 30.Korea Center for Disease Control and Prevention. The updates of COVID-19 (as of Feb.19) in Korea; 2020. Available from: https://www.cdc.go.kr/board/board.es?mid=a30402000000&bid=0030. Accessed March10, 2020..
- 31.Luo C, Yao L, Zhang L, et al. Possible Transmission of Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2) in a Public Bath Center in Huai’an, Jiangsu Province, China. JAMA Netw Open. 2020;3(3):e204583. doi: 10.1001/jamanetworkopen.2020.4583 [DOI] [PubMed] [Google Scholar]
- 32.Ghinai I, Woods S, Ritger KA, et al. Community Transmission of SARS-CoV-2 at Two Family Gatherings - Chicago, Illinois, February-March 2020. MMWR Morb Mortal Wkly Rep. 2020;69(15):446–450. doi: 10.15585/mmwr.mm6915e1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.The State Council of PRC. Inquiry of COVID-19 risk level (in Chinese); 2020. Available from: http://bmfw.www.gov.cn/yqfxdjcx/index.html. Accessed July20, 2020..
- 34.CCTV. Shanghai: GDP achieved positive growth in the second quarter, and the economy is picking up; 2020. Available from: http://news.cctv.com/2020/08/03/ARTISnjBDGFmJOSMCwe0GUt7200803.shtml. Accessed August4, 2020..
- 35.The Johns Hopkins Coronavirus Resource Center (CRC). The Johns Hopkins COVID-19 United States Cases; 2020. Available from: https://coronavirus.jhu.edu/map.html. Accessed July20, 2020..
- 36.Kissler SM, Tedijanto C, Goldstein E, Grad YH, Lipsitch M. Projecting the transmission dynamics of SARS-CoV-2 through the post-pandemic period. Science. 2020;368(6493):860–868. doi: 10.1126/science.abb5793 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Xu X, Wang S, Dong J, Shen Z, Xu S. An analysis of the domestic resumption of social production and life under the COVID-19 epidemic. PLoS One. 2020;15(7):e0236387. doi: 10.1371/journal.pone.0236387 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Barnes M, Sax PE. Challenges of “Return to Work” in an Ongoing Pandemic. N Engl J Med. 2020;10:1056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Noorbhai H. A mathematical model to guide the re-opening of economies during the COVID-19 pandemic. Ann Med Surg. 2020;57:5–6. doi: 10.1016/j.amsu.2020.06.041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Shaw WS, Main CJ, Findley PA, Collie A, Kristman VL, Gross DP. Opening the Workplace After COVID-19: what Lessons Can be Learned from Return-to-Work Research? J Occup Rehabil. 2020;30(3):299–302. doi: 10.1007/s10926-020-09908-9 [DOI] [PMC free article] [PubMed] [Google Scholar]