Abstract
The devastating impact of the ripple effect increases the importance of the reverse supply chain (RSC) design to ensure sustainability in the long-term. That being the case, in this study, a two-stage stochastic mixed-integer optimization model is proposed to design an RSC network under uncertainty sourcing from the ripple effect (i.e. external side of RSC) by considering the environmental and economic dimensions of sustainability. The environmental and economic disruptions of the ripple effect are represented by the increase in the carbon emission levels and the distance of roads, and the decrease in the capacity of facilities, respectively. Accordingly, a set of scenarios is considered based on the disruption levels (low- and high-impact) in case of the ripple effect. Furthermore, an -reliability constraint is integrated into the model to further analyze the occurrence of scenarios. The model allows us to make integrated operational and strategic decisions by placing an emphasis on the carbon emission levels (i.e. environmental dimension) and the total cost (i.e. economic dimension). To obtain some remarkable insights, the proposed model is validated through computational experiments based on data extracted from a real case. The computational results show that the ripple effect increases the emission level and total cost up to 40%. For this reason, it suggested that the regulations regarding WEEE (Waste Electrical and Electronic Equipment) should be prepared by considering sustainability in the entire RSC network. Besides, it is realized that the centralized distribution strategy leads to a more resilient RSC network design.
Keywords: Ripple effect, Reverse supply chain (RSC), Two-stage stochastic optimization
Highlights
-
•
The reverse supply chain design problem is explored for the ripple effect.
-
•
A two-stage stochastic optimization problem is developed.
-
•
The α-reliability approach is employed in the model.
-
•
A set of scenarios for the ripple effect is considered.
-
•
An industrial application is realized in the context of the ripple effect.
1. Introduction
There are some factors, such as legislation for recycling, ripple effect, awareness of environmental protection, and carbon policies shaped the way organizations operate their reverse supply chains (RSC). Over the last few decades, companies have invested in recovering processes to become sustainable, thereby; it motivates them to construct both efficient and responsive networks (Easwaran and Üster, 2010; Yılmaz, 2020a). Meanwhile, the RSC management from different perspectives has gained much attention (Mokhtar et al., 2019; Kushwaha et al., 2020).
RSC management is defined as a process for recovering products collected from end-users and disassembling them in an environmentally responsible way (Doan et al., 2019). Considering the fact that a triple bottom line approach (i.e. environmental, social, and economic) is adapted to sustainability (Ahi and Searcy, 2013), the RSC management becomes one of the most crucial topics considering the sustainability. With that in mind, there is a need for a systematic approach for putting environmental and economic concerns into practice regarding resilient RSC design (Mutingi, 2014). Such an RSC design with its integrated location and distribution decisions is more resilient and cost-effective than the traditional design approach in case of the ripple effect. Because the proper planning of this process considering the ripple effect is of great importance to fully realize the functions of RSC, in this study, environmental and economic dimensions of sustainability are taken into consideration.
The ripple effect, also known as risk propagation, is a phenomenon attracting attention from both scholars and practitioners due to the vulnerability of SCs. It is described as a sudden disruption at one or more points in (R)SC, which can greatly damage the remaining parts of the network in the long-term (Wang and Chen, 2020; Li and Zobel, 2020). Operational shutdowns can occur after the ripple effect because of various risks, such as earthquakes, floods, political decisions, terrorist attacks, health issues, disease, etc. (Ivanov, 2017a, 2017b, 2018). For instance, the transition between European and Middle Eastern countries is halted in 2020 due to Coronavirus (COVID-19) and the enterprises are faced with challenges while ensuring sustainability across the (R)SC. On one hand, from the RSC perspective, because of its design complexity and the difficulty of predicting the ripple effect, one or more stages of the RSC can be affected considerably (Dolgui et al., 2018; Ivanov, 2019a). Thereby, the RSC design may need to reconstruct in case of disruptions caused by the ripple effect (Gianesello et al., 2017; Ivanov, 2019b). Fig. 1 represents the stages of a ripple effect for two different disruption levels (low- and high-impact), in each of which the first three stages require a proactive strategy, whilst the fourth stage necessitates a reactive strategy. In this study, each disruption level is considered through a set of scenarios to gain more remarkable insights. For each level, a proactive strategy is considered by focusing on the first three stages to provide an ability to RSC to resist the devastating impact of the ripple effect and rapid recovery after the disruption. On the other hand, from an environmental perspective, the global CO2 emission is increased by 20% and 22% due to the main transportation activities in (R)SC (Budiman and Rau, 2019). On top of that, the ripple effect also leads to a negative impact on environmental pollution, since it destructs a well-developed (R)SC network. As seen from this dimension, while designing an RSC, consideration of the ripple effect is also important regarding the emission levels.
Fig. 1.
The stages of ripple effect on SC performance for two different cases: low-impact and high-impact.
Because the ripple effect is one of the striking issues, many studies have been focused on the ripple effect, disruptions, and resilience topics (See: Dolgui et al., 2018; Hosseini et al., 2019c). In this regard, a comprehensive literature matrix is presented in Table 1 to demonstrate the differences between the studies in the existing literature by highlighting two-way information: (i) the studies regarding RSC design (ii) the studies regarding the ripple effect on all types of SC.
Table 1.
The classification of studies according to the employed techniques.
(SC: Supply Chain - RSC: Reverse Supply Chain - CSC: Closed-loop Supply Chain - RE/D: Ripple Effect/Disruption - SM: Simulation Model - DOM: Deterministic Optimization Model -SOM: Stochastic Optimization Model - FM: Fuzzy Methods - ROM: Robust Optimization Model).
As seen from Table 1, the majority of the studies have focused on the uncertainties in RSC design. One of the most challenging issues in R(SC) management in the presence of the ripple effect is to cope with the uncertainty caused by the unpredictable disruptions and complex structure inherent of R(SC) (Sheffi and Rice, 2005). That being the case, the studies employing stochastic, robust, and fuzzy techniques rather than deterministic ones come into prominence (Rezapour et al., 2017; Kamalahmadi and Mellat-Parast, 2016). Besides, when considering the ripple effect, most of the studies have focused on the design of SC rather than RSC by employing many different techniques (Pavlov et al., 2018; Zhang et al., 2019).
In this study, the motivation behind employing stochastic programming comes from the ripple effect experienced in (R)SC. When relatively important situations are considered simultaneously, the stochastic programming can easily take disruptions into account thanks to scenario-based modeling (Sawik, 2016; Oksuz and Satoglu, 2020). There are also other techniques to solve problems involving uncertainty, such as robust programming and fuzzy optimization (Lim et al., 2013; Hasani and Khosrojerdi, 2016; Dolgui et al., 2020). Despite the several benefits of the robust programming, it directly focuses on the worst-case analysis, and all computations are carried out based on the corresponding scenario (Bertsimas and Sim, 2004; Schmitt et al., 2017; Ivanov et al., 2019). On the other hand, fuzzy optimization can prevent taking some important cases into account regarding the ripple effect (Samani and Hosseini-Motlagh, 2019; Özçelik et al., 2020). Therefore, aside from robust or fuzzy optimization, using a more comprehensive technique is essential to provide integrated operational and strategic decisions for RSC by considering most commonly encountered disruption threats at the same time through a set of scenarios. To this end, it is decided to employ the two-stage stochastic programming technique to ensure the sustainability of RSC and mitigate the consequences of the ripple effect. (For deep reviews regarding stochastic methods, consider the studies conducted by Khaloie et al., 2019; Khaloie et al., 2020a. For the implementation of stochastic methods to the supply chain, consider the studies performed by Cui et al., 2017; Cui et al., 2020a. On the other hand, for solving large-sized problems, consider the studies conducted by Cui et al., 2020b; Cui et al., 2020c. Further, for multi-stage stochastic approaches and fuzzy techniques, consider the studies carried out by Khaloie et al., 2020b; Khaloie et al., 2020c).
From Table 1, it is revealed that the impact of the ripple effect on RSC performance is less studied compared to SC. In this study, the ripple effect is included in the model for RSC with a set of scenarios considering possible disruptions on the roads and the capacities of collection centers. In the framework of the proposed two-stage stochastic model, the first stage is related to the location decisions (i.e. here-and-now), while the second stage considers the distribution decisions (i.e. wait-and-see). Besides, an -reliability constraint is used to ensure that the end-of-life products are returned to the primary collection centers according to a pre-determined rate. In the existing literature, there are several studies employing the -reliability constraint for the sensitivity analysis as in this study. (For further investigation considering -reliability, also known as chance constraint, we refer to the studies conducted by Taleizadeh et al., 2012; Oksuz and Satoglu, 2020; Ugranlı, 2020. Thanks to this constraint, sensitivity analysis can be performed in these studies to analyze the influence of service levels on the performance indicators.)
Being thus motivated, in this study, the following research questions are considered to be answered by solving the proposed optimization model. By doing so, further knowledge is gained regarding the RSC design in the context of the ripple effect from a variety of different perspectives.
-
-
How do strategic and operational decisions mitigate the impact of the ripple effect on RSC?
-
-
How does the ripple effect affect RSC performance in terms of responsiveness and efficiency?
-
-
How does the ripple effect affect the sustainability of RSC from economic and environmental dimensions?
The key contributions of this study are highlighted as follows. (I) From the theoretical perspective, it is the first time that the RSC design is considered through a two-stage stochastic optimization model to deal with the uncertainty caused by the ripple effect (i.e. the external side of the RSC). The minimization of the overall cost is determined as the objective function to focus on the economic dimension of sustainability. Additionally, the environmental dimension of sustainability is taken into consideration through model constraints to achieve long-term carbon emission reduction. (II) As for the managerial perspective, extensive-tested experiments are conducted by considering the northern region of Turkey. To this end, a set of scenarios is constructed to analyze the impact of the ripple effect on the RSC performance in terms of the total cost and the emission levels. Furthermore, we focused on service levels and different cases for sensitivity analysis from the point of disruption levels, and thus several key findings and managerial insights are obtained. Therefore, this study intends to create a framework for the academicians and practitioners focusing on RSC design in the presence of the ripple effect.
The rest of the study is structured as follows. The two-stage stochastic mixed-integer optimization model is presented to formulate the problem after the problem description is explained in Section 2. The computational experiments along with the results are presented in Section 3. The concluding remarks and future research directions are presented in Section 4.
2. Problem description and model formulation
2.1. Problem statement
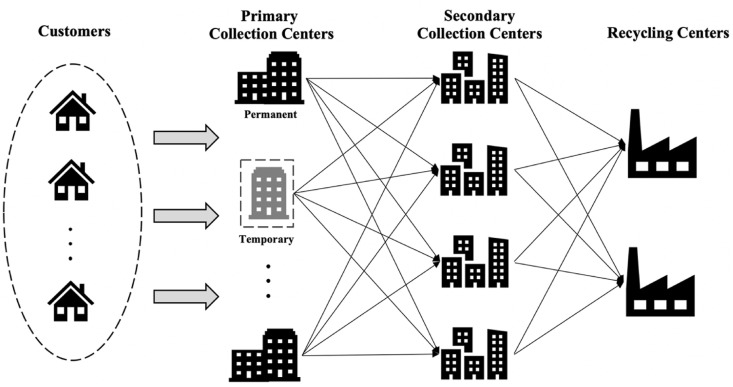
Formally, the addressed problem can be stated as follows: there are sets of , , and centers, i.e. primary collection, secondary collection, and recycling centers respectively. There are different product types and each of which must be collected through the collection centers. The possible disruptions caused by the ripple effect are represented by the set of S scenarios. The RSC network is comprised of three main stages. While the collection and transportation activities are realized in the first two stages, the recycling processes are performed in the facilities in the third stage. In the first stage of the RSC network, there are groups of and () primary collection centers, i.e. permanent and temporary facilities respectively. The permanent collection centers are employed to meet the requirement under normal circumstances. The temporary centers are considered to be served in case of the ripple effect. In such an environment, as the impact of the ripple effect increases, the number of temporary centers is expected to increase so as to satisfy the pre-determined service level. In the second stage, after the end-of-life products are collected from the end-users at primary centers, they are delivered to the secondary collection centers where the products are divided into batches and then sent to the recycling facilities. Finally, in the third stage, the recycling processes on the products are carried out in the recycling centers. The emission levels are affected not only by the transportation activities across the RSC but also recovering processes in recycling centers. The objective is to minimize the overall cost by considering the set of constraints.
In order to gain a better understating of the addressed problem, the representation of the considered RSC network is shown in Fig. 2 .
Fig. 2.
The visualization of considered RSC network.
The model is formulated under the following key assumptions which are also made in the study conducted by Özçelik et al. (2020).
Assumptions:
-
-
All collected end-of-life products are recovered in the recycling centers.
-
-
One year is considered to be a planning period.
-
-
Both distances and collection center capacities are affected by the ripple effect.
-
-
All temporary facilities are considered to be identical.
In section 2.2, the formulated optimization model is represented.
2.2. Optimization model
In this study, a two-stage stochastic mixed-integer optimization model is fundamentally proposed to minimize the total cost with the aim of designing a resilient RSC network in case of the ripple effect. The optimization model ensures that the emission levels are under control during the transportation and recovery processes. Further, -reliability constraints are included in the model to address the service levels. In doing so, the model becomes more sensitive to the changes in the regulations imposed by the government. The proposed model is tested through the computational experiments generated based on the data from a company recovering household appliances.
Nonetheless, the optimization model has some limitations: (i) the model does not allow considering more than one objective simultaneously, it only involves the total cost incurred in the RSC, and (ii) each route across the RSC network is defined independently. In order to handle the possible limitations of the model, in the first place, a multi-objective model can be developed, and an approach can be implemented to obtain the optimal or near-optimal Pareto-front. Moreover, all possible route combinations can be considered; however, it can cause some unrealistic circumstances.
In the following, the proposed stochastic optimization model is presented after the information is provided regarding the model.
Indices and sets
: index defined for the primary collection center
: index defined for the secondary collection center
: index defined for the recycling center
: index defined for the product type
: possible scenarios
set of temporary primary collection centers
set of permanent primary collection centers
set of primary collection centers
set of secondary collection centers
set of recycling centers
set of products
set of scenarios
Parameters
the distance from the collection center to the collection center
the distance from the collection center to the collection center
the fixed facility opening cost of the temporary collection center
the number of product bought by the customer in the previous planning period
: the percentage of the product which must be collected due to the regulations
the volume of the product
the capacity of the collection center in the current planning period
the capacity of the collection center in the current planning period
the capacity of the recycling center in the current planning period
the amount of carbon emission due to the transportation for per km (gram)
the amount of emission stem due to the recycling operations for per unit of product
the pre-determined target emission level (gram)
the fuel cost for per km
the number of available temporary primary collection centers in the current planning period
the distance increase ratio between the and the facilities in the scenario
the distance increase ratio between the and the facilities in the scenario
the capacity decrease ratio of the facility in the scenario
the capacity decrease ratio of the facility in the scenario
the capacity decrease ratio of the facility in the scenario
the occurrence probability of the scenario
reliability (service) level
a large number
First stage decision variables
1, if the facility is opened in the first stage, and 0, otherwise
Second stage decision variables
the number of transported products from the facility to the facility in the scenario
the number of transported products from the facility to the facility in the scenario
1, if the product is transported from the facility to the facility in the scenario by satisfying the legal limits, and 0, otherwise
Two-stage stochastic optimization model
Objective function
| (1) |
where
| (2) |
Equation (1) is the objective function, minimizing the overall cost associated with the opening cost of temporary facilities, and the expected total transportation cost, given in Equation (2), under the disruption possibility of the distances between the facilities. In the model, the reason behind why temporary collection centers can be employed is to implement a proactive strategy for the rapid response to the ripple effect. On the other side, , called as expected recourse function, is another part of the objective function and associates with the random vector consisting of uncertain data based on the scenarios. As known, where represents the occurrence probability of the scenario.
First stage constraints
| (3) |
Constraint set (3) guarantees that the number of temporary primary collection centers to be opened cannot exceed the number of available temporary primary collection centers in the current planning period.
First stage decision variables
| (4) |
Constraint set (4) represents the here-and-now decisions and relates to the binary decision variables in the first stage. denotes whether the temporary primary collection center is opened or not.
Second stage constraints
| (5) |
Constraint set (5) states that the CO2 emission amount caused by transportation and recycling activities cannot exceed the mandatory limit.
| (6) |
| (7) |
| (8) |
| (9) |
Constraint sets (6)–(9) are employed to control capacities by considering the capacity loss caused by disruptions in each scenario. Here, whilst constraint sets (6) and (7) implies that the total number of products delivered from the permanent primary collection center to the secondary collection center for the product cannot exceed the capacities of the and facilities respectively. Constraint set (8) ensures that the total number of products transported from secondary collection center to recycling center for the product cannot exceed the capacity of the facility. Similarly, Constraint set (9) guarantees that the total number of products delivered from the temporary primary collection center to the secondary collection center for the product cannot exceed the capacity of the facility if the temporary primary collection center is used.
| (10) |
Constraint set (10) is used to balance the number of delivered products between the stages on the RSC network, thereby; it prevents the products to be handled in the secondary collection center.
Chance constraints (-reliability)
The chance-constraints are added to ensure a certain service level in the presence of the ripple effect. In other words, the main reason for adopting the -reliability constraint in the developed model is to analyze the impact of various service levels on the system performance in terms of the operational cost and CO2 emission amounts. The -reliability approach, also known as chance constraint, was first presented by Daskin et al. (1997) for the facility location problem. Since then, it has been applied to SC design studies (Oksuz and Satoglu, 2020).
| (11) |
| (12) |
| (13) |
Constraint set (11) denotes the reliability of the system and ensures that the pre-determined -reliability level is satisfied by considering the scenarios. The -reliability level is satisfied by summing the occurrence probability of scenarios. A higher service level means more scenarios are addressed. Constraint sets (12) and (13) are either/or constraints and reveal that the service is provided or not. These constraints guarantee that the collected products are recovered by meeting the mandatory limit for each product and scenario. In other words, the scenario is included to the reliability set, if the product p is delivered from the facility to the facility by satisfying the limit.
Second stage decision variables
| (14) |
| (15) |
| (16) |
Constraint sets (14)–(16) represent the wait-and-see decisions. Constraint sets (14) define a binary decision variable indicating whether the scenario is included or not. Constraint sets (15) and (16) imply the nonnegativity for integer decision variables.
The optimization model including both stages is coded together by using CPLEX solver. The problems are solved by running the solver repeatedly for different parameter values. Since the problems at hand are not large-scale, the optimal solutions are obtained in seconds. However, heuristics methods can be implemented to cope with the difficulties in solving large-scale problems. To this end, single- or population-based metaheuristics (Ma and Li, 2018; Nikzad et al., 2019), scenario-based heuristics (Liu et al., 2019), and other problem-specific heuristics can be employed.
3. Computational experiments
3.1. Background of the real application case
In order to investigate the impact of the ripple effect on the RSC network design, the computational experiments are performed based on the data extracted from a company recovering household appliances. The company collects the end-of-life products all across Turkey to fulfill the strict requirements regarding WEEE (Waste Electrical and Electronic Equipment) obligated by the legislations. However, in this study, the collection of products is considered only for the northern region of Turkey (i.e. Black Sea region) due to heavy precipitation. The Black Sea region has a rough and steep topography. For this reason, heavy precipitation can cause floods and thereby landslide formation in this region (Özçelik et al., 2020).
The occurrence of flood and landslide (i.e. ripple effect) in the region has become more frequent over the last years. It causes disruptions on the roads and facilities. Fig. 3 represents an example of the ripple effect situation that occurred in the region.
Fig. 3.
The real ripple effect visualizations from the considered region (Özçelik et al., 2020).
In section 4.2, the experimental settings are provided.
3.2. Experimental settings
In this section, experimental settings are determined by considering the Northern region of Turkey. To develop a resilient RSC network in case of the ripple effect, all possible disruption scenarios should be considered while formulating the problem. Therefore, the proposed two-stage stochastic optimization model is validated by considering 27 different scenarios, including no disaster case.
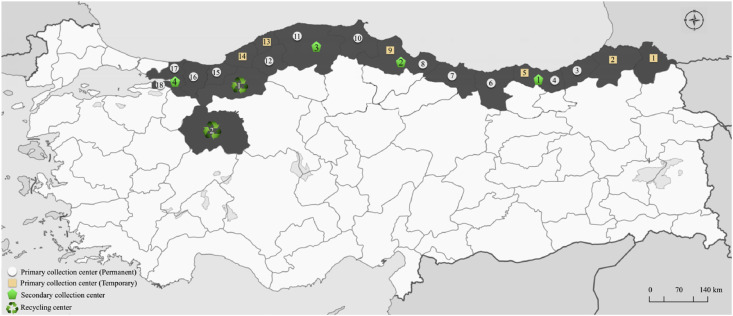
Fig. 4 shows the region considered within the context of the study, in which primary collection centers, secondary collection centers, and recycling centers are highlighted in distinctive symbols.
Fig. 4.
The visualization of the considered region in the industrial application.
As can be seen from Fig. 4, there are 18 different primary collection centers and six of them are candidate centers that can be employed in case of a disaster, i.e. temporary centers shown in the square. Similarly, 12 of them are permanent collection centers shown in the circle. There are four different secondary collection centers in the network, which are used to collect the end-of-life products transported from the primary collection centers. Lastly, the network has two different recycling centers for the recovering process of the products.
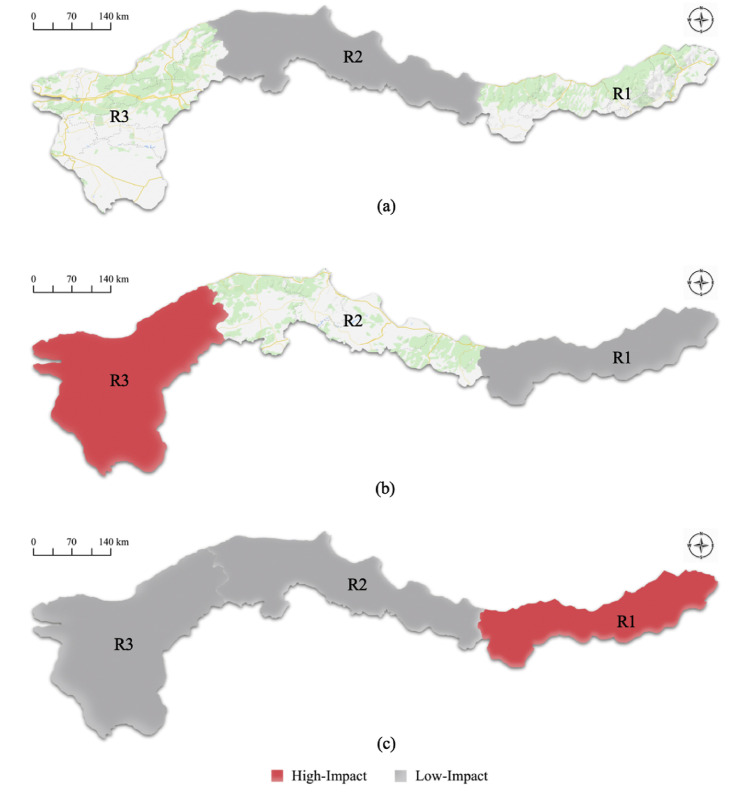
Because analyzing the impact of the ripple effect on the considered network is a major concern of the study, the scenarios are developed by considering all possible combinations of the disruption levels on the sub-regions. To generate the different disruption scenarios, the northern region of Turkey is divided into three different sub-regions, namely R1, R2, and R3, and each of which is accepted to be influenced by the ripple effect independently from each other. The occurrence probabilities are obtained from historical data of disasters in the region and vary from 0.01 to 0.07 (See: Table 2 ) to address the uncertainty regarding the scenarios generated based on two main disruption levels (low- and high-impact). As an example, the disruption levels on the areas are illustrated in Fig. 5 , in which (a), (b), and (c) correspond to the “low-impact on R2”, “high-impact on R3 and low-impact on R1”, and “low-impact on R2-R3 and high-impact on R1”, respectively.
Table 2.
The parameter values for scenarios (considered for Case 1).
Fig. 5.
The visualization of some scenarios regarding disruption levels in terms of low- and high-impact in case of the ripple effect: (a) scenario 2, (b) scenario 13, and (c) scenario 22.
When the disaster occurs, the distances between facilities and the facility capacities are affected. Thus, using increase ratios for the distances and capacities is plausible to represent the influence of the ripple effect on the network. The key parameters used in the industrial application are given in Table 2. Other parameter values are presented in Yılmaz (2020b).
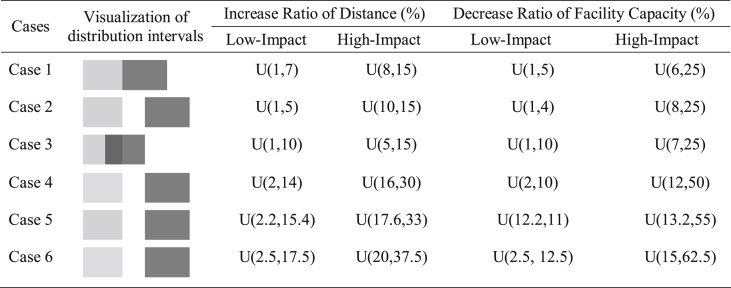
Six different cases, including extraordinary situations, are considered for all scenarios to specify the distance and capacity increase/damage ratios to better explain the importance of strategic decisions on the RSC performance. When different cases are implemented regarding the damage ratios, it becomes easier to evaluate the responsiveness of RSC. The damage ratio intervals for each case are indicated in Table 3 . Accordingly, the ratios are randomly generated with a continuous uniform distribution from these intervals.
Table 3.
The parameter values represent the disruption levels with respect to cases.
The cases differ from each other in terms of the determined distribution intervals for damage ratios. For case 1, the intervals are determined close to each other for the low- and high-impact levels in case of the ripple effect. It indicates that the impacts of disruption levels are different but close to each other. For case 2, the limits of intervals are specified to make a strict distinction between the low- and high-impact levels. On the contrary, for case 3, the intervals are considered to be intertwined with each other to represent that there is not a significant difference between the low- and high-impact levels.
On top of that, extraordinary situations may cause more destructive effects on the facilities’ capacities and distances between the facilities. Such challenging situations can hamper the feasibility of the solutions obtained from the proposed model. Therefore, extraordinary situations are included in experimental settings to obtain generalized results. Cases 4–6 represent extraordinary situations and have a stronger destructive impact than cases 1–3 (See: Table 3).
3.3. Computational results
The computational experiments are conducted to analyze the influence of the ripple effect on the performance indicators by focusing the interaction with other factors such as the service level and damage ratios (See: Table 2). The optimization model is coded by using GAMS® 23.6/CPLEX solver on a personal computer with 2.4 GHz Intel(R) Core™ i7-3630QM CPU and 16 GB of RAM. The addressed problem is solved through different parameter values for the sensitivity analysis, thereby 30 runs are performed with the CPLEX solver. All optimal results are achieved in seconds.
Table 4 reports the computational results for different cases in terms of the objective function values, the total number of temporary facilities, expected emission levels, and CPU times (in seconds). The last column of Table 4 represents the tractability of the proposed model.
Table 4.
The summary of computational results for cases 1–3 with respect to -reliability levels.
| α-levels | OFV | TNF | TNTF | EEL | CPU timea | |
|---|---|---|---|---|---|---|
| Case 1 | α = 0.80 | 1980.99 | 14 | 2 | 170.48 | 21.05 |
| α = 0.85 | 2108.25 | 14 | 2 | 182.12 | 21.50 | |
| α = 0.90 | 2236.53 | 14 | 2 | 193.85 | 22.30 | |
| α = 0.95 | 2364.76 | 15 | 3 | 200.18 | 20.15 | |
| α = 0.99 |
2471.34 |
15 |
3 |
209.92 |
21.03 |
|
| Case 2 | α = 0.80 | 1964.81 | 14 | 2 | 169.03 | 24.23 |
| α = 0.85 | 2089.29 | 14 | 2 | 180.41 | 21.54 | |
| α = 0.90 | 2215.83 | 14 | 2 | 191.99 | 22.24 | |
| α = 0.95 | 2347.34 | 15 | 3 | 198.62 | 25.29 | |
| α = 0.99 |
2453.79 |
15 |
3 |
208.35 |
19.39 |
|
| Case 3 | α = 0.80 | 1993.86 | 14 | 2 | 171.64 | 21.51 |
| α = 0.85 | 2120.80 | 14 | 2 | 183.25 | 21.18 | |
| α = 0.90 | 2250.40 | 14 | 2 | 195.10 | 20.24 | |
| α = 0.95 | 2384.24 | 15 | 3 | 201.93 | 19.15 | |
| α = 0.99 | 2549.18 | 16 | 4 | 211.53 | 19.44 | |
OFV: Objective Function Value.
TNF: Total Number of Facilities.
TNTF: Total Number of Opened Temporary Facilities.
EEL: The Expected Emission Level.
CPU Time in Seconds.
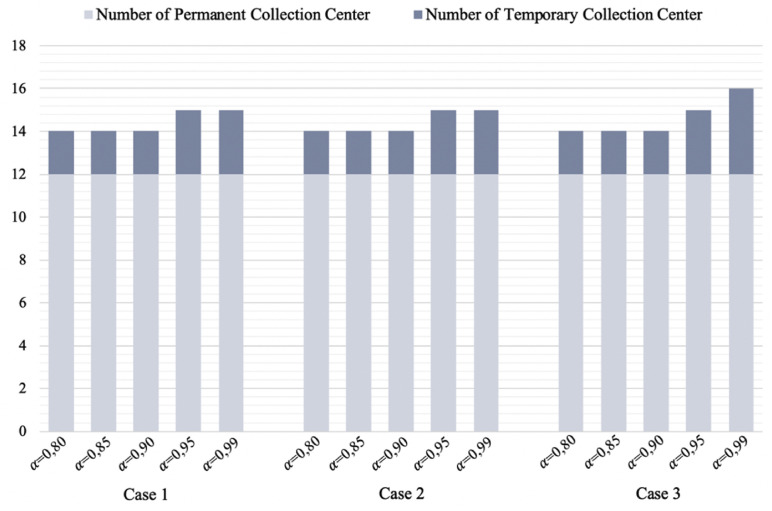
From Table 4, it is deduced that a decrease in -reliability levels leads to better results in terms of the objective function values and expected emission levels for each case. A similar trend is also observed for the total number of temporary facilities. The change in total number of temporary facilities with respect to service levels for cases 1–3 is visualized in Fig. 6 .
Fig. 6.
The visualization of the total number of facilities with respect to -reliability levels.
When the service level varies from 80% to 90%, the total number of temporary facilities is equal to two for cases 1–3. On the other side, when the service level varies from 95% to 99%, the total number of temporary facilities is equal to three, except for in case 3 (See: Table 4 and Fig. 6). The reason behind the exception is that the transportation cost is larger than the facility utilization cost for case 3, thus; opening a facility is plausible to decrease the overall cost.
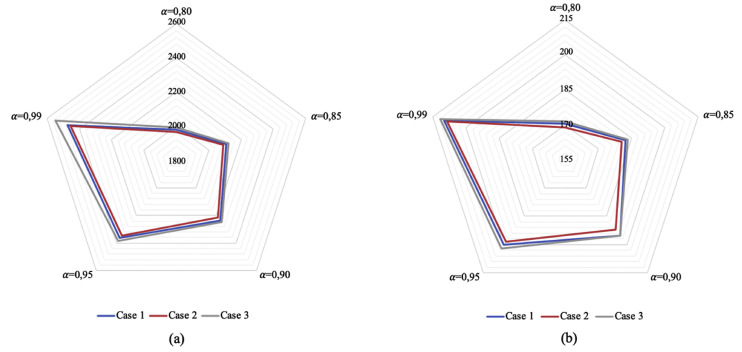
Fig. 7 reveals the change in the objective function and emission level values along with the service levels for each case simultaneously, in which (a) and (b) correspond to the overall cost and emission levels respectively. In this figure, each case is represented by a different color so as to perform the sensitivity analysis considering all service levels.
Fig. 7.
(a) The overall costs and (b) expected emission amounts for each case with respect to -reliability levels.
According to Fig. 7, despite there is not a considerable difference between cases in terms of the total cost and emission levels, changes in service levels have remarkable effects on the results which slightly differ at higher service levels. It can be seen from Fig. 7, as for the disruption level aspect, the worst results are obtained for case 3, in which there is not a strict difference between the low- and high-impact levels (i.e. intertwined intervals). That is why the RSC system design becomes more important when the low and high disruption levels show a similar impact in the presence of the ripple effect. On the basis of the computational analysis, it can be concluded that a change in the reliability level results in not only changes in the overall cost, but also the emission levels in the entire RSC.
Table 5, Table 6, Table 7 present all results regarding the emission levels and the amount of the collected products from the sub-regions (i.e. R1, R2, and R3) for each scenario with respect to each -level. In these tables, the scenarios, which do not affect the results, are represented by zero. For case 1, the total numbers of considered scenarios are 18, 21, 21, 25, and 26 for -levels 0.80, 0.85, 0.90, 0.95, and 0.99 respectively. For case 2, the total numbers of considered scenarios are 18, 20, 22, 25, and 26 for all -levels respectively. For case 3, the total numbers of considered scenarios are 18, 20, 22, 23, and 26 for all -levels respectively. For case 1, while the amount of emission varies between 192.63 and 246.36, the R1, R2, and R3 are in the range of 183–475, 561 to 789, 832 to 1028. For case 2, while the amount of emission varies between 192.63 and 252.18, the R1, R2, and R3 are in the range of 183–522, 585 to 789, 836 to 1028. For case 3, while the amount of emission varies between 192.63 and 245.26, the R1, R2, and R3 are in the range of 183–471, 576 to 789, 820 to 1028.
Table 5.
The computational results for case 1.
| Scenarios | Case 1 |
|||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| α = 0.80 |
α = 0.85 |
α = 0.90 |
α = 0.95 |
α = 0.99 |
||||||||||||||||
| Emission | R1 | R2 | R3 | Emission | R1 | R2 | R3 | Emission | R1 | R2 | R3 | Emission | R1 | R2 | R3 | Emission | R1 | R2 | R3 | |
| S1 | 202.62 | 258 | 714 | 1028 | 202.62 | 258 | 714 | 1028 | 202.62 | 258 | 714 | 1028 | 195.07 | 183 | 789 | 1028 | 195.07 | 183 | 789 | 1028 |
| S2 | 199.43 | 258 | 714 | 1028 | 199.43 | 258 | 714 | 1028 | 199.43 | 258 | 714 | 1028 | 193.32 | 183 | 789 | 1028 | 193.32 | 183 | 789 | 1028 |
| S3 | 216.70 | 331 | 641 | 1028 | 216.70 | 331 | 641 | 1028 | 216.70 | 331 | 641 | 1028 | 212.77 | 261 | 711 | 1028 | 212.77 | 261 | 711 | 1028 |
| S4 | 204.78 | 279 | 693 | 1028 | 204.78 | 279 | 693 | 1028 | 204.78 | 279 | 693 | 1028 | 200.20 | 208 | 764 | 1028 | 200.20 | 208 | 764 | 1028 |
| S5 | 227.22 | 434 | 714 | 852 | 227.22 | 434 | 714 | 852 | 227.22 | 434 | 714 | 852 | 221.03 | 359 | 789 | 852 | 221.03 | 359 | 789 | 852 |
| S6 | 205.74 | 304 | 714 | 982 | 205.74 | 304 | 714 | 982 | 205.74 | 304 | 714 | 982 | 200.30 | 229 | 789 | 982 | 200.30 | 229 | 789 | 982 |
| S7 | 230.61 | 401 | 571 | 1028 | 230.61 | 401 | 571 | 1028 | 230.61 | 401 | 571 | 1028 | 225.02 | 342 | 630 | 1028 | 225.02 | 342 | 630 | 1028 |
| S8 | 209.64 | 282 | 690 | 1028 | 209.64 | 282 | 690 | 1028 | 209.64 | 282 | 690 | 1028 | 202.86 | 210 | 762 | 1028 | 202.86 | 210 | 762 | 1028 |
| S9 | 223.42 | 400 | 572 | 1028 | 223.42 | 400 | 572 | 1028 | 223.42 | 400 | 572 | 1028 | 218.59 | 341 | 631 | 1028 | 218.59 | 341 | 631 | 1028 |
| S10 | 207.78 | 282 | 690 | 1028 | 207.78 | 282 | 690 | 1028 | 207.78 | 282 | 690 | 1028 | 202.19 | 210 | 762 | 1028 | 202.19 | 210 | 762 | 1028 |
| S11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 234.33 | 412 | 714 | 874 | 225.69 | 337 | 789 | 874 | 225.69 | 337 | 789 | 874 |
| S12 | 208.63 | 284 | 714 | 1002 | 208.63 | 284 | 714 | 1002 | 208.63 | 284 | 714 | 1002 | 201.23 | 209 | 789 | 1002 | 201.23 | 209 | 789 | 1002 |
| S13 | 231.53 | 439 | 714 | 847 | 231.53 | 439 | 714 | 847 | 231.53 | 439 | 714 | 847 | 224.22 | 364 | 789 | 847 | 224.22 | 364 | 789 | 847 |
| S14 | 207.48 | 298 | 714 | 988 | 207.48 | 298 | 714 | 988 | 207.48 | 298 | 714 | 988 | 201.59 | 223 | 789 | 988 | 201.59 | 223 | 789 | 988 |
| S15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 243.50 | 475 | 667 | 858 |
| S16 | 227.58 | 434 | 561 | 1005 | 227.58 | 434 | 561 | 1005 | 227.58 | 434 | 561 | 1005 | 223.34 | 371 | 624 | 1005 | 223.34 | 371 | 624 | 1005 |
| S17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 235.22 | 469 | 687 | 844 | 229.48 | 396 | 760 | 844 | 229.48 | 396 | 760 | 844 |
| S18 | 212.17 | 328 | 685 | 987 | 212.17 | 328 | 685 | 987 | 212.17 | 328 | 685 | 987 | 207.27 | 255 | 758 | 987 | 207.27 | 255 | 758 | 987 |
| S19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 246.36 | 405 | 725 | 870 | 246.36 | 405 | 725 | 870 |
| S20 | 0 | 0 | 0 | 0 | 229.40 | 380 | 627 | 993 | 229.40 | 380 | 627 | 993 | 223.78 | 316 | 691 | 993 | 223.78 | 316 | 691 | 993 |
| S21 | 0 | 0 | 0 | 0 | 237.37 | 423 | 694 | 883 | 0 | 0 | 0 | 0 | 229.83 | 352 | 765 | 883 | 229.83 | 352 | 765 | 883 |
| S22 | 219.08 | 310 | 696 | 994 | 219.08 | 310 | 696 | 994 | 219.08 | 310 | 696 | 994 | 212.88 | 238 | 768 | 994 | 212.88 | 238 | 768 | 994 |
| S23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| S24 | 0 | 0 | 0 | 0 | 230.36 | 427 | 577 | 996 | 0 | 0 | 0 | 0 | 225.56 | 368 | 636 | 996 | 225.56 | 368 | 636 | 996 |
| S25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 232.09 | 394 | 774 | 832 | 232.09 | 394 | 774 | 832 |
| S26 | 212.39 | 309 | 695 | 996 | 212.39 | 309 | 695 | 996 | 212.39 | 309 | 695 | 996 | 206.79 | 235 | 769 | 996 | 206.79 | 235 | 769 | 996 |
| S27 | 198.07 | 258 | 714 | 1028 | 198.07 | 258 | 714 | 1028 | 198.07 | 258 | 714 | 1028 | 192.63 | 183 | 789 | 1028 | 192.63 | 183 | 789 | 1028 |
R1: Sub-Region 1 R2: Sub-Region 2 R3: Sub-Region 3.
Table 6.
The computational results for case 2.
| Scenarios | Case 2 |
|||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| α = 0.80 |
α = 0.85 |
α = 0.90 |
α = 0.95 |
α = 0.99 |
||||||||||||||||
| Emission | R1 | R2 | R3 | Emission | R1 | R2 | R3 | Emission | R1 | R2 | R3 | Emission | R1 | R2 | R3 | Emission | R1 | R2 | R3 | |
| S1 | 203.10 | 258 | 714 | 1028 | 203.10 | 258 | 714 | 1028 | 203.10 | 258 | 714 | 1028 | 195.78 | 183 | 789 | 1028 | 195.78 | 183 | 789 | 1028 |
| S2 | 198.77 | 258 | 714 | 1028 | 198.77 | 258 | 714 | 1028 | 198.77 | 258 | 714 | 1028 | 193.04 | 183 | 789 | 1028 | 193.04 | 183 | 789 | 1028 |
| S3 | 218.14 | 343 | 629 | 1028 | 218.14 | 343 | 629 | 1028 | 218.14 | 343 | 629 | 1028 | 214.84 | 284 | 688 | 1028 | 214.84 | 284 | 688 | 1028 |
| S4 | 203.57 | 278 | 694 | 1028 | 203.57 | 278 | 694 | 1028 | 203.57 | 278 | 694 | 1028 | 198.77 | 206 | 766 | 1028 | 198.77 | 206 | 766 | 1028 |
| S5 | 0 | 0 | 0 | 0 | 228.05 | 431 | 714 | 855 | 228.05 | 431 | 714 | 855 | 221.89 | 356 | 789 | 855 | 221.89 | 356 | 789 | 855 |
| S6 | 203.23 | 284 | 714 | 1002 | 203.23 | 284 | 714 | 1002 | 203.23 | 284 | 714 | 1002 | 197.79 | 209 | 789 | 1002 | 197.79 | 209 | 789 | 1002 |
| S7 | 227.01 | 370 | 602 | 1028 | 227.01 | 370 | 602 | 1028 | 227.01 | 370 | 602 | 1028 | 221.59 | 307 | 665 | 1028 | 221.59 | 307 | 665 | 1028 |
| S8 | 208.60 | 277 | 695 | 1028 | 208.60 | 277 | 695 | 1028 | 208.60 | 277 | 695 | 1028 | 202.06 | 205 | 767 | 1028 | 202.06 | 205 | 767 | 1028 |
| S9 | 223.04 | 387 | 585 | 1028 | 223.04 | 387 | 585 | 1028 | 223.04 | 387 | 585 | 1028 | 218.40 | 319 | 653 | 1028 | 218.40 | 319 | 653 | 1028 |
| S10 | 203.53 | 279 | 693 | 1028 | 203.53 | 279 | 693 | 1028 | 203.53 | 279 | 693 | 1028 | 198.02 | 207 | 765 | 1028 | 198.02 | 207 | 765 | 1028 |
| S11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 231.85 | 405 | 714 | 881 | 223.79 | 330 | 789 | 881 | 223.79 | 330 | 789 | 881 |
| S12 | 208.77 | 281 | 714 | 1005 | 208.77 | 281 | 714 | 1005 | 208.77 | 281 | 714 | 1005 | 201.57 | 206 | 789 | 1005 | 201.57 | 206 | 789 | 1005 |
| S13 | 227.86 | 420 | 714 | 866 | 227.86 | 420 | 714 | 866 | 227.86 | 420 | 714 | 866 | 221.36 | 345 | 789 | 866 | 221.36 | 345 | 789 | 866 |
| S14 | 202.87 | 281 | 714 | 1005 | 202.87 | 281 | 714 | 1005 | 202.87 | 281 | 714 | 1005 | 197.12 | 206 | 789 | 1005 | 197.12 | 206 | 789 | 1005 |
| S15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 243.22 | 468 | 656 | 876 |
| S16 | 226.12 | 406 | 594 | 1000 | 226.12 | 406 | 594 | 1000 | 226.12 | 406 | 594 | 1000 | 222.20 | 345 | 655 | 1000 | 222.20 | 345 | 655 | 1000 |
| S17 | 227.51 | 414 | 698 | 888 | 227.51 | 414 | 698 | 888 | 227.51 | 414 | 698 | 888 | 222.05 | 341 | 771 | 888 | 222.05 | 341 | 771 | 888 |
| S18 | 206.28 | 306 | 691 | 1003 | 206.28 | 306 | 691 | 1003 | 206.28 | 306 | 691 | 1003 | 201.08 | 233 | 764 | 1003 | 201.08 | 233 | 764 | 1003 |
| S19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| S20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 227.58 | 352 | 651 | 997 | 227.58 | 352 | 651 | 997 |
| S21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 234.25 | 373 | 773 | 854 | 234.25 | 373 | 773 | 854 |
| S22 | 214.19 | 309 | 696 | 995 | 214.19 | 309 | 696 | 995 | 214.19 | 309 | 696 | 995 | 207.00 | 236 | 769 | 995 | 207.00 | 236 | 769 | 995 |
| S23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 252.18 | 522 | 642 | 836 | 252.18 | 522 | 642 | 836 |
| S24 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 230.04 | 406 | 592 | 1002 | 226.10 | 350 | 648 | 1002 | 226.10 | 350 | 648 | 1002 |
| S25 | 0 | 0 | 0 | 0 | 226.70 | 408 | 691 | 901 | 226.70 | 408 | 691 | 901 | 220.75 | 336 | 763 | 901 | 220.75 | 336 | 763 | 901 |
| S26 | 209.93 | 306 | 693 | 1001 | 209.93 | 306 | 693 | 1001 | 209.93 | 306 | 693 | 1001 | 204.49 | 234 | 765 | 1001 | 204.49 | 234 | 765 | 1001 |
| S27 | 198.07 | 258 | 714 | 1028 | 198.07 | 258 | 714 | 1028 | 198.07 | 258 | 714 | 1028 | 192.63 | 183 | 789 | 1028 | 192.63 | 183 | 789 | 1028 |
R1: Sub-Region 1 R2: Sub-Region 2 R3: Sub-Region 3.
Table 7.
The computational results for case 3.
| Scenarios | Case 3 |
|||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| α = 0.80 |
α = 0.85 |
α = 0.90 |
α = 0.95 |
α = 0.99 |
||||||||||||||||
| Emission | R1 | R2 | R3 | Emission | R1 | R2 | R3 | Emission | R1 | R2 | R3 | Emission | R1 | R2 | R3 | Emission | R1 | R2 | R3 | |
| S1 | 204.26 | 258 | 714 | 1028 | 204.26 | 258 | 714 | 1028 | 204.26 | 258 | 714 | 1028 | 196.61 | 183 | 789 | 1028 | 196.61 | 183 | 789 | 1028 |
| S2 | 199.02 | 258 | 714 | 1028 | 199.02 | 258 | 714 | 1028 | 199.02 | 258 | 714 | 1028 | 193.12 | 183 | 789 | 1028 | 193.12 | 183 | 789 | 1028 |
| S3 | 220.60 | 371 | 601 | 1028 | 220.60 | 371 | 601 | 1028 | 220.60 | 371 | 601 | 1028 | 217.15 | 312 | 660 | 1028 | 217.15 | 312 | 660 | 1028 |
| S4 | 205.75 | 300 | 672 | 1028 | 205.75 | 300 | 672 | 1028 | 205.75 | 300 | 672 | 1028 | 201.06 | 232 | 740 | 1028 | 201.06 | 232 | 740 | 1028 |
| S5 | 229.02 | 449 | 714 | 837 | 229.02 | 449 | 714 | 837 | 229.02 | 449 | 714 | 837 | 222.65 | 374 | 789 | 837 | 222.64 | 374 | 789 | 837 |
| S6 | 208.78 | 328 | 714 | 958 | 208.78 | 328 | 714 | 958 | 208.78 | 328 | 714 | 958 | 203.34 | 253 | 789 | 958 | 203.34 | 253 | 789 | 958 |
| S7 | 223.17 | 359 | 613 | 1028 | 223.17 | 359 | 613 | 1028 | 223.17 | 359 | 613 | 1028 | 217.74 | 294 | 678 | 1028 | 217.74 | 294 | 678 | 1028 |
| S8 | 209.41 | 294 | 678 | 1028 | 209.41 | 294 | 678 | 1028 | 209.41 | 294 | 678 | 1028 | 203.06 | 224 | 748 | 1028 | 203.06 | 224 | 748 | 1028 |
| S9 | 223.53 | 396 | 576 | 1028 | 223.53 | 396 | 576 | 1028 | 223.53 | 396 | 576 | 1028 | 218.53 | 335 | 637 | 1028 | 218.53 | 335 | 637 | 1028 |
| S10 | 208.75 | 294 | 678 | 1028 | 208.75 | 294 | 678 | 1028 | 208.75 | 294 | 678 | 1028 | 203.68 | 222 | 750 | 1028 | 203.68 | 222 | 750 | 1028 |
| S11 | 232.50 | 420 | 714 | 866 | 232.50 | 420 | 714 | 866 | 232.50 | 420 | 714 | 866 | 224.67 | 345 | 789 | 866 | 224.39 | 345 | 789 | 866 |
| S12 | 212.65 | 313 | 714 | 973 | 212.65 | 313 | 714 | 973 | 212.65 | 313 | 714 | 973 | 205.20 | 238 | 789 | 973 | 205.20 | 238 | 789 | 973 |
| S13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 235.01 | 466 | 714 | 820 | 228.01 | 391 | 789 | 820 | 227.62 | 391 | 789 | 820 |
| S14 | 213.22 | 314 | 714 | 972 | 213.22 | 314 | 714 | 972 | 213.22 | 314 | 714 | 972 | 206.43 | 239 | 789 | 972 | 206.43 | 239 | 789 | 972 |
| S15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 245.25 | 471 | 680 | 849 | 244.62 | 471 | 680 | 849 |
| S16 | 222.59 | 379 | 632 | 989 | 222.59 | 379 | 632 | 989 | 222.59 | 379 | 632 | 989 | 218.69 | 313 | 698 | 989 | 218.69 | 313 | 698 | 989 |
| S17 | 0 | 0 | 0 | 0 | 232.55 | 443 | 696 | 861 | 232.55 | 443 | 696 | 861 | 227.09 | 375 | 764 | 861 | 227.08 | 375 | 764 | 861 |
| S18 | 215.28 | 360 | 671 | 969 | 215.28 | 360 | 671 | 969 | 215.28 | 360 | 671 | 969 | 210.34 | 287 | 744 | 969 | 210.34 | 287 | 744 | 969 |
| S19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| S20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 233.23 | 365 | 694 | 941 | 232.73 | 365 | 694 | 941 |
| S21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 244.21 | 425 | 740 | 835 |
| S22 | 225.38 | 352 | 679 | 969 | 225.38 | 352 | 679 | 969 | 225.38 | 352 | 679 | 969 | 217.74 | 279 | 752 | 969 | 217.74 | 279 | 752 | 969 |
| S23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 239.02 | 439 | 682 | 879 |
| S24 | 0 | 0 | 0 | 0 | 230.86 | 425 | 609 | 966 | 230.86 | 425 | 609 | 966 | 226.02 | 362 | 672 | 966 | 225.85 | 362 | 672 | 966 |
| S25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 244.87 | 471 | 688 | 841 | 0 | 0 | 0 | 0 | 238.25 | 401 | 758 | 841 |
| S26 | 225.95 | 364 | 673 | 963 | 225.95 | 364 | 673 | 963 | 225.95 | 364 | 673 | 963 | 219.96 | 295 | 742 | 963 | 219.96 | 295 | 742 | 963 |
| S27 | 198.06 | 258 | 714 | 1028 | 198.06 | 258 | 714 | 1028 | 198.06 | 258 | 714 | 1028 | 192.63 | 183 | 789 | 1028 | 192.63 | 183 | 789 | 1028 |
R1: Sub-Region 1 R2: Sub-Region 2 R3: Sub-Region 3.
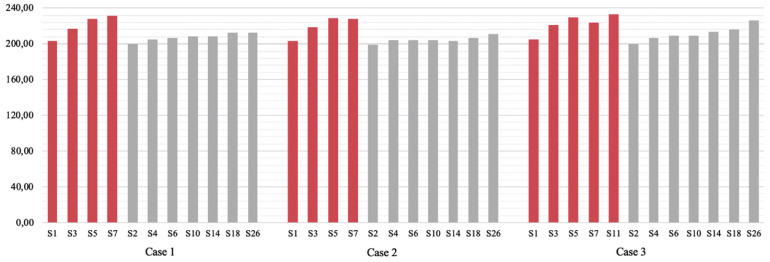
As noted earlier, two different disruption levels, namely low- and high-impact, are considered within the context of this study. To give an insight into the effect of low- and high-impact disruption levels on the emission levels in terms of scenarios, two different service levels ( and ) is considered. To this end, Fig. 8, Fig. 9 are drawn to further investigate the differences between the low- and high-impact disruption levels through scenarios in terms of the amount of the emission levels for and respectively.
Fig. 8.
The differences between disruption levels with respect to the emission levels for
Fig. 9.
The differences between disruption levels with respect to the emission levels for
In these figures, low- and high-impacts are highlighted in grey and red colors, respectively (See: Fig. 5 and Table 2). The changes in emission amounts along with the scenarios are measured for each case. Both figures indicate that emission levels increase rapidly under high disruption levels. That is to say, the model yields the most environmentally friendly results with the lowest emission amount for low disruption levels. Thus, it is easy to state that the sustainability of RSC is more vulnerable to high disruption levels. In brief, the results imply that the emission amounts are more stable for the low disruption level compared to the high disruption level. Besides, the amount changes according to the cases with respect to the service levels. Therefore, it is suggested to consider disruption levels and their impacts while making decisions on the environmental issues, i.e. emission amounts.
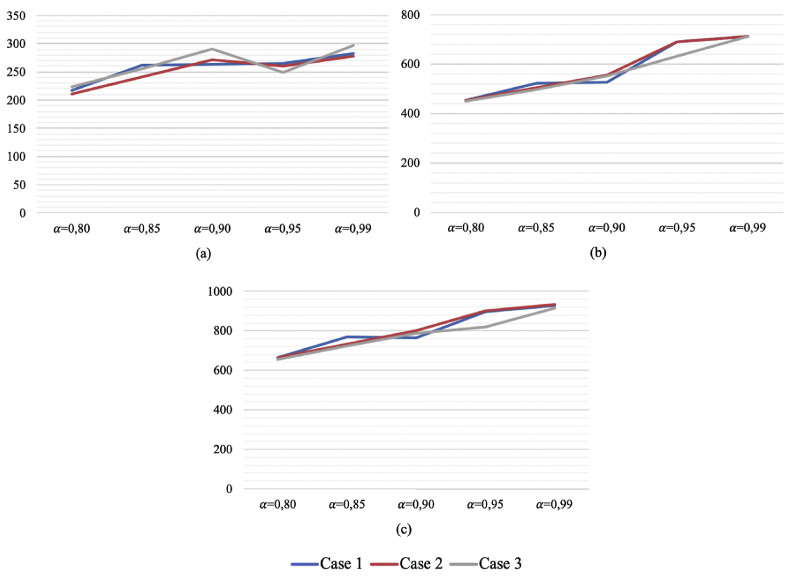
Fig. 10 , where (a), (b), and (c) represent R1, R2, and R3 sub-regions respectively, reveals the trends regarding the collected average number of products for each case. As expected, an increase in the -reliability level leads to an increase in the average number of collected products from sub-regions. A similar trend has been observed in all cases. It can be revealed from this figure that case 3 indicates a relatively small change in trend associated with the R1 whilst there is a regular and almost similar trend in R2 and R3 with respect to the -level. When the results are investigated regarding R1, 50% of the temporary collection centers are located in this region to ensure the determined service level. That is to say, a large ratio of temporary centers belongs to this region. Moreover, the centers located in this region are far away from the recycling centers. For these reasons, it can be deduced that the fluctuations are occurred due to the number of temporary collection centers and the high distance to the recycling centers.
Fig. 10.
The average number of collected products for each case with respect to -reliability levels.
Notably, the number of collected products shows an upward trend by increasing the -reliability level in R2 and R3 whereas there are some fluctuations in results regarding R1. But it can be still said that the value ranges are close for each service level. Overall, these results provide insights into the change in the -reliability level that does not yield a noteworthy effect.
The results contrasted in Fig. 10 also allow comparison of the centralized and decentralized distribution strategies. When the amounts of delivered products are explored with respect to the sub-regions, it is observed that the centralized strategy is more preferable than a decentralized strategy in the considered RSC network. The amount of product collected from the R1 is quite low compared to the R2 and R3 sub-regions and this situation promotes the centralized strategy.
Dividing the handled region to the sub-region provides more sensible results regarding the information on how the considered sub-regions are affected individually under disruptions. As can be also seen in Fig. 10 (a), it is suggested that the decision-makers should place an emphasis on sub-regions located away from recycling centers to avoid fluctuations or prevent the number of collected products from falling below a certain value. That is to say, RSC managers should collaborate with the government to prepare effective regulations to ensure the sustainability of RSC operations.
The box plots of emission levels are contrasted in Fig. 11 , in which (a), (b), and (c) represent case 1, case 2, and case 3, respectively. In all box plots, only occurred scenarios are considered to avoid the biasness. According to Fig. 11, long whiskers observed for all cases at higher -levels demonstrate that the data is over a wider interval. Whereas the short whiskers observed for all cases at lower -levels indicate that the data is within a narrower interval. Similarly, when considering IQRs (interquartile ranges) that measure the “spread” in a data set, it can be interpreted that all cases are almost the same and have consistent results. It is also worth to state that the emission data which has long whiskers or wide IQR can lead to biased interpretations for emission levels. It is justified by Fig. 11 that the distribution of emission levels is positively skewed for all -reliability levels, except for , for cases 1 and 2. Furthermore, the distribution of emission levels is negatively skewed for all -reliability levels, except for , for case 3. It can be emphasized that a uniformly distributed solution is attained in some of the box plots (for in case 1, and in case 3). Overall, it is suggested that the RSC managers should be aware of the fact that utilizing uniformly distributed and consistent data is crucial to avoid biased decisions when interpreting the emission levels.
Fig. 11.
The box plots of emission levels for each -reliability level: (a) Box plot for case 1, (b) box plot for case 2, and (c) box plot for case 3.
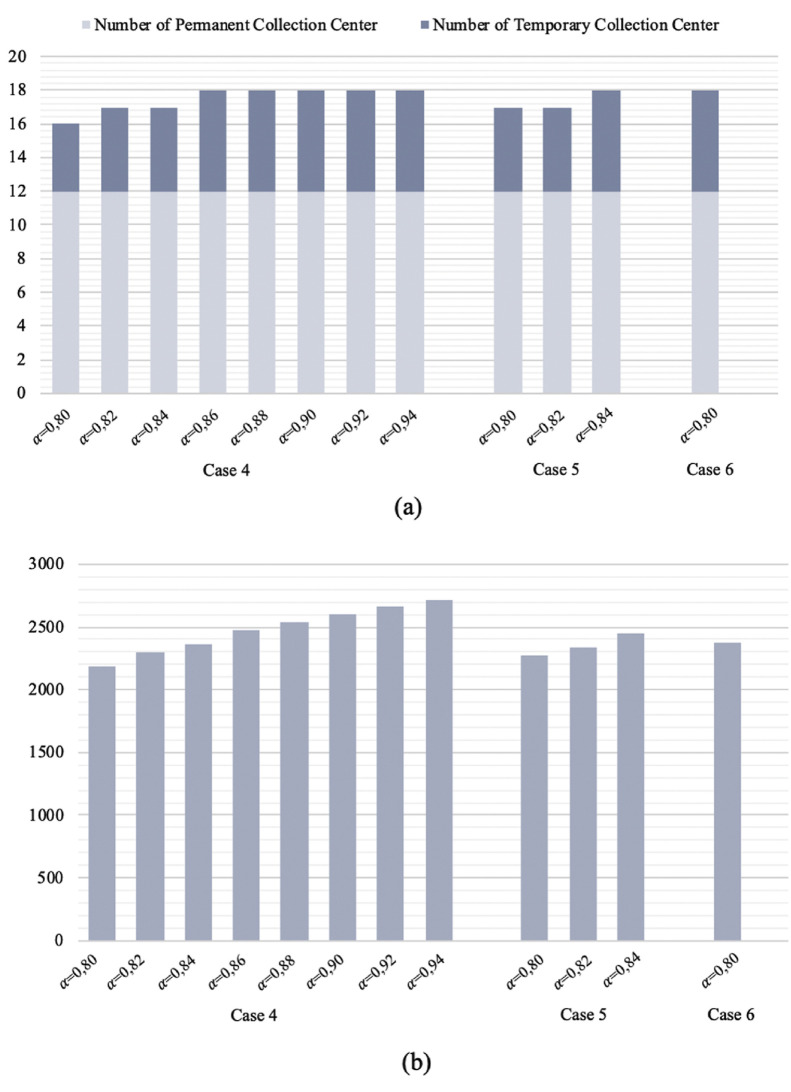
To provide a better understanding regarding the extraordinary situations, Table 8 is presented for the results of cases 4–6, which are designed to represent these situations. Additionally, the change in the total number of temporary facilities and the overall cost with respect to service levels for cases 4–6 is visualized in Fig. 12 (a) and (b), respectively. It is observed from the results that as the service level increases, the number of temporary facilities increases as well. This interrelation is observed more prominently in cases 4–6 since they correspond to the strong disruptions (See: Table 8 and Fig. 12 (a)). Overall, it can be interpreted that the total number of temporary facilities is larger for cases 4–6 compared to cases 1–3 under strong disruptions.
Table 8.
The summary of computational results for cases 4–6 with respect to -reliability levels.
| α-levels | OFV | TNF | TNTF | EEL | CPU timea | |
|---|---|---|---|---|---|---|
| Case 4 | α = 0.80 | 2186.73 | 16 | 4 | 178.18 | 20.34 |
| α = 0.82 | 2303.58 | 17 | 5 | 183.37 | 20.39 | |
| α = 0.84 | 2362.38 | 17 | 5 | 188.74 | 20.31 | |
| α = 0.86 | 2480.75 | 18 | 6 | 194.07 | 21.01 | |
| α = 0.88 | 2539.55 | 18 | 6 | 199.43 | 21.22 | |
| α = 0.90 | 2600.58 | 18 | 6 | 205.00 | 19.42 | |
| α = 0.92 | 2659.44 | 18 | 6 | 210.37 | 19.07 | |
| α = 0.94 | 2720.43 | 18 | 6 | 215.94 | 19.08 | |
| α = 0.96 |
infeasible |
|||||
| Case 5 | α = 0.80 | 2274.70 | 17 | 5 | 180.70 | 20.10 |
| α = 0.82 | 2334.33 | 17 | 5 | 186.14 | 19.52 | |
| α = 0.84 | 2454.49 | 18 | 6 | 191.62 | 19.33 | |
| α = 0.86 |
infeasible |
|||||
| Case 6 | α = 0.80 | 2379.53 | 18 | 6 | 184.73 | 18.18 |
| α = 0.82 | infeasible | |||||
OFV: Objective Function Value.
TNF: Total Number of Facilities.
TNTF: Total Number of Opened Temporary Facilities.
EEL: The Expected Emission Level.
CPU Time in Seconds.
Fig. 12.
(a) The total number of temporary facilities and (b) overall cost with respect to -reliability levels for cases 4-6.
From the feasibility aspect, when considering cases 4–6, the feasible solutions are only attained for , respectively. Therefore, it can be deduced from Table 8 that the feasibility of the solution becomes difficult as the destructive impact of the ripple effect increases.
It is also important to state that the service level indicates the sum of occurrence probability of scenarios. Accordingly, as stated earlier, six different cases are investigated to obtain more sensitive results regarding the scenarios. Computational results show that while more scenarios are considered for case 4, relatively fewer scenarios are addressed for other cases. For instance, the service level equals 0.94 for case 4 and 0.84 for case 5. In other words, more scenarios are addressed for case 4 compared to case 5. Thus, it is easy to conclude that the determined intervals affect the number of considered scenarios representing the ripple effect.
4. Conclusion
This study addresses the RSC network design problem through a two-stage stochastic mixed-integer optimization model to cope with uncertainty caused by the devastating impact of the ripple effect. Further, the -reliability approach, also known as service level, is adapted to the model to obtain a resilient RSC design. The computational experiments are carried out to validate the proposed model. The response variables measured to assess the RSC performance are the cost and emission amounts, which represent the economic and environmental dimensions of sustainability respectively. In order to evaluate the efficiency and responsiveness of obtained RSC design, the sensitivity analysis is performed by changing the parameter values, such as service levels and disruption level impacts. Accordingly, key findings and managerial insights are provided in the context of the sustainability of RSC in the case of the ripple effect.
Key findings and managerial insights are provided as follows:
-
-
The ripple effect has a significant impact on the overall cost and emission levels. More precisely, the regulations regarding the recycling operations should be eased to ensure sustainability in case of the ripple effect. This finding is not only valid for this specific case but can be generalized for other situations.
-
-
The resilient RSC system design becomes more important if there is not a strict difference between the low and high disruption levels, which should be considered to make environmentally friendly decisions. This finding is valid only for this specific case. For other situations, the disruption levels should be analyzed.
-
-
A centralized distribution strategy is more plausible compared to a decentralized strategy for the RSC network design under disruptions. This finding is not only valid for this specific case but can be generalized for other situations.
-
-
The -reliability level is important for environmental and economic dimensions of sustainability. This finding is not only valid for this specific case but can be generalized for other situations.
The novelty of this study is presented from several perspectives. (I) From research novelty, a two-stage stochastic optimization model is developed to make integrated strategic and operational decisions for RSC network design by focusing on the uncertainty caused by the ripple effect. (II) From knowledge advancement, the key findings and managerial insights are highlighted by exploring the relationship between the -reliability approach and disruption levels based on the scenarios. (III) From practical relevance, because this study provides a comprehensive framework to cope with the uncertainty for RSC network design, it has a wide range of implementation area.
This study may be modified in several research directions: (i) heuristic methods can be implemented for large-sized problems, (ii) multi-period can be considered while formulating the addressed problem, (iii) the problem can be explored with more than one objective, and (iv) last but not least, the recovering process can be included in the model in detail manner.
CRediT authorship contribution statement
Ömer Faruk Yılmaz: Supervision, Writing - original draft, Software, Conceptualization. Gökhan Özçelik: Writing - review & editing, Methodology, Formal analysis, Software. Fatma Betül Yeni: Visualization, Writing - review & editing, Validation, Resources.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Handling editor: Yutao Wang
References
- Ahi P., Searcy C. A comparative literature analysis of definitions for green and sustainable supply chain management. J. Clean. Prod. 2013;52:329–341. [Google Scholar]
- Bertsimas D., Sim M. The price of robustness. Oper. Res. 2004;52(1):35–53. [Google Scholar]
- Budiman S.D., Rau H. A mixed-integer model for the implementation of postponement strategies in the globalized green supply chain network. Comput. Ind. Eng. 2019;137:106054. doi: 10.1016/j.cie.2019.106054. [DOI] [Google Scholar]
- Cui L., Deng J., Liu F., Zhang Y., Xu M. Investigation of RFID investment in a single retailer two-supplier supply chain with random demand to decrease inventory inaccuracy. J. Clean. Prod. 2017;142:2028–2044. [Google Scholar]
- Cui L., Deng J., Liu R., Xu D., Zhang Y., Xu M. A stochastic multi-item replenishment and delivery problem with lead-time reduction initiatives and the solving methodologies. Appl. Math. Comput. 2020;374:125055. doi: 10.1016/j.amc.2020.125055. [DOI] [Google Scholar]
- Cui L., Deng J., Zhang Y., Tang G., Xu M. Hybrid differential artificial bee colony algorithm for multi-item replenishment-distribution problem with stochastic lead-time and demands. J. Clean. Prod. 2020;254:119873. doi: 10.1016/j.jclepro.2019.119873. [DOI] [Google Scholar]
- Cui L., Deng J., Zhang Y., Zhang Z., Xu M. The bare-bones differential evolutionary for stochastic joint replenishment with random number of imperfect items. Knowl. Base Syst. 2020;193:105416. doi: 10.1016/j.knosys.2019.105416. [DOI] [Google Scholar]
- Daskin M.S., Hesse S.M., Revelle C.S. α-reliable p-minimax regret: a new model for strategic facility location modeling. Locat. Sci. 1997;5(4):227–246. [Google Scholar]
- De Rosa V., Gebhard M., Hartmann E., Wollenweber J. Robust sustainable bi-directional logistics network design under uncertainty. Int. J. Prod. Econ. 2013;145(1):184–198. [Google Scholar]
- Darestani S.A., Hemmati M. Robust optimization of a bi-objective closed-loop supply chain network for perishable goods considering queue system. Comput. Ind. Eng. 2019;136:277–292. [Google Scholar]
- Demirel E., Demirel N., Gökçen H. A mixed integer linear programming model to optimize reverse logistics activities of end-of-life vehicles in Turkey. J. Clean. Prod. 2016;112:2101–2113. [Google Scholar]
- Doan L.T.T., Amer Y., Lee S.H., Phuc P.N.K. Optimizing the total cost of an E-waste reverse supply chain considering transportation risk. Oper. Supply Chain Manag. Int. J. 2018;11(3):151–160. [Google Scholar]
- Doan L.T.T., Amer Y., Lee S.H., Phuc P.N.K., Dat L.Q. A comprehensive reverse supply chain model using an interactive fuzzy approach–A case study on the Vietnamese electronics industry. Appl. Math. Model. 2019;76:87–108. [Google Scholar]
- Dolgui A., Ivanov D., Sokolov B. Ripple effect in the supply chain: an analysis and recent literature. Int. J. Prod. Res. 2018;56(1–2):414–430. [Google Scholar]
- Dolgui A., Ivanov D., Rozhkov M. Does the ripple effect influence the bullwhip effect? An integrated analysis of structural and operational dynamics in the supply chain. Int. J. Prod. Res. 2020;58(5):1285–1301. doi: 10.1080/00207543.2019.1627438. [DOI] [Google Scholar]
- Easwaran G., Üster H. A closed-loop supply chain network design problem with integrated forward and reverse channel decisions. IIE Trans. 2010;42(11):779–792. [Google Scholar]
- Fang H.W., Xiao R.B., Cai Z.Y. Disruption restoration model in production planning with the closed-loop supply chain between dual-channel. Control Decis. 2011;26(9):1303–1309. [Google Scholar]
- Ghadge A., Yang Q., Caldwell N., König C., Tiwari M.K. Facility location for a closed-loop distribution network: a hybrid approach. Int. J. Retail Distrib. Manag. 2016;44(9):884–902. [Google Scholar]
- Gu Q., Gao T. Proceedings of 2012 IEEE International Conference on Service Operations and Logistics, and Informatics. 2012, July. IEEE; 2012. Managing supply disruption for remanufacturer of reverse supply chain; pp. 331–335. [Google Scholar]
- Gianesello P., Ivanov D., Battini D. Closed-loop supply chain simulation with disruption considerations: a case-study on tesla. Int. J. Inventory Res. 2017;4(4):257–280. [Google Scholar]
- Hamdan B., Diabat A. Robust design of blood supply chains under risk of disruptions using Lagrangian relaxation. Transport. Res. E Logist. Transport. Rev. 2020;134:101764. doi: 10.1016/j.tre.2019.08.005. [DOI] [Google Scholar]
- Hasani A., Khosrojerdi A. Robust global supply chain network design under disruption and uncertainty considering resilience strategies: a parallel memetic algorithm for a real-life case study. Transport. Res. E Logist. Transport. Rev. 2016;87:20–52. [Google Scholar]
- Hasani A., Zegordi S.H., Nikbakhsh E. Robust closed-loop supply chain network design for perishable goods in agile manufacturing under uncertainty. Int. J. Prod. Res. 2012;50(16):4649–4669. [Google Scholar]
- Hasani A., Zegordi S.H., Nikbakhsh E. Robust closed-loop global supply chain network design under uncertainty: the case of the medical device industry. Int. J. Prod. Res. 2015;53(5):1596–1624. [Google Scholar]
- Hatefi S.M., Jolai F. Robust and reliable forward–reverse logistics network design under demand uncertainty and facility disruptions. Appl. Math. Model. 2014;38(9–10):2630–2647. [Google Scholar]
- Hatefi S.M., Jolai F., Torabi S.A., Tavakkoli-Moghaddam R. Reliable design of an integrated forward-revere logistics network under uncertainty and facility disruptions: a fuzzy possibilistic programing model. KSCE J. Civ. Eng. 2015;19(4):1117–1128. [Google Scholar]
- Hatefi S.M., Jolai F., Torabi S.A., Tavakkoli-Moghaddam R. Integrated forward-reverse logistics network design under uncertainty and reliability consideration. Sci. Iran. 2016;23(2):721–735. [Google Scholar]
- Hosseini-Motlagh S.M., Nouri-Harzvili M., Choi T.M., Ebrahimi S. Reverse supply chain systems optimization with dual channel and demand disruptions: sustainability, CSR investment and pricing coordination. Inf. Sci. 2019;503:606–634. [Google Scholar]
- Hosseini-Motlagh S.M., Samani M.R.G., Homaei S. Blood supply chain management: robust optimization, disruption risk, and blood group compatibility (a real-life case) J. Ambient Intell. Humanized Comput. 2020;11(3):1085–1104. [Google Scholar]
- Hosseini S., Sarder M.D. Ripple effect analysis of two-stage supply chain using probabilistic graphical model. In: Ivanov D., Dolgui A., Sokolov B., editors. vol. 276. Springer; Cham: 2019. pp. 181–191. (Handbook of Ripple Effects in the Supply Chain). [Google Scholar]
- Hosseini S., Ivanov D. A new resilience measure for supply networks with the ripple effect considerations: a bayesian network approach. Ann. Oper. Res. 2019:1–27. doi: 10.1007/s10479-019-03350-8. [DOI] [Google Scholar]
- Hosseini S., Ivanov D., Dolgui A. Ripple effect modelling of supplier disruption: integrated Markov chain and dynamic bayesian network approach. Int. J. Prod. Res. 2019:1–19. doi: 10.1080/00207543.2019.1661538. [DOI] [Google Scholar]
- Hosseini S., Morshedlou N., Ivanov D., Sarder M.D., Barker K., Al Khaled A. Resilient supplier selection and optimal order allocation under disruption risks. Int. J. Prod. Econ. 2019;213:124–137. [Google Scholar]
- Hosseini S., Ivanov D., Dolgui A. Review of quantitative methods for supply chain resilience analysis. Transport. Res. E Logist. Transport. Rev. 2019;125:285–307. [Google Scholar]
- Ivanov D. Simulation-based ripple effect modelling in the supply chain. Int. J. Prod. Res. 2017;55(7):2083–2101. [Google Scholar]
- Ivanov D. Simulation-based single vs. Dual sourcing analysis in the supply chain with consideration of capacity disruptions, big data and demand patterns. Int. J. Integrated Supply Manag. 2017;11(1):24–43. [Google Scholar]
- Ivanov D. Revealing interfaces of supply chain resilience and sustainability: a simulation study. Int. J. Prod. Res. 2018;56(10):3507–3523. [Google Scholar]
- Ivanov D. ‘A blessing in disguise’or ‘as if it wasn’t hard enough already’: reciprocal and aggravate vulnerabilities in the supply chain. Int. J. Prod. Res. 2019:1–11. doi: 10.1080/00207543.2019.1634850. [DOI] [Google Scholar]
- Ivanov D. Disruption tails and revival policies: a simulation analysis of supply chain design and production-ordering systems in the recovery and post- disruption periods. Comput. Ind. Eng. 2019;127:558–570. [Google Scholar]
- Ivanov D., Pavlov A., Sokolov B. Optimal distribution (Re) planning in a centralized multi-stage supply network under conditions of the ripple effect and structure dynamics. Eur. J. Oper. Res. 2014;237(2):758–770. [Google Scholar]
- Ivanov D., Sokolov B., Dolgui A. The ripple effect in supply chains: trade-off ‘efficiency-flexibility-resilience’ in disruption management. Int. J. Prod. Res. 2014;52(7):2154–2172. [Google Scholar]
- Ivanov D., Pavlov A., Dolgui A., Pavlov D., Sokolov B. Disruption-driven supply chain (re)-planning and performance impact assessment with consideration of pro-active and recovery policies. Transport. Res. E Logist. Transport. Rev. 2016;90:7–24. [Google Scholar]
- Ivanov D., Pavlov A., Pavlov D., Sokolov B. Minimization of disruption-related return flows in the supply chain. Int. J. Prod. Econ. 2017;183:503–513. [Google Scholar]
- Ivanov D., Dolgui A., Sokolov B. The impact of digital technology and Industry 4.0 on the ripple effect and supply chain risk analytics. Int. J. Prod. Res. 2019;57(3):829–846. [Google Scholar]
- Jabbarzadeh A., Fahimnia B., Seuring S. Dynamic supply chain network design for the supply of blood in disasters: a robust model with real world application. Transport. Res. E Logist. Transport. Rev. 2014;70:225–244. [Google Scholar]
- Jain V., Kumar S., Soni U., Chandra C. Supply chain resilience: model development and empirical analysis. Int. J. Prod. Res. 2017;55(22):6779–6800. [Google Scholar]
- John S.T., Sridharan R., Kumar P.R., Krishnamoorthy M. Multi-period reverse logistics network design for used refrigerators. Appl. Math. Model. 2018;54:311–331. [Google Scholar]
- Kamalahmadi M., Mellat-Parast M. Developing a resilient supply chain through supplier flexibility and reliability assessment. Int. J. Prod. Res. 2016;57(3):829–846. [Google Scholar]
- Khaloie H., Abdollahi A., Rashidinejad M., Siano P. Risk-based probabilistic-possibilistic self-scheduling considering high-impact low-probability events uncertainty. Int. J. Electr. Power Energy Syst. 2019;110:598–612. [Google Scholar]
- Khaloie H., Abdollahi A., Shafie-Khah M., Siano P., Nojavan S., Anvari-Moghaddam A., Catalão J.P. Co-optimized bidding strategy of an integrated wind-thermal-photovoltaic system in deregulated electricity market under uncertainties. J. Clean. Prod. 2020;242:118434. doi: 10.1016/j.jclepro.2019.118434. [DOI] [Google Scholar]
- Khaloie H., Abdollahi A., Shafie-Khah M., Anvari-Moghaddam A., Nojavan S., Siano P., Catalão J.P. Coordinated wind-thermal-energy storage offering strategy in energy and spinning reserve markets using a multi-stage model. Appl. Energy. 2020;259:114168. doi: 10.1016/j.apenergy.2019.114168. [DOI] [Google Scholar]
- Khaloie H., Abdollahi A., Nojavan S., Shafie-Khah M., Anvari-Moghaddam A., Siano P., Catalão J.P. Electricity Markets. Springer; Cham: 2020. Offering strategy of thermal-photovoltaic-storage based generation company in day-ahead market; pp. 113–133. [Google Scholar]
- Kim J., Do Chung B., Kang Y., Jeong B. Robust optimization model for closed-loop supply chain planning under reverse logistics flow and demand uncertainty. J. Clean. Prod. 2018;196:1314–1328. [Google Scholar]
- Kinra A., Ivanov D., Das A., Dolgui A. Ripple effect quantification by supplier risk exposure assessment. Int. J. Prod. Res. 2019:1–20. doi: 10.1080/00207543.2019.1675919. [DOI] [Google Scholar]
- Kushwaha S., Ghosh A., Rao A.K. Collection activity channels selection in a reverse supply chain under a carbon cap-and-trade regulation. J. Clean. Prod. 2020:121034. doi: 10.1016/j.jclepro.2020.121034. [DOI] [Google Scholar]
- Li Y., Zobel C.W. Exploring supply chain network resilience in the presence of the ripple effect. Int. J. Prod. Econ. 2020:107693. doi: 10.1016/j.ijpe.2020.107693. [DOI] [Google Scholar]
- Liu M., Liu X., Zhang E., Chu F., Chu C. Scenario-based heuristic to two-stage stochastic program for the parallel machine ScheLoc problem. Int. J. Prod. Res. 2019;57(6):1706–1723. [Google Scholar]
- Liao T.Y. Reverse logistics network design for product recovery and remanufacturing. Appl. Math. Model. 2018;60:145–163. [Google Scholar]
- Lim M.K., Bassamboo A., Chopra S., Daskin M.S. Facility location decisions with random disruptions and imperfect estimation. Manuf. Serv. Oper. Manag. 2013;15(2):239–249. [Google Scholar]
- Ma H., Li X. Closed-loop supply chain network design for hazardous products with uncertain demands and returns. Appl. Soft Comput. 2018;68:889–899. doi: 10.1016/j.asoc.2017.10.027. [DOI] [Google Scholar]
- Mokhtar A.R.M., Genovese A., Brint A., Kumar N. Improving reverse supply chain performance: the role of supply chain leadership and governance mechanisms. J. Clean. Prod. 2019;216:42–55. [Google Scholar]
- Mutingi M. The impact of reverse logistics in green supply chain management: a system dynamics analysis. Int. J. Ind. Syst. Eng. 2014;17(2):186–201. [Google Scholar]
- Niknejad A., Petrovic D. Optimisation of integrated reverse logistics networks with different product recovery routes. Eur. J. Oper. Res. 2014;238(1):143–154. [Google Scholar]
- Nikzad E., Bashiri M., Oliveira F. Two-stage stochastic programming approach for the medical drug inventory routing problem under uncertainty. Comput. Ind. Eng. 2019;128:358–370. [Google Scholar]
- Oksuz M.K., Satoglu S.I. A two-stage stochastic model for location planning of temporary medical centers for disaster response. Int. J. Disaster Risk Reduct. 2020;44:101426. doi: 10.1016/j.ijdrr.2019.101426. [DOI] [Google Scholar]
- Özçelik G., Yılmaz Ö.F., Yeni F.B. Robust optimisation for ripple effect on reverse supply chain: an industrial case study. Int. J. Prod. Res. 2020 doi: 10.1080/00207543.2020.1740348. [DOI] [Google Scholar]
- Pavlov A., Ivanov D., Dolgui A., Sokolov B. Hybrid fuzzy-probabilistic approach to supply chain resilience assessment. IEEE Trans. Eng. Manag. 2018;65(2):303–315. [Google Scholar]
- Pavlov A., Ivanov D., Pavlov D., Slinko A. Optimization of network redundancy and contingency planning in sustainable and resilient supply chain resource management under conditions of structural dynamics. Ann. Oper. Res. 2019:1–30. doi: 10.1007/s10479-019-03182-6. [DOI] [Google Scholar]
- Pishvaee M.S., Rabbani M., Torabi S.A. A robust optimization approach to closed-loop supply chain network design under uncertainty. Appl. Math. Model. 2011;35(2):637–649. [Google Scholar]
- Phuc P.N.K., Vincent F.Y., Tsao Y.C. Optimizing fuzzy reverse supply chain for end-of-life vehicles. Comput. Ind. Eng. 2017;113:757–765. [Google Scholar]
- Qiaolun G., Tiegang G. 2012 Fifth International Conference on Intelligent Networks and Intelligent Systems, 2012, November. IEEE; 2012. Simulation analysis for impacts of supply disruption on reverse supply chain; pp. 53–56. [Google Scholar]
- Qiaolun G., Tiegang G. Profits management for reverse supply chain with supply disruption. Int. J. Intell. Eng. Syst. 2013;6(1):1–9. [Google Scholar]
- Rezapour S., Farahani R.Z., Pourakbar M. Resilient supply chain network design under competition: a case study. Eur. J. Oper. Res. 2017;259(3):1017–1035. [Google Scholar]
- Samani M.R.G., Hosseini-Motlagh S.M. An enhanced procedure for managing blood supply chain under disruptions and uncertainties. Ann. Oper. Res. 2019;283(1):1413–1462. [Google Scholar]
- Samuel C.N., Venkatadri U., Diallo C., Khatab A. Robust closed-loop supply chain design with presorting, return quality and carbon emission considerations. J. Clean. Prod. 2020;247:119086. [Google Scholar]
- Sawik T. On the risk-averse optimization of service level in a supply chain under disruption risks. Int. J. Prod. Res. 2016;54(1):98–113. [Google Scholar]
- Sawik T. A portfolio approach to supply chain disruption management. Int. J. Prod. Res. 2017;55(7):1970–1991. [Google Scholar]
- Schmitt T.G., Kumar S., Stecke K.E., Glover F.W., Ehlen M.A. Mitigating disruptions in a multi-echelon supply chain using adaptive ordering. Omega. 2017;68:185–198. [Google Scholar]
- Setak M., Feizizadeh F., Tikani H., Ardakani E.S. A bi-level stochastic optimization model for reliable supply chain in competitive environments: hybridizing exact method and genetic algorithm. Appl. Math. Model. 2019;75:310–332. [Google Scholar]
- Sheffi Y., Rice J.B., Jr. A supply chain view of the resilient enterprise. MIT Sloan Manag. Rev. 2005;47(1):41. [Google Scholar]
- Suryawanshi P., Dutta P. International Conference on Information Technology and Applied Mathematics. Springer; Cham: 2019. March. A stochastic programming approach to design perishable product supply chain network under different disruptions; pp. 656–669. [Google Scholar]
- Taleizadeh A.A., Niaki S.T.A., Makui A. Multiproduct multiple-buyer single-vendor supply chain problem with stochastic demand, variable lead-time, and multi-chance constraint. Expert Syst. Appl. 2012;39(5):5338–5348. [Google Scholar]
- Tucker E.L., Daskin M.S., Sweet B.V., Hopp W.J. Incentivizing resilient supply chain design to prevent drug shortages: policy analysis using two-and multi-stage stochastic programs. IISE Trans. 2020;52(4):394–412. [Google Scholar]
- Ugranlı F. Probabilistic distribution planning: including the interactions between chance constraints and renewable energy. Sustainable Energy, Grids and Networks. 2020. 100372. [DOI]
- Wang C., Chen S. A distributionally robust optimization for blood supply network considering disasters. Transport. Res. E Logist. Transport. Rev. 2020;134:101840. doi: 10.1016/j.tre.2020.101840. [DOI] [Google Scholar]
- Wang H.F., Huang Y.S. A two-stage robust programming approach to demand-driven disassembly planning for a closed-loop supply chain system. Int. J. Prod. Res. 2013;51(8):2414–2432. [Google Scholar]
- Yılmaz Ö.F. Examining additive manufacturing in supply chain context through an optimization model. Comput. Ind. Eng. 2020;142:106335. doi: 10.1016/j.cie.2020.106335. [DOI] [Google Scholar]
- Yılmaz Ö.F. Ensuring sustainability in reverse supply chain in case of ripple effect: a two-stage stochastic optimization model (Parameters), GitHub-omerfarukktu repository. 2020. https://github.com/omerfarukktu/Parameters
- Yu H., Solvang W.D. A carbon-constrained stochastic optimization model with augmented multi-criteria scenario-based risk-averse solution for reverse logistics network design under uncertainty. J. Clean. Prod. 2017;164:1248–1267. [Google Scholar]
- Zhang S., Zhang P., Zhang M. Fuzzy emergency model and robust emergency strategy of supply chain system under random supply disruptions. Complexity. 2019. 3092514. [DOI]