Simulation of dose distribution and secondary particle production in proton therapy of brain tumor

Abstract

Aim

The aim of this study is simulation of the proton depth-dose distribution and dose evaluation of secondary particles in proton therapy of brain tumor using the GEANT4 and FLUKA Monte Carlo codes.

Background

Proton therapy is a treatment method for variety of tumors such as brain tumor. The most important feature of high energy proton beams is the energy deposition as a Bragg curve and the possibility of creating the spread out Bragg peak (SOBP) for full coverage of the tumor.

Materials and methods

A spherical tumor with the radius of 1 cm in the brain is considered. A SNYDER head phantom has been irradiated with 30−130 MeV proton beam energy. A PMMA modulator wheel is used for covering the tumor. The simulations are performed using the GEANT4 and FLUKA codes.

Results

Using a modulator wheel, the Spread Out Bragg Peak longitudinally and laterally covers the tumor. Flux and absorbed dose of secondary particles produced by nuclear interactions of protons with elements in the head are considerably small compared to protons.

Conclusions

Using 76.85 MeV proton beam and a modulator wheel, the tumor can be treated accurately in the 3-D, so that the distribution of proton dose in the surrounding tissues is very low. The results show that more than 99% of the total dose of secondary particles and protons is absorbed in the tumor.

1. Introduction

Research on the use of accelerator-produced proton beams in radiation therapy, which has been ongoing since 1946,¹ has been vastly progressed in recent years.2, 3, 4 Proton therapy is one of the external radiation therapy techniques to treat deep-seated tumors. Proton therapy takes advantage of the maximum and minimum dose reaching the tumor and the healthy tissue surrounding it, respectively.⁵ Comparison of proton therapy with advanced photon therapy methods such as intensity-modulated radiotherapy (IMRT) and volumetric modulated arc therapy (VMAT) shows that proton therapy provides better dose distributions and has a dosimetric advantage over photon therapy.6, 7, 8

The charged particles, such as protons, when passing through the material lose their energy, which can be expressed by Bethe-Bloch equation.⁹ The Bragg curve can be obtained by plotting the linear energy transfer (LET) of the charged particle as a function of depth in the stopping material. At the end range of the charged particles, LET reaches its maximum and then it quickly becomes zero. The very maximum is called Bragg peak.¹⁰ Bragg curve can be used in radiation therapy so that the Bragg peak is placed exactly at the tumor site. For large tumors, Bragg peak must cover the tumor size, namely Spread Out Bragg Peak (SOBP). The SOBP is obtained by adding several Bragg peaks that are created at different depths.11, 12, 13, 14 In order to do this, there are two main methods, namely passive scattering and active scanning.15, 16, 17 In the process of broadening the Bragg peak (creating SOBP) by using the passive scattering method, a range modulator is used in the proton beam line. This is because the geometry and the properties of the modulator are important in creating an equivalent dose distribution in the tumor volume.^18,19

In order to model the proton therapy treatment, the codes based on the Monte Carlo method are used. Numerous investigations on the proton therapy planning simulations have been carried out using the MCNPX (Monte Carlo N-Particle), GEANT4 (Geometry and Tracking) and FLUKA codes.20, 21, 22 A range modulator wheel for proton therapy in Italy has been simulated by the GEANT4 code as employed in the experiment.²³

Secondary particles are produced by the passage of protons within the body and their inelastic nuclear interactions with the nuclei of the elements of different tissues are scrutinized. Most of the important subatomic particles in this process are neutrons and gamma-rays. The secondary particles can move and lose their energy in various organs. The dose that is absorbed in other organs from these particles can be dangerous. Hence, measuring the flux and energy deposition of the secondary particles has an important role in radiotherapy.^24,25

Research has been done to optimize the material of the two-layer modulator in proton therapy with the presence of heterogeneous lung tissue.²⁶ Simulation of a slab head phantom has been conducted for evaluation of energy deposition, secondary particle production, range straggling and multiple scattering in proton therapy of brain tissue.^25,27 In these papers, the geometry of the head phantom is not real and more attention has been paid to the combination of the elements and the arrangement of the tissues. Phantom design and dosimetric characterization for multiple simultaneous cell irradiations have been performed for proton therapy of head and neck cancer with active pencil beam scanning.²⁸ In treatment planning, some parameters should be considered, such as the presence of inhomogeneity in tissue, the geometric shape of the phantom, the dose of primary particles and secondary particles in the tumor region and other tissues, etc, which were considered in this article.

The aim of this study was to calculate the total absorbed dose in different tissues of the SNYDER head phantom in the proton therapy of brain cancer using the GEANT4 and FLUKA Monte Carlo codes. By overlapping the pristine Bragg curves, a SOBP was created that covers the tumor. The energy spectrum and absorbed dose of the major secondary particles produced in nuclear reactions in the head phantom, gamma rays and neutrons were also calculated. Simulations have focused on the 3-dimensional (3D) coverage of the brain tumor while healthy brain tissue absorbs less radiation.

2. Materials and methods

2.1. Comparison of the Monte Carlo simulations and experimental results

A rectangular cube water phantom with dimensions of 40 × 30 × 30 cm³, which is irradiated with 108.8 MeV protons, was simulated using the GEANT4 toolkit by Park et al. and compared with experimental results.²⁹ In this paper a 40 × 30 × 30 cm³ rectangular cube of water irradiated with 108.8 MeV protons was simulated to evaluate the simulation results. The cubic voxel size was selected with dimensions of 1 × 1 × 1 mm³ to obtain the dose in each voxel. The Bragg curves obtained from simulation with the FLUKA code and GEANT4 toolkit with experimental results were shown in Fig. 1. It can be seen that there is a good agreement between the simulation results and the experimental results.

Fig. 1.

Comparison of the dose distribution created by 108.8 MeV proton beam in the water phantom, between simulations and measurements.

To further evaluate the simulations, phantoms of water, PMMA, soft tissue and compact bone were simulated with dimensions similar to those mentioned above. The phantoms were irradiated with 75 MeV proton beams and the Continuous Slowing Down Approximation range (CSDA range) of the protons was calculated in each phantom using the FLUKA code and GEANT4 toolkit. The results of the simulations and the International Commission on Radiation Units and Measurements report 49 (ICRU49)³⁰ are shown in Table 1. The results were in agreement with each other and the ICRU49 results.

Table 1.

Comparisons between the simulation results of the ranges of 75 MeV proton beam in different materials and ICRU49 report.³⁰

Material	FLUKA	GEANT4	ICRU49
Water PMMA Soft Tissue Compact Bone	4.552 4.665 4.614 4.921	4.572 4.697 4.623 4.902	4.618 4.742 4.668 4.984

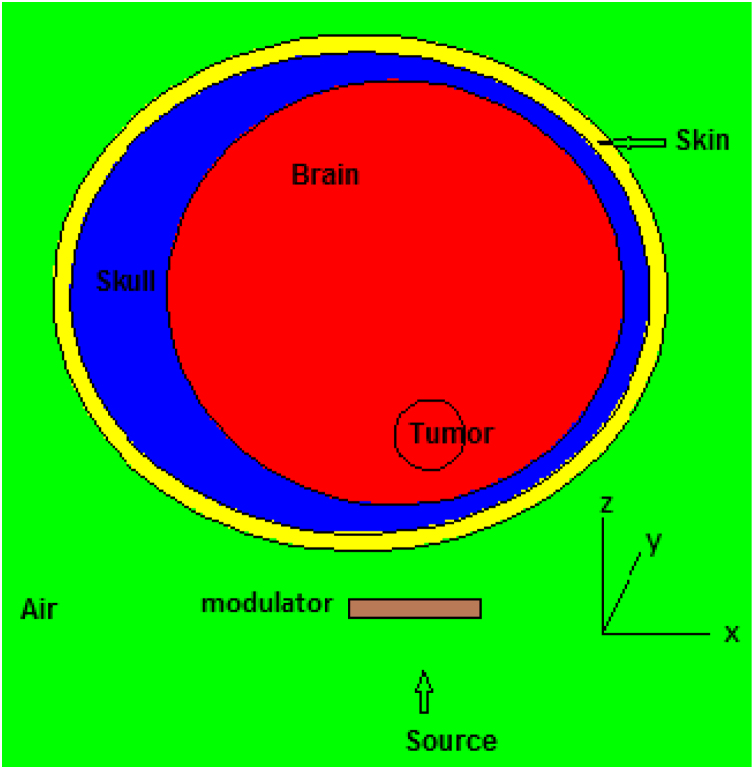
2.2. Head phantom definition

A SNYDER head phantom was used as shown in Fig. 2. The head phantom consists of the skin, skull, brain and tumor. The Snyder head phantom was defined by 3 elliptical layers with the following equations³¹:

$$Brain:{\left(\frac{x}{6}\right)}^2+{\left(\frac{y}{9}\right)}^2+{\left(\frac{z-1}{6.5}\right)}^2=1$$ (1)

$$Skull:{\left(\frac{x}{6.8}\right)}^2+{\left(\frac{y}{9.8}\right)}^2+{\left(\frac{z}{8.3}\right)}^2=1$$ (2)

$$Skin:{\left(\frac{x}{7.3}\right)}^2+{\left(\frac{y}{10.3}\right)}^2+{\left(\frac{z}{8.8}\right)}^2=1$$ (3)

Fig. 2.

Schematic view of the SNYDER head phantom used for proton therapy simulations.

The thickness of the skin was considered to be 0.5 cm and the skull has a variable thickness between 0.6 cm–2.8 cm. To investigate the treatment of a brain tumor using a proton beam, a spherical tumor with a radius of 1 cm at 1 cm from the surface of the brain was considered in the Snyder head phantom. Elemental compositions and atom fractions for the skin, skull and brain were taken from the Compendium of Material Composition Data for Radiation Transport Modeling³² and are shown in Table 2. Elemental composition of the tumor was contrived to be the same as the brain tissue composition. Simulations have been done using the GEANT4 and FLUKA codes. GEANT4 is a versatile C++ Monte Carlo simulation tool kit which simulates all kinds of particles. The G4VUserDetectorConstruction class was used to design the geometry using GEANT4 code. The material definitions using the G4Material class were in accordance with Table 2. A mono-energetic proton surface source was simulated as a disk with a radius of 1 cm and a distance of 17.5 cm from the center of the tumor and it was designed so that the proton beam penetrates the brain from the top of the phantom in the direction of the + Z axis. G4GeneralParticleSource class was used to simulate the source and generate the primary particles (protons) in the GEANT4 code. This class allows users to define spectral sources and sources with different spatial distributions. The physical reference QGSP_INCLXX was used to transport particles into matter and to consider interactions and production of secondary particles. This physical reference is for interactions involving protons and neutrons with energy of less than 3 GeV and is based on experimental information and has been proposed for medical and industrial applications. Boxmesh was used to obtain the Bragg curves in GEANT4. To obtain the secondary particles, several classes of the G4VPrimiiveScorer class were derived and recorded by the G4MultiFunctionalDetector. Each of these classes has a G4THitsMap object and records a value as a result.³³ In the simulation using the FLUKA code (version 2011.2c), geometry and source were designed exactly like simulations in the GEANT4 toolkit. The simulations were done in the HADROTHE mode, which was the most similar to the simulations done using the GEANT4 toolkit. This code is a general purpose tool for calculations of particle transport and interactions with materials. FLUKA can simulate the interaction and propagation in matter of about 60 various particles with high accuracy.³⁴ The number of protons transported in each simulation in both codes was 2 × 10⁷ and the error values were less than 1%.

Table 2.

Elemental composition, atom fractions and densities of materials used in the simulations.³²

Material	H	C	N	O	Mg	P	Cl	Ar	Density (g/cm3)
PMMA Skull Brain, Tumor Skin Air	0.533 0.528 0.655 0.620 –	0.333 0.192 0.062 0.118 –	– 0.016 0.006 0.021 0.784	0.133 0.213 0.275 0.240 0.211	– 0.001 – – –	– 0.019 0.001 – –	– 0.0305 0.0004 – –	– – – – 0.0047	1.19 1.85 1.03 1.1 0.001205

2.3. Simulation of a modulator

Proton deposits a small dose on its way when it enters the body. With increasing the depth and reducing the speed, the absorbed dose in the tissue increases. At the end of the proton range, the protons are stopped, albeit the absorbed dose rises to a peak. It is called the Bragg peak. The beam can be adjusted so that the Bragg peak is placed at the tumor site. The width of the Bragg peak is not enough to cover large tumors. The proton energy is changed by passing the beam through a modulator and many Bragg peaks occur at various depths. The Spread Out Bragg Peak was obtained from the superposition of multiple Bragg peaks. In this work, the SOBP was generated when the proton beam hits a wheel-shaped Poly Methyl Methacrylate (PMMA) as a range modulation. The PMMA was located perpendicular to the proton beam direction and rotating around the proton beam direction. The modulator has different steps and the thickness and the spanning angle vary at each step so that the protons pass thorough different thicknesses and consequently several Bragg peaks are produced. Without using a modulator, the Bragg peak of 76.85 MeV proton beam was placed at the end of the tumor volume (in the direction of the dropped protons on the tumor). From the collision of the 76.85 MeV proton beam with different thicknesses of a modulator, several Bragg peaks are created in the tumor region. With increasing the thickness of the modulator, the created Bragg peaks cover the entire tumor volume. The thickness of the PMMA changes from 0 to 16.8 mm in 25 steps meaning that the thickness increases by 0.7 mm at each step. The Spread Out Bragg Peak was obtained using the superposition of pristine Bragg curves with different weight coefficients., Bragg curves were assembled together according to the following relation²³:

$$w_1{D}_{i1}+w_2{D}_{i2}+\dots +w_N{D}_{iN}=D_{0}i=1,2,\dots N$$ (4)

Where w_i parameters are the weight coefficients which are dimensionless and calculated using MATLAB software. D_i parameters are the proton dose at each Bragg curve at a certain depth. D₀ is a constant value and related to the amount of dose in the SOBP region. N is the number of equations and represents the number of pristine Bragg curves. The role of each Bragg peak in creating the SOBP is proportional to the spanning angle of each thickness. In this modulator, the sum of weight coefficients is equivalent to 360 degrees. Thus, the spanning angle associated with each thickness of the modulator was calculated. Different thicknesses of PMMA create a continuous spectrum of the absorbed dose in the tumor region. These calculated angles and weights are shown in Table 3.

Table 3.

The characteristics of the range modulator used in the simulations.

Spanning angle (degree)	Relative weight	Thickness (mm)	Step number
90.486 27.352 24.166 19.563 17.356 14.403 13.475 12.326 11.408 11.173 10.275 9.513 9.629 8.451 8.454 8.114 7.561 7.703 7.290 6.779 7.149 6.666 6.153 5.838 8.713	5.142772 1.55456 1.373488 1.111897 0.986462 0.818624 0.765882 0.700552 0.648367 0.635031 0.584014 0.540668 0.547287 0.480308 0.480462 0.461173 0.42975 0.437821 0.414314 0.385301 0.406308 0.378858 0.349732 0.331832 0.495192	0 0.7 1.4 2.1 2.8 3.5 4.2 4.9 5.6 6.3 7.0 7.7 8.4 9.1 9.8 10.5 11.2 11.9 12.6 13.3 14.0 14.7 15.4 16.1 16.8	1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

3. Results

3.1. Proton depth-dose calculation

Comparison of the simulated and measured dose distribution created by 108.8 MeV proton beam was carried out in the water phantom. The simulation results and measured data are shown in Fig. 1 and were in good agreement with each other. The CSDA ranges of 75 MeV proton beam in water, PMMA, soft tissue and compact bone were calculated using the FLUKA and GEANT4 codes and are shown in Table 1. It can be seen that the simulation results were in good agreement with the ICRU49 report.³⁰ As already mentioned, a spherical shaped tumor with the same composition of the brain tissue has been irradiated from 30 MeV to 130 MeV proton beam along the beam with energy steps of 10 MeV. The absorbed dose of the protons was calculated as a function of the depth of the brain in rectangular voxels with a size of 2 × 2 × 0.1 mm³ using the GEANT4 and FLUKA codes. Fig. 3 illustrates the depth dose profiles.

Fig. 3.

Proton absorbed dose as a function of depth in the head phantom from protons with different energies using GEANT4 code.

By changing the energy of the proton beam, it can be seen that the appropriate proton energy for treatment is 76.85 MeV. Concerting this energy, the Bragg peak was located exactly at the end of the tumor volume. To achieve the flat dose distribution (Spread Out Bragg Peak) in the tumor volume, a modulator was designed in the form of a wheel. This wheel is made of PMMA and its thickness is variable as shown in Table 3. The 76.85 MeV proton beam strikes the modulator and, therefore, a lot of Bragg peaks in different depths of the brain are formed. Giving an appropriate weight to each Bragg peak and adding them (According to Eq. 4), the SOBP was obtained in the depth of the tumor. The resultant SOBPs are shown in Fig. 4. Characteristics of Bragg curves obtained from the two Monte Carlo codes are shown in Table 4. The range is the distal region of the Bragg peak, the penumbra width is the difference of 80% and 20% absorbed dose in the distal region and FWHM is Full Width at Half Maximum of the Bragg peaks.

Fig. 4.

Comparison of the Spread Out Bragg Peaks created by 76.85 MeV proton beam, using GEANT4 and FLUKA codes.

Table 4.

Comparison of the Bragg curve and SOBP parameters obtained from 76.85 MeV proton beam.

Monte Carlo code	Range (cm)	Penumbra width (cm)	FWHM (cm)	Penumbra width in SOBP (cm)
FLUKA GEANT4	4.13 4.11	0.07 0.08	0.41 0.42	0.1 0.09

The lateral dose distribution in the tumor has also been simulated as shown in Fig. 5. The penumbra width in SOBP is calculated using simulation codes and it is equal to 0.1 cm and 0.09 cm, which are calculated by the FLUKA and GEANT4 codes, respectively.

Fig. 5.

Comparison of the lateral dose distribution of 76.85 MeV proton beam at 3.1 cm depth from the surface of the skin, using GEANT4 and FLUKA codes.

The proton dose absorption in the tumor, skin, skull and brain tissues as a function of proton energy from 30 MeV to 130 MeV is shown in Fig. 6. It can be seen that the maximum absorbed dose was at the proton energy of 76.85 MeV. The energy deposition of 76.85 MeV protons in the tumor has been calculated using FLUKA-USRBIN and shown in Fig. 7.

Fig. 6.

Comparison of the proton absorbed dose in tumor, skin, skull and brain tissues as a function of proton energy with the energy range from 30 MeV to 130 MeV using GEANT4 code.

Fig. 7.

Energy deposition (x,z) profile of 76.85 MeV protons inside the tumor simulated using FLUKA-USRBIN.

3.2. Secondary neutrons and photons production

Due to the non-elastic nuclear interaction of protons with different elements inside the head, the secondary particles are produced, characterized by two main groups including neutrons and photons. The energy spectrum of the neutrons and photons per incident proton for 76.85 MeV proton beam were simulated using the GEANT4 toolkit and shown in Fig. 8. The neutrons and photons dose absorption in the tumor, skin, skull and brain tissues produced by 76.85 MeV proton beam is shown in Fig. 9. In this figure, it can be seen that the dose of secondary particles was absorbed more in the tumor region. The total fluxes of neutrons inside the head phantom were obtained as 2.52 × 10⁻³ 1/cm³ and 1.93 × 10^-3 1/cm³ and as for photons they were obtained as 2.81 × 10⁻³ 1/cm³ and 2.38 × 10^-3 1/cm³ using the GEANT4 and FLUKA codes, respectively. The average energy of neutrons obtained in the tumor, skin, skull, and brain were 11.87, 7.39, 7.57, and 7.97 MeV, respectively. While these values for photons were 4.55, 3.49, 3.74 and 3.42 MeV, respectively. The absorbed dose of secondary particles obtained were 0.00758 and 0.00693 Gy/proton in the tumor, 0.000307 and 0.000263 Gy/proton in the brain, 0.000131 and 0.000105 Gy/proton in the skull, 0.000163 and 0.000140 Gy/proton in the skin, using the GEANT4 and FLUKA codes, respectively.

Fig. 8.

Energy spectrum of (a) neutrons and (b) photons, produced by 76.85 MeV proton beam.

Fig. 9.

Comparison of the secondary neutrons and photons absorbed dose in tumor, skin, skull and brain tissues for 76.85 MeV proton beam energy using GEANT4 and FLUKA codes.

The total absorbed doses of protons and secondary neutrons and photons in various tissues of the head are shown in Table 5. The results show that more than 99% of the total dose was absorbed in the tumor.

Table 5.

Total absorbed dose in the head tissues.

Monte Carlo code	Tumor (nGy/proton)	Brain (nGy/proton)	Skull (nGy/proton)	Skin (nGy/proton)
FLUKA GEANT4	0.98123 0.93368	0.005543 0.003747	0.000627 0.000596	0.000572 0.000439

4. Discussion

From Fig. 3 it can be seen that by increasing the energy of the proton beam, Bragg peaks were created inside the brain region and they become shorter and wider. Research shows that with increasing energy, the range straggling increases and, therefore, the peaks become shorter and wider.²⁷ A spherical brain tumor was considered to be 1 cm in radius and 1 cm from the surface of the brain. The simulation results show that when the proton beam has energy of 76.85 MeV, the Bragg peak was formed at the end of the tumor region. Research shows that the location of the inhomogeneous tissue does not affect the shape of the Brag curve, while it affects the dose in the Bragg curve.³⁵ Research has been done to use low Z materials, such as PMMA, to change the range of protons and high Z materials, such as Pb, to create lateral scattering.^23,26 For treatment planning, to create a SOBP in the tumor region, a modulator with different thicknesses is required, which can be achieved by using a modulator wheel. By placing a modulator wheel with different thicknesses of PMMA in the path of the 76.85 MeV protons, a large number of Bragg peaks are formed in the tumor. Using the appropriate proton beam energy and a modulator, the SOBP was created that covers the entire tumor volume. The SOBP and lateral dose distribution of 76.85 MeV proton beam obtained using the GEANT4 and FLUKA codes, shown in Fig. 4, Fig. 5, were in good agreement with each other.

The deposited energy of the primary protons in the brain tumor is an important factor to determine the appropriate proton energy. This factor can be calculated using the Monte Carlo codes by changing the proton beam energy. According to the considered geometry, the simulation results show that the energy deposition in the tumor increases with increasing the proton energy up to 76.85 MeV, after which it decreases because of the deposition of a portion of the proton energy in the other organs surrounding the tumor. Fig. 6, Fig. 7 show that, at 76.85 MeV, the tumor absorbs the maximum dose and, also, the healthy tissues absorb the minimum dose emitted by the protons. In fact, the proton absorbed dose values in the tumor, brain, skull and skin were 99.2%, 0.41%, 0.16% and 0.23%, respectively.

Neutrons and photons are the most important secondary particles formed by the interaction of protons with elements. Positron emitter isotopes are also produced from non-elastic nuclear reactions of the primary protons with stable nuclei such as ¹²C, ³⁵Cl, ¹⁶O and other elements in the tissue from the (p,pn) reactions.³⁶ Figs. 8a and 8b show the energy spectrum of secondary neutrons and photons. The neutron energy spectra have a peak at low energies. The photon energy spectra have some peaks which are related to the characteristic gamma ray energies emitted from the excited carbon, chlorine and oxygen.²⁵ Nuclei such as ¹¹C, ³⁴Cl and ¹⁵O are positron emitters. After the positive beta decay, the positron moves in the tissues and loses its energy due to the coulomb interaction. Close to the end of its track, the positron combines with an atomic electron, the two annihilate each other, and at least two 0.511 MeV photons appear in opposite directions. By revealing these photons using PET camera, it can be possible to determine the location of the Bragg peak, which is very important in proton therapy.

The energy deposition of protons in a slab head phantom and calculated secondary neutrons and photons produced in proton therapy of the human brain have been evaluated using the MCNPX code.²⁵ They changed the energy from 40 MeV to 140 MeV. They found that for high energy proton beams, the amount of escaped energy by neutrons is almost 10 times larger than that by photons and it is around 1% at 110 MeV proton beam energy.

In this study, the results show that the average energy of neutrons in tumor, brain, skull and skin with a factor of 2.61, 2.33, 2.02, and 2.11 were higher than the average energy of photons, respectively. The absorbed dose of the secondary particles in different tissues that were simulated using the GEANT4 and FLUKA codes were in agreement with each other. The results of the simulations using the GEANT4 code show that the absorbed dose of secondary particles in tumor were 24.69, 57.86 and 46.50 times more than the absorbed dose in the brain, skull and skin, respectively. Mneanwhile these results obtained using the FLUKA code were 26.35, 66 and 49.50, respectively. It can be seen from Table 5 that the total absorbed dose in the tumor was 249.18 and 177.02 times higher than in the brain, 1566.58 and 1564.96 times higher than in the skull, 2126.83 and 1715.44 times higher than in the skin, calculated using the GEANT4 and FLUKA codes, respectively.

5. Conclusions

A SNYDER head phantom consisting of the skin, skull, brain and also tumor has been simulated using the GEANT4 and FLUKA codes. The brain tumor is considered as a sphere with a radius of 1 cm and is located 2.1 cm under the skin with the same elemental composition as the brain. The results show that by modulation of pristine Bragg peaks corresponding to the 76.85 MeV proton beam energy with their relevant weights, the SOBP can be obtained that longitudinally and laterally covers the tumor volume. The absorbed dose of the protons in the skin, skull, tumor and brain tissues was calculated for 76.85 MeV proton energies. It was found that 99.2% of the total dose for 76.85 MeV proton beam is absorbed in the tumor volume. Neutrons and photons have been considered as the most important secondary particles produced in the non-elastic nuclear reactions of the protons whose flux and absorbed dose have been calculated in different tissues. The absorbed dose of the protons and secondary neutrons and photons has been calculated in tumor, skin, skull and brain tissues. It was found that more than 99% of the total dose is absorbed in the tumor. Ultimately the tumor is irradiated in 3 dimensions while the healthy tissues absorb less radiation.

Conflict of interest

None.

Financial disclosure

None.