Gluten-free cookies with low glycemic index and glycemic load: optimization of the process variables via response surface methodology and artificial neural network

Abstract

This research investigates the effect of baking temperature and time on the resistant starch (RS), glycemic index (GI) and glycemic load (GL) of gluten-free cookies, optimized the processing parameter using a chemometrics approach of response surface methodology (RSM) and artificial neural network (ANN). The in-vitro starch digestibility of the formulated cookies exhibited a monophasic starch digestogram. Increase in resistant starch, and a decrease in the predicted GI of the cookies, was associated with low temperature and high baking time. The use of RSM and ANN modelling techniques accurately predict the RS, pGI and GL (coefficient of determinant, R² > 0.93 and root mean square of error = 0.43–0.62) of the gluten-free cookies. The optimal condition for the production of cookies with high RS, low pGI and GL were baking temperature of 158 °C and baking time of 20 min with predicted RS value of 19.61 g/100g of dry starch, pGI value of 56.98 and GL value 52.64.

Food science, Food technology, Food analysis, Celiac disease, Functional food, Chemometrics, Cardaba banana.

1. Introduction

In recent times, there had been increase in the demand for gluten-free (GF) food products such as bakery and pastry products with nutritive and sensory properties for partial replacement of traditional cereal-based products (Olawoye et al., 2017). The demand for GF food was due to the growing numbers of patients suffering from celiac disease. Celiac disease, an immune-mediated disorder, is a digestion condition in which an individual exhibits a negative reaction from the ingestion of gluten-containing grain. Food products made from wheat, rye, barley and oats contain gluten and may be injurious to the health of gluten-sensitive people. In these individuals, the ingestion of gluten-containing products led to the inflammation as well as mucosal damage of the small intestine. Owing to this, the only successful treatment for such patients is strict adherence to gluten-free foods and this had led to the production of gluten-free (GF) products from crops such as chickpea (Santos et al., 2020), plantain flour (Gutiérrez, 2018), pseudo cereal grain (Martínez-Villaluenga et al., 2020) and finally from grape peel and whey powder (Ungureanu-Iuga et al., 2020).

To formulate gluten-free food, there is a need for careful selection of raw materials. Several raw materials (maize, pseudo-cereal, sorghum etc.) used belong to the classes of medium-to-high glycemic index (GI) food (Chung et al., 2008; Ferrer-Mairal et al., 2012), as they are rapidly digested in the gastrointestinal tract compared to cardaba banana flour whose value were 53 and 40.44 for glycemic index and load, respectively (Ayodele and Godwin, 2010). Starch is one of the important raw materials used in the formulation of GF food and it's digested by alpha-amylase from the saliva as well as the pancreas followed by a border enzyme into glucose molecules in the gastrointestinal tract. This glucose provides the energy needed to carry out daily activities in human beings. However, the rate at which glucose is release into the bloodstream is of interest in the management of some degenerating diseases. Physiologically, Englyst et al. (1992) classified starch into Rapidly Digestible Starch (RDS), Slowly Digestible Starch (SDS), and Resistant Starch (RS). Food that contains high RDS resulted in high rate of glucose release into the bloodstream and hence, high GI. The GI is the degree at which the blood glucose level is raised two hours after the consumption of carbohydrate foods. Foods high in glycemic index (GI > 71) are found to be associated with degenerating diseases such as type 2 diabetes, cardiovascular diseases and obesity. On the other hands, SDS and RS starch fraction foods had been reported to have a low GI and help in the prevention of metabolic disorder such as hypolipoproteinaemia, as well as oxidative stress reduction. Resistant starch belongs to the starch fraction that is not digested in the small intestine but fermented by the colon microorganism to produce short-chain fatty acid (SCFA). This SCFA provides the body with additional energy as well as a high concentration of butyrate which is also beneficial in the reduction of colon cancer. Hence, it had been suggested that for health benefits, starch-baked food high in slowly digestible starch and resistant starch should be consumed (Olawoye and Gbadamosi, 2020c).

Several previous studies to improve the overall nutritional and sensorial characteristics of gluten-free products had been carried out (Malgor et al., 2020; Olawoye and Gbadamosi, 2020c; Rybicka et al., 2019). Owing to this, cookie could serve as a potentially nutritious gluten-free snack through careful selection of ingredients. The improvement of gluten-free cookie nutritionally as a result of decrease in the glycemic index, as well as the glycemic load, can be achieved through the modification of starch using either physical, chemical or enzymatic methods of starch modification. Chemical modification, depending on the degree and type of modification, the extent of starch gelatinization and sources of starch affects the rate of starch digestibility and glycemic response. Citric acid modification is a mild acid treatment of starch, which is relatively safe for industrial and pharmaceutical uses. Several researchers had reported the decrease in the GI of starch-modified through citric acid modification which they said was due to the increases in SDS and RS fractions of the starch. Remya et al. (2018), attributed the reduction in the glycemic index to the formation of bulky derivatizing group (mono, di and tri esters) which hinder the formation of the enzyme-substrate complex. Hence, cardaba banana starch modification using citric acid could find application in the production of gluten-free cookies. However, during the production of cookies, the thermal processing according Guillén et al. (2018), might lead to a reduction in resistant and slowly digestible starch, therefore, increase in the glycemic index of the formulated cookies. Hence, the need for the optimization of the baking process to minimize the glycemic response of the cookies.

Response surface methodology (RSM) is a combination of the mathematical and statistical method used for the design of experiment, model building, evaluation of the relationship between process variables as well as determining the optimum condition of variables for desire or targeted goals. It is regarded as an effective tool in optimizing complex process or reaction and had been applied by various researchers in food processing operations (Abd Rahman et al., 2017). Artificial Neural Network (ANN), on the other hand, is a collection of computational elements stimulated to imitate the human brain. Its advantage is that it is structurally generic and can learn from historical data. It is advantageous over RSM in that it doesn't need prior knowledge of the experimental data and can be used to estimate almost all types of non-linear models such as quadratic models (Khajeh et al., 2017). Although ANN had found application in modelling various biosystem, however, its application in optimizing the glycemic response in GF cookie is still limited. In this study, RSM and ANN were used to find the optimum process condition (baking temperature and time) for the preparation of GF cookies with low GI.

2. Materials and methods

2.1. Cardaba banana flour

The flour from cardaba banana used for the cookies production was produced as described by Olawoye and Gbadamosi (2020a). The de-bunched cardaba banana was peeled under water, sliced and dried at 50 °C for 8 h in a conventional hot air oven (Uniscope, SM9053, England). Following drying, the sliced bananas were milled and packed in an airtight container prior to use.

2.2. Extraction of cardaba banana starch

Cardaba banana was de-bunched, washed and peeled, the isolation of starch from the banana was done using a method described by Olawoye and Gbadamosi (2020a). Briefly, Cardaba banana was de-bunched from the stalk, washed, peeled and sliced. The banana slices were milled with the addition of water (1.5 L) for 10 min using Stephan milling machine (Stephan Universal Machine, Germany). The banana mash obtained after milling was suspended into distilled water (1.5 w/v). Following suspension, the mash was sieved using 200 μm mesh size and the corresponding starch slurry was allowed to stay overnight. The starch obtained was washed three times with distilled water until the starch slurry was free from non-starch material. After washing, the starch obtained was dried at 45 for 12 h and was subsequently packaged in airtight container until for further use.

2.3. Citric acid modification of cardaba banana starch

Citric acid modification was done according to the method described by Klaushofer et al. (1978) with some modifications. Cardaba banana starch (500g) was dissolved in 0.12M of citric acid (1:4 w/v) in a glass beaker. The starch slurry was stirred on a magnetic stirrer for 120 min with a continuous adjustment of the pH to 5.5 using 0.1M NaOH. The starch slurry was centrifuged at 3000 rpm for 5 min and subsequently washed three times with a twofold volume of distilled water to remove the unreacted citric acid. Finally, the washed starch was dried at 45 °C in a hot-air oven (Uniscope, SM9053, England) for 12 h, it was milled into powder and packed in airtight containers for further use.

2.4. Experimental design, RSM modelling and optimization

A central composite design (CCD) with a second-order polynomial model was used to evaluate the combined effect of the independent variables (baking temperature and time) on the resistant starch, glycemic index and glycemic load of the formulated GF cookies using Design Expert 12.0.3 (Stat-Ease. Inc. U.S.A.). The range of values considered for the independent variables were 150–180 °C and 10–20 min for the baking temperature and baking time, respectively (Table 1). A second-order polynomial model was used to fit the relationship between the independent variables and the response (Eq. (1)). The quality of the fitted model was evaluated using a significance test and analysis of variance (ANOVA). The effects of each model terms, as well as their interaction, were identified graphically using the Pareto chart.

$$Y=b_0+\sum _{i=1}^k{b}_i{X}_i+\sum _{i=1}^k{b}_{ii}{X}_i^2+\sum _{i<j}^k{b}_{ij}{X}_i{X}_j+e$$ (1)

where Y is the response variable, b₀ is the intercept value, b_i (I = 1, 2, …. k) is the first-order model coefficient, b_ij is the interaction effect, and b_ii represents the quadratic coefficient of X_i. X_i and X_j are the independent variables that affect the dependent (response) variables and ⅇ represents the random error.

Table 1.

Experimental and predicted values for the dependent variables.

Runs Code	A	B	Experimental			Predicted RS		Predicted PGI		Predicted GL
			RS	PGI	GL	RSM	ANN	RSM	ANN	RSM	ANN
C1	165	15	18.33	56.88	51.95	17.29	17.4199	56.90	56.89	51.45	51.45
C2	165	25	22.64	56.98	55.12	22.99	22.6307	56.98	56.97	55.28	55.12
C3	150	20	20.28	57.07	52.73	20.08	20.2528	57.07	57.07	52.67	52.73
C4	165	15	16.89	56.87	51.97	17.29	17.4199	56.90	56.89	51.45	51.45
C5	180	20	19.53	56.67	53.62	18.93	20.5958	56.67	56.67	53.30	53.62
C6	150	10	13.55	57.11	50.11	13.97	13.5848	57.10	57.11	50.30	50.11
C7	165	15	15.96	56.94	51.28	17.29	17.4199	56.90	56.89	51.45	51.45
C8	195	15	20.05	56.50	53.66	20.30	20.0537	56.50	56.50	53.82	53.66
C9	165	15	16.99	56.92	51.31	17.29	17.4199	56.90	56.89	51.45	51.45
C10	135	15	15.68	57.13	50.87	15.52	15.0143	57.14	57.13	50.77	50.87
C11	180	10	19.89	56.86	52.78	19.91	19.8946	56.86	56.86	52.72	52.78
C12	165	15	18.08	56.89	50.58	17.29	17.4199	56.90	56.89	51.45	51.45
C13	165	5	18.12	57.19	52.42	17.85	18.1411	57.20	57.19	52.33	52.42

∗A: Baking temperature (°C); B: Baking time (min); RS: Resistant starch (g/100 g dry starch); PGI: Predicted glycemic index; GI H₉₀: Glycemic index at 90 min; GL: Glycemic load.

2.5. Production of GF cookies

The gluten-free cookies were produced following the method described by Giuberti et al. (2015). Briefly, cardaba banana flour and citric acid modified cardaba banana starch were blended in the ratio of 20:80 (w/w). Unsalted buttercream (8.5% of the flour blends) was creamed, mixed with whole egg (12% of the flour blend) and 20 ml of distilled water and then added to the flour blends. Sugar was not added to the mixture to limit or control the glycemic index of the formulated cookies. The mixture blends were amalgamated to form a homogenous dough in a mixer (Kenwood KMM021, UK) for 7 min, after which a pasta roller was used to laminate the dough at 80 mm height and was allowed to rest at 4 °C for 30 min. The laminated dough was cut into a small size using a dough cutter and was baked at various temperature and time following experimental design data in a household oven (Cuisinart TOB-200, U.S.A.). After baking, the cookies were allowed to cool for 30 min and were packaged in separated Ziploc polythene nylon at room temperature until further analysis.

2.6. In-vitro starch digestibility and hydrolysis kinetics

The digestion rate of the cookies was evaluated according to the method described by Olawoye and Gbadamosi (2020a). The released glucose was determined colorimetrically as described by Olawoye and Gbadamosi (2020a). The rate of starch digestion was expressed as the percentage of total starch (TS) hydrolyzed at different times.

The digestion kinetics, as well as the pGI of the GF cookies, were calculated using the procedure described by (Goñi et al., 1997). Starch hydrolysis kinetics was described using a non-linear model as shown in Eq. (2).

C_t = C_∞ (1-e^-kt) (2)

where C_t is the concentration of product or reactant at time t, C_α is the corresponding equilibrium concentration and k is a pseudo-first-order rate constant (Goñi et al., 1997). The basis of fit of the model is a low mean relative deviation modulus (MRDM <10) and high coefficient of determinant (r²) greater than 0.7. The hydrolysis index (HI) was obtained by dividing the area under the hydrolysis curves (0–180 min) of the cookies by the area of reference sample (white bread). From the result of HI, predicted glycemic index (pGI) was computed using Eq. (3) below.

GI = 39.71 + 0.54 HI (3)

Also, the glycemic load per g solid (GL) was determined from the pGI as shown in Eq. (4)

$$GL=pGI\times \frac{TS}{100}$$ (4)

where TS is the total starch of the cookie sample.

2.7. Physical and textural characteristics of GF cookies

Diameter and thickness of some selected cookies, as well as the optimized cookie, were determined with a Vanier calliper at three different points. The colour of the cookie sample was determined by a method described by Olawoye and Gbadamosi (2020b). The colour which include L∗, lightness (0 = black, 100 = white), a∗ (-a = greenness, +a = redness) and b∗ (-b = blueness, +b = yellowness) of the cookies were obtained using HunterLab colorimeter coupled with an optical sensor (HunterLab, U.S.A.). Hardness analysis was performed with a TA-XT2i Texture Analyser (Stable Micro Systems, UK) fitted with a shape blade-cutting probe as described by (Sharma et al., 2016).

2.8. Modelling using ANN

In this study, a commercial software NeuralPower version 2.5 (CPC-X Software) was used to predict the glycemic index and glycemic load of the formulated cookies. The ANN architecture included an input layer with two neurons (baking temperature and time), an output layer consisting of three neurons (RS, pGI and GL) as well as a hidden layer. To develop an optimal network topology for the model, the number of neurons, as well as the transfer function of hidden and output layers, were determined iteratively through the development of many networks. Multilayer full feedforward (MFFF), as well as multilayer normal feedforward (MNFF) neural networks, were used to predict the output variables, while the training of the data sets was done using different learning algorithms such as incremental backpropagation (IBP), quickprob (QP), genetic algorithm (GA), batch backpropagation (BBP), and Levenberg-Marquardt algorithm (LM). The experimental data obtained from the central composite design was split into two: training and testing data sets. The training dataset consists of 8 experimental runs while the remaining dataset was used for testing.

3. Result and discussion

3.1. In vitro starch hydrolysis kinetics of the cookies

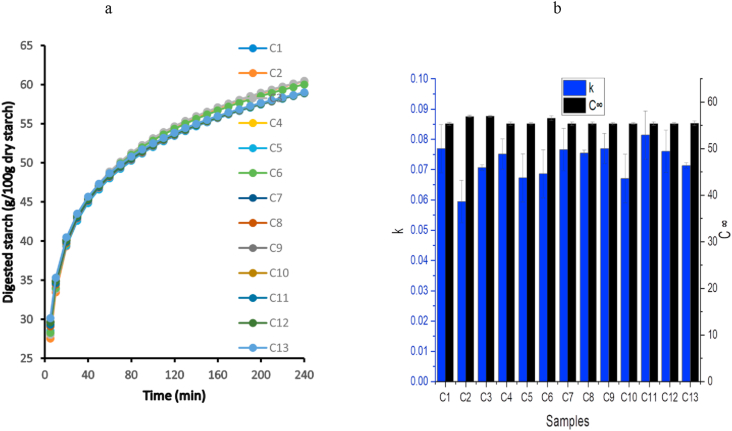
The in-vitro starch hydrolysis kinetics (digestogram) of the formulated cookies is shown in Figure 1a. The cookies, irrespective of their processing variables exhibited a monophasic starch digestogram in which the initial restriction to hydrolysis was insignificant. It could be seen that the quantity of digested starch increased with an increase in the digestion time at a different rate throughout the enzymatic hydrolysis of the cookies. This increase could be as a result of an increased in the interactions between the substrate (cookies) as reported by Mahasukhonthachat et al. (2010).

Figure 1.

(a) Starch digestogram of the gluten-free cookies; (b) Digestion parameters of the cookies.

To obtain more quantifiable information about the digestion properties of the cookies, a first-order kinetics model was applied to the cookies hydrolysis and a predictive parameter was obtained whose values (average r² = 0.760, SSE = 13, MRDM = 4%) affirmed the suitability of the approach in describing the cookies monophasic digestogram (Figure 1a). As it could be seen, the average value of the MDRM is lower than 10 which is an indication of a good model. The values of the digested starch equilibrium (C∞) and kinetic constant (k) which revealed the rate of digestion of the formulated cookies are shown in Figure 1b. The figure reveals the values ranged between 0.059 to 0.081 min⁻¹ and 55.39–56.98 g/100g dry starch for kinetics constant and digested starch equilibrium, respectively. The highest rate of digestion (k) was found in cookie sample C11 while it was observed cookie sample coded C2 had the lowest rate of digestion. The values of k reported in this study were slightly higher than the values reported by Giuberti et al. (2015) who reported an average of 0.61min⁻¹ for their gluten-free maize cookies. The kinetics constant (k) is an important property and index for the susceptibility of the cookies to amylase hydrolysis. The value of C∞ revealed that the cookies with the maximum digested starch were cookies coded C3 with 56.98 g/100 g dry starch.

3.2. Process optimization

3.2.1. Analysis of the model of resistant starch

The analysis of variance obtained for the models is presented in Table 2. The ANOVA of the regression model demonstrated that the experimental model was highly significant, an evident of its lower p-values (<0.001). Also, as it could be seen from the result, the linear terms (i.e. 1L and 2L), interaction parameter, as well as the quadratic term of the baking time were all observed to be highly significant (p < 0.001). However, the quadratic parameter of the baking temperature is not significant (p > 0.05). The predictive equation of the quadratic model was deduced taking into consideration only the significant terms with p < 0.001 as shown in Eq. (5).

$$RS=17.29+1.19A+1.28B-1.77AB+0.78B^2$$ (5)

Table 2.

Analysis of variance (ANOVA) of the dependent variables.

Factor	SS	df	MS	F	P
Resistant starch
Model	63.69	5	12.74	19.46	<0.001∗
(1)Baking Temperature(L)	17.13	1	17.13	26.17	0.0013
Baking Temperature(Q)	0.56	1	0.56	0.85	0.3870
(2)Baking Time(L)	19.79	1	19.79	30.24	<0.001∗
Baking Time(Q)	14.09	1	14.09	21.53	0.0023
1L by 2L	12.55	1	12.55	19.17	0.0032
Lack of fit	0.86	3	0.29	0.31	0.8202∗∗
Error	4.58	7	0.65
Total SS	68.27	12
R2	0.9329
Adjusted R2	0.8849
Predicted glycemic index
Model	0.42	5	0.08	168.01	<0.001∗
(1)Baking Temperature(L)	0.30	1	0.30	602.56	<0.001∗
Baking Temperature(Q)	0.01	1	0.01	19.65	0.003∗
(2)Baking Time(L)	0.04	1	0.03	71.51	<0.001∗
Baking Time(Q)	0.05	1	0.05	97.42	<0.001∗
1L by 2L	0.01	1	0.01	11.63	0.0112∗
Lack of fit	0.001	3	0.000	0.05	0.9853∗∗
Error	0.003	7	0.0005
Total SS	0.43	12
R2	0.9917
Adjusted R2	0.9858
Glycemic load
Model	22.30	5	4.46	20.24	<0.001∗
(1)Baking Temperature(L)	6.96	1	6.96	31.60	<0.001∗
Baking Temperature(Q)	1.03	1	1.03	4.67	0.068∗∗
(2)Baking Time(L)	6.53	1	6.53	29.63	<0.001∗
Baking Time(Q)	7.96	1	7.96	36.10	<0.001∗
1L by 2L	0.80	1	0.80	3.64	0.098∗∗
Lack of fit	0.22	3	0.07	0.22	0.8760∗∗
Error	1.54	7	0.22
Total SS	23.84	12
R2	0.9353
Adjusted R2	0.8891

Superscript ∗ are significant at P < 0.05; Superscript ∗∗ are not significant at p > 0.05.

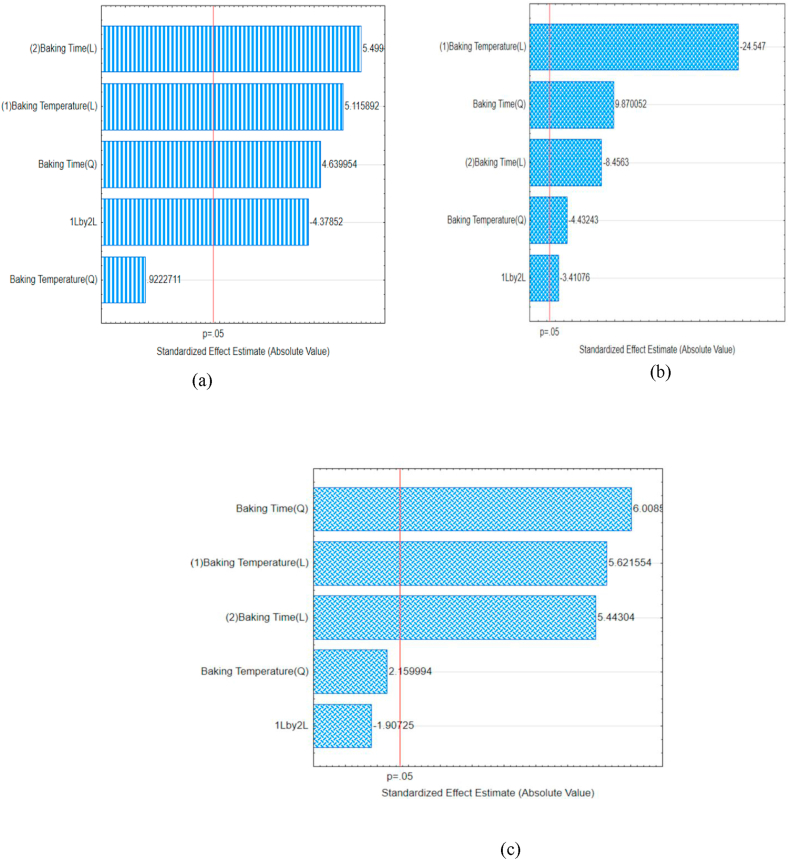
The relationship between the dependent variable (resistant starch) and the model terms are shown in Figure 2a. The result of the regression coefficient revealed that all the linear terms as well as the quadratic parameter of baking time had a positive regression coefficient and hence, a positive synergy between the experimental model terms and the experimental response. However, the interaction between the baking temperature and time had a negative coefficient hence, a negative impact on the resistant starch.

Figure 2.

Pareto chart of standardized effects for modification process.; L - linear; Q – quadratic. (a) Resistant starch; (b) glycemic index; (c) glycemic load.

The statistical significance and quality of the model as evaluated using an ANOVA test as presented in Table 2 suggest that the regression model could be employed in navigating the design space. The value of the coefficient of determinant (R²) is 0.9329 which indicated that 93.29% of the data variance was attributed to the independent variables while only 6.61% of the variation could not be explained. The closeness of the R² values to unity indicates the high significance of model terms. However, the coefficient of determinant alone does not make a good model or fit for use because it doesn't take into consideration the effect exhibited when a new term is added to the experimental process. Hence, it must be compared to the adjusted R² (08849) which measures the sample variance of the experimental process and take in consideration the addition of new independent variables and only increase when the model is being enhanced by the new terms. The lack of fit of the model was 0.8202 which is insignificant (p > 0.05).

3.2.2. Effect of independent variables on resistant starch

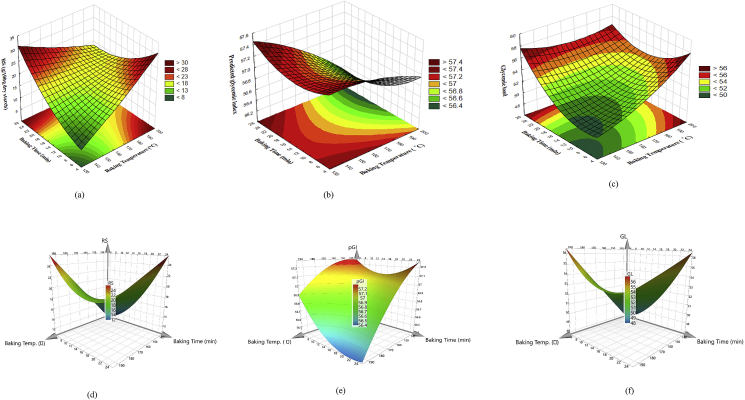
The simultaneous effect of the baking temperature and time on the resistant starch of the cookies is depicted in Figure 3a. The three-dimensional response surface plot revealed that the resistant starch of the cookies depends mainly on the baking time because both the linear and quadratic effects are highly significant with p < 0.001. The plot revealed an increase in the resistant starch of the cookies as both the baking temperature and time increases. Although the baking temperature of the cookies had no significant effect on the RS, its increase led to an increase in the resistant starch. The increase in the resistant starch fraction of the cookies could be attributed to the strong interaction between the molecular chains and the helical structure causing an orientation and formation of starch crystals after baking at high temperature. The formation of starch crystals in the cookies would lead to the resistance of the cookies against enzyme hydrolysis hence, an increase in the resistant starch. In their study, Ritudomphol and Luangsakul (2019), reported an increase in the resistance starch of an instant rice. They attributed this increase to the formation of starch crystal as a result of high processing temperature. The combined effect of both variables shows that a low temperature/high baking time is more effective in increasing the resistant starch of the gluten-free cookies than a high temperature/low baking time. The result obtained in this study commensurate with the findings of Liu et al. (2020). The optimal resistant starch conditions for this model were determined by maximizing desirability and were: baking temperature: 158 °C; baking time: 20 min of the cookie production have been investigated and the actual RS obtained under this conditions was 20.10 ± 1.04 g/100g against a predicted value of 19.61 g/100g of dry starch with no significant difference (p > 0.05).

Figure 3.

Effects of independent variables on (a) resistant starch (b) glycemic index (c) glycemic load for RSM model (d) resistant starch (e) glycemic index (f) glycemic load for ANN model.

3.2.3. Analysis of RSM model of predicted glycemic index

The result of the RSM model analysis of the pGI is shown in Table 2. For the predicted glycemic index, it could be seen from Table 2 that both the linear terms of the independent variables (1L and 2L), the quadratic parameter of the baking time was highly significant (p < 0.001), while the interaction between the independent variables as well as the quadratic parameter of the baking temperature was significant (p < 0.05). The final predictive equation for the predicted glycemic index was obtained and presented in Eq. (6).

$$pGI=56.90-0.16A-0.05B-0.04AB-0.02A^2+0.05B^2$$ (6)

From the result of the analysis of variance of the experimental result of pGI, the F value of the model was 168.01 and was highly significant (p < 0.001). Both the P and F value shows the significance of model terms, but they don't differentiate between the positive or negative significant effect on the model. Owing to this, the standard effect of the baking temperature and time, as well as their interaction on the predicted glycemic index, is visualized using the Pareto chart (Figure 2b). The negative coefficient of all the model terms except the quadratic term of the baking temperature showed an antagonist effect on the predicted glycemic index of the cookies. The statistical significance of the experimental model was evaluated using the coefficient of determinant and adjusted R². The value of the R² was 0.9917 which indicate that only 0.83% of the experimental data variation could not be explained by the independent variables. The adjusted R² of model 0.9858, a value close to the coefficient of determinant and hence the significance of the experimental model to adequately predict the dependent variable. Also, the insignificance of the lack of fit (0.9853) with p > 0.05 affirmed the adequacy of the experimental model.

3.2.4. Effect of independent variables on predicted glycemic index

The three-dimensional response surface profile of the predicted glycemic index is shown in Figure 3b. Both the independent variable had a significant effect (p < 0.001) on the pGI of the cookies. However, it was observed that the baking time had a linear effect on the pGI while the baking temperature exhibit a quadratic effect on the pGI of the cookies. The plot revealed a decrease in the predicted glycemic index as the baking temperature of the cookies increases. The decrease could be ascribed to the increase formation of resistant starch as a result of the crystallization of the amylose starch granule in the cookies. This result commensurate with the report of da Silva and Conti-Silva (2018) who also reported decrease in the glycemic index of gluten free cookies as the temperature of baking of the cookies increases. Minimal predicted glycemic index was observed when the baking time increased from 4 min to 18 min, however, a baking time above 18 min led to a significant increase in the pGI. The reason for the low pGI could probably be that the baking condition not only renders a fraction of the starch resistant due to amylose crystallization but also lower the rate of enzymatic digestion of the cookies non-RS fraction. The optimal conditions for the production of low glycemic index cookies after which the desirability had been maximized are: baking temperature: 158 °C; baking time: 20 min of the cookies production in which the actual predicted glycemic index obtained was 54.83 ± 0.92 against a predicted value of 56.98 with a significant difference (p < 0.05).

3.2.5. Analysis of RSM model of glycemic load

The analysis of variance results of the baking temperature and time effect on the glycemic load of cookies are resented in Table 2.

The results revealed that the linear parameters (i.e. baking temperature and time) are highly significant (p < 0.001). for the quadratic terms, only the baking time (Q) is highly significant (p < 0.001) while the baking temperature (Q) was found to be insignificant (p > 0.05). Finally, the interaction parameter of the baking temperature and time is insignificant with p > 0.05. The final equation for the prediction of the glycemic load of the cookies taking into consideration only the significant terms is presented in Eq. (7).

$$GL=51.45+0.76A+0.74B+0.59B^2$$ (7)

The analysis of the glycemic load model revealed the significance of the model owing to its high Fischer test value of 20.24. Both the P and F values of the model indicated the significance of the model terms, they however did not reveal the synergistic effects (positive or antagonist effect) of the model terms on the dependent variable (glycemic load). owing to this, the synergistic effects of the independent variables as well as their interaction on the glycemic load is presented visually using the Pareto chart (Figure 2c). The chart revealed that both the linear terms as well as the quadratic parameter of baking time (Q) had a positive coefficient and hence positive synergistic effect on the glycemic load of the cookies. The bar chart of the quadratic parameter of the baking temperature as well as that of interaction parameter was observed to fall below the threshold red line and hence their insignificant effect on the GL. The statistical quality of the experimental model was determined using the coefficient of determinant, adjusted R² as well as the lack of fit of the model. The values of the R², adjusted R² and the lack of fit of the model were 0.9353, 08891 and 0.8760, respectively. According to Olawoye and Gbadamosi (2020a), coefficient of determinant measures the extent of sample variation in the glycemic load, which can be explained by the baking temperature and time as well as the interaction between them. The R² value obtained in this study indicated that only 6.47% of the experimental data variations could not be explained by the processing factors as well as the interaction between them. The experimental model lack-of-fit is insignificant with p > 0.05.

3.2.6. Effect of independent variables on predicted glycemic loads

The three-dimensional response surface profile of the glycemic load of the formulated cookies is shown in Figure 3c. Both the baking temperature and time significantly affect the glycemic load. The baking temperature shows a linear effect on the GL while the baking time had a very highly significant quadratic effect on the glycemic load of the cookies. Increase in both the baking temperature and time was found to significantly increase the glycemic load of the cookies. However, the combined effect of both variables revealed that a low temperature/low baking time is more effective in reducing the glycemic load of the gluten-free cookies than a high temperature/high baking time. Punia et al. (2017) reported that the glycemic load of the cookies is dependent on both the glycemic index as well as the total starch content of the gluten-free cookies. For this experimental model, the optimal glycemic load conditions are baking temperature: 158 °C; baking time: 20 min of the cookies production and the actual glycemic load obtained under this condition was 50.47 ± 1.49 against a predicted value of 52.64. These optimization conditions were based on maximum desirability.

3.3. ANN modelling and process optimization

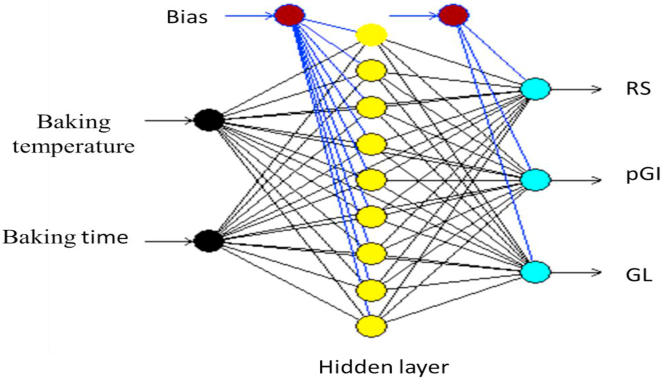
Optimal neural network topology and architecture selection is critical in the modelling of dependent variables using ANN. Owing to this, several neural architectures were developed and test for the prediction of the resistant, glycemic index and glycemic load. The result for the determination of optimal neural topology is summarized in Table 3 which revealed that the increment backpropagation (IBP) learning algorithm and multilayer normal feed-forward connection type best fits the experimental data. Furthermore, the type of transfer functions used affects both the learning rate as well as the performance of the network. In this research, among several transfer functions employed for the hidden and output layers, the sigmoid-sigmoid transfer functions bring about the acceptable model. The optimal number of hidden neurons needs to be carefully and its usually achieved by a trial by error method. According to Betiku and Taiwo (2015), the learning performance of the experimental model becomes better as the number of hidden neurons increases. The result which is based on the best goodness of fit is presented in Figure 4. Therefore, the optimum number of hidden for the neural architecture is 9 which also had 2 input neurons (baking temperature and time) as well as 3 output neurons (RS, pGI and GL). Many input and output transfer functions were used; however, the sigmoid-sigmoid transfer function was chosen which consist of a 2-9-3 topology as it gave the highest coefficient of determinant coupled with a very low root mean square of error. The result of the ANN modelling as shown in Table 3 revealed the value of 0.9915 and 0.062 were obtained for the coefficient of determinant (R²) and RMSE, respectively, for the training data set while the result of the testing revealed that the value of the coefficient of determinant (R²) and RMSE were 0.9904 and 0.337, respectively. The result obtained revealed that the relationship between the independent variables and the responses can adequately be predicted using artificial neural network.

Table 3.

R² and RMSE of the dependent variables as a function of different learning algorithm and connection types.

Model	Learning Algorithms	Connections Types	Output Layer Transfer Function	Input Layer Transfer Function	Training		Testing
					fR2	gRMSE	R2	RMSE
2-6-3	BBPa	MFFFb	Hyperbolic Tangent	Hyperbolic Tangent	0.9899	0.206	0.9871	1.78
2-6-3	IBPc	MFFF	Hyperbolic Tangent	Sigmoid	0.9902	0.105	0.9900	1.49
2-7-3	IBP	MNFFd	Sigmoid	Hyperbolic Tangent	0.9906	0.06	0.9902	0651
2-7-3	QPe	MFFF	Hyperbolic Tangent	Hyperbolic Tangent	0.9710	4.025	0.9793	4.83
2-8-3	IBP	MNFFd	Sigmoid	Hyperbolic Tangent	0.9907	0.064	0.9904	0.62
2-8-3	QPe	MFFF	Sigmoid	Hyperbolic Tangent	0.9164	3.037	0.9174	3.09
2-8-3	BBP	MFFF	Hyperbolic Tangent	Sigmoid	0.9897	0.113	0.9893	1.36
2-9-3	IBP	MNFF	Sigmoid	Sigmoid	0.9915	0.0623	0.9904	0.337
2-9-3	IBP	MFFF	Sigmoid	Hyperbolic Tangent	0.9906	0.0641	0.9905	0.314

^aBatch Back Propagation;

^bMultilayer Full Feed Forward;

^cIncremental back propagation;

^dMultilayer normal Feed Forward;

^eQuick Propagation;

^fCoefficient of determination;

^gRoot mean square deviation.

Figure 4.

Neural Network Topology of the dependent variables.

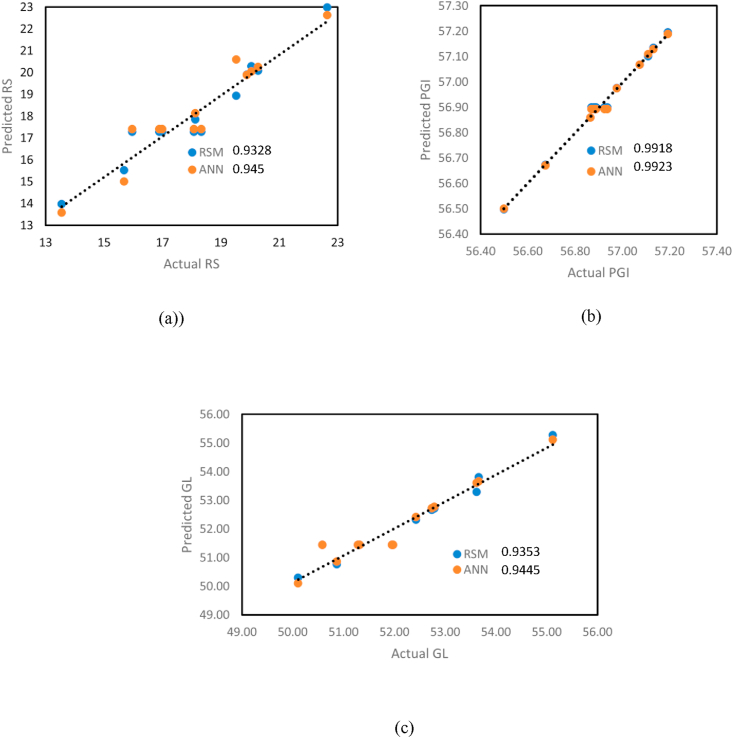
3.4. Comparison between RSM and ANN predicted values

Table 4 and Figure 5 revealed the predicted and actual values of resistant starch, glycemic index and glycemic load using RSM and ANN. The performance of both models was evaluated using the coefficient of determinant (R²) and root mean square of error (RMSE). Although both RSM and ANN model performed well, however, the ANN model approach performed better n both experimental data fitting as well as estimation capabilities than RSM model approach. This result was also supported by the parity plot between the predicted and experimental values. Akintunde et al. (2015) and Olawoye et al. (2020) also reported the superiority of ANN over RSM when optimizing the extraction of oil from Bauhinia monandra seed and cardaba starch respectively.

Table 4.

Optimal condition for RSM and ANN.

Model	Baking temperature (°C)	Baking time (min)	Predicted value			Actual value
			RS (g/100 g dry starch)	pGI	GL	RS (g/100 g dry starch)	pGI	GL
RSM	158	20	19.61	56.98	52.64	20.1	54.83	50.47
ANN	155	18.5	20.65	54.06	49.11	21.04	52.9	48.52

Figure 5.

Plot of predicted (RSM and ANN) values against Actual values:(a) resistant starch; (b) predicted glycemic index; (c) glycemic load.

3.5. Physical and textural properties of the gluten-free cookies

The physical characteristics (thickness, width and spread ratio) of the gluten-free cookies are presented in Table 5. The thickness and width of the cookie samples ranged between 0.60 - 0.79 mm and 3.52–4.15mm, respectively. The result revealed that the baking time had a pronounced effect on the thickness and width of the cookie samples. Cookie subjected to long baking time had the lowest thickness and width. The spread ratio of the cookie sample which was obtained by dividing the width to thickness of the cookie ranged from 5.46 to 6.23. Cookie formulated under the processing condition of 180 °C baking temperature and 20 min baking time had the highest spread ratio. The change in spread ratio values of the gluten-free cookie samples was consistent with the changes in thickness and width of the cookies.

Table 5.

Physical and textural characteristics of the gluten-free cookies.

Sample	Thickness (mm)	Width (mm)	Spread ratio	L∗	a∗	b∗	Hardness (N)
C1	0.72 ± 0.02a	4.01 ± 0.09a	5.57 ± 0.10b	60.21 ± 0.31a	-4.93 ± 0.03a	10.53 ± 0.13a	60.03 ± 0.91b
C5	0.60 ± 0.01b	3.74 ± 0.07a	6.23 ± 0.08a	49.83 ± 0.84b	-4.35 ± 0.01a	11.19 ± 0.17a	67.92 ± 1.06a
C8	0.63 ± 0.04a	3.52 ± 0.01b	5.59 ± 0.06b	56.42 ± 0.75b	-3.30 ± 0.05b	9.38 ± 0.21b	64.87 ± 0.77a
C13	0.76 ± 0.02a	4.15 ± 0.05a	5.46 ± 0.10b	61.39 ± 0.80a	-4.27 ± 0.03a	11.60 ± 0.09a	43.11 ± 0.53c
Copt	0.67 ± 0.03a	3.84 ± 0.04a	5.56 ± 0.10b	51.38 ± 0.47b	1.85 ± 0.01c	10.61 ± 0.11a	65.70 ± 1.78a

∗C_opt: cookies produced from optimum condition. Values are means of three replicates ±standard deviation (n = 3). Values in the row with the same letter in superscript are not significantly different from each other (p ≤ 0.05).

The L∗, a∗, b∗ values of the cookie samples ranged from 49.83 ± 0.84–61.39 ± 0.80, -4.93 ± 0.03–1.85 ± 0.01 and 9.38 ± 0.21–11.60 ± 0.09, respectively. The decrease in L and a value coupled with increased b values of the cookies as a result of an increase in baking temperature and time could probably be due to onset/acceleration of Maillard reaction in the production of cookies. The most obvious changes in the colour of the cookie (significant decrease in L and a value, as well as increase in b values) was observed in cookie sample formulated under the process conditions of 180 °C baking temperature and 20 min of baking time. The hardness of the cookie samples which is related to the force required to break the cookie samples varied from 43.11 ± 0.53 to 67.92 ± 1.06 N. The result obtained in this research revealed that the breaking strength of the cookies in increased with increase in baking time rather than the baking temperature.

4. Conclusion

In this study, the effects of baking temperature and time on the resistant starch, predicted glycemic index and glycemic load of cookies was evaluated to maximize the RS and minimize the pGI and GL. The second-order polynomial model fitted revealed a relationship exists between the independent variables and the dependent variables (RS, pGI and GL). Based on the statistical indices, the RSM had higher RMSE as well as lower coefficient of correlation (R), compared to ANN. Hence, ANN gave the best performance as a predictive model for the dependent variables. The optimal condition for the production of cookies with high RS, low pGI and GL were baking temperature of 158 °C and baking time of 20 min with predicted RS value of 19.61 g/100g of dry starch, pGI value of 56.98 and GL value 52.64. The findings of this research will enable the establishment of appropriate process conditions for the production of GF cookies with low glycemic index and load. It would then be possible to predict appropriately baking temperature and time which will facilitate the maximization of resistant starch as well as minimization of glycemic index and load of the formulated cookies.

Declarations

Author contribution statement

Babatunde OLAWOYE: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Saka O. GBADAMOSI: Conceived and designed the experiments; Wrote the paper.

Israel O. Otemuyiwa, Charles T. Akanbi: Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.