Deep Learning Based Noise Reduction for Brain MR Imaging: Tests on Phantoms and Healthy Volunteers

Abstract

Purpose:

To test whether our proposed denoising approach with deep learning-based reconstruction (dDLR) can effectively denoise brain MR images.

Methods:

In an initial experimental study, we obtained brain images from five volunteers and added different artificial noise levels. Denoising was applied to the modified images using a denoising convolutional neural network (DnCNN), a shrinkage convolutional neural network (SCNN), and dDLR. Using these brain MR images, we compared the structural similarity (SSIM) index and peak signal-to-noise ratio (PSNR) between the three denoising methods. Two neuroradiologists assessed the image quality of the three types of images. In the clinical study, we evaluated the denoising effect of dDLR in brain images with different levels of actual noise such as thermal noise. Specifically, we obtained 2D-T₂-weighted image, 2D-fluid-attenuated inversion recovery (FLAIR) and 3D-magnetization-prepared rapid acquisition with gradient echo (MPRAGE) from 15 healthy volunteers at two different settings for the number of image acquisitions (NAQ): NAQ2 and NAQ5. We reconstructed dDLR-processed NAQ2 from NAQ2, then compared with SSIM and PSNR. Two neuroradiologists separately assessed the image quality of NAQ5, NAQ2 and dDLR-NAQ2. Statistical analysis was performed in the experimental and clinical study. In the clinical study, the inter-observer agreement was also assessed.

Results:

In the experimental study, PSNR and SSIM for dDLR were statistically higher than those of DnCNN and SCNN (P < 0.001). The image quality of dDLR was also superior to DnCNN and SCNN. In the clinical study, dDLR-NAQ2 was significantly better than NAQ2 images for SSIM and PSNR in all three sequences (P < 0.05), except for PSNR in FLAIR. For all qualitative items, dDLR-NAQ2 had equivalent or better image quality than NAQ5, and superior quality to that of NAQ2 (P < 0.05), for all criteria except artifact. The inter-observer agreement ranged from substantial to near perfect.

Conclusion:

dDLR reduces image noise while preserving image quality on brain MR images.

Introduction

High-resolution MR images with high SNR enable better visualization of precise anatomical structures, improving diagnostic accuracy and facilitating early-stage diagnosis of various central nervous system diseases.^1–3 However, SNR decreases when high-resolution images are acquired in a short acquisition time. To obtain high-resolution MR images with high-SNR, there are several options, such as changing the acquisition bandwidth, using a high magnetic field strength, and increasing the number of image acquisition (NAQ). In the clinical setting, increasing NAQ is a common choice. However, an increase of NAQ results in a longer acquisition time. To improve the image quality in low SNR images, several denoising techniques have been used.^4–6 Recently, deep learning approaches for image noise reduction have been reported.^7–9

We have previously presented a MR image denoising method called the shrinkage convolutional neural network (SCNN),^10,11 based on the denoising CNN (DnCNN)⁸ approach. Unlike the DnCNN, the SCNN can be tuned to the noise power of the input image. This is achieved by using a CNN with soft-shrinkage activation functions. With this technique, the output is proportional to the input noise power. Therefore, setting an appropriate noise level for each target image in SCNN allows the use of a single network for a large variety of noise levels without training separate CNNs that are specific to each noise level. Such a noise-adaptive network is especially useful in MRI, where scans with different contrast, such as T₁-weighted imaging (T₁WI), T₂-weighted imaging (T₂WI), and proton-density-weighted imaging (PDWI), are often acquired in the same examination.

Based on SCNN, we have developed a denoising approach using deep learning-based reconstruction (dDLR) with a CNN. dDLR performs denoising by learning noise thresholds in the high frequency components extracted from images by a discrete cosine transform (DCT), whereas SCNN¹¹ performs denoising directly in the image domain.

The purpose of this study was to test whether our proposed dDLR technique can denoise thin-slice brain MR images effectively in experimental and clinical settings. In the experimental study, we compared the denoising performance of DnCNN, SCNN, and dDLR using artificially noise-added brain images with different noise levels. In the clinical study, we evaluated the denoising effect of dDLR using brain images acquired with different NAQ values that provided different noise levels.

Materials and Methods

Our experimental and clinical studies were separately approved by the Institutional Review Board at two different institutions. Informed consent was obtained from all volunteers.

Experimental study

Volunteers

Six healthy volunteers (6 men; mean age, 42.8 years; age range, 29–51 years) were enrolled to acquire training and validation data sets. Testing data sets were acquired on a different group of five healthy volunteers (5 men; mean age, 28.4 years; age range, 24–38 years).

Deep-CNN architecture of dDLR

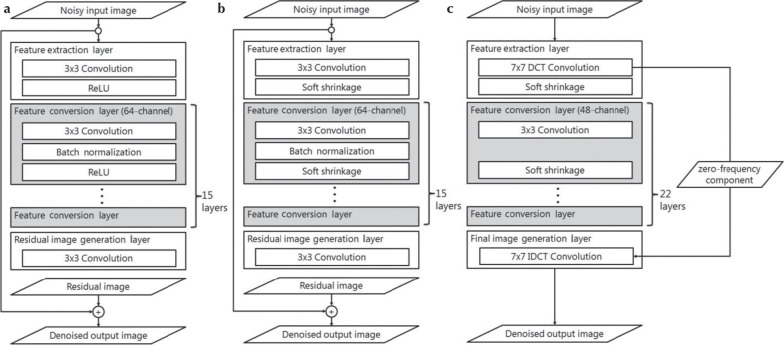
The CNN architectures of DnCNN, SCNN and dDLR used in this study are illustrated in Fig. 1. DnCNN and SCNN make use of residual learning and batch-normalization in hidden layers. In SCNN, the soft shrinkage function is used as an activation function, but it is not used in DnCNN. dDLR is based on a “plain” CNN without the skip connections featured in residual neural networks. dDLR does not have batch-normalization processing in any layers. As is the case with SCNN, the use of a soft-shrinkage activation function provides adaptive denoising at various noise levels using a single CNN without a requirement to train a unique CNN for each noise level.^10,11 Soft shrinkage has a threshold T which is calculated by multiplying the noise level σ of the input noisy image and a coefficient α which is one of the training parameters (Fig. 2). In the feature extraction layer, both SCNN and dDLR use convolution and the soft-shrinkage activation function. SCNN generates 64-channel feature maps with 64 3 × 3 convolution kernels, which are training parameters. dDLR derives 49 components with a fixed 7 × 7 DCT basis. Like wavelet shrinkage,¹² noise reduction is performed using the high frequency components of the image rather than the zero-frequency component that represents the mean gray-level value of the image. The zero-frequency component of DCT goes through a separate collateral path, while the other 48 high frequency components are processed as feature maps in the subsequent feature conversion layers. The zero-frequency component of a 7 × 7 DCT is equivalent to a 7 × 7 unweighted moving average filter. Separation of this zero-frequency component from the feature extraction layer allows the process to maintain the image contrast regardless of the scan type, such as T₁W, T₂W, etc. In contrast, the use of a 7 × 7 moving average filter loses the edges of detailed structure. Because the detailed structure information and noise are mainly in the high frequency components passing through the path of feature conversion layers, dDLR with a separated path of high frequency components can learn CNN parameters to remove noise and restore the lost detailed structure. In the feature conversion layers, convolution and the soft-shrinkage activation function are repeatedly applied to the feature maps. The kernel size of convolution layers is 3 × 3 in both SCNN and dDLR. The number of feature conversion layers is 15 in SCNN¹⁰ and 22 in dDLR. In dDLR, the CNN has more layers but fewer channels, and fewer total learning parameters than DnCNN and SCNN. Finally, in the image generation layer, the denoised image is generated by deconvolution with a 7 × 7 inverse DCT kernel followed by addition of the zero-frequency component from the other path in dDLR. To summarize, there are two kinds of learned parameters in the dDLR CNN: one kind is the 3 × 3 convolution kernels in the feature conversion layers, and the other is the coefficient of the soft-shrinkage activation function in the one feature extraction layer and the 22 feature conversion layers. The objective of the training process is to optimize the threshold coefficient (α) in the soft-shrinkage activation function in the feature extraction layer and the feature conversion layers, and the 3 × 3 convolution kernels in the feature conversion layers. These parameters are determined by minimizing a loss function based on the mean-square-error between ground-truth images and denoised images. To solve the loss function optimization problem, the Adam iterative stochastic optimization method¹³ is used as an optimizer with a step size of 0.0001. To evaluate our proposed method, a deep-CNN with the Chainer¹⁴ neural network framework was implemented. We trained the CNN over 400 epochs.

Fig. 1.

Convolutional neural network (CNN) architecture of (a) denoising convolutional neural network (DnCNN), (b) shrinkage convolutional neural network (SCNN) and (c) deep learning-based reconstruction (dDLR). (a) DnCNN is a conventional denoising method featuring residual learning and batch normalization in hidden layers. (b) SCNN differs from DnCNN in that the activation function is a soft-shrinkage function. (c) dDLR is a plain CNN, not a residual neural network. dDLR uses discrete cosine transform (DCT) convolution to divide the data into a zero-frequency component path and a path with 48 high frequency components for denoising. A soft-shrinkage activation function is applied in both SCNN and dDLR to provide adaptive denoising at various noise levels using a single CNN without a requirement to train a unique CNN at each level. IDCT, inverse discrete cosine transform; ReLU, Rectified Linear Unit.

Fig. 2.

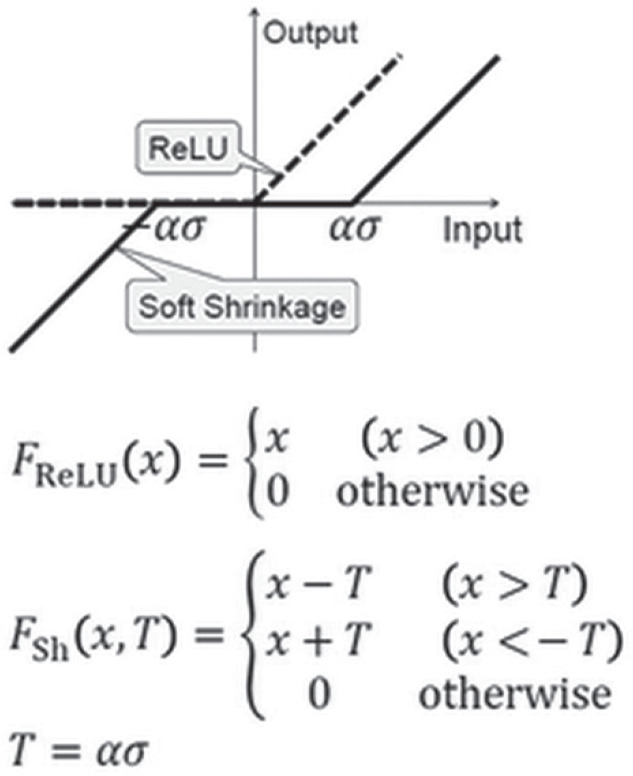
Activation function using soft-shrinkage. T is the threshold of the soft-shrinkage activation function. T is calculated by multiplying the noise level σ of the input noisy image and a coefficient α which is one of training parameters in our convolutional neural network. ReLU, Rectified Linear Unit.

Training and validation data sets

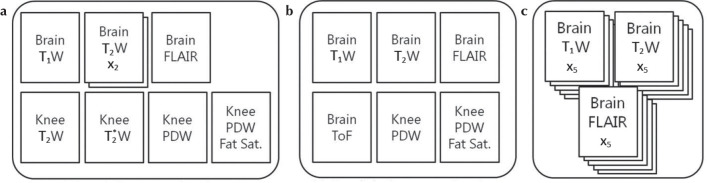
The training data sets comprised training image pairs of a high-SNR ground-truth image and a noisy input image, both acquired at the same anatomical location with the same imaging sequence. The high-SNR ground-truth images of brain and knee were acquired in eight examinations using T₁WI, T₂WI, fluid-attenuated inversion recovery (FLAIR) and PDWI (Fig. 3). Each sequence was acquired with 10 averaged repetitions (NAQ = 10). A scan with 10 averages requires a long acquisition time and is unrealistic in clinical situations. Then we obtained 10 images with one repetition (NAQ1) separately at the same anatomical location, and the resulting 10 images were registered using an in-plane rigid-body image registration method followed by averaging to generate the desired high-SNR ground-truth images. The noisy input images were generated from the ground-truth images by adding Gaussian noise with amplitude between 0% and 20% of the maximum intensity of the ground-truth image. Training data was augmented through horizontal and vertical flipping of the training image pairs. Finally, each training image pair was divided into nine patches, each of 256 × 256 matrix size, to obtain 32400 training image pairs. Validation loss was computed during training on six examinations that contained 660 training image pairs. The validation data sets were six examinations comprised of T₁WI, T₂WI, PDWI, FLAIR, and time-of-flight MRA of the brain, plus PDWI of the knee (Fig. 3). After noise addition, 660 validation pairs were obtained to validate the generalization capability of our proposed method: that it can be applied regardless of the type of MR contrast or the pulse sequence. In this study, the three deep learning-based denoising methods, DnCNN, SCNN and dDLR, were trained with these same training and validation data sets.

Fig. 3.

Training, validation, and test data sets. (a) Training data sets were generated from eight examinations (T₁WI, T₂WI, PDWI, etc.) from the brain and knee of five of the volunteers. After noise addition and data augmentation, 32400 patches of training pairs were obtained. (b) Validation data sets were created from six examinations such as T₁WI, T₂WI, PDWI, etc. of the brain and knee from four of the volunteers. After noise addition, 660 validation pairs were obtained. (c) Test data sets were obtained from three examinations of five volunteers. Oblique-coronal T₁WI, T₂WI and FLAIR images were acquired. Fat Sat., fat saturation; Brain ToF, time-of-flight images from brain MR angiography; FLAIR, fluid-attenuated inversion recovery; PDW, proton-density-weighted; T₁WI, T₁-weighted image; T₂WI, T₂-weighted image.

Test data sets

Test data sets were brain T₁WI, T₂WI and FLAIR oblique-coronal images oriented perpendicular to the hippocampus, obtained from five healthy volunteers (Fig. 3). The scan parameters are shown in Table 1. The 10-NAQ-like ground-truth images were created by averaging and in-plane registration. Noisy input images were generated by adding Gaussian noise levels at 1–10% of the maximum ground-truth image intensity.

Table 1.

MR scan parameters

	T1WI*	T2WI	FLAIR	MPRAGE**
Sequence	2D FSE	2D FSE	2D FSE	3D FFE
TR (ms)	2050	4000	10000	10.3
TE (ms)	15	92	136	3.4
TI (ms)		-	2700	900
Echo train lengths	6	13	29	-
Echo space (ms)	7.5	11.5	8.5	-
Flip angle (°)	90/140	90/180	90/150	13
Matrix	320 × 320	512 × 512	256 × 256	384 × 384
FOV (mm)	200 × 200	200 × 200	200 × 200	200 × 200
Thick/gap (mm)	2.5/2.5	2.5/2.5	2.5/2.5	1/0
No. of slices	10	10	10	30
Bandwidth (Hz)	325.5	195.3	244.1	177.5
Parallel imaging factor: (SPEEDER)	2	2	1.5	1.6
(NAQ)#	1	1, 2, 5	1, 2, 5	1, 2, 5
Total scan time (s)#
NAQ2#		164	130	122
NAQ5#		404	310	204

^*T₁WI was used in the experimental study.

^**MPRAGE was used in the clinical study.

^#NAQ1 images were used for the experimental study to generate the ground-truth images. NAQ2 and NAQ5 images were acquired in the clinical study. FLAIR, fluid-attenuated inversion recovery; NAQ, number of image acquisition.

Evaluation of denoising performance

Denoising convolutional neural network and shrinkage convolutional neural network were compared with dDLR on the same noise-added images. Denoised images processed with the different techniques were obtained at each different noise level. No post-processing was applied to the images denoised by each method shown in Fig. 1. Two quantitative metrics, peak signal-to-noise ratio (PSNR) and structure similarity (SSIM) index, were computed for images denoised with each technique compared with the ground-truth images. These metrics were used to evaluate the denoising performance. The PSNR shows pixel-wise differences between the ground-truth image and the denoised image. The SSIM shows the similarity of signal intensity, contrast, and structure for each local region, but not pixel-wise. When the denoising method works well, the denoised image will be similar to the ground-truth image. Thus, it is expected that PSNR and SSIM would increase. For each imaged volume, PSNR and SSIM were calculated as a mean across all slices for each type of contrast, e.g., T₁WI, T₂WI and FLAIR, with the 10-NAQ-like ground-truth images as reference. To assess subjective image quality, two board-certified neuroradiologists (M.K. with 28 years and H.U. with 12 years of neuroimaging experience), who were blinded to the type of denoising technique, assessed the image quality of the initial images without any denoising applied, as well as images processed with DnCNN, SCNN and dDLR. The two readers evaluated images from the five volunteers at each noise level (Gaussian noise levels at 1–10% of the maximum ground-truth image intensity) for T₁WI, T₂WI and FLAIR, and determined the upper limit of the noise level at which the images were acceptable for clinical evaluation. Specifically, the readers determined the noise level in consideration of excessive image noise, blurring of anatomical structural boundaries, and artificial texture of the images.

Statistical analysis

Statistical analysis of the difference in PSNR and SSIM values between DnCNN, SCNN and dDLR was performed using one-way analysis of variance (ANOVA) and Bonferroni correction for multiple comparisons. Differences with P < 0.05 were considered statistically significant. BellCurve for Excel version 2.15 (Social Survey Research Information Co., Ltd., Tokyo Japan) was used for the statistical analysis.

For the qualitative assessment, we did not perform statistical analysis because of the small number of evaluated images. The mean and standard deviation (SD) of the upper limit noise level at which the images were acceptable for clinical evaluation were calculated.

Clinical study

Volunteers

For the clinical study, from December 2017 to January 2018, we recruited 15 healthy volunteers (13 men and two women; mean age, 32.1 years; age range, 24–55 years).

MR image acquisition and image reconstruction using dDLR

All volunteers underwent MRI on a 3T MRI scanner (Vantage Galan 3T, Canon Medical Systems, Tochigi, Japan) with a 32-channel head coil. In the clinical study, we evaluated the performance of dDLR not only for denoising but also for delineation of brain anatomical structures, particularly in the hippocampus on T₂WI, FLAIR and 3D-magnetization-prepared rapid acquisition with gradient echo (MPRAGE) images. To evaluate the denoising effect of dDLR, we acquired images with different NAQ values and hence different noise levels, using those with two numbers of image acquisition (NAQ2) for comparison data and those with five numbers of image acquisition (NAQ5) for ground-truth data. NAQ5 was chosen because the resulting acquisition time for T₂WI images was approximately 7 min, which we considered an upper limit for minimizing unwanted subject motion. We also decided that using NAQ2 images for comparison data was appropriate in evaluating dDLR performance, because the SNR of NAQ2 images is approximately 60% compared with NAQ5 images. Two-dimensional fast spin echo (FSE) T₂WI, 2D-FLAIR and 3D-MPRAGE oblique coronal thin-slice images perpendicular to the hippocampus were acquired at the two NAQ settings (NAQ2 and 5). The scan parameters are described in Table 1. We then reconstructed images using dDLR processing on the NAQ2 data for each sequence (dDLR-NAQ2 images).

Three datasets for each sequence were used for image analysis: NAQ2, NAQ5 and dDLR-NAQ2 images. The denoising level was determined using the five volunteers’ images for each sequence. Specifically, one radiologist (M.K. with 10 years of experience in MRI) who was not involved in the performance evaluation of dDLR assessed dDLR-NAQ2 images processed with various denoising levels, and determined the maximum denoising level at which the delineation of the basal ganglia and the contrast between the cerebral cortex and white matter were sufficiently preserved. The same denoising level was applied across volunteers.

Performance evaluation of dDLR for thin-slice brain MR images

PSNR and SSIM were used for quantitative image analysis. These metrics were computed for both NAQ2 and dDLR-NAQ2 images compared with the ground-truth (NAQ5 images) to show the performance of the proposed dDLR technique. Before the quantitative image analysis, one radiologist (M.K. with 10 years of experience in MRI) confirmed no inter-scan motion between the ground-truth and NAQ2 images.

To assess subjective quality, two board-certified neuroradiologists (M.K. and H.U with 28 and 12 years of neuroimaging experience, respectively) separately and blindly rated NAQ5, NAQ2 and dDLR-NAQ2 images for T₂WI, FLAIR and 3D-MPRAGE. The window level and width values were chosen to best demonstrate the anatomy of interest. The readers assessed perceived SNR, image contrast, image sharpness, artifacts and overall image quality with a 4-point Scale (1 = poor; 2 = fair; 3 = good; 4 = excellent). Scoring criteria are shown in Table 2. Inter-reader disagreements were resolved by consensus during a joint reading to determine the final score.

Table 2.

Scoring of criteria used for evaluation of conventional and deep learning-based reconstruction (dDLR) images

Sore	Perceived signal-to-noise ratio	Image contrast*	Image sharpness	Identification of hippocampal layer structure	Artifacts disturbing evaluation	Overall image quality
1	Too noisy	One of the structures is not separated.	Poor	Obscure	Severe	Poor
2	Noise has an adverse effect on interpretation	All of the structures are separated, but the contrast is weak.	Fair	Partially identified	Moderate	Fair
3	No adverse effect for interpretation	All of the structures are mostly separated.	Good	Mostly identified	Mild	Good
4	Little or no noticeable noise	All of the structures are clearly separated.	Excellent	Entirely identified	Little or none	Excellent

^*Differentiation between cerebral spinal fluid (CSF), cerebral cortex, white matter, and basal ganglia.

Statistical analysis

All values are expressed as the mean ± SD. Differences with a P < 0.05 were considered statistically significant. The Wilcoxon signed-rank test was used for quantitative values. Friedman’s test was used for multiple comparisons of qualitative values. If a significant difference was found, pairwise comparisons were performed with the Scheffe’s test. The degree of inter-observer agreement for each qualitative assessment was determined by calculating Cohen’s κ coefficient; the scale for κ coefficients for inter-observer agreement was as follows: <0.20 = poor, 0.21–0.40 = fair, 0.41–0.60 = moderate, 0.61–0.80 = substantial, and 0.81–1.00 = near perfect. MedCalc version 17.9.2 (MedCalc Software, Ostend, Belgium) and BellCurve for Excel version 2.15 were used for the statistical analyses.

Results

Experimental study

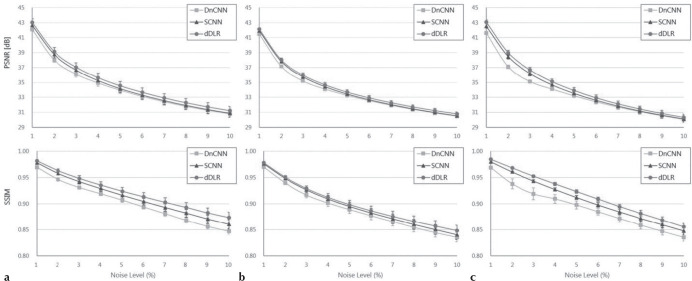
The PSNR and SSIM values for dDLR were statistically higher than those of DnCNN and SCNN across all noise levels from 1–10% (P < 0.001) (Fig. 4). Table 3 shows the mean and SD of the upper limit of clinically-acceptable noise level determined by two radiologists in the assessment of subjective quality. In all cases, the upper limit noise levels increased as follows: unprocessed noisy images <DnCNN < SCNN < dDLR. A visual comparison of noise reduction performance for DnCNN, SCNN and dDLR appears in Fig. 5.

Fig. 4.

Peak signal-to-noise ratio (PSNR) and structure similarity (SSIM) index values at different noise levels (1–10%) for DnCNN, SCNN, and dDLR on (a) T₁WI, (b) T₂WI, and (c) fluid-attenuated inversion recovery (FLAIR) images. Across all noise levels for all three types of images, dDLR was superior to DnCNN and SCNN with regard to both PSNR and SSIM (P < 0.01). dDLR, deep learning-based reconstruction; DnCNN, denoising convolutional neural network; SCNN, shrinkage convolutional neural network.

Table 3.

Mean upper limit of the noise level at which images were acceptable for clinical evaluation in non-denoised images and images denoised with DnCNN, SCNN and dDLR in five volunteers

	Reader A				Reader B
	Noisy	DnCNN	SCNN	dDLR	Noisy	DnCNN	SCNN	dDLR
T1WI	3.8% (0.7)	5.0% (0.6)	5.4% (0.5)	6.2% (0.4)	3.2% (0.7)	4.2% (0.7)	4.8% (0.7)	5.4% (0.5)
T2WI	4.4% (0.5)	6.8% (0.7)	7.4% (0.8)	8.6% (0.8)	4.2% (0.7)	6.6% (0.8)	7.4% (0.8)	8.6% (0.8)
FLAIR	3.0% (0.6)	4.0% (0.9)	4.4% (0.5)	4.8% (0.7)	2.8% (0.7)	3.6% (0.8)	4.6% (0.5)	4.8% (0.7)

Data in parentheses are standard deviations. FLAIR, fluid-attenuated inversion recovery; DnCNN, denoising convolutional neural network; SCNN, shrinkage convolutional neural network; dDLR, deep learning-based reconstruction; T₁WI, T₁-weighted image; T₂WI, T₂-weighted image.

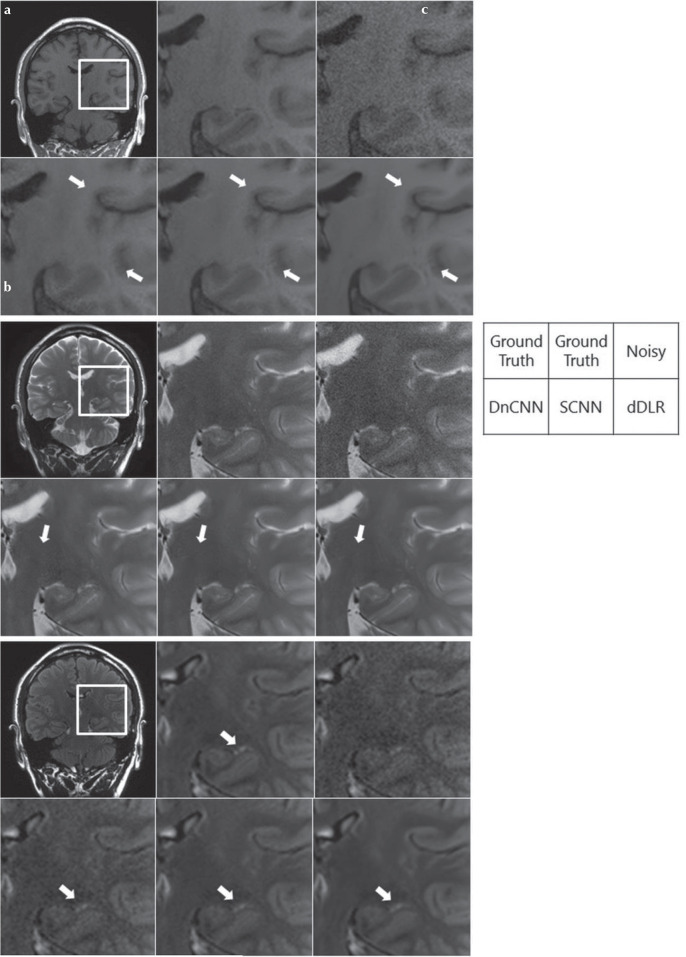
Fig. 5.

Visual comparison of noise reduction performance between DnCNN, SCNN and dDLR in a 38-year old male volunteer. Top-left is a ground-truth (10-number of image acquisition [NAQ]-like) image, and the others are magnified images of the rectangular annotated area in the ground-truth image. Top-center: magnified ground-truth image, top-right: magnified noise-added image without denoising, bottom-left: magnified image denoised with DnCNN, bottom-center: denoised with SCNN, and bottom-right: denoised with dDLR. Denoising was applied to the artificially noise-added images as follows: (a) T₁WI with 3% noise, (b) T₂WI with 4% noise, and (c) fluid-attenuated inversion recovery (FLAIR) with 2% noise. dDLR unambiguously reduced image noise while preserving intrinsic structures and structural boundaries (arrows) compared with DnCNN and SCNN images. dDLR, deep learning-based reconstruction; DnCNN, denoising convolutional neural network; SCNN, shrinkage convolutional neural network; T₁WI, T₁-weighted image; T₂WI, T₂-weighted image.

Clinical study

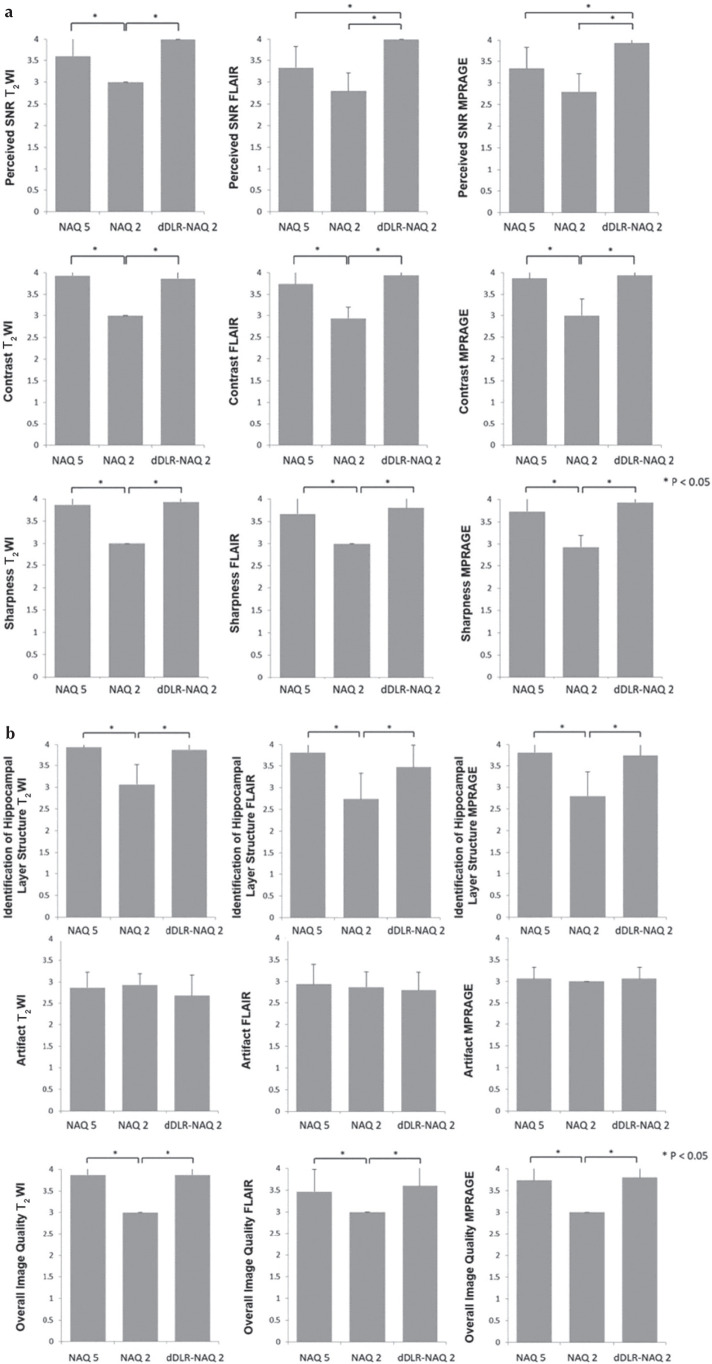
Quantitative and qualitative metrics are summarized in Table 4 and Fig. 6, respectively. The SSIM of dDLR-NAQ2 images was significantly higher than that of NAQ2 images in all sequences (P < 0.05). The PSNR of dDLR-NAQ2 images was significantly higher than that of NAQ2 images in all sequences (P < 0.05), except in FLAIR (P = 0.08).

Table 4.

Results of quantitative assessments

		NAQ 2 (mean ± SD)	dDLR-NAQ 2 (mean ± SD)	P
SSIM	T2WI	0.977 ± 0.012	0.981 ± 0.012	<0.05
	FLAIR	0.982 ± 0.010	0.984 ± 0.009	<0.05
	MPRAGE	0.992 ± 0.004	0.993 ± 0.004	<0.05
PSNR (dB)	T2WI	28.867 ± 2.875	29.628 ± 3.194	<0.05
	FLAIR	30.839 ± 2.635	31.026 ± 2.874	0.08
	MPRAGE	33.158 ± 1.684	33.736 ± 1.858	<0.05

SSIM, structural similarity index; PSNR, peak signal-to-noise ratio; SD, standard deviation; FLAIR, fluid-attenuated inversion recovery; MPRAGE, magnetization-prepared rapid acquisition with gradient echo; NAQ, number of image acquisitions.

Fig. 6.

(a) Results of qualitative assessments: perceived SNR, image contrast and image sharpness. Perceived SNR of dDLR-NAQ2 was significantly higher than that of NAQ2 in all sequences (P < 0.05). Perceived SNR of NAQ5 was significantly higher than that of NAQ2 in T₂WI (P < 0.05). In FLAIR and MPRAGE, perceived SNR of dDLR-NAQ2 was significantly higher than that of NAQ5 (both P < 0.05). Image contrast for both dDLR-NAQ2 and NAQ5 was significantly higher than that of NAQ2 in all sequences (P < 0.05), and there was no significant difference between dDLR-NAQ2 and NAQ5 (T₂WI: P = 0.95; FLAIR: P = 0.64; MPRAGE: P = 0.95). For image sharpness, dDLR-NAQ2 and NAQ5 were both significantly superior to NAQ2 in all sequences (P < 0.05), and there was no significant difference between dDLR-NAQ2 and NAQ5 (T₂WI: P = 0.95; FLAIR: P = 0.79; MPRAGE: P = 0.64). (b) Results of qualitative assessments: identification of hippocampal layer structure, artifact and overall image quality. For identification of hippocampal layer structure, dDLR-NAQ2 and NAQ5 were both significantly superior to NAQ2 in all sequences (P < 0.05), and there was no significant difference between dDLR-NAQ2 and NAQ5 (T₂WI: P = 0.94; FLAIR: P = 0.38; MPRAGE: P = 0.91). There were no significant differences in artifacts between NAQ5, NAQ2 and dDLR-NAQ2 (T₂WI: P = 0.20; FLAIR: P = 0.47; MPRAGE: P = 0.37). For overall image quality, dDLR-NAQ2 and NAQ5 were both significantly superior to NAQ2 for all sequences (P < 0.05), and there was no significant difference between dDLR-NAQ2 and NAQ5 (T₂WI: P = 1.00; FLAIR: P = 0.72; MPRAGE: P = 0.94). FLAIR, fluid-attenuated inversion recovery; dDLR, deep learning-based reconstruction; NAQ, number of image acquisition; MPRAGE, magnetization-prepared rapid acquisition with gradient echo; T₂WI, T₂-weighted image.

Perceived SNR of dDLR-NAQ2 and NAQ5 images was significantly higher than that of NAQ2 images in T₂WI (P < 0.05); however, there was no significant difference of perceived SNR between dDLR-NAQ2 and NAQ5 images (P = 0.17) (Figs. 6a and 7a). In FLAIR and MPRAGE, perceived SNR values for dDLR-NAQ2 images were significantly higher than those of both NAQ5 and NAQ2 images (both P < 0.05) (Figs. 6a, 7b and 7c). Image contrast and sharpness were significantly higher for dDLR-NAQ2 and NAQ5 images than for NAQ2 images in all sequences (P < 0.05), but there was no significant difference between dDLR-NAQ2 and NAQ5 images (T₂WI: P = 0.95 for image contrast, P = 0.95 for image sharpness; FLAIR: P = 0.64 for image contrast, P = 0.79 for image sharpness; MPRAGE: P = 0.95 for image contrast, P = 0.64 for image sharpness) (Figs. 6a and 7). For identification of hippocampal layer structure, dDLR-NAQ2 and NAQ5 images were superior to NAQ2 images in all sequences (P < 0.05), but there was no significant difference between dDLR-NAQ2 and NAQ5 images (T₂WI: P = 0.94; FLAIR: P = 0.38; MPRAGE: P = 0.91) (Figs. 6b and 7). There were no significant differences for artifact between NAQ5, NAQ2 and dDLR-NAQ2 images in all sequences (T₂WI: P = 0.20; FLAIR: P = 0.47; MPRAGE: P = 0.37). For overall image quality, dDLR-NAQ2 and NAQ5 images were superior to NAQ2 in all sequences (P < 0.05), and again, there was no significant difference between dDLR-NAQ2 and NAQ5 images (T₂WI: P = 1.00; FLAIR: P = 0.72; MPRAGE: P = 0.94) (Figs. 6b and 7). The inter-observer agreement ranged from substantial (κ = 0.61) to near perfect (κ = 1.00).

Fig. 7.

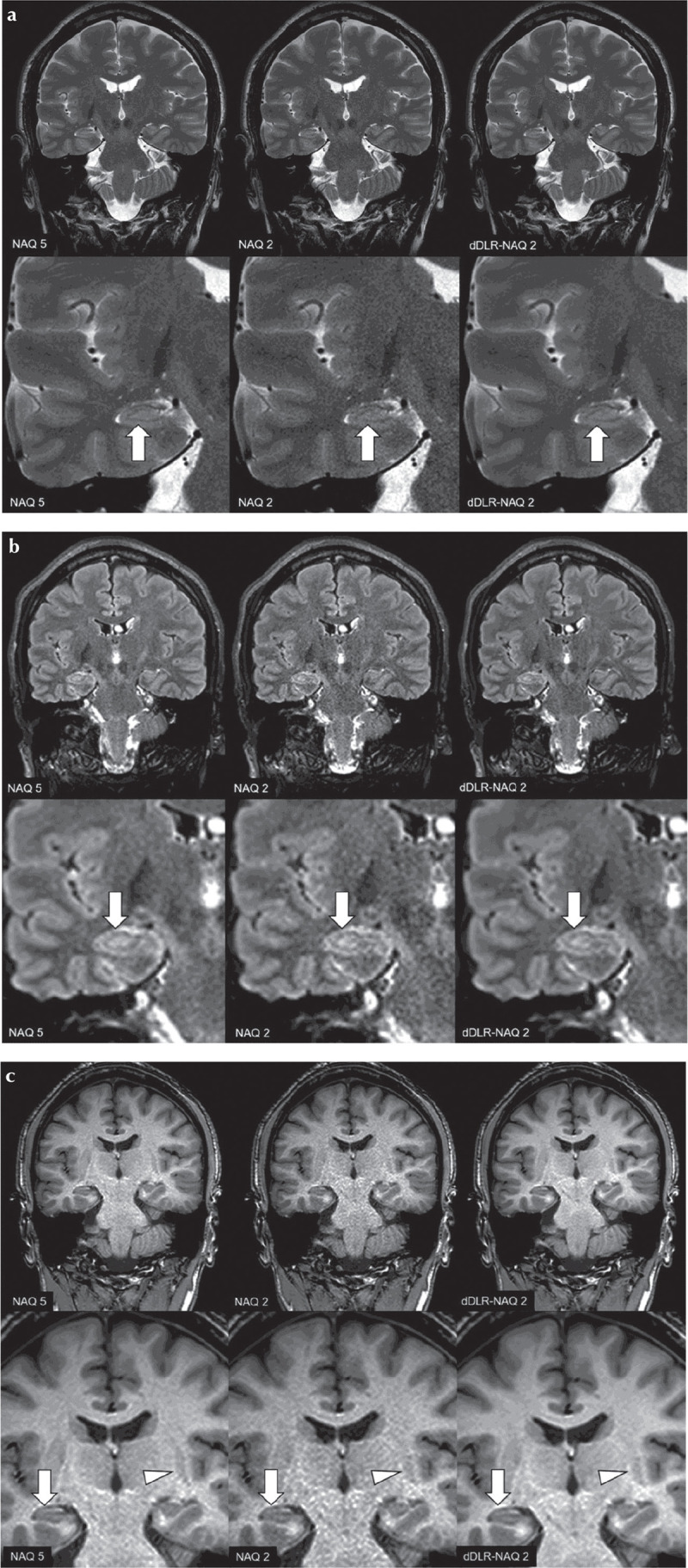
A 38-year-old male healthy volunteer. Upper row: original magnification, lower row: magnified image. (a) T₂-weighted image (T₂WI): A NAQ2 has higher image noise than NAQ5 and dDLR-NAQ2. Identification of the hippocampal layer structure is superior in both NAQ5 and dDLR-NAQ2 compared with NAQ2 (arrows). (b) FLAIR: NAQ2 demonstrates higher image noise than NAQ5 and dDLR-NAQ2. Identification of the hippocampal layer structure is again superior in NAQ5 and dDLR-NAQ2 compared with NAQ2 (arrows). (c) magnetization-prepared rapid acquisition with gradient echo (MPRAGE) NAQ2 demonstrates higher image noise than NAQ5 and dDLR-NAQ2. Identification of the hippocampal layer structure is superior in NAQ5 and dDLR-NAQ2 compared with NAQ2 (arrows). Contrast between the left putamen and its surrounding white matter is also superior in NAQ5 and dDLR-NAQ2 compared with NAQ2 (arrowheads). dDLR, deep learning-based reconstruction; NAQ, number of image acquisition.

Discussion

In the experimental study, dDLR outperformed DnCNN and SCNN for image denoising. dDLR removes image noise by learning various noise characteristics using training pairs of different noise level images and the respective ground-truth images. Similar to SCNN, soft-shrinkage seems to enable more adaptive noise removal than DnCNN. In addition, denoising of the high frequency components using the DCT layer, which separates the high frequency components from the zero-frequency component, may allow for more efficient noise reduction than is possible with DnCNN or SCNN.

Our clinical results showed that the dDLR approach drastically decreased image noise and generated thin-slice MR brain images with sufficient image quality to precisely evaluate fine anatomic details in a relatively short acquisition time. dDLR-NAQ2 images yielded equivalent or better image quality compared with NAQ5 images despite the shortened acquisition time (reduced by approximately 60% in all sequences). For evaluation of small anatomical structures such as the hippocampus, high-spatial-resolution images with high-SNR are required. To address this need, there are two methods. One is to increase the NAQs: image signal is added up, whereas the increase in noise is less than that of the image signal because of the randomness of noise. As a result, SNR increases. The other is denoising by noise removal from acquired data, and this technique can be achieved with deep learning. Our results indicate that our denoising method using deep learning works effectively even in images with small anatomical structures such as the hippocampus. In the qualitative evaluation for FLAIR, dDLR-NAQ2 images was superior to NAQ5 images in perceived SNR; however, there was no significant difference between dDLR-NAQ2 and NAQ5 images in identification of hippocampal layer structure. FLAIR imaging produces FSE T₂W cerebral spinal fluid-nulled images by adding inversion pulses to the sequence followed by long inversion times. This type of sequence can potentially decrease SNR due to partial suppression of tissue signal. In images with insufficient image quality and/or SNR, dDLR may not work effectively. Therefore, optimization of pre-dDLR image quality as well as the level of dDLR denoising according to the type of imaging sequence used and the anatomical targets of interest is required when using dDLR, especially in the evaluation of precise anatomical regions.

Adaptation of deep learning methods to improve disease detection and MR image analysis in neuroimaging has been shown to have a significant impact on medical imaging.^15–19 Despite the popularity of deep learning methods, there have been only a small number of studies on CNN-based MR image reconstruction^7,20,21; hence, the applicability of deep learning methods to neuroimaging has yet to be fully explored.

In clinical neuroimaging, disease-specific anatomical evaluation is required. The hippocampus has been implicated in a variety of disorders, including hippocampal sclerosis and Alzheimer’s disease.^3,22,23 Hippocampal sclerosis is a disorder characterized by hippocampal neuronal loss that causes medial temporal lobe epilepsy.³ Atrophy and/or signal change of the hippocampus on T₂WI and FLAIR images are characteristic findings. In addition, partial loss of hippocampal striation on high-resolution T₂WI images is a useful marker for diagnosis of hippocampal sclerosis.²⁴ In a recent report,²² combined volumetry and quantitative high-resolution FLAIR signal analysis clearly identified the specific histologic types of hippocampal sclerosis. Quantitative assessment of the hippocampus and adjacent structures using 3D-T₁WI techniques such as the MPRAGE sequence is also vital for early diagnosis of Alzheimer’s disease and accurate tracking of disease progression.²³ Even with images obtained in a relatively short acquisition time, use of optimized dDLR may improve the diagnostic accuracy of hippocampal abnormality. Furthermore, noiseless high-resolution 3D images can provide more accurate information compared with conventional images for brain volumetric analysis.

In the last decade, MRI technical improvements, including high-resolution imaging and high-field MRI, have yielded increased sensitivity in detecting subtle abnormalities.^25–29 However, a relatively long acquisition time is required for high-resolution images, which can be uncomfortable or inconvenient for patients and result in blurred images caused by patient motion. To reduce motion artifacts associated with a long acquisition time, the most effective solution is shortening the image acquisition time. Several techniques for reduction of image acquisition time have been used, including parallel imaging and compressed sensing.³⁰ While missing k-space data are interpolated based on a priori knowledge of coil sensitivity profiles with parallel imaging, compressed sensing interpolates the missing data by imposing an a priori transform domain sparsity constraint to regularize the reconstruction problem.³¹ In contrast, dDLR is a novel approach that allows for decreased image acquisition time without degrading image quality because this method can drastically reduce the noise independent of any data omitted in MR acquisitions. For image noise reduction, several techniques have also been used.^4–6 A frequently used approach is to recover the true intensity value of a voxel by averaging the intensity values of neighboring voxels.⁴ A Gaussian smoothing filter is a popular technique; however, this kind of local averaging will remove not only noise but also structural details such as anatomical boundaries. To address this issue, several advanced approaches^5,6 have been investigated. In this experimental study, we compared the image quality of brain MR images processed with dDLR, DnCNN and SCNN. The results showed that dDLR was superior to both DnCNN and SCNN in preserving image quality. Image blurring was more obvious in DnCNN and SCNN compared with dDLR.

Our study had some limitations. First, it included a relatively small number of volunteers. Moreover, the diagnostic accuracy of dDLR in clinical patients was not assessed. Second, we used dDLR for only T₁WI, T₂WI, FLAIR and MPRAGE images, although our dDLR technique can theoretically be applied as well to other MR sequences or even to CT. A multi-institutional study with a larger number of patients with various neurologic diseases and using a wider range of MR sequences would be necessary to fully validate our dDLR technique.

Conclusion

Deep learning-based reconstruction significantly reduces image noise while preserving image quality for brain MR images obtained in a relatively short acquisition time. To verify the expected diagnostic benefit of the dDLR technique, large-scale clinical studies are needed.