Abstract
The COVID-19 pandemic, which first spread to the People of Republic of China and then to other countries in a short time, affected the whole world by infecting millions of people and have been increasing its impact day by day. Hundreds of researchers in many countries are in search of a solution to end up this pandemic. This study aims to contribute to the literature by performing detailed analyses via a new three-staged framework constructed based on data envelopment analysis and machine learning algorithms to assess the performances of 142 countries against the COVID-19 outbreak. Particularly, clustering analyses were made using k-means and hierarchic clustering methods. Subsequently, efficiency analysis of countries were performed by a novel model, the weighted stochastic imprecise data envelopment analysis. Finally, parameters were analyzed with decision tree and random forest algorithms. Results have been analyzed in detail, and the classification of countries are determined by providing the most influential parameters. The analysis showed that the optimum number of clusters for 142 countries is three. In addition, while 20 countries out of 142 countries were fully effective, 36% of them were found to be effective at a rate of 90%. Finally, it has been observed that the data such as GDP, smoking rates, and the rate of diabetes patients do not affect the effectiveness level of the countries.
Keywords: Machine learning, Weighted stochastic imprecise data envelopment analysis, Clustering, COVID-19
Highlights
-
•
Efficiency analysis of 142 countries against COVID-19 was made by WSIDEA.
-
•
DEA-based model and machine learning algorithms are integrated.
-
•
Clustering analysis was done and differences between clusters were examined.
-
•
Effects of factors on number of infections, recovered, death cases were examined.
-
•
Most important factors affecting the efficiency levels of countries were examined.
1. Introduction
The recent contagious virus outbreak with an acute respiratory syndrome [SARS] -CoV-2 is one of the biggest public health problems that humanity has ever struggled with. It first reported at the end of 2019, in Wuhan/China [1]. Coronavirus infectious disease 2019 (COVID-19) is an extraordinary and enduring pandemic that has newly appeared and is defined as a human virus [2].
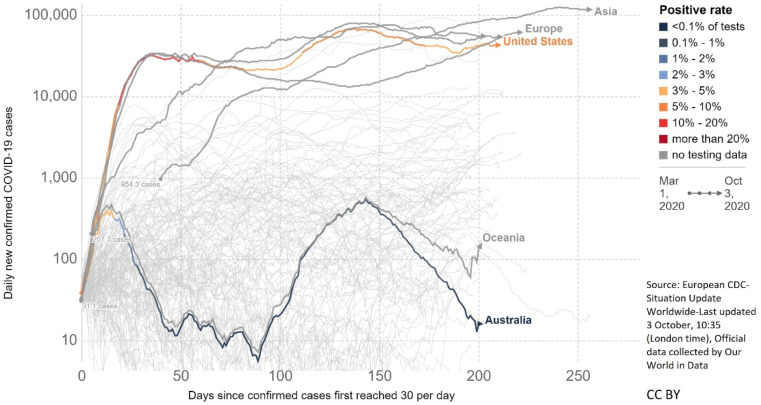
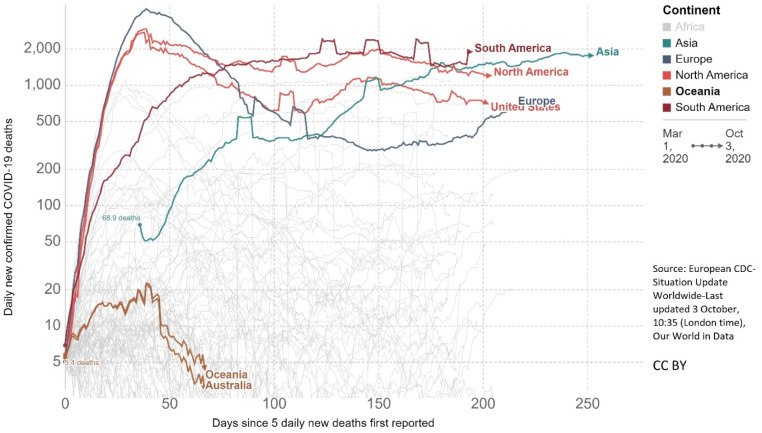
Only one month following the date of the first case, the COVID-19 is affirmed as an international public health disaster [3] and as a pandemic on March 11th, 2020 [4] by WHO. In few months, it appeared in all continents and in more than 210 countries. Since December 31st of 2019 and as of July 29th 2020, 16,708,920 cases and 660,123 deaths have been reported by [5], whereas, fortunately the amount of healing cases have also increased. Daily based statistics are reported in Fig. 1, Fig. 2 for cases and deaths by continent, respectively.
Fig. 1.
Number of the cases reported [6].
Fig. 2.
Number of deaths by continent [6].
The eruption of a disease has a huge impact on the welfare of society. The intensity level of a pandemic is related to the rate of conveyance, virulence, person-to-person contacts, robustness of immune system of a person, healthcare system, and climate [7]. So far, three world wide Influenza eruptions occurred in the last century. Considering the number of deaths they caused, COVID-19 has almost exceeded by ten times more than the later Influenza pandemic outbreak in terms of the number of cases recorded. To compress the growth of the COVID-19 effective protection actions as well as responsive healthcare systems have a vigorous significance. Considering the studies conducted and the information announced by the governments, the number of cases and loss of lives reported in the countries with insufficient health and economic systems are higher comparing to other countries. The absence of an effective drug or vaccine for COVID-19 causes the spread of the disease and worsen the conditions even more.
On the other hand, Fig. 1, Fig. 2 gave us the opportunity to compare the impact of the pandemic on a continental basis. For example, Europe was the continent most affected by the pandemic, while Africa was less affected than the others. Furthermore, while April was the month with the highest number of deaths (Fig. 1), Europe is the continent with the highest death rates (Fig. 2).
The aim of this study is to determine the factors affect the number of positive and death cases associated with COVID-19 pandemic via new three-stage model.
Particularly, firstly, the countries are clustered considering the data provided. Then, analysis is conducted based on the results of clustering algorithms, such as the number of clusters formed, the distinctive features of the clusters etc. Secondly, the efficiency of these clusters is assessed via WSIDEA. As a result of this analysis, the efficiency level of each cluster element is obtained. For both effective and ineffective countries, decision trees and random forest algorithms are utilized to analyze the factors that affect the effectiveness of these countries. Thirdly, used algorithms performances were compared in terms of success criteria and the most successful algorithm was investigated.
The contributions of the study may be shortened as follows:
-
A three-stage framework is presented to analyze the effectiveness of the countries against COVID-19.
-
In the study, both WSIDEA and machine learning tools are utilized.
-
To the best knowledge of authors, it is the first study that applies abovementioned algorithms together for COVID-19 analyses.
-
The obtained results provide a road map for decision makers and authorities to notice the factors that need to be considered in order to increase their effectiveness in response to COVID-19.
-
The developed framework can be applied not only to COVID-19 but also to any field given that the topic specific data is updated.
The rest of the paper is designed as follows: In Section 2, we introduced the relevant literature in terms of COVID-19 and machine learning algorithms applied. In Section 3, the used algorithms are explained, briefly. The results of analyses and discussions are presented in the Section 4 and in the last Section 5 conclusions and future research directions are provided.
2. Literature review
Since the first case reported, several studies have been conducted on COVID-19 by taking into account from different points of view. Some of the studies tried to anticipate the number of affected people [8], [9], [10] or death, some studied COVID-19‘s effects on economies [11], environment [12] or health [13], and some studied the effects that cause the spread of COVID-19 [14], [15]. Differently than all, in this study, we analyze the effectiveness of the countries in struggling with COVID-19 considering their performances since the end of 2019. Several models are utilized to conduct this research, in particular the WSIDEA and multiple tools of machine learning.
Machine learning have been applied to several topics in various disciplines, especially in the last decade. In Atalay and Çelik [16] detailed information on big data in the concept of machine learning and artificial intelligence are provided. Gök [17] investigated the success rates of secondary school students in Turkish and Mathematics courses using questionnaire data, which is conducted on 6th, 7th, and 8th grade students, and machine learning algorithms. In their study, linear regression, random forest algorithm, support vector machines and radian-based function were used. Rebai et al. [18], also, investigated the success of the secondary school education system in Tunis with a two-level algorithm. In the study, they utilized the decision tree and random forest algorithms, which provide results as inputs for the data envelopment analysis (DEA) method. Kaynar et al. [19] obtained new datasets using attribute selection algorithms over a dataset developed for attack detection systems, and then using these new datasets k-nearest neighbor algorithm, support vector machines and over learning machine algorithms are applied and compared. As a result, they observed that feature selection methods increase the success rate of all three machine learning algorithms. Further, Yiğiter et al. [20] used kNN algorithm to estimate the rental certificate prices. The model presented a successful performance in terms of estimating the prices for the next 1, 3 and 5 days. Zhou et al. [21] conducted a study on the use of machine learning algorithms in the field of material science and material design. They provided valuable information on the usage of machine learning algorithms and software to conduct these algorithms, i.e, Weka and Python, in the related field.
While Lavrov and Domashova [22] suggested a new model for the classification problems, Sağbaş and Ball [23] determined the type of communication of the users via smartphone sensors and machine learning algorithms. They determined random forest as the most promising algorithm, in where they applied GPS, naive bayes, kNN, random forest and C4.5 algorithms [22], [23].
On the other hand, after providing detailed information on deep learning, Seker et al. [24] applied data mining in social networks. In the study of Chen [25], a machine learning-based risk assessment tool is proposed for the assessment of a bank branches. They used support vector machines, random forest, C4.5, decision tree and synthetic minority over-learning (SMOTE) techniques as machine learning algorithms. As a result of the study, four important inferences were made: the accuracy of the model is 75%, the risk rating of the bank branches are sufficient, personal and corporate accounts have similar characteristics, and both types of accounts have similar classes as well. Jan et al. [26] made a comparative analysis of the methods used in the field of deep learning. Different models have been used in the study to process a large amount of data including different neurons and hidden layers. Similarly, Dos Santos et al. [27], using data mining and machine learning techniques, conducted a bibliometric analysis of the studies done between 2009 and 2018 on community health [27].
Considering the pandemic-based studies, Remuzzi and Remuzzi [28] suggested a model on how the pandemic process will develop and how the resources will be utilized for the countries with similar symptoms [28]. While, Dikmen et al. [29] conducted a qualified research on the etiology, and transmission rate of the disease, Parbat [30] estimated the number of COVID-19 based deaths, patients, and healings for India via support vector regression method. Differently than the literature, in this study, the factors that affect the number of positive and death cases associated with COVID-19 pandemic are determined and then the performances of the countries against COVID-19 are analyzed using WSIDEA, clustering algorithm, decision trees algorithm, random forest algorithm, and regression analysis.
Kishor and Venkateswarlu [31] suggested a novel algorithm named as A Novel Hybridization of Expectation Maximization and K-Means (NovHbEMKM) algorithms for Better Clustering Performance. The proposed algorithm has less computational time in comparison with other EM or K-means algorithms. They stated that new hybrid methods are more advantageous than traditional methods in some areas.
Fong et al. [32] proposed a model called Group of Optimized and Multi-source Selection (GROOMS), which provides the high possibly level to make predictions at a high probability level with low information and less data. The model they suggested came true in three processes. First of all, the dataset is transferred to the models that will make predictions. Afterwards, prediction models are brought to the highest performance levels with tune operations. Then, the most suitable model is selected and predicted. In addition, Fong et al. [33] proposed the composited Monte Carlo model (CMC) as a result of the hybridization of deep learning algorithms and fuzzy logic rules in their case study on the COVID-19 pandemic. The researchers put forward the argument in the study that structures with dynamic variables cannot be predicted with classical Monte Carlo, and therefore they proposed the CMC model. This proposed model was used with the Grooms model proposed by Fong et al. [32]. As a result of the study, they showed that, thanks to CMCM GROOMS, it can produce qualitative results for better decision support than any deterministic estimator [33]
In the COVID-19 literature several studies have been performed with different perspectives. However, an efficiency analysis of the countries, which are struggling with COVID-19, by DEA-based model and as it was done in this study has not been performed yet. The comparison table of similar studies is presented in Table 1, which supports the argument we put forward.
Table 1.
The comparison table of existing works.
| Study | Year | Scope | Method |
|||||
|---|---|---|---|---|---|---|---|---|
| COVID-19 | DEA based modeling | Machine learning |
||||||
| K-means | Hierarchical A. | Decision tree | Random forest | SVM | ||||
| Sarkodie and Owus , [34] | 2020 | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| Yeasmina et. al, [35] | 2020 | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ |
| Loey et. al, [36] | 2021 | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ |
| Ahamad, et al., [37] | 2020 | ✓ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ |
| Malki et. al, [38] | 2020 | ✓ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ |
| Sonbhadra et. al, [39] | 2020 | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | ✓ |
| Mahmoudi et. al, [40] | 2020 | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ |
| Khan et. al, [41] | 2020 | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| Imtyaz et. al, [42] | 2020 | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ |
| Amar et. al,[43] | 2020 | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| Guerrero et. al, [44] | 2020 | ✓ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ |
| Mei et. al, [45] | 2020 | ✓ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ |
| Salehi et. al, [46] | 2020 | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ |
| Pendharkar et. al, [47] | 2011 | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| Kheirkhah et. al, [48] | 2013 | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ |
| Jafarzadegan et. al, [49] | 2019 | ✗ | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ |
| Nandy et. al, [50] | 2020 | ✗ | ✓ | ✗ | ✗ | ✗ | ✓ | ✗ |
| Tayala et. al, [51] | 2020 | ✗ | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ |
| This Study | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✘ | |
| Study | Year | Scope of Paper | Method |
|||||
| COVID-19 | DEA based modeling | Machine Learning |
||||||
| ANN | MLP | Fuzzy Based A. | Other ML A. | PCA | ||||
| Sarkodie and Owus [34] | 2020 | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| Yeasmina et. al, [35] | 2020 | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| Loey et. al, [36] | 2021 | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ |
| Ahamad et al. [37] | 2020 | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ |
| Malki et. al, [38] | 2020 | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ |
| Sonbhadra et. al, [39] | 2020 | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ |
| Mahmoudi et. al, [40] | 2020 | ✓ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ |
| Khan et. al, [41] | 2020 | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| Imtyaz et. al, [42] | 2020 | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| Amar et. al, [43] | 2020 | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| Guerrero et. al, [44] | 2020 | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| Mei et. al, [45] | 2020 | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| Salehi et. al, [46] | 2020 | ✗ | ✓ | ✗ | ✓ | ✗ | ✓ | ✗ |
| Pendharkar et. al, [47] | 2011 | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ |
| Kheirkhah et. al, [48] | 2013 | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✓ |
| Jafarzadegan et. al, [49] | 2019 | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ |
| Nandy et. al, [50] | 2020 | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ |
| Tayala et. al, [51] | 2020 | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ |
| This Study | ✔ | ✔ | ✘ | ✘ | ✘ | ✘ | ✘ | |
ML: Machine Learning, SVM: Support Vector Machine, ANN: Artificial Neural Network, MLP: Multilayer Perception Machine, PCA: Principal Component Analysis.
As can be observed from Table 1, a three-staged framework used in this study is different in its structure from other studies. In proposed framework, both DEA-based mathematical modeling, clustering, classification and regression analysis were used together. Moreover, an efficiency analysis on COVID-19 has not yet been done. Therefore, the proposed study has novelties in providing a novel hybrid method to assess the performances of the countries and in being the first study to assess the countries performances against COVID-19 pandemics.
Besides, weighted stochastic imprecise data envelopment analysis (WSIDEA) model studied is a novel DEA-based model that has not been studied in the literature so far. Thus, this is the first study that presents the application of WSIDEA on a real case. Secondly, it is also the first application on COVID-19 as a DEA-based model. Lastly the framework proposed in the study is the first study in terms of combining WSIDEA and machine learning algorithms. In this respect the proposed study provides several technical novelties by proposing a new DEA model and machine learning algorithms. Further, Table 1 is a good indicator in this regard.
3. Methodologies
Almost eight months have been passed since the officially start date of the COVID-19 pandemic. In the past eight months, the corona virus outbreak has infected 19 million people worldwide, and about 730 thousand people lost their lives. Many countries around the world are struggling with the pandemic. The level of exposure of each country to the pandemic is different. Even though, the struggle way of each country with the pandemic looks similar, it varies within itself. In this respect, some countries are considered successful on the basis of combating pandemics, while others are considered unsuccessful. One of the aims of this study is to analyze the efficiency of countries in the pandemic process. The analysis to be made consists of three steps. First of all, using k-means and hierarchical clustering algorithms for all countries, the optimum number of classes, which country is in which class and what parameters constitute these classes will be investigated. After cluster analysis, the efficiency analysis of the countries in each class will be investigated separately with the weighted stochastic imprecise data envelopment analysis (WSIDEA) proposed by Aydin and Yurdakul [52]. In the third step, the analysis of the situations that causes these results for the effective and ineffective countries will be analyzed with the decision tree and random forest algorithms.
The proposed framework is a method in which a new mathematical model constructed based on DEA, which is named as WSIDEA, and the developed DEA based model is used together with the machine learning algorithms, such as decision trees, random forest, k-means and hierarchic clustering methods. The flow chart of the proposed framework is constructed as follows (see Fig. 3).
Fig. 3.
Flow chart of the proposed methodology.
The data used in the study consist of 14 different type of data set collected for 142 countries. While creating the data set, the number of cases, tests, deaths, patients recovering and active patients were collected on a daily basis between 21/01/2020 and 28/07/2020. The collected data were summed before being used in the analysis. GDP, diabetes prevalence, female smokers, male smokers, population and hospital beds.per.100k are the current data taken from www.kaggle.com website on 28.07.2020. The data consists of 142 rows and 14 columns, which are all continuous. The efficiency values obtained after the analysis with WSIDEA were added to the data set as a factor type. The obtained results were used as inputs to the random forest and decision tree algorithms. When adding efficiency values to the data set, the countries with an efficiency level of 90% and above were accepted as 1, and 0 for others.
On the other hand, these data consist of three different categories. The first category is the current and most general data on COVID-19, the second is the data on determining the social and economic structures of countries, and lastly, the data that are not frequently used in studies on COVID-19. In literature, the most preferred data are the number of total cases, total recovered, total tests, total deaths, active cases etc... Furthermore, the GDP, poverty index, population and similar data are the data that characterize the social and economic structures of the countries. Moreover, stringency index, cvd death rate is uncommonly used data in the literature, which are also considered in this study. The titles that make up the data set are listed as follows.
Sum of Total Deaths: Refers to the number of patients who died due to COVID-19 disease.
Stringency Index: The Stringency Index is a number from 0 to 100 that reflects indicators such as containment policies such as school and workplace closings, public events, public transport, stay at home policies of the governments. A higher index score indicates a higher level of stringency.
Extreme Poverty: Refers to the poverty rates of the countries. The high extreme poverty index indicates that the country is extremely poor and its level of development is low.
CVD Death Rate: It refers to the death rate due to heart attack.
Diabetes Prevalence: refers to the prevalence of diabetes patients in the countries.
Female Smokers: Refers to the number of women smoking in the country.
Male Smokers: Refers to the number of women smoking in the country.
Population: Refers to the number of residents in the country.
GDP: Gross domestic product (GDP) is the total monetary or market value of all the finished goods and services produced within a country’s borders in a specific time period.
Hospital.Beds.per.100k: Number of hospital beds per 100,000 people
Total Recovered: Refers to the number of people who were infected by COVID-19 but recovered.
Total Test: It refers to the Polymerase Chain Reaction (PCR) test to determination of COVID-19 infections for people.
Sum of Total Cases: Refers to people who have tested positive for COVID-19
Active Cases: Refers to patients who have been diagnosed with COVID-19 as of the date of data creation.
3.1. Data envelopment analysis
The DEA model, first proposed by Charnes, Cpooper and Rhodos [53], is a nonparametric method used to measure the efficiency levels of similar decision-making units over the same inputs and outputs at different rates [53], [54]. In particular, DEA analyzes the relative efficiency of similar decision-making units with each other. The first DEA model was named CCR using the authors’ initials.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
The variables and , shown in the model show the weights of the r output and i input respectively. In similar vein, the parameters and are output and input values of j DMU. When the model shown above is solved, it provided the efficiency value of each DMUs. When the value of efficiency level is equal to 1, it means that relevant DMU is considered fully efficiency [55], [55], [56], [57], [58].
DEA has been used in numerous studies by many researchers since the day it was first put forward. Today, it is possible to come across many different DEAs. One of them is the imprecise DEA model proposed by Cook and Zhu [59]. The reason why we say imprecise is because one or more data sets that we used in model is uncertain, either input or output. There is no rule about determining input and output data sets in DEA models. For this reason, the selection of input and output data is left to the researcher, even though it is obvious that some data are input or output. Cook and Zhu [59] proposed a new model to solve this problem.
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
show the weight of the output, input and flexible data set, respectively. Therewithal, another decision variable, is (0, 1) binary variable and determines category of the flexible data set. If d 1, the relevant flexible variable is included in the output set, and when d 0, it functions as the opposite.
Both of the introduced models are deterministic. In other words, both the model itself and the data used must be complete and precise. However, in some cases, these conditions may not be met or it may be desirable to use probabilistic data containing predictions about the future instead of deterministic data. For this reason, Charnes and Cooper [53] proposed the chance constraint DEA model. Post Charnes and Cooper, many scientists have developed different chance constrained DEA models. One of these models is the model developed by Sueyoshi [60]. Sueyoshi stated that future analysis is more important than today and proposed a new model based on chance constraint DEA. In his model, the input set is deterministic and the output set is stochastic. He named the model as the future DEA model of Sueyoshi [60].
| (16) |
S.t:
| (17) |
| (18) |
| (19) |
| (20) |
In the model shown above, denotes the expected value of the r output of the j decision making unit (DMU). While indicates the expected efficiency level of the j decision making unit, indicates the probability that the efficiency level is more than . One of the important criticisms about DEA is that the importance of input and output weights are uncertain.
Since the input and output weights are assigned by the model, the value of a data that is important to the researcher may be zero, while relatively less important data may have a much higher value. In this case, the accuracy of the model output can also be a matter of discussion. To solve this problem, researchers proposed weighted data envelopment models. It is possible to find many different weighted DEA models in the literature. Some of the most known of these are AR I (Assurance Region I), AR II (Assurance Region II), Cone Ratio, Bounded Method and Absolute Weight Restriction models.
3.1.1. Weighted stochastic imprecise data envelopment analysis (WSIDEA)
In the previous section, general DEA model and different DEA models suggested for different situations are mentioned. It is possible to talk about numerous models that can be encountered in the literature, unlike the models mentioned in the most general terms. As mentioned above, according to the model used, the efficiency levels of decision-making units may vary. Obviously, all the models described have different advantages and disadvantages. More precisely, the advantage of one is also the missing part of another. For example, while Sueyoshi’s proposed model allows the use of stochastic data, the model proposed by Cook and Zhu is designed for deterministic data. Likewise, while Indefinite DEA can determine the group of data sets that are not known to be input or output, we do not have this possibility in Sueyoshi’s model.
The WSIDEA model, which is proposed by Aydin and Yurdakul [52] used in this study is a hybrid of DEA models that can solve all the problems mentioned above. Thus, the WSIDEA model is a new approach of the stochastic imprecise DEA model proposed by Cosgun and Yurdakul [61], where decision variables are weighted and designed according to the order of importance of the data set. The proposed model has several advantages over existing models in the literature. The differences and advantages of this model from other DEA models are as follows: the category determination of data, which is not certain to be either input or output, is included. In other words, it enables the use of stochastic data. In addition, it is an approach that saves the weight of input and output sets that make up the efficiency score from zero and most importantly integrates expert opinions into the model.
| (21) |
S.t;
| (22) |
| (23) |
| (24) |
| (25) |
| (26) |
| (27) |
| (28) |
| (29) |
| (30) |
| (31) |
Within mathematical representation above, are variables of the model. , parameters represent the expected values of the r output and l flexible data, respectively. , are the standard deviation of the variables. This parameters represent the inverse value of the cumulative normal distribution. Lastly, represents the risk criteria of the decision maker. Therefore measurement shows the rate of reaching the requirements. Eqs ((26), (27)) shown in the model guarantee that the relevant decision variables do not take a zero value. Constraints ((28), (29)) show which data is more important according to the opinions of the experts. The efficiency score for each DMUs is calculated using the equation provided in (21).
3.2. Machine learning algorithms
The machine learning algorithms to be used in this study were explained in this sub-section. K-means and hierarchic clustering algorithms were used for cluster analysis, while decision tree and random tree algorithms were used for the analysis of parameters in the 3rd step. Algorithms used in analysis are machine learning algorithms, which are frequently used in the literature. Although there are many new and different algorithm proposals in recent past, decision tree, random forest, K-means or hierarchical clustering methods are still frequently used ones because of their effort and accurate results [62].
3.2.1. K-means algorithm
K-mean method is one of the commonly preferred techniques in the machine learning literature [63], [64]. The k-mean algorithm is constructed based on the principle of minimizing intra-cluster variance and maximizing the distance between clusters. It determines k points from the original data set as the starting set center. First of all, each datum in each data set is considered as a point, then the distance between these points and the central cluster point is calculated using the Euclidean distances. Clusters are formed according to these calculated distances. Finally, the average distance of the points in each cluster is calculated and the center of gravity of each cluster is determined. This process continues until the last cluster is created [65].
3.2.2. Hierarchic clustering algorithm
There are four different linkage methods in the hierarchical clustering method. These methods are complete, average, single, and ward methods, respectively. The initial steps of these methods in creating clusters are similar, but the paths they follow are different in setting the priorities.
3.2.3. Decision tree algorithm
Another method we used in the study is the decision tree algorithm. The decision tree algorithm is an important method that can be used for both classification and regression analysis. Its ruling structure is understandable, simple to display and interpret, and suitable for graphical representation. In tree-based classification, selection is made for at least two options. The result of the selection is branched from the left side of the tree and the reverse of the selection from the right side creates a tree. The first choice creates the first node, the root node. In the regression tree, the models are obtained by Repetitive positioning of all data concentrated on the root node which is determined by the most important independent variable and applying the appropriate predictive mode [66], [67].
3.2.4. Random forest algorithm
A random forest algorithm has been developed to improve the performance of the decision tree algorithms. While both the regression model and the classification models are constructed on a single tree in the decision tree algorithm, more than one tree algorithm is used in the random forest algorithm. In the random forest algorithm, the model is run repeatedly within a certain rule structure for each tree. The point to be noted here is that in the decision tree model, the root node branches start from the most important variable. In this case, the variable used in the root node will remain the same in every tree analysis to be performed with the same data set. This will have the following result: even if the algorithm is run many times, the results will always be the same. In order to eliminate this problem, it runs a series of tree algorithms by making bootstrap with training sets randomly created from the same data set in the random forest algorithm, and by taking the average of these models, higher performance is provided [18], [68].
4. Results and discussions
The analyses made in this study were collected in three steps. Before analyses, the data set related to the COVID-19 pandemic was collected and required arrangements were made. A data set of 142 (number of countries) * 14 (number of titles) is used. Since some missing values or data encountered, first, the imputation process is applied to the missing data. In other words, data assignments that do not change the mean and standard deviation were made instead of missing data. Next, scaling is applied: The data set consists of very different values (range and type) from each other. For example, while the total number of tests includes the values expressed in hundreds of thousands, the gross domestic product refers to hundreds of millions or the data on cigarette addiction are proportional values. For this reason, each value in the data set needs to be normalized. After making arrangements on the data set, as the first step, cluster analysis, was performed. With the cluster analysis, the answers to the questions such as what is the optimum number of clusters over the total data set, what are the characteristics of these clusters and which country is in which cluster were sought. After the clustering, the efficiency analysis of the countries which is the second step was made. Separate efficiency analysis was conducted for each cluster. The efficiency levels of the countries in the same cluster were examined. Then, in the third step of the analyses, the variables that form the efficiency levels of the countries were analyzed with decision tree and random forest algorithms. The results of each algorithm were compared with each other and the algorithm giving the best performance was researched. Comparison of the models was made using three criteria for regression analysis: R2, root mean square error (RMSE) and mean absolute errors (MAE). In the analysis, a computer with i7-CPU, 64-bit windows 10 professional operating system was used. GAMS modeling version 21.6 solver program was used for WSIDEA analysis and also R programming version 4.0.2 is used for the machine learning algorithms.
4.1. Clustering analysis
Clustering analysis was performed with k-mean algorithm using data from 142 different countries. As a result of the analysis made with “complete” method and “all” index, the following results are obtained.
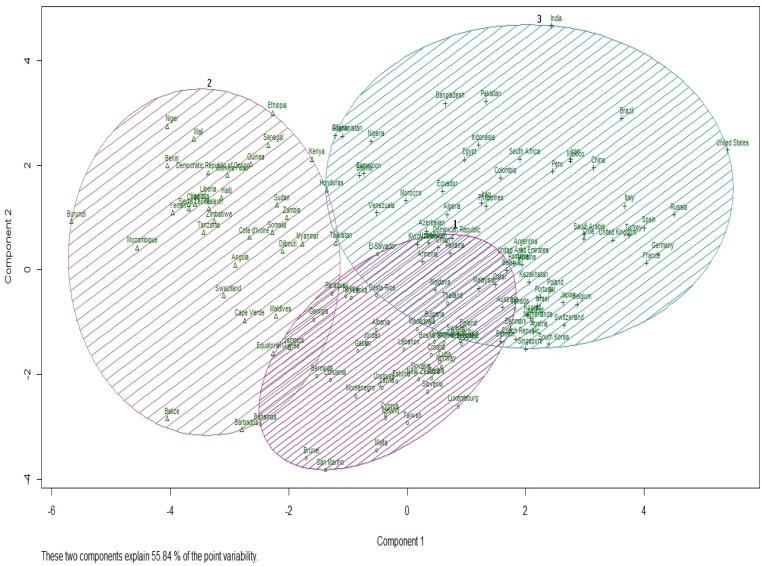
As reported in Table 2, the optimum number of clusters according to majority rule is three. The graphical representation of clusters and countries in the clusters are provided in Fig. 4.
Table 2.
K-means cluster results.
| 5 proposed 2 as the best number of clusters |
| 7 proposed 3 as the best number of clusters |
| 4 proposed 4 as the best number of clusters |
| 4 proposed 5 as the best number of clusters |
| 1 proposed 11 as the best number of clusters |
| 1 proposed 13 as the best number of clusters |
| 1 proposed 15 as the best number of clusters |
Fig. 4.
Plot of the cluster analyzing results.
Table 3 shows each cluster and the countries that make up these clusters.
Table 3.
List of the countries included in the clusters according to k-means algorithms.
| Cluster 1 | Cluster 2 | Cluster 3 | |||
|---|---|---|---|---|---|
| Albania | Angola | Afghanistan | Nigeria | ||
| Bahamas | Barbados | Algeria | Oman | ||
| Bermuda | Belize | Argentina | Pakistan | ||
| Bosnia and Herzegovina | Benin | Armenia | Panama | ||
| Brunei | Burkina Faso | Australia | Peru | ||
| Bulgaria | Burundi | Austria | Philippines | ||
| Canada | Cape Verde | Azerbaijan | Poland | ||
| Costa Rica | Chad | Bahrain | Portugal | ||
| Croatia | Cote d’Ivoire | Bangladesh | Qatar | ||
| Cuba | D. R. Congo | Belarus | Romania | ||
| Cyprus | Djibouti | Belgium | Russia | ||
| El Salvador | Equatorial Guinea | Bolivia | Saudi Arabia | ||
| Estonia | Ethiopia | Brazil | Singapore | ||
| Finland | Guinea | Cameroon | South Africa | ||
| Gabon | Haiti | Chile | South Korea | ||
| Georgia | Honduras | China | Spain | ||
| Greece | Jamaica | Colombia | Swaziland | ||
| Hungary | Kenya | Czech Republic | Turkey | ||
| Iceland | Liberia | Denmark | Ukraine | ||
| Jordan | Malawi | Dominican Republic | U. Arab Emirates | ||
| Latvia | Maldives | Ecuador | United Kingdom | ||
| Lebanon | Mali | Egypt | United States | ||
| Lithuania | Mozambique | France | Uzbekistan | ||
| Luxembourg | Myanmar | Germany | Venezuela | ||
| Macedonia | Niger | Ghana | |||
| Malta | Senegal | India | |||
| Montenegro | Sierra Leone | Indonesia | |||
| New Zealand | Somalia | Iran | |||
| Norway | Sudan | Iraq | |||
| Paraguay | Switzerland | Ireland | |||
| Puerto Rico | Tajikistan | Israel | |||
| San Marino | Tanzania | Italy | |||
| Serbia | Uganda | Japan | |||
| Slovakia | Yemen | Kazakhstan | |||
| Slovenia | Zambia | Kuwait | |||
| Sri Lanka | Zimbabwe | Kyrgyzstan | |||
| Sweden | Malaysia | ||||
| Taiwan | Mexico | ||||
| Thailand | Moldova | ||||
| Tunisia | Morocco | ||||
| Uruguay | Netherlands | ||||
As in Table 3, cluster 1 consists of 41 countries, cluster 2 consists of 36 countries and cluster 3 consists of 65 countries. The statistics of the clusters are provided in Table 4.
Table 4.
Statistic analyses of the clusters.
| Cluster 1 |
Cluster 2 |
Cluster 3 |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Max | Min | Ort | Max | Min | Ort | Max | Min | Ort | |
| Sum of total cases | 2 423 523 | 3644 | 158 241 | 1 542 486 | 765 | 61 021 | 48 945 768 | 4404 | 2 326 215 |
| Sum of total deaths | 143 146 | 55 | 8457 | 63 499 | 0 | 2360 | 2 677 247 | 51 | 157 053 |
| GDP | 94 277.97 | 7292.46 | 28 936.72 | 57 410.17 | 702.23 | 5734.15 | 116 935.60 | 1803.99 | 26 351.23 |
| Extreme poverty | 5.00 | 0.10 | 1.13 | 77.10 | 4.80 | 39.07 | 23.80 | 0.10 | 3.50 |
| Hospital beds | 7.45 | 1.13 | 3.77 | 5.80 | 0.10 | 1.39 | 13.05 | 0.50 | 3.48 |
| Total recovered | 40 776 | 32 | 2170 | 27 800 | 4 | 1023 | 370 973 | 0 | 29 328 |
| Active cases | 33 335 | 1 | 2066 | 2594 | 0 | 483 | 1 130 532 | 0 | 36 703 |
| Total tests | 1 375 126 | 1826 | 113 210 | 361 692 | 120 | 27 827 | 14 190 978 | 281 | 965 228 |
| Population | 69 799 978 | 33 938 | 7 648 506 | 114 963 583 | 287 371 | 23 499 211 | 1 439 323 774 | 1 160 164 | 96 474 052 |
As reported in Table 4, big differences occur between the statistics parameters of the clusters. Considering the total number of cases, the first cluster has 150 thousand on average, while the second cluster has 60 thousand and the third cluster has 2.5 million. Similar situations are valid for other parameters.
In clustering made via hierarchical clustering method, the results of four different linkage methods should be compared and the best result has to be analyzed in order to obtain the optimum number of clusters. There are two most commonly used algorithms in the hierarchical clustering methods to achieve the best results. The hierarchical clustering method works based on two basic algorithms: agglomerative and divisive. Agglomerative clustering is called AGNES for short.
Agnes algorithm starts clustering from the bottom to up. It starts performing as a single cluster first, then each cluster merges with the cluster that is most similar to itself. After these mergers, they form larger clusters. Divisive aggregate method is called DIANA for short. This method works exactly opposite to AGNES method. First, it starts as a large single cluster and then at each step the clusters are divided into two homogeneously.
Agglomerative Coefficient (AC) is a metric used to quantify hierarchical structures, proposed by Kaufman and Rousseeuw [69].
Where refers to the average distance of an object that is merged to (or more objects) for the first time. refers to the distance at where all objects came together in a single set. As stated above, with respect to clustering process of AGNES model, all objects cluster from bottom to top. First, the most similar objects form a cluster, then among these new clusters the most similar ones form a cluster until all clusters merge into a single cluster. The use of AC has been used frequently in many areas. In our study, four different linkage methods among hierarchical clustering methods were used, their results were compared, and the method with the highest agglomerative coefficient value was selected. As a result, Ward linkage method has been selected with a meaningful and sufficient value of 0.95375.
In the agglomerative clustering method, the optimum number of clusters is measured with the agglomerative coefficient (AC) parameter. The result with the highest AC value is taken as the best [69], [70], [71], [72].
In this study, Agnes algorithm is preferred and the results for “AC” values are presented in Table 5.
Table 5.
Ac values of linkage methods.
| Agglomerative coefficient (AC) | |
|---|---|
| Complete Agnes | 0.87469 |
| Single Agnes | 0.66476 |
| Average Agnes | 0.78413 |
| Award Agnes | 0.95378 |
Based on the results provided in Table 5, the best agglomerative coefficient score was obtained by the Award Agnes method. The cluster analysis results obtained by Award Agnes method are shown in Table 6.
Table 6.
List of the country included in cluster according to hierarchic algorithms.
| Cluster 1 | Cluster 2 | Cluster 3 | |||
|---|---|---|---|---|---|
| Afghanistan | Kuwait | Albania | Lebanon | Canada | |
| Algeria | Kyrgyzstan | Angola | Liberia | Mozambique | |
| Argentina | Malaysia | Australia | Lithuania | Serbia | |
| Armenia | Mexico | Bahamas | Luxembourg | Sweden | |
| Austria | Moldova | Barbados | Macedonia | ||
| Azerbaijan | Morocco | Belize | Malawi | ||
| Bahrain | Netherlands | Benin | Maldives | ||
| Bangladesh | Nigeria | Brunei | Mali | ||
| Belarus | Oman | Bulgaria | Malta | ||
| Belgium | Pakistan | Burkina Faso | Montenegro | ||
| Bermuda | Panama | Burundi | Myanmar | ||
| Bolivia | Peru | Cameroon | New Zealand | ||
| Bosnia and Herzegovina | Philippines | Cape Verde | Niger | ||
| Brazil | Poland | Chad | Norway | ||
| Chile | Portugal | Costa Rica | Paraguay | ||
| China | Puerto Rico | Cote d’Ivoire | San Marino | ||
| Colombia | Qatar | Croatia | Senegal | ||
| Czech Republic | Ecuador | Cuba | Sierra Leone | ||
| Denmark | Romania | Cyprus | Slovakia | ||
| Dominican | Russia | D. Republic of Congo | Slovenia | ||
| Egypt | Saudi Arabia | Djibouti | Somalia | ||
| El Salvador | Singapore | Equatorial Guinea | Sri Lanka | ||
| France | South Africa | Estonia | Sudan | ||
| Germany | South Korea | Ethiopia | Swaziland | ||
| Honduras | Spain | Finland | Taiwan | ||
| India | Switzerland | Gabon | Tajikistan | ||
| Indonesia | Thailand | Georgia | Tanzania | ||
| Iran | Turkey | Ghana | Tunisia | ||
| Iraq | Ukraine | Greece | Uganda | ||
| Ireland | U. Arab Emirates | Guinea | Uruguay | ||
| Israel | U. Kingdom | Haiti | Venezuela | ||
| Italy | U. States | Hungary | Yemen | ||
| Japan | Uzbekistan | Iceland | Zambia | ||
| Kazakhstan | Jamaica | Zimbabwe | |||
| Jordan | |||||
| Kenya | |||||
| Latvia | |||||
According to Table 6, a similar class number has been reached with the previous method, the k-mean method. In both methods, the optimum number of clusters is three. However, the number of countries that make up the clusters differentiate. Table 7 compares the outcomes.
Table 7.
K-means and Hierarchic cluster comparison table.
| Hierarchic cluster |
||||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| K-means cluster | 1 | 21 | 20 | 0 |
| 2 | 16 | 17 | 3 | |
| 3 | 30 | 34 | 1 | |
In the light of the information provided in Table 7, it can be inferenced that the two algorithms gave the same optimum number of sets, but the number of elements of the sets and these elements are different. While the number of elements of cluster 1 was 41 in the analysis made with K-means, it was 67 in the hierarchic method. Similarly, in the first method, cluster 2 consists of 36 elements, while cluster 2 consists of 71 elements. However, while United State and United Kingdom are in the 3rd cluster as a result of the first algorithm, they are in the 1st cluster as a result of the hierarchic clustering method.
The cluster-based efficiency analyses of the countries that make up each cluster were made using the WSIDEA method. Before applying the WSIDEA method, there are a few important phenomena to mention. First, input, output and flexible data sets should be created. In general DEA models, income indexed data constitute the output set, while the data affecting the cost form the input set. In addition, it creates a flexible data set that is not certain whether it is input or output. Since income or cost-based data are not used in this study, data related to COVID-19 were used while creating input and output data sets. Data such as total death cases, stringency index and poverty index were accepted as inputs. Data such as the number of patients recovered and GDP were accepted as outputs. In addition, the total number of cases and the number of active cases were included in the analysis as a flexible data set. On the other hand, experts’ opinions were sought to determine which data is important or is less important than others. The titles of the input, output and flexible data sets to be used in the analysis are as in Table 8.
Table 8.
Input and output data sets for WSIDEA.
| Input | Output | Flexible | |
|---|---|---|---|
| Sum of total deaths | Population | Sum of total cases | |
| Stringency index | GDP | Active cases | |
| Extreme poverty | Hospital beds | ||
| Cvd death rate | Total recovered | ||
| Diabetes prevalence | Total test | ||
| Female smokers | |||
| Male smokers |
4.2. Results of WSIDEA
In the light of outputs gathered from WSIDEA, when the efficiency analysis of the countries that make up each cluster is made, the results in Table 9, Table 10, Table 11 are created.
Table 9.
Efficiency results of cluster 1.
| Country | Efficiency level | Country | Efficiency level | |
|---|---|---|---|---|
| Albania | 0.801 | Lebanon | 0.863 | |
| Bahamas | 0.803 | Lithuania | 0.834 | |
| Bermuda | 0.809 | Luxembourg | 0.914 | |
| Bosnia and Herzegovina | 0.847 | Macedonia | 0.808 | |
| Brunei | 1.000 | Malta | 1.000 | |
| Bulgaria | 0.88 | Montenegro | 0.879 | |
| Canada | 0.98 | New Zealand | 0.915 | |
| Costa Rica | 0.989 | Norway | 1.000 | |
| Croatia | 0.843 | Paraguay | 0.934 | |
| Cuba | 0.852 | Puerto Rico | 0.87 | |
| Cyprus | 0.892 | San Marino | 0.838 | |
| El Salvador | 0.956 | Serbia | 0.92 | |
| Estonia | 0.885 | Slovakia | 0.895 | |
| Finland | 0.944 | Slovenia | 0.79 | |
| Gabon | 1.000 | Sri Lanka | 1.000 | |
| Georgia | 0.952 | Sweden | 0.945 | |
| Greece | 0.858 | Taiwan | 1.000 | |
| Hungary | 0.846 | Thailand | 1.000 | |
| Iceland | 1.000 | Tunisia | 0.82 | |
| Jordan | 1.000 | Uruguay | 0.969 | |
| Latvia | 0.907 |
Table 10.
Efficiency results of cluster 2.
| Country | Efficiency level | Country | Efficiency level |
|---|---|---|---|
| Angola | 0.983 | Liberia | 0.758 |
| Barbados | 0.811 | Malawi | 0.892 |
| Belize | 0.981 | Maldives | 1.000 |
| Benin | 1.000 | Mali | 0.796 |
| Burkina Faso | 0.782 | Mozambique | 0.726 |
| Burundi | 1.000 | Myanmar | 0.960 |
| Cape Verde | 0.897 | Niger | 0.842 |
| Chad | 0.788 | Senegal | 0.914 |
| Cote d’Ivoire | 0.874 | Sierra Leone | 0.784 |
| Democratic Republic of Congo | 0.808 | Somalia | 0.831 |
| Djibouti | 0.936 | Sudan | 0.797 |
| Equatorial Guinea | 0.958 | Swaziland | 1.000 |
| Ethiopia | 1.000 | Tajikistan | 0.866 |
| Guinea | 0.916 | Tanzania | 0.878 |
| Haiti | 0.809 | Uganda | 0.749 |
| Honduras | 0.756 | Yemen | 0.885 |
| Jamaica | 0.863 | Zambia | 0.944 |
| Kenya | 0.837 | Zimbabwe | 0.873 |
Table 11.
Efficiency results of cluster 3.
| Country | Efficiency level | Country | Efficiency level |
|---|---|---|---|
| Afghanistan | 0.894 | Kazakhstan | 1.000 |
| Algeria | 0.862 | Kuwait | 0.901 |
| Argentina | 0.867 | Kyrgyzstan | 0.916 |
| Armenia | 0.826 | Malaysia | 0.993 |
| Australia | 0.956 | Mexico | 0.786 |
| Austria | 0.785 | Moldova | 0.812 |
| Azerbaijan | 0.955 | Morocco | 0.863 |
| Bahrain | 0.982 | Netherlands | 0.759 |
| Bangladesh | 0.902 | Nigeria | 1.000 |
| Belarus | 0.949 | Oman | 0.981 |
| Belgium | 0.748 | Pakistan | 0.861 |
| Bolivia | 0.815 | Panama | 0.766 |
| Brazil | 0.765 | Peru | 0.770 |
| Cameroon | 0.851 | Philippines | 0.890 |
| Chile | 0.830 | Poland | 0.823 |
| China | 0.868 | Portugal | 0.767 |
| Colombia | 0.825 | Qatar | 1.000 |
| Czech Republic | 0.889 | Romania | 0.739 |
| Denmark | 0.809 | Russia | 0.931 |
| Dominican Republic | 0.757 | Saudi Arabia | 0.878 |
| Ecuador | 0.751 | Singapore | 1.000 |
| Egypt | 0.857 | South Africa | 0.885 |
| France | 0.729 | South Korea | 0.762 |
| Germany | 0.760 | Spain | 0.725 |
| Ghana | 0.999 | Switzerland | 0.796 |
| India | 0.868 | Turkey | 0.823 |
| Indonesia | 0.850 | Ukraine | 0.887 |
| Iran | 0.820 | United Arab Emirates | 0.853 |
| Iraq | 0.891 | United Kingdom | 0.770 |
| Ireland | 0.799 | United States | 0.764 |
| Israel | 0.855 | Uzbekistan | 1.000 |
| Italy | 0.700 | Venezuela | 1.000 |
| Japan | 0.956 |
Based on the WSIDEA results, nine out of 41 countries were fully efficient in cluster 1, while 21 countries had an efficiency of 90% or more. In the second cluster, five countries from 36 countries were fully effective and 13 countries reached an efficiency score of 90% and above. In the 3rd cluster with the highest number of members, 61 countries, six countries have a value at full efficiency level, while 18 countries have reached a value of 90% and above. The average efficiency scores of the clusters are shown in Table 12.
Table 12.
Average efficiency scores of clusters.
| Average efficiency level | |
|---|---|
| Cluster 1 | 0.9082 |
| Cluster 2 | 0.8748 |
| Cluster 3 | 0.8565 |
Based on the obtained analyses, some countries have reached full efficiency during the COVID-19 pandemic process, while some countries have remained at much lower levels.
4.3. Results of decision tree and random forest algorithms
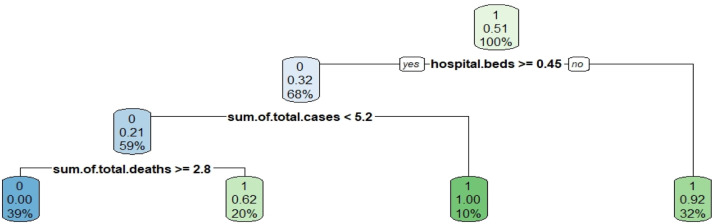
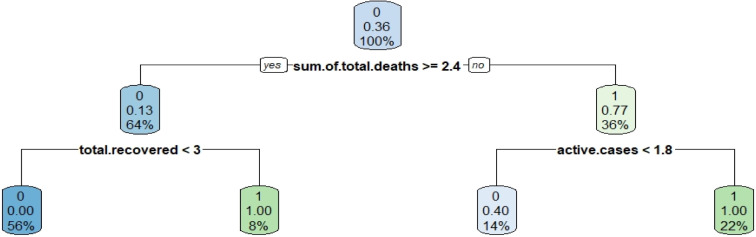
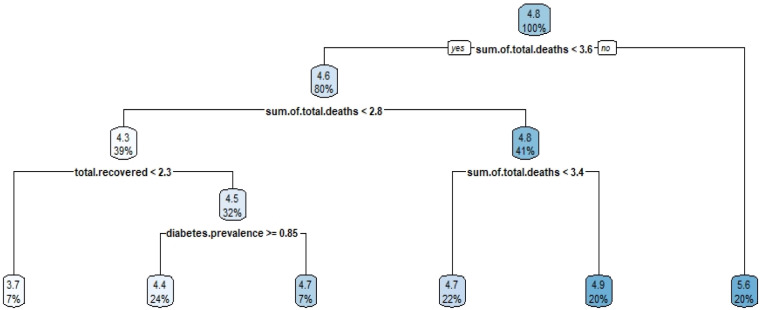
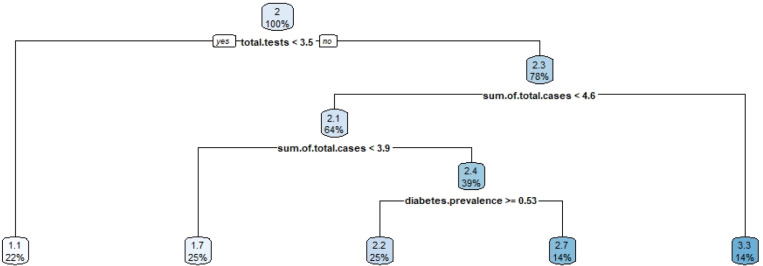
In this part, which is the third step of the study, the parameters that are directly effective in determining the efficiency levels of countries for each cluster will be analyzed with decision tree and random forest algorithms. Decision tree algorithm is a method frequently used in the literature that is able to explain independent variables with dependent variables. Analyzes were done separately for three different clusters. Four models were run for four different dependent variables in the analysis. The first of these dependent variables is the efficiency scores obtained in the previous analysis. Efficiency scores were added as a categorical variable to the data set. If a country has an efficiency score of 90% or more, it is accepted as 1, otherwise 0. Other variables are the total number of cases, deaths and recovered patients, respectively. When the efficiency score is taken as the dependent variable of the model as a parameter, we obtained the results provided in Fig. 5 for cluster 1.
Fig. 5.
Decision tree results for cluster 1 with efficiency variable.
Based on the results in Fig. 5, it is seen that the most important variable for efficiency score is the number of hospital beds. Countries with less than 0.45 hospital beds are 32% efficient countries. If the number of hospital beds and cases are greater than 0.45 and 5.2, respectively, then it is accepted as efficient. This means that the number of hospital beds in a country directly affects the country’s fight against the COVID-19 pandemic.
Likewise, when the analysis is made for the 2nd and 3rd clusters, the results in Fig. 6, Fig. 7 are obtained.
Fig. 6.
Decision tree results for cluster 2 with efficiency variable.
Fig. 7.
Decision tree results for cluster 3 with efficiency variable.
According to Fig. 6, it is seen that the most important variable affecting the efficiency score for the 2nd cluster countries is the total number of death cases. Likewise, this parameter has emerged as the most important parameter in the 3rd set as well.
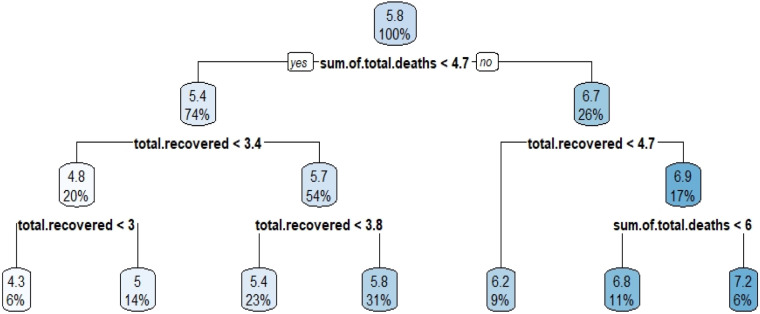
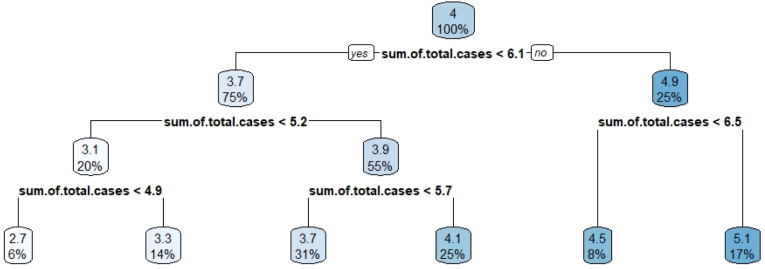
When similar analyses are conducted for the total death case parameter, the following results in Fig. 8 are obtained.
Fig. 8.
Decision tree results for cluster 1 with sum of total death variable.
For the countries in cluster 1, the most important variable affecting total death cases was the total number of cases, which is obviously an expected result. What is striking is that the stringency index is one of the independent variables used in the analysis, and, further, the variables such as GDP, smoking rates or diabetes prevalence have no effect on the total mortality rates. Another remarkable result is that the countries with an effective level of 1 or 0 in cases where the total number of cases is less than 4.4 did not affect the total death case parameter. In other words, whether any country is efficient on the basis of COVİD-19 and pandemic has no effect on the total death case parameter. The results for other two clusters are as in Fig. 9, Fig. 10.
Fig. 9.
Decision tree results for cluster 2 with sum of total death variable.
Fig. 10.
Decision tree results for cluster 3 with sum of total death variable.
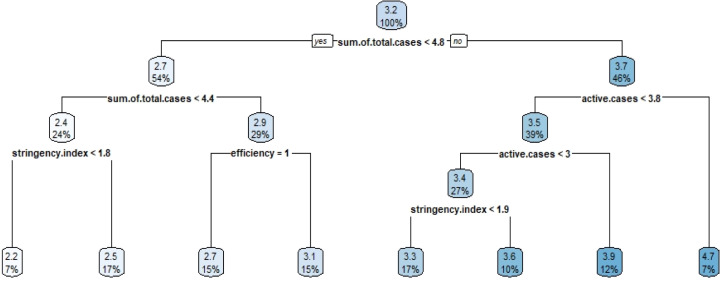
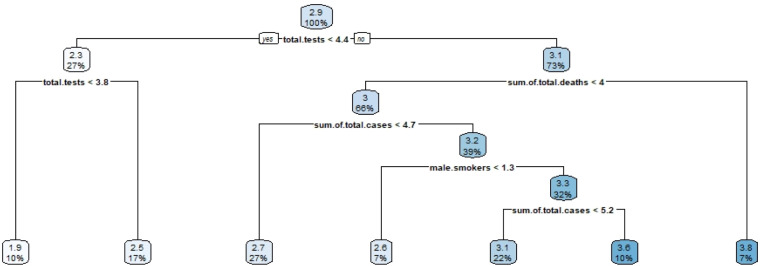
Based on the results provided in Fig. 9, Fig. 10, it is seen that the most important variable for the total death case parameter is the total number of cases. In cluster 2, following the total number of cases parameter, the next most important parameters are efficiency score and GDP, while in cluster 3, efficiency score and number of hospital beds are the next most important parameters. It is expected that the total number of cases will be the most important parameter. The striking result here is that the number of hospital beds and stringency index are among the variables used in the model. On the other hand, variables such as GDP, diabetes prevalence rate, cigarette addiction rate do not affect the total number of deaths. Similarly, when decision tree analyses are made for the total number of cases, the following results in Figs. 11, 12, and 13 are obtained.
Fig. 11.
Decision tree results for cluster 1 with sum of total case variable.
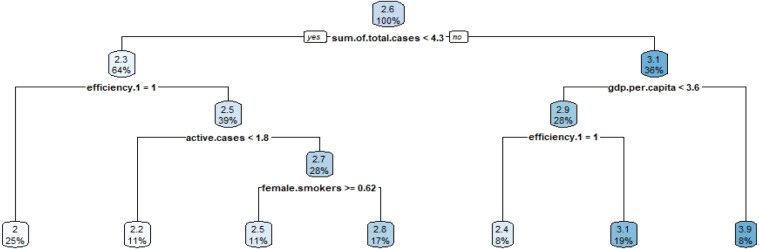
Fig. 12.
Decision tree results for cluster 2 with sum of total case variable.
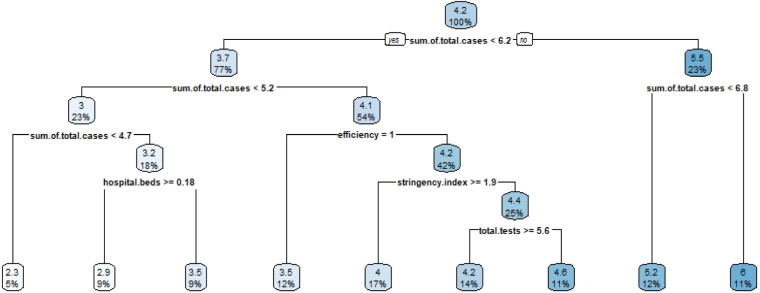
Fig. 13.
Decision tree results for cluster 3 with sum of total case variable.
Fig. 11 shows the results for the first cluster, while Fig. 12 shows the results of the second cluster and Fig. 13 shows the results of the third cluster. As can be seen from the graphic in Fig. 11, the most important variable that affected the total number of cases was the total death case parameter. Oppositely, the most important parameter for the second cluster was determined as the total number of healed patients, and similar result with cluster 1 obtained for cluster 3.
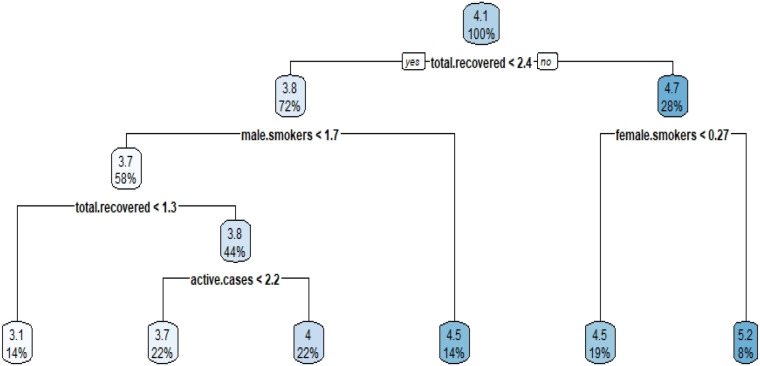
Finally, analyses were made for the total number of healing patients and the results are presented in Fig. 14, Fig. 15, Fig. 16.
Fig. 14.
Decision tree results for cluster 1 with number of recovered variable.
Fig. 15.
Decision tree results for cluster 2 with number of recovered variable.
Fig. 16.
Decision tree results for cluster 3 with number of recovered variable.
In the analyses performed for the first and second clusters, the most important variable for the parameter of the total number of healing patients is the total number of tests, while for the third cluster, this parameter is determined as the total number of cases. In cluster 1, the smoking addiction (male) parameter is another variable used in the model. Analyzing the outcomes for the 2nd cluster the following results are inferenced: In cluster 1, while smoking addiction rates were derived from important data affecting the total number of patients healed parameter, in cluster 2 this data group was excluded from the model. Instead, the diabetes prevalence parameter entered the model. In other words, in cases where the total number of cases is greater than 3.9, and if the diabetes prevalence is less than 0.53, the recovery rate of the patients is 25%. Otherwise, the recovery rate of patients has decreased to 14%.
The analysis and results made with the decision tree algorithm are as shown above. Additionally, the random forest algorithm is also applied. The random forest algorithm has been applied distinctly for the three clusters. Analyzes were performed for four different variables disjointedly, namely the level of efficacy, total number of cases, total deaths, and total number of patients recovered. Results of the algorithm are presented as follows:
The random forest algorithm was run on the activity variable for each cluster and the results are shown in Table 13. Efficiency value is actually a value obtained as a result of WSIDEA analysis. Particularly, the random forest algorithm was run by adding this obtained value to the model as a categorical variable. For this reason, this analysis is a classification analysis. In this respect, the accuracy values shown in Table 13 are acceptable for each cluster. Since other variables are discrete variables, regression analysis was performed. The analysis results are shown in Table 14. Based on the results in Table 14, the RMSE, MAE and R2 values obtained for each cluster are sufficient and acceptable.
Table 13.
Accuracy scores for efficiency variables.
| Cluster 1 | Cluster 2 | Cluster 3 | |
|---|---|---|---|
| Accuracy | 0.7916 | 0.7444 | 0.8833 |
Table 14.
Results of random forest analyses.
| RMSE | R2 | MAE | ||
|---|---|---|---|---|
| Cluster 1 | Sum of total cases | 0.2471 | 0.8359 | 0.2039 |
| Sum of total deaths | 0.3514 | 0.9920 | 0.3206 | |
| Total recovered | 0.0571 | 0.9784 | 0.0471 | |
| Cluster 2 | Sum of total cases | 0.4366 | 0.7178 | 0.3422 |
| Sum of total deaths | 0.4935 | 0.7235 | 0.4049 | |
| Total recovered | 0.2458 | 0.8709 | 0.2326 | |
| Cluster 3 | Sum of total cases | 0.2127 | 0.9437 | 0.1606 |
| Sum of total deaths | 0.4754 | 0.8151 | 0.4000 | |
| Total recovered | 0.0749 | 0.9771 | 0.0624 | |
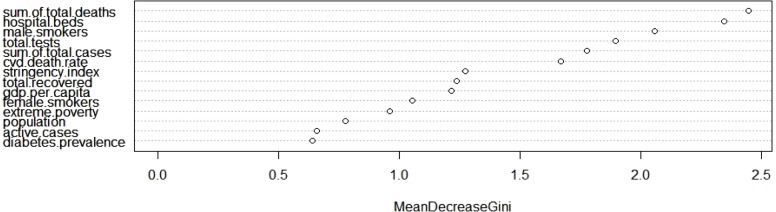
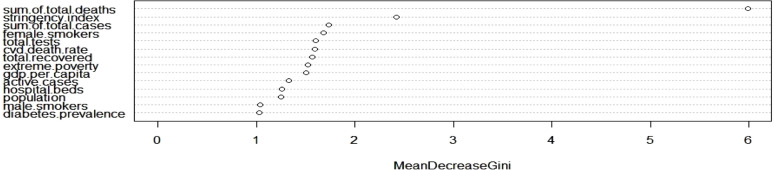
Furthermore, analyzing the mean decrease Gini graph (see Fig. 17) for the efficiency variable, it is determined that the most important variables for cluster 1 are the total death cases, hospital beds and smoking dependency rate (male). Differently, in cluster 2 the total death cases, total number of healed patients and CVD death rate are determined as the most important variables (see Fig. 18). For cluster 3, the total death cases, stringency index and total number of cases are obtained as the most important variables (see Fig. 19).
Fig. 17.
Mean Decrease Gini chart for cluster 1.
Fig. 18.
Mean Decrease Gini chart for cluster 2.
Fig. 19.
Mean Decrease Gini chart for cluster 3.
4.4. Discussions
Considering the results obtained in the light of the analysis, three remarkable outcomes have emerged. First of all, as a result of the clustering analysis, the optimum number of clusters of 142 countries is determined as three in both algorithms. However, the number of cluster memberships are different from each other. According to the K-means algorithm, the number of elements in the clusters are 41, 36 and 65, respectively, while they are 67, 71 and 4 in hierarchical clustering. Considering the K-means algorithm, the second cluster consists of the countries with low number of infectious and deaths. Similarly, the countries form the second cluster have low GDP, low hospital bed numbers and high poverty index. The third cluster consists of countries with the highest number of cases and mortality rates. However, the first cluster is the median cluster of the other data groups. Accordingly, it cannot be said that the number of hospital beds and GDP directly affects the total number of infectious and total deaths.
The second attention grabbing result appears in the efficiency analysis. According to the number of members in each cluster, the order of clusters in descending order is cluster 3, cluster 1 and cluster 2. If they are ranked according to the average efficiency level, it will be ranked as cluster 1, cluster 2 and cluster 3. In other words, the cluster with the highest number of members has the lowest average efficiency level.
As may be recalled from the cluster analysis (Table 3), the first cluster (cluster 1) is the cluster with the highest rate in terms of GDP and hospital beds, but has the lowest rate in terms of poverty index. On the other hand, cluster 1 is the cluster with the highest efficiency level in terms of average efficiency level. Even though the third cluster has the highest value in terms of total number of cases and total death cases it holds the lowest average efficiency level. In this respect, cluster analysis and efficiency analysis are seen to be consistent with each other.
As a summary the cluster with the lowest average efficiency level is the cluster with the highest level in terms of total number of cases, total number of deaths and population. Based on this, we can say that in terms of mean values, the cluster that was most affected by the COVID-19 pandemic was the cluster with the lowest efficiency level. In other words, there is an inverse ratio between efficiency level and COVID-19 values for countries.
Another remarkable outcome is that the data groups such as female and male smoking addiction rates, GDP and CVD death rate do not have significant effects on the total number of cases, total number of deaths and total number of recovered patients.
5. Conclusions
The COVID-19 pandemic, which emerged in the People’s Republic of China in December 2019 and then spread all over the world, has become one of the most dangerous epidemics the world has ever seen. Since it is an epidemic with a high rate of transmission, millions of people in many countries have suffered from the disease in a short time period and the hundreds of thousands of people have lost their lives.
Currently, many researchers are in search of a solution to end this disease. Besides researches for ending up the epidemic there are many qualified studies, which analyze the effects of the epidemic in different disciplines in the literature on the COVID-19 pandemic.
In this study, multidisciplinary analyses were made on the data of countries on pandemics. Unlike other studies, in this study, clustering studies of the countries affected by the pandemic were carried out and the optimum number of clusters and the characteristics of these clusters were examined. Afterwards, the efficiency levels of the countries that make up each cluster were investigated by a novel DEA based model. Thereafter, the effect of the data set on the efficiency results was investigated with decision tree and random forest algorithms. Considering the results of the research, both the K-means algorithm and the hierarchic clustering method showed that the optimum number of clusters for the data set consisting of 142 countries was three. When the efficiency levels of countries were analyzed on the basis of clusters, 20 out of 142 countries were fully effective, while the rate of countries reaching 0.9 and above efficiency levels was around 34%. Another analysis in the study was made with decision tree and random forest algorithms. As a result of these analyses, it was seen that the parameters such as stringency index, diabetes prevalence and number of hospital beds have a remarkable effect on fight against the COVID-19 pandemic. However, it was observed in the analysis results that the parameters such as GDP, both male/female cigarette smoker rate, extreme poverty, CVD death rate had no or minor effect. Furthermore, the situation of countries in the process of COVID-19 pandemic was tried to be examined by linear programming and machine learning-based methods, and 14 different data groups were used in this study.
The data set used in the study consists of 14 different data collected from 142 countries. Of course, the number of countries affected by the COVID-19 pandemic is higher than the countries covered in this study. However, since the data of all countries were not available, the study was limited to 142 countries. Therefore, when the data for other countries become available the study may be extended. Furthermore, one of the second objectives of this study was to research whether different parameters, such as the stringency index or diabetes prevalence, have an effect on the number of cases of COVID-19 pandemic. The factors that can be considered is not limited to above mentioned ones, thus, many similar factors or parameters such as air pollution, tourism intensity rates, mask effect, various lung diseases, hypertension, air travel may be considered for this purpose, as a future study. It is thought that it will be beneficial to conduct a research for these and similar or different parameters in the future studies. Moreover, based on the results obtained here, it may be useful to examine the factors affecting the number of cases, deaths due to pandemic and the number of patients recovering, in detail. Additionally, it can be investigated why the countries with low efficiency scores are at low efficiency levels based on the efficiency analysis results obtained in this study. Furthermore, detailed studies by increasing more number of countries and the data set may be useful in combating the COVID-19 pandemic.
CRediT authorship contribution statement
Nezir Aydin: Idea, Conceptualization, Software, Writing - review & editing, Supervision. Gökhan Yurdakul: Methodology, Developed the theory software, Validation, Data curation, Resources, Writing, Visualization preparation.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Du Z., Wang L., Cauchemez S., Xu X., Wang X., Cowling B.J., Meyers L.A. Risk for transportation of coronavirus disease from Wuhan to other cities in China. Emerg. Infect. Diseases. 2020;26(5):1049. doi: 10.3201/eid2605.200146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.WHO . 2020. Coronavirus. https://www.who.int/health-topics/coronavirus#tab=tab_1, (accessed 20 July 2020) [Google Scholar]
- 3.Chung M., Bernheim A., Mei X., Zhang N., Huang M., Zeng … X., Jacobi A. CT imaging features of 2019 novel coronavirus (2019-nCoV) Radiology. 2020;295(1):202–207. doi: 10.1148/radiol.2020200230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Li He, Xu Xiao-Long, Dai Da-Wei, Huang Zhen-Yu, Ma Zhuang, Guan Yan-Jun. Int. J. Infec. Dis. 2020 doi: 10.1016/j.ijid.2020.05.076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.ECDC . 2020. https://www.ecdc.europa.eu/en/geographical-distribution-2019-ncov-cases. [Last Access: 29 July, 2020] [Google Scholar]
- 6.Roser M., Ritchie H., Ortiz-Ospina E., Hasell J. 2020. Coronavirus pandemic (COVID-19) Received from OurWorldInData.org: https://ourworldindata.org/coronavirus#citation. [Google Scholar]
- 7.Pandemic plan . 2019. https://hsgm.saglik.gov.tr/tr/bulasicihastaliklar-haberler/ulusal-pandemi-hazirlik-plani.html. [Last Access: 29 July, 2020] [Google Scholar]
- 8.Maleki M., Mahmoudi M.R., Wraith D., Pho K.H. Time series modelling to forecast the confirmed and recovered cases of COVID-19. Travel Med. Infec. Dis. 2020 doi: 10.1016/j.tmaid.2020.101742. [DOI] [PubMed] [Google Scholar]
- 9.Tuli S., Tuli S., Tuli R., Gill S.S. Predicting the growth and trend of COVID-19 pandemic using machine learning and cloud computing. Internet Things. 2020 doi: 10.1016/j.iot.2020.100222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Salgotra R., Gandomi M., Gandomi A.H. Time series analysis and forecast of the COVID-19 pandemic in India using genetic programming. Chaos Solitons Fractals. 2020 doi: 10.1016/j.chaos.2020.109945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Açikgöz Ö., Günay A. The early impact of the Covid-19 pandemic on the global and turkish economy. Turkish J. Med. Sci. 2020;50(SI-1):520–526. doi: 10.3906/sag-2004-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sarkodie S.A., Owusu P.A. Global assessment of environment, health and economic impact of the novel coronavirus (COVID-19) Environ. Dev. Sustain. 2020:1–11. doi: 10.1007/s10668-020-00801-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fang Y., Zhang H., Xie J., Lin M., Ying L., Pang P., Ji W. Sensitivity of chest CT for COVID-19: comparison to RT-PCR. Radiology. 2020 doi: 10.1148/radiol.2020200432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Qi H., Xiao S., Shi R., Ward M.P., Chen Y., Tu … W., Zhang Z. COVID-19 transmission in Mainland China is associated with temperature and humidity: A time-series analysis. Sci. Total Environ. 2020 doi: 10.1016/j.scitotenv.2020.138778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Li H., Xu X.L., Dai D.W., Huang Z.Y., Ma Z., Guan Y.J. Air pollution and temperature are associated with increased COVID-19 incidence: a time series study. Int. J. Infect. Dis. 2020 doi: 10.1016/j.ijid.2020.05.076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Atalay M., Çelik E. Büyük veri analizinde yapay zekâ ve makine öğrenmesi uygulamalari-artificial intelligence and machine learning applications in big data analysis. Mehmet Akif Ersoy Üniv. Sos. Bilim. Enst. Derg. 2017;9(22):155–172. [Google Scholar]
- 17.M. Gök. Makine öğrenmesi yöntemleri ile akademik başarinin tahmin edilmesi. Gazi Üniv. Fen Bilim. Derg. C. 2017;5(3):139–148. [Google Scholar]
- 18.Rebai S., Yahia F.B., Essid H. A graphically based machine learning approach to predict secondary schools performance in Tunisia. Socio-Econ. Plan. Sci. 2020:1–14. [Google Scholar]
- 19.Kaynar o., Arslan H., Görmez Y., Işik Y.E. Makine öğrenmesi ve öznitelik seçim yöntemleriyle saldırı tespiti. Bilişim Teknol. Derg. 2018;11(2):175–185. [Google Scholar]
- 20.Yiğiter Ş.Y., Sarı S.S., Karabulut T., Başakın E.E. Kira sertifikası fiyat değerlerinin makine öğrenmesi metodu ile tahmini. Uluslar. İslam Ekon. Finans. Araştırmaları Derg. 2018;4(3):74–82. [Google Scholar]
- 21.Zhou T., Song Z., Sundmacher K. Big data creates new opportunities for materials research: A review on methods and applications of machine learning for materials design. Engineering. 2019;5(6):1017–1026. [Google Scholar]
- 22.Lavrov I., Domashova J. Constructor of compositions of machine learning models for solving classification problems. Procedia Comput. Sci. 2020;169:780–786. [Google Scholar]
- 23.Sağbaş E.A., Balli S. Akıllı telefon algılayıcıları ve makine öğrenmesi kullanılarak ulaşım türü tespiti. Pamukkale Univ. J. Eng. Sci. 2016;22(5) [Google Scholar]
- 24.Şeker A., Diri B., Balık H.H. Derin öğrenme yöntemleri ve uygulamaları hakkında bir inceleme. Gazi Mühendis. Bilim. Derg. 2017;3(3):47–64. [Google Scholar]
- 25.Chen T.H. Do you know your customer? Bank risk assessment based on machine learning. Appl. Soft Comput. 2020;86 [Google Scholar]
- 26.Jan B., Farman H., Khan M., Imran M., Islam I.U., Ahmad … A., Jeon G. Deep learning in big data analytics: A comparative study. Comput. Electr. Eng. 2019;75:275–287. [Google Scholar]
- 27.dos Santos B.S., Steiner M.T.A., Fenerich A.T., Lima R.H.P. Data mining and machine learning techniques applied to public health problems: A bibliometric analysis from 2009 to 2018. Comput. Ind. Eng. 2019;138 [Google Scholar]
- 28.Remuzzi A., Remuzzi G. COVID-19 and Italy: what next? Health Policy. 2020:1225–1228. doi: 10.1016/S0140-6736(20)30627-9. The Lancet. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Dikmen A.U., Kina M.H., Özkan S., Ilhan M.N. COVID-19 epidemiyolojisi: Pandemiden ne öğrendik. J. Biotechnol. Strateg. Health Res. 2020;4:29–36. [Google Scholar]
- 30.D. Parbat, A python based support vector regression model for prediction of Covid19 cases in India. Chaos Solitons Fractals, 109942. [DOI] [PMC free article] [PubMed]
- 31.Kishor D.R., Venkateswarlu N.B. A novel hybridization of expectation maximization and k-means algorithms for better clustering performance. Int. J. Ambient Comput. Intell. 2016;7(2):47–74. [Google Scholar]
- 32.Fong S.J., Li G., Dey N., Crespo R.G., Herrera-Viedma E. Finding an accurate earl forecasting model from small dataset: A case of 2019-nCoV novel coronavirus outbreak. Int. J. Interact. Multimedia Artif. Intell. 2020:132–140. [Google Scholar]
- 33.Fong S.J., Li G., Dey N., Crespo R.G., Herrera-Viedma E. Composite Monte Carlo decision making under high uncertainty of novel coronavirus epidemic using hybridized deep learning and fuzzy rule induction. Appl. Soft Comput. 2020 doi: 10.1016/j.asoc.2020.106282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Sarkodie S., Owus P. Impact of meteorological factors on 1 COVID-19 pandemic: Evidence from top 20 countries with confirmed cases. Environ. Res. 2020 doi: 10.1016/j.envres.2020.110101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Yeasmina S., Banik R., Hossain S., Hossain M.N., Mahmut R., Salma N., Hossain M.M. Impact of COVID-19 pandemic on the mental health of children in Bangladesh: A cross-sectional study. Child. Youth Serv. Rev. 2020:1–7. doi: 10.1016/j.childyouth.2020.105277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Loey M., Manogaran G., Taha M.H., Khalifa N.E. A hybrid deep transfer learning model with machine learning methods for face mask detection in the era of the COVID-19 pandemic. Measurement. 2021:1–11. doi: 10.1016/j.measurement.2020.108288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ahamad M.M., Aktar S., Rashed-AL-Mahfuz M., Uddin S., Liò P., Xu … H., Moni M. A machine learning model to identify early stage symptoms of SARS-Cov-2 infected patients. Expert Syst. Appl. 2020:1–10. doi: 10.1016/j.eswa.2020.113661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Malki Z., Atlam E.-S., Hassanien A.E., Dagnew G., Elhosseini M.A., Gad I. Association between weather data and COVID-19 pandemic predicting mortality rate: Machine learning approaches. Chaos Solitons Fractals. 2020:1–10. doi: 10.1016/j.chaos.2020.110137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sonbhadra S.K., Agarwal S., Nagabhushan P. Target specific mining of COVID-19 scholarly articles using one-class approach. Chaos Solitons Fractals. 2020:1–11. doi: 10.1016/j.chaos.2020.110155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Mahmoudi M.R., Baleanu D., Mansor Z., Tuan B., Pho K.-H. Fuzzy clustering method to compare the spread rate of Covid-19 in the high risks countries. Chaos Solitons Fractals. 2020:2–9. doi: 10.1016/j.chaos.2020.110230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Khan I., Haleem A., Javaid M. Analysing COVID-19 pandemic through cases, deaths, and recoveries. J. Oral Biol. Craniofac. Res. 2020:450–469. doi: 10.1016/j.jobcr.2020.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Imtyaz A., Haleem A., Javaid M. Analysing governmental response to the COVID-19 pandemic. J. Oral Biol. Craniofac. Res. 2020:504–513. doi: 10.1016/j.jobcr.2020.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Amar L.A., Taha A.A., Mohamed M.Y. Prediction of the final size for COVID-19 epidemic using machine learning: a case study of Egypt. Infect. Dis. Model. 2020 doi: 10.1016/j.idm.2020.08.008. Pre-Proof. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Guerrero M., Vanderloo L., Rhodes R., Faulkner G., Moore S., Tremblay M. Canadian children’s and youth’s adherence to the 24-h movement guidelines during the COVID-19 pandemic: A decision tree analysis. J. Sport Health Sci. 2020:313–321. doi: 10.1016/j.jshs.2020.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mei Y., Weinberg S., Zhao L., Frink A., Qi C. Risks tratification of hospitalized COVID-19 patients through comparative studies of laboratory results with in fluenza. E Clin. Med. 2020:2–8. doi: 10.1016/j.eclinm.2020.100475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Salehi V., Veitch B., Musharraf M. Measuring and improving adaptive capacity in resilient systems by means of an integrated DEA-machine learning approach. Applied Ergon. 2020:1–9. doi: 10.1016/j.apergo.2019.102975. [DOI] [PubMed] [Google Scholar]
- 47.Pendharkar P. A hybrid radial basis function and data envelopment analysis neural network. Comput. Oper. Res. 2011:256–266. [Google Scholar]
- 48.Kheirkhah A., Azadeh A., Saberi M., Azaron A., Shakouri H. Improved estimation of electricity demand function by using of artificial neural network, principal component analysis and data envelopment analysis. Comput. Ind. Eng. 2013:425–441. [Google Scholar]
- 49.Jafarzadegan M., Safi-Esfahani F., Beheshti Z. Combining hierarchical clustering approaches using the PCA method. Expert Syst. Appl. 2019:1–10. [Google Scholar]
- 50.Nandy A., Singh P.K. Farm efficiency estimation using a hybrid approach of machine learning and data envelopment analysis: Evidence from rural eastern India. J. Cleaner Prod. 2020:1–11. [Google Scholar]
- 51.Tayala A., Solankib A., Singh S.P. Integrated frame work for identifying sustainable manufacturing layouts based on big data, machine learning, meta-heuristic and data envelopment analysis. Sustainable Cities Soc. 2020:1–17. [Google Scholar]
- 52.Aydın N., Yurdakul G. 2020. Analyzing the Efficiency Bank Branches Via Novel Weighted Stochastic Imprecise Data Envelopment Analysis: [Working paper] [Google Scholar]
- 53.Charnes A., Cooper W.W. Chance-constrained programming. Manage. Sci. 1959;6:73–79. [Google Scholar]
- 54.Kayalıdere K., Kargın S. Çimento ve tekstil sektöründe etkinlik çalışması ve veri zarflama analizi. Doküz Eylül Üniv. Sos. Bilim. Derg. 2004:196–219. [Google Scholar]
- 55.Liua J.S., Lub L.Y., Luc W.-M. Research fronts in data envelopment analysis. Omega. 2016:33–45. [Google Scholar]
- 56.Olesen O.B., Petersen N.C. Stochastic data envelopment analysis-A review. Eur. J. Oper. Res. 2015:1–20. [Google Scholar]
- 57.Andersen P., Petersen N. A procedure for ranking efficient units in data envelopment analysis. Manage. Sci. 1993:1261–1264. [Google Scholar]
- 58.Bian Y., Yang F. Resource and environment efficiency analysis of provinces in Chine: A DEA approach based on Shannon’s entropy. Energy Policy. 2010:1909–1917. [Google Scholar]
- 59.Cook W.D., Zhu J. Classifying inputs and outputs in data envelopment analysis. Eur. J. Oper. Res. 2007:692–699. [Google Scholar]
- 60.Sueyoshi T. Stochastic DEA for restructure strategy: an application to a japanese petroleum company. Omega. 2000:385–398. [Google Scholar]
- 61.Cosgun Ö., Yurdakul G. Performance evaluation of an apparel retailer’s stores by using stochastic imprecise DEA. J. Mult.-Valued Logic Soft Comput. 2020 (Accepted November 3, 2019) [Google Scholar]
- 62.Kishor D., Venkateswarlu N. Hybridization of expectation-maximization and k-means algorithms for better clustering performance. Cybern. Inf. Technol. 2016:16–34. [Google Scholar]
- 63.Ziberna A. K-means-based algorithm for block modeling linked networks. Social Networks. 2020:153–169. [Google Scholar]
- 64.Ren Z., Sun L., Zhai Q. Improved kmeans and spectral matching for hyper spectral mineral mapping. Int. J. Appl. Earth Obs. Geoinf. 2020:1–12. [Google Scholar]
- 65.Yang W., Long H., Ma L., Sun H. 3rd International Conference on Mechatronics and Intelligent Robotics (ICMIR-2019) vol. 166. 2020. Research on clustering method based on weighted distance; pp. 507–511. (Procedia Computer Science). [Google Scholar]
- 66.Loh W.-Y. Classification and regression trees. WIREs Data Min. Knowl. Discovery. 2011:14–23. [Google Scholar]
- 67.Bosso M., Vasconselos K.L., Ho L.L., Bernucci L.L. Use of regression trees to predict overweight trucks from historical weigh-in-motion data. J. Traffic Transp. Eng. (English Ed.) 2019:1–17. [Google Scholar]
- 68.Peker M., Özkaraca O., Kesimal B. Enerji tasarruflu bina tasarımı için isıtma ve soğutma yüklerini regresyon tabanlı makine öğrenmesi algoritmaları ile modelleme. Bilişim Teknol. Derg. 2017:443–449. [Google Scholar]
- 69.Kaufman L., Rousseeuw P.J. Wiley; New York: 1990. Finding Groups in Data. An Introduction to Cluster Analysis. [Google Scholar]
- 70.Odong T.L., van Heerwaarden J., Jansen J., van Hintum T.J.L., van Eeuwijk F.A. Determination of genetic structure of germplasm collections: are traditional hierarchical clustering methods appropriate for molecular marker data? Theor. Appl. Genet. 2011:195–205. doi: 10.1007/s00122-011-1576-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Yeşilbudak M., Kahraman H.T., Karacan H. Veriİ madenciliğinde nesne yönelimli birleştirici hiyerarşik kümeleme modeli. J. Fac. Eng. Archit. Gazi Univ. 2011:27–39. [Google Scholar]
- 72.Xu Z., Xuan J., Liu J., Cui X. 2016 IEEE 23rd International Conference on Software Analysis, Evolution, and Reengineering (SANER) SANER; Suita: 2016. MICHAC: Defect prediction via feature selection based on maximal information coefficient with hierarchical agglomerative clustering; pp. 370–381. [Google Scholar]