Abstract
During the outbreak of the novel coronavirus pneumonia (COVID-19), there is a huge demand for medical masks. A mask manufacturer often receives a large amount of orders that must be processed within a short response time. It is of critical importance for the manufacturer to schedule and reschedule mask production tasks as efficiently as possible. However, when the number of tasks is large, most existing scheduling algorithms require very long computational time and, therefore, cannot meet the needs of emergency response. In this paper, we propose an end-to-end neural network, which takes a sequence of production tasks as inputs and produces a schedule of tasks in a real-time manner. The network is trained by reinforcement learning using the negative total tardiness as the reward signal. We applied the proposed approach to schedule emergency production tasks for a medical mask manufacturer during the peak of COVID-19 in China. Computational results show that the neural network scheduler can solve problem instances with hundreds of tasks within seconds. The objective function value obtained by the neural network scheduler is significantly better than those of existing constructive heuristics, and is close to those of the state-of-the-art metaheuristics whose computational time is unaffordable in practice.
Keywords: Emergency production, Flow shop scheduling, Neural network, Reinforcement learning, Public health emergencies
Graphical abstract

Highlights
-
•
We propose a neural network production scheduler with reinforcement learning.
-
•
The scheduler solves a problem instance within 1-2 s.
-
•
The scheduler achieves performance close to popular metaheuristics.
-
•
The scheduler was applied to medical mask production during COVID-19.
1. Introduction
Since the outbreak of the novel coronavirus pneumonia (COVID-19), there has been an ever-growing demand for medical masks. A mask manufacturer often receives a large amount of orders that must be processed within a short response time. Therefore, it is of critical importance for the manufacturer to schedule mask production tasks as efficiently as possible. Moreover, as new orders arrive continuously, the manufacturer also need to reschedule production tasks frequently. This brings a great challenge for the manufacturer to produce high-quality scheduling solutions rapidly.
The motivation of this paper comes from our cooperation with ZHENDE company, a medical apparatus manufacturer in Zhejiang Province, China, during COVID-19. The manufacturer has a mask production line that can produce different types masks, such as disposable medical masks, surgical masks, medical protective masks, and respiratory masks. The daily output is nearly one hundred thousand. However, on each day since the outbreak of COVID-19, it receives tens to hundreds of orders, the total demand of which ranges from hundreds of thousands to a million masks, and almost all orders have tight delivery deadlines. The manufacturer asked our research team to develop a production scheduler that can schedule hundreds of tasks within seconds. During the COVID-19 pandemic, a lot of medical supply manufacturers having similar requirements of production task scheduling.
Scheduling production tasks on a production line can be formulated as a machine scheduling problem which is known to be NP-hard [1]. Exact optimization algorithms (e.g., [2], [3], [4], [5]) often have very large computational times that are infeasible on even moderate-size problem instances. As for moderate- and large-size instances optimal solutions are rarely needed in practice, heuristic approximation algorithms, including constructive heuristics (e.g., [6], [7], [8]) and metaheuristic evolutionary algorithms (e.g., [9], [10], [11], [12], [13], [14], [15]), are more feasible to achieve a trade-off between optimality and computational costs. However, the solution fitness of constructive heuristics is often low for even moderate-size instances. For metaheuristics, the number of repeated generations and objective function evaluations for solving large-size instances still takes a relatively long time and, therefore, cannot satisfy the requirement of real-time scheduling. Table 1 gives an overview of main classes of algorithms for NP-hard production scheduling problems.
Table 1.
Advantages and disadvantages of main classes of algorithms for NP-hard production scheduling problems.
| Solution quantity | Computational time | Typical work | |
|---|---|---|---|
| Exact optimization algorithms | Optimality guarantee | Long (exponential in problem size) | [2], [3], [4], [5] |
| Constructive heuristics | Low for moderate and large problems | Short (typically polynomial in problem size) | [6], [7], [8] |
| Metaheuristics | Near-optimal or high-quantity | Moderate (polynomial in the number of generations times problem size) | [9], [10], [11], [12], [13], [14], [15] |
| Neural optimization | Typically between constructive heuristics and metaheuristics | Short (polynomial in problem size) | [16], [17] |
In this paper, we propose a deep reinforcement approach for scheduling real-time production tasks. The scheduler is a deep neural network (DNN), which consists of an encoder that takes a sequence of production tasks as inputs to predict a distribution over different schedules, and a decoder that predict the probability of selecting a task into the schedule at each time step. The network parameters are optimized by reinforcement learning using the negative total tardiness as the reward signal. After being trained on sufficient (unlabeled) instances following the distribution of the problem, the network can directly produce a solution for a new instance within a very short time. We applied the DNN scheduler to mask production scheduling in the ZHENDE manufacturer during the peak of COVID-19 in China. Computational results show that the proposed method can solve problem instances with hundreds of tasks within seconds. The objective function value (total weighted tardiness) produced by the DNN scheduler is significantly better than those of existing constructive heuristics such as the Nawaz, Enscore and Ham (NEH) heuristic [6] and Suliman heuristic [7], and is very close to those of the state-of-the-art metaheuristics whose computational time is obviously unaffordable in practice.
The remainder of this paper is organized as follows. Section 2 briefly reviews the related work on machine learning methods for scheduling problems. Section 3 describes the considered emergency production scheduling problem. Section 4 describes the DNN scheduler in detail, including the model architecture and learning algorithm. Section 5 presents the experimental results, and finally Section Section 6 concludes with a discussion.
2. Related work
To solve NP-hard combinatorial optimization problems, classical algorithms, including exact optimization algorithms, heuristic optimization algorithms, and metaheuristic algorithms, are essentially search algorithms that explore the solution spaces to find optimal or near-optimal solutions [8]. Using end-to-end neural networks to directly map a problem input to a solution is another research direction that has received increasing attention [17]. The earliest work dates back to Hopfield and Tank [18], who applied a Hopfield-network to solve the traveling salesman problem (TSP). Simon and Takefuji [19] modified the Hopfield network to solve the job-shop scheduling problem. However, the Hopfield network is only suitable for very small problem instances. Based on the premise that optimal solutions to a scheduling problem have common features which can be implicitly captured by machine learning, Weckman et al. [20] proposed a neural network for scheduling job-shops by capturing the predictive knowledge regarding the assignment of operation’s position in a sequence. They used solutions obtained by genetic algorithm (GA) as samples for training the network. To solve the flow shop scheduling problem, Ramanan et al. [21] used a neural network trained with optimal solutions of known instances to produce quality solutions for new instances, which are then given as the initial solutions to improve other heuristics such as GA. Such methods combining machine learning and metaheuristics are still time-consuming on large problems.
Recently, deep learning has been utilized to optimization algorithm design by learning algorithmic decisions based on the distribution of problem instances. Vinyals et al. [22] introduced the pointer network as a sequence-to-sequence model, which consists in an encoder to parse the input nodes, and a decoder to produce a probability distribution over these nodes based on a pointer (attention) mechanism over the encoded nodes. They applied the pointer network to solve TSP instances with up to 100 nodes. However, the pointer network is trained in a supervised manner, which heavily relies on sample instances with known optimal solutions which are expensive to obtain. Nazari et al. [23] addressed this difficulty by using reinforcement learning to calculate the rewards of output solutions and introducing an attention mechanism to address different parts of the input. They applied the model to solve the vehicle routing problem (VRP). Kool et al. [16] used a different decoder based on a context vector and improved the training algorithm based on a greedy rollout baseline. They applied the model to several combinatorial optimization problems including TSP and VRP. For online scheduling of vehicle services in large transportation networks, Yu et al. [24] also employed reinforcement learning to train a deep graph embedded pointer network, which employs an auxiliary critic neural network to estimate the expected output. Peng et al. [25] presented a dynamic attention model with dynamic encoder–decoder architecture to exploit hidden structure information at different construction steps, so as to construct better solutions. Solozabal et al. [26] extended the neural combinatorial optimization approach to constrained combinatorial optimization, where solution decisions are inferred based on both the reward signal generated from objective function values and penalty signals generated from constraint violations. However, to our knowledge, studies on deep learning approaches for efficiently solving emergency production scheduling problems are still few.
3. Medical mask production scheduling problem
In this section, we formulate the scheduling problem as follows (the variables are listed in Table 2). The manufacturer has orders, denoted by , to be processed. Each order is associated with a set of production tasks (jobs), and each task specifies the required type and number of masks. Each order has an expected delivery time and an importance weight defined according to its value and urgency. In our practice, the manager gives a score between 1–10 for each order, and then all weights are normalized such that .
Table 2.
Mathematical variables used in the problem formulation.
| Symbol | Description |
|---|---|
| The set of orders | |
| Number of orders | |
| Index of orders () | |
| Expected delivery time of order | |
| Importance weight of order | |
| Set of production tasks in order | |
| Set of all production tasks | |
| Number of tasks | |
| Index of tasks () | |
| Set of machines | |
| Number of machines | |
| Index of machines () | |
| Processing time of th operation of task (on machine ) | |
| A solution (sequence of tasks) to the problem | |
| Completion time of task on machine | |
| Completion time of order |
Let be the set of all tasks. These tasks need to be scheduled on a production line with machines, denoted by . Each task has exactly operations, where the th operation must be processed on machine with a processing time (). Each machine can process at most one task at a time, and each operation cannot be interrupted. The operations of mask production typically include cloth cutting, fabric lamination, belt welding, disinfection, and packaging.
The problem is to decide a processing sequence of the tasks. Let denote the completion time of task on machine . For the first machine , the tasks can be sequentially processed immediately one by one:
| (1) |
| (2) |
The first job can be processed on each subsequent machine immediately after it is completed on the previous machine :
| (3) |
Each subsequent job can be processed on machine only when (1) the job has been completed on the previous machine ; (2) the previous job has been completed on machine :
| (4) |
Therefore, the completion time of each order is the completion time of the last task of the order on machine :
| (5) |
The objective of the problem is to minimize the total weighted tardiness of the orders:
| (6) |
If all tasks are available for processing at time zero, the above formulation can be regarded as a variant of the permutation flow shop scheduling problem which is known to be NP-hard [1]. When there are hundreds of tasks to be scheduled, the problem instances are computationally intractable for exact optimization algorithms, and search-based heuristics also typically take tens of minutes to hours to obtain a satisfying solution. Moreover, in a public health emergency such as the COVID-19 pandemic, new orders may continually arrive during the emergency production and, therefore, it needs to frequently reschedule production tasks to incorporate new tasks into the schedules. The allowable computational time for rescheduling is even shorter, typical only a few seconds. Hence, it is required to design real-time or near-real-time rescheduling methods for the problem.
4. A neural network scheduler for emergence production task scheduling
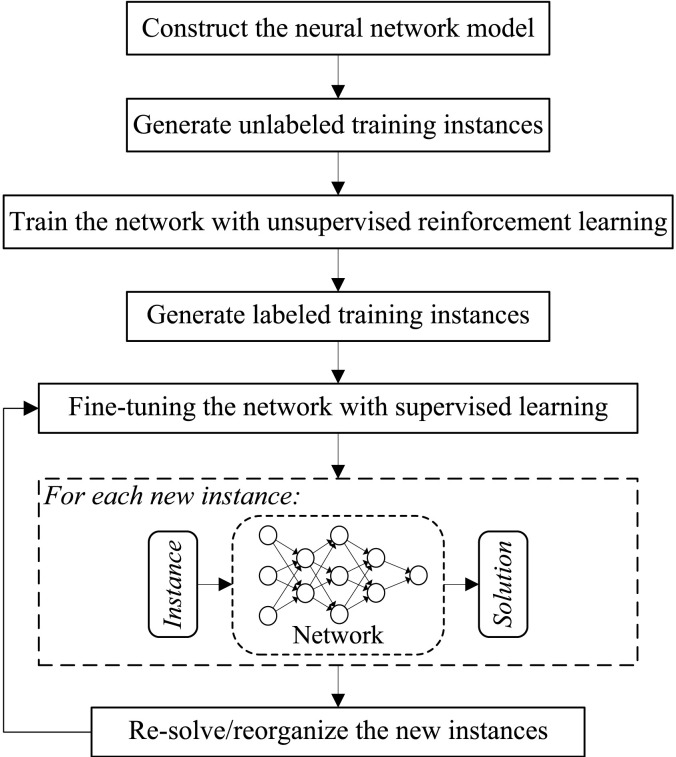
We propose a neural network scheduler to efficiently solve the above production task scheduling problem. The network takes a sequence of production tasks as inputs, and produce a schedule of the tasks by sequentially selecting a task into the schedule at each time step. We first use reinforcement learning to train the network on a large number of unlabeled instances (exact optimal solutions of which are not needed), and then use supervised learning to fine tune the network on some labeled instances (exact optimal solutions of which are known). Given a new instance as the input to the network, it is expected to produce a high-quality scheduling solution if the training instances well represent the distribution of the scheduling problem. Since the network is put into use, we periodically collect these real-world instances and solve them with state-of-the-art metaheuristics and, thus, construct new labeled instances to re-train the network. The basic flow to apply our machine learning approach is illustrated in Fig. 1.
Fig. 1.
Basic flow to apply the machine learning approach to solve the production task scheduling problem.
4.1. Neural network model
The proposed neural network scheduler is based on the encoder–decoder architecture [27]. Fig. 2 illustrates the architecture of the network. The input to the network is a problem instance represented by a sequence of tasks, each of which is described by a -dimensional vector that consists the processing times on the machines and the expected delivery time and weight importance of the corresponding order. To facilitate the processing of the neural network, all inputs are normalized into [0,1], e.g., each is transformed to , where and .
Fig. 2.
Architecture of the neural network scheduler.
The encoder is a recurrent neural networks (RNN) with long short-term memory (LSTM) [28] cells. An LSTM takes a task as input at a time and transforms it to a hidden state by increasingly computing the embedding of the inputs (where denotes the transformation by LSTM):
| (7) |
As a result, the encoder produces an aggregated embedding of all inputs as the mean of hidden states:
| (8) |
The decoder also performs decoding steps, each making a decision on which task should to be processed at the next step. At each th step, it constructs a context vector by concatenating and the hidden state of the previous LSTM. We use a five-layer DNN to implement the decoder. The first layer takes as input and transforms it into a -dimensional hidden vector ():
| (9) |
where is a weight matrix and is a -dimensional bias vector.
The second layer takes the concatenation of and context vector as input and transforms it into a -dimensional hidden vector ():
| (10) |
where denotes the horizontal concatenation of vectors, is a weight matrix and is a -dimensional bias vector.
Each of the remaining layers takes the hidden state of the previous layer and transforms it into a lower-dimensional hidden vector using ReLU activation. Finally, the probability that each task is selected at the th step is calculated based on the state of the top layer of the DNN:
| (11) |
At each step, the task that has the maximum probability is selected into the schedule.
4.2. Reinforcement learning of the neural network
A solution to the scheduling problem can be viewed as a sequence of decisions, and the decision process can be regarded as a Markov decision process [29]. According to the objective function (6), the training of the network is to minimize the loss
| (12) |
We employ the policy gradient using REINFORCE algorithm [30] with Adam optimizer [31] to train the network. The gradients of network parameters are defined based on a baseline as:
| (13) |
A good baseline reduces gradient variance and increases learning speed [16]. Here, we use both the NEH heuristic [6] and Suliman heuristic [7] to solve each instance , and use the better one as the .
During the training, we approximate the gradient via Monte-Carlo sampling, where problem instances are drawn from the same distribution:
| (14) |
The pseudocode of the REINFORCE algorithm for optimizing the network parameters according to is presented in Algorithm 1.
5. Computational results
5.1. Comparison of different baselines for the reinforcement learning algorithm
In the training phase, according to production tasks of the manufacturer during the peak of COVID-19 in China, we randomly generate 20,000 instances. The basic features of the instance distribution are as follows: (the number of machines in the ZHENDE company), follows a normal distribution , follows a normal distribution (in hours), and follows a uniform discrete distribution (in hours). To avoid training instances deviating too much from the distribution of the problem, any instance where the sum of all is larger than 1500 or less than 50 is considered as noise and is not included in the training set.
Our REINFORCE algorithm uses hybrid NEH and Suliman heuristics (denoted by NEH-Sul) as the baseline. For comparison, we also use three other baselines: the first is a greedy heuristic that sorts tasks in decreasing order of , and the second and the third are individual NEH heuristic and individual Suliman heuristic, respectively. For each baseline, we run 30 Monte Carlo simulations with different sequences of training instances. The maximum number of epochs for training the network is set to 100. The neural network model is implemented using Python 3.4, and the training heuristics are implemented with Microsoft Visual C# 2015 (snapshots are shown in Fig. 3 and codes can be download from http://compintell.cn/en/dataAndCode.html). The experiments are conducted on a computer with Intel Xeon 3430 CPU, 4G DDR4 Memory, and GeForce GTX 1080Ti GPU.
Fig. 3.
Snapshots of the codes of algorithmic programs.
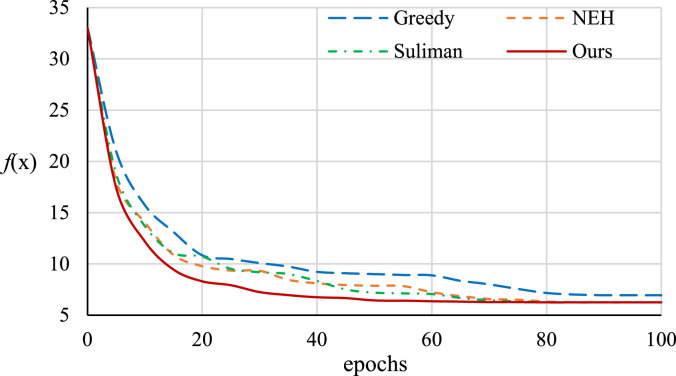
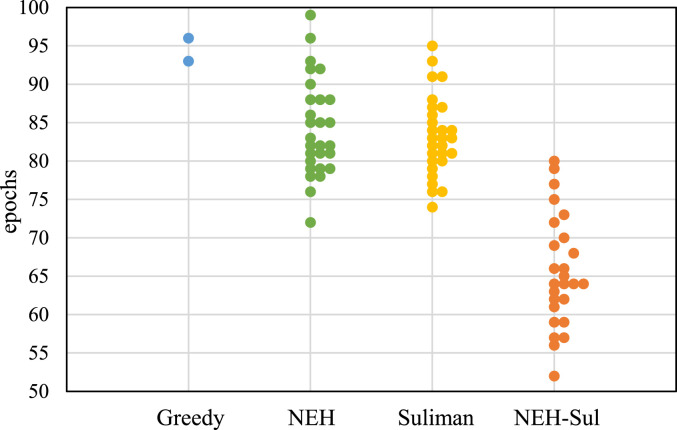
Fig. 4 presents the convergence curves of the four methods (averaged over the 30 Monte Carlo simulations) during the training process. The horizontal axis denotes the training epochs, and the vertical axis denotes the average objective function value of Eq. (6) obtained by the network. Among all simulations, the best average objective function value is approximately 6.25, and Fig. 5 presents the numbers of epochs at which the simulations converge to the best value within 1% error. The results show that, among 30 runs, the greedy method converges to the best value only twice, and in most cases it converges to local optima that are significantly worse than the best value. The individual NEH heuristic converges to the best value in 28 of the 30 runs, and the individual Suliman heuristic and our hybrid method converge to the best value in all 30 runs. In average, NEH and Suliman heuristics converge after 8085 epochs, while our method converges after 6065 epochs. This is because NEH and Suliman heuristics exhibit different performance on different instances, and using the baseline combining them can obtain solutions that are closer to the exact optima than either individual heuristic and, therefore, reduces gradient variance and increases learning speed. Moreover, as both NEH and Suliman heuristics are efficient constructive heuristics, using the hybrid baseline only incurs a slight performance overhead during the training process. The results demonstrate that, compared to the existing heuristic baselines, our method using hybrid NEH and Suliman heuristics as the baseline can significantly improve the training performance. This also provides an approach to improve reinforcement learning for neural optimization by simply combing two or more complementary baselines to a better baseline.
Fig. 4.
Convergence curves of the four methods for training the neural network.
Fig. 5.
Numbers of epochs of the four methods to reach the best value within 1% error.
5.2. Comparison of scheduling performance
Next, we test the performance of the trained neural network scheduler (denoted by NNS) for solving the scheduling problem by comparing with the NEH heuristic, Suliman heuristic, and five state-of-the-art metaheuristic algorithms including a shuffled complex evolution algorithm (SCEA) [32], an algebraic differential evolution (ADE) algorithm [33], a teaching–learning based optimization (TLBO) algorithm [34], a biogeography-based optimization (BBO) algorithm [35], [36], and a discrete water wave optimization (WWO) algorithm [15], [37]. Before applying the network to real-world instances, we select 50 instances with different sizes from the training instances, use the above five metaheuristics to solve each of them, and select the best solution obtained by them as the label of the instance. The network is fine-tuned using back-propagation on the labeled instances.
We select 146 real-world instances of the manufacturer from Feb 8 to Feb 14, 2020, the peak of COVID-19 in China. For each day, we need to first solve an instance with about 50200 tasks; during the daytime, with the arrival of new orders, we need to reschedule the production for 2040 times. Fig. 6 shows the distribution of number of tasks of the instances. After each day, we also select 24 scheduling/rescheduling instances, employ five metaheuristics to obtain solutions as the labels of the instances, and use the labeled instances to re-train the network. Such periodical re-training also increases the model robustness against noise.
Fig. 6.
Distribution of number of tasks of the real-world instances.
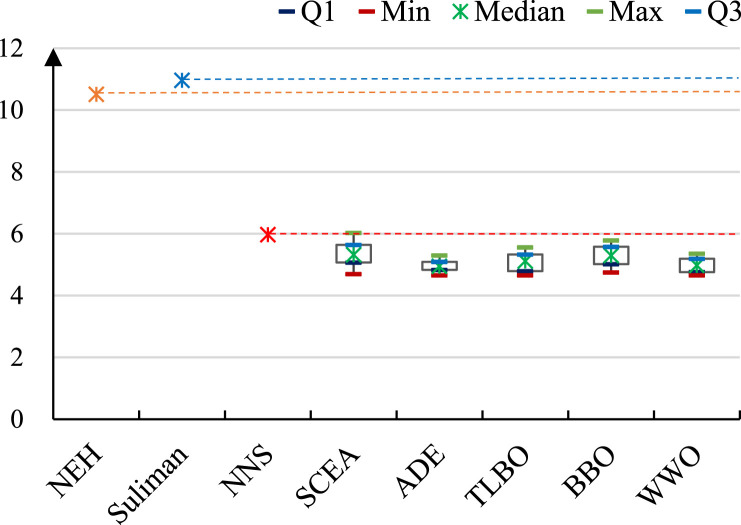
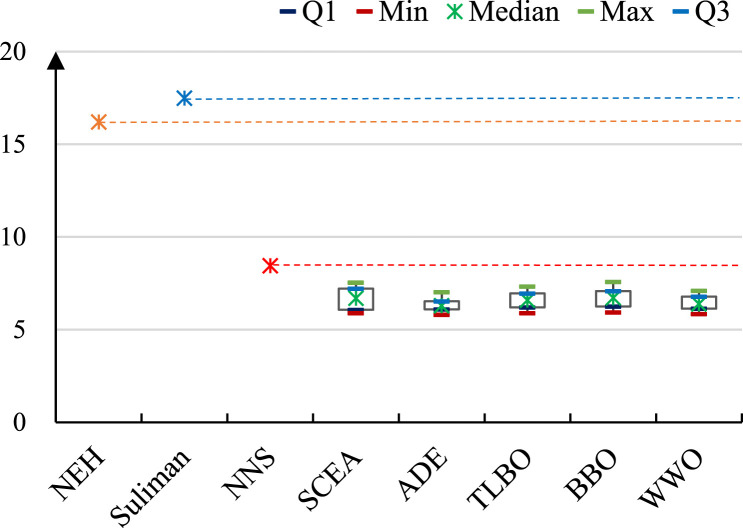
Fig. 7, Fig. 8, Fig. 9, Fig. 10, Fig. 11, Fig. 12, Fig. 13 present the resulting objective function values obtained by the different algorithms on the instances during Feb 8 to Feb 14. For the above five stochastic metaheuristic algorithms, we perform 50 Monte Carlo simulations on each instance, and present the maximum, minimum, median, first quartile (Q1), and third quartile (Q3) of the resulting objective function values in the plots. Table 3 presents the average CPU time consumed by the algorithms to obtain the solutions; for the five metaheuristic algorithms, the stop condition is that the number of fitness evaluations reaches 100,000.
Fig. 7.
Comparison of the results of the neural network scheduler, constructive heuristics, and metaheuristic algorithms on the instance of Feb 8.
Fig. 8.
Comparison of the results of the neural network scheduler, constructive heuristics, and metaheuristic algorithms on the instance of Feb 9.
Fig. 9.
Comparison of the results of the neural network scheduler, constructive heuristics, and metaheuristic algorithms on the instance of Feb 10.
Fig. 10.
Comparison of the results of the neural network scheduler, constructive heuristics, and metaheuristic algorithms on the instance of Feb 11.
Fig. 11.
Comparison of the results of the neural network scheduler, constructive heuristics, and metaheuristic algorithms on the instance of Feb 12.
Fig. 12.
Comparison of the results of the neural network scheduler, constructive heuristics, and metaheuristic algorithms on the instance of Feb 13.
Fig. 13.
Comparison of the results of the neural network scheduler, constructive heuristics, and metaheuristic algorithms on the instance of Feb 14.
Table 3.
CPU time (in seconds) consumed by the neural network scheduler, constructive heuristics, and metaheuristic algorithms on the test instances.
| Day | NEH | Suliman | NNS | SCEA | ADE | TLBO | BBO | WWO |
|---|---|---|---|---|---|---|---|---|
| Feb-8 | 0.63 | 0.93 | 0.75 | 545 | 516 | 525 | 524 | 520 |
| Feb-9 | 0.92 | 2.35 | 1.03 | 725 | 690 | 710 | 718 | 707 |
| Feb-10 | 1.71 | 4.59 | 1.32 | 1102 | 1027 | 1060 | 1089 | 1047 |
| Feb-11 | 2.13 | 5.26 | 1.57 | 1210 | 1097 | 1136 | 1165 | 1121 |
| Feb-12 | 2.30 | 5.96 | 1.72 | 1503 | 1312 | 1337 | 1422 | 1359 |
| Feb-13 | 0.97 | 2.64 | 1.09 | 940 | 851 | 890 | 908 | 883 |
| Feb-14 | 1.45 | 3.84 | 1.20 | 1013 | 948 | 970 | 993 | 956 |
As it can be observed from the results, the Suliman heuristic typically consumes more computational time than the NEH heuristic, because the former uses a bit more complex solution construction procedure, although both heuristics have time complexities that are polynomial in instance size. The overall performance of the two heuristics are similar: the Suliman heuristic obtains better solutions on three instances, while NEH performs better on the other four instances. The computational time of our NNS model is similar to NEH (and less than Suliman): as the NNS model iteratively process input tasks and select tasks into a schedule, its time complexity is also polynomial in instance size; the time consumed to process a task by NNS is similar to the time of a construction step in NEH. Nevertheless, the solutions produced by NNS are significantly better than those of both NEH and Suliman heuristics, which demonstrates that NNS trained on the large number of instances by reinforcement learning based on the hybrid NEH and Suliman baseline can effectively learn the problem distribution and map new instances to high-quality solutions, and such neural network mapping exhibits significant performance advantages over the construction procedures of Suliman and NEH.
The metaheuristic algorithms are more powerful in solving the production task scheduling problem, but their performance advantages are at expense of high computational cost. On the seven problem instances, their average solution times are 5001500 s, significantly longer than the 12 s of NNS. Nevertheless, the objective function values produced by NNS are only approximately 10%20% larger than the median objective function values of the metaheuristic algorithms. In some cases, the solutions of NNS are even better than the worst solutions produced by the metaheuristic algorithms (e.g., SCEA on the instance of Feb. 8 and BBO on the instance of Feb. 9). In general, compared to the state-of-the-art metaheuristics, NNS consumes about 1/1000 computational time to achieve similar performance. This is because, at each generation of the metaheuristics, the operations for evolving the solutions have time complexity polynomial in solution length (which is equivalent to instance size); as discussed above, the time complexity of NNS is also polynomial in instance size; however, the metaheuristics use approximately a thousand iterations in average. In emergency conditions, the computational time of the metaheuristics is obviously unaffordable, while the proposed NNS can produce high-quality solutions within seconds and, therefore, satisfy the requirements of emergency medical mask production.
6. Conclusion
In this paper, we propose a DNN with reinforcement learning for scheduling hundreds of emergency production tasks within seconds. The neural network consists of an encoder and a decoder. The encoder employs an LSTM-based RNN to sequentially parse the input production tasks, and the decoder employs a deep neural network to learn the probability distribution over these tasks. The network is trained by reinforcement learning using the negative total tardiness as the reward signal. We applied the proposed neural network scheduler to a medical mask manufacturer during the peak of COVID-19 in China. The results show that the proposed approach can achieve high-quality solutions within very short computational time to satisfy the requirements of emergency production.
Emergency production scheduling is an important function that determines the efficiency of a manufacturing system in response to unexpected emergencies. Most manufacturers have purchased OR tools with exact optimization algorithms, which are suitable for only small-size instances. Many manufacturers have also equipped heuristic and metaheuristic scheduling algorithms. Constructive heuristics can produce good solutions on small-size instances and occasionally on moderate-size instances, but there is no guarantee on the optimality or optimality gap. In general, we do not encourage directly using constructive heuristics to solve real-world emergency production scheduling instances; they can be used in combined with other methods, e.g., for generating initial solutions for metaheuristics or acting baselines for neural optimization models. Metaheuristics are suitable for moderate-size instances, but are not suitable for large-size instances under emergency conditions. The proposed neural optimization method is suitable for moderate- and large-size instances, but the main disadvantage is that it should have been trained on a large number of well-distributed instances. If the emergency will last for a certain period, we can first analyze the distribution of the problem and generate sufficient instances for model training, and use the trained network in the remaining stages. Managers of manufacturers should define a decision-making process on selecting the most suitable solution methods for different instances so as to efficiently respond to emergencies.
In our study, the baseline plays a key role in reinforcement learning. The baseline used in this paper is based on two constructive heuristics, which have much room to be improved. However, better heuristics and metaheuristics often require large computational resource and are not efficient in training a large number of test instances. Currently, we are incorporating other neural network schedulers to improve the baseline. Ongoing work also includes preprocessing training instances by clustering and re-sampling to improving learning performance [38] and using metaheuristic algorithms to optimize the parameters of the deep neural network [39]. Moreover, we believe that the proposed approach can be adapted or extended to many other emergency scheduling problems, e.g., disaster relief task scheduling [40] and online unmanned aerial vehicle scheduling [41], [42], in which short solution time is critical to the mission success.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work was supported by National Natural Science Foundation of China under Grant 61872123, Zhejiang Provincial Natural Science Foundation, China under Grant LR20F030002 and LQY20F030001, and Zhejiang Provincial Emergency Project for Prevention & Treatment of New Coronavirus Pneumonia, China under Grant 2020C03126.
References
- 1.Pinedo M. second ed. Prentice Hall; New York: 2002. Scheduling Theory, Algorithms, and Systems. [Google Scholar]
- 2.McMahon G.B., Burton P.G. Flow-shop scheduling with the branch-and-bound method. Oper. Res. 1967;15(3):473–481. doi: 10.1287/opre.15.3.473. [DOI] [Google Scholar]
- 3.Karlof J.K., Wang W. Bilevel programming applied to the flow shop scheduling problem. Comput. Oper. Res. 1996;23(5):443–451. doi: 10.1016/0305-0548(95)00034-8. [DOI] [Google Scholar]
- 4.Ziaee M., Sadjadi S. Mixed binary integer programming formulations for the flow shop scheduling problems, a case study: ISD projects scheduling. Appl. Math. Comput. 2007;185(1):218–228. doi: 10.1016/j.amc.2006.06.092. [DOI] [Google Scholar]
- 5.Gicquel C., Hege L., Minoux M., van Canneyt W. A discrete time exact solution approach for a complex hybrid flow-shop scheduling problem with limited-wait constraints. Comput. Oper. Res. 2012;39(3):629–636. doi: 10.1016/j.cor.2011.02.017. [DOI] [Google Scholar]
- 6.Nawaz M., Enscore E.E., Ham I. A heuristic algorithm for the -machine, -job flow-shop sequencing problem. Omega. 1983;11(1):91–95. doi: 10.1016/0305-0483(83)90088-9. [DOI] [Google Scholar]
- 7.Suliman S.M.A. A two-phase heuristic approach to the permutation flow-shop scheduling problem. Int. J. Prod. Econom. 2000;64(1):143–152. doi: 10.1016/S0925-5273(99)00053-5. [DOI] [Google Scholar]
- 8.Zheng Y., Xue J. A problem reduction based approach to discrete optimization algorithm design. Computing. 2010;88(1–2):31–54. doi: 10.1007/s00607-010-0085-0. [DOI] [Google Scholar]
- 9.Etiler O., Toklu B., Atak M., Wilson J. A genetic algorithm for flow shop scheduling problems. J. Oper. Res. Soc. 2004;55(8):830–835. doi: 10.1057/palgrave.jors.2601766. [DOI] [Google Scholar]
- 10.Onwubolu G., Davendra D. Scheduling flow shops using differential evolution algorithm. European J. Oper. Res. 2006;171(2):674–692. doi: 10.1016/j.ejor.2004.08.043. [DOI] [Google Scholar]
- 11.Liao C.J., Tseng C.T., Luarn P. A discrete version of particle swarm optimization for flowshop scheduling problems. Comput. Oper. Res. 2007;34(10):3099–3111. doi: 10.1016/j.cor.2005.11.017. [DOI] [Google Scholar]
- 12.Kuo I.H., Horng S.J., Kao T.W., Lin T.L., Lee C.L., Terano T., Pan Y. An efficient flow-shop scheduling algorithm based on a hybrid particle swarm optimization model. Expert Syst. Appl. 2009;36(3):7027–7032. doi: 10.1016/j.eswa.2008.08.054. [DOI] [Google Scholar]
- 13.Lin J. A hybrid discrete biogeography-based optimization for the permutation flow-shop scheduling problem. Int. J. Prod. Res. 2016;54(16):4805–4814. doi: 10.1080/00207543.2015.1094584. [DOI] [Google Scholar]
- 14.Zhao F., Liu H., Zhang Y., Ma W., Zhang C. A discrete water wave optimization algorithm for no-wait flow shop scheduling problem. Expert Syst. Appl. 2018;91:347–363. doi: 10.1016/j.eswa.2017.09.028. [DOI] [Google Scholar]
- 15.Zheng Y.-J., Lu X.-Q., Du Y.-C., Xue Y., Sheng W.-G. Water wave optimization for combinatorial optimization: Design strategies and applications. Appl. Soft Comput. 2019;83 doi: 10.1016/j.asoc.2019.105611. [DOI] [Google Scholar]
- 16.W. Kool, H. van Hoof, M. Welling, Attention, learn to solve routing problems! in: International Conference on Learning Representations, 2019.
- 17.Bengio Y., Lodi A., Prouvost A. Machine learning for combinatorial optimization: A methodological tour d’horizon. European J. Oper. Res. 2020 doi: 10.1016/j.ejor.2020.07.063. (in press) [DOI] [Google Scholar]
- 18.Hopfield J.J., Tank D.W. Neural computation of decisions in optimization problems. Bio. Cybern. 1985;52(3):141–152. doi: 10.1007/BF00339943. [DOI] [PubMed] [Google Scholar]
- 19.F.Y.-P. Simon, . Takefuji, Integer linear programming neural networks for job-shop scheduling, in: International Conference on Neural Networks, vol. 2, 1988, pp. 341–348, 10.1109/ICNN.1988.23946. [DOI]
- 20.Weckman G.R., Ganduri C.V., Koonce D.A. A neural network job-shop scheduler. J. Intell. Manuf. 2008;19(2):191–201. doi: 10.1007/s10845-008-0073-9. [DOI] [Google Scholar]
- 21.Ramanan T.R., Sridharan R., Shashikant K.S., Haq A.N. An artificial neural network based heuristic for flow shop scheduling problems. J. Intell. Manuf. 2011;22(2):279–288. doi: 10.1007/s10845-009-0287-5. [DOI] [Google Scholar]
- 22.Vinyals O., Fortunato M., Jaitly N. In: Advances in Neural Information Processing Systems, Vol. 28. Cortes C., Lawrence N.D., Lee D.D., Sugiyama M., Garnett R., editors. Curran Associates, Inc.; 2015. pp. 2692–2700. [Google Scholar]
- 23.Nazari M., Oroojlooy A., Snyder L., Takac M. Reinforcement learning for solving the vehicle routing problem. In: Bengio S., Wallach H., Larochelle H., Grauman K., Cesa-Bianchi N., Garnett R., editors. Advances in Neural Information Processing Systems, Vol. 31. Curran Associates, Inc; 2018. pp. 9839–9849. [Google Scholar]
- 24.Yu J.J.Q., Yu W., Gu J. Online vehicle routing with neural combinatorial optimization and deep reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2019;20(10):3806–3817. doi: 10.1109/TITS.2019.2909109. [DOI] [Google Scholar]
- 25.Peng B., Wang J., Zhang Z. A deep reinforcement learning algorithm using dynamic attention model for vehicle routing problems. In: Li K., Li W., Wang H., Liu Y., editors. International Symposium on Intelligence Computation and Applications. Springer Singapore; Singapore: 2020. pp. 636–650. [Google Scholar]
- 26.Solozabal R., Ceberio J., Takác̆č Z. 2020. Constrained combinatorial optimization with reinforcement learning. arXiv preprint arXiv:2006.11984. [Google Scholar]
- 27.Sutskever I., Vinyals O., Le Q.V. Sequence to sequence learning with neural networks. In: Ghahramani Z., Welling M., Cortes C., Lawrence N.D., Weinberger K.Q., editors. Advances in Neural Information Processing Systems, Vol. 27. Curran Associates, Inc.; 2014. pp. 3104–3112. [Google Scholar]
- 28.F. Gers, J. Schmidhuber, F. Cummins, Learning to forget: continual prediction with LSTM, in: International Conference on Artificial Neural Networks, Edinburgh, UK, 1999, pp. 850–855.
- 29.Bello I., Pham H., Le Q.V., Norouzi M., Bengio S. 2016. Neural combinatorial optimization with reinforcement learning. arXiv preprint arXiv:1611.09940. [Google Scholar]
- 30.Williams R.J. Simple statistical gradient-following algorithms for connectionist reinforcement learning. In: Sutton R.S., editor. Machine Learning. Springer US; Boston, MA: 1992. pp. 5–32. [DOI] [Google Scholar]
- 31.D.P. Kingma, J. Ba, Adam: A method for stochastic optimization, in: International Conference on Learning Representations, 2015, http://arxiv.org/abs/1412.6980.
- 32.Zhao F., Zhang J., Wang J., Zhang C. A shuffled complex evolution algorithm with opposition-based learning for a permutation flow shop scheduling problem. Int. J. Comput. Integ. Manuf. 2015;28(11):1220–1235. doi: 10.1080/0951192X.2014.961965. [DOI] [Google Scholar]
- 33.Santucci V., Baioletti M., Milani A. Algebraic differential evolution algorithm for the permutation flowshop scheduling problem with total flowtime criterion. IEEE Trans. Evol. Comput. 2016;20(5):682–694. doi: 10.1109/TEVC.2015.2507785. [DOI] [Google Scholar]
- 34.Shao W., Pi D., Shao Z. An extended teaching-learning based optimization algorithm for solving no-wait flow shop scheduling problem. Appl. Soft Comput. 2017;61:193–210. doi: 10.1016/j.asoc.2017.08.020. [DOI] [Google Scholar]
- 35.Simon D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008;12(6):702–713. doi: 10.1109/TEVC.2008.919004. [DOI] [Google Scholar]
- 36.Du Y.-C., Zhang M.-X., Cai C.-Y., Zheng Y.-J. Enhanced biogeography-based optimization for flow-shop scheduling. In: Qiao J., Zhao X., Pan L., Zuo X., Zhang X., Zhang Q., Huang S., editors. Bio-Inspired Computing: Theories and Applications. Springer; Singapore: 2018. pp. 295–306. (Commun. Comput. Inf. Sci.). [Google Scholar]
- 37.Zheng Y.-J. Water wave optimization: A new nature-inspired metaheuristic. Comput. Oper. Res. 2015;55(1):1–11. doi: 10.1016/j.cor.2014.10.008. [DOI] [Google Scholar]
- 38.Zheng Y.-J., Yu S.-L., Gan T.-E., Yang J.-C., Song Q., Yang J., Karatas M. Intelligent optimization of diversified community prevention of COVID-19 using traditional chinese medicine. IEEE Comput. Intell. Mag. 2020;15(4) doi: 10.1109/MCI.2020.3019899. [DOI] [Google Scholar]
- 39.Zhou X.-H., Zhang M.-X., Xu Z.-G., Cai C.-Y., Huang Y.-J., Zheng Y.-J. Shallow and deep neural network training by water wave optimization. Swarm Evol. Comput. 2019;50:1–13. doi: 10.1016/j.swevo.2019.100561. [DOI] [Google Scholar]
- 40.Zheng Y.-J., Ling H.-F., Xu X.-L., Chen S.-Y. Emergency scheduling of engineering rescue tasks in disaster relief operations and its application in China. Int. Trans. Oper. Res. 2015;22(3):503–518. doi: 10.1111/itor.12148. [DOI] [Google Scholar]
- 41.Du Y., Zhang M., Ling H., Zheng Y. Evolutionary planning of multi-UAV search for missing tourists. IEEE Access. 2019;7:73480–73492. doi: 10.1109/ACCESS.2019.2920623. [DOI] [Google Scholar]
- 42.Zheng Y., Du Y., Ling H., Sheng W., Chen S. Evolutionary collaborative human-UAV search for escaped criminals. IEEE Trans. Evol. Comput. 2020;24(2):217–231. doi: 10.1109/TEVC.2019.2925175. [DOI] [Google Scholar]