Standard state free energies, not pK_as, are ideal for describing small molecule protonation and tautomeric states

Abstract

The pK_a is the standard measure used to describe the aqueous proton affinity of a compound, indicating the proton concentration (pH) at which two protonation states (e.g A^- and AH) have equal free energy. However, compounds can have additional protonation states (e.g. AH₂⁺), and may assume multiple tautomeric forms, with the protons in different positions (microstates). Macroscopic pK_as give the pH where the molecule changes its total number of protons, while microscopic pK_as identify the tautomeric states involved. As tautomers have the same number of protons, the free energy difference between them and their relative probability is pH independent so there is no pK_a connecting them. The question arises: What is the best way to describe protonation equilibria of a complex molecule in any pH range? Knowing the number of protons and the relative free energy of all microstates at a single pH, ΔG°, provides all the information needed to determine the free energy, and thus the probability of each microstate at each pH. Microstate probabilities as a function of pH generate titration curves that highlight the low energy, observable microstates, which can then be compared with experiment. A network description connecting microstates as nodes makes it straightforward to test thermodynamic consistency of microstate free energies. The utility of this analysis is illustrated by a description of one molecule from the SAMPL6 Blind pK_a Prediction Challenge. Analysis of microstate ΔG°s also makes a more compact way archive and compare the pH dependent behavior of compounds with multiple protonatable sites.

1. Introduction

Acids and bases in solution bind and release protons in a process that changes their molecular charge distribution, influencing solubility, and molecular recognition and reactivity. Many biological and bio-active molecules have pK_as in the physiological pH range, existing in a mixture of protonation and tautomeric states. The knowledge of which protonation states are energetically accessible is important for the design of molecules with desired function [1,2]. The binding or loss of a proton represents one of the simplest reactions, so the calculation of the relative free energy of protonation states as a function of pH represents a powerful test of biomolecular modeling methodologies [3,4].

The recent SAMPL6 Blind pK_a Prediction Challenge focused on the prediction of pK_as for 24 small molecules [5]. As the participant submissions were analyzed and compared it became apparent that the description of the free energy landscape of molecules with multiple protonation states is not simple and that lists of many pK_a values is in fact not the best way to describe the behavior of the molecule as a function of pH. Attempting to capture all necessary information regarding pK_a predictions, SAMPL6 pK_a Challenge supported three different reporting schemes (submission types): microscopic pK_a values (type I), fractional populations of microstates with respect to pH (type II), and macroscopic pK_as (type III). These reporting schemes captured different aspects of the predictions however none of them has proved to be optimal. Here we present a different reporting scheme that provides a complete and concise description of thermodynamics of the behavior of molecules with multiple protonation and tautomeric states, and allows the derivation of pK_as.

1.1. Proteins can have innumerable protonation and tautomeric microstates

The complexity of protonation equilibria of a molecule can vary enormously depending on the number of possible titratable groups and the interactions amongst them. Thus, a simple molecule with a single titratable group has a single well-defined pK_a, which is the pH where the species with different numbers of protons have the same free energy and thus the same concentration. For a single protonatable group the reaction is:

$$\mathrm{AH}={\mathrm{A}}^{-}+{\mathrm{H}}^{+}$$ 1a

Defining the pK_a as -log₁₀K_eq leads to:

$${pK}_a=pH-{log}_{10}\frac{A^{-}}{AH}$$ 1b

We will define a protonation macrostate by the total charge of the molecule while the microstate defines the specific protonation and tautomeric state of all protonatable sites. As the number of protonatable sites in a molecule increases, the number of possible microstates the molecule can access increases. Proteins and other (bio)polymer polyelectrolytes [6] can have many acidic and basic substituents. If we only consider protonatable sites that can gain or lose a single proton (A^- vs AH or B vs BH⁺) then there are 2ⁿ different distributions of protonation states for n protonatable groups. On average, 25% of protein residues are either Asp, Glu, Lys, or Arg [7], providing a very large number of possible microstates. Long-range electrostatic interactions lead to the ionization of all residues being interdependent [8]. Computational tools have been developed that view the protein environment as perturbing the pK_as individual residues would have in solution [9–11]. Given the huge number of possible microstates, Metropolis Monte Carlo sampling is typically used to sample the Boltzmann distribution of protonation states at each pH [11]. Thus, proteins have many protonatable sites, where the interactions are not negligible, but can be treated as a sum of separable, individual interactions. Typically, calculations consider a relatively rigid protein and calculate the electrostatic interactions with the Poisson-Boltzmann equation of continuum electrostatics. Evolving methods allow the protein to move via classical MD simulations, with the protonation change sampled either by a separate MC analysis or by lambda dynamics within the MD trajectory [12–15]. However, these methods will not work to define the pH dependent behavior of small molecules with multiple protonation states.

1.2. SAMPL6 pK_a challenge targets are small molecules with multiple protonation and tautomeric microstates

Organic molecules with multiple protonatable sites play roles in metabolism and are design targets for drugs [1,2]. The pH dependent behavior of these molecules is at a level of complexity between a single protonatable group (eqn. 1) and a complex polyelectrolyte such as a protein. The SAMPL6 pK_a Challenge chose 24 extended organic compounds as a test case for a blind prediction of molecule pK_as. [5,16] (https://github.com/samplchallenges/SAMPL6/tree/master/physical_properties/pKa/microstates). All SAMPL6 molecules have multiple potential protonation macrostates (states with different total charge) as well as different energetically accessible tautomer states (same total charge but different protonation site), each of which represents a defined microstate. There are three to six protonatable sites in each molecule, substantially fewer than in proteins, but still sufficient to generate tens of protonation and tautomeric microstates (Fig 1) [4,5,17]. However, the coupling amongst the protonatable sites in these molecules does not allow separation into independent units, with simply summable interactions. Rather, each molecule must be treated as a whole with its microstate energy a function of the proton distribution and molecular conformation. The prediction methods used in submissions to the SAMPL6 pK_a Challenge range from knowledge-based empirical methods to detailed quantum mechanical simulations. Several recent papers have described some of the results [16,18–23] and [17] provides an analysis of the predictions submitted for all molecules.

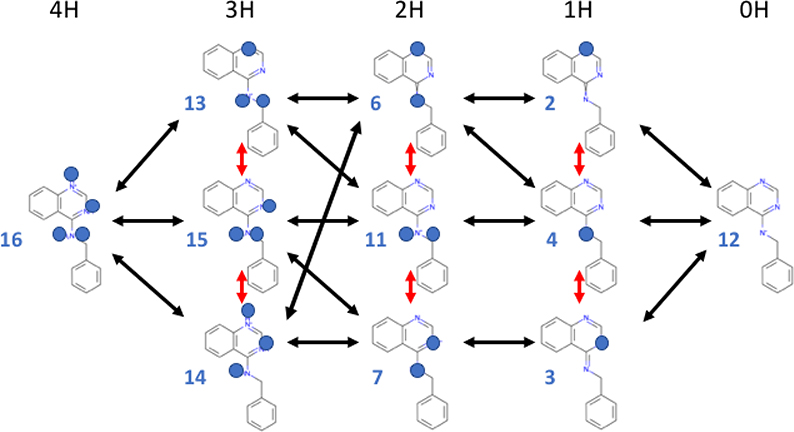
Fig 1. Network of protonation and tautomeric microstates for SAMPL6 pK_a challenge target SM07.

Only the subset of possible microstates identified as being of interest in the SAMPL6 challenge are shown. The protons of interest are denoted by blue balls on top of the nitrogen which is the proton acceptor. Each column has a different number of dissociable protons, indicated at the top. All microstates in a column are tautomers with the same total charge; their vertical order is arbitrary. All the tautomers in a column contribute to the macrostates states with 4 (4H) to zero (0H) dissociable protons. Black double-headed arrows indicate pK_as that were reported in the SAMPL6 Challenge; red arrows are the transitions between tautomers. Twenty four pK_as can be defined between all microstates in one column and all in the neighboring columns as they differ by one proton. Some transitions, such as between 13 and 7 required tautomer changes. Likewise, transitions between tautomers in the top and bottom rows (e.g. between microstates 2 and 3) are also well-defined, but are not shown here for clarity. The numbers associated with each microstate simplify the microstate IDs assigned by the SAMPL6 pKa Challenge, which have the form: SM07_microXXX, where XXX are three digits. For example, microstate 4 in this figure corresponds to SM07_micro004.

Figure 1 shows the network of 11 considered protonation and tautomeric microstates of the SAMPL6 pK_a Challenge molecule SM07, which will be described in detail here. While it is theoretically possible to enumerate additional microstates, this set of microstates a combines microstates suggested by SAMPL6 pKa Challenge organizers (using Epik from the Schrodinger Suite v3.4 and QUACPAC from the OpenEye Toolkit v2017.Feb.1) with any additional microstates included in SAMPL6 challenge submissions. Each column shows microstates with a different number of protons noted at the top of the figure, from 4 dissociable protons (4H) to none (0H). The tautomers are arranged (in arbitrary order) in a column. The sixteen black arrows show pK_as that connect microstates that were predictions in at least one submission. However, a pK_a can be defined between all microstates in adjacent columns. The red arrows show changes in proton positions between tautomers. Drawn in this way, it can be seen that there are many closed reaction cycles. One example, starts with state 4 (1H); the shift of a proton position leads to tautomeric microstate 2 (1H); the loss of a proton generates microstate 12 (0H); and proton binding regenerates microstate 4. In a network that is thermodynamically consistent the summed change in free energy for these three reactions should equal zero. The network shows cycles, including many with 3 microstates as well as larger ones such as those that connect microstates 12 (0H) and 16 (4H) through different tautomers of the intermediate protonation states. Thermodynamic consistency can provide a test of a set of calculations for a given molecule.

1.3. What information was requested for the SAMPL6 pK_a Challenge?

Three types of submissions for predictions were requested SAMPL6 pK_a Challenge: microscopic pK_as for related microstate pairs (type I), fractional microstate populations in the pH interval 2 to 12 (type II), and macroscopic pK_as (type III). We will see that type I and type II are formally identical as long as the same microstates are included in both descriptions and that type III misses important information needed to see if a numerical pK_a that matches an experimental value captures the correct protonation and tautomeric states.

Macroscopic pK_a entries were reported (type III submissions). Macroscopic states combine all the (tautomer) microstates that have the same number of protons and thus the same net charge. Macroscopic pK_as are closest to experiments that monitor the proton uptake of the molecule as a function of pH, such as electrochemical titrations or spectrophotometric titrations [5]. However, the macroscopic predictions did not require an assignment of which microstates are involved or even how many protons are associated with the beginning and end state. Thus, it may not be clear if the transition is, for example, between A^- and AH or between AH and AH₂^+. Unfortunately, this ambiguity is also a problem for many of the experimental measurements of these complex molecules. Thus, a spectroscopic or potentiometric titration provides information on the pK_a value of a proton binding event without knowing the macrostate (charge state) or microstate(s) (tautomer(s) with that charge) that is connected by the pH-dependent transition. This lack of specificity made it difficult to determine if different methods predicting a similar pK_a were referring to transitions between even the same macrostates of the molecule [5].

1.4. The minimum information needed to describe the network of protonation and tautomeric states: microstate ΔG°s at one pH provides one number to rule them all

The complexity of the SAMPL6 protonation and tautomer microstates for each molecule led to an unanticipated open question: What is the best way to report the predictions? The ideal description should provide the minimum information needed so the free energy landscape for all the protonation and tautomeric microstates in a network, such as that shown in Fig 1, can be described at each pH. It should allow easy comparison with experimental measurements and between multiple predictions for the same system. It should define the distribution of tautomeric microstates for each protonation macrostate and include information about high energy microstates, which could become important in a specific binding pocket or in a reaction mechanism. It should make it possible to check for thermodynamic consistency of cycle of changes in protonation and tautomer states such as seen if Figure 1.

SAMPL6 pK_a Challenge type I submissions report the predicted pK_as for transitions between selected pairs of prespecified microstates. This information is far richer than a list of macroscopic pK_as. However, as the list of individual microscopic pK_as were analyzed it became apparent that this format is also far from ideal. A list of pK_as provides only a local view of the relative proton affinity of pairs of states for the molecule. In addition, the list can have more information than is needed. For example, for SM07 (Fig 1) there are 24 possible pK_as between all pairs of microstates that vary by one proton (adjacent rows), of which 17 are shown. However, we will show that knowing the relative free energy of the 11 individual microstates at a single reference pH (ΔG°) can completely describe the free energy (ΔG) of all microstates at any pH. Populations of each microstate can then be obtained given the ΔGs to recover titration curves. In addition, is not readily apparent if the overall free energy landscape built up from the network of individual pairwise pK_as is thermodynamically consistent, while this is straightforward when each microstate of the molecule is associated with its relative free energy.

2. Deriving ΔG°s for a network of protonation and tautomeric states from a list of pK_as

2.1. Describing a molecule with 3 pK_as and no tautomeric states by the relative microstate free energy at pH 0 or 7

Currently, the information we have about the protonation and tautomeric states of protonatable molecules is often collected as a set of pK_as and this was the information submitted to SAMPL6. We will therefore show how to use these pK_as to build up a standard state free energy ladder, which is the free energy differences between microstates at one pH. The first example considers three pK_as separating four states, denoted A, B, C, and D (Table 1). A has three dissociable protons and D none. The analysis would be the same if the input pK_as come from experiment or simulation. Tautomeric microstates, with the same number of protons but at different locations on the molecule, will be considered in the next section. The pK_as are at −2.17, 5.61, and 13.77. These are taken from the EPIK predictions for the pK_a between the SM07 microstates 14, 7, 4, and 12 (Fig 1,2) [24]

Table 1:

The pK_as and number of protons provide the input information needed to describe a molecule with 4 protonation states separated by 3 pK_as

Molecule		XH33+		XH22+		XH+	X
microstate		A		B		C	D
Relative charge		i+3		i+2		i+1	i
pH where Gj=Gk	pKAB	−2.17	pKBC	5.61	pKCD	13.77
ΔGjk	ΔG°AB	2.17	ΔG°CB	−5.61	ΔG°DC	−13.77
ΔmB		1		0		−1	−2
ΔmC		2		1		0	−1

pK_jk=pK_kj is the pH where G_j=G_k; ΔG°_jk is the free energy difference between states j and k at pH 0. The reference state is the second term in the subscript. ΔG°_jk = −ΔG°_kj. Δm_j is the number of protons relative to the reference state, which is B or C here. As there are no tautomeric states in this simplified example, the microstates and macrostates are equivalent. Free energy (ΔG) is given as unitless free energies where a one unit change in ΔG yields a 10-fold population change.

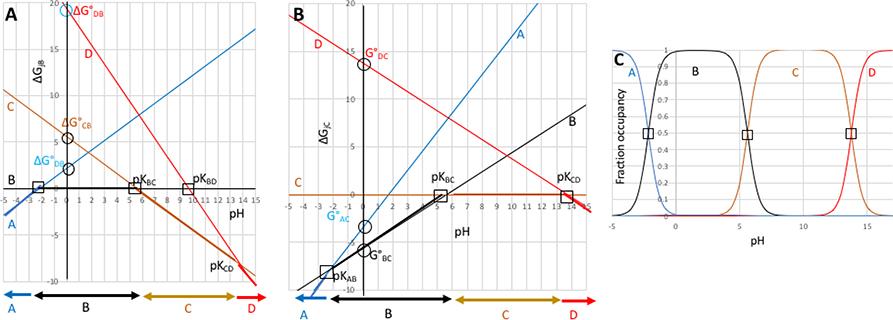
Figure 2. Relative standard state free energies (ΔG°) and relative number of protons (Δm) is all that is needed to completely describe the pH dependence of a system with multiple protonation states.

2A: The relative free energies of the states A,B,C, and D as a function of pH given the pK_as in Table 1 transformed to standard state free energies, ΔG° (Table 2). Relative free energies of microstates change linearly with respect to pH (eqn. 2b). Squares are input pK_as which can be experimentally observable. Circles mark ΔG°_jB, the free energies at pH 0 of the other three states relative to B. Horizontal arrows at the bottom show the state at lowest free energy (dominant population) in each pH range. 2B): states A, B, C and D with state C as the reference; 2C): Titration showing relative state populations vs pH predicted using ΔG°s in Table 2 and equations 3 and 4. This plot is the same independent of which state is used as the reference. ΔG is given in unitless free energies where a unit change in ΔG yields a 10-fold population change.

To determine the relative free energy of the four microstates at a single pH one state is chosen to be the reference state. The reference state and pH are arbitrary choices, but simply need to be applied consistently. We will describe the calculation of the relative state free energies with B as the reference (ΔG°_jB) and then show that using C as a reference (ΔG°_jC) provides the same relative energies between all states, but with a constant offset equal to the energy difference between microstates B and C (ΔG°_BC). The reference state is defined here as the second term in the subscript.

If B is the reference then its energy is zero and it is independent of pH, shown by the horizontal black line at ΔG=0 in Fig 2a. The pK_AB at −2.17 gives the pH where state A and B have equal energy so the line describing the pH dependence of the relative free energy of A crosses B here. The free energy difference between A and B at any other pH is:

$${\Delta G}_{AB}^{pH}={\Delta m}_{AB}{C}_{units}(pH-{pK}_{AB})$$ (2a)

ΔG_AB is 0 when the pH is equal to the pK_AB. C_units moves the values into the desired units of energy. It is 1.36 for kcal/mol or 5.69 for kJ/mol. We will use C_units=1, which is RTlog₁₀10. Thus, one unit of energy changes the equilibrium constant by a factor of 10 at the reference temperature. A change in pH of 1 unit leads to a 1 unit change in ΔG_AB if a proton is gained or −1 unit if a proton is lost. C_units can be referred to as pH units. As A has one more proton than B (Δm_AB=1) its energy increases with pH as the proton concentration decreases. The standard state reference energy for A is its energy relative to (the reference state) B at the (reference) pH of 0 is:

$${\Delta G}_{AB}^{°}={\Delta m}_{AB}{C}_{units}(-{pK}_{AB})$$ (2b)

ΔG°_AB is thus the y-intercept in Fig 2b. In biochemistry, the standard state (ΔG°’) is often defined at pH 7 not pH 0. ΔG°’ is provide in table 2, and can be read off figure 2a or b from the y value for each state at pH 7. At pH 7 the relative free energies are:

$${\Delta G}_{AB}^{°\prime }={\Delta G}_{AB}^7{=\Delta m}_{AB}{C}_{units}(7-{pK}_{AB})$$ (2c)

Table 2.

State energies derived from pK_as in Table 1 using different reference states or reference pHs.

		pH =0	pH=7		pH=0	ΔΔG°jC - ΔΔG°jB
State j	ΔmjB	ΔG°jB	ΔG°’jB	ΔmjC	ΔG°jC
A	1	2.17	9.17	2	−3.44	−5.61
B	0	0	0	1	−5.61	−5.61
C	−1	5.61	−1.39	0	0	−5.61
D	−2	19.37	5.37	−1	13.77	−5.61

With B as the reference state ΔG°_jB and ΔG°_jC obtained with eqn 2b given pK_AB and pK_CB; ΔG°_DB = ΔG°_DC+ΔG°_CB (Table 1). ΔG°’_jB, the relative state energies with the reference pH=7, is obtained with eqn 2c. When C is the reference state the ΔG° relative to states B and D are obtained directly from the reported pK_as using equation 2b. ΔG°_AC = ΔG°_AB+ΔG°_BC. There is a constant offset for all ΔG°s moving from a system that uses state B or state C as the reference state. ΔG represents unitless free energies where a unit change in ΔG yields a 10-fold population change.

The pK_a at pH 5.61 connects state C to the reference state B. The pK_BC is marked on Figure 2a as the point where the two states have equal energy. As C has one less proton than B (Δm_CB = −1) the free energy of C decreases relative to B with increasing pH, so its energy has a slope of −1 (in pH units). Extrapolation of the free energy as a function of pH back to the reference pH of 0 yields the ΔG°_CB of 5.61 (eqn 2b).

While the pK_as in Table 1 give the pairwise free energy difference between states A or C and B, there is no direct information about the transition between states B and D, which differ by 2 protons. The pK_CD at 13.77 connects states C and D. Thus, ΔG°_DC = Δm_DC(-pK_DC) = 13.77. ΔG°_DB= ΔG°_DC + ΔG°_CB (i.e. the free energy change from B to C plus that from C to D) (Table 2). The slope of ΔG°_DB is −2 as D has 2 fewer protons than B. The slope of ΔG°_DC with pH is −1, which is not easy to see from the graph, but will become apparent in the next section when C is used as the reference state. At each pH the predominant species will be the state at lowest energy shown by thicker lines in Figure 2a. Thus, below pH −2.17 this is state A; between −2.17 and 5.61 it is state B; and above 5.61 it is state C and above pH 13.77 D is the lowest energy and thus the predominant species.

Translating the pK_as, which each connect a pair of microstates, into relative ΔG° for the ensemble of four microstates provides additional information. Thus, the free energy difference between states not connected by a defined pK_a, such as a two proton transition between A and D, can be obtained from the sum of stepwise ΔGs at any pH. The crossing points between the any pair of lines on the free energy vs pH plot show the pH where two microstates have equal energy and thus equal probability.

The selection of the reference state is arbitrary. Figure 2b shows the graphical analysis of the same pK_as shown in table 1 but with state C as the reference, instead of B. Now C lies along the horizontal at ΔG=0. B has one more proton than C so the pH dependence of ΔG°_BC has a slope of 1 and crosses ΔG=0 at pK_BC. State D has one less proton than C so ΔG°_DC changes with pH with a slope of −1. ΔG_DC is 0 at pH 13.77, at pK_DC. Now it is the pK_AB at −2.17 that is not directly connected to the reference state. ΔG°_AC is ΔG°_AB+ΔG°_BC (Table 1, 2). The two graphs in Fig2a and b are the same except for a rotation to move from B being on the x axis to place C on this axis. For any microstate (j) ΔG°_jB and ΔG°_jC differ by the difference in energy between the states B and C (ΔG°_CB), which is −5.61 at pH 0. As the relative energy difference between all states are the same at each pH the lowest energy (and hence highest population) state at each pH is the same in Fig 2a and 2b.

Given the relative energy at pH 0, the relative energy of each state can be determined at any pH by:

$${\Delta G}_{jB}^{pH}={{\Delta G}_{jB}^{°}+\Delta m}_{jB}{C}_{units}(pH-{pH}_{ref})$$ (3)

Given the energy as a function of pH (ΔG^pH_jB) the fraction of each state, N_j, at each pH is obtained from the standard expression:

$$N_j^{pH}=\frac{{10}^{{-\Delta G}_{jB}^{pH}}}{{\sum }_i{10}^{{-\Delta G}_{iB}^{pH}}}$$ (4)

Plotting N^pH_j vs pH provides the titration curve. The crossing points of titration curves recover the initial, input pK_as (Fig 2c).

2.2. Microstate analysis of SM07

In the microscopic analysis of SAMPL6 pK_a challenge target SM07, eleven microstates were enumerated (Fig 1). There were 32 blind submissions of microscopic pK_a predictions from eight laboratories [16,21,24]. Four research groups submitted a single set of predictions, two submitted 2 distinct sets of predictions, another submitted 10 [19,25], and a final group 14 [23]. As few as a single pK_a was submitted for this compound (one prediction set) and as many as 17 pK_as were reported (24 prediction sets). We will show how converting all the pairwise pK_as to state ΔG°s will make it easier to compare the entire free energy landscape predicted by different methods, recognizing thermodynamic inconsistencies and ending with better appreciation of whether different calculation methods are converging to similar answers for states that are not experimentally accessible.

2.2.1. Choosing the reference state

We will first consider the values calculated with the program Epik [26–28]. From independent Epik calculations run with the -pH option at pH values between 2–12 (0.1 pH units apart), 8 microstates were predicted to be populated (Fig 3b, Table 3a)[24]. We will then describe the relative microstate energies obtained from the pK_as in all submissions, which describe as many as 11 microstates (Fig 1).

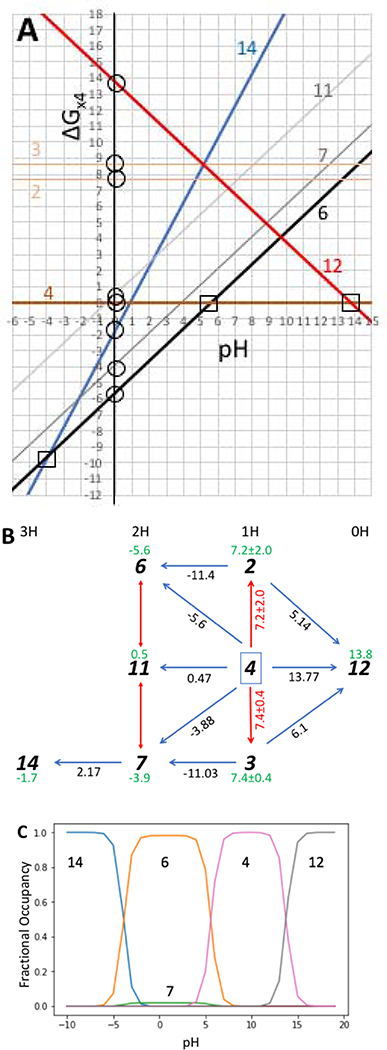
Figure 3. Graphical depiction of the microstate energy as a function of pH and resultant titration curve for the eight microstates of SM07 described in Table 2.

a) Graphical representation of the 8 microstate energies as a function of pH using ΔG°s and Δms from Table 3b. The squares show pK_as that would be seen experimentally as they connect the states that are at low energy at that pH and the triangles show pK_as that were the input to the calculation. There is an inconsistency in the relative energy of states 2 and 3 calculated when state 12 or state 6 or 7 are used to obtain the free energy difference from reference state 4 (Table 3b). b); The microstate network of 8 microstates of SM07 connected by pK_as calculated with Epik [24]. Microstates predicted by Epik are a subset of those shown in Fig 1. Dark blue arrows are the ΔG° between the two microstates; Red arrows are ΔG° between tautomers. The standard deviations for ΔG°_2,4 and ΔG°_3,4 represent the standard error for the free energy calculated around the two nearest closed triangular loops. Green numbers under microstate identifiers are ΔG°, the free energy relative to state 4 at pH=0._. c) The probability of each state as a function of pH. Note that while state 6 is the predominant microstate between pH −5 and 5, a small amount of tautomer microstate 7 is seen. ΔG represents unitless free energies where a unit change in ΔG yields a 10-fold population change. Python scripts and interactive Jupyter notebooks to generate networks and graphs of the relative free energy as a function of pH from a list of microscopic pKas can be found at http://github.com/choderalab/titrato

Table 3a.

Epik microscopic pK_as for SM07

Statej	Statek	pKj,k	Std err		ΔG°jk
2	12	5.14	1.47	ΔG°12,2	5.14
3	12	6.1	0.86	ΔG°12,3	6.1
4	12	13.77	0.73	ΔG°12,4	13.77
6	2	11.4	2.22	ΔG°6,2	−11.44
6	4	5.6	1.13	ΔG°6,4	−5.6
7	3	11.03	2.22	ΔG°7,3	−11.03
7	4	3.88	2.22	ΔG°7,4	−3.88
11	4	−0.47	0.92	ΔG°11,4	0.47
14	7	−2.17	2	ΔG°14,7	2.17

The standard error (Std err) is the value reported by the Epik calculations.

Knowing the structure of each state we can count the number of protons (Fig 1). As shown above the choice of reference state is arbitrary. One choice, which is easier to automate, is to use microstate 12 or 16 with the fewest or most protons (Fig.2). However, we chose state 4 as the reference as it has four reported pK_as. This allows the ΔG°_j4 for microstates 6, 7, 14 and 12 to be determined directly with Eqn 2b (Table 3b). ΔG°_14,4 is then the sum of ΔG°_14,7 + ΔG°_7,4.

Table 3b:

Epik SM07 microstate standard state free energies

state	Δmj,4	ΔG°j,4	source	ΔG°’j,4
12	−1	13.77	pK12,4	6.77
2	0	5.8 8.63	ΔG°6,4-ΔG°6,2 ΔG°12,4-ΔG°12,2	5.8 8.63
3	0	7.15 7.67	ΔG°7,4-ΔG°7,3 ΔG°12,4-ΔG°12,3	7.15 7.67
4	0	0	reference	0
6	1	−5.6	pK6,4	1.4
7	1	−3.88	pK7,4	3.12
11	1	0.47	pK11,4	7.47
14	2	−1.71	ΔG°14,7 + ΔG°7,4	12.29

Table 3a:. pK_a are obtained from [24]. Microstate j has one more proton than microstate k. ΔG°_jk is the free energy difference between states j and k at pH 0 (eqn 2b). State IDs are given in Figure 1 and 3b. Table 3b: Δm_j,4 is the change in the number of protons relative to state 4. ΔG°_j4 and ΔG°’_j4 are the relative microstate free energy at pH 0 and 7 respectively. Source: Where pK_j,k is indicated equation 2b and table 3a are used; otherwise the ΔG°s listed are summed to generate the energy difference between the desired microstate and microstate 4 using the network in Figure 3b.The energy of microstates 2 and 3 are obtained from the sum of the free energies around the indicated loop using the path described and the resultant ΔG° is the average of the two paths. ΔG presented as unitless free energies where a unit change in ΔG yields a 10-fold population change.

2.2.2. Determining the ΔG° between tautomers can uncover a lack of thermodynamic consistency

Microstates 2, 3, and 4 are tautomers with the same number of protons. Thus, their relative energy is independent of pH, so there is no pH where their energy is equal and thus no pK_a can be defined. However, examination of Fig 3b shows the ΔG° can be defined between these states by the summed energy along any path to the reference. For example, to determine ΔG°_2,4 we consider two short paths: one with state 6 as the intermediate, and one via state 12. The two paths give a different ΔG°_2,4 (Table 3b). This indicates that the closed reaction cycle from microstate 4 to 6 to 2 to 12 and back to 4 does not sum to zero as it should for a thermodynamically consistent method. The summed free energy for the protonation number and tautomer changes described in a loop is clear when the molecule is described as a network of protonation and tautomeric microstates with energies defined against a single reference state. When different cycles do not sum to zero there are multiple choices for the derived ΔG° values, from using one cycle, averaging the 2 shortest cycles as carried out here, to averaging the results from all possible cycles. When the thermodynamic cycles close properly there is no ambiguity in the relative free energy of the microstates.

2.2.3. Graphical analysis of the microstate energy as a function of pH

Fig. 3a provides a graphical picture of the microstate energy as a function of pH obtained from the pK_as in Table 3a. Plotted relative microstate free energy vs. pH shows the energy of each of the two groups of tautomers (1H macrostate, microstates 2, 3, 4) and (2H macrostate, microstates 6, 7, 11) are parallel to each other as the ΔG between them is independent of pH. The graph shows which state(s) are at experimentally accessible energy in any pH range. This is microstate 14 at low pH, a mixture of 6 and 7, then microstate 4 and at high pH microstate 12 predominates.

The nine pK_as that are given each represent crossing points between two lines on the graph. There are many other possible pK_as that can be read off the graph or obtained by determining the pH where two microstates with different numbers of protons have the same energy. For example, pK_7,14 is given but pK_6,14 might be more important as microstate 6 is at lower energy than the tautomer microstate 7. In addition, inconsistencies in the energies obtained for different pairs of pK_as are seen. Thus, the intersection of states 2 and 6 as well as that of 3 and 7 are different than the reported pK_as because the y intercept (ΔG°) represents the average of two thermodynamic cycles while the slope of the lines must be fixed at 0 as these microstate have the same number of protons as reference state 4, or the slope is 1 if the microstate has an additional proton (e.g. for 6,7, and 11). The derived titration curve highlights the low energy, experimentally accessible states. It should be noted that the titration covers a pH range that is higher and lower than most experiments. The 2H protonation state is found to be the most stable between pH −5 and 5. While tautomer 6 is dominant, the free energy analysis shows tautomer 7 is close in energy so would be predicted to be a minority species. The relative probability of microstates 6 and 7 is pH independent and their sum give the probability of the 2H macrostate as a function of pH..

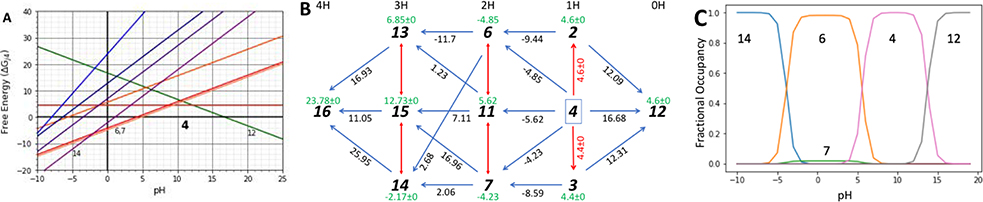
ECRISM-13 (SAMPL6 pK_a challenge submission ID 0xi4b) reported 17 pK_a values for SM07 (Figure 4) [23]. The network obtained from these pK_as show all closed paths around the network have a summed ΔG° of zero, indicating the reported values are, thermodynamically consistent (Fig 4a). Now there is data to characterize the free energy of tautomers 13, 14 and 15 as well as the highly protonated microstate 16. The pattern of relative microstate energies are in qualitative agreement with the Epik simulations and the resulting titration is also similar. The same microstates are at low energy (Fig 4c). Both calculations place the 2H microstates 6 and 7 close enough in energy that a mixture of tautomers are predicted to be seen (Fig 3c, 4c).

Fig 4: Graphical analysis of a network of 11 microstates SM07.

(a) Network of 11 SM07 microstates considered by calculation ECRISM-13 (ID 0xi4b) [23], their connecting pK_a (black 2-headed arrows); the resultant pairwise ΔG°_j4 (blue arrows) and microstate ΔG°_j4 relative to microstate 4 (green numbers). (b) ΔG_j4 as a function of pH for all microstates. ΔG°_j4 is ΔG_j4 at pH 0. ΔG represents unitless free energies where a unit change in ΔG yields a 10-fold population change. (c) Predicted titration curves given the microstate ΔGs as a function of pH. It should be noted that the pK_as shown in Fig 4c match the crossing points in Fig 4b that occur as one lowest energy state is replaced by another as the pH changes.

2.3. Overview of all submitted predictions for SM07: Do different calculation methods give similar values for ΔG°?

Table 3 gives the ΔG° for all predictions of all microstates of SM07 with microstate 4 as the reference state and pH 0 the reference pH. It is far more compact than a table of pK_as, requiring only a single value for each microstate. In contrast, a single microstate in the SM07 network of states described in Figure 2, can be connected by as many as six pKas to the six microstates that different by one proton. In addition, the pH independent ΔG° between tautomeric states are established, although there is no pK_a that can be defined for a pair of microstates with the same number of protons. As shown in Fig 2,3 and 4, knowledge of ΔG°_j4 at a single pH and the difference in the number of protons from the reference state (Δm_j4) can be used to find the microstate free energy differences at all pHs. The analysis shows where any two microstates are at the same energy either graphically or by calculation, and so identifies all possible microscopic pK_as. The pK_as can connect microstates at high energy or that differ by more than one proton. Knowing the microstate energies as a function of pH allows the calculation of their relative probability with pH. Plotting this probability as a function of pH generates a titration curve, visually identifying the low energy states and providing the macroscopic pK_as (Fig 2,3,4). Table 4, gives the ΔG°s at the reference pH of 0, although the table can be modified for any pH using eqn. 3 (e.g. table 2, 3b).

Table 4.

Microstate ΔG°_i4 for SM07 derived from pK_as submitted to the SAMPL6 Blind pK_a Challenge shows areas of qualitative agreement with significant differences in calculated energies.

		Microstate
		0H	1H			2H			3H			4H
ID		12	2	3	4	6	7	11	13	14	15	16	ΔG16–12	ΔGcycle
hgn83[25]	NHLBI-9	3.7	16.7	18.0	0	20.4	28.5	28.5	36.3	24.4	36.5	55.9	52.2	7.9
758j8[25]	NHLBI-8	8.3	12.4	17.3	0	15.8	23.9	25.6	32.6	28.8	41.1	57.4	49.1	7.9
z3btx[25]	NHLBI-7	9.7	17.0	17.3	0	14.4	23.2	21.8	30.0	18.4	30.2	49.7	40.0	8.3
0wfzo[25]	NHLBI-6	14.3	15.7	16.6	0	9.8	17.2	18.6	26.1	21.8	34.2	50.8	36.5	8.3
8toyp[23]	ECRISM-8	20.6	6.4	5.4	0	−1.4	−1.3	4.5	11.6	6.6	19.9	40.7	20.1	0
arcko[19]	NHLBI-4	16.8	6.9	6.2	0	−6.5	−2.7	6.8	12.9	4.7	20.5	36.2	19.4	0.9
wexjs[19]	NHLBI-5	17.8	6.8	5.9	0	−6.0	−2.4	7.5	13.7	5.1	20.5	36.9	19.1	0.3
w4z0e[19]	NHLBI-2	19.0	6.7	5.8	0	−5.4	−2.0	8.0	14.2	5.6	20.9	37.0	18.0	0.3
wcvnu[19]	NHLBI-3	18.1	6.8	6.5	0	−5.2	−1.9	7.8	13.3	4.7	19.5	36.0	17.9	0.5
ko8yx[19]	NHLBI-1	18.0	6.9	6.5	0	−5.3	−2.2	7.5	13.0	4.5	19.0	35.6	17.6	0.9
z7fhp[23]	ECRISM-7	20.2	6.3	5.4	0	−1.8	−1.6	4.0	10.2	5.2	18.4	37.6	17.4	0
kxztt[23]	ECRISM-1	15.9	5.4	4.1	0	−2.6	−2.6	2.0	7.0	3.7	13.3	30.1	14.2	0
nxaaw[23]	ECRISM-12	17.8	5.5	4.5	0	−4.8	−4.4	5.7	8.8	0.4	14.9	30.0	12.2	0
2umai[23]	ECRISM-5	16.7	4.7	4.0	0	−2.5	−2.4	1.9	5.7	2.0	11.8	25.7	9.0	0
cm2yq[23]	ECRISM-6	16.6	4.7	4.0	0	−2.5	−2.4	1.8	5.7	1.9	11.8	25.6	9.0	0
epvmk[23]	ECRISM-9	14.0	4.1	3.5	0	−2.9	−2.7	2.7	5.5	0.7	11.0	22.8	8.8	0
4o0ia[23]	ECRISM-11	13.8	3.9	3.4	0	−2.9	−2.7	2.5	5.3	0.6	10.5	22.1	8.3	0
xnoe0[23]	ECRISM-10	14.2	4.1	3.5	0	−3.1	−2.9	2.5	5.1	0.2	10.5	22.1	7.9	0
ktpj5[23]	ECRISM-3	16.5	4.7	4.0	0	−2.7	−2.6	1.6	4.9	1.1	11.0	24.0	7.5	0
wuuvc[23]	ECRISM-4	16.4	4.7	4.0	0	−2.7	−2.6	1.6	4.8	1.1	10.9	23.8	7.4	0
0xi4b[23]	ECRISM-13	16.7	4.6	4.4	0	−4.9	−4.2	5.6	6.9	−2.2	12.7	23.8	7.1	0
cywyk[23]	ECRISM-14	16.3	4.5	4.3	0	−5.0	−4.4	5.3	6.0	−2.8	11.7	21.9	5.6	0
ftc8w[23]	ECRISM-2	15.5	4.8	3.7	0	−4.7	−4.8	1.2	2.3	−2.6	7.9	18.5	3.0	0
gdqeg[23]	PCM-15	8.9	2.9	2.4	0	−7.2	−7.0	−1.4	−4.5	−9.4	−1.1	1.3	−7.6	0
6tvf8[16]	BannonOE-1	-	-	-	0	−7.1	−5.1	−0.5	−6.3	−9.5	−5.9	−12.9	NI	8.8
hdiyq	Rfraczkiewicz	-	-	-	0	−5.6	−3.7	−1.3	−5.4	−2.8	−2.1	−1.2	NI	0
ccpmw[21]	Wilcken2	15.8	-	-	0	−7.4	−6.0	3.4	-	−7.9	-	-	NI	NI
t8ewk	cosmologic_fine17	-	-	-	0	−7.4	−5.9	-	-	-	-	-	NI	NI
v8qph	KirilLanevskij-1	-	-	-	0	−5.5	-	-	-	-	-	-	NI	NI
[24]	EPIK	13.8	7.2	7.4	0	−5.6	−3.9	0.5	-	−1.7	-	-	NI

Energy of microstates of SM07 at pH 0, with state 4 used as the reference. ΔG in unitless free energies where a unit change yields a 10-fold population change. Microstate IDs as in Figure 1. The rows are ordered by ΔΔG°_16–12, which is the energy difference between the unique 4H and 0H microstates. The tautomers, with the same number of protons are grouped together (1H, 2H, 3H). Energies below zero are indicated in red. ΔG°_j4 values are derived from predicted pK_as found for the SAMPL6 pKa Challenge: (https://github.com/samplchallenges/SAMPL6/tree/master/physical_properties/pKa/analysis/analysis_of_typeI_predictions/typeI_predictions ). Superscript with the submission ID identifies published papers associated with each submission. Superscript is the reference. The Epik calculations do not have a SAMPL6ID. The only experimentally observed pK_a is 6.08 (ΔG°₆₄ = −6.08) is obtained by spectrophotometric method which technically measures the macroscopic pK_a for multiprotic molecules. NMR analysis identified microstate state 4 and 6 as dominant microstates that participate in this transition [5]. Values within 1 pH unit of the predicted pK_a are underlined. ΔG_cycle is the largest difference in energy calculated for the summed ΔG°s along all cycles of length 4 in the graph of SM07 microscopic equilibria for each of the submissions. NI indicates that too few pK_as were submitted to generate closed cycles to check for thermodynamic consistency.

2.3.1. Comparison of the calculated results with experiment

A single experimental pK_a value at pH 6.08 is available for SM07 [5,17]. SM07 was one of the few whose titration was followed by NMR showing the transition is between microstates 4 and 6. The NHLBI QM submissions (ko8yx, w4z0e, wcvnu, arcko, wexjs)[19] and the Fraczkiewicz submission (hdiyq) as well as the single KirilLanevskij submission (v8qph) predicts both the correct low energy microstates and the pK_a correctly (with a maximum error of 1 pH unit).

The ΔG° analysis gives access to the pH independent ΔΔG between tautomers, which can be compared with the experimental evidence for the transition between the 1H and 2H microstates described by experiment. All calculations put microstate 4 as the lowest energy 1H state, in agreement with experiment. However, the free energy of microstate 7 is often very close to that of 6, so it is often predicted to be a minority species in the titration (Fig 3c, 4c). It should be noted that in several cases the microscopic pK_as between microstates 7 and 4 is close to the experimental value. However, macroscopic titration will always predominantly involve microstate 6 as it is at lower energy.

2.3.2. The thermodynamic consistency of the submitted predictions for SM07

Viewing the molecule as a network of connected protonation and tautomeric states allows the self-consistency of the relative energies to be determined. If the sum of the ΔG° around a closed path deviates from zero by more than the likely error of the individual values, then this group of microstates energies are not thermodynamically consistent and something is wrong. We can see that different submissions have different degrees of internal constancy. The ΔG° were summed along all cycles of length 4 in the graph of SM07 microscopic equilibria for each of the submissions. Table 5 gives the largest value of the summed ΔG° for each prediction set (ΔG_cycle).

The submissions from ECRISM (kxztt, ftc8w, ktpj5, wuuvc, 2umai, cm2yq, z7fhp, 8toyp, epvmk, xnoe0, 4o0ia, nxaaw, 0xi4b, cywyk) [23] have closed free energy cycles, with the exception of rounding errors on the second decimal, as does the Fraczkiewicz submission (hdiyq). The NHLBI QM submissions (ko8yx, w4z0e, wcvnu, arcko, wexjs)[19] have closed cycles for some but not every 4-microstate cycle, but the mismatch are all below 1 ΔG unit. In contrast, NHLBI submissions using QM-MM (0wfzo, z3btx, 758j8, hgn83) [25], do not produce thermodynamically consistent cycles, with largest errors of around 8 ΔG units for the cycle containing microstates 4, 7, 15, and 11. The submission that used the Bannan OE method (6tvf8) [16] have cycles that do not sum to 0, with the largest cycle error being 8.75 ΔG units for the cycle between microstates 4, 11, 13, and 6.

It should be noted that the ΔG°_j4 connects the 1H microstate 4 to other microstates. As described in Table 2b the energy of tautomers is derived from the sum of free energies along a thermodynamic path and the energy of states that are separated from microstate 4 by more than 1 proton (3H and 4H microstates for SM07) are obtained by sums of ΔG°s along the path to the reference state 4. When the cycles do not close than the values in table 3 become dependent on which path is used or if multiple paths are averaged.

2.3.4. Overview of the SM07 landscapes show qualitative consistency, but large differences in values

Only one experimental value is available for SM07. Under these circumstances simulations can offer information if the calculations can be vetted in some manner. One check is the ability to match the single known pK_a, identifying the correct macrostates (1H to 2H here) and correct microstates (4 and 6). Another check is that the overall network is thermodynamically consistent. Lastly, we might say that the calculation of pK_as for molecules such as SM07 is ‘solved’ if the various submissions find similar answers for the relative state energies that can be checked against experiment for the few microstates that are experimentally inaccessible.

Table 4 allows evaluation of the consistency of the lowest energy microstate at the reference pH. Here this is pH 0, but the table to be remade at any pH (eqn. 3). It is apparent that at pH 0 the calculations do not agree on what is the lowest energy protonation state. It can be the 1H state (NHLBI-6 to 9), the 2H state or a 3 H state. Thus, the calculations do not agree on what is the net charge of the SM07 molecule at the reference pH.

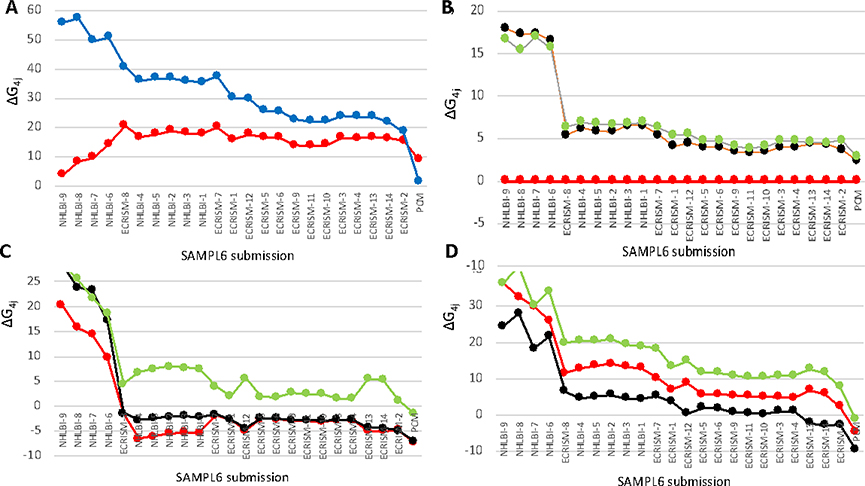
Another comparison amongst the calculations is to compare the ΔG°_j4 of individual microstates. The overall range of energy from the microstate with no protons (microstate 12) to that with 4 protons (16) varies enormously between the different calculations from −7.6 for PCM-1 to +52 for NCBLI-9 at pH 0. The calculations which are not thermodynamically consistent (NHBLI 6,7,8,9 (on the left in Figure 5) and PCM (on the right) are clearly different from the bulk of the calculations. The thermodynamically consistent networks still have a range of energy from the most to least protonated microstates of 20 to −7.6. As one unit of energy is sufficient to change the relative population by 10 fold, this represents a large variation. Thus, while the ΔG°_12,16 may not be significant experimentally, the difference in this value shows that the free energy landscape for this molecule is predicted to be radically different in the different calculations. The array of different values shows how SAMPL challenges allow the strengths and weaknesses of different computational to be seen. Outliers have much to teach us.

Figure 5. Overview of relative free energies for individual microstates for individual submissions to the SAMPL6 blind pK_a challenge.

All submissions that provided information about all 11 microstates are included, ordered by the free energy difference between the 4H microstate (16) and the 0H microstate (12). Data from Table 4; definition of microstates from Figure 1. a) Blue: microstate 16, Red: 12; b) Green: microstate 2; Black: 3; Red: 4 (reference state); c) Green: microstate 11; Black: 7; Red: 6; d) Green: microstate 15; Black: 14; Red: 13.

The relative tautomer energies are, perhaps, a simpler test of the various calculation methods, as the compounds have the same net charge so there is likely to be a smaller difference in solvation energy or influenced by the uncertainties in the calculation of the energy of the free proton. The relative energy of each set of tautomers is independent of pH. All calculations show microstates 2 and 3 of SM07 to be close in energy and at higher energy than microstate 4 (Fig 5b). Likewise, microstates 6 and 7 are generally close in energy with 6 being the lower and state 11 being significantly higher in energy (Fig. 5c). For the tautomers with three protons (microstates 13,14 and 15) microstate 14 is predicted to be the lowest energy microstate, but there is less agreement about the relative energy of these tautomers (Fig. 4d). Thus, overall comparison of the thermodynamically consistent networks of ΔG°s the relative tautomer free energies are in qualitative agreement.

Conclusion

The protonation and tautomer states of extended organic molecules will significantly influence their solubility, partition coefficients and binding affinities to biologically important macromolecules. Molecules used as drugs often have multiple protonation and tautomeric states. Thus, we need to be able to organize the information about the molecular macrostates (with different charge) and microstates (defining the position of all protons) so that under any set of conditions we can determine the dominant charge of the compound and its likely tautomeric state. The question addressed here is how to best organize the information we have about these complex molecules.

The SAMPLE6 Blind pK_a Challenge was the first SAMPL challenge directly focusing on the ability of simulation to predict pK_as of complex organic molecules [5]. Evaluating the submissions made it clear that the best way to describe the pH dependence of molecules with multiple protonation and tautomeric states was not a solved problem. It proved to be difficult to compare different calculations with each other using the complex lists of microstate pK_as. The work presented here shows that reporting only the free energy at a single pH, ΔG°, and change in the number of protons, Δm, each with respect to one (arbitrary) microstate is a better way to report information about protonation and tautomeric states. This procedure should be used for future SAMPL challenges, but it should also be useful as a general way to archive information about molecules with multiple protonation and tautomeric states more generally. It should be noted that this paper shows in detail how to back calculate all the microstate ΔG°s from a list of submitted pK_as. However, computer simulations will often calculate relative microstate ΔG°s, which were then submitted as pK_as.

There are a number of significant advantages to listing microstate ΔG°s for a network of states rather than a list of pairwise pK_a between specific states. The list of ΔG°s is more compact. Thus, for the SM07 microstates considered here, 11 ΔG°s and Δms provide all needed information to determine the free energy difference between any pair of states. In contrast, there are 24 pK_a that connect only states that different by one proton. The information provided by the ΔG°s is richer. It provides the ΔG°s between tautomers, which is never evident from lists of pK_as as the free energy difference between molecules with the same number of protons is pH independent (Fig 5b,c,d). The relative energy of microstates that differ by more than 1 proton is clearly defined (Fig 5a). The summed free energy around closed cycles in the network of microstates can be checked for thermodynamic consistency. As in any equilibrium system, knowledge of the free energy of all states determines its population of each state in the ensemble (eqn. 4). Knowing standard state ΔG°s and that the free energy varies linearly with pH with a slope of that reflects the change in the number of protons relative to the reference state (Δm) directly provides the relative free energy of all states at all pHs (eqn. 3).

The ensemble of all microstate ΔG° allows the calculations derived by all methods including empirically based methods such as machine learning and QSAR to be compared with each other to determine where all methods agree (Fig 5). In situations where experimental data is unavailable (and likely to remain so) convergence of values calculated in different ways lends support to the answers obtained by the simulations. The agreement can be qualitative, as often is here, where the ordering of the lowest to highest energy tautomeric state is the same for all calculations. But the numerical free energy differences between states can vary significantly showing that there is more work to be done for these simulation methods to be able to reliably substitute for experimental measurements.

If this round of calculations does lead to a second prediction challenge for pK_as, we would strongly suggest that only microscopic data be reported; that this should be given as the standard state ΔG°; and that only thermodynamically consistent networks of ΔG°s be submitted.