Study of global dynamics of COVID-19 via a new mathematical model

Abstract

The theme of this paper focuses on the mathematical modeling and transmission mechanism of the new Coronavirus shortly noted as (COVID-19), endangering the lives of people and causing a great menace to the world recently. We used a new type epidemic model composed on four compartments that is susceptible, exposed, infected and recovered (SEIR), which describes the dynamics of COVID-19 under convex incidence rate. We simulate the results by using nonstandard finite difference method (NSFDS) which is a powerful numerical tool. We describe the new model on some random data and then by the available data of a particular regions of Subcontinents.

Introduction

Very recently a dangerous outbreak due to coronavirus has been attacked the whole globe. This is the seventh generation of coronavirus and therefore researchers have named it COVID-19. Nearly $2.5$ millions people have been infected by the virus all over the world and $0.15$ million have been pushed to death in almost 180 countries of the world. Many countries of the world have ordered lockdown the cites and stop the air as well as plane traffic so that the infection may be controlled from further spreading. WHO announced it a global pandemic [45], [46]. The economic situation of many countries are going on worse position as well as health system of several countries. Historically in the end of 2019, the mentioned outbreak started from a seafood market of Wuhan city and within a month the whole city was attacked by the virus. The Chinees government on time lockdowned the whole city and the infected people were separated which they called the quarantined people and at this way the mentioned state after two month was able to control the infection in their country. But on the other hand due to immigration and transmission of people the infection was spreaded in two months in almost all countries of the world. Therefore researchers, physicians and policy makers have started work day and night to control this killer infection from further spreading. Each country has taken their own precautionary measure, for detail see [1], [2], [3], [4].

The greatest and difficult task for human beings is to control the same environment which they have inhabited. For this purpose, however, some guidelines have been issued or provided and limits have been fixed that beyond that nature/environment shouldn’t be disturbed. Epidemics is a real danger to human race and their economic conditions. Unless there is a proper comprehension of the disease, it can’t be controlled or eliminated from the community. The implementation of plans to stop the transmission of the disease has been considered a major challenge. Therefor as we know that mathematical models are powerful tools to understand the transmission dynamics of infectious diseases and to make future planing. In this regards large numbers of infectious models were developed corresponding to various infectious disease in history, we refer few as [5], [6], [7], [8]. One of the greatest assignments given to humankind is to control the environment within which they live. However, some instructions have been given and boundaries have been identified such that some law of nature should not be violated. Infectious diseases is a massive threat for humanity and can greatly effect the economy of a state. Proper understanding of a disease’ dynamics could play an important role in elimination of the infection from the community. Further, implementation of suitable control strategies against the disease transmission have been assumed a big challenge. The approach of mathematical modeling is one of the key tools for handling such and other challenges. A number of general and disease models have been investigated in existing literature which enables us to explore and control the spread of infectious diseases in a better way [9], [10], [11]. Also The aforementioned model have been studied under various incidence rates including concave, linear and nonlinear incidence rate. Each rate has its own importance see detail [12], [13]. But investigation of biological models under convex incidence rates are more informative as in such investigation a convex function of infected class under double exposure is taken. Such involvement of double exposure helps more in the spreading of infection and its dynamics is more powerful in forming control procedure [14], [15]. The area specified to investigate biological models for endemic diseases is warm area of research in current time. Various mathematical models have been found in the literature studying the theory of stability, existence results and optimization of biological models, referring to [20], [21], [22], [23], [24], [25], [26]. In the same manner of other morbidities (see [16], [17], [18]), COVID-19 (see [19]) can be medalled, and its future behavior can be predicted. It is also feasible to seek the prevention planning. Also, one can look for possible prevention strategies as well. Therefore motivated from the aforesaid discussion, we construct a new type model like SEIR for the current novel disease. Global and local dynamics are investigated by using the powerful tools of nonlinear analysis [27], [28], [29], [30], [31], [32], [33], [34], [35], [36], [37], [38], [39], [40], [41], [42], [43], [44]. For numerical simulation, we apply a famous numerical method called nonstandard finite difference scheme given in [47].

Model formulation

Here, we present a mathematical model to describe the problem. We divide the whole population into four classes susceptible class $S(t)$, exposed class $E(t)$, infected class $I(t)$ and recovered class $R(t)$. The model is analyze by the following differential equations[9], [10], [11].

$$\begin{array}{cc}\frac{\mathit{dS}(t)}{\mathit{dt}}\hfill & =a-\mathit{KI}(t)S(t)(1+\alpha I(t))-d_{0}S(t)\hfill \\ \frac{\mathit{dE}(t)}{\mathit{dt}}\hfill & =\mathit{KI}(t)S(t)(1+\alpha I(t))-(d_0+\gamma )E(t)\hfill \\ \frac{\mathit{dI}(t)}{\mathit{dt}}\hfill & =b+\gamma E(t)-(d_0+\mu +\beta )I(t)\hfill \\ \frac{\mathit{dR}(t)}{\mathit{dt}}\hfill & =\beta I(t)-d_{0}R(t),\hfill \end{array}$$ (1)

where $D=a-b$. For any values of the parameters, we consider the existence of equilibrium of model (1) has $H_0=(\frac{a+b}{d},0,0,0)$ disease-free equilibrium. To find out the non-negative equilibria, set

The description of the parameters and compartments is given in next Table 1 as

$$\begin{array}{cc}\hfill & a-\mathit{KI}(t)S(t)(1+\alpha I(t))-d_{0}S(t)=0\hfill \\ \hfill & \mathit{KI}(t)S(t)(1+\alpha I(t))-(d_0+\gamma )E(t)=0\hfill \\ \hfill & b+\gamma E(t)-(d_0+\mu +\beta )I(t)=0\hfill \\ \hfill & \beta I(t)-d_{0}R(t)=0\text{.}\hfill \end{array}$$

To find the Basic Reproduction Number $R_0$, let $x=(E(t),I(t))$, in system (1). Then

$$\frac{\mathit{dx}}{\mathit{dt}}=\mathcal{F}-\mathcal{V}$$

$$\mathcal{F}=\left(\begin{array}{c}\hfill \mathit{KI}(t)S(t)(1+\alpha I(t))\hfill \\ \hfill 0\hfill \\ \hfill \hfill \end{array}\right)$$

and

$$\mathcal{V}=\left(\begin{array}{c}\hfill (\gamma +d_0)E(t)\hfill \\ \hfill -\gamma E(t)+(d_0+\mu +\beta )I(t)\hfill \\ \hfill \hfill \end{array}\right)\text{.}$$

The Jacobian of $\mathcal{F}$ for the disease-free equilibrium is

$$F=\left(\begin{array}{cc}\hfill 0\hfill & \hfill {\mathit{KS}}^0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill \end{array}\right)\text{.}$$

And also the Jacobian of $\mathcal{V}$ for the disease-free equilibrium is

$$V=\left(\begin{array}{cc}\hfill \gamma +d_0\hfill & \hfill 0\hfill \\ \hfill -\gamma \hfill & \hfill \mu +d_0+\beta \hfill \\ \hfill \hfill \end{array}\right)\text{.}$$

Hence, for the model(1), by simple calculation, we have

$${\mathit{FV}}^{-}1=\left(\begin{array}{cc}\hfill \frac{\gamma {\mathit{KS}}^0}{(\gamma +d_0)(\mu +d_0+\beta )}\hfill & \hfill \frac{{\mathit{KS}}^0}{\mu +d_0+\beta }\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill \end{array}\right)\text{.}$$

Which implies that the basic reproduction number $R_0$ is,

$$R_0=\frac{K(a+b)}{d_0(\mu +d_0+\beta )}\text{.}$$ (2)

Theorem 1

From the model (1) it follows that

• $(i)$ There is no positive equilibrium of system, if $R_0\le 1$ ;
• $(\mathit{ii})$ There is a unique positive equilibrium $H^{\ast }=(S^{\ast }(t),E^{\ast }(t)I^{\ast }(t),R^{\ast }(t))$ of the model (1) , called the endemic equilibrium, if $R_0>1$ . Given by

$$\begin{array}{cc}\hfill & S^{\ast }(t)=\frac{a}{K(1+\alpha I^{\ast }(t))I^{\ast }(t)-d_0}\hfill \\ \hfill & E^{\ast }(t)=\frac{\mathit{aK}(1+\alpha I^{\ast }(t))I^{\ast }(t)}{(K(1+\alpha I^{\ast }(t))I^{\ast }(t)-d_0)(\gamma +d_0)}\hfill \\ \hfill & I^{\ast }(t)=\frac{-(d_0+\mu +\beta +b(\gamma +d_0)+\gamma \mathit{aK})+\sqrt{\mathrm{\Omega }}}{2\alpha (\gamma +d_0)(b+1)}\hfill \\ \hfill & R^{\ast }(t)=\frac{\beta }{d_0}{I}^{\ast }(t)\text{.}\hfill \end{array}$$

where $\mathrm{\Omega }$ is

$$\mathrm{\Omega }={\left(d_0+\mu +b(\gamma +d_0)+\gamma \mathit{aK}\right)}^2-4\alpha (\gamma +d_0)(b+1)(d_0+\mu +\beta -d_0-b(\gamma +d_0)d_0)\text{.}$$

Table 1.

The physical interpretation of the parameter.

Parameters	The physical interpretation
$S(t)$	Susceptible class
$E(t)$	Exposed class
$I(t)$	Infected class
$R(t)$	Recovered class
a	The population who test is negative
$d_0$	Natural death
$\mu$	Death due to corona
b	The population who test is positive
$\alpha$	Individuals lose immunity
K	Proportionality constant
$\gamma$	Infection rate
$\beta$	Recovered rete
D	Whole population

Dynamical behavior of the model

In this section of our work, we will study endemic and epidemic equilibria points. Also the qualitative aspect of the proposed system will be discussed. In order to study the dynamic of model (1) we present the following lemma.

Lemma 1

The model (1) has invariant manifold of plane $S(t)+E(t)+I(t)+R(t)=\frac{\mu -a-b}{d_0}$ , which is attracting in the first octant.

Proof

Assume $M(t)=S(t)+E(t)+I(t)+R(t)$. Add all of the equations of model (1), we get

$$\begin{array}{cc}\hfill & \frac{\mathit{dS}(t)}{\mathit{dt}}+\frac{\mathit{dE}(t)}{\mathit{dt}}+\frac{\mathit{dI}(t)}{\mathit{dt}}+\frac{\mathit{dR}(t)}{\mathit{dt}}=a+b-d_{0}S(t)-d_{0}E(t)-d_{0}I(t)-d_{0}R(t)-\mu \hfill \\ \hfill & \frac{d}{\mathit{dt}}(S(t)+E(t)+I(t)+R(t))=a+b-\mu -d_0(S(t)+E(t)+I(t)+R(t))\hfill \end{array}$$

implies that

$$\frac{\mathit{dM}(t)}{\mathit{dt}}=a+b-\mu -d_{0}M(t)\text{.}$$ (3)

$$M(t)=\frac{\mu -a-b}{d_0}$$

General solution of (3) is

$$M(t)=\frac{1}{d_0}\left[a+b-(a+b-\mathit{dN}(t_0))e^{-d_0(t-t_0)}\right]\text{.}$$

Which complete our proof.  □

It is clear that the limit set of model (1) is on the plane $S(t)+E(t)+I(t)+R(t)=\frac{\mu -a-b}{d_0}$. Therefore, we are going to reduced the system.

$$\begin{array}{cc}\frac{\mathit{dE}(t)}{\mathit{dt}}\hfill & =\frac{\mathit{aKI}(t)(1+\alpha I(t))}{\mathit{KI}(t)(1+\alpha I(t)-d_0)}-(\gamma +d_0)E(t)\stackrel{\mathrm{\Delta }}{=}\omega (E(t),I(t),R(t)),\hfill \\ \frac{\mathit{dI}(t)}{\mathit{dt}}\hfill & =b+\gamma E(t)-(d_0+\mu +\beta )I(t)\stackrel{\mathrm{\Delta }}{=}\mathrm{\Upsilon }(E(t),I(t),R(t)),\hfill \\ \frac{\mathit{dR}(t)}{\mathit{dt}}\hfill & =\beta I(t)-d_{0}R(t)\stackrel{\mathrm{\Delta }}{=}\xi (E(t),I(t),R(t))\text{.}\hfill \end{array}$$ (4)

We have the following theorem with regards to the non-existence of cyclical shells in system (4), which show the non-existence of cyclical shells of system (1) by above lemma.

Theorem 2

System (4) does not have nontrivial periodic orbits if $\alpha I(t)<-1$ .

Proof

We consider system(4) for$E(t)>0,I(t)>0$ and $R(t)>0$. Let the Dulac function is

$$D(E(t),I(t),R(t))=\frac{1+\alpha I(t)}{\mathit{KI}(t)}\text{.}$$ (5)

Then,we have

$$\begin{array}{cc}D\omega \hfill & =\frac{\mathit{aK}}{1+\alpha -d_0}-\frac{(\gamma +d_0)(1+\alpha I(t))}{\mathit{KI}(t)}E(t)\hfill \\ D\mathrm{\Upsilon }\hfill & =\frac{b(1+\alpha I(t))}{\mathit{KI}(t)}+\frac{(\gamma (1+\alpha I(t))}{\mathit{KI}(t)}E(t)-\frac{(\mu +\beta +d_0)(1+\alpha I(t))}{\mathit{KI}(t)}I(t)\hfill \\ D\xi \hfill & =\frac{\beta (1+\alpha I(t))}{K}\frac{d_0(1+\alpha I(t))R(t)}{\mathit{KI}(t)}\text{.}\hfill \\ \hfill \end{array}$$ (6)

Take partial derivative of (6) and then adding, we get

$$\frac{\partial (D\omega )}{\partial E(t)}+\frac{\partial (D\mathrm{\Upsilon })}{\partial I(t)}+\frac{\partial (D\xi )}{\partial R(t)}=-\frac{\gamma (1+\alpha I(t))}{\mathit{KI}(t)}-\frac{d_0(1+\alpha I(t))}{\mathit{KI}(t)}-\frac{\mathit{aK}\alpha }{{[1+\alpha I(t)-d_0]}^2}<0\text{.}$$ (7)

If

$$\alpha I(t)<-1$$

This complete our conclusion.  □

In order to investigate the properties of the disease-free equilibrium $H^0=(S^0,0,0,0)$ and the endemic equilibrium $H^{\ast }$, we rescale (4) with

$$x=\frac{K}{d_0}E(t)$$

$$y=\frac{K}{d_0}I(t)$$

$$z=\frac{K}{d_0}R(t)$$

$$\tau =d_{0}t\text{.}$$

Then we obtain the following

$$\begin{array}{cc}\frac{\mathit{dx}}{d\tau }\hfill & =\frac{\mathit{qx}}{\mathit{px}+\mathit{ry}}(B-x-y)-\mathit{Nx},\hfill \\ \frac{\mathit{dy}}{d\tau }\hfill & =b+\mathit{hx}-\mathit{wy}\hfill \\ \frac{\mathit{dz}}{d\tau }\hfill & =\mathit{Cy}-\mathit{gz}\text{.}\hfill \end{array}$$ (8)

where

$$q=\frac{\mathit{aK}\alpha }{d_0},$$

$$p=\frac{K(K+\alpha d_0)}{d_0}$$

$$r=\frac{K+\alpha d_0}{d_0}$$

$$N=\frac{d_0(d_0+\alpha )}{K}$$

$$B=\frac{\mathit{aK}}{d_0(d_0+\alpha )}$$

$$h=\frac{\gamma d_0}{K}$$

$$w=\frac{d_0+\mu +\beta }{K}$$

$$C=\frac{\beta d_0}{K}$$

$$g=\frac{d_0^2}{K}$$

Note: that the trivial equilibrium $(0,0,0)$ of system (8) is the disease-free equilibrium $H_0=(S^0,0,0,0)$ of system (1) and the unique positive equilibrium $(x^{\ast },y^{\ast })$ of system (8) is the endemic equilibrium $S^{\ast }$ of system (1) if and only if $q+\mathit{Nr}<0$, where

$$x^{\ast }=\frac{\mathit{wpB}-(q+\mathit{Nr})b}{w(q+\mathit{wp})+h(q+\mathit{Nr})}$$

$$y^{\ast }=\frac{b+{\mathit{hx}}^{\ast }}{w}$$

$$z^{\ast }=\frac{C(b+{\mathit{hx}}^{\ast })}{\mathit{gw}}$$

We first determine the stability and topological type of $(0,0,0)$. The Jacobian matrix of system (8) is

$$M_0=\left(\begin{array}{ccc}\hfill \mathit{Bq}-N\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill h\hfill & \hfill w\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill C\hfill & \hfill g\hfill \\ \hfill \hfill \end{array}\right)\text{.}$$

If $q+\mathit{Nr}=0$, then there exists a small neighborhood $N_0$ of (0, 0, 0) such that the dynamics of system (8) is equivalent to

$$\begin{array}{c}\frac{\mathit{dx}}{d\tau }=-\mathit{qxy}-x^2+O({(x,y,z)}^3)\hfill \\ \frac{\mathit{dy}}{d\tau }=b+\mathit{hx}-\mathit{wy}\hfill \\ \frac{\mathit{dz}}{d\tau }=\mathit{Cy}-\mathit{gz}\text{.}\hfill \end{array}$$ (9)

We know that $(0,0,0)$ is a saddle-node. Hence, we obtain the following result.

Theorem 3

The trivial equilibrium point of the system (1) possess the following properties.

• $(i)$ As a result the system is hyperbolic saddle, If $q+\mathit{Nr}<0$ .
• $(\mathit{ii})$ As a result the system is saddle node, If $q+\mathit{Nr}=0$ .
• $(\mathit{iii})$ As a result the system is stable hyperbolic node, If $q+\mathit{Nr}>0$ .

Proof

When $q+\mathit{Nr}<0$, we discuss the stability and topological type of the endemic equilibrium $(x^{\ast },y^{\ast },z^{\ast })$.

The Jacobian matrix of (8) at $(x^{\ast },y^{\ast },z^{\ast })$ is

$$M_1=\left(\begin{array}{ccc}\hfill \frac{({\mathit{px}}^{\ast }+\mathit{ry})+(B-x^{\ast }-y^{\ast })-N{({\mathit{px}}^{\ast }+{\mathit{ry}}^{\ast })}^2}{{({\mathit{px}}^{\ast }+{\mathit{ry}}^{\ast })}^2}\hfill & \hfill \frac{\mathit{rq}(B-x^{\ast }-y^{\ast })x^{\ast }}{{({\mathit{px}}^{\ast }+{\mathit{ry}}^{\ast })}^2}\hfill & \hfill 0\hfill \\ \hfill h\hfill & \hfill -w\hfill & \hfill 0\hfill \\ \hfill o\hfill & \hfill c\hfill & \hfill -g\hfill \end{array}\right),$$ (10)

where

$$\mathit{det}(M_1)=\frac{g\left(-w(({\mathit{px}}^{\ast }+\mathit{ry})(B-x^{\ast }-y^{\ast })-N{({\mathit{px}}^{\ast }+{\mathit{ry}}^{\ast })}^2)\right)}{{({\mathit{px}}^{\ast }+{\mathit{ry}}^{\ast })}^2}-\frac{\mathit{hrq}(B-x^{\ast }-y^{\ast })x^{\ast }}{{({\mathit{px}}^{\ast }+{\mathit{ry}}^{\ast })}^2}=\frac{-\mathit{gw}({\mathit{px}}^{\ast }+\mathit{ry})(B-x^{\ast }-y^{\ast })-\mathit{gN}{({\mathit{px}}^{\ast }+{\mathit{ry}}^{\ast })}^2-\mathit{hrq}(B-x^{\ast }-y^{\ast })x^{\ast }}{{({\mathit{px}}^{\ast }+{\mathit{ry}}^{\ast })}^2}\text{.}$$

The sign of $\mathit{det}(M_1)$ is arbitrate by

$$S_1\stackrel{\mathrm{\Delta }}{=}-\mathit{gw}({\mathit{px}}^{\ast }+\mathit{ry})(B-x^{\ast }-y^{\ast })-\mathit{gN}{({\mathit{px}}^{\ast }+{\mathit{ry}}^{\ast })}^2-\mathit{hrq}(B-x^{\ast }-y^{\ast })x^{\ast }\text{.}$$ (11)

Sice $q+\mathit{Nr}>0$ it show that $S1<0$. Which implies, $\mathit{det}(M1)<0$ and $(x^{\ast },y^{\ast },z^{\ast })$ is a node or a focus or a center. Also, for the stability of $(x^{\ast },y^{\ast },z^{\ast })$ we have the following result. □

Theorem 4

There is a unique local stability of $(x^{\ast },y^{\ast },z^{\ast })$ of system (8) , which is a stable node, when $q+\mathit{Nr}<0$ .

Proof

From $\mathit{tr}(M_1)$ we determined the stability of $(x^{\ast },y^{\ast },z^{\ast })$ is

$$\mathit{tr}(M_1)=\frac{({\mathit{px}}^{\ast }+{\mathit{ry}}^{\ast })(B-x^{\ast }-y^{\ast })-{({\mathit{px}}^{\ast }+{\mathit{ry}}^{\ast })}^2(N+w+g)}{{({\mathit{px}}^{\ast }+{\mathit{ry}}^{\ast })}^2}$$

To determined the sign of $\mathit{tr}(M_1)$, we take

$$S_2=-({\mathit{px}}^{\ast }+{\mathit{ry}}^{\ast })(x^{\ast }+y^{\ast }-B)\text{.}$$

Let assume that $S_2=0$. then $q+\mathit{Nr}<0$. Therefore $S_2\ne 0$, which follow that $\mathit{tr}(M1)\ne 0$. Therefore for any positive values of parameters and $q+\mathit{Nr}<0$ does not change the stability of $(x^{\ast },y^{\ast },z^{\ast })$. Which implies that $\mathit{tr}(M1)<0$ for $q+\mathit{Nr}<0$. This completes our conclusion. □

The following theorem concluding the results for the mathematical analysis of the original system (1) can be established.

Theorem 5

From (2) we define $R_0$ .

• $(i)$If ${\mathcal{R}}_0<1$, the model (1) have $H_0=(\frac{a+b}{d},0,0,0)$, has a unique disease-free equilibrium, which is a global attractor in the first octant.
• $(\mathit{ii})$If ${\mathcal{R}}_0=1$, then model (1) has a unique disease-free equilibrium $H_0=(\frac{a+b}{d},0,0,0)$ which is a attracts of all orbits in the interior of the first octant.
• $(\mathit{iii})$If ${\mathcal{R}}_0>1$, then model (1) has two equilibria, a disease-free equilibrium $H_0=(\frac{a+b}{d},0,0,0)$ and an endemic equilibrium $H^{\ast }(t)=(S^{\ast }(t),E^{\ast }(t),I^{\ast }(t),R^{\ast }(t))$. The endemic equilibrium $H^{\ast }(t)$ is a global attractor in the interior of the first octant.

Numerical results and conclusion

We present in this section numerical simulation for system (4). First we use nonstandard finite difference (NSFD) scheme [47] to write the model in difference form as: consider first equation of model (4)

$$\frac{\mathit{dS}(t)}{\mathit{dt}}=a-\mathit{KI}(t)S(t)(1+\alpha I(t))-d_{0}S(t)$$ (12)

which is decomposed in NSFD scheme as

$$\frac{S_{j+1}-S_j}{h}=a-{\mathit{KI}}_j(t)S_j(t)(1+\alpha I_j(t))-d_0{S}_j(t)$$ (13)

Like (13), we can decomposed the model (4) in NSFD scheme and write the whole system as

$$\begin{array}{cc}\hfill S_{j+1}=& S_j+h\left(a-{\mathit{KI}}_j(t)S_j(t)(1+\alpha I_j(t))-d_0{S}_j(t)\right)\hfill \\ \hfill E_{j+1}=& E_j+h\left({\mathit{KI}}_j(t)S_j(t)(1+\alpha I_j(t))-(d_0+\gamma )E_j(t)\right)\hfill \\ \hfill I_{j+1}=& I_j+h\left(b+\gamma E_j(t)-(d_0+\mu +\beta )I_j(t)\right)\hfill \\ \hfill R_{j+1}=& R_j+h\left(\beta I_j(t)-d_0{R}_j(t)\right)\text{.}\hfill \end{array}$$ (14)

Using the scheme developed in (14) and we plot the model corresponding to the given values as.

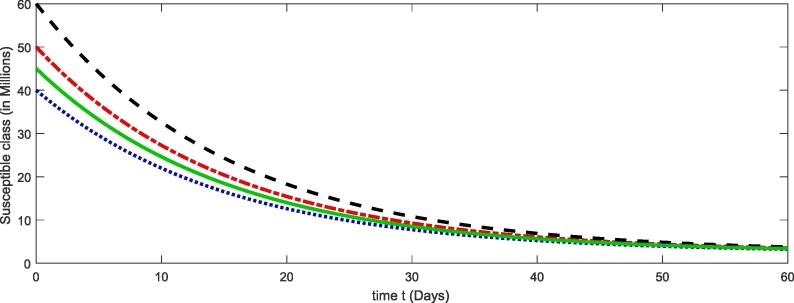
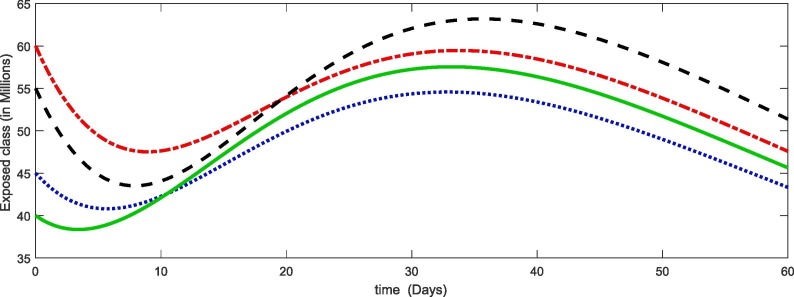
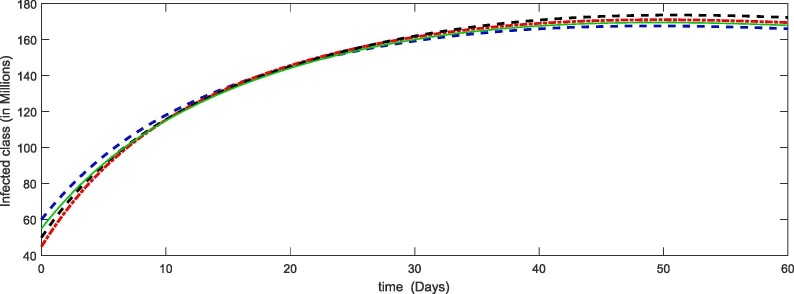
From Fig. 1, Fig. 2, Fig. 3, Fig. 4 , we have plotted the different compartment of the model corresponding to different initial values. As susceptibility is decreasing which caused the increase in exposure and hence the infection also increasing. Due to more death cases together with cure the recovery class also increasing. see Table 2 .

Fig. 1.

Plots of susceptible compartment for the given initial values of the considered model (4).

Fig. 2.

Plots of exposed compartment for the given initial values of the considered model (4).

Fig. 3.

Plots of infected compartment for the given initial values of the considered model (4).

Fig. 4.

Plots of recovered compartment for the given initial values of the considered model (4).

Table 2.

The physical interpretation of the parameters and numerical values.

Parameters	The physical interpretation	Numerical value
a	The population who test is negative	0.73 Millions
$d_0$	Natural death	0.02
$\mu$	Death due to corona	0.0009
b	The population who test is positive	0.06003
$\alpha$	Individuals lose immunity	0.00009
K	Proportionality constant	0.098601
$\gamma$	Infection rate	0.00007
$\beta$	Recovered rete	0.01

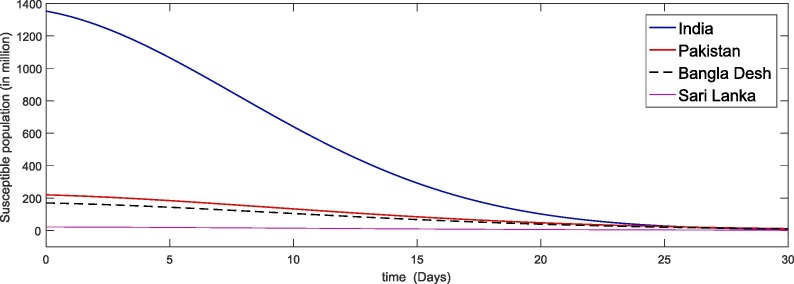
Now with the values we use are given in Table 3 are taken from WHO [46] about the four countries India, Pakistan, Bangla Desh and Sari Lanka respectively as: as

Table 3.

The physical interpretation of the parameters and numerical values.

Parameters	The physical interpretation	Numerical value
$S_0(t)$	Initial susceptible class	1353, 220, 170, 21.6 Millions
$E_0(t)$	Initial exposed class	800, 100, 70, 10 Millions
$I_0(t)$	Initial infected class	0.027977, 0.013328, 0.005149,0.000523 Millions
$R_0(t)$	Initial recovered class	0.007407, 0.003310, 0.000267, 0.000127 Millions

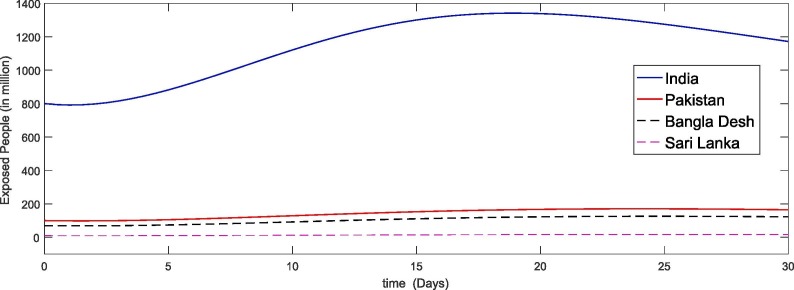
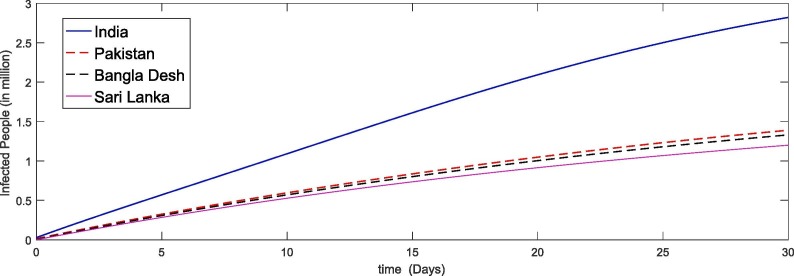
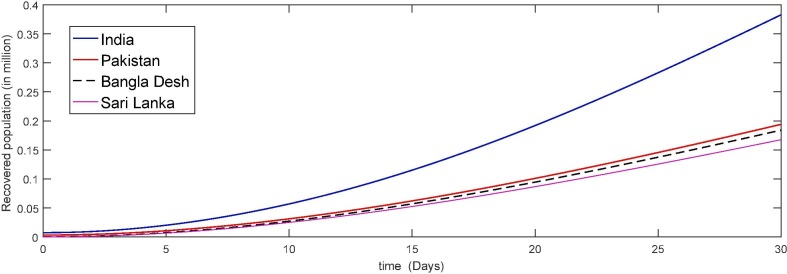
In Fig. 5, Fig. 6, Fig. 7, Fig. 8 we simulate the results for the last thirty days in the four different countries of the world. We see that due to large papulation the precipitability ratio in India is fastest than the other three countries as in Fig. 5 and then the second number is of Pakistan and so on. As the susceptible compartment deceasing the papulation of more people is going to exposed and hence the infection rate is also increasing with rapid increase in India due to large papulation. In Pakistan, Bangla Desh the infection flow is more faster than Sari Lanka as shown in Fig. 6, Fig. 7 respectively. Further the recovered class is also increasing which is either due to death or getting ride from infection. Here again the death ratio in India is faster than the other three countries as in Fig. 8.

Fig. 5.

Plots of susceptible compartment for the given initial values of the considered model (4).

Fig. 6.

Plots of exposed compartment for the given initial values of the considered model (4).

Fig. 7.

Plots of infected compartment for the given initial values of the considered model (4).

Fig. 8.

Plots of recovered compartment for the given initial values of the considered model (4).

Conclusion

We have established a four compartments model for the description of the current COVID-19. We have established global and local dynamics for the constructed model. Further we have simulated the results by using nonstandard finite difference scheme. In last, we have testified the results by a real data of four different countries. We concluded that the infection spread in these four countries with different rate. In India and Pakistan the ratio is fast as compared to the other two countries because huge papulation produce greater chance to more people infected.

CRediT authorship contribution statement

Rahim ud Din: Data curation, Writing - original draft. Aly R. Seadawy: Conceptualization, Methodology, Writing - review & editing. Kamal Shah: Visualization, Investigation, Software, Validation. Aman Ullah: Software. Dumitru Baleanu: Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.