Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Oct 1;5(40):25723–25732. doi: 10.1021/acsomega.0c03016

Effects of the van der Waals Interactions on Structural and Electronic Properties of CH3NH3(Pb,Sn)(I,Br,Cl)3 Halide Perovskites

Narasak Pandech †,‡, Thanundon Kongnok †,‡, Nirawith Palakawong †,‡, Sukit Limpijumnong †,§, Walter R L Lambrecht ∥, Sirichok Jungthawan †,‡,⊥,*
PMCID: PMC7557212  PMID: 33073098

Abstract

graphic file with name ao0c03016_0011.jpg

In hybrid perovskite materials like CH3NH3PbI3, methylammonium (MA) lead iodide (MAPI), the orientation of the MA+ cations and their ordering can significantly affect the structure of the inorganic framework. Although the states near the band edges are known to be primarily derived from the Pb and halogen orbitals rather than from the organic ion, the latter may have an indirect effect through their impact on the structural relaxation. In this work, we investigate both the structural relaxation effects of the inorganic framework in response to the MA+ orientation and their impact on the electronic structure near the band edges. Calculations are performed for MA(Pb,Sn)X3 with (X = I, Br, and Cl) materials for both Pb- and Sn-based compounds. The work focuses on the high-temperature α-phase, which is nominally cubic if averaged over all possible MA orientations and in which no alternating rotations of the octahedral occur, so that the unit cell is the smallest possible. The effects of van der Waals (vdW) corrections to density functional theory on the structural relaxation are investigated. Our results reveal that the vdW interactions between the MA+ cation and the inorganic framework can strongly affect the optimized orientation and position of the molecule and the resulting distortion of the inorganic framework. Consequently, it also affects the electronic properties of the materials and specifically can change the band structure from direct to indirect band gaps. The robustness of this result is studied by comparing hybrid functional calculations and quasiparticle self-consistent GW calculations as well as spin–orbit coupling.

Introduction

Perovskites are crystalline materials with an ABX3 structure similar to the CaTiO3 mineral. The A-site cations are 12-fold coordinated, and divalent B-site cations are 6-fold coordinated. In the class of organic–inorganic halide perovskite materials, the A-site is a monovalent organic cation, for example, methylammonium (CH3NH3+, MA+), the B-site is a divalent metal, for example, Pb2+, Sn2+, Ge2+, and the X-site is occupied by the halogen ions, for example, I–, Br–, and Cl–. Recently, hybrid halide perovskite materials have emerged as new promising materials in photovoltaic applications. This class of materials has been known for a long time and has been studied in relation to their very particular dielectric properties.1 However, the first application of organo-halide perovskite materials in photovoltaics can be traced back to 2009, with the work of Kojima and co-workers.2 After the pioneering work, the number of applications of the hybrid perovskite in photovoltaics rapidly increased, especially in the case of lead-halide perovskite materials.3−5 Notably, the solar cell efficiencies of halide perovskites have remarkably risen to about 20% such that they are a good alternative to Si solar cells.6−8 However, their stability and structural transformations remain a challenge.

The crystal structures of Pb- and Sn-based halide perovskite materials are temperature-dependent. Their exact structures are still under dispute because of the complexity introduced by the MA+ cation group. Experimentally, many research groups have attempted to identify the structures of the materials using neutron powder diffraction and also synchrotron X-ray powder diffraction.5,9 At high temperature, the α-structure is cubic (with the space group Pm3̅m if the molecular orientations are ignored or MA is replaced by a symmetric Cs ion). However, the Pb or Sn ferroelectric displacement in its octahedron or the MA in-phase orientation can lead to a non-centrosymmetric tetragonal P4mm space group.3 The β-phase occurs by alternatingly tilting the octahedra clock and counterclockwise about a single axis, thereby doubling the unit cell to a 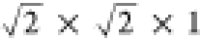Inline graphic cell and making the system tetragonal. In CsSnI3, this leads to the P4/mbm group because the tilts are in phase in the c-direction. However, with the additional ferroelectric symmetry breaking of the MA ions, the space group becomes I4cm.3 Others however assigned the I4/mcm spacegroup5 to this phase in MAPbI3. This phase occurs in SrTiO3 where it also exhibits rotation of the octahedra about the z-axis but which alternates between clockwise and counterclockwise along the c-axis, thereby doubling the cell again to Inline graphic. On the other hand, the I4/mcm phase which does maintain an inversion symmetry could also result from alternating the MA dipole orientations.10 The transition temperature to this phase depends on the material and occurs at ∼180 K in MAPbI35 and 200 K in MASnI3.3 Finally, a second transition occurs at a lower temperature to an orthorhombic γ-phase in which octahedral tilts occur about two orthogonal axes, and the cell is doubled in the c-direction. The full space group determination in this phase has not been achieved for the different organic ions but is Pnma in the case of the symmetric A ion and is thus assumed to be derived from this phase.5 In MAPbI3, this transition occurs between 100 and 150 K,5 while for the Sn case, it occurs closer to 100 K.3 In the low-temperature structure, the BX6 octahedra are strongly deformed and restrict the rotational motion of MA+ cations.5 In this case, the organic cations are fully ordered and pinned and can rotate only along the C–N axis.5,9 When the temperature increases, tetragonal and cubic structures appear. In the high-temperature structures, the organic cations become free to rotate inside the dodecahedral cages, and they are disordered.5,9 Nuclear magnetic resonance measurements11 have shown that the probable location of the MA cations cannot be determined in the cubic phase, and the reorientation time of the MA cations is in the order of picoseconds. Therefore, the presence of organic molecules and their mobility are a challenge in the study of these types of materials.

In organic–inorganic halide perovskite materials, the MA-cation groups reside within the network of corner-sharing BX6 octahedra and are stabilized by van der Waals (vdW) interactions. Some previous theoretical works12−15 have already revealed the importance of the presence of dispersive forces in these types of materials on structural properties. The effect of the MA orientations on the electronic structure is less clear. Because the states near the band edges are either Pb-s, I-p mixed at the valence band maximum (VBM) or Pb-p like at the conduction band minimum (CBM), one may think that the MA has little effect on them. On the other hand, the MA orientations can affect the overall symmetry and this may lead to splitting of the CBM.

In this work, we conducted vdW-corrected density functional theory (DFT) calculations to examine the importance of vdW interactions on the MA-cation structural parameters and consequently to examine the electronic properties of the MABX3 (B = Pb, Sn; X = I, Br, Cl) halide perovskite materials. Our results reveal that the inclusion of the vdW interactions in DFT calculations affects the MA-cation orientation, which influences the structural properties of the inorganic network and consequently affects the electronic properties of the materials. Because the Perdew–Burke–Ernzerhof (PBE) and even vdW-corrected DFT can significantly underestimate the gap, we also conduct calculations of the same structures using the quasiparticle self-consistent GW (QSGW) method. Finally, spin–orbit coupling (SOC) is known to be important in particular in the Pb-based compounds. Thus, we study the effect of both GW self-energy corrections and SOC on the electronic structure in relation to the orientation of the MA molecules and their corresponding induced structural distortions. The SOC in combination with the electric field-induced symmetry breaking arising from the dipolar molecules leads to the Rashba effect, which can affect the location of CBM in k-space.

Results and Discussion

Structural Relaxation

Before we go into our calculated results, we want to refer to two previous studies of the molecular orientations in the cubic phase of MAPbI3 that are particularly relevant to our study. Motta et al.16 performed a full structural optimization of MAPbI3 within generalized gradient approximations (GGAs) including vdW corrections. It has been found that the results are sensitive to the initial orientation of the molecule being along [100] or [111]. In the former case, the molecule rotates toward a [110] or equivalent direction, while in the latter case, it remains in the [111] direction. Both the [110] and [111] orientations thus appear to be the favored orientations. We here extend that approach to the other halogens and to the case of Sn instead of Pb. Bechtel et al.,17 on the other hand, took a more systematic approach for mapping out the energy landscape. They define all possible rotation degrees of freedom of the molecule, defined by a polar angle θ and azimuthal angle ϕ of the C–N axis of the molecule versus the [001] and [100] cubic axes, the rotation angle α of the molecule about its own axis, and the displacement of the molecule from its center along its own axis. They then map out the energy of the molecule as a function of these variables but while keeping the inorganic framework fixed. They found that the molecule translates along its own direction away from the nominal center of the dodecahedral site, in other words, the displacement of the molecule is important. The favored orientations found in this work are close [100] and [111] directions. Consequently, the initial orientation of the molecule for structural relaxations is either [100], [110], or [111] direction. The molecule and the framework are fully allowed to relax. Subsequently, we also performed calculations with constraint where the position of the molecule is kept at some angle as in the energy landscape studies of Bechtel et al.,17 but the inorganic framework is allowed to fully relax along with the possible displacement of the molecule relative to the framework. All of these calculations were then performed with and without vdW corrections to ascertain their importance. After discussing the structural results, we will then examine their effect on the electronic band structure in the next section. Ferroelectric ordering was found to be slightly preferable energetically by Quarti et al.10 On the other hand, Weller et al.5 indicate the disordered alternating non-polar orientation of the MA molecules.

Let us start the discussion by presenting the relaxed crystal geometries. Initially, the structural optimizations have been performed at the level of the GGA–PBE calculations with and without including the vdW interactions for revealing the effects of internal interactions between the organic cation and the BX6 inorganic framework. We perform a full structural relaxation without any symmetry constraints from the ideal cubic perovskite structure with staggered H-atoms arrangement (the H-atoms on the C-end and on the N-end are not aligned with each other but rotated with respect to each other by 60°) adopted from Motta et al.’s calculation,16 as depicted in Figure 1. The relaxations have been performed with various initial configurations of the MA cation, namely, oriented along the [100], [110], or [111] directions, as listed in Table 1. We note that the relaxation process is extremely sensitive to the initial MA-cation orientation. For example, when we started the relaxation with the MA+ cation oriented along the [111] direction, the relaxed structure preserves its original MA+ cation orientation in both cases of with and without including vdW interactions, as depicted in Figure 2c,d, respectively. This result is similar to that of Motta et al.16 The calculated change in angle (Δθ) of the C–N axis with respect to its initial orientation direction is very small, as shown in Table 1. In contrast, if we start the structural relaxation with the MA+ cation oriented along the [100] direction, the relaxed structure does not preserve its original MA+ cation orientation, instead, it may end up with the MA+ cation orientated along the [10–1] direction, as depicted in Figure 2a,b. The reason why particularly the [10–1] direction is favored as opposed to the in-principle equivalent [1±10] or [101] depends on the particular chosen orientation of the molecule about its own axis. As we will show later, the H atoms are in such positions to favor rotating in this particular direction by optimizing the hydrogen bonds with the halogen. This is why the vdW interactions are important in the structural optimization of these types of materials. In this case, the MA+ cation shifts down along the x–z plane (see the inset of Figure 3) with the change in angle, (Δθ) around 18° (in the case of MAPbI3) when including the vdW interaction, as shown in Table 1. However, if one does not include the vdW interaction in the calculation, the calculated Δθ in this case is around 7.8° and the relaxed structure is less distorted, as shown in Figure 2b. Including the vdW interaction, the calculated Δθ of the C–N axis with respect to the [100] direction increases when the halogen atom is changed from I– to Br– to Cl– in both Pb- and Sn-based cases, as shown in Figure 3. The increase of the angle indicates a stronger interaction between the organic MA+ cation and the BX6 inorganic framework and causes the relaxed structure to become more distorted, as indicated by a B–X–B bond angle tabulated in Table 1. The calculated lattice parameters, when including the vdW interaction, are in very good agreement with the experimental values, with an error less than 1%. If the calculation does not include the vdW interaction, the calculated lattice parameters are larger than the experimental values by an error more than 3%. The calculated lattice constants of the MAPbX3 (X = I, Br, and Cl) with vdW-included are 6.34, 5.96, and 5.71 Å which are in good agreement with the experimental values of 6.33, 5.90, and 5.67 Å, respectively.1 For the MASnX3 (X = I, Br, and Cl), the calculated lattice constants with vdW-included are 6.25, 5.89, and 5.68 Å, which are also in good agreement with the experimental values of 6.23, 5.88, and 5.67 Å, respectively.3,18

Figure 1.

Figure 1

Open in a new tab

Illustration of the ideal cubic structure of CH3NH3BX3 with staggered H-atoms arrangement in CH3NH3 molecule which is oriented along the [100] direction viewed along (a) b-crystallographic axis and (b) arbitrary crystallographic axis. Green, cyan, blue, orange, and red spheres represent the B-site atoms, X-site atoms, N-atoms, C-atoms, and H-atoms, respectively.

Table 1. Calculated Lattice Constants a, b, and c (Å), Unit Cell Volume V (Å3), Deviate Angle from the Given Initial MA Orientation, Δθ (in Degree), Relative Energy (Rel. Energy, in meV), B–X–B Bond Angle (in Degree), and Hydrogen Bond Length (Å) of MABX3a.

    calculated structural parameters
   H-bonding
compounds int. MA orient. rel. energy Δθ a b c V B–X–B bond angle HN–X HC–X
MAPbI3 [100] 0.00 18 (7.8) 6.34 (6.48) 6.30 (6.43) 6.38 (6.49) 254.7 (270.2) 169.5 (174) 2.72 (2.8) 3.36 (3.6)
  [110] 14.4 9 (5.6) 6.34 (6.48) 6.40 (6.57) 6.27 (6.32) 252 (270.4) 175 (175) 2.75 (2.8) 3.40 (3.6)
  [111] 21.0 0.9 (0.5) 6.34 (6.47) 6.34 (6.47) 6.34 (6.47) 255.3 (270.4) 178 (178) 2.71 (2.7) 3.38 (3.6)
MAPbBr3 [100] 0.00 23 (12.7) 5.94 (6.03) 5.89 (6.03) 6.03 (6.13) 211 (222.8) 169.1 (172) 2.45 (2.5) 3.31 (3.4)
  [110] 18.6 6.8 (4.6) 5.98 (6.08) 5.98 (6.08) 5.89 (6.03) 209.8 (221) 174 (173) 2.55 (2.5) 3.50 (3.5)
  [111] 35.4 0.9 (1.2) 5.97 (6.08) 5.97 (6.08) 5.97 (6.08) 212.7 (223.4) 177 (177) 2.41 (2.5) 3.10 (3.5)
MAPbCl3 [100] 0.00 26 (17.5) 5.67 (5.74) 5.63 (5.73) 5.79 (5.90) 184.7 (193.8) 168 (171) 2.3 (2.4) 3.17 (3.2)
  [110] 23.1 6.6 (4.6) 5.73 (5.83) 5.73 (5.83) 5.63 (5.73) 184.2 (193.9) 174 (175) 2.3 (2.4) 3.3 (3.2)
  [111] 46.4 0.8 (1.3) 5.73 (5.83) 5.73 (5.83) 5.73 (5.83) 187.6 (197.2) 175 (176) 2.3 (2.4) 2.9 (3.2)
MASnI3 [100] 0.00 20.1 6.26 6.19 2.27 243 172 2.7 3.3
  [110] 6.4 8.5 6.26 6.26 6.17 241.3 172 2.8 3.4
  [111] 20.3 0.01 6.24 6.24 6.24 243.4 177.4 2.7 3.3
MASnBr3 [100] 0.00 26.5 5.89 5.80 5.95 202.9 170.6 2.43 3.2
  [110] 9.00 8.6 5.91 5.91 5.80 201.6 171 2.45 3.1
  [111] 34.6 0.03 5.88 5.79 5.95 204.5 176 2.47 3.05
MASnCl3 [100] 0.00 28.4 5.72 5.55 5.75 182.6 171 2.25 2.89
  [110] 8.92 4.6 5.71 5.71 5.54 179.2 172 2.25 2.86
  [111] 33.17 0.03 5.70 5.70 5.70 185.4 176 2.26 2.85
Open in a new tab
a

The numbers in parenthesis are obtained without including vdW.

Figure 2.

Figure 2

Open in a new tab

Illustration of relaxed structures of the cubic CH3NH3PbI3 with and without vdW interactions (left and right panels, respectively) for different orientations of the MA+ cation. (a,b) Relaxed structure of the MA cation initially oriented along the [100] direction. (c,d) Relaxed structure of the MA cation initially oriented along the [111] direction. The pictures are viewed along the y-axis or showing the x–z plane.

Figure 3.

Figure 3

Open in a new tab

vdW-calculated tilting angle of the MA cation with respect to the initial [100] orientation (Δθ), as represented in an inserted picture.

If we focus on the relaxed structures, the significant difference between these structures is the deformation of the BX6 octahedra. In the case of initial [100] orientation, the relaxation of the MA+ cation induces the deformation and the symmetry reduction of the inorganic BX6 octahedra. Such distortion causes the B–X–B bonds to not lie parallel to the crystal directions but instead be slightly tilted by ∼10° from the ideal cubic structure when the vdW interaction is included (see Table 1). However, when excluding vdW interactions, they only tilted by ∼5° from the ideal cubic structure. In the case of [111] orientation, the B–X–B bond angles are very close to 180°, indicating that the relaxed structure preserves a high symmetry cubic structure. In this case, the relaxed structure of the [111] orientation is still simple cubic (see Table 1). In contrast, the relaxed structure of the initial [100] orientation becomes tetragonal (c/a ≠ 1).

Additionally, the hydrogen bond lengths were calculated and are listed in Table 1. The results show that the hydrogen atoms on the NH3-side are closer to the BX6 inorganic framework than those of the CH3-side. It can be implied that the hydrogen atoms in NH3-side dominate the strong interaction with the BX6 inorganic framework. Although the relaxed structure is sensitive to the initial MA+ cation configuration, it is worth noting that the energy difference between these configurations is very small. The energy difference is calculated to be in the 21–50 meV range in favor of a direction near the [10–1] direction (tilted from [100] by Δθ ∼ 18° in the case of MAPbI3), which is consistent to the previous studies of MAPbI3.16,17 The lowest energy structure we found (MAPbI3 case) is consistent with the lowest energy structure calculated by Qiaoling Xu et al.19 using 2 × 2 × 2 supercell calculations, the MA cations are found in favored orientation to the [012] direction with the relative energy of ∼60 meV per formula unit. Indeed, it can be implied that these MA+ cation configurations represent the local energy minima.

After the full structural relaxation of the initial [100] orientation has been carried out, it is still unclear why the MA+ cation rotated downward in the x–z plane instead of other directions. Therefore, we have chosen the MAPbI3 case as an example for further study. We performed the ground state energy calculation as a function of the rotational angle of the C–N axis with respect to the [100] direction, including the vdW interactions. Several pathways, namely, [100] → [10–1], [100] → [110], and [100] → [111] are considered. In the calculations, the staggered H-atoms arrangement is applied, the C–N axis and C–N bond length are fixed at each rotational angle while the other atoms and cell volume are allowed to relax. The calculated energies as a function of rotational angle in different pathways are depicted in Figure 4. From the plot, we can see that the calculated energies in the [100] → [10–1] pathway decrease until the rotational angle is around 20° and then the energy increases. This is consistent with the full unconstrained minimization presented above. At the lowest energy structure, three hydrogen atoms in NH3-side bond with I– atoms almost equally, as depicted in Figure 4a. The energy difference between [100] and [10–1] orientations is very small, 3.5 meV. On the other hand, the calculated energies in the [100] → [110] pathway slightly fluctuate with the rotational angle and end up with the energy 10 meV higher than that of the [100] orientation. In this case, at the lowest energy point, one of the hydrogen atom in NH3-side bonds with the I– atom stronger than other two hydrogen atoms, as depicted in Figure 4b. In the case of the [100] → [111] pathway, the calculated energy slightly increases and then decreases until the rotational angle is around 22°, then increase and end up with the energy 9 meV higher than that of the [100] orientation. In this case, at the lowest energy structure, two of hydrogen atoms on the NH3-side present stronger bonds with the I– atoms than the other hydrogen atom, as depicted in Figure 4c. The lowest energies along the [100] → [110] and [100] → [111] pathways are ∼7 meV higher than along the [100] → [10–1] pathway. In addition, we can see that the energy difference in the 15–25° range of the [100] → [10–1] pathway is very shallow, indicating several local minima around that point. The difference in these different pathways lies in the way that the molecule’s H-atoms are positioned relative to the halogen atoms along these paths. The more complex behavior for other than the optimal rotation pathway (a) shows that there is some optimal orientation of the molecule about its own axis such that it best optimizes the H bonds with the halogens.

Figure 4.

Figure 4

Open in a new tab

(a−c) Calculated relative energy and (d−f) variation of the band gap, for MAPbI3 case, as a function of the rotational pathway of the C–N axis with respect to the [100] direction. (a,d) [100] → [10–1], (b,e) [100] → [110], and (c,f) [100] → [111]. The C–N atoms are fixed at each rotational angle, while the other atoms are allowed to relax. The inserts show the orientation and the hydrogen bond lengths (red dashed lines) that can be formed with the nearest halogen atoms near the minimum configuration.

From our calculated ground state energies in different pathways, we conclude that the fully structural relaxation process of the initial [100] orientation with the given staggered H-atoms arrangement, including the vdW interaction, ends up with the MA+ cation rotated downward in the x–z plane from [100] toward [10–1] in a local minimum energy near the [10–1] direction with the deviate angle, Δθ, listed in Table 1.

Electronic Properties

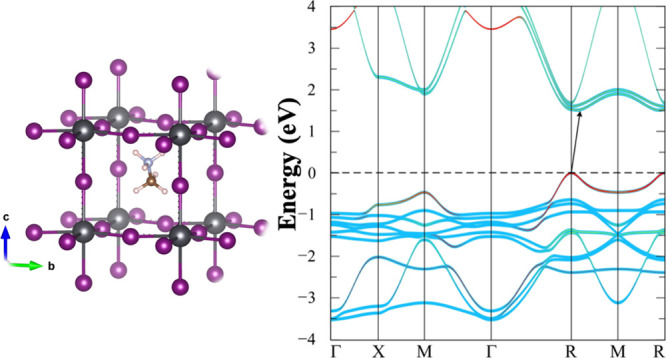
The significant differences in the structural geometries are expected to impact on the electronic structure of the studied MABX3. First, let us pick MAPbI3 as an example to explain the effect of the vdW interaction on the electronic properties of the studied materials. The electronic band structures along the high symmetry points of the Brillouin zone calculated by using the GGA–PBE without SOC with different MA+ cation orientations of the MAPbI3 are depicted in Figure 5. Our GGA–PBE calculated band structures reveal that the orientations of the MA+ cation have a profound impact on the nature of the band gap of MAPbI3. In the case of the [111] orientation, the relaxed structure keeps the high symmetry of the cubic structure and gives the direct band gap at the R-point (0.5, 0.5, 0.5) of the Brillouin zone both with and without vdW interactions, as depicted in Figure 5b,d. On the other hand, in the case of the initial [100] orientation, the relaxed structures are strongly distorted due to the cation rotation and consequently affect the band structure: the CMB shifts along the R → Γ line, the band gap becomes indirect, as depicted in Figure 5c. These results are in good agreement with Motta et al.16 Please note that the Grimme DFT-D3 approach changes the total energy and hence relaxation but not the exchange correlation potential used for the band structure calculations. In the case of exclusion of vdW interactions, the calculated band gap remains direct for both [100] and [111] orientations, as depicted in Figure 5a,b, respectively. This indicates that the relaxed structures do not present enough distortion to modify the band structure significantly, and the vdW correction is necessary for the structural relaxation of the halide perovskite systems.

Figure 5.

Figure 5

Open in a new tab

Calculated band structures without SOC of the CH3NH3PbI3 for (a,b) PBE without including vdW, (c,d) PBE with including vdW, and (e,f) Heyd–Scuseria–Ernzerhof (HSE) with including vdW. Left and right panels represent the MA+ cation initially orientated along [100] and [111] directions. The red, skyblue, and lime colors of each band represent the spd-projected wavefunction character of s, p, and d orbitals, respectively. The calculated VBM energies were shifted to zero.

The vdW-calculated band gap without SOC of MAPbI3 lies in the 1.45–1.55 eV (see Table 2) range close to the experimental value of about 1.55 eV,2,20 while the calculated band gap without vdW-interaction lies in 1.6–1.7 eV, slightly larger than the experimental values. The GGA–PBE calculations usually underestimate the band gap of semiconductors. However, as already shown in the case of MAPbI3,21 the agreement here is due to a fortuitous cancellation of the errors of the GGA underestimated band gap and the lack of spin–orbit interactions which would tend to overestimate the gap. To test the robustness of the indirect band gap, we also used the HSE06 hybrid functional to calculate the electronic band structures of the MAPbI3 by using the GGA–PBE + vdW-relaxed structures. The band structures of the MAPbI3 calculated by the HSE-functional without SOC are also depicted in Figure 5e,f, and we can see that the indirect band gap persists when the screened hybrid functional is included. However, the calculated band gap of the MAPbI3 by using the HSE06 lies in the range of 1.90–1.95 eV (see Table 2), larger than that one from the experimental value, as expected.

Table 2. Calculated Band Gaps (in eV) of the Studied MABX3 Compounds for Different MA Orientations at Varying Levels of Approximation and Compared with the Available Experimental Dataa.

      calculated band gap (eV)
    
compounds int. MA orient. PBE PBE+SOC HSE QSGW QSGW+SOC expt.
MAPbI3 [100] 1.55 0.47 1.99 2.47 1.79 1.55
  [110] 1.50 0.48        
  [111] 1.45 0.44 1.95 2.40 1.65  
MAPbBr3 [100] 1.93 0.84 2.51 3.13 2.55 2.30
  [110] 1.86 0.84        
  [111] 1.80 0.70 2.43 3.01 2.28  
MAPbCl3 [100] 2.41 1.30 3.10 3.91 3.49 2.90
  [110] 2.30 1.33        
  [111] 2.31 1.23 3.04 3.80 3.33  
MASnI3 [100] 0.50 0.10 1.29     1.20
  [110] 0.47 0.10        
  [111] 0.49 0.10 1.26 (0.77)      
MASnBr3 [100] 0.76 0.32 1.90     2.14
  [110] 0.76 0.38        
  [111] 0.75 0.30 1.88      
MASnCl3 [100] 1.83 1.46 3.10     3.6
  [110] 1.33 1.03        
  [111] 1.49 1.06 2.94      
Open in a new tab
a

Note: the HSE band gaps of Pb-based are obtained with 25% exact exchange, while the HSE band gaps of Sn-based are obtained with 55% exact exchange based on the experimental band gap of MASnI3, and a number in parenthesis is obtained with 25% exact exchange.

We note that indirect gaps or, more specifically, a displacement of the CBM away from the high symmetry point has previously been obtained due to the Rashba15 effect. However, the results here are obtained without SOC and thus have a different origin: namely the distortions of the inorganic framework in response to the orientation of the MA molecules. The B-6p contributes to the CMB, while the X-5p and B-6s contribute to the VMB of these materials. From our calculated results, it is clear that the molecular orientation can strongly influence the electronic structure of the hybrid perovskites by affecting the X–B–X inorganic framework which take part in the frontier orbital and a little bit change the band gap of the materials, which will be discussed in the next section.

For the other studied compounds, the direct band gaps are also found in the case of the [111] orientation, while the indirect band gaps are found in all cases of distorted BX6 octahedral due to the cation rotation. However, the GGA–PBE calculations now underestimate the band gap, as shown in Table 2, when compared with the experimental values. This shows that the good agreement for MAPbI3 is really a coincidence, and less perfect cancellation of errors occurs in the other cases. The full band structures in GGA–PBE without SOC have significant errors even for methylammonium lead iodide. The electronic band structures of the other compounds are depicted in Figure 6. We can also see that the indirect band gaps persist for all studied compounds in the case of initial [100] orientation when the screened hybrid functional is included. The HSE-calculated band gap without SOC of MAPbBr3 and MAPbCl3 lies between 2.43 and 2.51 eV and 3.04 and 3.10 eV, respectively (see Table 2), which is slightly larger than the experimental values. The HSE-calculated band gap without SOC of Sn-based compounds lies in the 1.26–1.29 eV range for MASnI3, 1.88–1.90 eV for MASnBr3, and 2.94–3.10 eV for MASnCl3 which is slightly smaller than the experimental values (see Table 2).

Figure 6.

Figure 6

Open in a new tab

HSE-calculated band structures without SOC of the other studied compounds. (a,b) for MAPbBr3, (c,d) for MAPbCl3, (e,f) for MASnI3, (g,h) for MASnBr3, and (i,j) for MASnCl3. Left and right panels represent the MA+ cations initially orientated along [100] and [111] directions, respectively.

While the above study indicates that the indirect gap found in the structures obtained from the initial [100] direction of the molecule is robust when considering different functionals, we need to further study the combined effect of SOC and the gap corrections beyond semilocal functionals. In fact, the distortion-induced shift of the CBM may be related to the closeness of the bands which remain nearly degenerate at the R-point when SOC is neglected. One might expect that adding SOC could remove this effect. However, when we add SOC alone without using hybrid functionals to open the gap, the latter will be so strongly reduced that the CBM is then close to the VBM and this may then lead to other artifacts. Instead of combining HSE with SOC, we decided here to use the QSGW+SO because it is in principle an even more accurate approach.

The band structures of the Pb-based compounds in QSGW approximation and at the GGA–PBE-relaxed structures are shown in Figure 7. We can see from our calculated results that the QSGW band structures of the initial [111] MA orientation exhibit the direct band gap at R-point both with and without SOC. On the other hand, the QSGW band structures of the near [10–1] MA+ orientation are different: the CBM is slightly shifted from R → Γ as found in our DFT band structures without SOC. This indirect nature is already obtained in QSGW even without SOC. Nonetheless, the band structures are still substantially different when SOC is included, namely, they are spin-split and the origin of the indirect gap is now clearly affected by the Rashba effect.

Figure 7.

Figure 7

Open in a new tab

Calculated band structures in QSGW approximation with (red) and without (blue) SOC of the (a,b) CH3NH3PbI3, (c,d) CH3NH3PbBr3, and (e,f) CH3NH3PbCl3. Left and right panels represent the MA+ cation initially orientated along [100] and [111] directions, respectively.

Our calculated QSGW band structures in the case of MAPbI3 are qualitatively consistent with the studies of Brivio et al.15 results in which the representative [100] configuration of the MA+ cation was selected. In their work, a similar spin-splitting of the CBM and a shift of the CBM away from the R-point is found. On the other hand, for a smaller NH4 molecule instead of the MA, this Rashba effect is not observed. This is because the NH4 molecule has a much smaller molecular dipole character than the MA molecule. In recent work, the size of this effect was studied as a function of local distortions obtained from molecular dynamics snapshots and found to be present even in CsPbI3 due to the possibility of local Pb off-centering which like the MA molecules also can lead to the required symmetry breaking to have a Rashba effect.15 Their calculated QSGW band gaps are 2.70 eV (SOC = 0) and 1.67 eV (added SOC). Our calculated band gaps in QSGW approximation are also listed in Table 2. We can see that the QSGW band gaps calculated without SOC are much larger than the experimental values, and the gaps are reduced by approximately 0.7 ± 0.1 eV when the SOC is considered. We note here that the orientations of the MA+ cation are found to have an important impact on the nature of the band gap also at the level of QSGW approximation.

To further describe the indirect band gap, let us define the energy difference between the CBM and the conduction band at R-point of the Brillouin zone, ΔE ≡ ER – ECBM, as shown by an inset in Figure 9. The PBE calculated ΔE of the studied compounds is depicted in Figure 9. From our calculated results, we can see that the ΔE of the Pb-based compounds is larger than that of the Sn-based compounds. This is resulting from the more distorted structure of the Pb-based compounds compared to the Sn-based ones. We note that the band gap shifting does not occur only with the [10–1] orientation, the indirect band gap does appear for the equivalent orientations, for examples, [10±1], [01±1], and [1±10]. In addition, in the case of the [101] orientation, the CBM shifts along the R → M line (Supporting Information, Figure S1).

Figure 9.

Figure 9

Open in a new tab

PBE-calculated energy difference, ΔE between the CBM and the conduction band at R-point (π/a, π/a, and π/a) of the Brillouin zone in the case of the indirect band gap.

The MA+ cation has often been assumed to not have any significant contribution to the electronic structure around the band edges. From our calculated DOS results of MAPbI3, it is obviously seen that the bottom of the conduction band mainly consists of the p orbitals of the Pb atom, while the top of the valence band is mainly derived from the p orbital of the I atoms and the Pb-s orbital, as depicted in Figure 8b. When considering the organic molecule, the highest occupied molecular orbital of the MA+ cation is found deep below the valence band, ∼5 eV below the VBM. Thus, one may argue that there is no effect of the MA+ cation in the optical and electronic response of such materials, rather it does only contribute to their structural cohesion by donating its charge to the rest of the system. However, a closer inspection of the DOS projected on the various atoms (Figure 8a) reveals that there is a small contribution of the MA cation, ∼0.5 eV below the VBM. This indicates that indeed there is an interaction between the MA cation and the inorganic PbI6 octahedral framework in the form of hydrogen bonding. To further understand the effect of the interactions between the MA cation and the inorganic framework in electronic properties of these materials, we removed the MA cation from the PBE + vdW-relaxed structure of the initial [100] orientation and calculated the electronic band structures. This is to check the interactions between the MA cation and the framework. Note that, by removing the MA cation, one electron is missing from the band, therefore there is a hole in the valence band and the Fermi-level shifted down, below the VBM. To do charge neutralizing, we added one electron to the system and then calculated the band structure. The calculated band structure in this case preserves the same feature of indirect band gap as one obtained from the MAPbI3 unit cell (Supporting Information, Figure S2). This indicates that the MA cation in the system just donates its electron to the inorganic framework, it does not affect the band structure near the band edge. However, its orientations played a role in the relaxed structure of the inorganic framework and caused the structural distortion of the framework, leading to the symmetry breaking and the CBM is a bit shifted away from high symmetry point. In our cases, the rotation of the MA cation can create a variation of the band gap of MAPbI3 ∼0.2 eV (∼13% wrt. experimental gap of 1.55 eV), as shown in Figure 4d−f. Therefore, in the real system, the cation rotations would slightly change the band gap. The lowest and highest band gaps are found to be 1.43 and 1.64 eV which correspond to the calculated absorption spectrum of ∼865 and ∼756 nm, respectively. It is expected that the variation of the band gap for this material would be within 0.2 eV. The average band gap of MAPbI3 is 1.54 eV which corresponded to the calculated absorption spectrum ∼805 nm. From all our calculated results, it has been revealed that the vdW correction is important to obtain an accurate description of the interactions between the MA cation and the inorganic framework for the structural relaxation of the halide perovskite system. This interaction induces the deformation of the PbI6 octahedral framework, leading to the distorted structure of PbI6 framework; the band structure is changed from direct to indirect band gap.

Figure 8.

Figure 8

Open in a new tab

(a) Calculated total density of states (DOS) (dashed line) of CH3NH3PbI3 for the case of [111]-oriented molecule and projected DOS (PDOS) on the Pb atom (red), I-atoms (green), and CH3NH3 (blue). (b) PDOS on orbitals of the Pb atom and I atoms.

Conclusions

In this work, we have performed DFT + vdW correction calculations with various initial MA+ cation orientations, namely [100], [110], and [111] for revealing the effects of the internal interactions between the MA+ cation and the BX6 inorganic framework of the CH3NH3BX3 (B = Pb, Sn; X = I, Br, Cl) halide perovskite materials. Our calculations reveal that the vdW interactions between the MA+ cation and the inorganic framework are critical for internal geometry optimization and electronic properties calculations. Full structural relaxations, including vdW-corrected DFT, give the better agreement of the lattice parameters with the experimental values than obtained without them. More importantly, full relaxations, including vdW interactions of the MA cation initially oriented along the [100] direction, give a strongly distorted structure of the BX6 inorganic framework, which results from the MA+ cation rotation and consequently affects the electronic band structure, which changes from direct to indirect band gap. On the other hand, the relaxations without vdW correction do not present enough distortion of the BX6 inorganic framework, the electronic band structures remain direct band gap.

This result is found to be robust when considering different halogens and occurs in both Sn- and Pb-based compounds. It is also robust when using a more accurate hybrid functional or the GW method. Finally, the indirect gap is maintained for this orientation when including both quasiparticle self-energy corrections at the GW level and SOC. The latter leads to the Rashba effect which spin-splits the bands, but the indirect nature is already present before adding the SOC. This clearly demonstrates that the main origin of the indirect gap lies in the distortions resulting from the structural distortions of the organic ion with the inorganic framework.

Computational Methods

The structural properties of studied materials were predicted using the first-principle DFT which is implemented in the Vienna ab initio simulation package (VASP) code.22,23 The semilocal GGAs combined with the PBE24 functional are used as the primary exchange–correlation functional. The vdW corrections were also employed to study their effects on the structural and electronic properties of the materials. The projected augmented wave23,25 method with plane-wave basis set cut-off energy of 520 eV is employed in all calculations. The conjugate gradient algorithm26 is used for the structural optimization until the change of the energy on each atom is less than 1 × 10–4 eV. For the structural optimization and electronic properties calculations, the Monkhorst–Pack k-points sampling27 with 8 × 8×8 mesh is used for the Brillouin-zone integrations. Recent studies12−14 revealed that vdW force plays an important role in the range of materials with weak interactions, such as organic–inorganic halide perovskite compounds, especially in their geometry optimization. Therefore, in order to study the effects of internal interactions between the MA+ cation and BX6 inorganic framework, full structural relaxations (volume and atomic position are allowed to relax), including vdW interactions, have been performed using the zero damping DFT-D3 method described by Grimme et al.28 Then, the relaxed structures have been used to calculate the corresponding electronic band structures both at the DFT and many-body perturbation theory GW level.29−31

The cubic primitive cell of the MABX3 (12 atoms per unit cell) has been used in this work. As a matter of fact, under working temperature, the MA molecules are nearly free to rotate inside the cuboctahedral BX6. It is more important to investigate the range of the change in the energy level near the band edge. In this work, various MA orientations within the cubic unit cell have been studied in order to determine the range of variation of electronic structures as molecules rotating inside the perovskite cage. Our calculated results are able to qualitatively explain the change of CBM of MAPbI3 which is affected by molecular rotational and is in good agreement with both other calculations using the supercell approach13,16,19 and the experiment performed by Hutter et al.32 The orientation of the MA cation significantly affects the BX6 inorganic framework and consequently the electronic properties of the materials.

It is well known that the GGA–PBE usually underestimates band gaps of semiconductors. However, for MAPbI3, the GGA–PBE without SOC gives fortuitously good agreement of the calculated band gap with the experimental measurement. This is due to a compensation of the errors of the GGA–PBE and the lack of SOC. Therefore, the more accurate HSE-screened hybrid functional (HSE06)33 is also used to calculate the band structures without including SOC for the band gaps. It is well known that the DFT method treats core electrons by effective pseudopotential. In order to study the effects of core electrons, one may need the full-potential all-electron methods to explain the electronic properties of the materials. Subsequently, to compare with the DFT method, we also calculated the band structures using the full-potential linearized muffin-tin orbital all-electron method,34,35 as implemented in Questaal Suite.31 In this method, the band structures are calculated using the QSGW method.35,37 The GW method is a many-body perturbation theoretical method introduced by Hedin38,39 in which the self-energy is approximated in terms of the one-electron Green’s function G and screened Coulomb interaction, W, schematically Σ = iGW. While the GW self-energy operator is energy-dependent and non-Hermitian in the QSGW approach, we replace it by an energy-independent but still non-local operator, determined in a self-consistent manner. From a starting independent particle Hamiltonian H0, and its eigenvalues and eigenfunctions, we obtain both the Green’s function G0 and the polarization function P0. The screened Coulomb interaction is then given by W = v + vP0W, and the self-energy is obtained as Σ = iG0W0. This quantity is actually obtained in the basis set of the eigenstates of H0. From it, we then extract a correction to the exchange correlation potential

graphic file with name ao0c03016_m003.jpg

which is added to the previous H0 to obtain a new H0, and the procedure is iterated until Δvxc = 0. At convergence, the quasiparticle energies equal the Kohn–Sham eigenvalues. Hence, the name quasiparticle self-consistent. The energy dependence of the GW self-energy and its imaginary part or lifetime are thus ignored, but the quasiparticle energies are correctly including the dynamical effects of the electron–electron interaction.

Acknowledgments

This work was supported by the Suranaree University of Technology (SUT) and by the Office of the Higher Education Commission under NRU Project. N. Pandech was supported by the Development and Promotion of Science and Technology Talents Project (DPST, Thailand). Computations made use of the High Performance Computing Resource in the Core Facility for Advanced Research Computing at Case Western Reserve University.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c03016.

  • Band structures of the fully relaxed crystal structure including vdW interactions calculated using the GGA–PBE without SOC of MAPbI3 for the MA cation initially orientated along the [101] direction; calculated band structures of the PBE + vdW-relaxed structure of the MAPbI3 unit cell with the MA cation initially orientated in the [100] direction; and calculated band structures of the PBE + vdW-relaxed structure of Pb–I host without the MA cation in the structure (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao0c03016_si_001.pdf (242.4KB, pdf)

References

  1. Poglitsch A.; Weber D. Dynamic disorder in methylammoniumtrihalogenoplumbates (II)observed by millimeter-wave spectroscopy. J. Chem. Phys. 1987, 87, 6373–6378. 10.1063/1.453467. [DOI] [Google Scholar]
  2. Kojima A.; Teshima K.; Shirai Y.; Miyasaka T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. 10.1021/ja809598r. [DOI] [PubMed] [Google Scholar]
  3. Stoumpos C. C.; Malliakas C. D.; Kanatzidis M. G. Semiconducting Tin and Lead Iodide Perovskites with Organic Cations: Phase Transitions, High Mobilities, and Near-Infrared Photoluminescent Properties. Inorg. Chem. 2013, 52, 9019–9038. 10.1021/ic401215x. [DOI] [PubMed] [Google Scholar]
  4. Park J.-S.; Choi S.; Yan Y.; Yang Y.; Luther J. M.; Wei S.-H.; Parilla P.; Zhu K. Electronic Structure and Optical Properties of α-CH3NH3PbBr3 Perovskite Single Crystal. J. Phys. Chem. Lett. 2015, 6, 4304–4308. 10.1021/acs.jpclett.5b01699. [DOI] [PubMed] [Google Scholar]
  5. Weller M. T.; Weber O. J.; Henry P. F.; Di Pumpo A. M.; Hansen T. C. Complete structure and cation orientation in the perovskite photovoltaic methylammonium lead iodide between 100 and 352 K. Chem. Commun. 2015, 51, 4180–4183. 10.1039/c4cc09944c. [DOI] [PubMed] [Google Scholar]
  6. Sahoo S. K.; Manoharan B.; Sivakumar N.. Chapter 1—Introduction: Why Perovskite and Perovskite Solar Cells? In Perovskite Photovoltaics; Thomas S., Thankappan A., Eds.; Academic Press, 2018; pp 1–24. [Google Scholar]
  7. Tonui P.; Oseni S. O.; Sharma G.; Yan Q.; Tessema Mola G. Perovskites photovoltaic solar cells: An overview of current status. Renewable Sustainable Energy Rev. 2018, 91, 1025–1044. 10.1016/j.rser.2018.04.069. [DOI] [Google Scholar]
  8. Shi Z.; Jayatissa A. Perovskites-Based Solar Cells: A Review of Recent Progress, Materials and Processing Methods. Materials 2018, 11, 729. 10.3390/ma11050729. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Whitfield P. S.; Herron N.; Guise W. E.; Page K.; Cheng Y. Q.; Milas I.; Crawford M. K. Structures, Phase Transitions and Tricritical Behavior of the Hybrid Perovskite Methyl Ammonium Lead Iodide. Sci. Rep. 2016, 6, 35685. 10.1038/srep35685. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Quarti C.; Mosconi E.; De Angelis F. Interplay of Orientational Order and Electronic Structure in Methylammonium Lead Iodide: Implications for Solar Cell Operation. Chem. Mater. 2014, 26, 6557–6569. 10.1021/cm5032046. [DOI] [Google Scholar]
  11. Knop O.; Wasylishen R. E.; White M. A.; Cameron T. S.; Oort M. J. M. V. Alkylammonium lead halides. Part 2. CH3NH3PbX3 (X = Cl, Br, I) perovskites: cuboctahedral halide cages with isotropic cation reorientation. Can. J. Chem. 1990, 68, 412–422. 10.1139/v90-063. [DOI] [Google Scholar]
  12. Egger D. A.; Kronik L. Role of Dispersive Interactions in Determining Structural Properties of Organic–Inorganic Halide Perovskites: Insights from First-Principles Calculations. J. Phys. Chem. Lett. 2014, 5, 2728–2733. 10.1021/jz5012934. [DOI] [PubMed] [Google Scholar]
  13. Li J.; Rinke P. Atomic structure of metal-halide perovskites from first principles: The chicken-and-egg paradox of the organic-inorganic interaction. Phys. Rev. B 2016, 94, 045201. 10.1103/physrevb.94.045201. [DOI] [Google Scholar]
  14. Yin W.-J.; Shi T.; Yan Y. Unusual defect physics in CH3NH3PbI3 perovskite solar cell absorber. Appl. Phys. Lett. 2014, 104, 063903. 10.1063/1.4864778. [DOI] [Google Scholar]
  15. Brivio F.; Butler K. T.; Walsh A.; van Schilfgaarde M. Relativistic quasiparticle self-consistent electronic structure of hybrid halide perovskite photovoltaic absorbers. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 89, 155204. 10.1103/physrevb.89.155204. [DOI] [Google Scholar]
  16. Motta C.; El-Mellouhi F.; Kais S.; Tabet N.; Alharbi F.; Sanvito S. Revealing the role of organic cations in hybrid halide perovskite CH3NH3PbI3. Nat. Commun. 2015, 6, 7026. 10.1038/ncomms8026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Bechtel J. S.; Seshadri R.; Van der Ven A. Energy Landscape of Molecular Motion in Cubic Methylammonium Lead Iodide from First-Principles. J. Phys. Chem. C 2016, 120, 12403–12410. 10.1021/acs.jpcc.6b03570. [DOI] [Google Scholar]
  18. Chiarella F.; Zappettini A.; Licci F.; Borriello I.; Cantele G.; Ninno D.; Cassinese A.; Vaglio R. Combined experimental and theoretical investigation of optical, structural, and electronic properties of CH3NH3SnX3 thin films (X=Cl, Br). Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 77, 045129. 10.1103/physrevb.77.045129. [DOI] [Google Scholar]
  19. Xu Q.; Stroppa A.; Lv J.; Zhao X.; Yang D.; Biswas K.; Zhang L. Impact of organic molecule rotation on the optoelectronic properties of hybrid halide perovskites. Phys. Rev. Mater. 2019, 3, 125401. 10.1103/physrevmaterials.3.125401. [DOI] [Google Scholar]
  20. Lee M. M.; Teuscher J.; Miyasaka T.; Murakami T. N.; Snaith H. J. Efficient Hybrid Solar Cells Based on Meso-Superstructured Organometal Halide Perovskites. Sci 2012, 338, 643. 10.1126/science.1228604. [DOI] [PubMed] [Google Scholar]
  21. Mosconi E.; Amat A.; Nazeeruddin M. K.; Grätzel M.; De Angelis F. First-Principles Modeling of Mixed Halide Organometal Perovskites for Photovoltaic Applications. J. Phys. Chem. C 2013, 117, 13902–13913. 10.1021/jp4048659. [DOI] [Google Scholar]
  22. Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169–11186. 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
  23. Kresse G.; Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758–1775. 10.1103/physrevb.59.1758. [DOI] [Google Scholar]
  24. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/physrevlett.77.3865. [DOI] [PubMed] [Google Scholar]
  25. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 17953–17979. 10.1103/physrevb.50.17953. [DOI] [PubMed] [Google Scholar]
  26. Golub G. H.; Ye Q. Inexact Preconditioned Conjugate Gradient Method with Inner-Outer Iteration. SIAM J. Sci. Comput. 1999, 21, 1305–1320. 10.1137/s1064827597323415. [DOI] [Google Scholar]
  27. Monkhorst H. J.; Pack J. D. Special points for Brillouin-zone integrations. Phys. Rev. B: Condens. Matter Mater. Phys. 1976, 13, 5188–5192. 10.1103/physrevb.13.5188. [DOI] [Google Scholar]
  28. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  29. Bhandari C.; Lambrecht W. R. L.; van Schilfgaarde M. Quasiparticle self-consistent GW calculations of the electronic band structure of bulk and monolayer V2 O5. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 91, 125116. 10.1103/physrevb.91.125116. [DOI] [Google Scholar]
  30. Bhandari C.; van Schilgaarde M.; Kotani T.; Lambrecht W. R. L. All-electron quasiparticle self-consistent GW band structures for SrTiO3 including lattice polarization corrections in different phases. Phys. Rev. Mater. 2018, 2, 013807. 10.1103/physrevmaterials.2.013807. [DOI] [Google Scholar]
  31. Pashov D.; Acharya S.; Lambrecht W. R. L.; Jackson J.; Belashchenko K. D.; Chantis A.; Jamet F.; van Schilfgaarde M. Questaal: A package of electronic structure methods based on the linear muffin-tin orbital technique. Comput. Phys. Commun. 2020, 249, 107065. 10.1016/j.cpc.2019.107065. [DOI] [Google Scholar]
  32. Hutter E. M.; Gélvez-Rueda M. C.; Osherov A.; Bulović V.; Grozema F. C.; Stranks S. D.; Savenije T. J. Direct–indirect character of the bandgap in methylammonium lead iodide perovskite. Nat. Mater. 2017, 16, 115–120. 10.1038/nmat4765. [DOI] [PubMed] [Google Scholar]
  33. Heyd J.; Scuseria G. E.; Ernzerhof M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. 10.1063/1.1564060. [DOI] [Google Scholar]
  34. Methfessel M.; van Schilfgaarde M.; Casali R. A. In A Full-Potential LMTO Method Based on Smooth Hankel Functions, Electronic Structure and Physical Properties of Solids; Dreyssé H., Ed.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2000; pp 114–147. [Google Scholar]
  35. Kotani T.; van Schilfgaarde M.; Faleev S. V. Quasiparticle self-consistent GW method: A basis for the independent-particle approximation. Phys. Rev. B: Condens. Matter Mater. Phys. 2007, 76, 165106. 10.1103/physrevb.76.165106. [DOI] [Google Scholar]
  36. van Schilfgaarde M.; Kotani T.; Faleev S. Quasiparticle Self-Consistent GW Theory. Phys. Rev. Lett. 2006, 96, 226402. 10.1103/PhysRevLett.96.226402. [DOI] [PubMed] [Google Scholar]
  37. Hedin L. New Method for Calculating the One-Particle Green’s Function with Application to the Electron-Gas Problem. Phys. Rev. 1965, 139, A796–A823. 10.1103/physrev.139.a796. [DOI] [Google Scholar]
  38. Hedin L.; Lundqvist S.. Effects of Electron-Electron and Electron-Phonon Interactions on the One-Electron States of Solids. In Solid State Physics; Seitz F., Turnbull D., Ehrenreich H., Eds.; Academic Press, 1970; Vol. 23, pp 1–181. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao0c03016_si_001.pdf (242.4KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES