Abstract
Here, a self-developed experimental system of diffusion at high temperatures and pressures was utilized to clarify the impacts of high pressure and temperature (303, 323, 343, and 363 K; 2, 6, 12, and 20 MPa) and coal ranks on diffusion properties in coal. At constant temperature and pressure, the diffusion coefficients of CH4 gradually decrease with increasing particle size and increase gradually with the increasing pressure and temperature. However, the diffusion coefficients first decrease and then increase with the increasing coal rank. The minimum diffusion coefficients occur at about Ro,max = 1.7%. The temperature and pressure sensitivity of CH4 diffusion was quantified via the experimental data. The increase extent first increases and then decreases with the increasing pressure. The peak pressure for the increase extent was 6 MPa for all coals. The increments of diffusion rate per pressure unit were 1.50, 0.90, and 0.61%, indicating that the impact of pressure at the low-pressure stage (2–6 MPa) was more significant than that at the high-pressure stage (6–20 MPa). At the same pressure, the diffusion rates overall increase with the increasing temperature. At the low-pressure stage (2–6 MPa), the impacts of pressure were more significant than at the high-pressure stage. However, as for the temperature dependence, the impacts of temperature were more significant at the high-pressure stage than at the low-pressure stage.
1. Introduction
Knowledge of gas transport properties of coal is important for coalbed methane (CBM) production and recovery by CO2/N2 injection into coal seams.1 During the CBM engineering, CH4 first desorbs from the optimized adsorption sites2−4 in the microporous (<2 nm) surface, then diffuses into the meso- (2–50 nm) and macropores (>50 nm), and finally is extracted through permeation flow.5−7 Thus, the diffusion properties of CH4 in a coal matrix are crucial to impact the CBM production. Diffusion is a kind of migration phenomenon induced by the random movement of guest particles driven by concentration gradient,8 mainly occurring in the pore system of host structures, and is frequently characterized by Fick’s first and second laws of diffusion.9,10 The diffusion coefficient (D) of coal refers to the amount of gas passing through the coal matrix per unit cross-sectional area in unit time at unit concentration gradient depending mainly on the gas composition, coal quality, temperature, pressure, and stress conditions.11−16 The geological conditions of CBM resources are complex and difficult to exploit ,17,18 and there exist extremely high geological temperatures and pressures in deep strata. Thus, the investigation of the CH4 diffusion characteristics of coal at high temperature and pressure is of great theoretical and practical significance for the exploration of deep CBM resources and prevention of mine gas disasters.
In the desorption of CH4 from the adsorption sites to the steady Darcy flows, there exist four microscopic diffusion mechanisms including self-diffusion (randomized Brownian motions from one site to another and characterized by self-diffusion coefficients), Fickian diffusion (dominated by molecule–molecule collisions and characterized by Fickian/transport diffusion coefficients), Knudsen diffusion (dominated by molecule–wall collisions and characterized by Knudsen diffusion coefficients), and surface diffusion (transport through a physically adsorbed layer characterized by surface/Maxwell–Stefan diffusion coefficients).3,7,17,18 Among these four diffusion processes, the transport diffusion represents particle motions driven by chemical or concentration gradient, which results in net mass transport.2,4 Thus, it is more relevant to the technological applications. Scholars at home and abroad have carried out a lot of research work on the isothermal adsorption diffusion experiment of coal, especially under high temperature and high pressure.1,19,20 However, the research on the diffusion of methane in coal is mainly focused on high temperature, and there are few reports on the diffusion experiment under high pressure (>5 MPa).
Experimentations have been frequently conducted to obtain the transport diffusions of CH4 in coal, and significant progress has been made since the last decades. Saghafi et al.13 measured the diffusion coefficients of CH4 in sub-bituminous to bituminous rank, ranging from 0.66 to 1.45% in mean maximum vitrinite reflectance from Sydney Basin coals using the and found that obtain the diffusivity (diffusion coefficient) of CH4 in the Sydney Basin coals varying from 0.6 × 10–6 to 5.1 × 10–6 cm2/s. Cui et al.1 quantified the apparent diffusivities of CH4 through numerical simulations using a bidisperse model (0.5–1 nm in size) in a macropore and micropore based on the experimental gas adsorption data, obtained the apparent micropore diffusivity of CH4 (2.5 × 10–5–3.5 × 10–4 s–1 at 0.12–4.39 MPa), and proposed that the dynamic radius of the diffusion particle is crucial for the diffusion coefficients. Additionally, it is also found that the apparent diffusivity strongly decreases with an increase in gas pressure, which may be attributed to coal matrix swelling caused by gas adsorption. The International Union of Pure and Applied Chemistry (IUPAC) has proposed the classification scheme (microporpus, <2 nm in size; mesoporous, 2–50 nm in size; macroporous, >50 nm in size) for pore structures,21 and the specific surface area of pores is primarily contributed by the micropores (accounting for more than 96.64–99.56%).22 Thus, the diffusion process in micropores has attracted growing attention, and several models have been proposed to calculate the diffusion coefficients such as unipore,5,11 bidisperse,7 and modified bidisperse (also known as Fickian diffusion–relaxation model) models.1,15 These models varied significantly in pore size, and the unipore models (d ∼ 0.3 nm) are consisted of spherical particles with a uniform size (particle size φ ∼ 0.5 mm),5,11 while the bidisperse models (d: 0.5–1 nm) are characterized by spheres of two distinct sizes, i.e., macrospherical particles (φ: 0.35–0.7 mm) and microspheres containing an assemblage of uniform size (φ: 0.04–0.06 mm).7,23 The apparent diffusivities obtained through these physical porous models are 10–14–10–11 m2/s for CH4. The differences in the models with uniform size have indicated that the particle sizes of the diffusion host impact significantly the diffusion coefficients.
The diffusion of CH4 was sensitive to the depressurization and temperature rise. Increasing temperature can reduce the ability of methane to adsorb onto the coal matrix, promoting the rapid diffusion of CH4 and effectively solving the problem of insufficient driving force for CH4.3,22 Nandi and Walker24 conducted experiments on the adsorption equilibrium of CH4 in coal at 323–630 K and calculated the effective diffusion coefficient based on the t1/2 model via the constant temperature diffusion experimentations. The results indicated the increasing trends of the effective diffusion coefficient with the increasing temperature. Fan et al.25 investigated the desorption of CH4 at various temperatures and proposed that the desorption quantity increases with the increasing temperature and CH4 is easy to desorb to a free state under the thermal conditions. Charrière et al.5 carried out a series of constant-temperature (at 283–333 K) diffusion experiments at constant pressure and found that D increases gradually with the increasing temperature in the first 10 min. Zhao et al.26 investigated the influences of temperature and moisture on the methane diffusion rate and revealed that both the abilities of desorption and diffusion of CH4 increase with the increasing temperature after water injection. Wen et al.27 explored the temperature dependence of diffusion and specific heat capacity for coal and discovered that thermal diffusivity and conductivity become constant at high temperature. Charrière et al.5 highlighted the effect of temperature on diffusion of CH4 in coal from the Lorraine basin and proposed that both the effective diffusion (De) and the diffusion coefficient (D) (∼10–12 m2 s–1) estimated from modeling experimental data by assuming Fickian and unipore diffusion increased with increasing temperature. Jiang et al.28 conducted experiments on the adsorption equilibrium for experimental coal samples with initial temperature and pressure and found that the diffusion parameter B decreases with increasing temperature via the temperature-rising diffusion experiment of CH4. Li et al.29,30 proposed that D of methane in coal particles increases with the increase of temperature.
For the diffusion coefficients of pressure dependence, international scholars have conducted numerical and molecular simulations to highlight the pressure dependence. There exists disagreement on whether D increases or decreases with the increasing pressure. Even with similar models, some authors have found that diffusion coefficients increase with the increasing pressure.12,31 Others proposed that the variations of diffusion coefficients for pressure dependence are determined by the models used.11 Staib et al.15 conducted a brief review for the pressure dependence of diffusion coefficients and found that both the primary and secondary diffusion coefficients decrease with the increasing pressure. The lack of consistency in the deduced effects of pressure could be due to the (i) choice of model, (ii) choice of experimental conditions, or (iii) choice of coal.15
As mentioned above, plenty of research has been carried out on CH4 desorption and diffusion characteristics in coal under high temperatures and pressures, and fruitful results have been achieved; however, there are still some problems to be further explored. There exist deficiencies in the following two aspects in previous investigations on the diffusion of CH4 in coal: (1) The diffusion characteristics of CH4 in coal were explored mainly via experiments, and they were mainly focused on high-temperature experiments. The diffusion of CH4 in coal under high pressures (>5 MPa) has been minimally reported to date. (2) As the previous investigations were mainly focused on the impacts of pressure and temperatures, there are few explorations to reveal the influences of coal rank on diffusion properties. Here, a self-developed experimental system of diffusion at high temperatures and pressures was utilized to clarify the impacts of high pressure and temperature (303, 323, 343, and 363 K; 2, 6, 12, and 20 MPa) and coal ranks on diffusion properties in coal. The temperature and pressure sensitivity analyses of CH4 diffusion were also conducted, and this work is of great theoretical and practical significance for the exploration of deep CBM resources and prevention of mine gas disasters.
2. Sample Preparation
To comprehensively reveal the diffusion properties of CH4 in coal, four samples of various ranks were collected, and they were from the Yujialiang Colliery of Shendong Coalfield (YJL), Zhuxianzhuang Colliery of Huaibei Coalfield (ZXZ), Yuanxiang Colliery of Xishan Coalfield (YX), and Duanshi Colliery of Qinshui Coalfield (DS). The sampling scheme and density examination (using an UltraPYC1200e density analyzer) followed the national standards proposed in 2008 (GB/T 482-2008) and 2010 (GB/T 6949-2010), respectively. The samples were crushed and ground to <0.2 mm and dried under vacuum in accordance with GB/T 477-2008. These samples were prepared in sextuplicate, and >200 g for each portion was sealed up for industrial analysis (5E-MAG6600 analyzer). The maceral analysis and vitrinite reflectance for these four samples were conducted on an AXIOSKOP 40 microscope (GB/T8899-2013) and an MSP UV–vis 2000 microspectrophotometer.
For the diffusion samples, the blocky samples were crushed to <6 mm (following GB/T 477-2008) and sieved out to obtain the specific samples of particle sizes 0.17–0.25, 0.5–1, and 1–3 mm. These different samples were prepared in triplicate (∼200 g for each) and dried (375 K) in a high-temperature oven for more than 2 h. Finally, these samples were cooled and sealed for the diffusion experiments at high temperatures and pressures.
3. Methods
For the diffusion of gas in a coal matrix, there are two main deficiencies in the current experimental platforms: (1) Low experimental efficiency: the experimental devices are frequently equipped with one to two sample tanks with long test cycle and thus reducing the experimental efficiency. (2) Imperfect temperature control system: the constant temperature device often controls the temperature between in the reference tank and the sample tank, and the constant temperatures of the gas injection pipeline and the pipeline connecting the reference tank were often ignored, which affects the accuracy of CH4 diffusion in coal particles, especially at the high-temperature stage. In view of the above problems, the existing experimental equipment is improved based on MT/T752-1997 and GB/T 19560-2008. A high-temperature and high-pressure methane diffusion simulation experiment platform was built, and its working principle is depicted in Figure 1.
Figure 1.
Schematic diagram of a methane diffusion experimental platform under high temperature and high pressure. 1: Gas cylinder of CH4; 2: air compressor; 3: gas turbocharged pump; 4: high-pressure gas holder; 5: safety valve; 6: buffer tank; 7: vacuum pump; 8: standard room; 9(9′): pressure sensor of reference cylinder; 10(10′): pressure sensor of sample cylinder; 11(11′): reference cylinder; 12(12′): sample cylinder; 13–16: pressure reducing valve; 17–23: precise pressure gauge; 24–38: valve; 39(39′): constant temperature system; 40(40′): vent solenoid valve; 41(41′): pressure sensor; 42(42′): servo motor; 43(43′): liquid storage cup; 44(44′): gas storage tank; 45(45′): drive screw; 46–47(47′): intake solenoid valve; 48: controlling system; and 49: high-precision pressure sensor.
This experimental system was composed of controlling systems for volume calibration, vacuum degassing, high-pressure gas injection, inflation adsorption balance, temperature control, and diffusion quantitative control. The coal matrix is an organic rock and is sensitive to the response of reservoir pressures and temperatures, and both of them are also the most critical factors to control the diffusion characteristics of CBM.32,33 The mechanical properties of deep coal seams are obviously different from those of shallow coal seams. To simulate the true geological conditions, it is crucial to determine the reasonable reservoir pressure and temperature of deep coal seams. According to the actual situation of the strata in the coal-bearing area, the simulated pressure and temperature parameters of this experiment are finally determined as 2, 6, 12, and 20 MPa and 303, 323, 343, and 363 K, respectively. To make the data of various experimental conditions comparable, the experimental diffusion quantity was transformed to volume in standard conditions based on the following empirical equation
| 1 |
where Qgt is the diffusion quantity of CH4 at the moment tmin under the standard conditions, cm3/g. Qt′ is the diffusion quantity of CH4 under the experimental temperatures. T is the water temperature in the measuring tube (K) and Pa depicts the atmospheric pressure (Pa) under experimental conditions. hw is the height of water column in the measuring tubes (mm), and Ps is the saturated steam pressure at temperature T (Pa).
4. Results and Discussion
4.1. Coal Basic Properties
The results for coal petrology and the density and proximate analysis are depicted in Tables 1 and 2, respectively. The coal macerals are dominated by vitrinite, and the Ro,max varies 0.56–2.93, covering the low, medium, and high ranks for the YJL, ZXZ, YX, and DS. All of the samples used here were collected from an undeformed or a weakly deformed tectonic region and differ significantly in thermal evolution degree, resulting in their diversities in Ro,max. The gas behaviors in coal are affected by its rank, moisture, maceral composition, and fracture–pore systems.5,7 The four low-, medium-volatile (7.12–27.54 wt %, dry basis) dried coal (Ro,max = 0.68–0.75%) samples were selected from a larger pool according to their typical macro- and microstructural characteristics.
Table 1. Results of Maceral and Vitrinite Reflectance.
| sample no. | vitrinite (%) | inertinite (%) | exinite (%) | minerals (%) | Ro,max (%) |
|---|---|---|---|---|---|
| YJL | 60.51 | 23.22 | 1.40 | 20.67 | 0.56 |
| ZXZ | 71.06 | 21.57 | 5.65 | 3.35 | 0.89 |
| YX | 68.38 | 27.54 | 0 | 4.02 | 1.68 |
| DS | 88.69 | 7.12 | 0 | 2.76 | 2.93 |
Table 2. Results of True Density, Apparent Density, and Proximate Analysisa.
| sample no. | Mad (%) | Aad (%) | Vdaf (%) | FCad (%) | TRD (g/m3) | ARD (g/m3) | porosity (%) |
|---|---|---|---|---|---|---|---|
| YJL | 8.72 | 11.35 | 39.71 | 44.87 | 1.38 | 1.27 | 7.97 |
| ZXZ | 1.94 | 13.43 | 33.45 | 55.52 | 1.49 | 1.42 | 4.70 |
| YX | 0.96 | 14.17 | 22.32 | 72.35 | 1.60 | 1.51 | 5.63 |
| DS | 1.37 | 13.46 | 7.24 | 80.13 | 1.53 | 1.45 | 5.23 |
Mad, moisture content; Aad, ass content from the air drying basis; Vdaf, dry ash-less base; FCad, fixed carbon content; ARD, apparent density; and TRD, true density.
The typical scanning electron microscopy images for these samples are shown in Figure 2. All of these samples have macropores (>1000 nm), and they vary significantly in pore morphology. For YJL, there exists high density of the macropores and mesopores and the distribution is relatively homogeneous. These pores mainly manifest as intercrystalline types with fine fissures, and the connectivity is relatively good (Figure 2a). The clay and carbonate minerals are occasionally occupied in the pores and fine fissures (Figure 2b). The surface of ZXZ is overall smooth, and crystalline mineral particles develop frequently on it (Figure 2c). The fractures among the pores developed primarily in this sample (Figure 2d). For YX, the granular minerals are mingled with the coal matrix the fracture surface is large (Figure 2e). Fusinite or semifusinite can be seen, and the pores developed locally (Figure 2f). There are plenty of continuous pores of various shapes in sample DS (Figure 2g), belonging to the stomata formed by overflow of gas in the coalification process (Figure 2h). This indicates the strong aerogenesis process and provides the sufficient storage space for CH4.
Figure 2.
Scanning electron microscopy pictures of coal samples: (a, b) YJL; (c, d) ZXZ; (e, f) YX; and (g, h) DS.
4.2. Effects of Particle Size on Diffusion
International scholars have reached a consensus that the diffusion quantity of CH4 in coal is related to the time via exponential solutions.11,34,35 The forms of the exponential solutions vary due to the variations in the hypothesis of the boundary conditions. D was frequently obtained via the calculation of the diffusion rate based on the quantity obtained from the experimentations.33,36
For eq 1, t was 120 min and Qt was the total diffusion quantity within 120 min. Then, the diffusion data was plugged into eq 1, where Q∝ was the ultimate diffusivity of CH4. To date, there has also been disagreement on the calculation methods of the ultimate diffusivity.37−42 Among these calculation methods, the one based on Langmuir adsorption theory proposed by Harpalani and Chen39 has been most widely utilized, where the ultimate diffusivity was the difference in the total amount of adsorption quantity corresponding to the experimental and atmospheric pressures. At the pressure >20 MPa, the adsorption process will access the multilayer adsorption stage.43−45 Thus, to enhance the reproduction of the experimental data, the ultimate diffusivity here was obtained through the experimental measurement. The diffusion process at 303 K in different-sized coal particles and the relationship between diffusion coefficients and coal particle size are depicted in Figure 3a–c,d, respectively.
Figure 3.
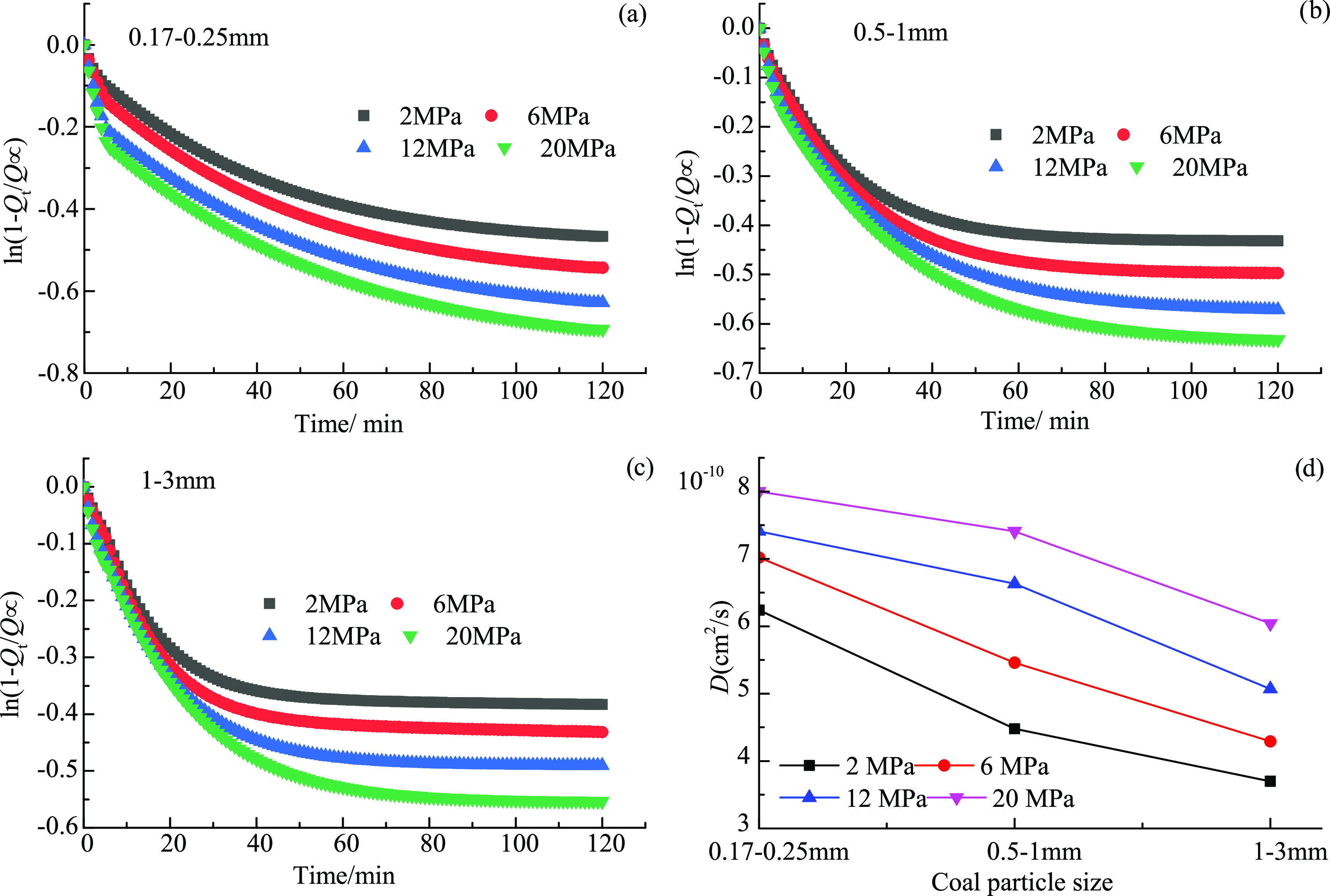
Diffusion process of CH4 in different-sized particles of (a) 0.17–0.25 mm, (b) 0.5–1.0 mm, and (c) 1–3 mm and (d) relationship between coal particle size and diffusion coefficients.
For the same particle size of coal, the diffusion rate decreases significantly in the first 40 min and then decreases slightly (even keeps stable) as the diffusion process continues. The diffusion coefficients range from (3.7 to 8.0) × 10–10 cm2/s, lower than the apparent diffusivities obtained through the unipore5,11 and bidisperse7 models (10–14–10–11 m2/s) and the molecular simulation results (10–9–10–11 m2/s).3,4,46 The differences in the unipore and bidisperse models are induced by the structural differences in constitutive characteristics and pore size distribution. The unipore and bidisperse models are based on the uniform microsphere,11 and the pore size distribution is highly heterogeneous, resulting in the lower diffusion coefficients in experimental data. Additionally, these lower diffusion coefficients than in the molecular simulation used here are induced because the macromolecules used for the dynamic simulation were constructed based on aromatic clusters and aliphatic chains and were free of minerals.3,4,6 The Aad for the samples used here was >10%, which is indicative of the higher mineral content, which can fill the diffusion channel and thus hinder the diffusion process.
At constant temperature and pressure, the diffusion coefficients of CH4 gradually decrease with increasing particle size (Figure 3d). At 303 K and 12 MPa, the diffusion coefficients are 7.11 × 10–10, 6.63 × 10–10, and 5.07 × 10–10 cm2/s for particle sizes of 0.17–0.25, 0.5–1, and 1–3 mm, respectively. The decrease in diffusion coefficients with the increasing particle size is due to the fact that the diffusion path of CH4 from the adsorption sites of the micropores to the fracture channels is shorter for the coal samples of smaller particle size. For the coal samples of lower particle size, there is higher surface area exposed per mass, and a large number of closed pores can be exposed under the comminution process, which macroscopic manifests as higher diffusion quantity for CH4.
4.3. Effects of Gas Pressure on Diffusion
To investigate the impacts of pressure, the diffusion coefficients were calculated via eq 1 for samples YJL, ZXZ, YX, and DS. The diffusion processes for these four samples are depicted in Figures 5–8, respectively. There is disagreement on whether diffusion coefficients increase or decrease with the increasing pressure. Clarkson and Bustin11 proposed that different models display different pressure dependences of diffusion coefficients, which is determined by the used model and even using the same data. By the unipore model, the scholars such as Ciembroniewicz and Marecka,31 Charrière et al.,5 and Jian et al.12 found that the diffusion coefficients increase with the increasing pressure. Furthermore, the results obtained through the modified unipore models of Shi and Durucan17 and Cui et al.1 indicated the decreasing trend with the increasing pressure. However, Busch et al.36 also used the two exponential unipore models, and the results show that the diffusion coefficients of CO2 and CH4 decrease for the “slow” term at elevated pressures (≤6.38 MPa), as well as the results of Pone et al.47 (≤3.10 MPa). Figure 4a–d depicts the CH4 diffusion processes at different pressures for YJL, ZXZ, YX, and DS, respectively. Combined with Figure 5, it can be concluded that the diffusion coefficients of CH4 increase gradually with the increasing pressure for all of the ranks used here (Figure 5a–d), consistent with the works of Ciembroniewicz and Marecka,31 Charrière et al.,5 and Jian et al.12 For YJL (Figure 5a), ZXZ (Figure 5b), YX (Figure 5c), and DS (Figure 5d), the diffusion coefficients increase with the increasing pressure. Taking the sample DS for instance, the diffusion coefficients are 8.00 × 10–10, 9.17 × 10–10, 1.13 × 10–9, and 1.19 × 10–9 cm2/s for 2, 6, 12, and 20 MPa, respectively, at 303 K.
Figure 5.

Relationship between different pressures and diffusion coefficients of the following four coal samples: (a) YJL, (b) ZXZ, (c) YX, and (d) DS.
Figure 8.

(a) Diffusion process and the (b) variations of diffusion coefficients in coals of various ranks.
Figure 4.


CH4 diffusion processes at different pressures for (a) YJL, (b) ZXZ, (c) YX, and (d) DS.
High pressure can increase the adsorption quantity of CH4 into the coal matrix and thus microscopically enhance the collision probabilities of molecules. With the increasing molecular motion, the CH4 molecules in the adsorption state in the microporous surface will desorb into free gases and the concentration gradient about the coal matrix increases, resulting in a higher diffusion quantity. On the other hand, the transport channel of the closed pores enlarges or unfolds through the swelling of the coal matrix and further decreases the resistance force of CH4 diffusion.
4.4. Effects of Temperature on Diffusion
The impacts of temperature on diffusion processes for these four samples are depicted in Figure 6a,b. At the same pressures, the diffusion coefficients increase with the increasing temperature (Figure 6a). Taking the ZXZ for instance, the diffusion coefficients were 5.64 × 10–10, 7.81 × 10–10, 1.03 × 10–9, and 1.80 × 10–9 cm2/s for 303, 323, 343, and 363 K, respectively (Figure 6b). Other scholars such as Nandi,24 Yang,48 Schueller and Yang,49 Charrière,5 and Wang50 also reported the increase in the diffusion coefficients with the temperature. The influence of temperature on the diffusion coefficient is realized by changing the average kinetic energy of the CH4 molecule. With the increase in temperature, the vibration frequency and amplitude of CH4 molecules can be increased, and the movement of gas molecules can be accelerated simultaneously. The CH4 molecules can escape from the adsorption sites to the free state when the kinetic energy of CH4 molecules is higher than the surface free energy of gas adsorption on the coal matrix. Then, the concentration gradient above the coal matrix increases, and the diffusion kinetic energy enhances finally.
Figure 6.
(a) Diffusion processes for the four samples and (b) the relationship between diffusion coefficients and the temperature for ZXZ.
4.5. Effects of Coal Rank on Diffusion
The diffusion quantity of CH4 in all of the four coals used here increases as the diffusion process continues and their growth rates gradually decrease as the diffusion processes continue for the following conditions: 303 K, 2 MPa (Figure 7a); 323 K, 6 MPa (Figure 7b); 343 K, 12 MPa (Figure 7c); and 363 K, 20 MPa (Figure 7d). For the sample temperature and pressure, the coals of higher rank show a high diffusion quantity in the same duration (Figure 7a–d). At 323 K and 6 MPa, the diffusion quantities in the first 120 min were 4.23, 6.02, 7.91, and 14.22 cm3/g for YJL, ZXZ, YX, and DS, respectively (Figure 7a). For the variations of diffusion quantity in other conditions, refer to Figure 7c,d. In addition, it can also be concluded that the greater differences in coal rank can also result in higher differences in diffusion quantity. The diffusion quantities in DS in the first 120 min were 1.80, 2.36, and 3.36 times higher than in YX, ZXZ, and YJL, respectively.
Figure 7.
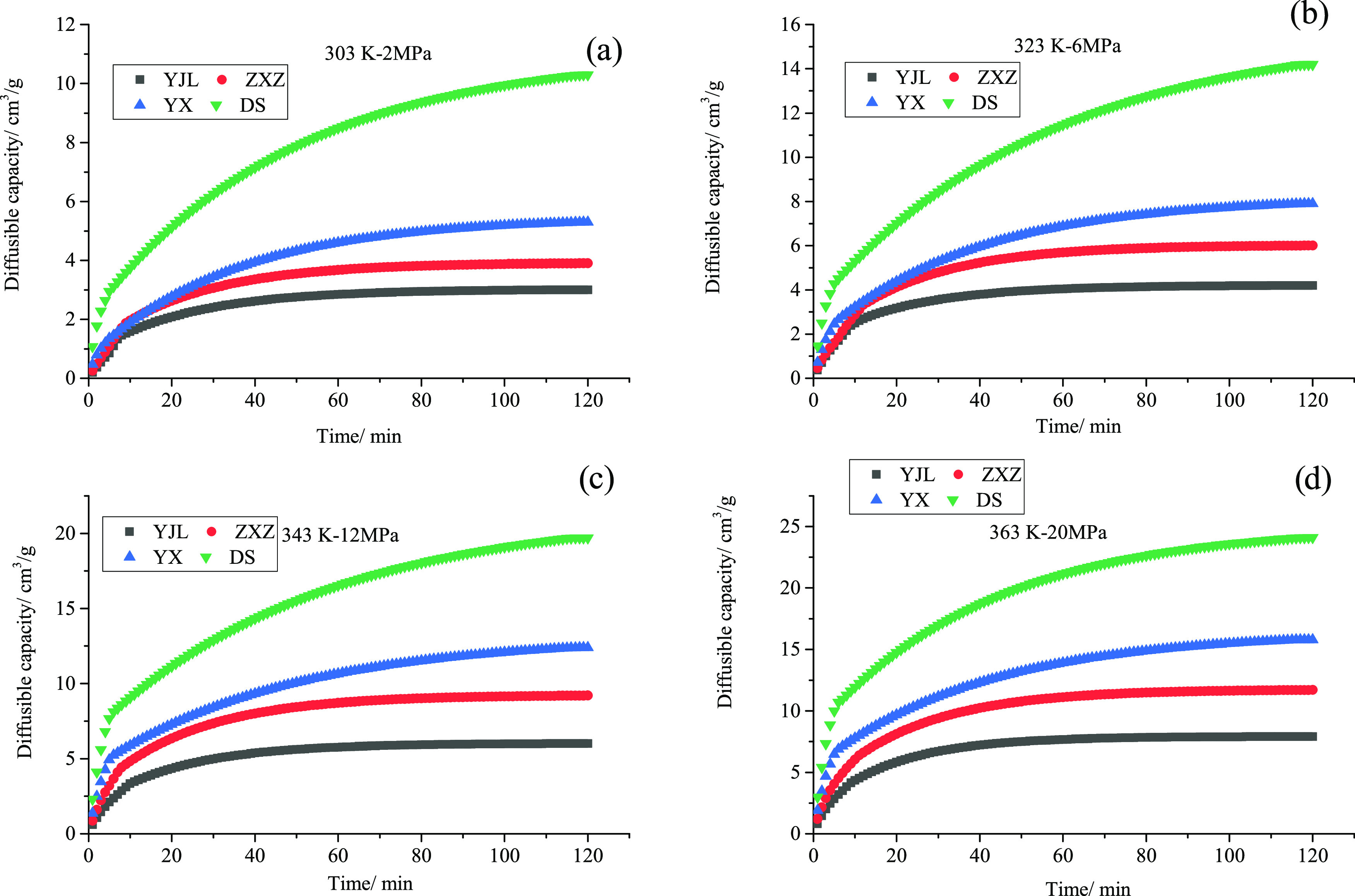
Curves of CH4 diffusion quantity in coals of different ranks: (a) 303 K, 2 MPa; (b) 323 K, 6 MPa; (c) 343 K, 12 MPa; and (d) 363 K, 20 MPa.
The diffusion processes and the variations of diffusion coefficients in coals of different ranks are depicted in Figure 8a,b, respectively. At constant pressure and temperature, the diffusion coefficients of CH4 first decrease and then increase with the increasing coal rank (Figure 8b). The minimum diffusion coefficients usually occur at about Ro,max = 1.7%. The differences in diffusion coefficients of CH4 in different ranks are induced by the variations in the adsorption capacity and pore size distribution of the various ranks.51,52 The micropores develop more frequently, and their specific surface area increases with the increasing coal rank, resulting in a higher adsorption capacity than that of the low- and middle ranks. This also ensures the long diffusion time for the high-rank coals, and the strong process of surface diffusion in micropores also contributes to higher diffusion coefficients. The low-rank coals have lower compaction degree and show higher development of natural fractures and macropores, which is also the cause of their higher diffusion coefficients than those of the middle ranks (Figure 9).
Figure 9.

Changes in (a) CH4 diffusivity and (b) incremental percentage per pressure unit at the same temperature (for the DS).
4.6. Temperature and Pressure Sensitivity Analysis of CH4 Diffusion
As an organic rock, coal is more sensitive to temperature and pressure.53−57 The temperature and pressure sensitivity of CH4 diffusion was quantified via the experimental data. Taking the sample DS at 303 K for instance, the diffusion rate (Qt/Q∝) at 303 K and 2 MPa was selected as the unified datum, and then the increase extent of the diffusion rate per unit pressure or temperature was indicative of the sensitivity. The diffusion rate and the variations of the increase extent per unit temperature for the DS are depicted in Figure 10a,b, respectively, and other coals have shown similar rules.
Figure 10.

Changes in (a) methane diffusivity and (b) incremental percentage per unit temperature (for DS).
At the same temperature, the diffusion rates of CH4 increase and the increase extent per unit first increases and then decreases with the increasing pressure. The peak pressure for the increase extent was 6 MPa for all of the samples used here. At 323 K, the diffusion rate at 2 MPa was 0.54%, and then it increases to 0.60, 0.63, and 0.65% at 6, 12, and 20 MPa, respectively. The increments of diffusion rate per unit pressure were 1.50, 0.90, and 0.61%, respectively, indicating that the impact of pressure at the low-pressure stage (2–6 MPa) was more significant than that at the high-pressure stage (6–20 MPa). The variations of increments of the diffusion rate per unit pressure also have a similar pattern. Additionally, the impacts of pressure on the diffusion rate reduced with the increasing temperature. At 6 MPa, the diffusion rates at 303 and 363 K were 1.25 and 0.50%, respectively, indicating that the higher temperature can weaken the effects of pressure on the diffusion rate. The variations at other temperatures also support this weakening effect.
The changes in CH4 diffusivity and incremental percentage per unit temperature for DS are depicted in Figure 10a,b, respectively. At the same pressure, the diffusion rates of CH4 gradually increase and the diffusion rates per unit temperature overall increase with the increasing temperature. At 2 MPa, the diffusion rate at 303 K was 0.45%, and it increased to 0.54, 0.64, and 0.80% when the temperature was increased to 323, 343, and 363 K, respectively. Additionally, the impacts of temperature on diffusion ability of CH4 gradually weakened with the increasing pressure. The diffusion rates at constant temperature were 0.48 and 0.38% for 2 MPa (343 K) and 20 MPa (343 K), respectively, indicating that the high pressure can weaken the impacts of temperature on CH4 diffusion. The variations at other pressures also support this viewpoint.
As mentioned above, the dominant factors at various diffusion stages vary. At the low-pressure stage (2–6 MPa), the impacts of pressure were more significant than at the high-pressure stage. However, as the temperature dependence, the impacts of temperature were more significant at the high-pressure stage than at the low-pressure stage. High temperature and high pressure can weaken the impacts of pressure and temperature, respectively, for the diffusion rate, indicating that diffusion mechanisms for the deep CBM resources differ significantly from those for the shallow resources.
5. Conclusions
Here, a self-developed experimental system of diffusion at high temperatures and pressures was utilized to clarify the impacts of higher pressure and temperature (303, 323, 343, and 363 K; 2, 6, 12, and 20 MPa) and coal ranks on diffusion properties in coal. The temperature and pressure sensitivity analysis of CH4 diffusion was also conducted, as well as the influences of particle size of coal, rank, temperature, and pressure. The main conclusions can be summed up as follows:
-
(1)
For the same particle size of coal, the diffusion rate decreases significantly in the first 40 min and then decreases slightly (even keeps stable) as the diffusion process continues. At the constant temperature and pressure, the diffusion coefficients of CH4 gradually decrease with increasing particle size. The variations of the diffusion coefficients are consistent for all of the ranks used here, and they increase gradually with the increasing pressure and temperature.
-
(2)
At constant pressure and temperature, the diffusion coefficients first decrease and then increase with the increasing coal rank. The minimum diffusion coefficients occur at about Ro,max = 1.7%, induced by their variations in adsorption capacity and pore size distribution of various ranks. The temperature and pressure sensitivity of CH4 diffusion was quantified via the experimental data. The increase extent first increases and then decreases with the increasing pressure. The peak pressure for the increase extent was 6 MPa for all coals. At 323 K, the diffusion rate at 2 MPa was 0.54% and then it increases to 0.60, 0.63, and 0.65% at 6, 12, and 20 MPa, respectively. The increments of diffusion rate per unit pressure were 1.50, 0.90, and 0.61% respectively, indicating that the impact of pressure at the low-pressure stage (2–6 MPa) was more significant than that at the high-pressure stage (6–20 MPa).
-
(3)
At the same pressure, the diffusion rates overall increase with the increasing temperature. At the low-pressure stage (2–6 MPa), the impacts of pressure were more significant than at the high-pressure stage. However, as for the temperature dependence, the impacts of temperature were more significant at the high-pressure stage than at the low-pressure stage.
Acknowledgments
This work is supported by the National Natural Science Foundation of China (51874122 and 51704100), the Program for Innovative Research Team of Henan Polytechnic University (T2019-4), the Key Research Projects of Henan Higher Education Institutions (18A440004 and 15A440007), the State Key Laboratory Cultivation Base for Gas Geology and Gas Control (Henan Polytechnic University) (WS2019A06), the Key R&D and Extension Projects of Henan Province (202102310223), and the Doctoral Fund of Henan Polytechnic University (B2020-8).
The authors declare no competing financial interest.
References
- Cui X.; Bustin R. M.; Dipple G. Selective transport of CO2, CH4, and N2 in coals: insights from modeling of experimental gas adsorption data. Fuel 2004, 83, 293–303. 10.1016/j.fuel.2003.09.001. [DOI] [Google Scholar]
- Hu H.; Du L.; Xing Y.; Li X. Detailed study on self-and multicomponent diffusion of CO2-CH4 gas mixture in coal by molecular simulation. Fuel 2017, 187, 220–228. 10.1016/j.fuel.2016.09.056. [DOI] [Google Scholar]
- Hu H.; Li X.; Fang Z.; Wei N.; Li Q. Small-molecule gas sorption and diffusion in coal: Molecular simulation. Energy 2010, 35, 2939–2944. 10.1016/j.energy.2010.03.028. [DOI] [Google Scholar]
- Zhao Y.; Feng Y.; Zhang X. Molecular simulation of CO2/CH4 self- and transport diffusion coefficients in coal. Fuel 2016, 165, 19–27. 10.1016/j.fuel.2015.10.035. [DOI] [Google Scholar]
- Charrière D.; Pokryszka Z.; Behra P. Effect of pressure and temperature on diffusion of CO2 and CH4 into coal from the Lorraine basin (France). Int. J. Coal Geol. 2010, 81, 373–380. 10.1016/j.coal.2009.03.007. [DOI] [Google Scholar]
- Moore T. A. Coalbed methane: a review. Int. J. Coal Geol. 2012, 101, 36–81. 10.1016/j.coal.2012.05.011. [DOI] [Google Scholar]
- Pan Z. J.; Connell L. D.; Camilleri M.; Connelly L. Effects of matrix moisture on gas diffusion and flow in coal. Fuel 2010, 89, 3207–3217. 10.1016/j.fuel.2010.05.038. [DOI] [Google Scholar]
- Weissberg H. L. Effective diffusion coefficient in porous media. J. Appl. Phys. 1963, 34, 2636–2639. 10.1063/1.1729783. [DOI] [Google Scholar]
- Paradisi P.; Cesari R.; Mainardi F. The fractional Fick’s law for non-local transport processes. Phys. A 2001, 293, 130–142. [Google Scholar]
- Webb S. W.; Pruess K. The use of Fick’s law for modeling trace gas diffusion in porous media. Transp. Porous Media 2003, 51, 327–341. 10.1023/A:1022379016613. [DOI] [Google Scholar]
- Clarkson C. R.; Bustin R. M. The effect of pore structure and gas pressure upon the transport properties of coal: a laboratory and modeling study. 1. Isotherms and pore volume distributions. Fuel 1999, 78, 1333–1344. 10.1016/S0016-2361(99)00055-1. [DOI] [Google Scholar]
- Jian X.; Guan P.; Zhang W. Carbon dioxide sorption and diffusion in coals: experimental investigation and modeling. Sci. China Earth Sci. 2012, 55, 633–643. 10.1007/s11430-011-4272-4. [DOI] [Google Scholar]
- Saghafi A.; Faiz M.; Roberts D. CO2 storage and gas diffusivity properties of coals from Sydney Basin, Australia. Int. J. Coal Geol. 2007, 70, 240–254. 10.1016/j.coal.2006.03.006. [DOI] [Google Scholar]
- Song Y.; Jiang B.; Li F.; Liu J. Structure and fractal characteristic of micro- and meso-pores in low, middle-rank tectonic deformed coals by CO2 and N2 adsorption. Microporous Mesoporous Mater. 2017, 191. [Google Scholar]
- Staib G.; Sakurovs R.; Gray E. M. A. A pressure and concentration dependence of CO2 diffusion in two Australian bituminous coals. Int. J. Coal Geol. 2013, 116–117, 106–116. 10.1016/j.coal.2013.07.005. [DOI] [Google Scholar]
- Yu S.; Yan-ming Z.; Wu L. Macromolecule simulation and CH4 adsorption mechanism of coal vitrinite. Appl. Surf. Sci. 2017, 396, 291–302. 10.1016/j.apsusc.2016.10.127. [DOI] [Google Scholar]
- Shi J.; Durucan S. A bidisperse pore diffusion model for methane displacement desorption in coal by CO2 injection. Fuel 2003, 82, 1219–1229. 10.1016/S0016-2361(03)00010-3. [DOI] [Google Scholar]
- Yu S.; Bo J.; Meijun Q. Molecular dynamic simulation of self-and transport diffusion for CO2/CH4/N2 in low-rank coal vitrinite. Energy Fuels 2018, 32, 3085–3096. 10.1021/acs.energyfuels.7b03676. [DOI] [Google Scholar]
- Cai Y.; Liu D.; Pan Z.; Yao Y.; Li J.; Qiu Y. Pore structure and its impact on CH4 adsorption capacity and flow capability of bituminous and subbituminous coals from Northeast China. Fuel 2013, 103, 258–268. 10.1016/j.fuel.2012.06.055. [DOI] [Google Scholar]
- Chengyang W.; Shixiong H.; Wenjing S.; Wei C. Fractal dimension of coal particles and their CH4 adsorption. Int. J. Min. Sci. Technol. 2012, 22, 855–858. 10.1016/j.ijmst.2012.11.003. [DOI] [Google Scholar]
- Sing K. S. W.; Everett D. H.; Haul R. A. W.; Moscou L.; Pierotti R. A.; Rouquerol J.; Siemieniewska T. Commission on colloid and surface chemistry including catalysis. Pure Appl. Chem. 1985, 57, 603–619. 10.1351/pac198557040603. [DOI] [Google Scholar]
- Yu S.; Bo J.; Jie-gang L. Nanopore structural characteristics and their impact on methane adsorption and diffusion in low to medium tectonically deformed coals: case study in the Huaibei coal field. Energy Fuels 2017, 31, 6711–6723. 10.1021/acs.energyfuels.7b00512. [DOI] [Google Scholar]
- Ruckenstein E.; Vaidyanathan A. S.; Youngquist G. R. Sorption by solids with bidisperse pore structures. Chem. Eng. Sci. 1971, 26, 1305–1318. 10.1016/0009-2509(71)80051-9. [DOI] [Google Scholar]
- Nandi S. P.; Walker P. L. Activated diffusion of methane in coal. Fuel 1970, 49, 309–323. 10.1016/0016-2361(70)90023-2. [DOI] [Google Scholar]
- Fan C.; Elsworth D.; Li S.; Zhou L.; Yang Z.; Song Y. Thermo-hydro-mechanical-chemical couplings controlling CH4 production and CO2 sequestration in enhanced coalbed methane recovery. Energy 2019, 173, 1054–1077. 10.1016/j.energy.2019.02.126. [DOI] [Google Scholar]
- Zhao D.; Feng Z.; Zhao Y. Experiment Study on Affected Factors to Seam Gas Desorption Law. Coal Sci. Technol. 2010, 5. [Google Scholar]
- Wen H.; Lu J.; Xiao Y.; Deng J. Temperature dependence of thermal conductivity, diffusion and specific heat capacity for coal and rocks from coalfield. Thermochim. Acta 2015, 619, 41–47. 10.1016/j.tca.2015.09.018. [DOI] [Google Scholar]
- Jiang Y. D.; Xian X. F.; Yi J.; Liu Z.; Guo C. Experimental and mechanical on the features of ultrasonic vibration stimulating the desorption of methane in coal. J. China Coal Soc. 2008, 33, 675–680. [Google Scholar]
- Li Z.; Wang D.; Song D. Influence of temperature on dynamic diffusion coefficient of CH4 into coal particles by new diffusion model. J. China Coal Soc. 2015, 40, 1055–1064. 10.13225/j.cnki.jccs.2014.1218. [DOI] [Google Scholar]
- Li Z. Q.; Cheng Q.; Duan Z. P.; Song D. Y.; Wen Z. H. Determination of adsorption saturation and diffusion time of gas in cylindrical coal core under different temperatures and pressures. J. Saf. Sci. Technol. 2017, 13, 92–99. [Google Scholar]
- Ciembroniewicz A.; Marecka A. Kinetics of CO2 sorption for two Polish hard coals. Fuel 1993, 72, 405–408. 10.1016/0016-2361(93)90062-7. [DOI] [Google Scholar]
- Jamialahmadi M.; Emadi M.; Müller-Steinhagen H. Diffusion coefficients of methane in liquid hydrocarbons at high pressure and temperature. J. Pet. Sci. Eng. 2006, 53, 47–60. 10.1016/j.petrol.2006.01.011. [DOI] [Google Scholar]
- Pillalamarry M.; Harpalani S.; Liu S. Gas diffusion behavior of coal and its impact on production from coalbed methane reservoirs. Int. J. Coal Geol. 2011, 86, 342–348. 10.1016/j.coal.2011.03.007. [DOI] [Google Scholar]
- Barrer R. M.Diffusion in and through Solids; Cambridge University Press: London, 1951. [Google Scholar]
- Sevenster P. G. Diffusion of gases through coal. Fuel 1958, 38, 403–418. [Google Scholar]
- Busch A.; Gensterblum Y.; Krooss B. M.; Littke R. Methane and carbon dioxide adsorption–diffusion experiments on coal: upscaling and modeling. Int. J. Coal Geol. 2004, 60, 151–168. 10.1016/j.coal.2004.05.002. [DOI] [Google Scholar]
- Ball R. C.; Bowler N. E.; Sander L. M.; Somfai E. Off-lattice noise reduction and the ultimate scaling of diffusion-limited aggregation in two dimensions. Phys. Rev. E 2002, 66, 026109 10.1103/PhysRevE.66.026109. [DOI] [PubMed] [Google Scholar]
- Grushka E.; Kikta E. J. Jr.; Cullinan H. T. Jr. Binary liquid diffusion prediction in infinitely diluted systems using the ultimate volume approach. J. Phys. Chem. A 1976, 80, 757–761. 10.1021/j100548a020. [DOI] [Google Scholar]
- Harpalani S.; Chen G. Estimation of changes in fracture porosity of coal with gas emission. Fuel 1995, 74, 1491–1498. 10.1016/0016-2361(95)00106-F. [DOI] [Google Scholar]
- Nguyen B. S.; Lin J. F.; Perng D. C. 1-nm-thick graphene tri-layer as the ultimate copper diffusion barrier. Appl. Phys. Lett. 2014, 104, 082105 10.1063/1.4866857. [DOI] [Google Scholar]
- Nie B.; Yang T.; Li X. C.; Li L.; Lu H. Research on diffusion of methane in coal particles. J. China Univ. Min. Technol. 2013, 42, 975–980. [Google Scholar]
- Nie B.; Guo Y.; Wu S.; Zhang L. Theoretical model of gas diffusion through coal particles and its analytical solution. J. China Univ. Min. Technol. 2001, 30, 19–22. [Google Scholar]
- Arami-Niya A.; Rufford T. E.; Zhu Z. Activated carbon monoliths with hierarchical pore structure from tar pitch and coal powder for the adsorption of CO2, CH4 and N2. Carbon 2016, 103, 115–124. 10.1016/j.carbon.2016.02.098. [DOI] [Google Scholar]
- Kelemen S. R.; Kwiatek L. M. Physical properties of selected block Argonne Premium bituminous coal related to CO2, CH4, and N2 adsorption. Int. J. Coal Geol. 2009, 77, 2–9. 10.1016/j.coal.2008.05.020. [DOI] [Google Scholar]
- Pini R.; Ottiger S.; Storti G.; Mazzotti M. Pure and competitive adsorption of CO2, CH4 and N2 on coal for ECBM. Energy Procedia 2009, 1, 1705–1710. 10.1016/j.egypro.2009.01.223. [DOI] [Google Scholar]
- Xiang J. H.; Zeng F. G.; Liang H. Z.; Li B.; Song X. X. Molecular simulation of the CH4/CO2/H2O adsorption onto the molecular structure of coal. Sci. China Earth Sci. 2014, 57, 1749. 10.1007/s11430-014-4849-9. [DOI] [Google Scholar]
- Pone J. D. N.; Halleck P. M.; Mathews J. P. Sorption capacity and sorption kinetic measurements of CO2 and CH4 in confined and unconfined bituminous coal. Energy Fuels 2009, 23, 4688–4695. 10.1021/ef9003158. [DOI] [Google Scholar]
- Yang R. T.Gas Separation by Adsorption Processes; Imperial College Press: London, 1997. [Google Scholar]
- Schueller B. S.; Yang R. T. Ultrasound enhanced adsorption and desorption of phenol on activated carbon and polymeric resin. Ind. Eng. Chem. Res. 2001, 40, 4912–4918. 10.1021/ie010490j. [DOI] [Google Scholar]
- Wang Z. F.; Tang X.; Yue G.; Kang B.; Xie C.; Li X. Physical simulation of temperature influence on methane sorption and kinetics in coal: Benefits of temperature under 273.15 K. Fuel 2015, 158, 207–216. 10.1016/j.fuel.2015.05.011. [DOI] [Google Scholar]
- Li Y.; Yang J.; Pan Z.; Tong W. Nanoscale pore structure and mechanical property analysis of coal: An insight combining AFM and SEM images. Fuel 2020, 260, 116352 10.1016/j.fuel.2019.116352. [DOI] [Google Scholar]
- Li Y.; Zhang C.; Tang D.; Gan Q.; Niu X.; Wang K.; Shen R. Coal pore size distributions controlled by the coalification process: an experimental study of coals from the Junggar, Ordos, and Qinshui basins in China. Fuel 2017, 206, 352–363. 10.1016/j.fuel.2017.06.028. [DOI] [Google Scholar]
- Cai H. Y.; Güell A. J.; Chatzakis I. N.; Lim J. Y.; Dugwell D. R.; Kandiyoti R. Combustion reactivity and morphological change in coal chars: effect of pyrolysis temperature, heating rate and pressure. Fuel 1996, 75, 15–24. 10.1016/0016-2361(94)00192-8. [DOI] [Google Scholar]
- Fermoso J.; Arias B.; Plaza M. G.; Pevida C.; Rubiera F.; Pis J. J.; García-Peña F.; Casero P. High-pressure co-gasification of coal with biomass and petroleum coke. Fuel Process. Technol. 2009, 90, 926–932. 10.1016/j.fuproc.2009.02.006. [DOI] [Google Scholar]
- Tremel A.; Haselsteiner T.; Kunze C.; Spliethoff H. Experimental investigation of high temperature and high pressure coal gasification. Appl. Energy 2012, 92, 279–285. 10.1016/j.apenergy.2011.11.009. [DOI] [Google Scholar]
- Li Y.; Wang Y.; Wang J.; Pan Z. Variation in permeability during CO2–CH4 displacement in coal seams: Part 1-Experimental insights. Fuel 2020, 116666 10.1016/j.fuel.2019.116666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Q. M.; Liu S. M.; Wang G.; Cheng W. M. Evaluating the changes of sorption and diffusion behaviors of Illinois coal with various water-based fracturing fluid treatments. Fuel 2021, 283, 118884 10.1016/j.fuel.2020.118884. [DOI] [Google Scholar]






