Abstract
The COVID-19 virus outbreak has affected most of the world in 2020. This paper deals with artificial intelligence (AI) methods that can address the problem of predicting scale, dynamics and sensitivity of the outbreak to preventive actions undertaken with a view to combatting the epidemic. In our study, we developed a cellular automata (CA) model for simulating the COVID-19 disease spreading. The enhanced infectious disease dynamics (Susceptible, Exposed, Infectious, and Recovered) model was applied to estimate the epidemic trends in Poland, France, and Spain. We introduced new parameters into the simulation framework which reflect the statistically confirmed dependencies such as age-dependent death probability, a different definition of the contact rate and enhanced parameters reflecting population mobility. To estimate key epidemiological measures and to predict possible dynamics of the disease, we juxtaposed crucial CA framework parameters to the reported COVID-19 values, e.g. length of infection, mortality rates and the reproduction number. Moreover, we used real population density and age structures of the studied epidemic populations. The model presented allows for the examination of the effectiveness of preventive actions and their impact on the spreading rate and the duration of the disease. It also shows the influence of structure and behavior of the populations studied on key epidemic parameters, such as mortality and infection rates.
Although our results are critically dependent on the assumptions underpinning our model and there is considerable uncertainty associated with the outbreaks at such an early epidemic stage, the obtained simulation results seem to be in general agreement with the observed behavior of the real COVID-19 disease, and our numerical framework can be effectively used to analyze the dynamics and efficacy of epidemic containment methods.
Keywords: Novel coronavirus, Cellular automata, SEIR model, Epidemic spread model, Mathematical model
Highlights
-
•
Cellular Automata include density population of Poland, France, Spain in SEIR model.
-
•
We analyze influence of parametric adjustment for modeling pandemic prevention.
-
•
The earlier reduction of personal contacts the faster reduction of infections number.
-
•
Age dependent mortality rates are explored to reflect the real features of COVID-19.
-
•
Our approach allows for modeling of COVID-19 presumable dynamics.
1. Introduction
In December 2019 coronavirus disease (COVID-19) emerged in China. Within a few weeks, the disease spread far beyond China, reaching countries in all parts of the globe. At the beginning of March 2020, the governments in most countries, including Europe, closed the borders for international movement. Also, the freedom to travel within the countries has been significantly curbed. This is associated with the decision to take immediate actions to limit the spread of the COVID-19 virus(Wu, Leung, & Leung, 2020). Actions taken include stopping the inflow of people from abroad, and limiting or eliminating the possibility of gathering people in larger clusters and social groups(Lloyd-Smith, Schreiber, Kopp, & Getz, 2005). All persons coming to these countries are subject to quarantine for at least 14 days, while citizens are asked to minimize their stay away from home, and are encouraged to stay at home to decrease virus transmission (similar processes have been previously described in relation to the SARS epidemic(Chowell and Lee, 2015, Kucharski, 2015, Riley et al., 2005). At the same time, a few European governments adopted a strategy of maximum hygiene, self-control, and elimination of social activities of these groups of citizens who are particularly exposed to the risk of infection. The main attention was directed to the elderly people whose stay at home was highly recommended(Alwan et al., 2020).
Despite the weakening of the epidemic dynamics spread in most regions, forecasting the development of the COVID-19 remains an issue that plays an important role, helping to quantify possible control and manageable levels of the disease. Due to the global nature of the phenomenon, though the incomplete clinical COVID-19 description, the scale of availability and amount of collected epidemic data(World Health Organization, 2020) is unique and allows extensive use of data mining and modeling methods, which become essential parts of assessing the impacts of mitigation strategies(Anderson, Heesterbeek, Klinkenberg, & DeirdreHollingsworth, 2020). In this context, mathematical models of infectious disease transmission dynamics remain one of the most useful and popular methods, that allow to predict, assess, and control potential epidemic outbreaks(Djordjevic et al., 2018, Rachah and Torres, 2018).
Traditionally, differential equations have been used to describe the spreading of a contagious disease(Murray, 1993). An epidemic model usually falls under one of the following types: , , or . This involves taking into account in our model parameters specific to the models. The components of these models, i.e.individuals susceptible (), exposed (), infected () and recovered (), change their value over the time according to time-dependent differential equations(Fu and Milne, 2003, Liu et al., 2006, Milne et al., 2008, Pfeifer et al., 2008). Recently, more complex compartmental models have been proposed for COVID-19 analysis, i.e. model with death () class(Fanelli & Piazza, 2020) and model with new super-spreaders (), asymptomatic (), hospitalized (), fatality () classes(Ndairou, Area, Nieto, & Torres, 2020). These models introduce new groups of population, which appear to be relevant in the context of medical reports, but still do not take into account the local characteristics of the epidemic spread process, individual contact processes and their effects, spatial aspects of the spread of the epidemic, and different vulnerability patterns groups of individuals(White, del Rey, & Sanchez, 2007).
In this paper we applied an improved cellular automata (CA) approach to verify (using available epidemiological and social data) the potential causes of the observed epidemic features and help to develop guidelines which will be more effective in terms of government goals. Our analyses are based on the use of a modified influenza spread model, which we presented in our earlier paper(Holko, Medrek, Pastuszak, & Phusavat, 2016). Our model remove the drawbacks of traditional models(Achmed & Agiza, 1998) by the inclusion of external infections attributed to moving individuals(Boccara & Cheong, 1993) and reflecting the realistic age structure of the population with age dependent vulnerability of individuals(White et al., 2007) and real population density distribution. Although classic CA model has some limitations like shape of cells, the regular neighbors pattern and simple rules of interconnections between people, researches try to overcome these disadvantages integrating e.g.the geographical assumptions necessary for studying the epidemics spread in a realistic way(Zhong, Huang, & Song, 0000). Our model develops such approach and introduces factors related to the actual demographic and geographic profiles of the simulated population. Consequently, we can now present a novel, complete model to simulate the epidemic spread based on CA. The simulation results obtained seem to be in agreement with the observed features of the COVID-19 epidemic. The considerations presented in the paper are aimed mainly at presenting a new simulation model and detailed analysis of the results of modeling in the social and economic perspectives will be the subject of our further work.
The paper is organized as follows: the next Section presents numerical model. The spatial and social parameters used in our simulations are described briefly in Section3. Section4 contains results of numerical simulations. The paper is concluded by a short summary of main results.
2. Numerical epidemic model
Most epidemic models which incorporate death causing diseases and varying total population assume a population of size N which is partitioned into separated subclasses of individuals who are susceptible () i.e.who can contract the disease, who are infectious () and who have recovered ()(Anderson & May, 1979). The size of each class of the population varies in time and the whole population size is given by
| (1) |
In the model(Aron & Schwartz, 1984) and additional compartment is incorporated and it describes those exposed who are infected but not yet infectious (denoted by ). The time evolution of the population compartments model is described by set of differential equations(Pfeifer et al., 2008)
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
where is time, and are death and birth rates, is the mean latent period for the disease, is the mean infectious period and is the contact rate which denotes the probability of getting the disease through contacts between susceptible and infectious individuals. The basic reproduction number which determines whether an infectious disease can spread () is given by
| (7) |
and it measures the number of secondary cases that can be expected from a single case of the disease.
Since the SEIR model does not reflect the behavior of individuals and it shows the infection on the population level we use as the basis in our simulation framework an enhanced model(Holko et al., 2016), which introduces into the system additional coefficients that reflects some demographic interactions and geographical configuration.
2.1. Cellular automata model
We use CA model where the finite set of states can be observed in the cellular two-dimensional space , with rows and columns iterated by and , respectively. The CA system is defined by tuple , where is a function of the Moore neighborhood(del Rey et al., 2006, Delorme, 1999) with a distance of one and is a local transition function of cell at the instant of time. Fig.1 shows the example of a state of an –th cell at the time described by equations
| (8) |
| (9) |
where is the whole population of the cell, and are respectively numbers of susceptible and recovered individuals and and are the numbers of exposed and infective individuals in a –th day of the given stage of an infection, where and are the periods of exposed and infective stages in days.
Fig. 1.
Illustration of number of individuals in cell in different states at instant of time, Eq.(9).
In the CA model, we assume that the exposed state has no any infectivity capability. However, there are many reports that infected persons who have no any symptoms yet can infect others(Ferretti et al., 2020, Hu et al., 2020). In our opinion such presymptomatic cases can be included into the presented model through the extension of the length of the infective state (reduction of the length of exposed state ) in Eq.(9), since the only difference between and is the ability to infect. Including new compartments (besides SEIR) into the model requires the consensus on the values of the parameters characterizing these new groups — as far as we know, there is no such agreement yet because of the early stage of the pandemic.
In the next part of this section we present some new components which we introduced into the model of Holkoetal. (Holko et al., 2016) to reflect the condition of individuals and population dynamics over time, that appear to be relevant to COVID-19 epidemic.
2.1.1. Improved daily commutes model
We introduced into the daily commutes model the assumption that exposed () and recovered () travelers are irrelevant to the spread of the epidemic since they cannot infect anyone and re-infect themselves. The numbers of individuals who travel to another cell at the instant of time is denoted by the
| (10) |
where and denote the fractions of healthy and infective individuals commuting outside the cell, respectively. The states of the source and destination cells are defined by
| (11) |
Moreover, we assume that the destination cell is randomly selected from the three cells with largest population over a neighborhood defined by the Chebyshev distance (Abello, Pardalos, & Resende, 2002) between the and cell given by
| (12) |
2.1.2. Direct contact rate
In our model the transition function is defined by the set of the following equations:
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
where and denote the day number of and states respectively, and are natural deaths and births rates (Eq.(23)), is the COVID-19 mortality rate. Descriptions and initial values of all parameters used in eqs.(13)–(18) are listed in Table2. Additionally we introduced the direct contact rate which corresponds to the number of direct contacts of susceptible individuals () with infectious (), which may reflect the population density(Hu, Nigmatulina, & Eckhoff, 2013), the epidemic phase and prevention. New infections appear according toEq.(14) where is the random probability of infection given by
| (19) |
| (20) |
where is a Gaussian random number with mean value defined by the binomial probability of infection in direct contacts between susceptible and infectious individuals, is the total number of contacts a person has with other people, is the straight probability of infection given by the ratio of infectious in the whole population, and is the variance of the Gaussian generator. Fig.2(a) shows the mean value of probability of infection as a function of direct contact rate for four cases of straight probability .
Table 2.
Initial parameters of the model.
| Parameter | Description | Initial value | References — estimation source |
|---|---|---|---|
| Fixed length in days of the exposed state (). | 5 | [28] | |
| Fixed length in days of the infective state (). | 7 | [26] | |
| Individual contact rate between individuals in a cell. | from 0.15 to 2.00 | [30] | |
| Variation coefficient of the infection probability. | 0.1 | ||
| New births per one individual per time step.a | [42] | ||
| Natural deaths per one individual per time step.a | [42] | ||
| Mortality rate per time step, i.e. probability of a death of an infected individual. | Eq. (21) | [46] | |
| Fraction of a healthy population commuting outside of their cell. | 0.037 | [17] | |
| Fraction of an infected population commuting outside of their cell | 0.021 | [26] | |
| Fraction of commuters commuting outside of their neighborhood. | 0.23 | [17] |
Values for Poland, France, and Spain respectively.
Fig. 2.
(a): mean value of the infection probability in particular cell for four different values of the straight probability of infection as a function of individual contact rate , according to Eq.(19). (b): map plot of as a function of and , with four isolines for .
2.1.3. Variable mortality rate
To reflect different mortality for various age ranges of a population we introduced into our model variable mortality rate , which is randomly chosen with the probability density which reflects the demographical structure of the population:
| (21) |
| (22) |
where is the age range and is the probability density of belonging the individual to chosen age range. The values of we select with particular attention to empirical data(Lin et al., 2020) in Section2.2.
2.2. Geographical and demographical configurations
Our CA simulation system is based on heterogeneous distribution of the population across the cells (Fig.3) and can change over time due to births and deaths. We use numerical grids of population counts for Poland, France and Spain with the cell size km (Poland), km (France) and km (Spain) where initial values we set according to CIESIN population counts, v.3(Center for International Earth Science Information Network (CIESIN) / Columbia University; United Nations Food and Agriculture Programme (FAO); Centro Internacional de Agricultura Tropical (CIAT), 2005).
Fig. 3.
Simulation grids with the populations counts of Poland (a), France (c), and Spain (e).
Since the mortality rate in our simulation varies for different age ranges of individuals (see Eq.(21)) we use the actual age distribution of Poland(CentralStatisticalOffice, 2017), France and Spain(United Nations, Department of Economic and Social Affairs, Population Division, 2020) to set the appropriate mortality rates for each age range of these populations (Fig.4).
Fig. 4.
Age structure of the population of Poland, France, and Spain (a) and COVID-19 mortality rates(World Health Organization, 2020) as a function of different age ranges (b).
According to recent reports COVID-19 mortality rate differs not only by age, but also by gender of the individuals. Although male COVID-19 mortality rate is generally higher than the COVID-19 female mortality rate across all ages in all countries, there are some notable differences between individual countries. Table1 shows the GMR (gender mortality ratio) defined by
for age ranges reported by Reinsurance Group of America(Ng, Bakrania, Russell, & Falkous, 2020) for Spain (data for age groups , and Poland and France were not accessible). We use the GMR values and the age–gender structure of Spanish population(United Nations, Department of Economic and Social Affairs, Population Division, 2020) to obtain corresponding mortality rates for males and females in all age groups — they are presented in two last columns of Table1.
Table 1.
COVID-19 mortality rates for different genders and age groups in Spain.
| Age range | Fraction of population |
Mortality rate | GMR | Age–gender mortality rate |
||
|---|---|---|---|---|---|---|
| Male | Female | see Fig.4 | Male | Female | ||
| 40–49 | 0.086 | 0.084 | 0.0040 | 1.6 | 0.0049 | 0.0031 |
| 50–59 | 0.074 | 0.074 | 0.0130 | 2.2 | 0.0179 | 0.0081 |
| 60–69 | 0.053 | 0.057 | 0.0360 | 2.3 | 0.0509 | 0.0221 |
| 70–79 | 0.039 | 0.046 | 0.0800 | 2.3 | 0.1153 | 0.0501 |
| 80 | 0.023 | 0.039 | 0.1480 | 1.5 | 0.1873 | 0.1248 |
3. COVID-19 numerical model parametrization
At initial stages of an epidemic, numerical modeling can help understand the dynamics of a new disease and identify key parameters affecting the speed of its spread. Table2 shows the initial values of key model parameters which we estimate according to recent reports from the regions that were affected by the COVID-19 epidemic — estimation sources are listed in the last column. The lengths of exposed (Eq.(3)) and infective (Eqs.(4), (5)) states we set according to median incubation period of COVID-19 (5.1 days) reported by Lauer etal.(Lauer et al., 2020) and most infectious period (7 days) reported by Kelvin Kai Wang etal.(Kai-WangTo, 2020).
Our simulations are geographically located in three countries: Poland, France, and Spain. Fig.3 (left panel) shows the grids configuration for selected regions. Moreover, to show the age structure for each country we divided each population into age ranges corresponding to different reported mortality ratios of COVID-19. Fig.3 shows the structure of populations provided by Countrymeters.info database(CountryMeters, 2020) and corresponding COVID-19 mortality ratios(WorldoMeters, 2020). Respective values of natural birth and natural death rates per one time step (1 day) for each countries we calculated using demographic data on the number of births and deaths in Poland, France, and Spain(United Nations, Department of Economic and Social Affairs, Population Division, 2020) according to equation
| (23) |
where is the total population of each country.
Since the probability of dying from the disease depends on the age of an individual we use heterogeneous and age-dependent mortality rate per time step , which is chosen according to age population structure (Fig.4(a)) and age distribution of COVID-19 mortality rate (Fig.4(b)). Additionally, our model includes daily commutes of individuals with different commuters ratio for healthy and infected individuals and commuting over a longer distance (Holko et al., 2016). These parameters we estimate according to “Statistics on commuting patterns at regional level” provided by Eurostat(Eurostat, 2016), where the number of people commuting to another region (NUTS, level 2) is assessed to 8.1% of total persons in employment, which gives the number of daily commuters about 3.7% of total population (with respect to employment rate and the percentage of people of working age in Europe,(Eurostat, 2020). The fraction of commuting infected population we estimate as of the value of daily commuters according to the median interval between symptom onset and hospitalization (isolation) (4 days) reported by epidemiologists(Kai-WangTo, 2020) while the mean length of the infective state we previously assessed to days.
4. Results of the simulation
To organize our simulations, we divided them into three parts. Section4.1 concerns the dependence of reproduction number (Eq.(7)) on the contact factor describing the interaction between individuals in and groups of the population. Section4.2 describes the dynamics of the epidemic and the impact of various intervention scenarios for Poland. The last part (Section4.3) compares the most important results for all countries under analysis (Poland, France, and Spain).
4.1. Basic reproduction number
As reproduction number is the critical conditioning parameter for the disease, we started by determining the relationship between and the parameter of our simulation — contact rate (Eq.(20)). To set , we use the equation
| (24) |
according toHolko et al..
Fig.5 shows that grows with and which corresponds to the estimated value of reproduction number for COVID-19(Hellewell et al., 2020). The direct contact rate meets the case when an infectious individual has contacts with susceptible person once every two days. For values of we can expect epidemic progress while for smaller values of the epidemic is suppressed.
Fig. 5.
Mean value of as a function of contact rate .
Additionally we empirically verified that the relationship of is independent of the geometry of simulation and the population structure; therefore we can assume that it is the same for all countries considered.
4.2. Dynamic of the epidemic
All results presented in this part are ensemble-averaged over runs performed for the same initial configuration of infected individual, which was generated by a random selection of 15 cells with the population above and moving in each of these cells a group of individuals to the infectious state. We ensured that averaging over a larger number of realizations gave no significant changes in the results.
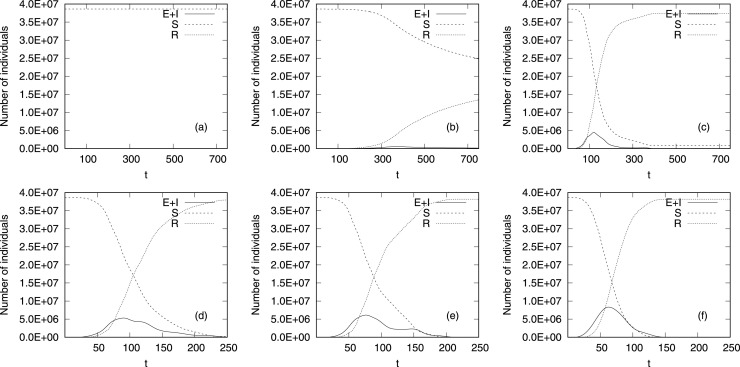
First, we perform simulation of spreading disease for set values of , corresponding to the most likely values, in the vicinity of reported . Fig.6 displays the time history (with time step in days, horizontal axis) of the number of individuals in compartments . Since in the upper row of Fig.6(a)–(c) we present results for smaller and the disease lasts much longer than for bigger (lower row of Fig.6(d)–(f)), we set the range of -axis to and days for upper and lower row of Fig.6, respectively.
Fig. 6.
Average number of for (a), (b), (c), (d), (e) and (f) as a function of time step .
Fig.6 shows that for all values of contact rate the number of susceptible individuals (dash–dot line) decreases, while the number of recovered ones (dotted line) grows with time. It is the result of an ongoing epidemic whose intensity depends on the number of the infected (solid line). For very small values of the number of never falls below the number of the recovered (Fig.6(a)–(b)), which means that the disease affected less than half of the population. For the epidemic spreads for limited time ( days) but the numbers of and is much smaller than and they are not discernible on Fig.6(a).
The dynamic of the disease hinges on the values of contact rate parameter (). Higher values of accelerate the disease (lower row of Fig.6, from (d) to (f)) and the number of infected individuals () reaches its maximum value faster if the is greater. The maximum value of increases with the contact rate, the disease is accumulated in time for higher values of , while for low contact rates the number of infected individuals is blurred in time and becomes less intense.
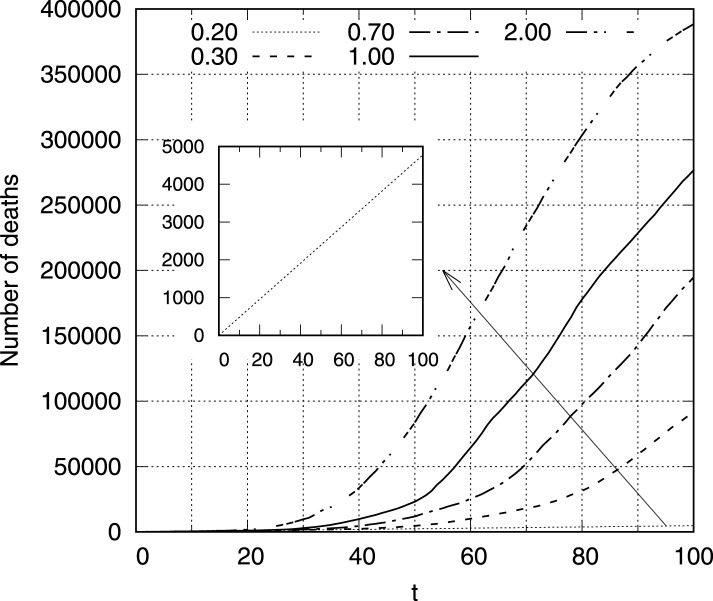
Fig.7 illustrates the number of deaths for days of epidemic for different values of contact rate . It is noticeable that this relationship is more non-linear for larger values of , while for small (which corresponds to ) the number of victims increases almost linearly (internal enlarged panel in Fig.7). Observed dependency is in general agreement with epidemic patterns shown in Fig.6, where the nonlinearity of grows for larger values.
Fig. 7.
The number of deaths as a function of time step for (internal panel enlarges the dependency for to ensure the sufficient visibility).
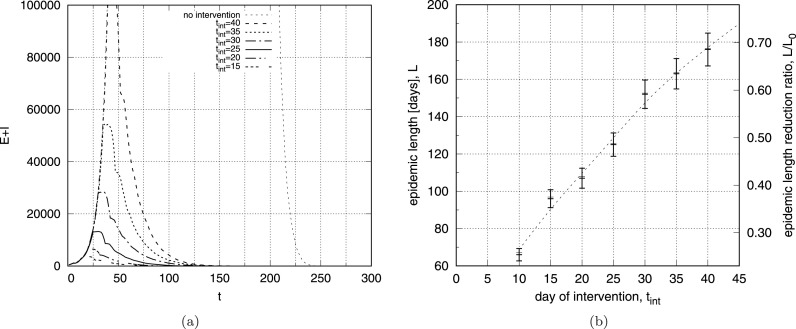
The disease reveals time signatures that follow similar scenario for the constant values of : a rapid increase in the number of and a slower decrease after it reaches its maximum (Fig.6). In order to simulate preventive measures that inhibit the development of an epidemic, we conducted simulations with value which changes in time – Fig.8. To reflect the preventive action taken at various stages of the epidemic development we use initial configurations with () and reduce it times, at day of the disease. It corresponds to a five-fold reduction in the number of direct contacts among people in the epidemic population. The left panel of Fig.8 shows the number of as a function of time and it confirms that such a strong reduction of (corresponding to ) stops the development of the epidemic and reduces the number of infected individuals faster if the reduction occurs earlier. However, this relation is not linear and the effect of shortening the epidemic is stronger for smaller (right panel of Fig.8): intervention at reduces the length of the disease to of its original length, while changing at gives the epidemic reduction time up to . It means that strong intervention taken even later in the development of epidemic can effectively shorten its duration.
Fig. 8.
The number of exposed and infected individuals as a function of time step for and for different days of intervention (a) and epidemic length as a function of day of intervention (b).
Another way to reduce the spread of an epidemic may be decreasing the population mobility. In our model we have three commuting rates, separately for healthy population (), infected population () and for individuals commuting outside their neighborhoods () – typical values of these parameters are presented in Table2.
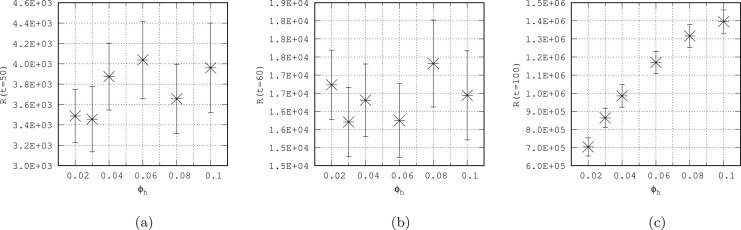
To verify the influence of such defined mobility of individuals on the spread of the disease, we set at 20 infectious in the most dense cell of our system (with the population of over 112 000) and check how the disease develops for different values of commuting ratio ( and - see Table2). The results are presented in Fig.9 where (a) shows the evolution of infection for and (b) for increased mobilities . A much faster development of the epidemic is noticeable (Fig.9(b)) due to greater population mobility and this relationship is quantitatively confirmed by the time history of number for different values of , presented on Fig.9(c). The difference between number for growing commuting ratios is more discernible for larger which suggests, that in the early stages of an epidemic , the impact of mobility of individuals on the speed of epidemic development may be less. To check it we plot on Fig.10 the number of as a function of commuting ratio for three instants of time: (a), (b) and (c). Our results confirm that the acceleration of the epidemic due to increased mobility is clearly visible after some period of time (, Fig.10(c)), while at shorter intervals (Fig.10(a), (b)) it is not clearly visible. It may be the result of acquiring population resilience over time due to the larger compartment in limited area (Fig.10(a), (b)), whereas for longer time the disease propagates to new regions (CA cells) and the epidemic suppression effect for higher values of commuting ratio is not so significant (Fig.10(c)).
Fig. 9.
The map plot of the number of recovered individuals for and commuting rates (a), (b) at days. Figure(c) presents time history of the number of recovered for different values of commuting rates and .
Fig. 10.
The number of recovered individuals for as a function of commuting ratio for three instants of time (a), (b) and (c).
Table 3.
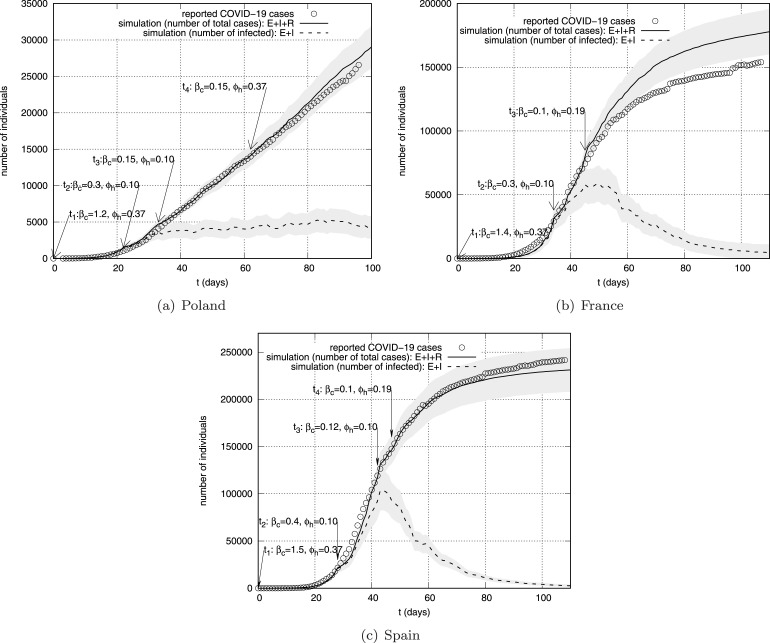
Estimated model parameters values for the COVID-19 disease cases presented on Fig.12.
| Country | Time step t | Contact rate | Commuting rates | Date |
|---|---|---|---|---|
| Poland Fig.12(a) | 1.20 | 0.37 | 04.03.2020 | |
| 0.30 | 0.10 | 26.03.2020 | ||
| 0.15 | 0.10 | 05.04.2020 | ||
| 0.15 | 0.37 | 05.05.2020 | ||
| France Fig.12(b) | 1.40 | 0.37 | 23.02.2020 | |
| 0.30 | 0.10 | 27.03.2020 | ||
| 0.10 | 0.19 | 08.04.2020 | ||
| Spain Fig.12(c) | 1.50 | 0.37 | 22.02.2020 | |
| 0.40 | 0.10 | 15.03.2020 | ||
| 0.12 | 0.10 | 04.04.2020 | ||
| 0.10 | 0.19 | 10.04.2020 | ||
Fig. 12.
The number of reported COVID-19 cases (circles) and corresponding simulation results: mean cumulative number of infections (solid line) and the number of infected (dashed line) as a function of time for Poland (a), France (b), and Spain (c). Shaded areas represent reference ranges.
4.3. Influence of the population age structure on the epidemic mortality rate
In this section we consider the impact of the age structure of the population on the mortality rate , which we define as an indicator quantifying the increase or decrease in mortality due to the epidemics, i.e.
| (25) |
where and denote the number of recovered and deaths from the disease, respectively. To verify the impact of the age structure of the population in real conditions, we conducted simulations for three selected countries whose populations show discernible differences — the right panel of Fig.3 shows population structures of Poland, France, and Spain in the analyzed age ranges. In the case of Poland, the largest age groups are in the range of 20–69years, and the number of older people (70+) is rapidly decreasing. In the case of Spain, and France especially, the oldest groups (70+), for which the observed mortality rate is the highest (8% for 70–79 and over 14% for the 80+ group) are much more numerous. Moreover, France has the most balanced age structure — all groups below 70years are similar.
To reflect the age structure we used in our model heterogeneous mortality, which was introduced into the numerical system as the COVID-19 mortality rate per time step selected according to different age structures for countries analyzed (Fig.4).
Fig.11 presents averaged (over 10 runs) mortality rate as a function of the contact rate for the analyzed populations, for the first days of the epidemic. The highest values of were obtained for France, which has the highest percentage of age group 60+. Slightly lower values of occur for Spain, which has a similar percentage in the 60+ age group, but in this case the number of people in the 0-29 age group is much smaller than in France. For Poland, whose population is relatively the most numerous in the 0-39 age range, the mortality rate is the lowest, regardless of . In general, the values of mortality rates for France range from about (corresponding to 4.5%) to (2%). The lowest values of were obtained for Poland, and they are in the range , while for Spain we received intermediate values of . Our results confirm expectations related to the impact of the size of most exposed age groups (which are the biggest in France), on the mortality rate expressed for the entire population.
Fig. 11.
Mortality ratio as a function of for Poland, France and Spain.
Another interesting effect is the dependence of on the value of contact rate : mortality rates are lower for bigger values of . Since increasing value of accelerates the spread of the epidemic we conclude that this relationship is the result of a faster reduction in the number of the most vulnerable population age groups (60+), which follows more intensively in the beginning of disease.
Finally, to test the impact of the gender (different mortality rates for males and females) on total mortality rate , we run some simulation for Spain with age–gender dependent mortalities provided by Reinsurance Group of America (see Table1). Received values of for where consistent (within the error limits) with values presented in Fig.11. We conclude that such result confirms our findings and to assess the value of total mortality ratio we can use the averaged mortalities for different age groups (regardless of gender).
4.4. Model calibration for the COVID-19 outbreak in Poland, France, and Spain
A common approach to quantify model parameters that cannot easily be measured directly is to adjust the parameters until the model output closely matches empirical data. This approach is known as inverse modeling or model calibration(Schittkowski, 2002). We infer the model parameters based on the data provided by European Centre for Disease Prevention and Control(ECDC, 2020) about the evolution of COVID-19. Fig.12 shows the best fit of cumulative number of infection we have been able to get for Poland (a), France (b), and Spain (c). To estimate the values of the parameters , that should realistically reproduce the data, we use a best-fit approach: (1) we started with initial values of contact rate and commuting ratios reported in Table3 for , (2) then we checked if the simulation results deviate from the data by more than 10% for the subsequent time steps ; (3) if so, we tried to adjust the parameters to achieve the assumed compliance. At the beginning of the calibration process for each country, we set the initial configuration of infected individuals, which was generated by a random selection of 5 cells with the population above of inhabitants and moving in these cells a group of 5 individuals to the infective state. The estimated values of the model parameters are presented in Table2.
For the very early stage of the epidemic (Fig.12, ) we estimated the highest value of (which corresponds to the reproduction number ) for Spain, while for France it is () and for Poland (). Received values of are slightly overestimated in comparison with values of reported by Liu etal. (Liu, Gayle, Wilder-Smith, & Rocklov, 2020) and Yuan etal.(Yuan, Li, G., & Lu, 2020). However, the effective reproduction number values estimated for other -type models are higher than for different methods (e.g.statistical exponential Growth, statistical maximum likelihood estimation)(Liu et al., 2020) and it may be the result the significant impact of the initial configuration of the system. For longer time we can observe significant reduction in the contact rate and commuting rates , first for Poland and Spain () and then for France (). This is the result of introducing prevention, travel limitation and quarantine. The imposed restrictions were initially the largest in Poland (e.g.relatively the earliest closing of schools after registering the first cases of COVID-19), but over time France and Spain introduced stricter restrictions (especially in terms of freedom of communication) which are maintained in a mild form up today, while in Poland after about 60 days travel restrictions were lifted. Such scenario is in general agreement with our findings (Fig.12), where initial value of is reduced to for France and Spain (), and to for Poland (). The number of infected individuals for France and Spain after and (respectively) clearly drops (Fig.12(b)–(c), dashed lines) which corresponds to the effective suppression of the epidemic, while for Poland the size of compartment is not reduced in time (Fig.12(a), dashed line), which can be interpreted as a sign of lower effectiveness of the preventive action taken ( is close to 1).
Obtained simulations results show also a good agreement with the reported COVID-19 data for active cases (). Fig.13 presents the time history of the active cases for Poland (a), France (b), and Spain (c) for the configuration from Table3 (dotted line) and reported values (circles)(WorldoMeters, 2020). The number of CA based active cases (dotted lines) is close to the real values for all countries. Solid lines on Fig.13 show the numbers of active cases for reduced length of exposed state and extended length of infective state (respectively, and parameters from Table2). We made such modification since there are many reports that the transmission of the virus may be presymptomatic(Ferretti et al., 2020, Wei et al., 2020). We tried to check the impact of such presymptomatic infections on the disease spreading by changing the duration of and states. Received results indicate high dependence on lengths of and states: with the reduction to days (extension to days) the number of active cases (Fig.13, solid lines) increases rapidly and significantly exceeds the observed values (Fig.13, circles). Better results we received for the previous model configuration (Fig.13, dotted lines) which confirms the typical duration of the exposed ( days) and infective ( days) states.
Fig. 13.
The number of reported COVID-19 cases (circles) and corresponding simulation results for different lengths of the exposed state (dotted line) and (solid line) as a function of time for Poland (a), France (b), and Spain (c).
5. Conclusions and future research
We investigate numerically the epidemic model for the novel coronavirus spreading. Our model uses two-dimensional cellular automata. Numerical simulations were performed for three countries affected by the epidemic, i.e.Poland, France, and Spain. Although the results obtained refer to the models described in earlier publications, the approach we propose includes new elements that increase the scientific and practical value of the models used so far.
Since the empirical data show a strong relationship between the age of infected people and the level of mortality, we introduced into the system probability of death which depends on the age structure of the populations under analysis. Numerical results show varying mortality rates for different countries, e.g.for France, where the fraction of people in the most vulnerable age group 60+ is high, the mortality is higher than that determined for Spain and Poland, where the group of 60+ is smaller, which is in general agreement with the statistical mortality values of COVID-19(ECDC, 2020). Moreover, we examined the relationship of the basic reproduction number and direct contact rate between individuals. The results show that one per two days contact of infectious people leads to infection over three individuals. The mobility of population also influences the speed of the epidemic spreading: increasing the population mobility leads to a growth in the number of people infected, particularly in the long term and this finding is consistent with the results of global metapopulation disease transmission model(Chinazzi et al., 2020). Our model also enables an analysis of the optimal response time in the early period of the epidemic development, which may be the basis for taking appropriate actions as a function of the expected effects, described by the parameters of duration of the epidemic and the level of disease incidence of citizens. Numerical simulations show that the implementation of prevention by limiting the number of contacts in a population significantly reduces the duration of the epidemic. However, even the earliest application and continuous maintenance of strong restrictions on people-to-people contacts does not shorten the epidemic duration below 120 days. Our study also confirms that to control the pandemic it might not be enough to limit the mobility of individuals () and that contact rates () reduction interventions will provide the greatest benefit for mitigating the epidemic(Chinazzi et al., 2020, Wei et al., 2020). Moreover, the calibration of our model on real epidemic data from Poland, France, and Spain allows us to reconstruct the real course of the epidemic in these countries, and the obtained reproduction ratio values at the beginning and current stage of the epidemic ( and ) are qualitatively consistent with the reported data(Yuan et al., 2020).
We conclude that because CA based numerical framework reproduces several observed features of coronavirus disease, it can be a useful tool to study the mechanism of the COVID-19 epidemic spread and it may create a broad spectrum of new useful data. In every aspect of social life our framework can be used to model the impact of the epidemic on the social and economic environment, where the number of people available on the market or excluded from participating in its processes is important.
Although the model presented has some limitations, we believe that it may constitute an area for future research to be carried out by other authors. We plan to focus future work on the applicability of the CA model in modeling different preventing scenarios and in applying the same in social and economic processes.
CRediT authorship contribution statement
M. Medrek: Conceptualization, Methodology, Software, Formal analysis, Investigation, Writing - original draft, Visualization. Z. Pastuszak: Conceptualization, Methodology, Validation, Writing - review & editing, Text structuring.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors thank Arkadiusz Holko for his support in the programming framework and to unknown referees for detailed comments on the paper.
Footnotes
This article is dedicated to John Horton Conway (1937–2020), a professor at Princeton University who died of coronavirus infection. Prof. Conway developed the theory of cellular automata (by Stanisław Ulam and John von Neumann), and one of the best-known examples of cellular automata is Conway’s “Game of Life”.
References
- Abello J., Pardalos P., Resende M. Springer; 2002. Handbook of massive data sets. [Google Scholar]
- Achmed E., Agiza H. On modeling epidemics including latency, incubation and variable susceptibility. Physica A. Statistical Mechanics and its Applications. 1998 [Google Scholar]
- Alwan R., Burgess R., Colburn T., Cuevas L., Smith G. Evidence informing the UK’s COVID-19 public health response must be transparent. Lancet. 2020;20 doi: 10.1016/S0140-6736(20)30667-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson R., Heesterbeek H., Klinkenberg D., DeirdreHollingsworth T. How will country-based mitigation measures influence the course of the COVID-19 epidemic? The Lancet. 2020;395:931–934. doi: 10.1016/S0140-6736(20)30567-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson R., May R. Population biology of infectious disease: Part I. Nature. 1979 doi: 10.1038/280361a0. [DOI] [PubMed] [Google Scholar]
- Aron J.L., Schwartz I.B. Seasonality and period-doubling bifurcations in an epidemic model. Journal of Theoretical Biology. 1984;110(4):665–679. doi: 10.1016/s0022-5193(84)80150-2. [DOI] [PubMed] [Google Scholar]
- Boccara N., Cheong K. Critical behaviour of a probabilistic automata network SIS model for the spread of an infectious disease in a population of moving individuals. Journal of Physics A: Mathematical and General. 1993;26(15):3707–3717. doi: 10.1088/0305-4470/26/15/020. [DOI] [Google Scholar]
- Center for International Earth Science Information Network (CIESIN) / Columbia University; United Nations Food and Agriculture Programme (FAO); Centro Internacional de Agricultura Tropical (CIAT) N. NASA Socioeconomic Data and Applications Center (SEDAC); Palisades, NY: 2005. Gridded population of the world, Version 4 (GPWv4): Population count grid. Retrieved from http://sedac.ciesin.columbia.edu/data/collection/gpw-v4. (Accessed 2020-03-07) [Google Scholar]
- CentralStatisticalOffice N. 2017. Population by sex and age group. Retrieved from https://bdl.stat.gov.pl/BDL/metadane/metryka/2137. (Accessed 15 March 2020) [Google Scholar]
- Chinazzi M., Davis J.T., Ajelli M., Gioannini C., Litvinova M., Merler S. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science. 2020;368(6489):395–400. doi: 10.1126/science.aba9757. URL https://science.sciencemag.org/content/368/6489/395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chowell F., Lee S. Transmission characteristics of MERS and SARS in the healthcare setting: a comparative study. BMC Medicine. 2015;13:210. doi: 10.1186/s12916-015-0450-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- CountryMeters F. 2020. Population of the world and countries. https://countrymeters.info/en. (Accessed 17 March 2020) [Google Scholar]
- del Rey A.M., White S.H., Sánchez G.R. Cellular automata. Springer; 2006. A model based on cellular automata to simulate epidemic diseases; pp. 304–310. [Google Scholar]
- Delorme M. An introduction to cellular automata. Mathematics and its Application. 1999;460:5–50. [Google Scholar]
- Djordjevic J., Silva C.J., Torres D.F. A stochastic SICA epidemic model for HIV transmission. Applied Mathematics Letters. 2018;84:168–175. doi: 10.1016/j.aml.2018.05.005. [DOI] [Google Scholar]
- ECDC J. 2020. COVID-19 situation update for the EU/EEA and the UK. Retrieved from https://data.europa.eu/euodp/pl/data/publisher/ecdc. (Accessed 09 June 2020) [Google Scholar]
- Eurostat J. 2016. Statistics on commuting patterns at regional level. Retrieved from https://ec.europa.eu/eurostat/statistics-explained/pdfscache/50943.pdf. (Accessed 27 March 2020) [Google Scholar]
- Eurostat J. 2020. Statistics explained. Retrieved from https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Statistics_Explained:About. (Accessed 07 April 2020) [Google Scholar]
- Fanelli D., Piazza F. Analysis and forecast of COVID-19 spreading in China, Italy and France. Chaos, Solitons & Fractals. 2020;134 doi: 10.1016/j.chaos.2020.109761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferretti L., Wymant C., Kendall M., Zhao L., Nurtay A., Abeler-Dörner L. Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science. 2020;368(6491) doi: 10.1126/science.abb6936. URL https://science.sciencemag.org/content/368/6491/eabb6936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu, S., & Milne, G. (2003). Epidemic modelling using cellular automata. In Proc. of the Australian conference on artificial life.
- Hellewell J., Abbot S., Gimma A., Bosse N., Ch. J. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. The Lancet. 2020;8:488–496. doi: 10.1016/S2214-109X(20)30074-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holko A., Medrek M., Pastuszak Z., Phusavat K. Epidemiological modeling with apopulation density map-based cellular automata simulation system. Expert Systems With Applications. 2016;48:1–8. [Google Scholar]
- Hu H., Nigmatulina K., Eckhoff P. The scaling of contact rates with population density for the infectious disease models. Mathematical Biosciences. 2013;244:125–134. doi: 10.1016/j.mbs.2013.04.013. [DOI] [PubMed] [Google Scholar]
- Hu Z., Song C., Xu C.e.a. Clinical characteristics of 24 asymptomatic infections with COVID-19 screened among close contacts in Nanjing, China. Science China Life Sciences. 2020;63:706–711. doi: 10.1007/s11427-020-1661-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kai-WangTo K.e.a. Temporal profiles of viral load in posterior oropharyngeal saliva samples and serum antibody responses during infection by SARS-CoV-2: an observational cohort study. The Lancet. 2020;20(5):565–574. doi: 10.1016/S1473-3099(20)30196-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kucharski C. The role of superspreading in Middle East respiratory syndrome coronavirus (MERS-CoV) transmission. Euro Surveill. 2015;20:14–18. doi: 10.2807/1560-7917.es2015.20.25.21167. [DOI] [PubMed] [Google Scholar]
- Lauer S., Grantz K., Bi Q., Jones F., Zheng Q., Meredith H. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: Estimation and application. Annals of Internal Medicine. 2020;172(9):577–582. doi: 10.7326/M20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Q., Shi Z., Daozhou G., Yijun L., Shu Y., Salihu S. A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. International Journal of Infectious Diseases. 2020;93:211–216. doi: 10.1016/j.ijid.2020.02.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linka K., Peirlinck M., Kuhl E. 2020. The reproduction number of COVID-19 and its correlation with public health interventions. medRxiv. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y., Gayle A., Wilder-Smith A., Rocklov J. The reproductive number of COVID-19 is higher compared to SARS coronavirus. Journal of Travel Medicine. 2020;27 doi: 10.1093/jtm/taaa021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Q.X., Jin Z., Liu M.X. Spatial organization and evolution period of the epidemic model using cellular automata. Physical Review E. 2006;74(3) doi: 10.1103/PhysRevE.74.031110. [DOI] [PubMed] [Google Scholar]
- Lloyd-Smith J., Schreiber S., Kopp P., Getz W. Superspreading and the effect of individual variation on disease emergence. Nature. 2005;438:355–359. doi: 10.1038/nature04153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milne G., Fermanis C., Johnston P. A mobility model for classical swine fever in feral pig populations. Veterinary Research. 2008;39(6) doi: 10.1051/vetres:2008029. 53–53. [DOI] [PubMed] [Google Scholar]
- Murray J. Springer-Verlag; 1993. Mathematical Biology. [Google Scholar]
- Ndairou F., Area I., Nieto J.J., Torres D.F. Mathematical modeling of COVID-19 transmission dynamics with a case study of Wuhan. Chaos, Solitons & Fractals. 2020;135 doi: 10.1016/j.chaos.2020.109846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ng J., Bakrania K., Russell R., Falkous C. 2020. Covid-19 mortality rates by age and gender: why is the disease killing more men than women? https://www.rgare.com/knowledge-center/media/research/covid-19-mortality-rates-by-age-and-gender-why-is-the-disease-killing-more-men-than-women. (Accessed 19 July 2020) [Google Scholar]
- Pfeifer B., Kugler K., Tejada M.M., Baumgartner C., Seger M., Osl M. A cellular automaton framework for infectious disease spread simulation. The Open Medical Informatics Journal. 2008;2:70. doi: 10.2174/1874431100802010070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rachah A., Torres D. Dynamics and optimal control of ebola transmission. Mathematical Computational Sciences. 2018;10:331–342. doi: 10.1007/s11786-016-0268-y. [DOI] [Google Scholar]
- Riley S., C. F., Donnelly C. Transmission dynamics of the etiological agent of SARS in Hong Kong: impact of public health interventions. Nature. 2005;438:355–359. doi: 10.1126/science.1086478. [DOI] [PubMed] [Google Scholar]
- Schittkowski K. Springer, Boston, MA; 2002. Numerical data fitting in dynamical systems. [Google Scholar]
- United Nations, Department of Economic and Social Affairs, Population Division K. 2020. World population prospects: The 2019 revision. Retrieved from https://population.un.org/wpp/. (Accessed 15 March 2020) [Google Scholar]
- Wei W., Li Z., Chiew C., Yong S., Toh M., Lee V. Presymptomatic transmission of SARS-CoV-2 ? Singapore, January 23March 16, 2020. MMWR Morb Mortal Wkly Rep. 2020;69:411–415. doi: 10.15585/mmwr.mm6914e1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White S.H., del Rey A.M., Sanchez G.R. Modeling epidemics using cellular automata. Applied Mathematics and Computation. 2007;186(1):193–202. doi: 10.1016/j.amc.2006.06.126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- World Health Organization S.H. 2020. Report of the WHO-China joint mission on coronavirus disease 2019 (COVID-19) Retrieved from https://www.who.int/docs/default-source/coronaviruse/who-china-joint-mission-on-covid-19-final-report.pdf. (Accessed 15 March 2020) [Google Scholar]
- WorldoMeters S.H. 2020. Age of Coronavirus deaths. Retrieved from https://www.worldometers.info/coronavirus/coronavirus-age-sex-demographics/. (Accessed 17 March 2020) [Google Scholar]
- Wu J.T., Leung K., Leung G. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in wuhan, China: a modelling study. Lancet. 2020;395:689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan L., Li M., G. L., Lu Z. Monitoring transmissibility and mortality of COVID-19 in Europe. International Journal of Infectious Diseases. 2020;95:311–315. doi: 10.1016/j.ijid.2020.03.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong, S., Huang, Q., & Song, D. (0000). Simulation of the spread of infectious diseases in a geographical environment. Science in China Series D: Earth Sciences, 52. 10.1007/s11430-009-0044-9. [DOI] [PMC free article] [PubMed]