Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2020 Sep 30;5(40):25968–25972. doi: 10.1021/acsomega.0c03409

Insights into the Dielectric Loss Mechanism of Bianisotropic FeSi/SiC Composite Materials

Prasun Banerjee †, Nagasamudram Suresh Kumar ‡, Adolfo Franco Jr §, Akshaya Kumar Swain ∥, Kadiyala Chandra Babu Naidu †,*
PMCID: PMC7558038  PMID: 33073123

Abstract

graphic file with name ao0c03409_0006.jpg

High magnitudes of permittivity with the permeability of the materials help to absorb electromagnetic waves more efficiently. Snoek’s limit directly puts a constraint on the enhancement of the permeability of the material. However, the incorporation of the lossy material may help to enhance the permittivity abruptly. In this study, we prepared a FeSi/SiC composite material with the mechanical ball milling method and investigated its enhancement of the dielectric behavior. The bianisotropic nature was observed along with the phase purity in the morphological studies. The Cole–Cole relaxation mechanisms were observed to validate a complex relaxation mechanism with 104 times higher dielectric loss in the composite material. The detection of the Warburg capacitance using the impedance technique sheds new light on the ion diffusion mechanism in the metallic composite materials.

Introduction

The absorption of electromagnetic (EM) waves by the materials, especially coming from the RADAR is the crucial requirement for the development of the stealth technologies.1,2 In principle, the higher loss of the materials transformed the incident EM waves into heat energy.3 The typical household application of technology is a microwave oven. Here, orientational polarization of the electric dipoles of the water molecules generates heat energy within the food items because of the applied alternating EM field.4 However, over a long period silicon carbide was found to be the most suitable material for industrial applications because of its smaller absorption magnitude as well as the thinner width of the absorption.5 Nevertheless, these materials were widely used as a supplementary material because of their single absorption capacity. Hence, in the search for primary absorbing materials, they need to have higher permeability as well as higher dielectric loss.6−10 Here, the role of the higher permeability forces the EM wave passes through the material compulsorily.11 In contrast, the role of the higher dielectric loss is to convert the EM waves into other forms of energy, for instance, heat energy to absorb the EM wave completely.12−15

Several approaches have been taken to date to achieve the above criteria. For instance, Liu et al.16 chose FeSi powder as an absorbing material. They milled the spherical shape particles of FeSi alloy for several hours to achieve a flaky shape. Because of the flaky shape of the 12 h milled FeSi powder, they reported an increase of permeability values. It also suggested mixing paraffin along with the FeSi powder to make a composite with having higher permeability along with the higher dielectric loss with the resonant frequency within the L–S band.17

Hence, ferromagnetic FeSi alloy is a perfect material for the primary absorbing material because of its higher permeability values with soft nature.18−20 However, Snoek’s limit put constraints in increasing the permeability values as it directly affects the resonant frequency.21 Therefore, if we try to enhance the permeability values, it may result in the depletion of the resonant frequency sometimes under the microwave frequency. On the other hand, if we add SiC along with the FeSi alloy powder may result in higher dielectric loss along with the high permeability and high permittivity.

Hence, we investigated the dielectric effect of SiC on the flaky FeSi alloy composite powder within the phase limit using ball milling techniques to enhance its loss factor.

Experimental Details

Synthesis

FeSi powders synthesized commercially with gas atomization techniques were acquired as the primary absorbing material with a mesh size of 150. The composition study showed that it had 6.02 wt % silicon, 0.04 wt % chromium, and balance iron. The raw powders mixed with the SiC (99.9%, Alpha Chemika) with 2.5, 5.0, and 7.5 wt %, namely, FeSi@2.5%SiC, FeSi@5%SiC, and FeSi@7.5%SiC, respectively, within the phase purity limit. The mixed powders placed inside polyvinyl jars along with yttrium-stabilized ZrO2 balls. The ball to powder ratio was maintained at a value of 25:1 and wet milling was performed in ethanol medium for 7 days at 150 rpm speed. After milling, wet powders were collected and washed several times with ethanol and finally dried in the final form in a hot air oven for 12 h at 60 °C temperature. Pellets with 1.1 cm diameter and 0.17 cm thickness obtained with a uniaxial pressing with 4 tons of pressure for 10 min.

Characterization

Bruker D8 Advance powder X-ray diffraction (XRD) was utilized to find the limit of phase purity of the materials within the 30° ≤ 2θ ≤ 80° values. The indexing performed comparing with the PDF-2 (2018) database. The flaky shape of the particles along with the composite type of powders performed with scanning electron microscopy (SEM) techniques (Hitachi S 3500). The pellets painted with the silver paste. The dielectric and impedance properties determined with a Hioki IM3536 LCR meter within the 4 Hz to 8 MHz range of frequencies.

Results and Discussion

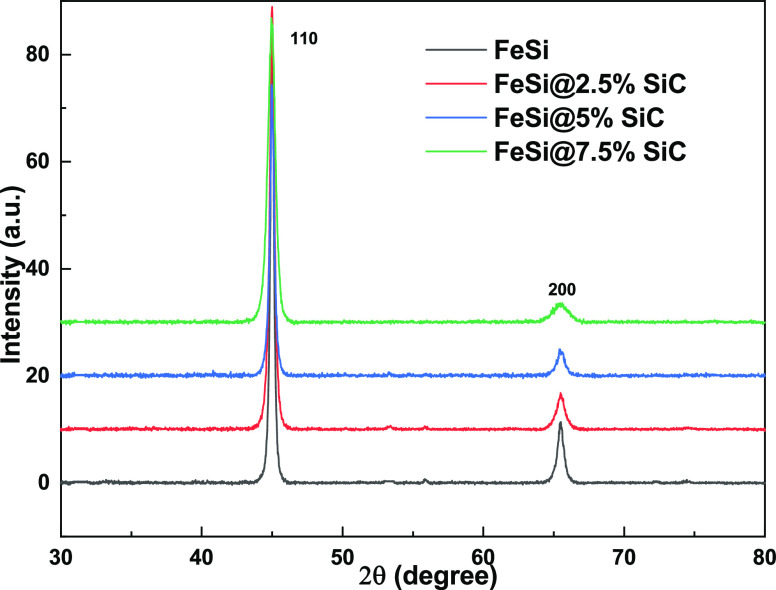
The XRD patterns for the pure and composite powders are shown in Figure 1. The reflection peaks were obtained for the (110) and (200) miller indices planes only.16 This suggests a high crystallinity nature along with the absence of any spurious secondary peaks up to 7.5 wt % for the FeSi@7.5%SiC composite powder. It also suggests that long hours of the milling process did not initiate any chemical decomposition in the composite matrices. However, with the increase of the SiC content peak broadening along with the reduced intensity of the peaks are visible. The peaks also shifted to the high value of Bragg angles with the SiC content. These suggested that a lower atomic radii of Si (1.18 Å) than that of the Fe (1.24 Å) and caused distortion because of the shrinkage of the lattice structure. Hence, the increased defect density may be responsible for the peak shifting as well as the peak broadening phenomenon. The D·β cos θ = nλ formula of Debye–Scherrer was utilized to determine the distribution of the particle size from the intensity peaks of the XRD data.22 Here, diffraction peak width β obtained from the full width at half-maximum value of the (110) plane and λ = 1.5418 Å. The distribution result suggests 10.46, 28.2, and 60.33% presence of the D10, D50, and D90 size of the particles. The obtained value of the bulk density was found to be 3.92 g/cm3 for the FeSi in good agreement with the literature.23

Figure 1.

Figure 1

Open in a new tab

XRD pattern for the FeSi/SiC composite powders.

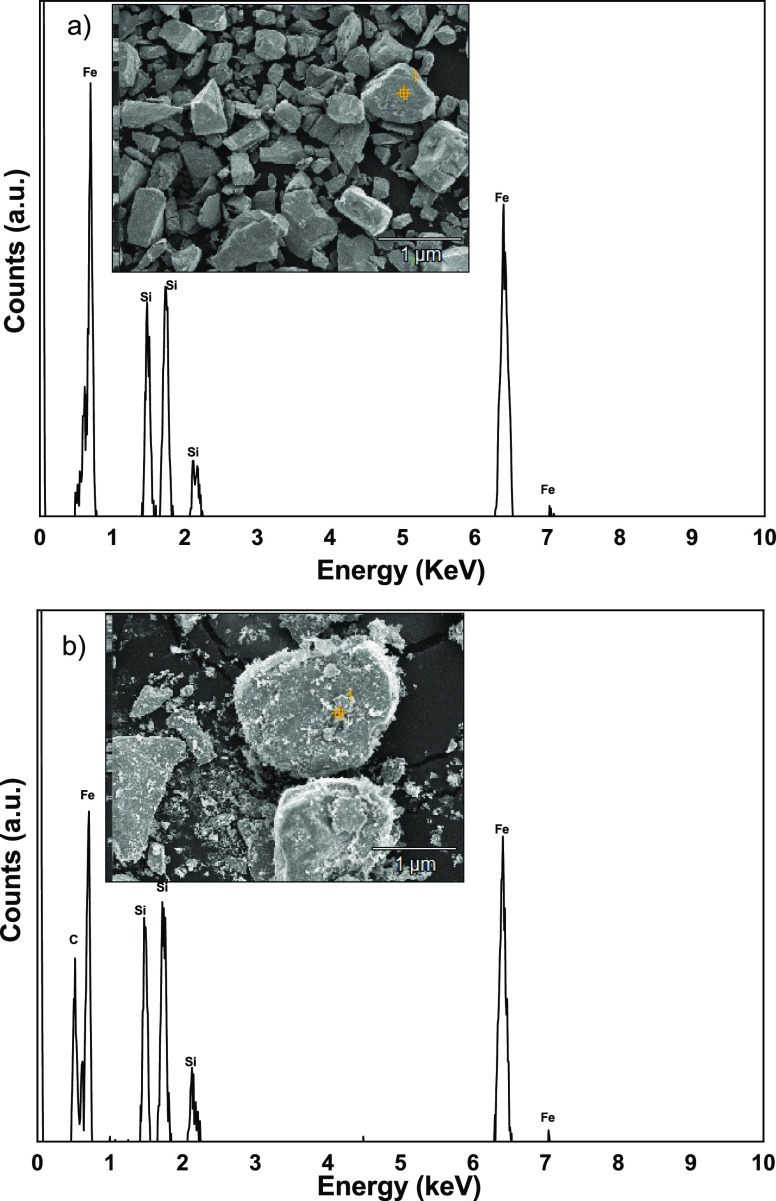
The SEM–energy-dispersive X-ray (EDX) analysis of the samples is presented in Figure 2. The brittle nature of the FeSi alloy powder is visible here with heterogeneous sizes because of long hours of milling. The composite nature of the FeSi@5%SiC powder was observed at the inset of Figure 2b. Here, the SiC particles provided a lamellar outer layer sandwiched with FeSi central cores. The presence of the SiC was also detected in the elemental analysis with EDX. The same has not been observed in the XRD till the 7.5 wt % of SiC because of the high degree of crystallinity of the FeSi primary phases. The presence of the secondary SiC phases around the surface of the FeSi primary phases also initiated shape bianisotropy.24 Hence, it may lead to the quick magnetization as well as the effects the complex permittivity of the composite powders.

Figure 2.

Figure 2

Open in a new tab

SEM–EDX analysis for (a) FeSi and (b) FeSi@5%SiC powders.

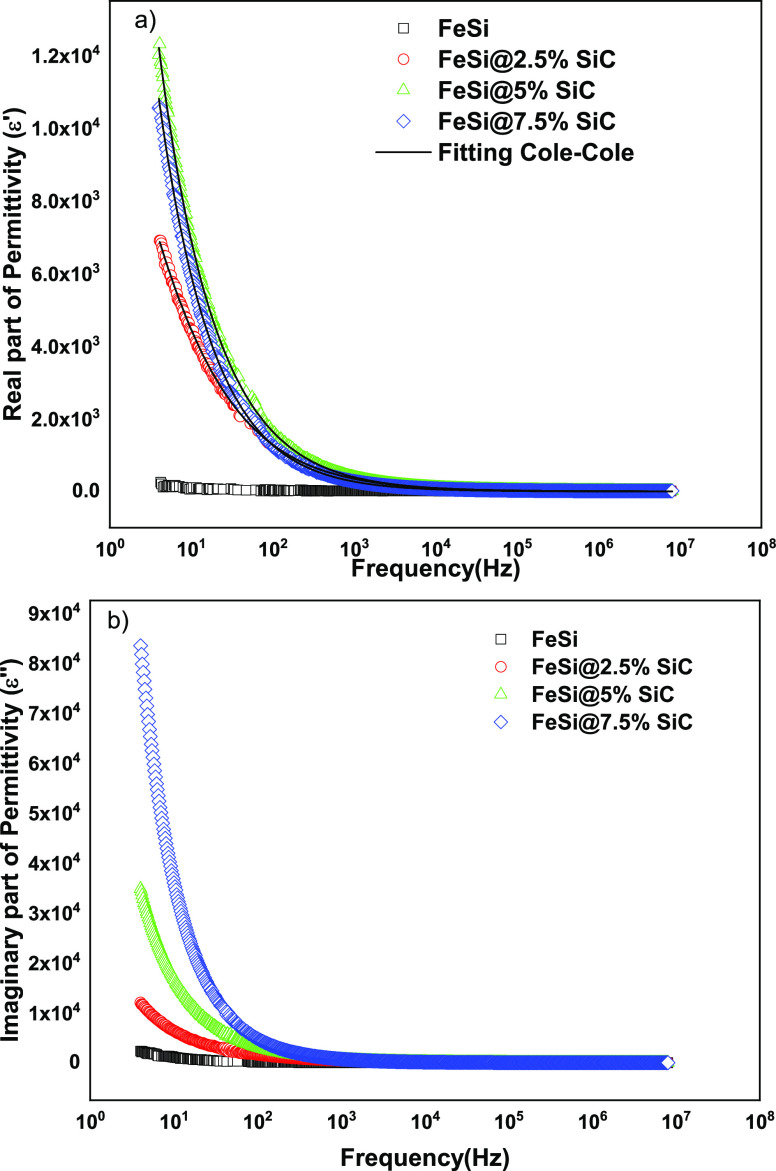
The graph of the real and imaginary parts of permittivity at room temperature with the frequency is presented in Figure 3. The composite materials here show more enhanced dielectric properties than the pure FeSi alloy. In general, the low-frequency dielectric constants directly depend on the orientational polarization mechanism, whereas the atomic and electronic contribution to the dielectric constant comes at the optical frequency regions. Hence, with an application of the alternating field at a low-frequency region, the electric dipoles try to follow toward the direction of the field. The addition of SiC in the composite material generates additional dipole presence inside the material. At the same time, the pure FeSi powder contains a single dipolar mechanism. Therefore, the real part of permittivity at lower frequencies for the FeSi@5%SiC and FeSi@7.5%SiC materials exhibited nearly 104 times higher permittivity than that of the pure FeSi powders. When the applied alternating electric field changes direction, the dipoles also try to change the direction with the applied field known as the relaxation mechanism.25 This leads to the loss inside the material. The presence of the distributed relaxation mechanism leads to the higher loss inside the material; hence, in this work, FeSi@7.5%SiC exhibited maximum dielectric loss. With the increase of the frequencies, the dipoles failed to align themselves with the alternating electric field; hence, the orientational polarization contribution to the dielectric behavior also minimizes.

Figure 3.

Figure 3

Open in a new tab

(a) Real and (b) imaginary parts of permittivity vs frequency for FeSi/SiC powders. The solid lines represent the fitting of the dielectric data with the Cole–Cole relaxation model.

The single relaxation mechanism of the pure FeSi powders is represented by the Debye model26

graphic file with name ao0c03409_m001.jpg 1

Whereas the distributed relaxation mechanism for the composite bianisotropic material follows the Cole–Cole model27

graphic file with name ao0c03409_m002.jpg 2

Here, the stretching component of the relaxation behavior expressed with the 1 – γ terms in the equation. The resonance phenomenon is said to happen if the magnitude of the 1 – γ term exceeds the value of unity. To fit the dielectric data of the composite material, the eq 2 is extended to its trigonometric form as28

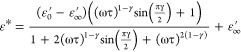graphic file with name ao0c03409_m003.jpg 3

Hence, we fitted the composite material dielectric data with the eq 3. The fitting results indicated that the value of the stretching component equals to the 0.58, 0.62, and 0.68 for the FeSi@2.5%SiC, FeSi@5%SiC, and FeSi@7.5%SiC, respectively. This indicates that the spectra are within the relaxation mode and can be extendable to GHz frequency for the spectra to behave in the resonance mode. They are indicating well below the Snoek’s limit. Hence, the bianisotropic composite material can have high permeability and high permittivity well below the Snoek’s limit.

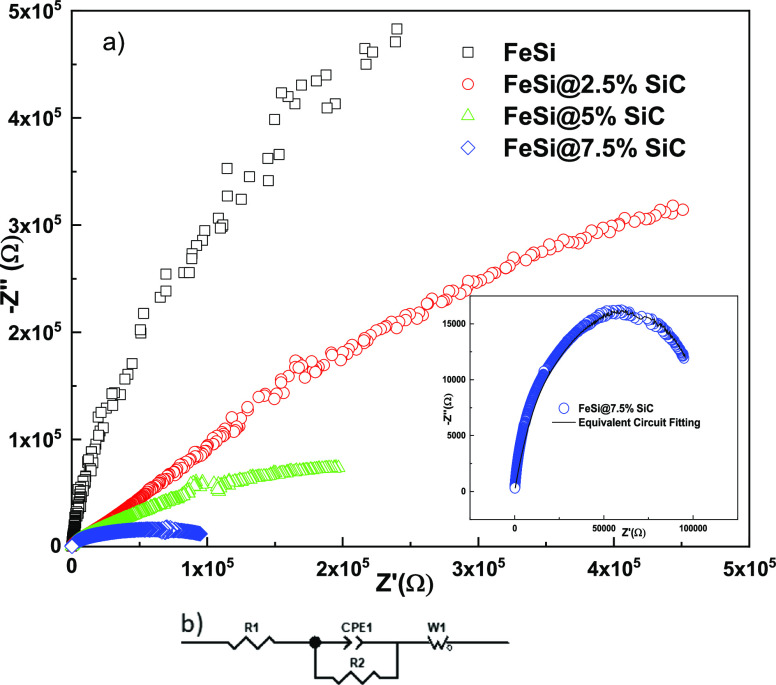
Moreover, the impedance characteristics of the pure and composite material are presented in Figure 4. It is observed that the pure FeSi resulted in a poorly resolved semicircle impedance spectrum. However, with the addition of SiC the semicircle arcs start forming and finally resolved into a clear semicircular arc for the FeSi@7.5%SiC samples. Here, the proposed equivalent circuit for the FeSi@7.5%SiC samples is shown in Figure 4b. The significance of the R2 term is purely ohmic resistance where the dispersion behavior resulted because of the constant phase element part. The Warburg element signifies diffusive nature.29 Hence, impedance data fitted well for the diffusive contribution of the SiC material in the FeSi@7.5%SiC samples, as shown in the inset of Figure 4a. Hence, the diffusion of ions resulted in a higher loss in the FeSi@7.5%SiC material.

Figure 4.

Figure 4

Open in a new tab

(a) Impedance characteristics of the pure and composite materials. Inset shows the fitting result obtained with (b) equivalent circuit for the FeSi@7.5%SiC samples.

Conclusions

In summary, FeSi/SiC composite materials were prepared with a mechanical ball milling method along with commercially available FeSi alloy powders. The uniform dispersion of the FeSi alloy into the SiC materials formed a bianisotropic nature into the composite materials. The SiC particles provided a lamellar outer layer sandwiched with FeSi central cores. The incorporation of additional SiC electric dipoles and ion diffusion mechanism into the composite resulted in 104 times of dielectric loss inside the material with respect to the pure FeSi alloy powder. Hence, the material can absorb a broad part of the EM wave to transform it into the heat energy efficiently. The Cole–Cole relaxation mechanism confirms the presence of the stretching component well below the resonance within the Snoek’s limit. The presence of the Warburg capacitance leads to the ion diffusion through the FeSi/SiC composite materials for higher losses. Hence, it is possible to obtain a high magnitude of permeability and permittivity FeSi/SiC materials for the efficient absorption of EM waves to tackle the EM pollution.

Acknowledgments

P.B. would like to thank UGC, New Delhi for start-up research grant with no F.30-457/2018 (BSR).

The authors declare no competing financial interest.

References

  1. Yan J.; Huang Y.; Wei C.; Zhang N.; Liu P. Covalently bonded polyaniline/graphene composites as high-performance electromagnetic (EM) wave absorption materials. Compos. Appl. Sci. Manuf. 2017, 99, 121–128. 10.1016/j.compositesa.2017.04.016. [DOI] [Google Scholar]
  2. Micheli D.; Vricella A.; Pastore R.; Marchetti M. Synthesis and electromagnetic characterization of frequency selective radar absorbing materials using carbon nanopowders. Carbon 2014, 77, 756–774. 10.1016/j.carbon.2014.05.080. [DOI] [Google Scholar]
  3. Liu W.; Liu L.; Ji G.; Li D.; Zhang Y.; Ma J.; Du Y. Composition design and structural characterization of MOF-derived composites with controllable electromagnetic properties. ACS Sustainable Chem. Eng. 2017, 5, 7961–7971. 10.1021/acssuschemeng.7b01514. [DOI] [Google Scholar]
  4. Borhan N.; Gheisari K.; Shoushtari M. Z. Dielectric properties of nanocrystalline Zn-doped lithium ferrites synthesized by microwave-induced glycine–nitrate process. J. Supercond. Novel Magn. 2016, 29, 145–151. 10.1007/s10948-015-3225-0. [DOI] [Google Scholar]
  5. Chiu S.-C.; Yu H.-C.; Li Y.-Y. High electromagnetic wave absorption performance of silicon carbide nanowires in the gigahertz range. J. Phys. Chem. C 2010, 114, 1947–1952. 10.1021/jp905127t. [DOI] [Google Scholar]
  6. Liang H.; Liu J.; Zhang Y.; Luo L.; Wu H. Ultra-thin broccoli-like SCFs@ TiO2 one-dimensional electromagnetic wave absorbing material. Compos. B Eng. 2019, 178, 107507. 10.1016/j.compositesb.2019.107507. [DOI] [Google Scholar]
  7. Xiang Z.; Song Y.; Xiong J.; Pan Z.; Wang X.; Liu L.; Liu R.; Yang H.; Lu W. Enhanced electromagnetic wave absorption of nanoporous Fe3O4@ carbon composites derived from metal-organic frameworks. Carbon 2019, 142, 20–31. 10.1016/j.carbon.2018.10.014. [DOI] [Google Scholar]
  8. Dai X.; Du Y.; Yang J.; Wang D.; Gu J.; Li Y.; Wang S.; Xu B. B.; Kong J. Recoverable and self-healing electromagnetic wave absorbing nanocomposites. Compos. Sci. Technol. 2019, 174, 27–32. 10.1016/j.compscitech.2019.02.018. [DOI] [Google Scholar]
  9. Xu X.; Ran F.; Fan Z.; Lai H.; Cheng Z.; Lv T.; Shao L.; Liu Y. Cactus-inspired bimetallic metal-organic framework-derived 1D-2D hierarchical Co/N-decorated carbon architecture toward enhanced electromagnetic wave absorbing performance. ACS Appl. Mater. Interfaces 2019, 11, 13564–13573. 10.1021/acsami.9b00356. [DOI] [PubMed] [Google Scholar]
  10. Qi Y.; Yin P.; Zhang L.; Wang J.; Feng X.; Wang K.; Zhao L.; Sun X.; Dai J. Novel Microwave Absorber of NixMn1-xFe2O4/Carbonized Chaff (x = 0.3, 0.5, and 0.7) Based on Biomass. ACS Omega 2019, 4, 12376–12384. 10.1021/acsomega.9b01568. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Zhang L.; Zhou F.; Zhang S.; Wang Y.; Wang J.; Wang J. Investigation of water-sensitivity damage for tight low-permeability sandstone reservoirs. ACS Omega 2019, 4, 11197–11204. 10.1021/acsomega.9b01286. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Lucas de Sousa e Silva R.; Banerjee P.; Franco A. Jr. Functional properties of donor-and acceptor-co-doped high dielectric constant zinc oxide ceramics. Phys. Chem. Chem. Phys. 2019, 21, 9456–9464. 10.1039/c9cp01140d. [DOI] [PubMed] [Google Scholar]
  13. Banerjee P.; Franco A. Jr. Substitution-induced near phase transition with Maxwell Wagner polarization in SrBi2 (Nb1- xAx) 2O9 ceramics [A= W, Mo and x= 0, 0.025R. Phys. Status Solidi A 2017, 214, 1700067. 10.1002/pssa.201700067. [DOI] [Google Scholar]
  14. Banerjee P.; Franco A. Jr. Role of higher valent substituent on the dielectric and optical properties of Sr0. 8Bi2. 2Nb2O9 ceramics. Mater. Chem. Phys. 2019, 225, 213–218. 10.1016/j.matchemphys.2018.12.075. [DOI] [Google Scholar]
  15. Banerjee P.; Ghosh G.; Biswas S. K.. A system to measure dielectric constant and loss of liquids at microwave frequencies. 2009 Applied Electromagnetics Conference (AEMC), 2009; pp 1–2.
  16. Liu C.; Yuan Y.; Jiang J.-t.; Gong Y.-x.; Zhen L. Microwave absorption properties of FeSi flaky particles prepared via a ball-milling process. J. Magn. Magn. Mater. 2015, 395, 152–158. 10.1016/j.jmmm.2015.06.085. [DOI] [Google Scholar]
  17. Liu L.; Duan Y.; Guo J.; Chen L.; Liu S. Influence of particle size on the electromagnetic and microwave absorption properties of FeSi/paraffin composites. Phys. B Condens. Matter 2011, 406, 2261–2265. 10.1016/j.physb.2011.03.045. [DOI] [Google Scholar]
  18. Dosoudil R.; Franek J.; Slama J.; Usakova M.; Gruskova A. Electromagnetic wave absorption performances of metal alloy/spinel ferrite/polymer composites. IEEE Trans. Magn. 2012, 48, 1524–1527. 10.1109/tmag.2011.2172779. [DOI] [Google Scholar]
  19. Lauda M.; Füzer J.; Füzerová J.; Kollár P.; Strečková M.; Fáberová M. Magnetic Properties of Soft Magnetic FeSi Composite Powder Cores. Acta Phys. Pol., A 2014, 126, 144. 10.12693/aphyspola.126.144. [DOI] [Google Scholar]
  20. Strečková M.; Füzer J.; Kobera L.; Brus J.; Fáberová M.; Bureš R.; Kollár P.; Lauda M.; Medvecký Ĺ.; Girman V.; et al. A comprehensive study of soft magnetic materials based on FeSi spheres and polymeric resin modified by silica nanorods. Mater. Chem. Phys. 2014, 147, 649–660. 10.1016/j.matchemphys.2014.06.004. [DOI] [Google Scholar]
  21. Nakamura T. Snoeks limit in high-frequency permeability of polycrystalline Ni-Zn, Mg-Zn, and Ni-Zn-Cu spinel ferrites. J. Appl. Phys. 2000, 88, 348–353. 10.1063/1.373666. [DOI] [Google Scholar]
  22. Holzwarth U.; Gibson N. The Scherrer equation versus the’Debye-Scherrer equation’. Nat. Nanotechnol. 2011, 6, 534. 10.1038/nnano.2011.145. [DOI] [PubMed] [Google Scholar]
  23. Cao L.; Jiang J.-T.; Wang Z.-Q.; Gong Y.-X.; Liu C.; Zhen L. Electromagnetic properties of ake-shaped Fe-Si alloy particles prepared by ball milling. J. Magn. Magn Mater. 2014, 368, 295–299. 10.1016/j.jmmm.2014.05.032. [DOI] [Google Scholar]
  24. Asadchy V. S.; RaDi Y.; Vehmas J.; Tretyakov S. Functional metamirrors using bianisotropic elements. Phys. Rev. Lett. 2015, 114, 095503. 10.1103/physrevlett.114.095503. [DOI] [PubMed] [Google Scholar]
  25. Franco A. Jr.; Banerjee P.; Romanholo P. L. Effect of composition induced transition in the optical band-gap, dielectric and magnetic properties of Gd doped Na0. 5Bi0. 5TiO3 complex perovskite. J. Alloys Compd. 2018, 764, 122–127. 10.1016/j.jallcom.2018.06.007. [DOI] [Google Scholar]
  26. Banerjee P.; Franco A. Jr. Enhanced dielectric and magnetic properties in multiferroic Bi0. 99Y0. 01Fe0. 99Ni0. 01O3 ceramic. Mater. Lett. 2016, 184, 17–20. 10.1016/j.matlet.2016.08.009. [DOI] [Google Scholar]
  27. Franco A.; Banerjee P.; Lima R. J. S. Dielectric and magnetic properties of three-layers laminated ceramic composite, K 0.5 Na 0.5 NbO 3/CoFe 2 O 4/K 0.5 Na 0.5 NbO 3. J. Mater. Sci.: Mater. Electron. 2018, 29, 4357–4364. 10.1007/s10854-017-8384-2. [DOI] [Google Scholar]
  28. Silva R. L. d. S. E.; Banerjee P.; Franco Júnior A. Functional properties of donorand acceptor-co-doped high dielectric constant zinc oxide ceramics. Phys. Chem. Chem. Phys. 2019, 21, 9456–9464. 10.1039/c9cp01140d. [DOI] [PubMed] [Google Scholar]
  29. Skale S.; Doleček V.; Slemnik M. Substitution of the constant phase element by Warburg impedance for protective coatings. Corros. Sci. 2007, 49, 1045–1055. 10.1016/j.corsci.2006.06.027. [DOI] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES