Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Sep 9;36(40):11929–11937. doi: 10.1021/acs.langmuir.0c02005

Elastohydrodynamic Dewetting of Thin Liquid Films: Elucidating Underwater Adhesion of Topographically Patterned Surfaces

Maciej Chudak †, Vaishali Chopra ‡, René Hensel ‡, Anton A Darhuber †,*
PMCID: PMC7558345  PMID: 32903008

Abstract

graphic file with name la0c02005_0012.jpg

In underwater adhesion of a topographically patterned surface with a very soft material such as human skin, the elastic deformation can be large enough to achieve solid-on-solid contact not only on top of the hills but also in the valleys of the substrate topography. In this context, we have studied the dynamics of dewetting of a thin liquid film confined between a rigid, periodic micropillar array and a soft, elastic sphere. In our experiments, we observed two very distinct dewetting morphologies. For large ratios of array period to micropillar height and width, the dewetted areas tend to have a diamond-like shape and expand with a rate similar to a flat, unpatterned substrate. When the array period is reduced, the morphology of the dry spot becomes irregular and its expansion rate is significantly reduced. We developed a fully coupled numerical model of the dewetting process that reproduces the key features observed in experiments. Moreover, we performed contact mechanics simulations to characterize the deformation of the elastomer and the shape of the dewetted area in a unit cell of the micropillar array.

Introduction

Surfaces with topological patterns can exhibit remarkable wetting and adhesion properties. Many examples are found in nature: geckos can locomote on a ceiling.1,2 Lotus leaves do not get wet in the rain.3 Springtails can breathe underwater.4,5 There is ongoing interest in replicating these properties and designing bio-inspired micro- and nanopatterned surfaces.

In the context of adhesion, micropatterned surfaces commonly adhere better to smooth and even rough substrates as stresses at the contact interface are distributed more homogeneously and cracks are blunted upon detachment of single fibrils.6−8 Furthermore, micropatterned surfaces show great potential for improving adhesion under wet conditions and underwater.9−23

At first glance, this observation is counterintuitive from a hydrodynamic perspective. The presence of liquids such as water between two surfaces is generally detrimental to achieving a high adhesion strength as liquids are essentially incompressible and thus prevent close contact. Moreover, they can reduce the effective Hamaker constant by up to a factor of 10.24 Consequently, the complete removal of liquid between the contacting materials is conducive to a high underwater adhesion performance. Therefore, a detailed understanding of the dewetting dynamics of micropatterned surfaces is desirable.

Arrays of pillars are often used as a model system to study the wetting of rough surfaces.25−31 Extrand et al. and Ishino et al. described32,33 how liquid droplets in a Wenzel state can spread through a pillar array through wicking in the form of a precursor film slightly thinner than the pillar height. Courbin et al. demonstrated34 how this process can be anisotropic, with the precursor film spreading in a circular, octagonal, or square shape. Chu et al. developed35 a system with slanted pillars, which caused the deposited droplet to spread unidirectionally. Further research36−38 focused on the details of anisotropy in contact line movement on patterned surfaces, showing how it can be considered as a series of pinning or depinning events.

In this manuscript, we studied the dewetting dynamics of a thin, partially wetting liquid film confined between a rigid, periodic micropillar array and a soft, elastic sphere. We systematically studied the impact of the array period on the expansion rate and the morphology of the dewetted areas. Moreover, we performed fully coupled three-dimensional numerical simulations, which reproduce the observed phenomena qualitatively well.

Experimental Section

Experimental Procedure

Figure 1 illustrates the geometry and the time evolution of a typical experiment. A soft elastic hemisphere (radius of curvature: 2 ± 0.5 mm) is pushed onto a rigid glass substrate with an initially thick, intervening liquid layer. The elastomers used were silicone-based, heat-curable, two-component polymer resins (Smooth-On Encapso K, Young’s modulus Y = 1.365 MPa and Sylgard 527, Y = 11.28 kPa). The liquid is a perfluoropolyether (Solvay, Fomblin Y LVAC 14/6, average molecular weight 2500, viscosity μ = 0.2646 Pa s, surface tension γL = 22 mN/m). Its contact angles on the elastomer surface and the substrate base plane are both θ = 30° ± 10°. The substrate contains a microscopic surface pattern in the form of a square array of cylindrical pillars. Upon approaching the substrate, the bottom of the hemisphere elastically deforms. This leads to the formation of a well-defined contact spot [Figure 1b] that defines the lateral extension rcs of the sub-micron thick liquid film [dashed lines in Figures 1b and 2b]. The compressive force acting exerted on the hemisphere is in the range of 0.1–30 mN and is kept constant during an experiment. The specific value is chosen to obtain a contact radius of 250 ± 50 μm depending on the Young’s modulus of the elastomer used. We have monitored the thickness of the ultrathin liquid film using optical interferometry (450 nm wavelength). The experimental setup is described in detail in ref (39).

Figure 1.

Figure 1

Open in a new tab

(a) Side-view sketch of the experimental geometry. A soft elastic hemisphere is pushed onto a glass substrate with an intervening liquid layer. The substrate contains a microscopic surface pattern in the form of a square array of cylindrical pillars. (b) A thin liquid film is formed in the contact spot. The radius of the contact spot rcs is highlighted. (c) Magnified view of the nucleation of a dewetted area. (d) The dewetted area grows over time, pushing the liquid out of the contact spot. The extension of the dewetted area radius rcl is highlighted, defined relative to the nucleation center.

Figure 2.

Figure 2

Open in a new tab

(a) 3D sketch of the pillar array. (b) Bottom-view sketch of the computational domain. The dashed line corresponds to the radius of the contact spot.

Micropillar Array Fabrication

Microscopic pillars were made from a negative tone photoresist (IP-Dip, Nanoscribe) using a two-photon lithography system (Professional GT, Nanoscribe). The nominal pillar height hp and diameter 2rp were 1 and 7 μm, respectively. The pillars were arranged in a square array with center-to-center distance dp varied between 10 and 50 μm. Fused silica slides with a coating of 3-methacryloxypropyl trichlorosilane (product number AB109004, abcr) were used as substrates. The structures were generated using the so-called “dip-in mode”, where the objective was dipped directly into the resist. Exposure parameters were a power scaling of 0.86, a laser power of 25 mW, and a scan speed of 10 mm/s. After exposure, the micropillars were developed using propylene glycol monomethyl ether acetate (product number 484431, Sigma Aldrich) for 20 min and post-cured to enhance the mechanical stability.40 For post-curing, the micropillars were exposed to 365 nm ultraviolet light (OmniCure S1500A, 200 W, igb-tech) in a nitrogen atmosphere. The elastic modulus of the micropillars is approximately 1 GPa.41

Numerical Models

Dewetting Simulations

We developed a three-dimensional, fully coupled finite element method model of the elastic deformation of the hemisphere, the thinning and dewetting of the thin liquid film. The model combines the stationary Cauchy momentum equation for soft, linear, non-dissipative, isotropic, and homogeneous elastic materials

graphic file with name la0c02005_m001.jpg 1

in the absence of body forces, with the Reynolds equation for thin film flow

graphic file with name la0c02005_m002.jpg 2

Here, σij is the stress tensor, h is the liquid film thickness, t is the time, η is the dynamic viscosity of the liquid, pf is the pressure in the liquid film, and v⃗e and v⃗s are the tangential velocities of the liquid–elastomer interface and the substrate surface, respectively, which are computed from the elastic displacements. The partial wettability of the liquid is implemented using a disjoining pressure formalism. All simulations have been performed for the material parameters Y = 1.365 MPa and ν = 0.499, which is close to the value of 0.5 corresponding to incompressible elastomers.42,43

The geometry of the pillar array and the computational domain used in the model are sketched in Figure 2. We assume that the pillar array has an even number of columns and rows and that the apex of the hemisphere is moving vertically downward along the surface normal of the substrate above the center of the array. In this fashion, the system exhibits mirror symmetry planes parallel to the axes and the main diagonals of the square array. The existence of these symmetry planes allows us to restrict the computational domain to the 45° slice shown in Figure 2b. Outside of the contact spot, a Dirichlet boundary condition for the pressure p = pamb is applied, where the constant ambient pressure pamb is set to zero.

Details of the model can be found in ref (39). Only Eq. (16) in ref (39) requires modification to account for the non-flat topography: the function zd(r⃗) is replaced by

graphic file with name la0c02005_m003.jpg 3

where the summation is over all micropillars in the array with corresponding center positions r⃗i. The function

graphic file with name la0c02005_m004.jpg 4

describes the axisymmetric shape of a single pillar, where sp = 2.5 μm is the radial distance over which zp changes smoothly from hp to 0 and fhs is the smoothed Heaviside function, defined by Eq. (14) in ref (39). The nucleation of dewetting was induced by a topographic defect in ref (39). In contrast, we now used a small chemical defect, i.e., a circular region with a locally higher contact angle, in the center of the domain.

Contact Mechanics Simulations

In addition to the fully coupled model described above, we also performed contact mechanics simulations of a single unit cell of the micropillar array. We solve the stationary Cauchy momentum equation (eq 1) in the absence of any intervening liquid. This implies that the resulting elastomer configuration corresponds to the long-time limit of a simulation including liquid if permanent trapping of liquid cannot occur. The latter condition is fulfilled in our model including liquid because, in the context of the disjoining pressure formalism, an ultrathin precursor layer is present, which provides a small but nonzero hydraulic conductivity toward the surrounding liquid bulk.

The conceptual setup, the computational domain, and relevant boundary conditions (BCs) of the contact mechanics simulations are illustrated in Figure 3a–d. Typically, one unit cell of the micropillar array is much smaller than both the radius of curvature of the elastomer hemisphere and the radius of the contact spot. Therefore, for simplicity, we have assumed that the elastomer is an elastic layer of large thickness H ≫ dp and H ≫ hp, approximating the behavior of an elastic half-space. This allows us to reduce the size of the computational domain [indicated by the pink triangle in Figure 3c] to one-eighth of a unit cell by exploiting symmetry boundary conditions. The elastic displacements vanish normal to the vertical mirror symmetry planes of the micropillar array indicated by the dashed lines in Figure 3c. The elastomer is assumed to be attached to a rigid support. Consequently, zero displacement BCs apply at large depths z = H.

Figure 3.

Figure 3

Open in a new tab

(a) At zero applied pressure, the pillar array just touches the elastomer layer of thickness H ≫ dp without deforming it. The elastomer is backed by a fixed, rigid support. (b) Definition of the protrusion depth δ + Δz of a deformed elastomer layer in contact with a rigid pillar array. The red dashed line indicates the position of the elastomer–pillar interface for zero applied pressure. (c) Top-view of the three-dimensional computational domain (pink triangle) of the contact mechanics simulations. Its vertical boundaries (indicated by the dashed lines) are mirror symmetry planes of the micropillar array. The points labeled α and β are the midpoints between pairs of neighboring pillars along the x axis and the array diagonal, respectively. (d) Illustration of the contact pressure BC for the case where the elastomer protrusions contact the substrate base plane.

The rigid pillar array is pushed upward with an applied average pressure pav and thereby indents and deforms the elastomer. Figure 3b provides a definition of the protrusion depth δ + Δz of the deformed elastomer layer. Here, δ is the (position-independent) indentation depth of the tops of the pillars and Δz(x, y) the (position-dependent) protrusion amplitude relative to the surface level of the undeformed elastomer (as indicated by the red dashed line). We have implemented two different models depending on whether the pillar height was larger or smaller than the protrusion depth δ + Δz. In the first case, the applicable BCs sketched in Figure 3b are zero shear stress σxz = σyz = 0 and constant vertical displacement uz = δ at the tops of the pillars (indicated by ②) and zero shear and zero normal stress at the elastomer–air interface (indicated by ①). The average applied pressure pav, which is linearly related to the indentation depth δ, is determined from the computed stress distribution σzz at the tops of the pillars. In the second case, where the protrusion depth is sufficient to make contact with the base plane of the pillar array, we implemented an empirical contact pressure pc boundary condition [indicated by ③ in Figure 3d] at the solid–elastomer interfaces. The contact pressure pc depends on the overlap distance δw that the elastomer and the substrate would have in the absence of a contact condition

graphic file with name la0c02005_m005.jpg 5

Here, Cf = 1017 Pa m–3/2 is an interaction stiffness parameter, chosen to be as high as possible without foregoing the model’s convergence. All elastomer–solid interfaces are assumed to be frictionless. At the elastomer–air interfaces, again zero shear and zero normal stress BCs apply.

Results and Discussion

Experimental Results

The elastic deformation of the hemisphere induces a non-uniform pressure distribution, with a local maximum in the center and ambient pressure just outside the contact spot.44,45 The ensuing pressure gradient pushes the intervening liquid out of the contact spot. At some point, the deformed hemisphere contacts the top of the pillars. Since the height hp = 1 μm of the pillar array is much smaller than the array period dp = 15–50 μm, the deformed elastomer squeezes into the interstitial region between neighboring pillars and eventually contacts the glass substrate [Figure 1c]. Since the liquid is partially wetting, the liquid film becomes unstable and dewets below a minimum film thickness determined by the disjoining pressure.39,46−48 The dewetted area grows over time, pushing further liquid out of the contact spot [Figure 1d]. Depending on the pillar array period, dewetted areas with very different morphologies were observed during dewetting. For a large pillar spacing, the dewetting dynamics is similar to that of a flat surface.39,46,47Figure 4a shows the anisotropic growth of a dewetted area for pillar spacing dp = 21 μm and a very soft polymer Y = 11.28 kPa. The non-circular shape of the dewetted area is caused by an anisotropy of the time-averaged contact line speed. Its motion is essentially unhindered along the axes but slowed down along the main diagonal of the square array. In the experiment shown in Figure 4b, a more rigid polymer (Y = 1.365 MPa) and a denser array (dp = 14 μm) were used, which gave rise to the occurrence of many irregular-shaped dry spots.

Figure 4.

Figure 4

Open in a new tab

(a) Square-shaped dewetted area observed 14 s after dewetting nucleation in a system with pillar spacing dp = 21 μm and elastic modulus Y = 11.28 kPa. (b) Using a denser array (dp = 14 μm) and a more rigid polymer (Y = 1.365 MPa) results in the formation of a multitude of irregular-shaped dewetted areas that grow relatively slowly. The image was acquired 12 s after dewetting nucleation.

The expansion of the dewetted area in Figure 4a proceeds in a concerted and time-correlated fashion all along its perimeter, otherwise the square shape would randomize and be lost. In contrast, the expansion of the dewetted area in Figure 4b occurs in a spatially uncorrelated fashion, leading to the irregular shape. The red arrow indicates the localized spreading of the dewetted area into a neighboring unit cell of the array.

Numerical Results

Figure 5 shows snapshots during the expansion of dewetted areas nucleated in arrays with different pillar spacings. The five columns represent the moments when the advancing contact line reaches distances rcl/hp of 20, 40, 60, 80, and 100 measured from the center of the array along the x axis. The scale bar applies to all images. For dp/hp ≥ 25, the dewetted area is diamond-shaped. For dp/hp ≤ 20, it appears more round and dp/hp = 22 is an intermediate case, where the dewetted area is initially square but gets rounder as it grows.

Figure 5.

Figure 5

Open in a new tab

Numerical simulations of the expansion of the dewetted areas for different pillar spacing dp. The five columns correspond to the moments when rcl/hp is equal 20, 40, 60, 80, and 100. The shape of the dry spot changes qualitatively for dp/hp between 22 and 25. The colors represent the liquid film thickness as indicated by the colorbar underneath the figure. The scale bar applies to all images.

Figure 6 shows a comparison between the dewetting mode in Figure 4 and analogous numerical results. Figure 6b shows anisotropic growth of a dewetted area, similar to the one in Figure 4a. The contact line moves faster along the axes of the square array and slower along its main diagonal, resulting in a square shape. Figure 6c,d shows in magnification how a dewetted area expands from one unit cell of the array to a neighboring one. The colorbar in Figure 5 also applies to Figure 6b,d.

Figure 6.

Figure 6

Open in a new tab

(a) Time evolution of the dry spot in Figure 4a. The panels correspond to 2.8, 5.3, 7.9, 9.8, and 11.8 s after dewetting nucleation. (b) A numerical simulation for dp = 50 μm and Y = 1.365 MPa yields similar results, a square-looking dry spot. (c) Magnification of Figure 4b illustrating the dry spot growth mechanism. The contact line slowly advances between pillars to a neighboring unit cell of the array. The panels correspond to 11.8, 11.9, 12, 12.1, and 12.2 s after dewetting nucleation. (d) A numerical simulation for dp = 15 μm and Y = 1.365 MPa predicts a similar behavior. The colorbar in Figure 5 also applies to (b) and (d).

Figure 7a shows the position of the advancing contact line as a function of time measured along the x axis (solid curves, circles) and along the main diagonal of the array (y = x, dashed lines, stars). The solid black line corresponds to a flat substrate without pillar array (dp = ∞). Along the main diagonal [solid lines in Figure 7a], the contact line moves until it reaches a pillar, where it gets pinned temporarily. It propagates around the pillar and eventually reaches the other side of the pillar, where it detaches and continues its motion. Along the x axis [dashed lines in Figure 7a], the contact line moves faster and with relatively uniform speed for dp ≥ 25 μm. For dp ≤ 22 μm, the speed shows strong modulations due to the influence of nearby pillars.

Figure 7.

Figure 7

Open in a new tab

(a) Position of the contact line measured along the “fast” direction (x axis, solid lines) and the “slow” direction (main diagonal y = x, dashed lines) in simulations with different pillar spacings. Inset: equivalent experimental data corresponding to Figure 4a. (b) Square root of the dry spot area as a function of time extracted from numerical simulations with varying pillar spacing. The curves are accelerating for dp ≥ 25 μm (above the gray dashed line) but decelerating for dp ≤ 22 μm (below the gray dashed line). An analogous simulation with a flat substrate (dp = ∞) is shown for comparison.

The inset in Figure 7a presents equivalent experimental data corresponding to Figure 4a. The qualitative behavior is completely analogous to the simulations; however, the timescales do not match. This discrepancy is mainly due to the large number of input parameters of the numerical model that are not accurately known, such as the disjoining pressure parameters and the interfacial energies.39 Moreover, the nucleation point of dewetting was located off center in Figure 4a, which implies that the contact line could only be traced for a fraction of rcs. In contrast, in the simulations, the nucleation center was located in the center of the contact spot, such that the contact lines could be traced along the entire contact spot radius rcs.

Figure 7b shows the time dependence of the square root of the dry area 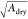Inline graphic at the glass–elastomer interface, not including the dry pillar–elastomer interface. The origin of the abscissa t = 0 corresponds to the time at which the dewetting started. For dp ≥ 25 μm (i.e., for curves above the gray dashed line), Inline graphic is accelerating in time, but for dp ≤ 22 μm (curves below the gray dashed line), it is decelerating. The black line shows the result from an analogous simulation with a flat substrate (i.e., without micropillars, dp = ∞). The initial jump at t ≪ 0.1 s is due to the chemical defect.

Figure 8a,b shows profiles of the liquid–elastomer interface and the pressure along the x axis (i.e., in between two rows of pillars), right before dewetting commenced. For dp = 50 and 100 μm, the liquid film thickness decreases toward the edge of the contact spot, similar to the case of a flat substrate. For dp ≤ 25 μm, the liquid film thickness increases toward the edge of the array. The liquid film outside of the array, but inside the contact spot, is thinner for dp ≤ 22 μm because the dewetting starts later in these cases. The primary reason for the delay is the reduced squeeze-out flow speed for a denser array of micropillars.

Figure 8.

Figure 8

Open in a new tab

Numerical simulations of (a) the liquid film thickness h(x, y = 0) and (b) the pressure pf (x, y = 0) right before dry spot nucleation for hp = 1 μm and different values of dp. The red dotted line in the inset of (b) defines the cross section, along which h and pf are plotted. The green cross indicates the origin (x, y) = (0, 0), i.e., the center of the contact spot.

Figure 9 presents numerical simulations of the dependence of δ and δ + Δz on the gap width between neighboring pillars at constant average pressure. The data correspond to a system in a steady state, after transient effects have faded. The curves labeled α and β correspond to the symmetry points on the axis and the main diagonal of the square array, respectively, as illustrated in the inset. We conclude that, for large array periods, Δz becomes negligible compared to δ.

Figure 9.

Figure 9

Open in a new tab

Numerical simulations of the deformation amplitude of a soft elastic half-space (Y = 1.365 MPa, ν = 0.499) indented by a rigid pillar array as a function of the gap width between neighboring pillars at constant average pressure. The inset defines the points α on the axis and β on the main diagonal of the square array. The yellow shaded area indicates the range of array periods used in the experiments. The triangle indicates a power law scaling of δ + Δz ∼ (dp – 2rp) 2.

In the stationary simulations shown in Figure 9, the pillar height hp was assumed to be essentially infinite, i.e., a possible solid-on-solid contact in the valleys between the pillars was not taken into account. A finite hp would imply that δ + Δz does not exceed a maximum value of hp in Figure 9. This is rectified in the steady-state simulations in Figure 10, where we allowed for a frictionless solid–solid contact according to eq 5.

Figure 10.

Figure 10

Open in a new tab

(a) Numerical simulations of the extension of the elastomer–substrate dry contact region for dp = 17 μm and different values of the force per pillar Fp. The gray shaded areas represent the pillars. (b) Extension of the dry contact spot along the main diagonal (solid lines) and the axis (dashed lines) of the square array for different values of dp. The symbols overlaid on the lines for dp = 17 μm correspond to the data shown in (a).

In Figure 10a, we plot the shape and size of the elastomer–substrate dry contact region for dp/hp = 17 and different values of Fp. At a certain critical value F1 of Fp, the elastomer makes contact with the substrate in the center of a unit cell of the square array, i.e., in the point labeled β in Figure 10a. For larger values of Fp, the dry contact region increases in size. At a second critical value F2 of Fp, the previously disconnected contact of neighboring unit cells merge and become connected over a length scale by far exceeding the array period dp. This is a prerequisite for dewetting the entire pillar array. For Fp ≪ F1, the regions available to the liquid are continuous and connected, whereas for Fp > F2, they become disconnected rings around the individual pillars as visible in Figures 4–6.

Figure 10b shows the extension of the dry contact spot scl relative to the point labeled β along the main diagonal (solid lines) and the axis (dashed lines) of the square array for different values of dp. The dashed lines terminate at a value of scl = dp/2. The solid lines asymptote to a value of 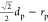Inline graphic in the limit of Fp → ∞. For dp ≫ 2rp, the critical values F1 and F2 are of similar magnitude, whereas F2 can greatly exceed F1 for dp ≈ 2rp.

Discussion

There exists a minimum value of dp or conversely maximum values of hp or Y , below or above which dewetting of the interstitial regions can no longer occur. The reason is that the applied force becomes insufficient for the protrusions of the deformed hemisphere to reach the bottom of the substrate.

To develop intuition, we consider the classical problem of contact mechanics of a single, rigid cylindrical punch indenting an elastic half-space.49 In this case, the steady-state indentation depth δ ∼ Fp/Y is proportional to the applied force and inversely proportional to Young’s modulus. We expect that this scaling applies to the case of a pillar array indenting an elastic half-space at large values of the array period dp. In this case, the force per micropillar is given by Fp ≈ dp2pav, where pav is the average pressure acting on the pillar array. Consequently, we expect the indentation depth to scale as

graphic file with name la0c02005_m009.jpg 6

The triangle in Figure 9 indicates that, for large periods, a power law relation δ + Δz ∼ (dp – 2rp)2 is a good approximation to the numerical data. Since, in the limit of large periods, Δz ≪ δ and dp ≫ 2rp hold, we indeed recover the expected scaling. We note that, in our experiments, we kept the contact spot radius constant, which implies that the average pressure scales with Young’s modulus. This does not affect the δ ∼ dp2 scaling; however, it makes the static deformation insensitive to Y.

For dense arrays, the non-linear relation eq 6 implies that locally larger periods induce locally larger protrusion amplitudes δ + Δz and locally higher film pressures pf, both of which speed up film thinning and dry spot nucleation. In other words, unavoidable fluctuations in the pillar spacings or pillar dimensions are amplified in terms of their impact on where dewetted areas nucleate for small values of dp/hp. We believe that this increased sensitivity to the array imperfections is a contributing factor to the irregular shapes of the dewetted areas observed in Figure 4b as dp/hp decreases.

As indicated by Figures 7a and 8a, the dewetting time and the expansion rate of the dewetted area along the array axes are almost the same for sparse arrays dp/hp ≥ 25. For dense arrays dp/hp ≤ 22, the dewetting time increases and the expansion rate significantly decreases. The origin of the slowdown is the concomitant reduction of the pressure pf in between rows of pillars as visible in Figure 8b for dp ≤ 25 μm. A larger fraction of the externally applied, overall contact force is acting on top of the pillars and used up in generating the protrusions, which explains the decreased values of pf and dpf/dx. It is the gradient of the pressure distribution, which determines the speed with which the liquid is driven out of the array and out of the contact spot.

In our experience, dewetting in an elastomer (Fomblin Y)–glass system in the absence of pillars suffers from sensitivity to surface heterogeneities and the boundaries of the contact area tend to have a ragged morphology. For a system containing micropillars, as pointed out above, the contact pressure in the interstitial space between neighboring pillars is greatly reduced for small values of dp. Consequently, we expect an increased sensitivity of the dry spot morphology to surface imperfections in this regime. Besides geometric fluctuations, therefore, also fluctuations in the elastic properties and the surface energies can contribute to the irregular growth mode observed in Figure 4b.

An interesting question concerns the nature of the correlation between the dewetting behavior studied in this manuscript and the achievable adhesion strength. Li et al. presented experiments of the adhesion between a flat elastomer layer and a plano-convex glass lens.50 They observed dewetting of the contact spot for pure water, whereas for SDS surfactant concentrations exceeding 0.03%, dewetting no longer occurred, which they attributed to the stabilizing effect of double-layer repulsion. The measured adhesion strength diminished by a factor of 4 compared to the case of pure water.

Generally, dewetting is controlled by the disjoining pressure isotherm, which is a material property reflecting molecular interactions between all solid and liquid phases involved. The same interactions also govern the van der Waals attraction responsible for the dry adhesion of molecularly smooth solid surfaces. In practice, surfaces are rarely molecularly flat and a plethora of other phenomena determine the effective strength of adhesion, such as surface roughness,51,52 viscous forces,53,54 surface tension forces,54,55 non-Newtonian liquid rheology,56 the three-dimensional surface geometry,57 or viscoelastic bulk properties of soft materials.51,58 Therefore, the correlation between dewetting and adhesion needs to be studied separately in each case.

For technological applications, the time required until a high adhesive state is reached and dewetting is complete is relevant. This lag time is composed of the thinning time of the liquid film in between the objects until dewetting commences and the subsequent dewetting time until the dewetted area reaches the edge of the contact spot. As shown in Figure 7, the dewetting time increases with decreasing pillar spacing. The thinning time can be divided into the time Δttop until the tops of the pillars dewet and Δtbase until the base plane of the pillar starts dewetting. Δttop benefits from a larger dp due to channeling,59−61 i.e., the efficient removal of the intervening liquid through the interstitial space between the pillars. Δtbase increases with decreasing dp due to the reduced effective contact pressure in between the pillars. In our experiments using Fomblin Y, the overall timescale typically ranged from 0.5 to 5 min. For water, which has a much lower viscosity, we expect this time to be reduced by two orders of magnitude.

Summary and Conclusions

The morphology of dewetted areas forming in a thin liquid film confined between a periodic micropillar array and a soft, elastic surface depends sensitively on the pillar height and spacing. For large ratios of array period to micropillar height and width, the dewetted areas tend to be diamond-shaped and expand at a rate almost the same as for a flat, unpatterned substrate. For a small ratio, the shapes of the dewetted areas become irregular and their expansion rate is significantly reduced.

We developed a fully coupled numerical model based on linear elasticity, the Reynolds equation, and a disjoining pressure formalism. The simulations reproduce the key features observed in the experiments very well. We found that, for the smallest array periods studied, the pressure gradient becomes noticeably smaller inside the array, which explains the observed delay of the onset of dewetting. For a larger average contact pressure, the elastomer protrudes further into the gap space between neighboring pillars. We found that the protrusion amplitude scales to good approximation as the square of the array period at constant pressure. This non-linear dependence implies an increased sensitivity of the dewetting dynamics to fluctuations in the pillar shape, height, and spacing in the limit of small periods. Furthermore, systems with small pillar spacing exhibit a reduced interstitial contact pressure, which makes them more sensitive to any material or surface irregularities. These two effects combined are the likely origin of the observed morphological difference.

In underwater adhesive systems, the adhesion force is usually provided by solid–solid contact of the tops of the pillars. The interstitial space between the pillars has a passive role of enabling a fast and efficient drainage of the liquid phase.59−61 Micropillar arrays are advantageous in that respect due to the connectedness of their interstitial space. We have considered a very soft material with a Young’s modulus comparable to human skin62 that deforms elastically upon contact and thereby induces dewetting in between the pillars. In this fashion, the area of solid-on-solid contact is increased, thereby likely enhancing adhesion. Moreover, we expect that the elastic deformation of the soft surface increases the stability of the adhesive contact to lateral motion due to mechanical interlocking.

Acknowledgments

This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 642861.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.langmuir.0c02005.

The authors declare no competing financial interest.

Supplementary Material

la0c02005_si_001.avi (3.9MB, avi)
la0c02005_si_002.avi (9.2MB, avi)

References

  1. Autumn K.; Liang Y. A.; Hsieh S. T.; Zesch W.; Chan W. P.; Kenny T. W.; Fearing R.; Full R. J. Adhesive force of a single gecko foot-hair. Nature 2000, 405, 681–685. 10.1038/35015073. [DOI] [PubMed] [Google Scholar]
  2. Arzt E.; Gorb S.; Spolenak R. From micro to nano contacts in biological attachment devices. Proc. Natl. Acad. Sci. U. S. A. 2003, 100, 10603–10606. 10.1073/pnas.1534701100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Barthlott W.; Neinhuis C. Purity of the sacred lotus, or escape from contamination in biological surfaces. Planta 1997, 202, 1–8. 10.1007/s004250050096. [DOI] [Google Scholar]
  4. Hensel R.; Helbig R.; Aland S.; Braun H.-G.; Voigt A.; Neinhuis C.; Werner C. Wetting resistance at its topographical limit: the benefit of mushroom and serif T structures. Langmuir 2013, 29, 1100–1112. 10.1021/la304179b. [DOI] [PubMed] [Google Scholar]
  5. Hensel R.; Helbig R.; Aland S.; Voigt A.; Neinhuis C.; Werner C. Tunable nano-replication to explore the omniphobic characteristics of springtail skin. NPG Asia Mater. 2013, 5, e37 10.1038/am.2012.66. [DOI] [Google Scholar]
  6. Kamperman M.; Kroner E.; del Campo A.; McMeeking R. M.; Arzt E. Functional adhesive surfaces with “gecko” effect: The concept of contact splitting. Adv. Eng. Mater. 2010, 12, 335–348. 10.1002/adem.201000104. [DOI] [Google Scholar]
  7. Hensel R.; Moh K.; Arzt E. Engineering Micropatterned Dry Adhesives: From Contact Theory to Handling Applications. Adv. Funct. Mater. 2018, 28, 1800865. 10.1002/adfm.201800865. [DOI] [Google Scholar]
  8. Barreau V.; Hensel R.; Guimard N. K.; Ghatak A.; McMeeking R. M.; Arzt E. Fibrillar Elastomeric Micropatterns Create Tunable Adhesion Even to Rough Surfaces. Adv. Funct. Mater. 2016, 26, 4687–4694. 10.1002/adfm.201600652. [DOI] [Google Scholar]
  9. Li M.; Xie J.; Dai Q.; Huang W.; Wang X. Effect of wetting case and softness on adhesion of bioinspired micropatterned surfaces. J. Mech. Behav. Biomed. Mater. 2018, 78, 266–272. 10.1016/j.jmbbm.2017.11.036. [DOI] [PubMed] [Google Scholar]
  10. Xie J.; Li M.; Dai Q.; Huang W.; Wang X. Key parameters of biomimetic patterned surface for wet adhesion. Int. J. Adhes. Adhes. 2018, 82, 72–78. 10.1016/j.ijadhadh.2018.01.004. [DOI] [Google Scholar]
  11. Li M.; Dai Q.; Huang W.; Wang X. Pillar versus dimple patterned surfaces for wettability and adhesion with varying scales. J. R. Soc., Interface 2018, 15, 20180681. 10.1098/rsif.2018.0681. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Meng F.; Liu Q.; Wang X.; Tan D.; Xue L.; Barnes W. J. P. Tree frog adhesion biomimetics: opportunities for the development of new, smart adhesives that adhere under wet conditions. Phil. Trans. R. Soc. A 2019, 377, 20190131. 10.1098/rsta.2019.0131. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Hosoda N.; Gorb S. N. Underwater locomotion in a terrestrial beetle: combination of surface de-wetting and capillary forces. Proc. R. Soc. Lond. B: Biol. Sci. 2012, 279, 4236–4242. 10.1098/rspb.2012.1297. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Rao P.; Sun T. L.; Chen L.; Takahashi R.; Shinohara G.; Guo H.; King D. R.; Kurokawa T.; Gong J. P. Tough Hydrogels with Fast, Strong, and Reversible Underwater Adhesion Based on a Multiscale Design. Adv. Mater. 2018, 30, 1801884. 10.1002/adma.201801884. [DOI] [PubMed] [Google Scholar]
  15. Federle W.; Barnes W. J. P.; Baumgartner W.; Drechsler P.; Smith J. M. Wet but not slippery: boundary friction in tree frog adhesive toe pads. J. R. Soc., Interface 2006, 3, 689–697. 10.1098/rsif.2006.0135. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Barnes W. J. P. Biomimetic Solutions to Sticky Problems. Science 2007, 318, 203–204. 10.1126/science.1149994. [DOI] [PubMed] [Google Scholar]
  17. Glass P.; Chung H.; Washburn N. R.; Sitti M. Enhanced Wet Adhesion and Shear of Elastomeric Micro-Fiber Arrays with Mushroom Tip Geometry and a Photopolymerized p(DMA-co-MEA) Tip Coating. Langmuir 2010, 26, 17357–17362. 10.1021/la1029245. [DOI] [PubMed] [Google Scholar]
  18. Glass P.; Chung H.; Washburn N. R.; Sitti M. Enhanced Reversible Adhesion of Dopamine Methacrylamide-Coated Elastomer Microfibrillar Structures under Wet Conditions. Langmuir 2009, 25, 6607–6612. 10.1021/la9009114. [DOI] [PubMed] [Google Scholar]
  19. Majumder A.; Sharma A.; Ghatak A. A Bioinspired Wet/Dry Microfluidic Adhesive for Aqueous Environments. Langmuir 2010, 26, 521–525. 10.1021/la9021849. [DOI] [PubMed] [Google Scholar]
  20. Soltannia B.; Sameoto D. Strong, Reversible Underwater Adhesion via GeckoInspired Hydrophobic Fibers. ACS Appl. Mater. Interfaces 2014, 6, 21995–22003. 10.1021/am5075375. [DOI] [PubMed] [Google Scholar]
  21. Langowski J. K. A.; Dodou D.; Kamperman M.; van Leeuwen J. L. Tree frog attachment: mechanisms, challenges, and perspectives. Front. Zool. 2018, 15, 32. 10.1186/s12983-018-0273-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Wang Y.; Kang V.; Arzt E.; Federle W.; Hensel R. Strong Wet and Dry Adhesion by Cupped Microstructures. ACS Appl. Mater. Interfaces 2019, 11, 26483–26490. 10.1021/acsami.9b07969. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Ma Y.; Ma S.; Wu Y.; Pei X.; Gorb S. N.; Wang Z.; Liu W.; Zhou F. Remote Control over Underwater Dynamic Attachment/Detachment and Locomotion. Adv. Mater. 2018, 30, 1801595. 10.1002/adma.201801595. [DOI] [PubMed] [Google Scholar]
  24. Israelachvili J. N.Intermolecular and surface forces; Academic Press, 2011. [Google Scholar]
  25. Yoshimitsu Z.; Nakajima A.; Watanabe T.; Hashimoto K. Effects of surface structure on the hydrophobicity and sliding behavior of water droplets. Langmuir 2002, 18, 5818–5822. 10.1021/la020088p. [DOI] [Google Scholar]
  26. Lundgren M.; Allan N. L.; Cosgrove T.; George N. Molecular dynamics study of wetting of a pillar surface. Langmuir 2003, 19, 7127–7129. 10.1021/la034224h. [DOI] [Google Scholar]
  27. He B.; Patankar N. A.; Lee J. Multiple equilibrium droplet shapes and design criterion for rough hydrophobic surfaces. Langmuir 2003, 19, 4999–5003. 10.1021/la0268348. [DOI] [Google Scholar]
  28. Patankar N. A. Transition between superhydrophobic states on rough surfaces. Langmuir 2004, 20, 7097–7102. 10.1021/la049329e. [DOI] [PubMed] [Google Scholar]
  29. Krupenkin T. N.; Taylor J. A.; Schneider T. M.; Yang S. From rolling ball to complete wetting: The dynamic tuning of liquids on nanostructured surfaces. Langmuir 2004, 20, 3824–3827. 10.1021/la036093q. [DOI] [PubMed] [Google Scholar]
  30. Fan J. G.; Dyer D.; Zhang G.; Zhao Y. P. Nanocarpet effect: Pattern formation during the wetting of vertically aligned nanorod arrays. Nano Lett. 2004, 4, 2133–2138. 10.1021/nl048776b. [DOI] [Google Scholar]
  31. Martines E.; Seunarine K.; Morgan H.; Gadegaard N.; Wilkinson C. D. W.; Riehle M. O. Superhydrophobicity and superhydrophilicity of regular nanopatterns. Nano Lett. 2005, 5, 2097–2103. 10.1021/nl051435t. [DOI] [PubMed] [Google Scholar]
  32. Extrand C. W.; Sung I. M.; Hall P.; Schmidt D. Superwetting of structured surfaces. Langmuir 2007, 23, 8882–8890. 10.1021/la700816n. [DOI] [PubMed] [Google Scholar]
  33. Ishino C.; Reyssat M.; Reyssat E.; Okumura K.; Quéré D. Wicking within forests of micropillars. Europhys. Lett. 2007, 79, 8–12. [Google Scholar]
  34. Courbin L.; Denieul E.; Dressaire E.; Roper M.; Ajdari A.; Stone H. A. Imbibition by polygonal spreading on microdecorated surfaces. Nat. Mater. 2007, 6, 661–664. 10.1038/nmat1978. [DOI] [PubMed] [Google Scholar]
  35. Chu K. H.; Xiao R.; Wang E. N. Unidirectional liquid spreading on asymmetric nanostructured surfaces. Nat. Mater. 2010, 9, 413–417. 10.1038/nmat2726. [DOI] [PubMed] [Google Scholar]
  36. Kim S. J.; Moon M. W.; Lee K. R.; Lee D. Y.; Chang Y. S.; Kim H. Y. Liquid spreading on superhydrophilic micropillar arrays. J. Fluid Mech. 2011, 680, 477–487. 10.1017/jfm.2011.210. [DOI] [Google Scholar]
  37. Gauthier A.; Rivetti M.; Teisseire J.; Barthel E. Role of kinks in the dynamics of contact lines receding on superhydrophobic surfaces. Phys. Rev. Lett. 2013, 110, 046101 10.1103/PhysRevLett.110.046101. [DOI] [PubMed] [Google Scholar]
  38. Yuan Q.; Huang X.; Zhao Y. P. Dynamic spreading on pillar-arrayed surfaces: Viscous resistance versus molecular friction. Phys. Fluids 2014, 26, 092104. [Google Scholar]
  39. Chudak M.; Kwaks J. S.; Snoeijer J. H.; Darhuber A. A. Non-axisymmetric elastohydrodynamic solid-liquid-solid dewetting: Experiments and numerical modelling. Eur. Phys. J. E: Soft Matter Biol. Phys. 2020, 43, 2. 10.1140/epje/i2020-11926-3. [DOI] [PubMed] [Google Scholar]
  40. Purtov J.; Verch A.; Rogin P.; Hensel R. Improved development procedure to enhance the stability of microstructures created by two-photon polymerization. Microelectron. Eng. 2018, 194, 45–50. 10.1016/j.mee.2018.03.009. [DOI] [Google Scholar]
  41. Jayne R. K.; Stark T. J.; Reeves J. B.; Bishop D. J.; White A. E. Dynamic Actuation of Soft 3D Micromechanical Structures Using Micro-Electromechanical Systems (MEMS). Adv. Mater. Technol. 2018, 3, 1700293. 10.1002/admt.201700293. [DOI] [Google Scholar]
  42. Hensel R.; McMeeking R. M.; Kossa A. Adhesion of a rigid punch to a confined elastic layer revisited. J. Adhesion 2019, 95, 44–63. 10.1080/00218464.2017.1381603. [DOI] [Google Scholar]
  43. Müller A.; Wapler M. C.; Wallrabe U. A quick and accurate method to determine the Poisson’s ratio and the coefficient of thermal expansion of PDMS. Soft Matter 2019, 15, 779–784. 10.1039/C8SM02105H. [DOI] [PubMed] [Google Scholar]
  44. Hertz H. R. Über die Berührung fester elastischer Körper. J. Pure Appl. Math. 1882, 92, 156–171. [Google Scholar]
  45. Johnson K. L.; Kendall K.; Roberts A. D. Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. A 1971, 324, 301–313. 10.1098/rspa.1971.0141. [DOI] [Google Scholar]
  46. Martin P.; Brochard-Wyart F. Dewetting at soft interfaces. Phys. Rev. Lett. 1998, 80, 3296. 10.1103/PhysRevLett.80.3296. [DOI] [Google Scholar]
  47. Martin A.; Buguin A.; Brochard-Wyart F. Dewetting nucleation centers at soft interfaces. Langmuir 2001, 17, 6553–6559. 10.1021/la010503y. [DOI] [Google Scholar]
  48. Chudak M.; Kwaks J. S.; Snoeijer J. H.; Darhuber A. A. Escape dynamics of liquid droplets confined between soft interfaces: non-inertial coalescence cascades. Soft Matter 2020, 16, 1866–1876. 10.1039/C9SM01992H. [DOI] [PubMed] [Google Scholar]
  49. Johnson K. L.Contact Mechanics; Cambridge University Press, 1985. 10.1017/CBO9781139171731 [DOI] [Google Scholar]
  50. Li M.; Xie J.; Shi L.; Huang W.; Wang X. Controlling direct contact force for wet adhesion with different wedged film stabilities. J. Phys. D: Appl. Phys. 2018, 51, 165305. 10.1088/1361-6463/aab58d. [DOI] [Google Scholar]
  51. Lorenz B.; Krick B. A.; Mulakaluri N.; Smolyakova M.; Dieluweit S.; Sawyer W. G.; Persson B. N. J. Adhesion: role of bulk viscoelasticity and surface roughness. J. Phys.: Cond. Matt. 2013, 25, 225004. [DOI] [PubMed] [Google Scholar]
  52. Lorenz B.; Krick B. A.; Rodriguez N.; Sawyer W. G.; Mangiagalli P.; Persson B. N. J. Static or breakloose friction for lubricated contacts: the role of surface roughness and dewetting. J. Phys.: Cond. Matt. 2013, 25, 445013. [DOI] [PubMed] [Google Scholar]
  53. Dhong C.; Fréchette J. Coupled effects of applied load and surface structure on the viscous forces during peeling. Soft Matter 2015, 11, 1901–1910. 10.1039/C4SM02616K. [DOI] [PubMed] [Google Scholar]
  54. Dirks J.-H. Physical principles of fluidmediated insect attachment - Shouldn’t insects slip?. Beilstein J. Nanotechnol. 2014, 5, 1160–1166. 10.3762/bjnano.5.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Pinchasik B.-E.; Steinkühler J.; Wuytens P.; Skirtach A. G.; Fratzl P.; Möhwald H. From Beetles in Nature to the Laboratory: Actuating Underwater Locomotion on Hydrophobic Surfaces. Langmuir 2015, 31, 13734–13742. 10.1021/acs.langmuir.5b03821. [DOI] [PubMed] [Google Scholar]
  56. Barral Q.; Ovarlez G.; Chateau X.; Boujlel J.; Rabideau B.; Coussot P. Adhesion of yield stress fluids. Soft Matter 2010, 6, 1343–1351. 10.1039/B922162J. [DOI] [Google Scholar]
  57. Chen Y.; Meng J.; Gu Z.; Wan X.; Jiang L.; Wang S. Bioinspired Multiscale Wet Adhesive Surfaces: Structures and Controlled Adhesion. Adv. Funct. Mater. 2020, 30, 1905287. 10.1002/adfm.201905287. [DOI] [Google Scholar]
  58. Greenwood J. A.; Johnson K. L. The mechanics of adhesion of viscoelastic solids. Philos. Mag. A 1981, 43, 697–711. 10.1080/01418618108240402. [DOI] [Google Scholar]
  59. Gupta R.; Fréchette J. Measurement and scaling of hydrodynamic interactions in the presence of draining channels. Langmuir 2012, 28, 14703–14712. 10.1021/la303508x. [DOI] [PubMed] [Google Scholar]
  60. Pilkington G. A.; Gupta R.; Fréchette J. Scaling hydrodynamic boundary conditions of microstructured surfaces in the thin channel limit. Langmuir 2016, 32, 2360–2368. 10.1021/acs.langmuir.5b04134. [DOI] [PubMed] [Google Scholar]
  61. Chastel T.; Mongruel A. Squeeze flow between a sphere and a textured wall. Phys. Fluids 2016, 28, 023301 10.1063/1.4941301. [DOI] [Google Scholar]
  62. Kalra A.; Lowe A.; Al-Jumaily A. M. Mechanical behaviour of skin: a review. J. Mater. Sci. Eng. 2016, 5, 1000254. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

la0c02005_si_001.avi (3.9MB, avi)
la0c02005_si_002.avi (9.2MB, avi)

Articles from Langmuir are provided here courtesy of American Chemical Society

RESOURCES