Second magnetization peak, rhombic-to-square Bragg vortex glass transition, and intersecting magnetic hysteresis curves in overdoped BaFe₂(As_1−xP_x)₂ single crystals

Abstract

The second magnetization peak (SMP) in the fourfold symmetric superconducting single crystals (such as iron pnictides and tetragonal cuprates) has been attributed to the rhombic-to-square transition (RST) of the quasi-ordered vortex solid (the Bragg vortex glass, BVG). This represents an alternative to the pinning-induced BVG disordering as the actual SMP mechanism. The analysis of the magnetic response of BaFe₂(As_1−xP_x)₂ specimens presented here shows that the SMP is not generated by the RST. However, the latter can affect the pinning-dependent SMP onset field if this is close to the (intrinsic) RST line, through the occurrence of a “shoulder” on the magnetic hysteresis curves m(H), and a maximum in the temperature variation of the DC critical current density. These features disappear in AC conditions, where the vortex system is dynamically ordered in the RST domain, emphasizing the essential role of vortex dislocations for an efficient accommodation of the vortex system to the pinning landscape and the SMP development. The m(H) shoulder is associated with a precipitous pinning-induced proliferation of dislocations at the RST, where the BVG elastic “squash” modulus softens. The DC magnetization relaxation indicates that the pinning-induced vortex system disordering continues above the RST domain, as the basic SMP mechanism.

Introduction

Vortex pinning enhancement at high external magnetic fields H in superconducting single crystals with randomly distributed vortex pinning centres is one of the most relevant aspects for the understanding of the vortex-phase diagram of superconductors. In the case of weakly pinned specimens, one has the so called peak effect^1–6, where the maximum in the magnetic field dependence of the critical current density J_c (proportional to the irreversible magnetic moment) is rather sharp and located close to the DC irreversibility line (defined in the magnetic field-temperature T plane by a vanishing irreversible magnetization).

When vortex pinning is stronger, the peak effect is substituted by a wide second magnetization peak (SMP) in increasing H, with the onset field H_on and the peak field H_p far below the irreversibility line, leading to fishtail-shaped DC magnetic hysteresis m(H) curves. Among many SMP mechanisms and models (see, for example,^7–20), a pinning-induced disordering of the low-H quasi-ordered vortex solid (the Bragg vortex glass^21,22, BVG, stable against dislocation formation) has been considered to be at the origin of the SMP for various superconducting single crystals^9,14–18.

Significant progress for the understanding of the vortex phase diagram and the occurrence of the SMP has been made by considering the competition between the thermal energy, the pinning energy, and the elastic energy in the vortex system¹¹. In the low-T domain, the thermal energy can be neglected, and the simple energy balance relation leads to an onset field which is independent of temperature. This is also the result of the order–disorder transition derived in Ref.¹². It has been later shown¹⁴ that the upward curvature of the H_on(T) variation in the low-T range can be explained by taking into account the reduction of the effective pinning energy at low temperatures, where the probing current density is closer to J_c. This approach was suggested by the often observed time evolution of the SMP, with the characteristic fields decreasing at high relaxation levels. Since the SMP extends over a large magnetic field interval, it has been proposed that the pinning-induced BVG disordering is continuous^15,17, starting at H_on, where the energy for the plastic vortex deformation²³ is smaller than the effective pinning energy, and finishing at H_p, where the vortex system is amorphous. The essential point is the proliferation of dislocations in the vortex system for H between H_on and H_p (at large scales first), where the pinning increase is caused by the efficient accommodation of vortices to the pinning centres in the presence of vortex dislocations. This idea is strongly supported by the repeatedly reported elastic vortex creep-plastic creep crossover across the SMP^9,24–26.

Alternatively, is has been argued that in (tetragonal) La_2−xSr_xCuO₄ single crystals, with fourfold symmetric inter-vortex interactions, the SMP is the direct result of the characteristic, structural rhombic-to-square transition (RST) of the BVG¹³, in which case the upward curvature in H_on(T) at low T results directly (see below). It is known for a long time that in certain anisotropic low-T_c superconductors (such as borocarbides, Nb, and V₃Si) the vortex solid undergoes the RST, as noted in¹³. Using small-angle neutron scattering experiments, the crossover toward a square vortex arrangement with increasing magnetic field was clearly seen in La_2−xSr_xCuO₄²⁷, which may reflect the importance of the anisotropic vortex cores in the d-wave superconductors. The main aspect is the softening of the BVG elastic “squash” modulus C_sq at the RST line in the (H, T) plane²⁸, and it has been predicted in Ref.²⁹ that this BVG softening should lead to a maximum of the critical current density J_c(H, T) in the elastic (collective) pinning regime, with

$$J_{\text{c}}\propto 1/C_{\text{sq}}.$$ 1

However, the vortex pinning in the BVG (rhombic or square) is generally weak, and a better compliance of vortices to the pinning structure in the elastic regime may not be able to generate the observed, pronounced SMP.

The 122-type iron pnictide single crystals in H parallel to the crystallographic c axis exhibit a well-developed SMP^30,31, and the above RST-related SMP model has been extended to these fourfold symmetric superconductors, as in the case of Ba(Fe_0.925Co_0.075)₂As₂³² and BaFe₂(As_0.68P_0.32)₂³³ (for which the existence of the BVG has been proven³⁴). The SMP in LiFeAs (from the 111 family) received the same interpretation³⁵. The anisotropic interaction with fourfold symmetry induces a rhombic rather than hexagonal vortex arrangement, which transforms into a square one when the vortex separation decreases. Thermal fluctuations assist in breaking the rhomb symmetry, lowering the transition field H_RST as the temperature increases. By minimizing the free energy of a square vortex lattice with respect to the elastic moduli, it was found that

$$H_{\text{RST}}\left(T\right)\propto (T_0-T)T^{-\nu }{\lambda }^{2(1-\nu )},$$ 2

where λ is the London magnetic penetration depth, which is ~ 108 nm in the low-T limit for BaFe₂(As_0.68P_0.32)₂³³, T₀ is a constant lower than the critical temperature T_c, and the exponent ν is close to unity¹³. The location of the RST line relative to H_on and H_p is controversial. An exclusive relationship between the SMP and the RST implies the identification of H_RST(T) with H_p(T), as proposed for La_2−xSr_xCuO₄¹³, whereas in the case of Ba(Fe_0.925Co_0.075)₂As₂ it has been argued³² that the RST line should lie between H_on(T) and H_p(T), where the normalized magnetization relaxation rate has a minimum.

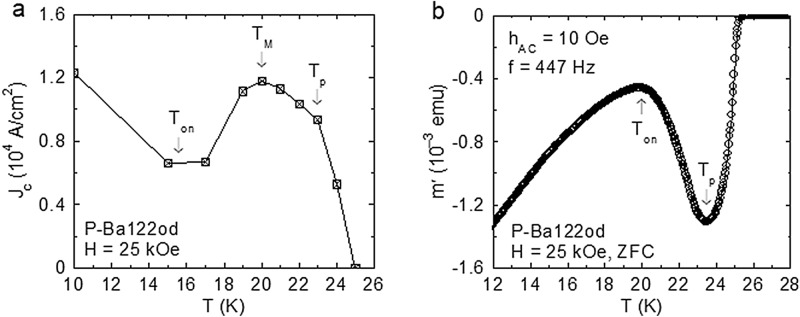
In this context, we recall the interpretation of the SMP in the fourfold symmetric superconductors by analysing the magnetic response of BaFe₂(As_1−xP_x)₂ (P-Ba122) single crystals. It was found that the SMP cannot be generated by the (elastic) rhombic-to-square BVG transition, but the RST can influence the SMP onset field if this is close to the intrinsic RST transition field, as revealed for overdoped specimens. In such a situation, the RST manifests itself through the occurrence of a “shoulder” on the magnetic hysteresis curves m(H), i.e., a relatively rapid increase of the effective pinning with increasing H for a limited magnetic field domain located just above H_on. The evolution of the m(H) shoulder with temperature leads to the intersection of the isothermal magnetic hysteresis curves, and, consequently, to a peak in the temperature variation of the DC critical current density J_c(T). The AC magnetic measurements performed by us indicate that when the vortex system is dynamically ordered in the RST domain the above features disappear. This suggests that the m(H) shoulder is associated with a precipitous proliferation of dislocations in the vortex system on crossing the RST line, where the softening of the BVG elastic squash modulus appears. Analysis of the DC magnetization relaxation shows that the pinning-induced vortex-system disordering continues above the RST range, as the basic mechanism for the occurrence of the SMP in the case of superconductors with fourfold inter-vortex interactions, as well.

Results and discussion

It is well established that by increasing the P doping level beyond the optimal one (where T_c is maximum) the critical current density of P-Ba122 single crystals decreases. A quantitative analysis of the J_c(T) dependence³¹ indicated that the characteristic pinning mechanisms [related to the spatial variation of T_c (δT_c pinning) and the fluctuations in the charge carrier mean free path] are enhanced for optimally doped and underdoped samples. The P-Ba122 specimen thoroughly investigated here is an overdoped single crystal, with the nominal x ~ 0.33, denoted below P-Ba122od, which has the critical temperature T_c = 27.5 K (determined at the onset of the diamagnetic signal, see Methods). This is similar to the single crystal investigated in Ref.³³, for which the occurrence of the RST has been signalled using DC magnetic measurements. To highlight the specific shape of the magnetic hysteresis curves of overdoped samples, an optimally doped single crystal (P-Ba122op, x ~ 0.30, T_c = 29 K), with stronger pinning, has been considered.

Figure 1 (main panel) illustrates the J_c(H) variation for P-Ba122od and P-Ba122op at T = 10 K, where J_c has been determined with the Bean model for rectangular specimens³⁶ from the descending branches of the m(H) curves plotted in the inset. By increasing doping from ~ 0.30 to ~ 0.33, J_c for H around the SMP onset at T = 10 K decreases from ~ 7 × 10⁴ to ~ 10⁴ A/cm². The particular difference between the m(H) curves of P-Ba122od and of the optimally doped specimen P-Ba122op is that in the former case there is a wide magnetic field range of weak elastic (collective) pinning (in the BVG), followed by an increase of ∣m∣ around H = 60 kOe on the ascending m(H) branch (see the inset of Fig. 1). We associate below the RST with this precipitous enhancement of the effective pinning in increasing H just above H_on.

Figure 1.

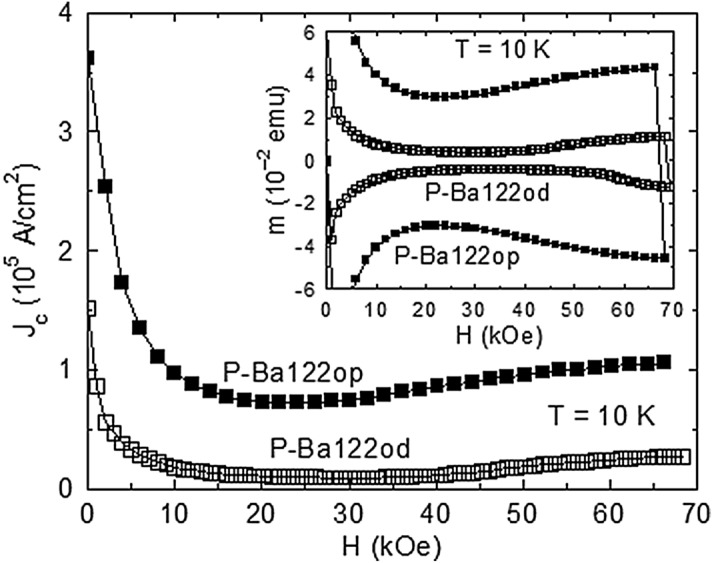
Main panel: Magnetic field H variation of the DC critical current density J_c determined for the optimally doped specimen P-Ba122op and the overdoped single crystal P-Ba122od (of similar dimensions) from the descending branches of the magnetic hysteresis curves m(H) at the temperature T = 10 K plotted in the inset. The particular difference between the DC magnetic hysteresis curves m(H) from the inset is that in the case of P-Ba122od there is a wide H range of weak collective (elastic) pinning in the low-field quasi-ordered vortex solid (the Bragg vortex glass), followed by a precipitous increase of ∣m∣ at H ~ 60 kOe on the ascending m(H) branch.

The DC magnetic hysteresis curve of P-Ba122od at T = 20 K is plotted in Fig. 2, where H_on and H_p of the SMP are indicated by arrows. One notes the development of an intriguing m(H) “shoulder” (leading to “pear-like” shaped hysteresis curves), which was observed for other overdoped P-Ba122 and K-Ba122 specimens³¹. The m(H) shoulder exhibits history effects. On the descending m(H) branch, the vortex system seems to remain trapped in more strongly pinned high-H states (see the inset of Fig. 1). For this reason, we considered the shoulder on the ascending m(H) branch, and the transition field H_RST has been taken at the local minimum of dm/dH, as illustrated in Fig. 2.

Figure 2.

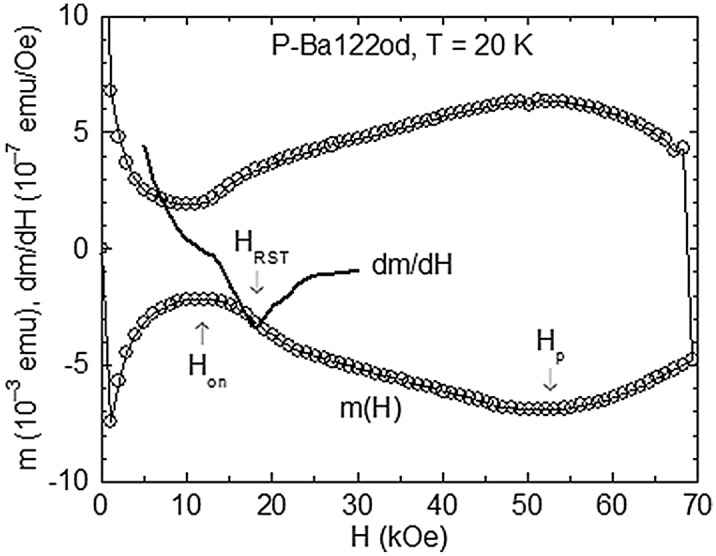
The DC magnetic hysteresis curve m(H) of P-Ba122od at T = 20 K, with the onset field H_on and the peak field H_p of the SMP indicated by arrows. We associate the structural rhomb-to-square vortex phase transition with the “step-like” enhancement of ∣m∣ in increasing H, giving rise to an m(H) shoulder. The structural transition field H_ST has been taken at the local minimum of dm/dH (represented by a continuous line).

The evolution of the m(H) shoulder with temperature is depicted in Fig. 3. As T decreases, the collective pinning in the rhombic BVG of P-Ba122od remains weak and the m(H) shoulder becomes more pronounced, generating the intersection of the m(H) curves (Fig. 3). The dashed line on the m(H) curve at T = 19 K illustrates a linear fit of the m(H) data just above the shoulder, to estimate the transition width. The temperature variation of the transition field H_RST determined as in Fig. 2, H_on(T), and H_p(T) are plotted in Fig. 4. The vertical segments on H_RST(T) represent the transition width extracted for several T values (by considering the RST symmetric relative to H_RST), showing that H_on is close to the lower H edge of the RST. One notes the upward curvature on H_RST(T), which is no longer present on H_p(T) below ~ 21 K. The H_RST(T) dependence determined by us is in agreement with (2), by considering the two-fluid model for λ(T)^23,33. The fit of the H_RST(T) variation from Fig. 4 supplies T₀ = 26.5 K < T_c, and ν = 0.8 (close to unity), as predicted by the RST theory¹³). At this point, it is worthy to note that if one takes H_RST as the field value where the shoulder in ∣m(H)∣ is completed in increasing H, it results T₀ > T_c, which is in conflict with (2).

Figure 3.

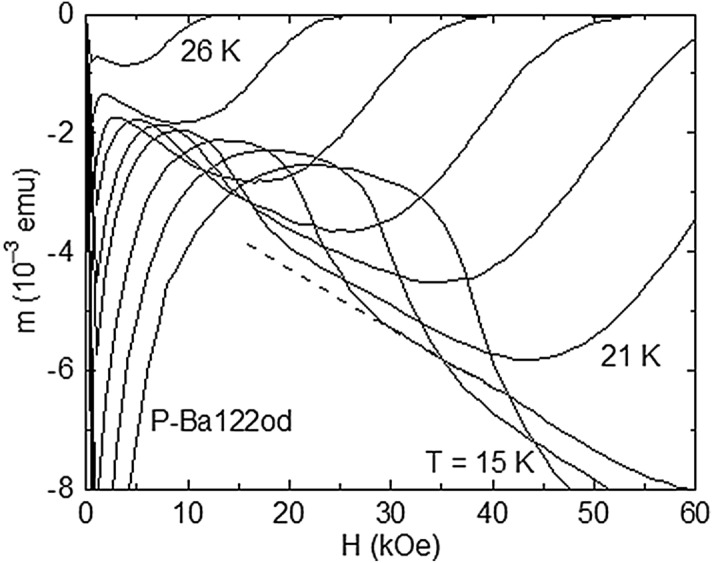
Evolution of the m(H) shoulder in increasing H observed for P-Ba122od with decreasing temperature T (from 26 to 21 K with a step of 1 K, and from 21 to 15 K, step of 2 K), leading to the intersection of the m(H) curves. The dashed line related to the m(H) curve at T = 19 K represents a liner fit of the m(H) data just above the shoulder, to estimate the width of the associated structural vortex phase transition.

Figure 4.

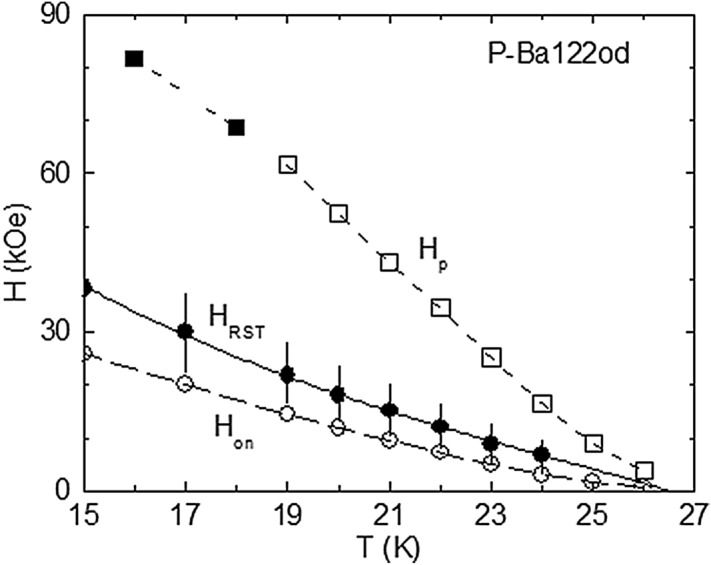
Temperature variation of the structural transition field H_ST (determined as in Fig. 2), the onset field H_on(T), and the peak field H_p(T). The vertical segments on H_ST(T) illustrate the transition width extracted for several temperatures (by taking the structural transition symmetric relative to H_ST). The continuous line represents the fit of the H_ST(T) dependence with (2), by considering the two-fluid model for the temperature variation of the magnetic penetration depth. The filed-symbol H_p(T) values have been determined from the magnetic hysteresis curves registered with the PPMS.

For intersecting isothermal m(H) curves, the m(T) variation obtained for a constant H with m taken from the magnetic hysteresis curves registered at different T values is obviously nonmonotonic, leading to a J_c(T) peak, as illustrated in Fig. 5a for H = 25 kOe. When m(T) is directly measured in increasing T at a constant H applied in ZFC conditions, the nonmonotonic dependence does not appear³³. This is because the external magnetic field is kept constant, and no inductive processes to bring the screening current density close to the critical value J_c are present. Thus, by entering a domain of stronger pinning, one can get at most a slowdown of the magnetic relaxation, i.e., a slower decrease of ∣m∣ with increasing temperature.

Figure 5.

(a) Temperature variation of the DC critical current density J_c(T) determined with the Bean model using the magnetic moment m(T) of P-Ba122od in H = 25 kOe, with m taken from the isothermal magnetic hysteresis curves m(H) registered at different T values (Fig. 3). The DC onset temperature T_on (around 16 K) and the DC peak temperature T_p = 23 K represent, in agreement with the m(H) curves from Fig. 3, the T values where the applied field H = 25 kOe equals H_on(T) and H_p(T), respectively. The J_c(T) maximum at T_M = 20 K (between T_on and T_p) is directly related to the ∣m(T)∣ values where the m(H) shoulder is completed, and, due to the large transition width, T_M is significantly higher that the structural transition temperature T_RST(H = 25 kOe) ~ 18 K in Fig. 4. (b) Temperature dependence of the in-phase component m′ of the AC magnetic moment (directly related to the density of the macroscopic screening currents) for P-Ba122od in H = 25 kOe (ZFC, h_AC = 10 Oe, f = 447 Hz). The onset temperature T_on and the peak temperature T_p (indicated by arrows) correspond to the SMP generated in the sample region penetrated by the AC critical state (see text). Note that in b there is no feature to correspond to the J_c(T) maximum at T_M in a.

On the J_c(T) variation from Fig. 5a one can distinguish the DC SMP onset temperature T_on around 16 K, and the DC peak temperature T_p = 23 K, representing, in agreement with the m(H) curves from Fig. 3, the T values where the applied field H = 25 kOe equals H_on(T) and H_p(T), respectively. The J_c(T) maximum at T_M = 20 K (located between T_on and T_p) is directly related to the ∣m(T)∣ values where the m(H) shoulder is completed, and, due to the large transition width, T_M is significantly higher that T_RST(H = 25 kOe) ~ 18 K in Fig. 4.

The main issue is to find out if the m(H) shoulder [leading to the DC J_c(T) maximum at T_M in Fig. 5a] corresponds, through (1), to the RST in the elastic pinning regime²⁹. Alternatively, in the SMP model based on the pinning-induced BVG disordering^14,15,17,18, this can be the result of a precipitous proliferation of dislocations at the RST, where the BVG elastic squash modulus softens²⁸. At this point, the use of AC magnetic measurements becomes helpful, offering the possibility to have an unambiguously ordered (dislocation free) vortex system across the RST domain. The dynamic ordering of the vortex system (i.e., healing of dislocations) at high drives^37,38 and “shaking” the vortices³⁹ has been proven. For this purpose, the presence of the nonlinear AC magnetic response with a large AC critical-state penetration is essential. It has been recently shown⁴⁰ that when pinning is strong and the demagnetization effects are negligible the AC magnetic signal at usual frequencies and amplitudes remains in the linear (Campbell) regime⁴¹ up to close to the irreversibility line, and the SMP (a bulk phenomenon) does not develop, regardless of the H and T setting protocol. The situation changes drastically for P-Ba122od, due to the relatively weak pinning and pronounced demagnetization effects in perpendicular magnetic fields, where the AC field amplitude at the sample edge is strongly enhanced. In these conditions, the nonlinear regime with a large AC critical-state penetration is reached far below the irreversibility line. For AC magnetic measurements where H is constant, the effective inductive processes during the AC cycles (enhanced by demagnetization effects) keep the screening current density close to the critical value. The SMP is generated in the sample region penetrated by the AC critical state, and the temperature variation of the induced current density is modulated accordingly, as presented below.

Figure 5b illustrates the temperature dependence of the in-phase component m′ of the AC magnetic moment (directly related to the density J of the macroscopic screening currents⁴²) for P-Ba122od in H = 25 kOe, obtained with the nominal AC field amplitude h_AC = 10 Oe and the frequency f = 447 Hz. The represented m′(T) has been registered in the ZFC protocol. Actually, the FCC m′(T) (not shown) and the ZFC m′(T) almost overlap, indicating an extended AC critical-state penetration. The onset temperature T_on ~ 20 K (where the induced J and |m′| are minimum), and the peak temperature T_p ~ 23.5 K (where J and |m′| are maximum) in the used AC conditions correspond to the SMP generated in the sample region penetrated by the AC critical state. By difference with the DC SMP (Fig. 3), the characteristic fields for the AC SMP are shifted to higher values. In the SMP model based on the pinning-induced proliferation of dislocations, this is the manifestation of the dynamic ordering of the vortex system. The ordering effect is large at the onset of the SMP, where the dislocation density is reduced. At H = 25 kOe, one has the AC T_on = 20 K (Fig. 5b), which means that the AC H_on(T = 20 K) = 25 kOe. This is considerably higher than the DC H_on ~ 12.5 kOe located on the magnetic hysteresis curve at T = 20 K, overcoming the upper edge of the RST (see Fig. 2). Thus, in the used AC conditions, the vortex system is ordered in the RST domain. The striking result is the absence of any significant feature on the m′(T) variation which could be related to the DC J_c(T) peak temperature T_M ~ 20 K from Fig. 5a, or, through (1), to the structural transition temperature T_RST(H = 25 kOe) ~ 18 K (see Fig. 4). This means that the DC J_c(T) peak at T_M ~ 20 K from Fig. 5a does not correspond to the RST in the elastic pinning regime. The effect of the elastic compliance of the BVG to the pinning landscape at the RST appears to be too small to generate the SMP. For random pinning, an efficient accommodation of vortices to the pinning centres necessitates the presence of dislocations in the vortex system. The m(H) shoulder can easily be generated by a precipitous, pinning-induced vortex-system disordering triggered by the C_sq softening at H_RST, where one has a transition between the rhombic BVG and a partially dislocated (disordered) square BVG. The proliferation of dislocations at H_RST is favoured, since H_RST is close to H_on, where the energy balance relation should be fulfilled.

The pinning-induced vortex system disordering continues above the RST range, as indicated by the analysis of DC magnetization relaxation. The inset of Fig. 6 illustrates the relaxation time t dependence of the absolute value of the DC irreversible magnetic moment ∣m_irr∣ in log–log scales for P-Ba122od at several temperatures in H = 30 kOe (applied in ZFC conditions). The considered temperature interval is above the RST domain, where the history effects are negligible. As known, when the relaxation time window t_w is moderate, in the representation from the inset of Fig. 6 the relaxation m_irr(t) curves are linear, with the slope of the linear fit supplying the normalized magnetization relaxation rate S =  − dln(∣m_irr∣)/dln(t) and the corresponding normalized vortex-creep activation energy U* = T/S^43,44. For a given H well below the irreversibility line (where the pinning potential is not reduced significantly by thermal vortex fluctuations) and a fixed t_w, the U*(T) variation obtained in the framework of the general vortex creep equation is approximated by

$$U\ast \left(T\right)\sim U_{\text{c}}+pTln\left(t_{\text{w}}/t_0\right),$$ 3

where U_c represents the characteristic pinning energy, p is the vortex creep exponent (positive in the case of an elastic vortex creep process⁴⁵ and negative (around − 1/2⁹) for plastic creep, whereas t₀ is the macroscopic time scale for creep²³. The resulting U*(T) variation, plotted in the main panel of Fig. 6, exhibits a maximum at the creep-crossover temperature T_cr, where, according to (3), the creep exponent changes sign, signalling the vortex system disordering across the SMP. This sign changing is possible through an increase of the characteristic pinning energy U_c, owing to a better accommodation of vortices to the pinning centres in a disordered vortex phase. The applied field H = 30 kOe is close to the midpoint between H_on and H_p at T = T_cr (see Fig. 3), which is expected using global magnetic measurements⁴⁶.

Figure 6.

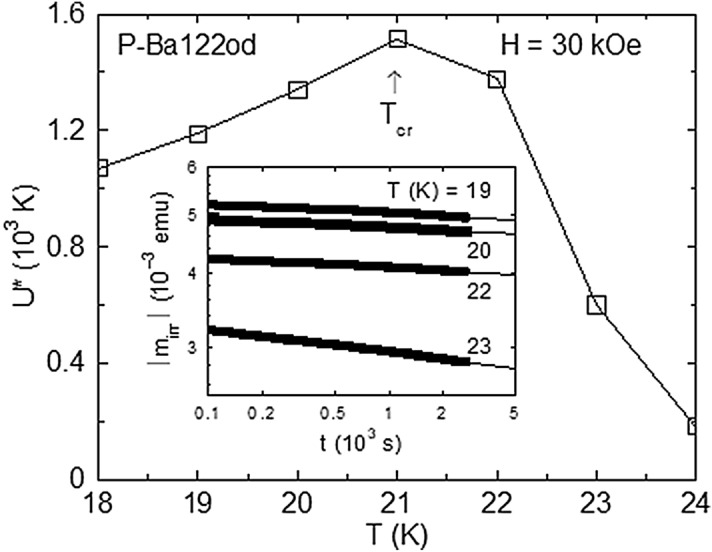
Inset: Time t dependence of the absolute value of the irreversible DC magnetic moment ∣m_irr∣ in log–log scales for P-Ba122od in H = 30 kOe (applied in ZFC conditions) at several temperatures T ≥ 18 K. In this representation, the relaxation curves are linear, with the slope of the linear fit (the continuous line) supplying the normalized magnetization relaxation rate S =  − dln(∣m_irr∣)/dln(t) and the corresponding normalized vortex-creep activation energy U* = T/S. Main panel: The resulting U*(T) variation exhibits a maximum at the creep-crossover temperature T_cr, signalling the vortex system disordering across the second magnetization peak.

The existence of a maximum in U* (Fig. 6, main panel) means a minimum of the normalized magnetization relaxation S = T/U*, and it is tempting to locate the RST at this S minimum³². However, as it can be seen in Fig. 3, there is no maximum in ∣m∣ at H = 30 kOe on the magnetic hysteresis curve registered at T = T_cr = 21 K. Similarly, since the long-time relaxation measurements²⁵ and structural investigations using muon-spin rotation and small-angle neutron scattering experiments^47,48 showed that at the peak field H_p the vortex system is completely disordered, the identification of the RST line with H_p(T) is ruled out.

Finally, the absence of the m(H) shoulder in the case of optimally doped and underdoped single crystals (the inset of Fig. 1 and³¹) can easily be explained in terms of the pinning-induced disordering of the vortex system across the SMP. A stronger pinning will shift H_on well below the intrinsic H_RST(T) line, and the RST cannot manifest in a significantly disordered vortex system.

Conclusions

In summary, we investigated the magnetic response of overdoped BaFe₂(As_1−xP_x)₂ single crystals, to clarify the relationship between the second magnetization peak and the characteristic structural rhomb-to-square transition of the Bragg vortex glass in the fourfold symmetric superconductors. It was found that the (elastic) RST does not generate the SMP, but the RST can influence the pinning-dependent SMP onset field when this is close to the intrinsic RST line, through the appearance of a shoulder on the magnetic hysteresis m(H) curves. The temperature evolution of the m(H) shoulder leads to the intersection of isothermal m(H) curves (a rare phenomenon), and, consequently, to a peak in the temperature variation of the DC critical current density J_c(T). However, this particular peak does not appear in the temperature variation of the screening current in AC magnetic measurements where the vortex system is dynamically ordered in the RST domain. This emphasizes the essential role of vortex dislocations for an effective accommodation of the vortex system to the pinning landscape and the occurrence of the SMP.

We conclude that the observed DC m(H) shoulder is the effect of a precipitous pinning-induced proliferation of dislocations when the BVG elastic squash modulus softens at the structural transition between a rhombic and a partially disordered square BVG. The pinning-induced vortex-system disordering continues above the RST domain (as indicated by the magnetization relaxation results), and represents the basic SMP mechanism for the fourfold symmetric superconductors, as well. The absence of a notable effect of the RST on the SMP in the case of optimally doped and underdoped P-Ba122 single crystals can easily be explained in terms of the pinning-induced disordering of the vortex system across the SMP. The stronger pinning exhibited by optimally doped and underdoped P-Ba122 single crystals shifts the onset field well below the structural transition field, and the RST cannot manifest in a significantly disordered vortex system.

Methods

The improved quality of iron-based superconducting single crystals^49,50 made possible the observation of ordered vortex phases^34,50,51. It is now established that the overdoped 122-type specimens exhibit a relatively weak, point-like δT_c pinning⁵² and a pronounced SMP develops³¹. The P-Ba122 single crystals analysed in this work have been grown by the Ba₂As₃/Ba₂P₃-flux method⁵³ at the Institute of Physics, Chinese Academy of Sciences. They have been selected by the width ΔT of the diamagnetic transition in the m′(T) variation registered with H = 0, f = 447 Hz, and h_AC = 1 Oe, as illustrated in Fig. 7 for P-Ba122od, where ΔT ~ 1 K. The measured samples are square-shaped (with the side l ~ 1.7 mm), with the thickness t (in the direction of the crystallographic c axis) of ~ 50 μm.

Figure 7.

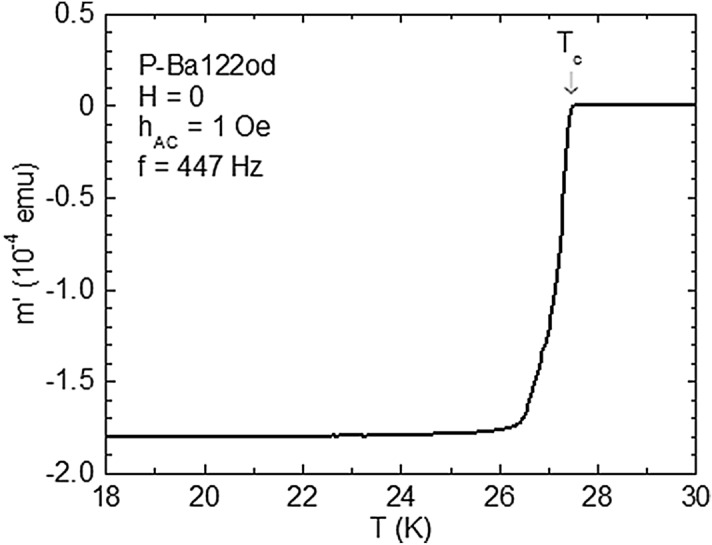
Temperature variation of the in-phase (screening) component m′ of the AC magnetic moment for P-Ba122od in H = 0 registered in increasing temperature with h_AC = 1 Oe and f = 447 Hz. The critical temperature T_c has be taken at the onset of the diamagnetic signal, and the width of the diamagnetic transition is around 1 K, reflecting the good quality of the thoroughly investigated single crystal.

The DC and AC magnetic fields have been oriented along the c axis, when the demagnetization factor⁵⁴ D ~ 0.9. Thus, the AC field amplitude h_AC at the sample edge is enhanced by a factor 1/(1 − D) ~ 10. The DC critical current density J_c (in A/cm²) has been determined as 60 |m_irr|/l³t³⁶, with l and t in cm, and the irreversible magnetic moment m_irr = (m₊ − m₋)/2, with m₊ (m₋) representing the magnetic moment (in emu) measured in increasing (decreasing) H. When the reversible magnetic moment is negligible, |m_irr| can be approximated by m₋.

The DC m(H) curves were usually obtained with a commercial Quantum Design Magnetic Property Measurement System (MPMS), whereas the AC magnetic moment was registered with a Physical Property Measurement System (PPMS). The presented AC results for finite H correspond to h_AC = 10 Oe, and the frequency f = 447 Hz. The relatively high h_AC and the strong demagnetization effects allow attaining the nonlinear AC regime with a large AC critical state penetration far below the DC irreversibility line of overdoped P-Ba122 single crystals.

The temperature and DC magnetic field setting followed the zero-field cooling protocol (ZFC), obtained by fast cooling the sample (~ 10 K/min) in H = 0 from above T_c down to T < T_c, then applying H, and measuring m(H) or the AC magnetic signal in increasing temperature at a slow rate (~ 0.05 K/min). For comparison, the field cooling on cooling procedure (FCC) has also been used, with H applied above T_c, and then measuring the AC magnetic moment in decreasing T at the slow rate. Well below the irreversibility line, the contribution of the reversible magnetic moment to the DC m(H) curves is negligible. However, in the case of magnetization relaxation data registered over a large temperature interval, the irreversible magnetic moment m_irr has been taken into account.

Author contributions

A.M.I., D.M., M.B., D.B., and P.B. performed the DC magnetic measurements and carried out the analysis of magnetization relaxation. A.C. measured the AC magnetic response, and L.M. wrote the paper with contributions of all authors.

Data availability

The data sets that support the findings in this study are available from the corresponding author upon reasonable request.

Competing interests

The authors declare no competing interests.