NIST’s Digital Library of Mathematical Functions

The Information Technology Revolution is creeping into all aspects of our lives. Today, more and more of us rely on digital information for both personal and professional purposes than ever before. It is so much easier to go to the Web to locate information or to purchase whatever widget you are looking for than to go out to a retail store. Similarly, for most scientific needs, journal articles and books are far easier to access on-line than in the older more conventional methods. While there are many examples of online scientific material that go beyond their print equivalents, the real power of the Web to transcend the printed page is still in its infancy.

One place the IT revolution has radically impacted a classic reference is the Handbook of Mathematical Functions, edited by Milton Abramowitz and Irene A. Stegun(A&S)[1] (see first sidebar). In this article, we discuss how A&S was transformed into an on-line 21^st century resource, known as the Digital Library of Mathematical Functions (DLMF) and importantly how this new and modern resource enables far more information to be available to the user and available in ways that are quite different from the past (see second sidebar). The DLMF contains far more material than A&S and where appropriate, older material has been updated or expanded. The current article is focused on providing readers of Physics Today with an overview of the DLMF and how it can be extremely useful tool for both research and educational purposes.

To set the stage for what follows, consider the following somewhat hypothetical situation. A researcher, who we will call Bill, found the much more extensive and up-to-date treatment of orthogonal polynomials in the DLMF extremely useful. Many years ago Bill was working on the problem of finding solutions to the radial Schrödinger equation for the attractive and repulsive Coulomb potential in terms of a set of square-integrable orthogonal functions. He had previously shown that it was indeed possible to expand the solutions to that problem in some complete, discrete set of functions and to relate the expansion coefficients to some set of orthogonal polynomials. For the Coulomb potential, the expansion coefficients satisfy a three term recursion relationship which is found to be that of the Pollaczek polynomials. When A&S was written, there was very little known about these polynomials and Bill and his colleagues had to work out many of their properties on their own. Bill has recently returned to the problem in order to generalize the older results to physical parameters not treated in the original work. But, much to his surprise and delight, the DLMF has a much more extensive treatment of many special functions, the orthogonal polynomials included, and does treat the case of the Pollaczek polynomials in some detail. Had that information been easily available at the time Bill and his students were originally working on the project, it would have made their life significantly easier. In addition, Bill found many useful references and notes in the metadata given in the “information boxes” (see below). Bill is now actively extending the earlier research to these physically important ranges of the nuclear charge and energies for the attractive Coulomb potential and producing some interesting and very useful new results.

Not your thesis advisor’s Handbook

Once you broaden your perspective first from a traditional printed handbook to a ‘book on the web’, and then on to a full-fledged electronic resource on the internet, the power of hypertext and the vast resources of the web itself open up a rich tableau of possibilities to enhance the information, its utility, and ease of use. For the developer, this abundance can be frustrating as there are so many choices and possibilities to be explored; moreover the evolution of the web takes place in fits and starts, with promising technologies sometimes stalling, other times becoming suddenly mandatory.

And yet, the traditional handbook has evolved virtues worth preserving such as conciseness, stability and permanence. By adopting an enriched authoring markup for the source documents and leveraging hyper-text we are able to ‘layer’ the information. On the one hand, we keep the concise surface ‘telegraphic style’ focused on the essential selected properties of the functions. Most users will find the information they need by simply using the time-honored method of scanning the relevant sections.

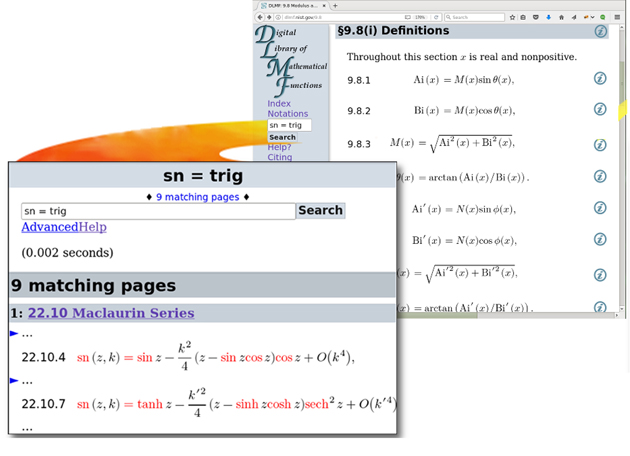
When that is not sufficient, we provide a search engine; once our friend Bill realized that Pollaczek polynomials were relevant to his problem, he might search for pollaczek recurrence to locate the relation he needed. That’s fine as far as it goes, but in a context so full of mathematical formula but bereft of text, the usual text search is insufficient; it cries out for a math-aware search engine. Our search tool[8] is aware not only of the mathematical notations, but the semantics of the symbols as well. Thus proper and common names of functions or their classification can be used as search terms (see Figure 1).

Figure 1. Math-aware search.

We incorporate in the DLMF a math-aware search engine. Beyond the usual searching for textual terms, queries that appear to be ‘mathematical’, namely using math operators or conventional LATEX commands are recognized. These latter are then matched against the mathematical expressions within the DLMF.

Moreover, the meaning of the symbols is also recognized, so that for example either J or Bessel would match the Bessel function J_ν. Above, we show the result of searching for the Jacobian elliptic function sn in terms of trigonometric functions. While the sn obviously matches the appropriate elliptic function, the term trig (or trigonometric) matches any trigonometric function, such as sine, cosine and even the hyperbolic tangent.

A benefit of technologies such as MathML is that we’re able to highlight the portions of the formula that match the query terms. providing a reassuring bit of feedback to the user.

For the interested researcher wishing to dig a bit deeper, an additional layer of information reveals the symbols used, sources of information, cross-references and so on (see Figure 2). The mathematical symbols themselves are linked to their definitions to reduce ambiguities of notation. The selective nature of a handbook virtually guarantees that not every useful relation will be presented. But by indicating the specific source of each equation or methods by which it can be derived, along with other expository annotations, our researcher will be able to find alternative sources of information, or guidance on how to derive what she needs for her application.

Figure 2. Layered Information in DLMF.

There’s more than immediately meets the eye! Hovering or clicking the ‘info’ icon () reveals a variety of metadata — data about the data — relating to the formula. In this case including listings of the symbols defined or used; links to original sources; cross-references; alternative formats (TEX code, MathML, images). The permalink gives the permanent URL for this formula, indicating that the number 9.8.3 will always refer to this formula independent of errata, updates or future editions of DLMF. Other metadata include any relevant keywords; links to A&S; notes on the formula’s derivation; as well as other annotations, classifications and errata for the object.

In addition to the list of symbols used, the individual mathematical symbols in the formula itself hyper-link to their definition within the DLMF (another benefit of MathML), in order to clarify and disambiguate similar appearing notations – there are, after all, several distinct functions denoted by P and Q!

But just what kind of ‘enriched’ markup can enable these features? Most mathematicians prefer to write using LATEX, a powerful, expressive markup system providing for high-quality typesetting. That it is extensible makes it notoriously difficult to convert to HTML for the web, and yet, that is exactly it’s strength for our application. A system of ‘semantic’ macros for many mathematical functions and concepts assures that we retain the underlying meaning. Converting this enriched LATEX markup into an intermediate XML representation allows for the layering of information to capture both the surface presentation and a database of information which we can mine for connections and information about the functions. It is exactly that extra information — metadata — which we use to link symbols to their definitions, to populate indices, notation lists and the ‘info boxes’ and enriches the search indices. The tools for this not being available off-the-shelf, we’ve created such a system, LATEXML[7], which converts the author’s LATEX into XML and thence to HTML and MathML. The benefits of this approach are illustrated in Figures 1 and 2.

The stability of traditional handbooks is maintained by committing to securing, across updates and even new editions of DLMF, the connection between equations, their reference numbers (such as Eq. 9.8.3), and permanent URL’s (so-called permalinks, such as http://dlmf.nist.gov/9.8.E3), so that the DLMF can be used as a resource for the long haul. These permalinks, moreover, provide for convenient means for corresponding researchers to exchange information contained within the DLMF.

Graphics

The graphs and visualizations in the DLMF are ‘hidden gems’ overlooked by many users as they peruse the website. There are many steps a researcher can take to gain a deeper understanding of a function that models interesting mathematical or physical phenomena, including studying its differential equation or other defining information, computing or approximating its zeros using Newton-type methods or asymptotic expansions, and using other numerical and analytical techniques to examine the function; however, an accurate graphical representation can provide that ‘Aha, just what I thought’ moment or quickly send a researcher back for more analysis and computations when the plot differs from what is expected. Our plots of the complex zeros of Bessel functions of positive integer order alerted us to inaccuracies in diagrams published in Olver’s 1954 asymptotic expansion paper [9], inaccuracies that were repeated in figures placed in A&S. The new plots showed that the infinite arrangement of nonreal zeros needed to be moved to the opposite side of the asymptote lines. (See http://dlmf.nist.gov/10.21.ix).

Our development of graphics for the DLMF evolved with the advancement of technology for viewing graphics on the web, making it possible to replace the few static graphs in the original handbook with close to 600 2D and 3D figures, including 200 rendered as 3D visualizations where users can interactively explore function surfaces. The clarity and responsiveness of the visualizations are a product of X3DOM/WebGL technology for rendering 3D graphics [3] and our careful attention to both plot and data accuracy. The WebGL application programming interface (API) provides portability, allowing users to view our visualizations in major web browsers without downloading a 3D graphics plugin. WebGL was developed by the Khronos WebGL Working Group (http://www.khronos.org/webgl/), a consortium focused on royalty-free standards for cross-platform 3D graphics APIs.

We achieved plot accuracy, that is, graphically representing function features accurately, by designing computational grids, or meshes, that effectively capture key function attributes such as zeros, poles and branch cuts[11]. To tackle the issue of data accuracy, we computed function values using at least two different methods, with codes from reliable repositories, standard computer algebra packages, or even personal codes from DLMF chapter authors; and we resolved discrepancies through discussions with the chapter author along with a close examination of function definitions and properties.

Although illustrative diagrams and graphs are located throughout the DLMF, most figures representing function curves or surfaces can be found in the Graphics sections of each Chapter. Clicking on a static 3D image opens a page with an array of interactive options, allowing users to rotate, scale, zoom or otherwise probe function graphs. Users will note that visualizations of each function have the same look and feel to facilitate familiarity with the controls. Figures 3, 4, and 5 highlight some of the interesting capabilities available.

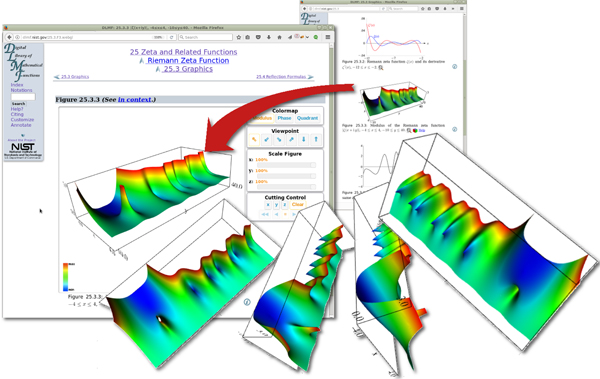
Figure 3. Interactive visualizations in the DLMF.

Images of the modulus of the Riemann zeta function |ζ(x + iy)|, an important function in number theory, quantum field theory and other areas of mathematics and physics, illustrate the difficulty in displaying key features of a function surface with a single static image. In the DLMF, we offer interactive 3D visualizations where users can rotate a function surface in any direction or use specially designed tools to explore the surface further. Clicking on the static image of the Riemann zeta function in the DLMF web page (top right) opens a new page (top left) containing an embedded visualization with control panels offering a variety of options. The original static image shows the simple pole at x = 1, but obscures the non-trivial zeros on the critical line (x = 0.5) where the Riemann Hypothesis asserts they will lie. Rotating the surface allows the user to see the function’s features more clearly. We used X3DOM/WebGL technology to design visualizations that users can view inside a web page on multiple platforms without downloading a special graphics plugin. (For more information on X3DOM and WebGL see [3] and http://www.khronos.org/webgl/.)

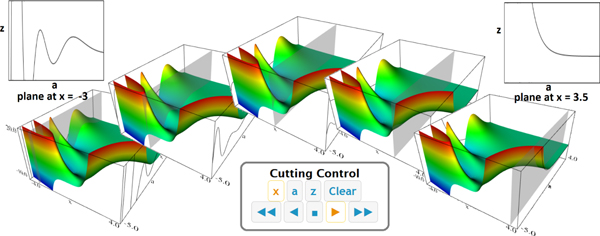
Figure 4. Cutting through a surface.

One of the options offered in the DLMF visualizations is cutting plane control. Observing the intersection of a plane with a function surface can provide the viewer with a unique perspective. The images above show a cutting plane moving in the x direction through a surface representing the incomplete gamma function γ*(a, x). As the plane cuts through the surface, intersection curves are projected onto opposite ends of the bounding box and also displayed in a pop-up window. In any coordinate direction, users can manipulate standard media controls to create an animation, or manually move the plane by using a slider bar. Of course, in the Riemann zeta function surface (Figure 3) yet another view of the non-trivial zeros is revealed by stopping a plane moving in the x direction at x = 0.5. (See DLMF chapters on Incomplete Gamma and Related Functions or Zeta and Related Functions for more information on these functions.)

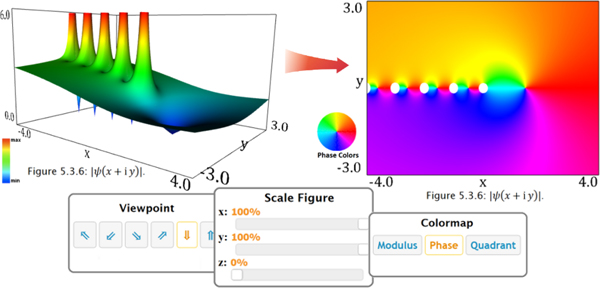
Figure 5. Density plots.

Options may be combined to produce graphical displays that illuminate significant function features more clearly. The graph on the left represents the modulus of the complex digamma, or psi function, defined by ψ(x + iy) = Γ′(x + iy)/Γ(x + iy). A user can construct a density plot by viewing the surface from the top and rescaling the vertical axis to zero. Selecting the phase color map then yields a density plot based on the phase, or arg, values as seen in the image on the right. Like the gamma function, the psi function has simple poles at the negative integers. When one moves counter-clockwise around a pole, that is, in our image, around the holes shown along the negative real axis, one travels clockwise one full rotation around the color wheel, indicating a phase change of 2π. However, unlike the gamma function, the psi function has zeros between the poles. Around the zeros, the direction of the colors is reversed, indicating that the phase sign is opposite to that around the poles. DLMF Physical Sciences Editor Charles Clark observed that the pattern is analogous to what one would see in fluid flow generated by a semi-infinite line of vortices with alternating lines of circulation, producing a near cancellation of flow far from the real axis. One can see the contrast with the gamma function, where there are poles but no zeros in-between, by creating a phase density plot using the gamma function visualization in the DLMF Gamma Function chapter.

DLMF Future

Firstly, NIST has a commitment to the long-term maintenance and further development of the DLMF, both in the evolution of the mathematical content and in its manifestation on the web. We will continue issuing quarterly updates including errata, corrections and clarifications that have been reported or discovered. As we track the evolving technologies of the web (e.g. HTML5, MathML, WebGL), and different usage patterns, we add new features and capabilities. Over time, we will make improvements to accessibility and add support for mobile devices.

Occasionally, additions of new material that is becoming more relevant to applications are included. Currently, a revision of the Orthogonal Polynomials and Painléve Transcendents chapters and a brand new chapter on Orthogonal Polynomials of Several Variables are in progress, and we expect more to come.

The metadata behind the scenes continues to be improved, refining the sources of information and semantic connections between formulas. At present, this metadata is given in human-readable form, but we are exploring ontologies to recast this data in machine-readable forms (such as RDFa) which can enable more powerful search and discovery capabilities by global search engines. Our first focus in representing the mathematical formulas was to generate Presentation MathML for display in browsers, but our longer term goal is to to develop Content MathML representations which could be exported to applications for direct use in computations and would further improve accessibility.

Beyond that, several spin-off projects have been started. The motivation for one, the DLMF Standard Reference Tables on Demand Project (DLMF Tables), is succinctly described by a user’s post to DLMF Feedback:

It is no longer useful to include large tables of function values for the purpose of interpolation. But a set of test values for each function with various decimal precisions would be useful for developers as they try to test implementations of special functions. This could be the beginning of a benchmark for numeric software. [12]

Our goal is an online testing service where users can generate high precision tables of special function values with an error certification for comparison to their own uploaded function data. A collaborative effort between the NIST Applied and Computational Mathematics Division and the University of Antwerp Computational Mathematics Research Group (CMA) has already produced a fully operational beta version, publicly available at http://dlmftables.uantwerpen.be/. The site’s computational engine is based on MpIeee, an IEEE 754/854 compliant C++ library for mixed precision floating point arithmetic developed by CMA[2].

Another project is the Digital Repository of Mathematical Formulae (DRMF), the development of a wiki-based compendium of formulas for orthogonal polynomials and special functions (OPSF) to promote interaction within the OPSF community. The DRMF will be expandable, but moderated, allowing the input of new formulas from the literature after review. To create a solid foundation, the wiki is being seeded with formula data from the DLMF and other sources, requiring the extension and development of a variety of format conversion processors[5].

Concluding Remarks

With the Digital Library of Mathematical Functions, NIST has attempted to create a worthy and modern successor to Abramowitz and Stegun’s handbook. Its best characteristics have been preserved while exploiting the capabilities of the web and modern technologies. It is a vibrant and evolving product that is drawing on new knowledge of special functions discovered since 1964, as well as correcting and expanding older material as demanded by its users. A group of Associate Editors, experts in various special functions, serve to provide continuing advice on individual chapters, while a group of Senior Associate Editors provide overall advice to the project.

Our main message is to invite the reader to explore the DLMF; hover the mouse over potentially interesting objects, symbols and graphics to see what is behind the scenes; open the ‘info boxes’ to see what additional, possibly useful, data is available. We believe that it will prove to be as useful to scientists and engineers today and in the future as A&S has been since 1964. We welcome comments (or corrections) from readers about how we can further improve the DLMF: dlmf-feedback@nist.gov.

Abramowitz & Stegun.

In 1964, the National Bureau of Standards (NBS) published the Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, as Applied Mathematics Series 55, edited by Milton Abramowitz and Irene A. Stegun[1]. Originally intended as a compendium of numerical tables for evaluating the special functions, it was augmented with selected properties and identities to ease the use of the tables. Ironically, it was that additional material that was responsible for its long-term popularity! Fondly referred to as ‘Abramowitz and Stegun’, or even ‘A&S’, it became the most widely distributed and cited NBS publication in the first 100 years of the institution’s existence. Its success derived from concisely providing critically useful mathematical data. Moreover, A&S served to standardize definitions and notations for special functions; providing standard reference data of this type being a core function of NBS.

The DLMF Project.

By the late 90’s, A&S was showing its age and due for more than a simple update with errata. Inportant advances in the special functions had taken place: more properties of many functions had been discovered and advances in mathematics had considerably enlarged the field to include many new and useful functions. Significantly, the advent of the World Wide Web had also opened up unique opportunities for publishing.

In 1998, a project was initiated at NBS, now transformed into the National Institute of Standards and Technology (NIST), to assemble the available information on the current state of special functions into a freely accessible on-line resource taking advantage of the (then) relatively new potential of the Web.

Over the ensuing decade, with the generous sponsorship of the National Science Foundation’s Knowledge and Distributed Intelligence program, and continuing internal support from NIST, 29 experts in the various special functions were contracted to write material for the new handbook. All chapters were validated by other experts. While roughly half of A&S consisted of numerical tables, the DLMF would have none. Instead, the amount of mathematical content was doubled. New chapters on Lamé, Heun and Painlevé functions, as well as integrals with coalescing saddles were included, resulting in 36 chapters and an extensive bibliography. Being a handbook, mathematical proofs were not included, but great care was taken to provide all relevant constraints on the validity of all formulas, as well as to track their original sources. Significantly more graphs and visualizations were also included. In 2010, after 11 years of dedicated effort, the enhanced online resource[6] was released as the ‘Digital Library of Mathematical Functions,’ while the printed handbook[10] was published as the ‘NIST Handbook of Mathematical Functions’. See also [4].