A Novel Attribute-based Symmetric Multiple Instance Learning for Histopathological Image Analysis

Abstract

Histopathological image analysis is a challenging task due to a diverse histology feature set as well as due to the presence of large non-informative regions in whole slide images. In this paper, we propose a multiple-instance learning (MIL) method for image-level classification as well as for annotating relevant regions in the image. In MIL, a common assumption is that negative bags contain only negative instances while positive bags contain one or more positive instances. This asymmetric assumption may be inappropriate for some application scenarios where negative bags also contain representative negative instances. We introduce a novel symmetric MIL framework associating each instance in a bag with an attribute which can be either negative, positive, or irrelevant. We extend the notion of relevance by introducing control over the number of relevant instances. We develop a probabilistic graphical model that incorporates the aforementioned paradigm and a corresponding computationally efficient inference for learning the model parameters and obtaining an instance level attribute-learning classifier. The effectiveness of the proposed method is evaluated on available histopathology datasets with promising results.

I. Introduction

Histopathological image analysis is a critical task in cancer diagnosis. Generally, this process is performed by pathologists who are capable of identifying problem-specific cues in a digital image, or a whole slide image (WSI), in order to classify it into one of the disease categories. In recent years, there have been an increasing interest in the application of automatic histopathological image analysis using machine learning algorithms [1], [2]. The advantages of this approach include (i) reducing variability in human interpretations and hence improving classification accuracy, (ii) eliminating a significant amount of trivial cases to ease the burden on pathologists, and (iii) providing quantitative image analysis in the context of one specific disease.

Most conventional approaches to automatic histopathological image analysis fall into the category of fully supervised learning, where training labels are available for the WSI and all of its patches (small blocks extracted from the image). These methods often rely on feature extraction techniques that are customized for a variety of problems, namely texture features [3], [4], spatial features [5], [6], graph-based features [7], [8], and morphological features [9], [10]. Those features can then be used by various classification algorithms such as random forest, support vector machines (SVM), and convolutional neural networks (CNN). Recently, automatic feature discovery framework has also been proposed by Vu et al. [11]. Their discriminative feature-oriented dictionary learning (DFDL) method was shown to outperform many competing methods, particularly in low training scenarios. Nevertheless, one major disadvantage of the fully-supervised approach is the labeling cost. Since each WSI typically comprises hundreds of patches, it requires a large amount of labor to create even a small number of training data. Moreover, labeling a histopathology image at the region-level could be a challenging task with inherent uncertainty, even for experts in the field. To address these issues, many researchers have been studying weakly-supervised learning that focuses on coarse-grain annotations, i.e., only WSI labels are given.

Multiple Instance Learning (MIL) is a framework for weakly supervised learning (limited supervision) that relies on a training set of bags of instances labeled at the bag level only. In our scenario, each WSI (bag) contains a collection of tissue segments (instances), but the annotation of cancer-type is only available at the image/bag level. The goal is to develop a classifier to predict both bag level and instance level labels. Various MIL-based approaches have been applied successfully in biochemistry [12], [13], image classification and segmentation [14]-[16], text categorization [17], [18], object recognition, tracking and localization [19]-[21], behavior coding [22], anomaly detection [23], and co-saliency detection [24]. In histopathological image classification, only a limited number of MIL approaches have been studied in literature. In [25], Dundar et al. introduced a multiple instance learning approach (MILSVM) based on the implementation of the large margin principle with different loss functions defined for positive and negative samples. Later on, Xu et al. [26] adopted the clustering concept into MIL to propose an integrated framework of segmentation, clustering, and classification named multiple clustered instance learning (MCIL). The authors also extended their work by taking into consideration the contextual prior in the MIL training stage to reduce the intrinsic ambiguity. Most recently, a comparison of general MIL-based methods on histopathological image classification, namely, mi-SVM and MI-SVM [27], miGraph and MIGraph [28] has also been reported in [29]. All of the aforementioned methods, nonetheless, deal with predicting the presence or absence of cancer, and are based on an asymmetric assumption that all instances in a negative bag are negative while each positive bag contains at least one positive instance. This commonly-used MIL assumption may be not suitable for other MIL setting such as predicting the cancer type based on histopathology images. In this case, only a fraction of the tissue segments can be useful towards recognizing the cancer type of each WSI, and such MIL setting is symmetric in that both positive and negative bags contain stereotypical instances featured for each cancer type along with irrelevant ones.

In this paper, we consider the binary classification problem of cancer types based on histopathology images. Our contribution in this paper is as follows. First, we introduce a novel symmetric MIL where both negative and positive bags contain relevant and irrelevant instances. Second, we propose a probabilistic graphical model, named Attribute-based Symmetric Multiple Instance Learning (AbSMIL), that incorporates cardinality constraints on the relevant instances in each bag to leverage possible prior knowledge and develop a forward-backward dynamic programming algorithm for learning model parameters. To facilitate efficient inference, the online learning version of our algorithm is also presented. Finally, the advantages of the proposed framework are demonstrated by experiments on instance annotation and bag level label prediction using classical multi-instance image recognition datasets as well as histopathology datasets.

II. Related work

In MIL setting, it is important to make assumptions regarding the relationship between the instances within a bag and the class label of the bag. Most of the MIL algorithms follow the standard assumption that each positive bag contains at least one positive instance and negative bags contain only negative instances. In one of the early works, Maron and Lozano-Pérez [30] introduced the concept point that is close to one instance in each positive bag and far from all instances in negative bags. The diverse density (DD) framework [31], [32] is then developed based on the idea of finding the best candidate concept. Later on, Andrew et al. [27] extended SVM approach to mi-SVM and MI-SVM by finding a separating hyperplane such that at least one instance in every positive bag is located on one side and all instances in negative bags are located on the other side of the hyperplane. In a different approach, Zhou et al. [28] proposed MIGraph and miGraph methods that map every bag to a graph and explicitly model the relationships among the instances within a bag. A number of single-instance algorithms have also been adapted to a multiple-instance context such as MIL-Boost [33], KI-SVM [34], Latent SVM [35], MI-CRF [36]. They all maintain the classical asymmetric assumption in their algorithms.

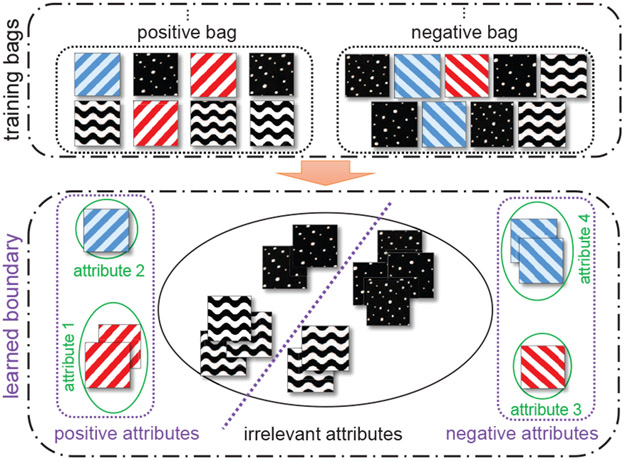
For some MIL applications where the class of a bag is defined by instances belonging to more than one concept, the standard assumption may be viewed as too strict. Therefore, researchers have recently shown a general interest in other more loose assumptions such as the collective assumption [37], [38]. In this paper, we consider the problem of predicting cancer types in histopathology images and propose a symmetric assumption that treats classes equally (see Fig. 1). In a positive bag, there is at least one relevant instance that demonstrates certain attributes associated with the positive class (e.g., stripes going from bottom-left to top-right). Similarly, a negative bag also contains at least one relevant instance that demonstrates certain negative attributes (e.g., stripes going from bottom-right to top-left). Finally, both bags contain some irrelevant instances whose attributes do not contribute to the difference between the two classes (e.g., dotted and wave). The goal is to learn the positive, negative, and irrelevant attributes and use them to address various classification tasks within this framework.

Fig. 1.

The setting of the proposed attribute-based symmetric MIL framework. The goal is to classify positive and negative bags and to figure out distinctly positive and negative relevant attributes (stripes going from bottom-left to top-right or bottom-right to top-left, respectively) and irrelevant attributes (dotted and wave) in each bag category. The proposed model helps control the relevant instance proportions in the bags.

Our assumption is motivated by multi-instance multi-label learning (MIML), a generalization of single-instance binary classifiers to the multiple-instance case. In MIML setting, each instance is associated with a latent instance label and each bag is the union of its instance labels [39]. With the presence of novel class instances [40], the bag label only involves the known instance classes and does not provide information about the presence or absence of the novel class. This consideration is similar to our symmetric MIL setting where only a small portion of the relevant instances are labeled and irrelevant instances are often ignored by pathologists. However, a simple reduction of the model for MIML would fail in the cancer classification problem as the bag labels in MIL are binary but not a subset of the class labels. Recently, You et al. [41] introduced cardinality constraints to the MIML setting and demonstrated that optimizing the control over the maximum number of instances per bag can significantly improve the performance of the model. Motivated by the result, we propose using cardinality constraints to limit the number of relevant attributes in each bag. Given that there are hundreds of instances per bag, cardinality constraints can help control the model complexity. While the probabilistic machinery for implementing cardinality constraints is similar to the approach in You et al. [41], the graphical model and inference methods differ. The modeling difference: instance-level labels include unknown attribute/cluster labels (see Fig. 1), whereas in the MIML setting in [41] instance-level labels are taken directly from bag-level labels (e.g., the bag-level label {2, 5} implies that relevant instances must have labels of either 2 or 5). The inference difference: (i) to promote the cluster diversity, we introduce entropy regularization to the original log-likelihood objective, (ii) to reduce the computational burden of large histopathology images, we apply a stochastic gradient descent approach. Both of which are not included in [41].

III. Problem formulation and proposed model

In this section, we formulate the problem of cancer type classification and describe our proposed AbSMIL approach.

A. Problem Formulation

We consider a collection of B bags and their labels, denoted by $\{{\mathit{X}}_b,Y_b{\}}_{b=1}^B$. The bag level label Y_b ∈ {0, 1} represents each of the two cancer types. The bth bag contains n_b instances ${\mathit{X}}_b=\{x_{bi}{\}}_{i=1}^{n_b}$ where ${\mathit{x}}_{bi}\in {\mathbb{R}}^d$ is a feature vector for the ith instance. Our goal is to predict the bag label based on the set of feature vectors for its instances. Moreover, we would like to learn a robust model that are capable of explaining the labeling decision. To that end, we consider the following attribute-based assumption on the data.

Relevant/irrelevant instances and attributes assumption.

We assume that each instance in a bag can be either relevant or irrelevant. Relevant instances provide useful information towards a specific class. Further, there may be more than one types of relevant instances for the same class, which we capture as instance attributes (clusters). In Fig. 1, for example, the positive (or negative) class always has two relevant attributes: 1 and 2 (or 3 and 4). Formally, we assume the attribute z_bi, corresponding to the ith instance in the bth bag, belongs to the set $\{0,1,\dots ,\mathbb{C}\}$, where 0 is reserved for irrelevant instances and the non-zero integers represent $\mathbb{C}$ attributes for relevant instances. For the bth bag, we denote the set of hidden attributes for all instances by z_b = [z_b1, z_b2, … , z_nb]^T, and the binary vector indicating the presence/absence of relevant attributes by ${\mathit{y}}_b=[y_{b1},y_{b2},\dots ,y_{b\mathbb{C}}{]}^T\in \{0,1{\}}^{\mathbb{C}}$.

No mixed-class attributes assumption.

Let us call attributes that provide sufficient information for predicting the positive bag as positive attributes (PAs) and similarly, for negative bags as negative attributes (NAs). Since the goal is to find distinct attributes that discriminate the two classes, we assume there is no shared relevant attribute between positive bags and negative bags. To be more specific, we consider the first half of the attribute set $C^{+}=\{1,\dots ,\frac{\mathbb{C}}{2}\}$ as PAs and the second half $C^{-}=\{\frac{\mathbb{C}}{2}+1,\dots ,\mathbb{C}\}$ as NAs ($\mathbb{C}$ is even in our assumption). Although we focus on a balanced number of PAs and NAs, the proposed model is not limited to this symmetry when extending to other settings.

Relevance cardinality constraints.

In many applications, the domain knowledge may provide practical information regarding the number of relevant instances. Such heuristics can be exploited with constraints on the maximum number of relevant instances per bag, i.e.,

$$\sum _{i=1}^{n_b}{I}_{z_{bi}\ne 0}\le n_{\max },\text{for}b=1,\dots ,B,$$

where I_σ denotes the indicator function taking the value 1 if σ is true and 0 otherwise. Unlike the standard MIL assumption, the relevance cardinality constraints require both positive and negative bags to have a bounded number of relevant instances. In our discriminative model, n_max is a tuning parameter that can be optimized to improve the classification performance. Although those make our model more amenable to cancer type recognition, we note that they are not equivalent to sparsity-promoting prior in generative models such as Laplacian [42] or spike-and-slab [43].

Potential extension to multinomial classification.

As the no mixed-class attributes assumption and relevance cardinality constraint apply for every bag, we can easily extend our model to the problem of multinomial MIL classification by considering more categories of attributes. For three-cancer-type classification, by way of illustration, we can consider three groups of labels $\{1,\dots ,\frac{\mathbb{C}}{3}\}$, $\{\frac{\mathbb{C}}{3}+1,\dots ,\frac{2\mathbb{C}}{3}\}$ and $\{\frac{2\mathbb{C}}{3}+1,\dots ,\mathbb{C}\}$.

B. Attribute-Based Symmetric MIL Model

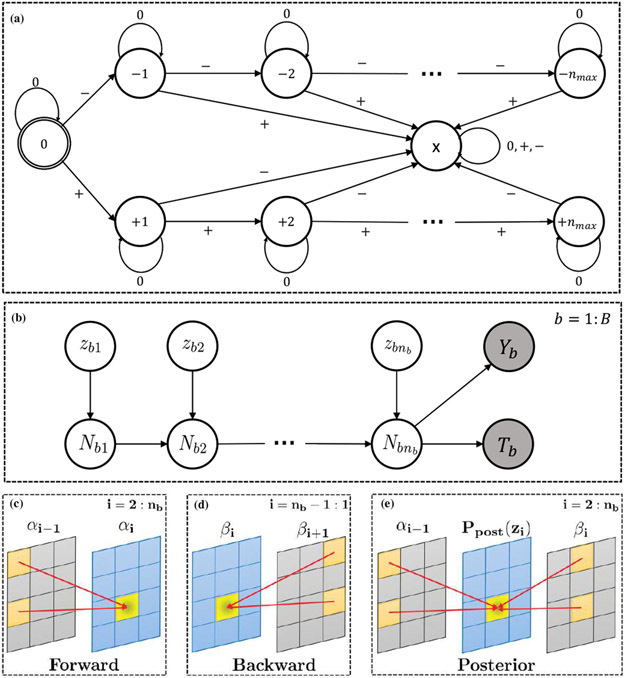
The graphical representation of the proposed model is illustrated in Fig. 2. We assume that instances are independent given all the feature vectors in the bag. We follow the discriminative approach in [39] to model the relationship between the attribute of an instance z_bi and its feature vector x_bi by a multinomial logistic regression function

$$P_{bic}(\mathit{w})=P(z_{bi}=c\mid {\mathit{x}}_{bi},\mathit{w})=\frac{e^{{\mathit{w}}_c^T{\mathit{x}}_{bi}}}{{\sum }_{c=0}^{\mathbb{C}}{e}^{{\mathit{w}}_c^T{\mathit{x}}_{bi}}},$$ (1)

where ${\mathit{w}}_c\in {\mathbb{R}}^d$ is the weight for the cth attribute and $\mathit{w}=[{\mathit{w}}_0,{\mathit{w}}_1,{\mathit{w}}_2,\dots ,{\mathit{w}}_{\mathbb{C}}]$. For the cth attribute in the bth bag, a presence or absence indicator y_bc is computed following the standard assumption [44]

$$y_{bc}=1-\prod _{i=1}^{n_b}{I}_{z_{bi}\ne c},\text{for}c=1,\dots ,\mathbb{C}.$$

Fig. 2.

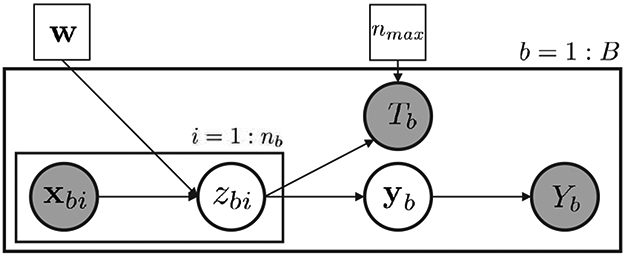
Graphical model for the proposed AbSMIL model. Observed variables are shaded.

To encode the cardinality constraint ${\sum }_{i=1}^{n_b}{I}_{z_{bi}\ne 0}\le n_{\max }$ for the bth bag, we introduce an binary observation variable

$$T_b=\left(I_{{\sum }_{i=1}^{n_b}{I}_{z_{bi}\ne 0}\ge 1}\right)\left(I_{{\sum }_{i=1}^{n_b}{I}_{z_{bi}\ne 0}\le n_{\max }}\right).$$

By letting T_b = 1, we enforce the constraint on the number of relevant instances per bag during training stage. The bag level label Y_b is computed based on the presence of positive and negative attributes

$$Y_b\mid {\mathit{y}}_b=\{\begin{array}{c}0,\text{for}(\bigcap _{c=1}^{\frac{\mathbb{C}}{2}}\{y_{bc}=0\})\bigcap (\bigcup _{c=\frac{\mathbb{C}}{2}+1}^{\mathbb{C}}\{y_{bc}=1\}),\hfill \\ 1,\text{for}(\bigcup _{c=1}^{\frac{\mathbb{C}}{2}}\{y_{bc}=1\})\bigcap (\bigcap _{c=\frac{\mathbb{C}}{2}+1}^{\mathbb{C}}\{y_{bc}=0\}),\hfill \\ 2,\text{otherwise}.\hfill \end{array}\phantom{\}}$$

For the completeness, the model may allow Y_b = 2; however, the considered dataset contains only positive bags Y_b = 1 and negative bags Y_b = 0. Thus, we can ignore the case Y_b = 2 in our derivation. To summarize, our model includes the observation $\{Y_b,T_b,{\mathit{X}}_b{\}}_{b=1}^B$, unknown classifier parameter w, hidden variables $\{{\mathit{y}}_b,z_b{\}}_{b=1}^B$ and a tuning parameter n_max.

IV. Inference

This section provides details of our graphical model, including the derivation of the incomplete log-likelihood, the expectation maximization (EM) approach to estimate the model parameters and the prediction of both instance and bag level labels. To facilitate efficient inference, we further present the dynamic programming method for the expectation step in combination with online learning for the maximization step.

A. Regularized Maximum Likelihood

Since the bags are independent, the normalized negative incomplete log-likelihood is given by

$${\mathbb{L}}_{incm}(\mathit{w})=-\frac{1}{B}\sum _{b=1}^B\left(\log P(Y_b,T_b\mid {\mathit{X}}_b,\mathit{w})+\log P({\mathit{X}}_b)\right)$$

where we assume that P(X_b) is a constant w.r.t. w. To ensure the attributes are distinctly different, we introduce entropy regularization that quantifies the cluster diversity (see [45], [46]):

$${\mathbb{H}}_b(\mathit{w})=\sum _{i=1}^{n_b}\left(-\sum _{c=0}^{\mathbb{C}}{P}_{bic}(\mathit{w})\log P_{bic}(\mathit{w})\right),$$ (2)

and a quadratic penalty to control the complexity of the model and avoid over-fitting. Now let us denote ${\mathbb{L}}_b(\mathit{w})=-\log P(Y_b,T_b\mid {\mathit{X}}_b,\mathit{w})$, the objective in our approach can be formulated as

$$\mathbb{L}(\mathit{w})=\frac{1}{B}\sum _{b=1}^B\left({\mathbb{L}}_b(\mathit{w})+{\lambda }_e{\mathbb{H}}_b(\mathit{w})\right)+\frac{{\lambda }_q\Vert \mathit{w}{\Vert }^2}{2},$$ (3)

where λ_q, λ_e are parameters of the quadratic regularizer and the entropy minimizer, respectively. Following the principle of maximum likelihood estimation (MLE), our goal is to minimize $\mathbb{L}(\mathit{w})$. However, this optimization problem is challenging as the probability P(Y_b, T_b ∣ X_b, w) in the objective function is not trivial to compute. For instance, to obtain P(Y_b = 1, T_b ∣ X_b, w), we marginalize the joint probability model of all the model variables over the hidden variables:

$$P(Y_b=1,T_b\mid {\mathit{X}}_b,\mathit{w})=\sum _{{\mathit{z}}_b,{\mathit{y}}_b}P(Y_b=1,T_b,z_b,{\mathit{y}}_b\mid {\mathit{X}}_b,\mathit{w}).$$

Using the graphical model in Fig. 2, we can expand the joint probability as

$$\begin{gathered} P(Y_b=1,T_b,{\mathit{z}}_b,{\mathit{y}}_b\mid {\mathit{X}}_b,\mathit{w}) \\ =P(Y_b=1\mid {\mathit{y}}_b)P({\mathit{y}}_b\mid z_b)P(T_b\mid z_b)P(z_b\mid {\mathit{X}}_b,\mathit{w}) \end{gathered}$$ (4)

Finally, by substituting (4) into the marginalization, we obtain

$$\begin{gathered} P(Y_b=1,T_b\mid {\mathit{X}}_b,\mathit{w}) \\ =\sum _{{\mathit{z}}_b,{\mathit{y}}_b}P(Y_b=1\mid {\mathit{y}}_b)P({\mathit{y}}_b\mid z_b)P(T_b\mid z_b)P(z_b\mid {\mathit{X}}_b,\mathit{w}) \\ =\sum _{{\mathit{z}}_b}{I}_{{\sum }_{i=1}^{n_b}{I}_{z_{bi}\ne 0}\ge 1}{I}_{{\sum }_{i=1}^{n_b}{I}_{z_{bi}\ne 0}\le n_{\max }}\prod _{i=1}^{n_b}P(z_{bi}\mid {\mathit{x}}_{bi},\mathit{w}) \end{gathered}$$

where the summation in the intermediate step is over $z_b\in \{0,1,\dots ,\mathbb{C}{\}}^{n_b}$ and ${\mathit{y}}_b\in \{0,1{\}}^{\mathbb{C}}$, while the latter summation is over $z_b\in \{0,1,\dots ,\frac{\mathbb{C}}{2}{\}}^{n_b}$. Notice that this summation includes a total of approximately ${\sum }_{k=1}^{n_{\max }}(\begin{array}{c}\hfill n_b\hfill \\ \hfill k\hfill \end{array})(\frac{\mathbb{C}}{2}{)}^k$ terms, and hence, is computationally expensive or even intractable when n_max is large. Therefore, we consider an EM approach as the alternative approach to efficiently minimizing $\mathbb{L}(\mathit{w})$.

B. Estimation of Model Parameters

Let us begin by identifying the negative complete log-likelihood as

$${\mathbb{L}}_{cm}(\mathit{w})=-\frac{1}{B}\sum _{b=1}^B\log P(Y_b,T_b,{\mathit{y}}_b,z_b\mid {\mathit{X}}_b,\mathit{w})+K,$$

where K corresponds to the term $\frac{1}{B}{\sum }_{b=1}^B$ log P(X_b) independent of the parameter vector w. Substituting the model dependence structure from (4) into ${\mathbb{L}}_{cm}$ and absorbing terms that do not depend on w into the constant yields

$${\mathbb{L}}_{cm}(\mathit{w})=\frac{1}{B}\sum _{b=1}^B\sum _{i=1}^{n_b}\left(-\sum _{c=0}^{\mathbb{C}}{I}_{z_{bi}=c}{\mathit{w}}_c^T{\mathit{x}}_{bi}+\log (\sum _{c=0}^{\mathbb{C}}{e}^{{\mathit{w}}_c^T{\mathit{x}}_{bi}})\right)$$

up to a constant. The EM algorithm seeks to find the minimum of $\mathbb{L}(\mathit{w})$ by iteratively applying the following two steps:

E-step.

The surrogate function is obtained by taking the expectation with respect to the current conditional distribution of the latent data {y, z} given the observed data {Y, T, X} and the current estimates of the parameters w^(k)

$$E_{\mathit{y},\mathit{z}\mid Y,T,\mathit{X},{\mathit{w}}^{(k)}}\left[{\mathbb{L}}_{cm}(\mathit{w})\right]=\frac{1}{B}\sum _{b=1}^B{\mathbb{J}}_b(\mathit{w},{\mathit{w}}^{(k)})$$

where ${\mathbb{J}}_b(\mathit{w},{\mathit{w}}^{(k)})$ is defined as

$$\sum _{i=1}^{n_b}\left(-\sum _{c=0}^{\mathbb{C}}{P}_{bic}^{post}({\mathit{w}}^{(k)})\cdot {\mathit{w}}_c^T{\mathit{x}}_{bi}+\log \left(\sum _{c=0}^{\mathbb{C}}{e}^{{\mathit{w}}_c^T{\mathit{x}}_{bi}}\right)\right)$$ (5)

and $P_{bic}^{post}({\mathit{w}}^{(k)})=P(z_{bi}=c\mid Y_b,T_b,{\mathit{x}}_{bi},{\mathit{w}}^{(k)})$ denotes the posterior probability. Thus, our surrogate function with regularization is given by

$$\mathbb{Q}(\mathit{w},{\mathit{w}}^{(k)})=\frac{1}{B}\sum _{b=1}^B\left({\mathbb{J}}_b(\mathit{w},{\mathit{w}}^{(k)})+{\lambda }_e{\mathbb{H}}_b(\mathit{w})+\frac{{\lambda }_q\Vert \mathit{w}{\Vert }^2}{2}\right).$$ (6)

In order to compute $\mathbb{Q}(\mathit{w},{\mathit{w}}^{(k)})$, it is necessary to compute the posterior probability $P_{bic}^{post}({\mathit{w}}^{(k)})$. Using the conditional rule, this probability can be then determined by

$$P_{bic}^{post}({\mathit{w}}^{(k)})=\frac{P(z_{bi}=c,Y_b,T_b\mid {\mathit{x}}_{bi},{\mathit{w}}^{(k)})}{{\sum }_{t=0}^{\mathbb{C}}P(z_{bi}=t,Y_b,T_b\mid {\mathit{x}}_{bi},{\mathit{w}}^{(k)})}.$$ (7)

We provide a detailed calculation of (7) in Section IV-C.

M-step.

Since we consider the negative log-likelihood as the objective, this step is essentially to minimize the surrogate $\mathbb{Q}$ by solving

$${\mathit{w}}^{(k+1)}=\underset{\mathit{w}}{\text{argmin}}\mathbb{Q}(\mathit{w},{\mathit{w}}^{(k)}).$$

Generally, minimizing $\mathbb{Q}(\mathit{w},{\mathit{w}}^{\prime })$ is a non-trivial optimization problem. Alternatively, we use the Generalized EM approach to facilitate a descent approach by taking steps along the gradient of $\mathbb{Q}(\mathit{w},{\mathit{w}}^{\prime })$. By Fisher’s identity, this gradient coincides with the gradient of the objective function

$${\phantom{\mid }\frac{\partial \mathbb{L}(\mathit{w})}{\partial \mathit{w}}\mid }_{\mathit{w}={\mathit{w}}^{\prime }}={\phantom{\mid }\frac{\partial \mathbb{Q}(\mathit{w},{\mathit{w}}^{\prime })}{\partial \mathit{w}}\mid }_{\mathit{w}={\mathit{w}}^{\prime }}={\phantom{\mid }\frac{1}{B}{\sum }_{b=1}^B\frac{\partial {\mathbb{Q}}_b(\mathit{w},{\mathit{w}}^{\prime })}{\partial \mathit{w}}\mid }_{\mathit{w}={\mathit{w}}^{\prime }}.$$

The gradient $\frac{\partial {\mathbb{Q}}_b(\mathit{w},{\mathit{w}}^{\prime })}{\partial {\mathit{w}}_c}$ can be computed as follows

$$\begin{gathered} \frac{\partial {\mathbb{Q}}_b(\mathit{w},{\mathit{w}}^{\prime })}{\partial {\mathit{w}}_c}=\sum _{i=1}^{n_b}\left(P_{bic}(\mathit{w})-P_{bic}^{post}({\mathit{w}}^{\prime })\right){\mathit{x}}_{bi}+ \\ {\lambda }_e\sum _{i=1}^{n_b}{P}_{bic}(\mathit{w})\left(\sum _{t=0}^{\mathbb{C}}{P}_{bit}(\mathit{w})({\mathit{w}}_t-{\mathit{w}}_c{)}^T{\mathit{x}}_{bi}\right){\mathit{x}}_{bi}+{\lambda }_q{\mathit{w}}_c. \end{gathered}$$ (8)

The full gradient involves enumerating all the bags. To reduce the computation per iteration, we further propose a single-bag-based stochastic gradient descent approach in the flavor of the Pegasos algorithm [47], [48]. At the kth iteration, a random bag b_k is chosen and a single-bag-based gradient is computed as follows

$${\mathit{w}}^{(k+1)}={\Pi }_{\tau }\left({\mathit{w}}^{(k)}-{\eta }_k{\phantom{\mid }\frac{\partial {\mathbb{Q}}_{b_k}(\mathit{w},{\mathit{w}}^{(k)})}{\partial \mathit{w}}\mid }_{\mathit{w}={\mathit{w}}^{(k)}}\right),$$

where ${\eta }_k=\frac{1}{k{\lambda }_q}$, $\tau =\sqrt{\frac{2({\lambda }_e+1)n_b}{{\lambda }_q}\log (\mathbb{C}+1)}$, and ${\Pi }_{\tau }(\mathit{v})=\text{min}\left\{1,\frac{\tau }{\Vert \mathit{v}\Vert }\right\}\mathit{v}$. Detailed derivation of the stochastic gradient update is provided in Appendix A.

C. Proposed Dynamic Programming for E-step

The brute-force calculation of P(z_bi = c, Y_b, T_b ∣ x_bi, w^(k)) in (7) requires marginalization over all other instance attributes (i.e., z_bj for j = 1, … , n_b and j ≠ i), which is exponential in the number of instances per bag ($O({\mathbb{C}}^{n_b-1})$). Traditional approaches to address such intractable problems often resort to approximation techniques such as approximate inference [49], variational approximation [50], and black-box alpha [51]. In a recent line of work [39], [40], [52], Pham et al. proposed a dynamic programming approach for exact and efficient computation of the posterior. Motivated by the result, we follow a similar idea of converting the V-structure to the chain structure for efficient inference. Specifically, we define a new latent variable N_bi as the “signed” number of relevant attributes in the first i instances of the bth bag. The representation of N_bi is given by the finite state machine in Fig. 3(a). Each instance in a bag is represented by one of the input symbols {0, +, −} (corresponding to an irrelevant instance, a relevant instance in the positive class, or a relevant instance in the negative class, respectively). The number of relevant instances is represented by the set of states {0, ±1, ±2,…, ±n_max}, where the sign indicates whether instances are belong to the positive class or the negative class. For the completeness, we introduce the error state {x} for the case there is a mix of positive and negative attributes in the bag. Practically, this state will not be reached due to our no mixed-class attributes assumption. Thanks to the introduction of N_bi, the posterior probability can be calculated efficiently using the forward and backward message passing on the chain structure (see Fig. 3(b)-(e)). To further simplify our forward-backward message passing derivation, let us denote

$$P_{bi}^0=P_{bi0}(\mathit{w}),P_{bi}^{+}=\sum _{c\in C^{+}}{P}_{bic}(\mathit{w}),P_{bi}^{-}=\sum _{c\in C^{-}}{P}_{bic}(\mathit{w})$$ (9)

where the parameter w is omitted for simplicity. Below is the details of our dynamic programming algorithm for computing the posterior.

Fig. 3.

(a) The number of positively- (negatively-) labeled instances in the first i instances, N_bi, as a finite state machine. (b) A reformulation of Fig. 2 as a chain on N_bi², and (c)-(e) recursive calculation of forward, backward messages, and posterior probability.

Step 1. Forward message passing.

This step computes the forward messages defined as

$${\alpha }_{bi}(l)\triangleq P(N_{bi}=l\mid {\mathit{X}}_b,\mathit{w})\text{for}l=0,\pm 1,\dots ,\pm n_{\max }.$$

The first message is initialized by

$${\alpha }_{b1}(l)=I_{l=0}{P}_{b1}^0+I_{l=1}{P}_{b1}^{+}+I_{l=-1}{P}_{b1}^{-},$$ (10)

The update equation for subsequent messages is given by

$$\begin{gathered} {\alpha }_{bi}(l)=P_{bi}^0{\alpha }_{b(i-1)}(l)+I_{l>0}{P}_{bi}^{+}{\alpha }_{b(i-1)}(l-1) \\ +I_{l<0}{P}_{bi}^{-}{\alpha }_{b(i-1)}(l+1), \end{gathered}$$ (11)

for i = 2,…, n_b.

Step 2. Backward message passing.

This step computes the backward messages defined as

$${\beta }_{bi}(l)\triangleq P(Y_b,T_b\mid N_{bi}=l,{\mathit{X}}_b,\mathit{w}).$$

The first backward message is initialized by

$${\beta }_{b{n}_b}(l)=I_{Y_b=1}{I}_{0<l\le n_{\max }}+I_{Y_b=0}{I}_{-n_{\max }\le l<0},$$ (12)

The update equation for subsequent messages is given by

$$\begin{gathered} {\beta }_{bi}(l)=P_{b(i+1)}^0{\beta }_{i+1}(l)+I_{0\le l<n_{\max }}{P}_{b(i+1)}^{+}{\beta }_{i+1}(l+1) \\ +I_{0\ge l>-n_{\max }}{P}_{b(i+1)}^{-}{\beta }_{i+1}(l-1), \end{gathered}$$ (13)

for i = n_b – 1, … , 1.

Step 3. Joint probability calculation.

This step computes the joint probability defined as

$$P_{bic}^{joint}(\mathit{w})\triangleq P(z_{bi}=c,Y_b,T_b\mid {\mathit{x}}_{bi},\mathit{w}),\text{for}c=0,1,\dots ,\mathbb{C},$$

First, initialize $P_{b1c}^{joint}(\mathit{w})$ by

$$(I_{c=0}{\beta }_1(0)+I_{c\in C^{+}}{\beta }_1(1)+I_{c\in C^{-}}{\beta }_1(-1))P_{b1c}(\mathit{w})$$ (14)

Next, for i = 2, … , n_b, perform the update for $P_{bic}^{joint}(\mathit{w})$ by

$$\begin{gathered} (I_{c=0}\sum _{l=-n_{\max }}^{+n_{\max }}{\beta }_i(l){\alpha }_{i-1}(l)+I_{c\in C^{+}}\sum _{l=0}^{n_{\max }-1}{\beta }_i(l+1){\alpha }_{i-1}(l)\phantom{)} \\ +\phantom{(}{I}_{c\in C^{-}}\sum _{l=-n_{\max }+1}^0{\beta }_i(l-1){\alpha }_{i-1}(l))P_{bic}(\mathit{w}). \end{gathered}$$ (15)

The detailed derivation for the forward messages, backward messages, and joint probability calculation are given in Appendix B, C, and D, respectively. We summarize the proposed AbSMIL approach in Algorithm 1.

D. Prediction

After learning the weight vector w, the instance level label for new test data can be predicted as follows:

$${\widehat{z}}_{bi}={\text{argmax}}_{0\le c\le \mathbb{C}}P(z_{bi}=c\mid {\mathit{x}}_{bi},\mathit{w}).$$

Note that this prediction is made without knowing the bag label. To this end, the bag level label can be predicted as

$${\widehat{Y}}_b={\text{argmax}}_{m\in \{0,1\}}P(Y_b=m,T_b=1\mid {\mathit{X}}_b,\mathit{w})$$

Algorithm 1 Attribute-based Symmetric Multiple Instance Learning (AbSMIL)

$$\begin{array}{cc}\hfill & 1:\mathrm{Input}:\text{Training data}\{{\mathit{X}}_b,Y_b{\}}_{b=1}^B,\text{cardinality constraint}\hfill \\ \hfill & n_{\max },\text{positive constants}{\lambda }_q\text{and}{\lambda }_e,\text{initial weight}{\mathit{w}}^{(0)}\hfill \\ \hfill & 2:\mathrm{Output}:\{{\mathit{w}}^{(k)}\}\hfill \\ \hfill & 3:k=0\hfill \\ \hfill & 4:\mathbf{repeat}\hfill \\ \hfill & 5:\text{Select a random bag}b\hfill \\ \hfill & 6:∕∕\mathbf{E}\text{-}\mathrm{step}:\hfill \\ \hfill & 7:\text{Compute prior probability}{P}_{bic}({\mathit{w}}^{(k)})\text{using (1)}\hfill \\ \hfill & 8:\text{Compute prior probability}{P}_{bi}^0,P_{bi}^{+}\text{and}{P}_{bi}^{-}\text{using (9)}\hfill \\ \hfill & 9:\text{Compute}\text{forward}\text{message}{\alpha }_{bi}(l)\text{for}i=1,\dots ,n_b\text{and}\hfill \\ \hfill & l=0,\pm 1,\dots ,\pm n_{\max }\text{using (10) and (11)}\hfill \\ \hfill & 10:\text{Compute}\text{backward}\text{message}{\beta }_{bi}(l)\text{for}i=n_b,\dots ,1\hfill \\ \hfill & \text{and}l=0,\pm 1,\dots ,\pm n_{\max }\text{using (12) and (13)}\hfill \\ \hfill & 11:\text{Compute}\text{joint}\text{probability}{P}_{bic}^{joint}({\mathit{w}}^{(k)})\text{for}i=\hfill \\ \hfill & 1,\dots ,n_b\text{and}c=0,1,\dots ,\mathbb{C}\text{using (14) and (15)}\hfill \\ \hfill & 12:\text{Compute}\text{posterior}\text{probability}{P}_{bic}^{post}({\mathit{w}}^{(k)})\text{for}i=\hfill \\ \hfill & 1,\dots ,n_b\text{and}c=0,1,\dots ,\mathbb{C}\text{using}(7)\hfill \\ \hfill & 13:∕∕\mathbf{M}\text{-}\mathrm{step}:\hfill \\ \hfill & 14:\tau =\sqrt{\frac{2({\lambda }_e+1)n_b}{{\lambda }_q}\log (\mathbb{C}+1)}\hfill \\ \hfill & 15:\text{Compute}\frac{\partial {\mathbb{Q}}_b(\mathit{w},{\mathit{w}}^{(k)})}{\partial {\mathit{w}}_c}\text{for}c=0,1,\dots ,\mathbb{C}\text{using}(8)\hfill \\ \hfill & 16:{\mathit{w}}^{(k+1)}={\Pi }_{\tau }\left({\mathit{w}}^{(k)}-\frac{1}{k{\lambda }_q}\frac{\partial {\mathbb{Q}}_b(\mathit{w},{\mathit{w}}^{(k)})}{\partial {\mathit{w}}^{(k)}}\right)\hfill \\ \hfill & 17:k=k+1\hfill \\ \hfill & 18:\mathbf{until}\text{stopping criteria is met}\hfill \end{array}$$

where P(Y_b = m, T_b = 1 ∣ X_b, w) is given by

$$\{\begin{array}{cc}{\sum }_{l=1}^{n_{\max }}{\alpha }_{b{n}_b}(l)\hfill & \text{for}m=1,\hfill \\ {\sum }_{l=n_{-\max }}^{-1}{\alpha }_{b{n}_b}(l)\hfill & \text{for}m=0.\hfill \end{array}\phantom{\}}$$

E. Complexity Analysis

To compute the posterior probability $P_{bic}^{post}({\mathit{w}}^{\prime })$, we need to obtain the forward and backward messages over all instances of the bag (n_b) and all possible numbers of relevant instances (2n_max + 1). Given the label Y_b of the bag, the overall complexity of the E-step is O(n_bn_max). Our proposed dynamic programming approach offers an efficient computation that is linear with the number of instances per bag n_b when the number of relevant instances is constrained to be small. On the other hand, the M-step requires $O(n_b\mathbb{C}d)$ to compute each single bag-based stochastic gradient. Thus, the total complexity per iteration is $O(n_b(\mathbb{C}d+n_{\max }))$. When each instance is a high-dimensional vector, i.e., d ≫ n_max, the M-step dominates other steps and the overall complexity per iteration of our algorithm is $O(\mathbb{C}{n}_{b}d)$. In terms of memory, the dominant factor stems from forward and backward messages. In order to store all possible messages, the space complexity per bag is O(n_bn_max), which is often smaller than that of the instances per bag (O(dn_b)) in practice.

Non-linear extension.

If there is a large number of attributes, a kernel extension can be used as an alternative to the linear model. By introducing non-linear kernel functions, data is transformed to capture the clustering nature of multiple attributes without assigning additional clusters. In practice, $\mathbb{C}=2$ is often sufficient for binary classification. To implement a radial basis function (RBF) kernel, one can follow the approach of [53], replacing x with

$$\varphi (x)=\frac{1}{\sqrt{k}}[\cos (g_1^T\mathit{x}),\sin (g_1^T\mathit{x}),\dots ,\cos (g_k^T\mathit{x}),\sin (g_k^T\mathit{x}){]}^T$$ (16)

where $g_1,\dots ,g_k\stackrel{i.i.d.}{\sim }\mathcal{N}(0_d,{\sigma }_g^2{I}_d)$. We demonstrate the effectiveness of the non-linear extension through the experiment in Section V-D.

V. Experiments

In this section, we evaluate the performance of the proposed algorithm (AbSMIL) in terms of runtime and classification accuracy. We compare its performance with state-of-the-art MIL frameworks on a number of datasets, including 4 different histopathology datasets.

A. Datasets

We consider 2 sets of experiments to evaluate the runtime (see V-C) and classification performance (see V-D). Firstly, in order to evaluate the runtime performance of AbSMIL, we create a synthetic MIL-based dataset from the MNIST dataset as follows. We select all the images of digits 0, 1, 2 and manually label the right/left-tilted 0s and 1s as the positive/negative relevant instances, and 2s as the irrelevant instances. Then, for each positive (negative) bag, we randomly select n_rel relevant instances from the images of right-tilted (left-tilted) digits and n_b – n_rel irrelevant instances from the images of 2. The total number of bags is B = 200, with a balanced number between positive and negative bags. The goal is to learn the orientation (left-tilted versus right-tilted) of 0 and 1 while the orientation of 2 is ignored.

Secondly, in order to evaluate the classification performance of AbSMIL, we use seven benchmark datasets in a wide range of applicability. (i) The first group includes three datasets popularly used in studies of MIL: Tiger, Fox, and Elephant datasets (see [12], [27], [28], [54], [55]). There are 200 bags in which 100 positive bags associated with the target animal images and 100 negative bags associated with other kinds of animal. For each of these datasets, 140 images are used for training and 60 images for test. The maximum number of instance per bag is 13. More details of these datasets can be found in [27]. (ii) The second group contains histopathology images of mammalian organs, provided by the Animal Diagnostics Lab (ADL) at Pennsylvania State University. Each of the three datasets (kidney, lung and spleen) contains 300 images of size 4000×3000 from either inflammatory or healthy tissues. A healthy tissue image largely consists of healthy patches while an inflammatory tissues have a dominant portion of diseased patches. 250 samples are used for training and the remaining ones are used for testing. There are 130 instances per bag in each dataset. More details of ADL datasets can be found in [11]. (iii) The last dataset, referred as the TCGA dataset [56], contains WSIs of brain cancer from The Cancer Genome Atlas (TCGA), provided by the National Institute of Health. This dataset contains 96 histopathology samples of two types of glioma: 48 samples for astrocytoma and 48 samples for oligodendroglioma. In each WSI (as one bag), cancerous regions occupy only a small portion of various shapes and color shading, and this portion is usually surrounded by benign cells, making the TCGA dataset inherently harder than the ADL datasets [11]. Noticeably, the problem of classifying cancer types in the TCGA dataset fits well the symmetric setting of AbSMIL. To obtain instances from each WSI, we first remove some redundant parts such as glass or folding areas, then randomly select a set of 100×100×3 patches in the image (with potential overlaps). The instances are obtained by featurizing these patches using 84 features including histogram of oriented gradients, histogram of gray images and SFTA-texture features [57]. The maximum number of instances per bag is 1258. A split of 76 training versus 20 test images is considered in our experiment. In all of these datasets, a balanced number of positive/negative bags is used in both training and testing stages.

B. Baselines

In our experiment, we compare the proposed method with a variety of popular approaches, including mi-SVM [27], MIL-Boost [33], miGraph [28], MCIL [26], DFDL [11], ORLR [39] and MIML-NC [40]. The first four methods are MIL-based approaches that utilize the standard asymmetric assumption. In particular, mi-SVM assumes that there is at least one pattern from every positive bag in the positive halfspace, while all patterns belonging to negative bags are in the negative halfspace. In [28], miGraph implicitly constructs a graph that model each bag and the relations among the instances within the bag. Both of these methods were previously used on the Tiger, Fox, Elephant datasets. In histopathological image classification, MCIL and DFDL are the state-of-the-art methods. While MCIL is designed for MIL setting and can be used directly in our experiment, DFDL learns a dictionary bases using manually extracted regions in the WSIs (i.e., annotating at instance level). In order to adapt DFDL to the MIL setting, we resort to assuming that all instances in positive bags are positive and all instances in negative bags are negative (similar to [11]). MIL-Boost can be seen as a special case of MCIL where there is one cluster in positive bags. The last two methods, ORLR and MIML-NC, are generally designed for the multiple instance multiple label learning (MIML) setting. As discussed in Section II, MIML setting is similar to our symmetric MIL assumption where both positive and negative bag contains instances from multiple clusters. However, while the MIML-based models are designed for a more general setting where the bag label is the union of all instance labels, the proposed AbSMIL method is designed for the specific setting of HIC where bag labels are binary based on the relevant instances.

C. Runtime Evaluation

In the following, we present the experiment to evaluate and compare the runtime performance of AbSMIL with the aforementioned algorithms.

Setting.

In the first set of simulations, we test the impact of the cardinality constraint n_max on the computational performance of AbSMIL by varying n_b through the set of values {500, 1000, 2000, 5000} and n_max through the set of values {2, 5, 10, 20, 50, 100, 200, 500, 1000, 2000, 5000} (such that n_max ≤ n_b). Since among the aforementioned values we include fairly large values of n_b and n_max, we consider the following to reduce the runtime. First, the original 784 = 28 × 28 image vector is trimmed down to a 30-dimensional vector by selecting only the first d = 30 elements. Next, the number of attributes is set to $\mathbb{C}=2$ and the parameters λ_q and λ_e are fixed to 10⁻⁶ and 10⁻², respectively. We also adjust the number of epochs inversely proportional to n_max so that each setting takes approximately the same amount of time. Finally, we report the average running time per epoch for each setting. In the second set of simulations, we test the impact of the number of attributes $\mathbb{C}$ on the computational performance of AbSMIL by varying n_max through the set of values {50, 100, 200, 500} and $\mathbb{C}$ through the set of values {2, 4, 10, 20, 50, 100, 200, 500, 1000, 2000, 5000}. The same setting for $\mathbb{C}$, d, λ_q and λ_e from the first simulation is used in this simulation and the average running time per epoch is then reported. To reduce the runtime variance, each setting is repeated 10 times on the same computer.

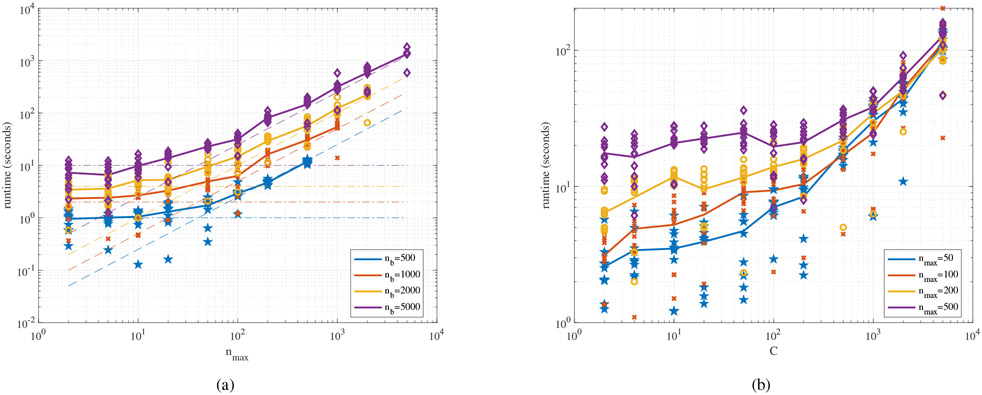
Results and Analysis.

We plot our results from the simulations in Fig. 4. The left plot shows the average running time of AbSMIL as a function of n_max. It can be seen that the running time exhibits two different modes with respect to the change in n_max. Recall that our overall complexity per bag is $O(n_b(\mathbb{C}d+n_{\max }))$. When n_max is small, the dominant term in the sum is $\mathbb{C}d$ (here, $\mathbb{C}d=60$) and we observe a flat region at the beginning of the four curves for different values of n_b. When n_max becomes larger, linear behavior (i.e., runtime ∝ n_max) is observed as n_max gains dominance over $\mathbb{C}d$. Note that in practice, the implementation of AbSMIL for the special case when n_max = n_b is less costly than reported and this case is equivalent to AbSMIL with no constraint. In the right plot, a similar behavior is observed: the running time remains stable when $\mathbb{C}$ is small and a linearly increasing runtime is observed when $\mathbb{C}$ is large. Note that for different values of n_max, the running time converges since the $\mathbb{C}d$ becomes dominant, thereby making the different values of n_max negligible. Similar to the number of weak classifiers T in MCIL, the number of attributes $\mathbb{C}$ in our algorithm also contributes as a linear term in the computational complexity. We also notice variation in the running time due to the differences among the computational cluster nodes used in this experiment.

Fig. 4.

Running time of AbSMIL as a function of the cardinality constraint n_max (a) and the number of attributes $\mathbb{C}$ (b) in log-log scale. Each curve corresponds to a different setting in terms of n_b (a) and in terms of n_max (b). The runtime values in each curve are calculated by averaging the runtime across 10 different runs (indicated by the markers). In (a), the dash-dotted lines and the dashed lines are added to demonstrate the asymptotic behavior of analytical complexity $O(n_b(\mathbb{C}d+n_{\max }))$ when n_max is small and when n_max is large, respectively.

D. Real-world Datasets

This subsection presents the experiment to evaluate and compare the accuracy performance of AbSMIL with the baseline algorithms on different real-world datasets.

Settings.

Since instance labels are unavailable for the aforementioned real-world datasets, all the results are evaluated using bag level prediction with 10-fold cross validation [61]. The value of n_max is selected in the set {5%, 10%, 20%, 30%, 40%, 50%, 100%} of n_b in Tiger, Fox, and Elephant datasets; {5%, 10%, 20%, 50%, 75%} of n_b in Kidney, Lung, Spleen datasets; and {1%, 2%, 5%, 10%, 20%} of n_b in TCGA dataset. Note that x_bi’s are assumed to be normalized such that the mean of each entry over the data is zero and the variance of each entry is 1. In AbSMIL, λ_q and λ_e are searched in a grid of {10⁻⁶, 10⁻⁵, 10⁻⁴, 10⁻³, 10⁻²}. For each setting, AbSMIL is initialized ten times, and the model that yields the lowest training negative log-likelihood is chosen to report the performance. We also report the results for two variants of the proposed method: AbSMIL - No constraint and AbSMIL - Kernel. AbSMIL - No constraint is essentially AbSMIL without using cardinality constraint. AbSMIL - Kernel is mentioned in (16), and its hyperparameter ${\sigma }_g^2$ is selected in {0.999, 0.998, 0.995, 0.99, 0.98, 0.95, 0.9, 0.8, 0.5}. For mi-SVM, we change the loss constant C ∈ {10⁻², 10⁻¹, 1, 10, 10²} and choose a linear kernel function. In MIL-Boost and MCIL, we search over the generalized mean (GM), the log-sum-exponential (LSE) softmax function with parameter named r ∈ {15, 20, 25} and the number of weak classifiers named T ∈ {150, 200, 250}. In miGraph, we tune the number of classes C ∈ {50, 100, 150, 200, 500}, RBF kernel γ ∈ {1, 5, 10, 15, 20, 25, 50} and threshold used in computing the weight of each instance ϵ ∈ {0.1, 0.2, 0.3, 0.4, 0.5}. ORLR and MIML-NC are tuning-free methods. For DFDL, we tune the regularization parameter ρ ∈ {10⁻⁵, 10⁻⁴, 10⁻³, 10⁻², 10⁻¹}, sparsity level parameter λ ∈ {10⁻⁵, 10⁻⁴,10⁻³, 10⁻², 10⁻¹}, and the number of dictionary bases k ∈ {100, 200, 500}. These tuning values are extracted from the corresponding aforementioned publications.

Results and Analysis.

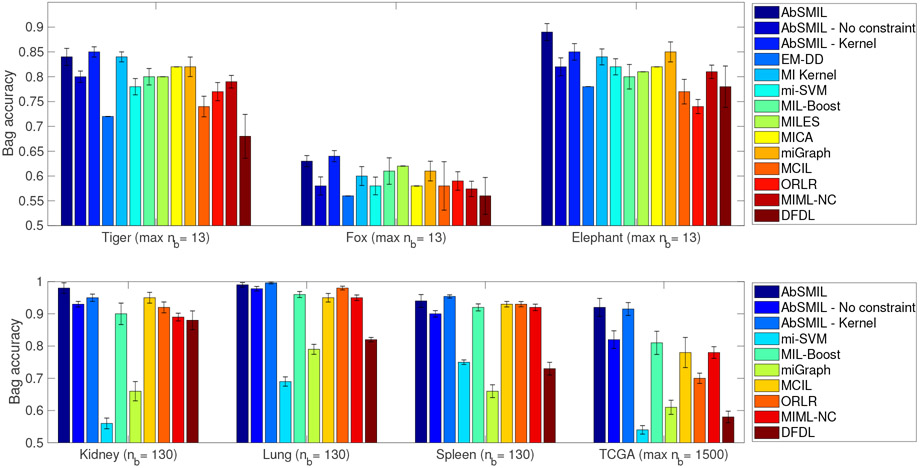
Fig. 5 demonstrates the bag level accuracy of the aforementioned methods on different real-world datasets. Overall, the proposed AbSMIL method shows a competitive performance with other state-of-the-art methods for various datasets in our experiment. Additionally, we observe a major improvement by adding the cardinality constraint to the AbSMIL model. Let us discuss the detail of each group of datasets below.

Fig. 5.

Bag level accuracy various algorithms in seven real-world datasets. The proposed AbSMIL method shows a competitive performance with other state-of-the-art methods for various datasets in our experiment. Especially for the case of TCGA dataset, the outstanding result of AbSMIL indicates that the symmetric MIL assumption and the cardinality constraint are more suitable to such settings. The results with EM-DD [31], MI Kernel [58], MILES [59], and MICA [60] are observed from [60] and [55].

Tiger, Fox, and Elephant datasets:

Overall, Fig. 5 shows that AbSMIL obtains the highest accuracy on Elephant dataset, while AbSMIL - Kernel outperforms other methods on Fox and Tiger datasets. As pointed out in [27], due to the limited accuracy of the image segmentation, the relatively small number of region descriptors, and the small training set size, Fox dataset yields a harder classification problem than the other two datasets. Regarding result of ‘AbSMIL-No constraint’, it can be seen that removing the cardinality constraint lessens the performance of AbSMIL significantly (e.g., roughly 7%).

Kidney, Lung, and Spleen datasets:

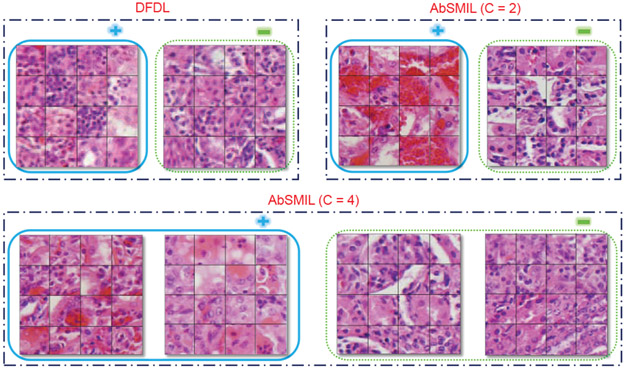
The results reported for AbSMIL are obtained by setting n_max at 20% of the total instances per bag in Kidney and Lung datasets and at 50% in Spleen dataset. Again, it can be seen that AbSMIL and AbSMIL - Kernel slightly outperform other methods in terms of bag level accuracy. A comparison of images of instances from the same attribute obtained by AbSMIL and DFDL on Kidney dataset are shown in Fig. 6. For $\mathbb{C}=2$, the cancerous tissue recognized by AbSMIL appears as a mixture of vascular proliferation (red parts) and necrosis (areas with no nuclei - appeared as the purple dot in the image). On the other hand, for $\mathbb{C}=4$, cancerous tissue splits into two distinctly different categories. In comparison, the performance of DFDL appears worse since in this MIL setting, DFDL assumes that all instances in positive bags are positive and all instances in negative bags are negative.

Fig. 6.

Groups of instances in the same class predicted by AbSMIL and DFDL. Cancer groups are in solid blue while normal ones in dotted green. Compared to two DFDL bases, AbSMIL exhibits distinctly different tissue types between the two categories with $\mathbb{C}=2$ and can be clustered to distinguish phenomenon in each category with $\mathbb{C}=4$.

TCGA dataset:

The result obtained by AbSMIL in this experiment is at n_max of nearly 5% the total number of instances in a bag. As in Fig. 5, AbSMIL and AbSMIL - Kernel significantly outperform the other frameworks. This improvement is remarkable compared to the previous experiment and matches with our intuition on the TCGA dataset: in each WSI, cancerous regions occupy only a small portion, as opposed to the ADL dataset where inflammatory tissues dominate the entire WSI. Thereby, the cardinality constraint offers an advantage to AbSMIL over other methods in effectively gathering information from patches.

VI. Conclusion

In this paper, we introduced Symmetric MIL, a novel setting for multiple-instance learning where both positive and negative bags contain relevant class-specific instances as well as irrelevant instances that do not contribute to differentiating the classes. We presented a probabilistic model for attribute-based Symmetric MIL that accommodates for the presence of numerous irrelevant instances in the data, and takes into account prior information about the sparsity of the relevant instances. We developed an efficient inference approach that is linear in the number of instances and is suitable for the online learning scenario, updating the model using one bag at a time. We evaluated our framework on the real-world datasets: Tiger, Fox, Elephant, Kidney, Lung, Spleen, and TCGA. We obtained competitive results on all datasets and in particular for TCGA where bags contain mainly irrelevant instances. The results validate the merit of the proposed symmetric MIL framework.

Appendix A Gradient Derivation

From (6), the gradient of ${\mathbb{Q}}_b$ w.r.t. w_c can be decomposed into

$$\frac{\partial {\mathbb{Q}}_b(\mathit{w},{\mathit{w}}^{\prime })}{\partial {\mathit{w}}_c}=\frac{\partial {\mathbb{J}}_b(\mathit{w},{\mathit{w}}^{\prime })}{\partial {\mathit{w}}_c}+\frac{\partial {\mathbb{H}}_b(\mathit{w})}{\partial {\mathit{w}}_c}+{\lambda }_q{\mathit{w}}_c.$$ (17)

On the one hand, differentiating ${\mathbb{J}}_b$ from (5) yields

$$\frac{\partial {\mathbb{J}}_b(\mathit{w},{\mathit{w}}^{\prime })}{\partial {\mathit{w}}_c}=-\sum _{i=1}^{n_b}{P}_{bic}^{post}({\mathit{w}}^{\prime }){\mathit{x}}_{bi}+\sum _{i=1}^{n_b}{P}_{bic}(\mathit{w}){\mathit{x}}_{bi}.$$

On the other hand, differentiating ${\mathbb{H}}_b$ from (2) yields

$$\begin{gathered} \frac{\partial {\mathbb{H}}_b(\mathit{w})}{\partial {\mathit{w}}_c}=\frac{\partial }{\partial {\mathit{w}}_c}\left(-\sum _{i=1}^{n_b}\sum _{t=0}^{\mathbb{C}}{P}_{bit}(\mathit{w})\log P_{bit}(\mathit{w})\right) \\ =-\sum _{i=1}^{n_b}\sum _{t=0}^{\mathbb{C}}\left(1+\log P_{bit}(\mathit{w})\right)P_{bit}(\mathit{w})\left(I_{t=c}-P_{bic}(\mathit{w})\right){\mathit{x}}_{bi} \\ =\sum _{i=1}^{n_b}{P}_{bic}(\mathit{w}){\mathit{x}}_{bi}\left(\sum _{t=0}^{\mathbb{C}}{P}_{bit}(\mathit{w})(\log P_{bit}(\mathit{w})-\log P_{bic}(\mathit{w}))\right) \\ =\sum _{i=1}^{n_b}{P}_{bic}(\mathit{w})\left(\sum _{t=0}^{\mathbb{C}}{P}_{bit}(\mathit{w})({\mathit{w}}_t-{\mathit{w}}_c{)}^T{\mathit{x}}_{bi}\right){\mathit{x}}_{bi} \\ =\sum _{i=1}^{n_b}{P}_{bic}(\mathit{w})\left(\sum _{t=0}^{\mathbb{C}}{P}_{bit}(\mathit{w})({\mathit{w}}_t^T{\mathit{x}}_{bi}-\sum _{t=0}^{\mathbb{C}}{P}_{bit}(\mathit{w}){\mathit{x}}_{bi}\right){\mathit{x}}_{bi}. \end{gathered}$$

Thus, substituting the results back into (17) yields

$$\begin{gathered} \frac{\partial {\mathbb{Q}}_b(\mathit{w},{\mathit{w}}^{\prime })}{\partial {\mathit{w}}_c}=\sum _{i=1}^{n_b}\left(P_{bic}(\mathit{w})-P_{bic}^{post}({\mathit{w}}^{\prime })\right){\mathit{x}}_{bi}+ \\ {\lambda }_e\sum _{i=1}^{n_b}{P}_{bic}(\mathit{w})\left(\sum _{t=0}^{\mathbb{C}}{P}_{bit}(\mathit{w})({\mathit{w}}_t-{\mathit{w}}_c{)}^T{\mathit{x}}_{bi}\right){\mathit{x}}_{bi}+{\lambda }_q{\mathit{w}}_c. \end{gathered}$$

The ball radius τ is then computed as follows. Let ${\mathit{w}}^{\ast }={\text{argmin}}_{\mathit{w}}{\mathbb{Q}}_b(\mathit{w},{\mathit{w}}^{\prime })$. Then the following always holds

$$\begin{gathered} {\mathbb{Q}}_b({\mathit{w}}^{\ast },{\mathit{w}}^{\prime })\le {\mathbb{Q}}_b(0,{\mathit{w}}^{\prime }) \\ \iff {\mathbb{J}}_b({\mathit{w}}^{\ast },{\mathit{w}}^{\prime })+{\lambda }_e{\mathbb{H}}_b({\mathit{w}}^{\ast })+\frac{{\lambda }_q\Vert {\mathit{w}}^{\ast }{\Vert }^2}{2} \\ \le \sum _{i=1}^{n_b}\log (\mathbb{C}+1)+{\lambda }_e\sum _{i=1}^{n_b}\log (\mathbb{C}+1) \\ \Rightarrow \frac{{\lambda }_q\Vert {\mathit{w}}^{\ast }{\Vert }^2}{2}\le ({\lambda }_e+1)n_b\log (\mathbb{C}+1) \\ \iff \Vert {\mathit{w}}^{\ast }{\Vert }^2\le \frac{2({\lambda }_e+1)n_b\log (\mathbb{C}+1)}{{\lambda }_q} \\ \iff \tau =\Vert {\mathit{w}}^{\ast }\Vert \le \sqrt{\frac{2({\lambda }_e+1)n_b}{{\lambda }_q}\log (\mathbb{C}+1)} \end{gathered}$$

where (*) stems from the fact that both ${\mathbb{J}}_b({\mathit{w}}^{\ast },{\mathit{w}}^{\prime })$ and ${\mathbb{H}}_b({\mathit{w}}^{\ast })$ are non-negative.

Appendix B Forward Message Derivation

Initialize α_i(l) for i = 1 and l = −n_max, … ,n_+max:

$$\begin{gathered} {\alpha }_1(l)=P(N_1=l\mid {\mathit{X}}_b,\mathit{w}) \\ =\sum _{c}P(N_1=l,z_{b1}=c\mid {\mathit{x}}_{b1},\mathit{w}) \\ =\sum _{c}P(N_1=l\mid z_{b1}=c)P_{b1c}(\mathit{w}) \\ =\sum _c\left(I_{l=0}{I}_{c=0}+I_{l=1}{I}_{c\in C^{+}}+I_{l=-1}{I}_{c\in C^{-}}\right)P_{b1c}(\mathit{w}) \\ =I_{l=0}{P}_{b10}+I_{l=1}\sum _{c\in C^{+}}{P}_{b1c}+I_{l=-1}\sum _{c\in C^{-}}{P}_{blc} \\ =I_{l=0}{P}_{b1}^0+I_{l=1}{P}_{b1}^{+}+I_{l=-1}{P}_{b1}^{-}. \end{gathered}$$

Update α_i(l) for i = 2, … , n_b and l = n_max, … , +n_max:

$$\begin{gathered} {\alpha }_i(l)=P(N_i=l\mid {\mathit{X}}_b,\mathit{w}) \\ =\sum _{c,k}P(N_i=l,N_{i-1}=k,z_{bi}=c\mid {\mathit{X}}_b,\mathit{w}) \\ =\sum _{c,k}P(N_i=l\mid N_{i-1}=k,z_{bi}=c) \\ \cdot P(N_{i-1}=k\mid {\mathit{X}}_b,\mathit{w})P_{bic}(\mathit{w}) \\ =\sum _{c,k}(I_{c=0}{I}_{k=l}+I_{l\ge 1}{I}_{c\in C^{+}}{I}_{k=l-1}\phantom{)} \\ +\phantom{(}{I}_{l\le -1}{I}_{c\in C^{-}}{I}_{k=l+1}){\alpha }_{i-1}(k)P_{bic}(\mathit{w}) \\ ={\alpha }_{i-1}(l)P_{bi}^0+I_{l>0}{\alpha }_{i-1}(l-1)P_{bi}^{+}+I_{l<0}{\alpha }_{i-1}(l+1)P_{bi}^{-}. \end{gathered}$$

Appendix C Backward Message derivation

Initialize β_i(l) for i = n_b and l = −n_max, … , +n_max:

$$\begin{gathered} {\beta }_{n_b}(l)=P(Y_b,T_b=1\mid N_{n_b}=l,{\mathit{X}}_b,\mathit{w}) \\ =P(T_b=1\mid N_{n_b}=l)P(Y_b\mid N_{n_b}=l) \\ =I_{Y_b=1}{I}_{0<l\le n_{\max }}+I_{Y_b=0}{I}_{-n_{\max }\le l<0}. \end{gathered}$$

Update β_i(l) for i = n_b – 1, … , 1, l = −n_max, … , +n_max:

$$\begin{gathered} {\beta }_i(l)=P(Y_b,T_b=l\mid N_i=l,{\mathit{X}}_b,\mathit{w}) \\ =\sum _{c,k}P(Y_b,T_b=1,N_{i+1}=k,z_{b(i+1)}=c\mid N_i=l,{\mathit{X}}_b,\mathit{w}) \\ =\sum _{c,k}P(Y_b,T_b=1\mid N_{i+1}=k,{\mathit{X}}_b,\mathit{w}) \\ \cdot P(N_{i+1}=k\mid N_i=l,z_{b(i+1)}=c)P_{b(i+1)c}(\mathit{w}) \\ =\sum _{c,k}{\beta }_{i+1}(k)(I_{c=0}{I}_{k=l}+I_{0\le l<n_{\max }}{I}_{c\in C^{+}}{I}_{k=l+1}\phantom{)} \\ +\phantom{(}{I}_{0\ge l>-n_{\max }}{I}_{c\in C^{-}}{I}_{k=l-1})P_{b(i+1)c}(\mathit{w}) \\ ={\beta }_{i+1}(l)P_{b(i+1)}^0(\mathit{w})+I_{0\le l<n_{\max }}{\beta }_{i+1}(l+1)P_{b(i+1)}^{+} \\ +I_{0\ge l>-n_{\max }}{\beta }_{i+1}(l-1)P_{b(i+1)}^{-}. \end{gathered}$$

Appendix D Joint Probability Derivation

For valid Y_b and T_b, the state machine will not travel through the invalid state x. So we can safely ignore the invalid state x in our derivation and only consider valid states 0, ±1, … , ±n_max. Initialize $P_{bic}^{joint}(\mathit{w})$ for i = 1:

$$\begin{gathered} P_{b1c}^{joint}(\mathit{w})=P(z_{b1}=c,Y_b,T_b=1\mid {\mathit{X}}_b,\mathit{w}) \\ =\sum _{k}P(Y_b,T_b=1,N_1=k,z_{b1}=c\mid {\mathit{X}}_b,\mathit{w}) \\ =\sum _{k}P(Y_b,T_b=1\mid N_1=k,{\mathit{X}}_b,\mathit{w}) \\ \cdot P(N_1=k\mid z_{b1}=c)P_{b1c}(\mathit{w}) \\ =\sum _k{\beta }_1(k)(I_{c=0}{I}_{k=0}+I_{c\in C^{+}}{I}_{k=1}\phantom{)} \\ \phantom{(}+I_{c\in C^{-}}{I}_{k=-1})P_{b1c}(\mathit{w}) \\ =\left(I_{c=0}{\beta }_1(0)+I_{c\in C^{+}}{\beta }_1(1)+I_{c\in C^{-}}{\beta }_1(-1)\right)P_{b1c}(\mathit{w}). \end{gathered}$$

Update rule for i = 2,…, n_b – 1:

$$\begin{gathered} P_{bic}^{joint}(\mathit{w})=P(z_{bi}=c,Y_b,T_b=1\mid {\mathit{X}}_b,\mathit{w}) \\ =\sum _{k,l}P(Y_b,T_b=1,N_i=k,N_{i-1}=l,z_{bi}=c\mid {\mathit{X}}_b,\mathit{w}) \\ =\sum _{k,l}P(Y_b,T_b=1\mid N_i=k,{\mathit{X}}_b,\mathit{w})\cdot \\ P(N_i=k\mid N_{i-1}=l,z_{bi}=c)P(N_{i-1}=l\mid {\mathit{X}}_b,\mathit{w})P_{bic}(\mathit{w}) \\ \sum _{k,l}{\beta }_i(k)(I_{c=0}{I}_{k=l}+I_{l<n_{\max }}{I}_{c\in C^{+}}{I}_{k=l+1}\phantom{)} \\ \phantom{(}+I_{l>-n_{\max }}{I}_{c\in C^{-}}{I}_{k=l-1}){\alpha }_{i-1}(l)P_{bic}(\mathit{w}) \\ =\left(I_{c=0}\sum _l{\beta }_i(l){\alpha }_{i-1}(l)+I_{c\in C^{+}}\sum _{l=0}^{n_{\max }-1}{\beta }_i(l+1){\alpha }_{i-1}(l) \\ +I_{c\in C^{-}}\sum _{l=-n_{\max }+1}^0{\beta }_i(l-1){\alpha }_{i-1}(l)\right)P_{bic}(\mathit{w}). \end{gathered}$$