Abstract
Biological excitable media, such as cardiac or neural cells and tissue, exhibit memory in which a change in the present excitation may affect the behaviors in the next excitation. For example, a change in calcium (Ca2+) concentration in a cell in the present excitation may affect the Ca2+ dynamics in the next excitation via bi-directional coupling between voltage and Ca2+, forming a delayed feedback loop. Since the Ca2+ dynamics inside the excitable cells are spatiotemporal while the membrane voltage is a global signal, the feedback loop is then a delayed global feedback (DGF) loop. In this study, we investigate the roles of DGF in the genesis and stability of spatiotemporal excitation patterns in periodically-paced excitable media using mathematical models with different levels of complexity: a model composed of coupled FitzHugh-Nagumo units, a 3-dimensional physiologically-detailed ventricular myocyte model, and a coupled map lattice model. We investigate the dynamics of excitation patterns that are temporal period-2 (P2) and spatially concordant or discordant, such as subcellular concordant or discordant Ca2+alternans in cardiac myocytes or spatially concordant or discordant Ca2+ and repolarization alternans in cardiac tissue. Our modeling approach allows both computer simulations and rigorous analytical treatments, which lead to the following results and conclusions. When DGF is absent, concordant and discordant P2 patterns occur depending on initial conditions with the discordant P2 patterns being spatially random. When the DGF is negative, only concordant P2 patterns exist. When the DGF is positive, both concordant and discordant P2 patterns can occur. The discordant P2 patterns are still spatially random, but they satisfy that the global signal exhibits a temporal period-1 behavior. The theoretical analyses of the coupled map lattice model reveal the underlying instabilities and bifurcations for the genesis, selection, and stability of spatiotemporal excitation patterns.
Author summary
Understanding the mechanisms of pattern formation in biological systems is of great importance. Here we investigate the dynamical mechanisms by which delayed global feedback affects excitation pattern formation and stability in periodically-paced biological excitable media, such as cardiac or neural cells and tissue. We focus on the formation and stability of the temporal period-2 and spatially in-phase and out-of-phase excitation patterns. Using models of different levels of complexity, we show that when the delayed global feedback is negative, only the spatially in-phase patterns are stable. When the feedback is positive, both spatially in-phase and out-of-phase patterns are stable, and the out-of-phase patterns are spatially random but satisfy that the global signals are temporal period-1 solutions.
Introduction
Pattern formation is ubiquitous in biological systems, ranging from biological development [1, 2], ecosystems [3], to disease development [4]. Many of the pattern formation processes can be explained by Turing instability in reaction-diffusion (or activator-inhibitor) systems [5, 6]. However, pattern formation via other mechanisms has also been proposed, in particular for spatiotemporal patterns, which are also widely observed in biological systems [7–12]. The fundamental processes causing temporal and spatiotemporal dynamics in biological systems are positive and negative feedback loops [5, 6, 13]. While many studies investigated the roles of local and instantaneous feedback loops in pattern formation, studies have also carried out to investigate the roles of instantaneous global feedback and time delay global feedback (DGF) loops, such as the ones demonstrated in oscillatory media of chemical reactions [14–19]. In this study, we focus on the roles of DGF in excitation pattern formation in a class of biological systems, i.e., excitable media subjected to periodic global stimulation. Examples of pattern formation in such biological systems include subcellular calcium (Ca2+) release patterns in neural or cardiac cells (see examples in S1 Fig) or repolarization (voltage) patterns in cardiac tissue or cluster firings in neural networks, as described in more detail below.
In the chemical reaction experiments [17, 19], the DGF loops were explicitly implemented. However, the DGF loops are not obvious at all in the excitable biological systems. Here we use intracellular Ca2+ signaling, which is required for many biological functions [20, 21], as an example to explain the existence of DGF. The fundamental unit of Ca2+ signaling in a cell is called Ca2+ release unit (CRU) (Fig 1A). Ca2+ entering the cell from the voltage-gated Ca2+ channels triggers the opening of the Ca2+ release channels to release Ca2+ from the internal Ca2+ stores. The open probability of the Ca2+ release channels is further enhanced by the released Ca2+. This process is known as Ca2+-induced Ca2+ release (CICR), which is an instantaneous local feedback loop responsible for a rich spectrum of Ca2+ dynamics widely observed in biological systems [22–26]. Besides this instantaneous feedback loop, implicit delayed feedback loops exist, i.e., Ca2+ in the present beat may affect itself in the next beat (Fig 1B). This feedback can be mediated by the Ca2+ current (ICa) of the voltage-gated Ca2+ channels or the Ca2+ release properties of the internal stores through either voltage or Ca2+-dependent signaling pathways. For example, in cardiac myocytes, Ca2+ is coupled to voltage via Ca2+-dependent ion channels and pumps. Changing Ca2+ in the present beat changes the action potential (AP) duration (APD) and thus the following diastolic interval (DI), affecting the recovery of voltage-gated Ca2+ channels in the next beat. As a result, the change in the recovery alters ICa and hence Ca2+, forming a delayed feedback loop. Note that in excitable cells, ion channels generally remain in closed or inactivation states in the quiescent phase. Therefore, the effects of this delayed feedback are manifested in the next beat. In other words, the time delay of the feedback loop is simply the pacing period T.
Fig 1. Schematic diagrams of Ca2+ cycling and a generic model of coupled excitable units with DGF.
a. Schematic diagram of a basic Ca2+ release unit (CRU) in excitable cells. Ca2+ from voltage gated Ca2+ channels (VCCs) triggers the opening of the inositol trisphosphate receptors (IP3Rs) or ryanodine receptors (RyRs), releasing the Ca2+ stored in the endoplasmic or sarcoplasmic reticulum (ER/SR). The released Ca2+ further triggers more IP3Rs/RyRs to open, forming a positive feedback loop. This process is called Ca2+-induced Ca2+ release (CICR). Ca2+ is extruded by Na+-Ca2+ exchange (NCX) or other Ca2+ pumps and uptaken back into the ER/SR via sarco/endoplasmic reticulum Ca2+ ATPase (SERCA). b. Schematic diagram of delayed feedback in Ca2+ signaling via Ca2+ current (ICa). T is the pacing period. c. Schematic diagram of a generic model of coupled excitable units (e.g., CRUs) with a DGF loop of time delay T.
A cell consists of thousands of CRUs which are coupled via Ca2+ diffusion. The CRUs are themselves excitable units [24, 27–29], which are triggered by a global signal, i.e., voltage. Therefore, one can simplify the Ca2+ signaling system into a coupled array of excitable units under a global stimulation with a DGF loop (Fig 1C). Since voltage is the global signal, under normal conditions, depolarization of the cell synchronizes the firings of the CRUs, resulting in a synchronous whole-cell Ca2+ release, such as Ca2+ release in neurons (S1A Fig) [30]. The synchronous Ca2+ release is essential for muscle contraction [21] and many other types of biological functions [20]. However, under abnormal or diseased conditions, dyssynchronous Ca2+ releases can occur, such as subcellular spatially discordant Ca2+ alternans widely observed in cardiac myocytes (S1B Fig) [31–33]. It is clear that voltage serves as the global signal to synchronize the CRU releases, but it is unclear how dyssynchronous or discordant patterns are formed. Furthermore, the roles of the DGF in maintaining the synchronous release patterns or the development of the dyssynchronous release patterns are not well understood.
In addition to intracellular Ca2+ signaling, other biological systems can also be described by the simplified scheme in Fig 1C, such as the excitation dynamics in cardiac tissue or neural networks. In cardiac tissue, myocytes are electrically excitable units that are coupled via gap junctions. Contraction of the heart can serve as the global signal, which may mediate DGF via mechano-electric feedback through activating mechano-sensitive channels and affecting intracellular Ca2+ release [34–36]. This DGF may play essential roles in arrhythmogenic pattern formation in the heart, such as the widely observed spatially discordant APD alternans [37, 38]. In neural networks, the roles of delayed feedback in neural firing dynamics have been investigated [39–41], and DGF may also play essential roles in the formation and stability of clustered firing of neurons [42].
This study was set to investigate the roles of DGF in the genesis and stability of spatiotemporal patterns in periodically-paced biological excitable media, focusing on temporal period-2 (P2) and spatially concordant (in-phase) or discordant (out-of-phase) patterns. Mathematical models of different levels of complexity were used to allow both computer simulations and rigorous analytical treatments. First, a generic model consisting of a coupled array of excitable units described by the FitzHugh-Nagumo (FHN) model was used, and simulations were carried out to reveal the pattern dynamics caused by DGF. To validate the findings of the generic model, we used a 3-dimensional (3D) ventricular myocyte model and carried out simulations to investigate the roles of DGF in spatially concordant and discordant Ca2+ alternans dynamics. Of note, the term “alternans” in the context of the cardiac systems refers to a P2 state. Finally, a coupled map lattice (CML) model was used to perform detailed theoretical analyses, which provide a general mechanistic understanding of the roles of DGF in pattern formation, selection, and stability in periodically-paced biological excitable media. Our approach or objective is to use the generic FHN model to demonstrate that the DGF induced dynamics are general, use the detailed ventricular cell model to validate the general dynamics in a realistic biological system, and use the CML model to reveal the underlying dynamical mechanisms. We argue (as detailed in Discussion) that besides the subcellular spatiotemporal Ca2+ dynamics in ventricular myocytes, due to the generality of the simple models, the mechanistic insights shall also be applicable to spatially discordant APD alternans in cardiac tissue or cluster firings in neural networks when global feedback or DGF exists. The theoretical insights may also be helpful for understanding the mechanisms of pattern formation induced by global feedback or DGF in oscillatory chemical media shown in previous studies [14–19].
Results
DGF in the genesis of spatiotemporal dynamics in an array of coupled FHN units
We used a generic model consisting of a one-dimensional (1D) array of coupled FHN units to investigate the spatiotemporal excitation patterns. The governing differential equations are:
| (1) |
in which j = 1, 2, …, L is the spatial index of the FHN units with L being the length of the 1D array. We used the standard FHN kinetics, i.e.,
| (2) |
where c is the activator and w the inhibitor. cth = 0.5 is a parameter determining the threshold for excitation, and D = 0.1 is the coupling strength. I(t) in Eq 1 is the external stimulus pulse. No-flux boundary condition was used.
As implied in Fig 1B, ICa that triggers the Ca2+ release and mediates the feedback is a spiky current, which only occurs at the beginning of each pacing beat. Therefore, instead of adding a time-continuous feedback term to Eq 1, we add the feedback to the stimulus pulse, which is then formulated as
| (3) |
In Eq 3, n is the index of the beat number, T is the pacing period, ΔT is the pulse duration, and α is the feedback strength. is the peak value of the spatial average of c (denoted as ) at the (n-1)th beat. is the reference value for the feedback. Here we define α>0 as positive feedback (α<0 as negative feedback), since in an uncoupled FHN unit, a larger cn−1 gives rise to a larger I(t), and thus a larger cn. We set I0 = 1.2, ΔT = 0.5, and . The value is roughly the steady-state value of c at the bifurcation point from P1 to P2 of an FHN unit without feedback. We find that other choices do not change the general results but exhibit certain quantitative differences.
Random initial conditions are used to induce spatially discordant patterns. Specifically, at t = 0, we set the variable w to be a spatially random distribution, i.e., w(j,0) = 0.5+δξ(j) (j = 1,2,…,L) with ξ(j) being a uniform random number in [–1,1]. δ is the parameter determining the extent of the spatial heterogeneity and the initial condition becomes uniform when δ = 0.
Excitation patterns without DGF
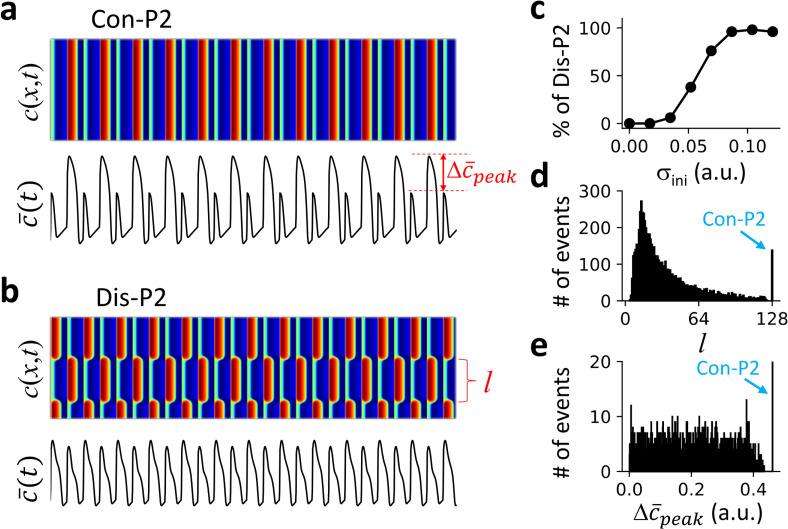
In the absence of DGF, i.e., α = 0 in Eq 3, a bifurcation from temporal P1 to P2 occurs as the pacing period T decreases in an uncoupled FHN unit (S2 Fig). We use spatially random initial conditions as detailed above to induce discordant patterns in the 1D array. We find that when T first passes through the bifurcation point, the system can only exhibit a spatially concordant P2 (Con-P2) pattern independent of initial conditions. As T decreases further, the system can exhibit a Con-P2 (Fig 2A) or a spatially discordant P2 (Dis-P2) pattern (Fig 2B) depending on the initial condition. The probability of forming a Dis-P2 pattern increases as the spatial heterogeneity of the initial condition increases (Fig 2C). Moreover, the Dis-P2 patterns are spatially random and selected by initial conditions. To quantify this property, we measured the spatial domain sizes (see Fig 2B for definition) from 2000 random trials for a given standard deviation of the spatial heterogeneity of the initial condition, and plotted the corresponding histogram in Fig 2D. It shows that the domain size can be any value as long as it is greater than a minimum domain size lmin, i.e., the domain sizes distribute between lmin and L-lmin. Because of this randomness in pattern selection, the corresponding histogram of the global P2 amplitude ( as defined in Fig 2A) also exhibits a continuous distribution (Fig 2E).
Fig 2. Excitation patterns and dynamics in a 1D array of coupled FHN units without DGF.
The pacing period T = 45 and system size L = 128. a. An example of Con-P2 patterns and the corresponding global signal . b. An example of Dis-P2 patterns with a different initial condition from panel a, and the corresponding . c. Percentage of Dis-P2 patterns versus the standard deviation (σini of the random initial conditions. . We performed 100 trials for each σini value in the plot. d. Histogram of domain size l (segment between two neighboring nodes, as indicated in panel b) from 2000 trials of random initial conditions with δ = 0.15. For each trial, 2000 beats were applied for the system to reach a steady state. The domain size was measured using the last two beats. e. Histogram of global P2 amplitude , (difference between the peak values of two consecutive beats, as indicated in panel a) for the simulations in d. was measured using the last two beats.
Effects of DGF on pattern selection and stability
To investigate the effects of DGF on the spatiotemporal pattern dynamics, we carried out simulations by scanning the pacing period T and DGF strength α (Fig 3A). There are four distinct regions: uniform P1 pattern (yellow), Con-P2 pattern only (cyan), Dis-P2 pattern only (black), and both concordant and discordant P2 (Con/Dis-P2) patterns (red). The blue curve is the stability boundary between P1 and P2 for an uncoupled FHN unit. For α<0, only uniform P1 and Con-P2 patterns were observed, independent of initial conditions. The uniform P1 and Con-P2 patterns are separated by the stability boundary (blue line) of the uncoupled FHN unit, indicating that the dynamics in the 1D array is the same as in the uncoupled FHN unit. For α>0, a transition from uniform P1 to Dis-P2 occurs as T decreases (from yellow to black), which is caused by a spatial-mode instability of the uniform P1 state. As T decreases further (red region), both Con-P2 and Dis-P2 patterns can occur depending on the initial conditions (Fig 3B).
Fig 3. Excitation patterns and dynamics in a 1D array of coupled FHN units with DGF.
a. Phase diagram of excitation dynamics. The blue line is the bifurcation boundary from P1 to P2 in an uncoupled unit with DGF. Color dots mark the different behaviors in the 1D array: yellow—uniform P1; black—Dis-P2; cyan—Con-P2; and red—Con/Dis-P2. b. A Dis-P2 pattern (upper) and a Con = P2 pattern (lower) for α = 0.2 and T = 45 obtained with two different initial conditions. c. Left, histogram of domain size l from 2000 trials. α = 0.4 and T = 45.5. The random initial conditions were set the same way as described in Fig 2 legend with δ = 3. For each trial, 2000 beats were applied for the system to reach a steady state. Right, corresponding histogram of global P2 amplitude from the same simulations. d. Same as panel c but for α = 0.2, T = 45, and δ = 0.09.
Furthermore, we performed the same statistical analysis as in the case of no DGF (Fig 2D and 2E) for different regions of the phase diagram in Fig 3A. In the Dis-P2 only region (Fig 3C), the domain sizes distribute between 0 to L/2 (more accurately, the domain size can be L/2 and any value between lmin and L/2-lmin), but remains zero for all patterns. In the Con/Dis-P2 region (Fig 3D), the distributions are similar to those in Fig 3C except for the existence of the Con-P2 pattern. Similar to the case of no DGF (α = 0), the domain size distributions are continuous, indicating that the Dis-P2 patterns are spatially random (including the periodic ones) and depend on initial conditions. However, differing from the case of no DGF, the global signals of the Dis-P2 patterns are always P1 solutions i.e., (Fig 3C and 3D). Moreover, the maximum domain size of Dis-P2 patterns is L/2. This is because if there is a domain greater than L/2, the sum of all other domains must be smaller than L/2, and thus when the patterns reverse in the next beat, the global signal cannot be the same, violating the requirement of a global P1 solution.
Therefore, in the absence of DGF (α = 0), both Con-P2 and Dis-P2 patterns can occur, and the Dis-P2 patterns are spatially random. In the presence of DGF, only Con-P2 patterns can exist when the DGF is negative (α<0). When the DGF is positive (α>0), both Con-P2 and Dis-P2 patterns can exist depending on the pacing period T and initial conditions. The Dis-P2 patterns are also spatially random but satisfy that the global signals are always P1 solutions.
Ca2+ release patterns in a physiologically detailed ventricular myocyte model
To validate the spatiotemporal dynamics in a realistic biological system, we carried out simulations in a physiologically detailed 3D ventricular myocyte model (see Methods), which can well capture the spatiotemporal Ca2+ dynamics widely observed in experiments [29, 43–45]. The model undergoes a bifurcation from P1 to P2 (alternans) as the pacing period T decreases (S2 Fig). We investigated the subcellular Ca2+ release patterns under both AP clamp and free-running conditions (see S1 Text). Under AP clamp, the voltage is no longer described by the differential equation but a pre-set function of time with a period T (see S3 Fig for the waveform used in this study). Under this condition, Ca2+ is decoupled with voltage, and therefore, there is no DGF. Under the free-running condition, the cell is stimulated by a current pulse (0.5 ms duration and -80 μA/μF amplitude, see Methods), and voltage is a free running signal. Under this condition, Ca2+ and voltage are coupled, and therefore, DGF is present due to Ca2+ and voltage coupling (as indicated in Fig 1B and 1C). The DGF properties can be changed by altering the ionic currents, as will be detailed below.
Ca2+ release patterns under AP clamp
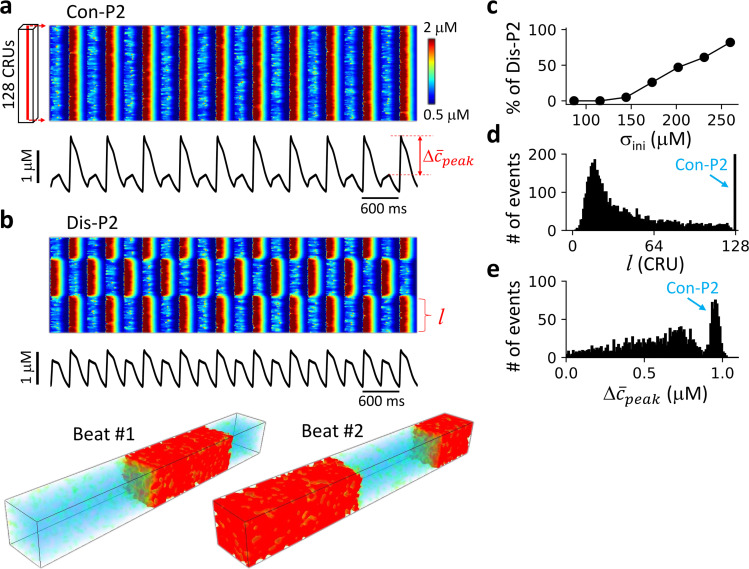
Under AP clamp, Ca2+ is decoupled with voltage and thus no DGF. We used spatially random initial conditions to induce Dis-P2 patterns (see Fig 4 legend for the details of the random initial conditions). In the alternans regime (e.g., T = 300 ms), both Con-P2 (Fig 4A) and Dis-P2 (Fig 4B) patterns occur in the cell depending on initial conditions. The probability of forming a Dis-P2 pattern increases as the spatial heterogeneity of initial conditions increases (Fig 4C). The Dis-P2 patterns are spatially random as indicated by the histograms of domain size (Fig 4D) and whole-cell alternans amplitude (Fig 4E). These behaviors are the same as those for the model of coupled FHN units without DGF (Fig 2), albeit some smearing in the histograms due to ion channel stochasticity (see Methods).
Fig 4. Ca2+ release patterns and dynamics in the 3D ventricular myocyte model under AP clamp.
a. Upper panel shows a linescan (time-space plot) of cytosolic Ca2+ concentration showing a Con-P2 pattern. Lower panel shows the corresponding whole-cell Ca2+ transient. The recording line was in the center of the cell as indicated on the left. b. Same as panel a. with a different random initial condition resulting in a Dis-P2 pattern. The middle panel is the corresponding whole-cell Ca2+ transient. The bottom panels are 3D views of Ca2+ from two consecutive beats. c. Percentage of Dis-P2 patterns versus the standard deviation (σini)of initial SR Ca2+ load. The random spatial distribution of the SR Ca2+ load was set as CaSR(j) = Ca0+ΔCaSR∙ξ(j)·(j = 1,2,…,L) with ξ(j) being a uniform random number in [–1,1]. . We set Ca0 = 500 μM. We performed 100 trials for each σini value in the plot. d. Histogram of domain size l (as marked in panel b) with ΔCaSR = 450 μM. e. Histogram of global P2 amplitude (as marked in panel a) from the same simulations in panel d. For panel d and e, 2000 trials were performed. For each trial, the cell was paced 2000 beats to reach a steady state. The domain size was computed using the last 50 beats to account for beat-to-beat variation (see SI for details) due to the intrinsic noise of ion channel stochasticity. was measured using the last two beats. The pacing period T = 300 ms.
Ca2+ release pattern dynamics with positive and negative Ca2+-to-APD coupling
Under free running, however, Ca2+ is coupled with voltage, and changing Ca2+ may change APD. If increasing the Ca2+ transient amplitude results in a longer APD in the same beat, then it is called positive Ca2+-to-APD coupling, and the opposite is called negative Ca2+-to-APD coupling [46, 47]. As shown in previous studies [46, 48, 49], the coupling properties can be altered by altering the properties of ICa and the Na+-Ca2+ exchange current (INCX). However, since ICa and INCX also directly affect the Ca2+ dynamics, it becomes difficult to only change the Ca2+-to-APD coupling without affecting the Ca2+ dynamics. To avoid this complexity, we added two new currents to the ventricular model: the non-specific Ca2+-activated cation current (InsCa) and the small conductance Ca2+-activated potassium current (ISK). InsCa is mainly an inward current [50] and increases as the intracellular Ca2+ concentration increases. Therefore, increasing the conductance of InsCa increases APD and promotes positive Ca2+-to-APD coupling. InsCa is small under normal conditions but becomes large under conditions of Ca2+ overload [50]. ISK is an outward current which also increases with the intracellular Ca2+ concentration, and thus ISK promotes negative Ca2+-to-APD coupling. Under normal conditions, ISK only presents in atrial myocytes, but under heart failure, it also presents in ventricular myocytes [51–53]. Since the charge carriers of both currents are not Ca2+, unlike ICa and INCX, they do not directly affect intracellular Ca2+ dynamics. Here we altered the maximum conductance of these two currents to alter the Ca2+-to-APD coupling properties. Note that DGF is not explicitly present in the model but indirectly via the Ca2+-to-APD coupling, as we explained in Introduction. We first investigated the effects of Ca2+-to-APD coupling properties on Ca2+ release patterns and then linked them to DGF.
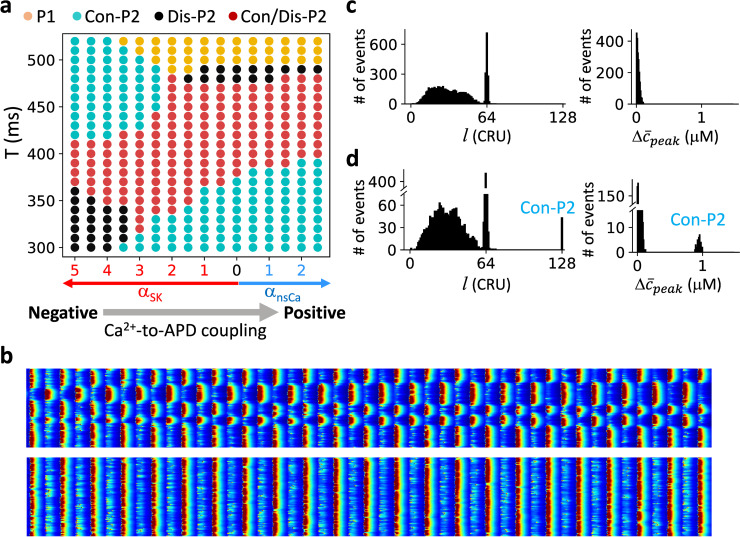
We systematically explored the spatiotemporal dynamics by altering the pacing period T and the maximum conductance of the two currents, as summarized in Fig 5A. We used the same spatially random initial conditions as in Fig 4 for the simulations. Note that due to dynamical instabilities and intrinsic noise of the sarcolemmal Ca2+ channels and Ca2+ release channels (see Methods), heterogeneous initial conditions are not needed for the formation of the Dis-P2 patterns in the Dis-P2 only region. When the Ca2+-to-APD coupling is negative (large ISK), a transition from uniform P1 to Con-P2 patterns occurs as T decreases, and this transition occurs at a larger T value as the maximum ISK conductance increases. When the coupling is positive (large InsCa), a transition from uniform P1 to Dis-P2 patterns (yellow to black) occurs as T decreases. Under both coupling conditions, as T decreases further, the system enters the Con/Dis-P2 regime (red), in which both Con-P2 and Dis-P2 patterns can occur depending on initial conditions (Fig 5B). However, as T decreases even further, the Con/Dis-P2 regime switches into a Dis-P2 only regime when the Ca2+-to-APD coupling is negative (large ISK) and into a Con-P2 only region when the Ca2+-to-APD coupling is positive (large InsCa). Therefore, for the same Ca2+-to-APD coupling, as T decreases, the spatiotemporal patterns change from Con-P2 only to Dis-P2 only through a Con/Dis-P2 region or in reverse order depending on the coupling properties.
Fig 5. Ca2+ release pattern dynamics in the ventricular myocyte model with positive and negative Ca2+-to-APD coupling.
a. Phase diagram of Ca2+ release dynamics versus pacing period and Ca2+-to-APD coupling properties. In this diagram, the x-axis is the fold increase of either InsCa (blue arrow) or ISK (red arrow), and the y-axis is the pacing period T. Gray arrow indicates the change from negative to positive Ca2+-to-APD coupling. Same color codes of the pattern dynamics as in Fig 3A were used. b. A Dis-P2 pattern (upper) and a Con = P2 pattern (lower) for αSK = 3.5 and T = 350 ms obtained with two different initial conditions. c. Left: Histogram of domain size l. The pacing period T = 330 ms, αSK = 4.5, The random initial conditions were set the same way as in Fig 4 with ΔCaSR = 500 μM. Two thousand trials were performed. For each trial, the cell was paced 2000 beats to reach a steady state. The domain size was computed using the last 50 beats. Right: Histogram of global P2 amplitude from the same simulations. was measured using the last two beats. d. Same as panel c but T = 350 ms and αSK = 3.5.
To reveal the statistical properties of the Dis-P2 patterns, we show the histograms of domain sizes and the whole-cell alternans amplitude for a parameter point in the Dis-P2 region (Fig 5C) and a point in the Con/Dis-P2 region (Fig 5D). The domain size distributions for Dis-P2 patterns are continuous, and the whole-cell alternans amplitudes always remain zero, indicating that the patterns are spatially random but always satisfy that the global signals are P1 solutions. These behaviors are the same as in the model of a coupled array of FHN units (Fig 3).
Linking the Ca2+-to-APD coupling properties to DGF
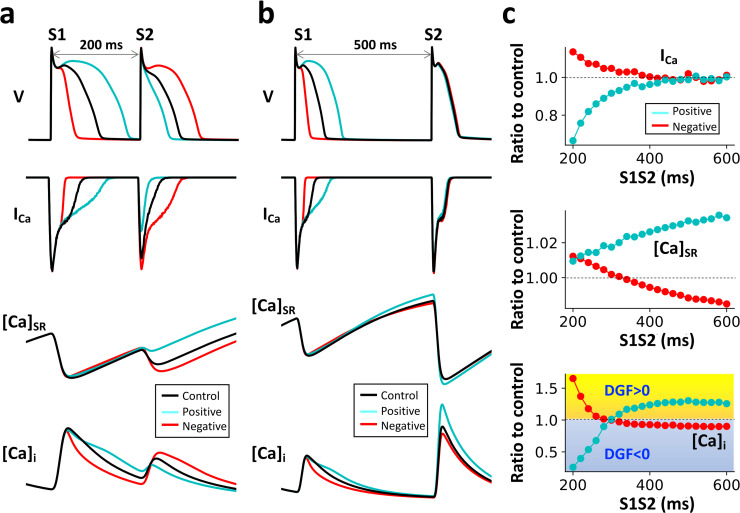
As shown above, the Ca2+ dynamics in the detailed ventricular myocyte model agree well with those of the generic FHN array with DGF. To link the spatiotemporal Ca2+ dynamics to the DGF properties, we performed a quantitative analysis to reveal the DGF properties and their relationship with the Ca2+-to-APD coupling properties. We carried out simulations of the ventricular cell model using an S1S2 protocol. In this protocol, a train of external stimuli (S1) was given at a fixed period (T = 300 ms) for the cell to reach the steady state, and a stimulus (S2) was then applied after a variable interval (denoted as S1S2 interval) from the last S1 beat. We measured the peak values of ICa, SR Ca2+ and cytosolic Ca2+ on the S2 beat, which were considered as control. Next, we repeated the same simulations except that on the last S1 beat, we increased αSK to shorten the APD (Fig 6A, red) or increased αnsCa to lengthen the APD (Fig 6A, cyan). This method enhanced the negative (increased αSK) or the positive (increased αnsCa) Ca2+-to-APD coupling from the control case. In Fig 6C, we plot the ratios of the peak values of ICa, SR Ca2+ and cytosolic Ca2+ of the two coupling cases to the control values on the S2 beat.
Fig 6. Relationship between the Ca2+-to-APD coupling properties and DGF.
a. Time traces of voltage, ICa, SR Ca2+, and cytosolic Ca2+ for control (black), enhanced positive coupling in the S1 beat (cyan) and enhanced negative coupling in the S1 beat (red). S1S2 = 200 ms. b. Same as in a. but S1S2 = 500 ms. c. Ratios of ICa peak, SR Ca2+ load, and [Ca2+]i peak on the S2 beat under positive (cyan) or negative (red) coupling conditions to the corresponding quantities at control v.s. S1S2 interval. Here, αnsCa = 0 for all the cases. In the S1 beat, αSK is 5, 0, and 30 for control, enhanced positive, and enhanced negative cases, respectively. In the S2 beat, αSK is 5 for all the cases.
For short S1S2 intervals (e.g., S1S2 = 200 ms, Fig 6A), the enhanced positive Ca2+-to-APD coupling case (cyan) results in a smaller ICa (ratio <1, see Fig 6C, top panel) and almost unchanged SR load compared to those of the control case on the S2 beat. The reason is that the longer APD caused by the positive Ca2+-to-APD coupling results in a shorter DI and thus less recovery of ICa. The net effect is to result in a smaller Ca2+ transient (ratio < 1, see Fig 6C, bottom panel) than that of the control case because of a smaller ICa. This indicates that the global feedback results in a negative gain on the Ca2+ signal on the next beat, i.e., the DGF is negative. For the negative Ca2+-to-APD coupling case (Fig 6A, red), the consequences are reversed, resulting in a positive DGF (Fig 6C, bottom panel). These results suggest that for short S1S2 intervals, the DGF properties are primarily determined by the recovery property of ICa.
For long S1S2 intervals (e.g., S1S2 = 500 ms, Fig 6B), the Ca2+-to-APD coupling properties have negligible effects on ICa (both ratios are ~1, see Fig 6C, top panel) since ICa fully recovers due to a long DI. However, the SR Ca2+ load is lower (ratio<1) for the negative Ca2+-to-APD coupling and higher (ratio>1) for the positive Ca2+-to-APD coupling (Fig 6C, middle panel). Therefore, for the negative Ca2+-to-APD coupling case, the feedback results in a smaller Ca2+ in the next beat because of a lower SR Ca2+ load, i.e., the DGF is negative. For the positive Ca2+-to-APD coupling case, the DGF is positive. These results suggest that for long S1S2 intervals, the DGF properties are primarily determined by the SR Ca2+ load.
Therefore, for short S1S2 intervals (<300 ms), positive or negative Ca2+-to-APD coupling leads to negative or positive DGF, respectively, primarily mediated by ICa recovery. For long S1S2 intervals (>300 ms), the relationships are reversed, i.e., positive or negative Ca2+-to-APD coupling leads to positive or negative DGF, respectively. The DGF is primarily mediated by SR Ca2+ load since with long S1S2 intervals the Ca2+-to-APD coupling properties show almost no effects on ICa due to full recovery. Knowing the relationships between Ca2+-to-APD coupling properties and the DGF properties, one can then link the DGF properties to the Ca2+ release patterns in the ventricular cell model. Based on the analysis above and the Ca2+ release patterns shown in Fig 5A, we can link the Ca2+ release patterns to the sign of DGF, which is summarized in Table 1. It shows that negative DGF leads to Con-P2 patterns, while positive DGF leads to Dis-P2 patterns. Note that we were not able to quantitatively distinguish the boundaries between positive and negative DGF in the phase diagram (Fig 5A) using this analysis, but it is likely that in the Con/Dis-P2 region, the DGF is also positive. Therefore, we can obtain the same conclusion as that from the generic FHN model.
Table 1. Links between Ca2+-to-APD coupling, Ca2+ release patterns, and DGF for the detailed ventricular cell model.
The sign in parenthesis is the sign of DGF.
| Negative Ca2+-to-APD coupling | Positive Ca2+-to-APD coupling | |
|---|---|---|
| Slow pacing | Con-P2, DGF (-) | Dis-P2, DGF (+) |
| Fast pacing | Dis-P2, DGF (+) | Con-P2, DGF (-) |
Theoretical insights from a CML model
To reveal analytically the instabilities and bifurcations leading to the spatiotemporal dynamics, we used a CML model to describe the system. CML, as a generic model for investigating spatiotemporal dynamics of nonlinear systems, has been widely used [54, 55]. In a previous study [56], we developed a CML model to investigate the spatiotemporal APD dynamics in cardiac tissue. Here we modified the 1D array CML model by adding a DGF term. The governing equation is,
| (4) |
where n is the temporal index and j the spatial index. cn(j) describes the peak signal in the jth lattice of the nth beat. f is the map function: , in which γ and μ determine the midpoint and the slope of the curve, respectively. M is the coupling length, and wm is the coupling strength described by a Gaussian function: in which Nw is the normalization constant. is the spatial average of cn−1(j), and satisfying cs = f(cs). We set μ = 0.1, M = 15, and σ = 3. Note that concrete forms of map functions for investigating intracellular Ca2+ dynamics were developed previously [47, 57]. However, for the sake of simplicity and generality, we chose a simple function f, which can give rise to a bifurcation from P1 to P2, similar to those of the FHN model and the detailed ventricular myocyte model (see S2 Fig).
Note that in Eq 4, instead of using a linear feedback term: , we used a nonlinear term with the map function f, i.e., , to maintain the convergence of iteration. The negative sign was used because f is a decreasing function (f′<0). Linearization of this nonlinear term around the uniform steady-state gives rise to a term proportional to , and thus α>0 corresponds to positive feedback, the same as in the FHN model.
1) Stability of an uncoupled unit. For an uncoupled unit, the map equation with DGF becomes
| (5) |
The stability of the steady-state solution is determined by the eigenvalue,
| (6) |
where is independent of α since the steady state is independent of α. Eq 6 indicates that α<0 destabilizes the steady state, and α>0 stabilizes the steady state. The stability boundary is shown as the dashed line in Fig 7A.
Fig 7. Bifurcations and spatiotemporal dynamics in the CML model.
a. Phase diagram in the α-γ space showing stability boundaries and spatiotemporal dynamics of the CML model. The same color codes as in Fig 3A and Fig 5A were used. The solid line is the stability boundary of uniform P1 determined by Eq 7. The dashed line is the stability boundary of P1 in an uncoupled unit determined by Eq 6. The dash-dot line is the stability boundary of Con-P2 determined by Eq 8. The vertical dotted line is the stability boundary of Dis-P2 determined by numerical simulations of the CML model. Inset is the blowup of the marked region, showing that all the stability boundaries meet at a common point. b. Histograms of domain size at different locations in the phase diagram marked by numbers. The coordinates (α, γ) from location 1 to 3 are: (0, 0.7), (0.3, 0.7), and (0.55, 0.7). c. Sample spatiotemporal patterns (top) and the corresponding global signals (bottom) from different regions of the phase diagram. Number ranges above each pattern indicate the locations in the phase diagram where the specific pattern can be seen.
2) Stability of the spatially uniform P1 state. The spatially uniform P1 state (see Stability analyses of the CML model in SI) is determined by the eigenvalues:
| (7) |
in which k is the wave number of the Fourier mode (λk vs. k for different α values are shown in S4 Fig). The spatially uniform P1 state is stable when |λk|<1 for any k. The stability of the 0-mode is the same as that of an uncoupled unit. Since λk for k>0 in Eq 7 does not depend on α, then the feedback has no effects on the stability of the uniform P1 state for non-zero mode. Because of this, the stability boundary separating uniform P1 from Dis-P2 appears to be a horizontal line independent of α (Fig 7A, solid).
3) Stability of the Con-P2 state. Following the same procedure as for the uniform P1 state, we obtained the eigenvalues for the spatially uniform P2 state as
| (8) |
where and are the two derivatives of f at the P2 solution of Eq 5. Since the P2 solution depends on α, and are functions of α. Therefore, the stability boundary also depends on α (Fig 7A, dashed-dotted).
4) Stability of the Dis-P2 states. The stability of the Dis-P2 states cannot be analytically obtained. We used numerical simulations of the CML model (Eq 4) to determine the stability boundary (Fig 7A, dotted). No stable Dis-P2 patterns were obtained on the left side of the dotted line.
Spatiotemporal dynamics via numerical simulations of the CML model are also shown in Fig 7A, which are colored the same way as in Fig 3A and Fig 5A. The Dis-P2 only region exists between the uniform P1 stability boundary (solid line) and the Con-P2 stability boundary (dash-dotted line). The Con/Dis-P2 region exists between the Con-P2 stability boundary (dashed-dotted line) and the Dis-P2 stability boundary (dotted line). The Con-P2 only region exists between the uniform P1 stability boundary (dashed line) and the Dis-P2 stability boundary (dotted line). Note that the dotted line is almost identical to α = 0 except at the vicinity where all phases meet (inset in Fig 7A), indicating that stable Dis-P2 patterns can only exist when α>0. Histograms of domain size and example spatial patterns from three locations marked in Fig 7A are plotted (Fig 7B and 7C). The structure of the phase diagram and the statistical properties of the spatial patterns of the CML model match well with those of the generic FHN model and the ventricular myocyte model.
Discussion
We investigated the roles of DGF in the genesis, selection, and stability of spatiotemporal patterns in periodically-paced excitable media. We used three models with different complexities, which allowed us to perform both numerical simulations and rigorous analytical treatments. The dynamical behaviors are well conserved in the three types of models, and the CML model reveals the dynamical mechanisms. Our major findings are as follows:
In the absence of DGF, both Con-P2 and Dis-P2 can occur depending on the pacing period and initial conditions. The Dis-P2 patterns are spatially random, determined by the initial conditions. The global signal (the spatial average) is a temporal P2 solution (alternans) with the alternans amplitude being randomly distributed between zero and the maximum amplitude (Con-P2).
In the presence of DGF, the pattern dynamics are determined by the sign of the DGF. When the DGF is negative, only Con-P2 patterns can exist, no spatial mode instabilities emerge, and all the Dis-P2 solutions are unstable. When the DGF is positive, both Con-P2 and Dis-P2 patterns can occur, depending on the pacing period and initial conditions. The Dis-P2 patterns are also spatially random but must satisfy that the global signals are temporal P1 solutions (no temporal alternans).
Bifurcation analyses of the CML model reveal the spatial-mode instabilities leading to the spatiotemporal patterns.
By linking the Ca2+-to-APD coupling properties to the DGF properties, we have shown that the spatiotemporal pattern dynamics of Ca2+ release in cardiac myocytes agree very well with the findings in the simple models, validating the theoretical predictions in a realistic system.
Therefore, our simulations and theoretical analyses reveal the underlying dynamical mechanisms and roles of DGF in the genesis, selection, and stability of spatiotemporal patterns in periodically-paced excitable media. The uniqueness of the conclusions drawn from the three types of models implies that the insights obtained in this study may apply to many excitable as well as oscillatory biological media. Here we discuss two examples below.
A unified theory for subcellular Ca2+ alternans dynamics in cardiac myocytes
At the subcellular level, both Con-P2 and Dis-P2 Ca2+ release patterns (spatially concordant and discordant alternans) have been observed experimentally [31–33, 58, 59], but the underlying mechanisms remain incompletely understood. As shown in this study, the subcellular Ca2+ alternans dynamic of the ventricular myocyte model agree well with those of the simplified models, indicating that the generic mechanisms of pattern formation and selection are also applicable to Ca2+ alternans dynamics in cardiac myocytes. Both spatially concordant and discordant Ca2+ alternans (Con-P2 and Dis-P2 patterns) have been observed experimentally in cardiac myocyte [31–33, 59]. Shiferaw and Karma [60] developed a theory showing that a Turing instability caused by negative Ca2+-to-APD coupling is responsible for the formation of Dis-P2 patterns. A direct experimental demonstration of this theory was carried out by Gaeta et al. [33], who developed a method that could change the sign of Ca2+-to-APD coupling. However, Dis-P2 patterns have also been observed experimentally under voltage-clamp [32, 59] and free-running conditions without showing negative coupling [61]. Furthermore, previous simulation studies [44, 48] and this study have also shown that Con-P2 patterns can occur under negative Ca2+-to-APD coupling, and Dis-P2 patterns can occur under positive Ca2+-to-APD coupling and voltage-clamp conditions. These complex Ca2+ release behaviors cannot be well explained by the Turing instability mechanism alone. On the other hand, our study unifies the complex subcellular Ca2+ alternans dynamics under a single theoretical framework of DGF, providing a general mechanistic understanding of the subcellular Ca2+ alternans dynamics.
Previous studies [33, 48, 60] showed that the sign of Ca2+-to-APD coupling determines the occurrence of subcellular discordant Ca2+ alternans. One can achieve this by properly tuning the relative contributions of ICa and INCX [48, 49, 60]. Here we show that changing the maximum conductance ISK or InsCa provides a more straightforward way of changing the coupling properties. Gaeta et al. [33] used a feedback control method to alter the coupling relationship and demonstrated in both simulations and experiments that the sign of the coupling controls the transitions between concordant and discordant Ca2+ alternans. However, our study shows that altering the Ca2+-to-APD coupling properties does not guarantee that one can control the transition between concordant and discordant Ca2+ alternans. The unique dynamical factor controlling the transition between concordant and discordant Ca2+ alternans is the sign of DGF, which is not uniquely determined by the sign of Ca2+-to-APD coupling. This is because Ca2+-to-APD coupling affects the recovery of ICa and SR Ca2+ loading which contribute oppositely to DGF.
Applications to tissue-scale dynamics of excitable biological media
Cardiac and neural tissue are typical excitable media. In cardiac tissue, spatially concordant and discordant APD alternans have been widely observed in experiments [37, 62–64], and mechanisms have been revealed in mathematical modeling and theoretical studies [38, 65, 66]. However, in the real heart, electrical excitations cause mechanical contraction, and the contraction and stretch of the heart cells may result in the opening of the mechano-sensitive ion channels or alteration of intracellular Ca2+ cycling properties, a phenomenon called mechano-electric feedback [34–36]. Since contraction is a mechanical response of cardiac tissue, which is nearly a global signal, it is possible that the mechano-electric feedback can serve as global feedback or a DGF to affect the discordant APD alternans dynamics. This needs to be investigated in future studies using models with mechano-electric feedback [67–69].
In neural tissue, cluster firing and other firing patterns have been widely observed [70–73]. The role of delayed feedback or DGF in the formation of firing patterns has been investigated in computer models [39–41]. In a simulation study by Golomb and Rinzel [42], the authors showed similar Dis-P2 patterns of firing as the discordant patterns shown in our present study. We believe that the theoretical insights from our simple FHN model or the CML model will help shed light on the formation of the firing patterns.
Links to pattern dynamics in oscillatory media with DGF
Our study focused on the roles of DGF in pattern formation and stability in periodically-paced excitable media. In a previous study in oscillatory chemical reaction experiments, Kim et al. [17] showed DGF caused clustering patterns similar to the Dis-P2 patterns in this study. Their observations were also demonstrated in computer simulations [19]. Since, in their studies, the DGF is an externally controlled signal, the delay time is a variable parameter. However, the DGF is intrinsic in the excitable biological media we investigated, and the delay time is simply the excitation period. Because of this, we can represent the system with a CML model that is able to capture the dynamics and the underlying bifurcations accurately. Since an excitable medium can become an oscillatory medium, the theories from our study may provide mechanistic insights into pattern dynamics of oscillatory media, such as the cluster patterning in the chemical reactions [14–19] or neural tissue [42].
Methods
The present study involved three mathematical models at different levels of complexity. The model of a coupled array of FHN units and the 1D CML model are described in the Result section. A brief summary of the 3D ventricular cell model and numerical methods is given below.
The 3D ventricular cell model
The ventricular cell model has been described in detail in our previous studies [44, 45], similar to other previous models [74–78]. Here we give a brief description of the model. The 3D cell model consists of 128×16×16 CRUs. Each CRU includes five sub-compartments: bulk cytosol, submembrane, dyad, junctional SR and network SR. The volumes of these sub-compartments are based on experimental data. The Ca2+ within a CRU cycles through these sub-compartments via diffusion, buffering/unbuffering, SR release and SERCA pump. The flow of Ca2+ between CRUs is via diffusion in the cytosol, submembrane and network SR. The exchange of Ca2+ between intracellular and extracellular space is regulated by ICa and Na+-Ca2+ exchanger (NCX). The model is described by differential equations that are coupled via Ca2+ and voltage. The closing and opening of L-type Ca2+ channels and the ryanodine receptors are simulated using stochastic Markov transitions. Therefore, intrinsic spatiotemporal noise exists in the model.
We added two new currents, InsCa and ISK, to the model for altering Ca2+-to-APD coupling. The InsCa formulation was adopted from the 1994 Luo and Rudy model [50] with the following parameter changes: Pns(Ca) = 3.5×10−5 cm/s and Km,ns(Ca) = 1.5 μM. ISK was formulated based on Komendantov et al. [79] as follows:
| (9) |
where GSK = 0.005 mS/F and Kd = 0.6 μM.
The differential equation for voltage is then
| (10) |
where Cm = 1 μF/cm2 is the membrane capacitance. αnsCa and αSK are the parameters controlling the maximum conductance of InsCa and ISK, respectively. Isti is the stimulus current density which is a square pulse with the amplitude -80 μA/μF and the duration 0.5 ms.
Computer simulations and algorithms
Both the model of a coupled array of FHN units and the CML model were programmed with Python 3, and the corresponding simulations were carried out on our cluster with 24 Intel Xeon CPUs. The 3D ventricular cell model was programmed with CUDA C++, and the corresponding simulations were carried out on Nvidia Tesla K20c, K80, and GTX 1080 Ti GPU cards. The detailed algorithms for detecting spatiotemporal excitation patterns in this study are described in the S1 Text and S5 Fig.
Supporting information
The online supporting information includes: A. AP clamp and free running protocols. B. Stability analysis of the CML model. C. Automatic detection algorithms for spatiotemporal excitation patterns. D. Boundary between discordant P2 and uniform P2 in the CML model.
(DOCX)
a). Data from Roome et al.[1] showing a spatiotemporal map of spontaneous dendritic voltage signal obtained from 5 s of linescan recording. Filled triangles indicate dendritic complex spikes (DCS). Subthreshold dendritic voltage modulation is also visible in the spatiotemporal voltage map. Red trace shows spatially averaged voltage, recorded at 2 kHz resolution. Corresponding spatiotemporal map for dendritic Ca2+ is also recorded. Green trace shows spatially averaged Ca2+. b). Data from Diaz et al.[2] showing spatiotemporal Ca2+ signals under control and ryanodine receptor blocker tetracaine with a voltage clamp protocol. Linescan recordings reveal out-of-phase spatial patterns of intracellular Ca2+ transient from beat to beat. Bottom two traces show fluorescence measured as a function of time at the regions indicated by arrows (i and ii).
(EPS)
a). Bifurcation diagram showing c vs. T for the single-element FHN model. b). Bifurcation diagram showing the peak values of the whole-cell average Ca2+ transient, vs. T for the detailed ventricular myocyte model. c). Bifurcation diagram showing c vs. γ for the single-element CML model.
(EPS)
The voltage trace is the last action potential recorded in the simulation of the physiologically detailed myocyte model. The model was paced for 100 beats to reach the steady state at the pacing period T = 450 ms. This voltage trace was used in the AP clamp simulations.
(EPS)
λk vs. k for α = 0.2 (black), 0 (red) and -0.2 (blue) are numerically computed based on Eq 7 in the main text. γ = 1.057, which is the bifurcation point in S2C Fig.
(EPS)
a). Top shows an example of discordant P2 patterns for the 1D FHN model. Bottom shows the relationship of Δcn+1(j) vs. j where the domain size l determined by the pattern recognition algorithm is marked by the double-arrow red line. b). Same as a), but for the 1D CML model. c). Same as a), but for the detailed myocyte model. Note that the gray and black traces are for m = 1 and 50 in S10 Eq, respectively. We used m = 50 to extract the domain size for the detailed myocyte model in our study.
(EPS)
Data Availability
All relevant data are within the manuscript and its Supporting Information files.
Funding Statement
Z.Q. received the grant from National Institutes of Health R01 HL134709 and R01 HL133294 (https://www.nih.gov/grants-funding). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Wolpert L. Pattern Formation in Biological Development. Sci Am. 1978;239(4):154–65. 10.1038/scientificamerican1078-154 [DOI] [PubMed] [Google Scholar]
- 2.Pourquié O. Vertebrate Segmentation: From Cyclic Gene Networks to Scoliosis. Cell. 2011;145(5):650–63. 10.1016/j.cell.2011.05.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kefi S, Rietkerk M, Alados CL, Pueyo Y, Papanastasis VP, Elaich A, et al. Spatial vegetation patterns and imminent desertification in Mediterranean arid ecosystems. Nature. 2007;449(7159):213–7. Epub 2007/09/14. 10.1038/nature06111 . [DOI] [PubMed] [Google Scholar]
- 4.Garfinkel A, Tintut Y, Petrasek D, Bostrom K, Demer LL. Pattern formation by vascular mesenchymal cells. Proc Natl Acad Sci U S A. 2004;101(25):9247–50. 10.1073/pnas.0308436101 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Meinhardt H, Gierer A. Pattern formation by local self-activation and lateral inhibition. BioEssays. 2000;22(8):753–60. . [DOI] [PubMed] [Google Scholar]
- 6.Kondo S, Miura T. Reaction-diffusion model as a framework for understanding biological pattern formation. Science. 2010;329(5999):1616–20. 10.1126/science.1179047 . [DOI] [PubMed] [Google Scholar]
- 7.Gomez C, Ozbudak EM, Wunderlich J, Baumann D, Lewis J, Pourquie O. Control of segment number in vertebrate embryos. Nature. 2008;454(7202):335–9. 10.1038/nature07020 . [DOI] [PubMed] [Google Scholar]
- 8.Vasiev BN, Hogeweg P, Panfilov AV. Simulation of Dictyostelium Discoideum aggregation via reaction-diffusion model. Phys Rev Lett. 1994;73(23):3173–6. 10.1103/PhysRevLett.73.3173 [DOI] [PubMed] [Google Scholar]
- 9.Kerr RA, Levine H, Sejnowski TJ, Rappel W-J. Division accuracy in a stochastic model of Min oscillations in Escherichia coli. Proc Natl Acad Sci USA. 2006;103(2):347–52. 10.1073/pnas.0505825102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kohyama S, Yoshinaga N, Yanagisawa M, Fujiwara K, Doi N. Cell-sized confinement controls generation and stability of a protein wave for spatiotemporal regulation in cells. eLife. 2019;8:e44591 10.7554/eLife.44591 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ivanov V, Mizuuchi K. Multiple modes of interconverting dynamic pattern formation by bacterial cell division proteins. Proceedings of the National Academy of Sciences. 2010;107(18):8071–8. 10.1073/pnas.0911036107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Cheng X, Ferrell JE. Spontaneous emergence of cell-like organization in Xenopus egg extracts. Science. 2019;366(6465):631–7. 10.1126/science.aav7793 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tyson JJ, Chen KC, Novak B. Sniffers, buzzers, toggles and blinkers: dynamics of regulatory and signaling pathways in the cell. Curr Opin Cell Biol. 2003;15(2):221–31. 10.1016/s0955-0674(03)00017-6 . [DOI] [PubMed] [Google Scholar]
- 14.Falcke M, Engel H. Pattern formation during the CO oxidation on Pt(110) surfaces under global coupling. The Journal of Chemical Physics. 1994;101(7):6255–63. 10.1063/1.468379 [DOI] [Google Scholar]
- 15.Falcke M, Engel H, Neufeld M. Cluster formation, standing waves, and stripe patterns in oscillatory active media with local and global coupling. Phys Rev E. 1995;52(1):763–71. 10.1103/PhysRevE.52.763 [DOI] [PubMed] [Google Scholar]
- 16.Vanag VK, Yang L, Dolnik M, Zhabotinsky AM, Epstein IR. Oscillatory cluster patterns in a homogeneous chemical system with global feedback. Nature. 2000;406(6794):389–91. 10.1038/35019038 [DOI] [PubMed] [Google Scholar]
- 17.Kim M, Bertram M, Pollmann M, Oertzen Av, Mikhailov AS, Rotermund HH, et al. Controlling Chemical Turbulence by Global Delayed Feedback: Pattern Formation in Catalytic CO Oxidation on Pt(110). Science. 2001;292(5520):1357–60. 10.1126/science.1059478 [DOI] [PubMed] [Google Scholar]
- 18.Yang L, Dolnik M, Zhabotinsky AM, Epstein IR. Oscillatory clusters in a model of the photosensitive Belousov-Zhabotinsky reaction system with global feedback. Phys Rev E. 2000;62(5):6414–20. 10.1103/PhysRevE.62.6414 [DOI] [PubMed] [Google Scholar]
- 19.Bertram M, Mikhailov AS. Pattern formation in a surface chemical reaction with global delayed feedback. Phys Rev E. 2001;63(6):066102 10.1103/PhysRevE.63.066102 [DOI] [PubMed] [Google Scholar]
- 20.Berridge MJ, Lipp P, Bootman MD. The versatility and universality of calcium signalling. Nat Rev Mol Cell Biol. 2000;1(1):11–21. 10.1038/35036035 . [DOI] [PubMed] [Google Scholar]
- 21.Bers DM. Cardiac excitation-contraction coupling. Nature. 2002;415(6868):198–205. 10.1038/415198a [DOI] [PubMed] [Google Scholar]
- 22.Lechleiter J, Girard S, Peralta E, Clapham D. Spiral calcium wave propagation and annihilation in Xenopus laevis oocytes. Science. 1991;252(5002):123–6. 10.1126/science.2011747 . [DOI] [PubMed] [Google Scholar]
- 23.Cheng H, Lederer WJ. Calcium Sparks. Physiol Rev. 2008;88(4):1491–545. 10.1152/physrev.00030.2007 [DOI] [PubMed] [Google Scholar]
- 24.Falcke M. Reading the patterns in living cells—the physics of ca2+ signaling. Advances in Physics. 2004;53(3):255–440. 10.1080/00018730410001703159 [DOI] [Google Scholar]
- 25.Shuai JW, Jung P. Optimal ion channel clustering for intracellular calcium signaling. Proc Natl Acad Sci U S A. 2003;100(2):506–10. 10.1073/pnas.0236032100 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nivala M, Ko CY, Nivala M, Weiss JN, Qu Z. Criticality in intracellular calcium signaling in cardiac myocytes. Biophys J. 2012;102(11):2433–42. Epub 2012/06/21. S0006-3495(12)00520-6 [pii]. 10.1016/j.bpj.2012.05.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sobie EA, Dilly KW, dos Santos Cruz J, Lederer WJ, Jafri MS. Termination of cardiac Ca(2+) sparks: an investigative mathematical model of calcium-induced calcium release. Biophys J. 2002;83(1):59–78. 10.1016/s0006-3495(02)75149-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Stern MD, Rios E, Maltsev VA. Life and death of a cardiac calcium spark. J Gen Physiol. 2013;142(3):257–74. 10.1085/jgp.201311034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Song Z, Karma A, Weiss JN, Qu Z. Long-Lasting Sparks: Multi-Metastability and Release Competition in the Calcium Release Unit Network. PLoS Comput Biol. 2016;12(1):e1004671 10.1371/journal.pcbi.1004671 PubMed Central PMCID: PMC4701461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Roome CJ, Kuhn B. Simultaneous dendritic voltage and calcium imaging and somatic recording from Purkinje neurons in awake mice. Nature communications. 2018;9(1):3388 10.1038/s41467-018-05900-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kockskamper J, Blatter LA. Subcellular Ca2+ alternans represents a novel mechanism for the generation of arrhythmogenic Ca2+ waves in cat atrial myocytes. J Physiol. 2002;545(Pt 1):65–79. 10.1113/jphysiol.2002.025502 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Diaz ME, Eisner DA, O'Neill SC. Depressed ryanodine receptor activity increases variability and duration of the systolic Ca2+ transient in rat ventricular myocytes. Circ Res. 2002;91(7):585–93. 10.1161/01.res.0000035527.53514.c2 [DOI] [PubMed] [Google Scholar]
- 33.Gaeta SA, Bub G, Abbott GW, Christini DJ. Dynamical mechanism for subcellular alternans in cardiac myocytes. Circ Res. 2009;105(4):335–42. 10.1161/CIRCRESAHA.109.197590 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kohl P, Ravens U. Cardiac mechano-electric feedback: past, present, and prospect. Prog Biophys Mol Biol. 2003;82(1–3):3–9. 10.1016/s0079-6107(03)00022-1 . [DOI] [PubMed] [Google Scholar]
- 35.ter Keurs HE, Wakayama Y, Sugai Y, Price G, Kagaya Y, Boyden PA, et al. Role of sarcomere mechanics and Ca2+ overload in Ca2+ waves and arrhythmias in rat cardiac muscle. Ann N Y Acad Sci. 2006;1080:248–67. 10.1196/annals.1380.020 . [DOI] [PubMed] [Google Scholar]
- 36.Iribe G, Ward CW, Camelliti P, Bollensdorff C, Mason F, Burton RA, et al. Axial stretch of rat single ventricular cardiomyocytes causes an acute and transient increase in Ca2+ spark rate. Circ Res. 2009;104(6):787–95. 10.1161/CIRCRESAHA.108.193334 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Pastore JM, Girouard SD, Laurita KR, Akar FG, Rosenbaum DS. Mechanism linking T-wave alternans to the genesis of cardiac fibrillation. Circulation. 1999;99(10):1385–94. 10.1161/01.cir.99.10.1385 [DOI] [PubMed] [Google Scholar]
- 38.Qu Z, Garfinkel A, Chen PS, Weiss JN. Mechanisms of discordant alternans and induction of reentry in simulated cardiac tissue. Circulation. 2000;102(14):1664–70. 10.1161/01.cir.102.14.1664 [DOI] [PubMed] [Google Scholar]
- 39.Batista CAS, Lopes SR, Viana RL, Batista AM. Delayed feedback control of bursting synchronization in a scale-free neuronal network. Neural Networks. 2010;23(1):114–24. 10.1016/j.neunet.2009.08.005 [DOI] [PubMed] [Google Scholar]
- 40.Rusin CG, Johnson SE, Kapur J, Hudson JL. Engineering the synchronization of neuron action potentials using global time-delayed feedback stimulation. Phys Rev E. 2011;84(6):066202 10.1103/PhysRevE.84.066202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Huang S, Zhang J, Wang M, Hu C-K. Firing patterns transition and desynchronization induced by time delay in neural networks. Physica A: Statistical Mechanics and its Applications. 2018;499:88–97. 10.1016/j.physa.2018.01.039. [DOI] [Google Scholar]
- 42.Golomb D, Rinzel J. Clustering in globally coupled inhibitory neurons. Physica D: Nonlinear Phenomena. 1994;72(3):259–82. 10.1016/0167-2789(94)90214-3. [DOI] [Google Scholar]
- 43.Song Z, Ko C Y, Nivala M, Weiss James N, Qu Z. Calcium-Voltage Coupling in the Genesis of Early and Delayed Afterdepolarizations in Cardiac Myocytes. Biophys J. 2015;108(8):1908–21. PubMed Central PMCID: PMC4407256. 10.1016/j.bpj.2015.03.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Song Z, Liu MB, Qu Z. Transverse tubular network structures in the genesis of intracellular calcium alternans and triggered activity in cardiac cells. J Mol Cell Cardiol. 2018;114:288–99. 10.1016/j.yjmcc.2017.12.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Song Z, Qu Z, Karma A. Stochastic initiation and termination of calcium-mediated triggered activity in cardiac myocytes. Proceedings of the National Academy of Sciences. 2017;114(3):E270–E9. 10.1073/pnas.1614051114 PubMed Central PMCID: PMC5255629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Shiferaw Y, Sato D, Karma A. Coupled dynamics of voltage and calcium in paced cardiac cells. Phys Rev E. 2005;71(2 Pt 1):021903 10.1103/PhysRevE.71.021903 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Qu Z, Shiferaw Y, Weiss JN. Nonlinear dynamics of cardiac excitation-contraction coupling: an iterated map study. Phys Rev E. 2007;75(1 Pt 1):011927 . [DOI] [PubMed] [Google Scholar]
- 48.Restrepo JG, Karma A. Spatiotemporal intracellular calcium dynamics during cardiac alternans. Chaos. 2009;19(3):037115 10.1063/1.3207835 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wan X, Cutler M, Song Z, Karma A, Matsuda T, Baba A, et al. New experimental evidence for mechanism of arrhythmogenic membrane potential alternans based on balance of electrogenic INCX/ICa currents. Heart Rhythm. 2012;9(10):1698–705. 10.1016/j.hrthm.2012.06.031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Luo CH, Rudy Y. A dynamical model of the cardiac ventricular action potential: I. simulations of ionic currents and concentration changes. Circ Res. 1994;74(6):1071–96. 10.1161/01.res.74.6.1071 [DOI] [PubMed] [Google Scholar]
- 51.Tuteja D, Xu D, Timofeyev V, Lu L, Sharma D, Zhang Z, et al. Differential expression of small-conductance Ca2+-activated K+ channels SK1, SK2, and SK3 in mouse atrial and ventricular myocytes. American Journal of Physiology—Heart and Circulatory Physiology. 2005;289(6 58–6):H2714–H23. 10.1152/ajpheart.00534.2005 [DOI] [PubMed] [Google Scholar]
- 52.Chua SK, Chang PC, Maruyama M, Turker I, Shinohara T, Shen MJ, et al. Small-conductance calcium-activated potassium channel and recurrent ventricular fibrillation in failing rabbit ventricles. Circ Res. 2011;108(8):971–9. Epub 2011/02/26. CIRCRESAHA.110.238386 [pii]. 10.1161/CIRCRESAHA.110.238386 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Hamilton S, Polina I, Terentyeva R, Bronk P, Kim TY, Roder K, et al. PKA phosphorylation underlies functional recruitment of sarcolemmal SK2 channels in ventricular myocytes from hypertrophic hearts. The Journal of Physiology. 2019;0(0). 10.1113/jp277618 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Kaneko K. Overview of coupled map lattices. Chaos. 1992;2(3):279–82. 10.1063/1.165869 . [DOI] [PubMed] [Google Scholar]
- 55.Qu Z, Hu G, Ma B, Tian G. Spatiotemporally periodic patterns in symmetrically coupled map lattices. Phys Rev E. 1994;50(1):163–70. [DOI] [PubMed] [Google Scholar]
- 56.Wang S, Xie Y, Qu Z. Coupled iterated map models of action potential dynamics in a one-dimensional cable of coupled cardiac cells. New Journal of Physics. 2007;10:055001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Qu Z, Liu MB, Nivala M. A unified theory of calcium alternans in ventricular myocytes. Scientific reports. 2016;6:35625 10.1038/srep35625 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Karma A, Gilmour RF. Nonlinear dynamics of heart rhythm disorders. Physics Today. 2007;60(3):51–7. [Google Scholar]
- 59.Xie LH, Weiss JN. Arrhythmogenic consequences of intracellular calcium waves. Am J Physiol Heart Circ Physiol. 2009;297(3):H997–H1002. 10.1152/ajpheart.00390.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Shiferaw Y, Karma A. Turing instability mediated by voltage and calcium diffusion in paced cardiac cells. Proc Natl Acad Sci U S A. 2006;103(15):5670–5. 10.1073/pnas.0511061103 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Aistrup GL, Shiferaw Y, Kapur S, Kadish AH, Wasserstrom JA. Mechanisms underlying the formation and dynamics of subcellular calcium alternans in the intact rat heart. Circ Res. 2009;104(5):639–49. 10.1161/CIRCRESAHA.108.181909 . [DOI] [PubMed] [Google Scholar]
- 62.Mironov S, Jalife J, Tolkacheva EG. Role of Conduction Velocity Restitution and Short-Term Memory in the Development of Action Potential Duration Alternans in Isolated Rabbit Hearts. Circulation. 2008;118(1):17–25. 10.1161/CIRCULATIONAHA.107.737254 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Gizzi A, Cherry EM, Gilmour RF Jr., Luther S, Filippi S, Fenton FH. Effects of pacing site and stimulation history on alternans dynamics and the development of complex spatiotemporal patterns in cardiac tissue. Front Physiol. 2013;4:71 10.3389/fphys.2013.00071 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Lau E, Kossidas K, Kim TY, Kunitomo Y, Ziv O, Song Z, et al. Spatially Discordant Alternans and Arrhythmias in Tachypacing-Induced Cardiac Myopathy in Transgenic LQT1 Rabbits: The Importance of IKs and Ca2+ Cycling. PLoS ONE. 2015;10(5):e0122754 10.1371/journal.pone.0122754 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Echebarria B, Karma A. Instability and spatiotemporal dynamics of alternans in paced cardiac tissue. Phys Rev Lett. 2002;88(20):208101 10.1103/PhysRevLett.88.208101 [DOI] [PubMed] [Google Scholar]
- 66.Huang C, Song Z, Landaw J, Qu Z. Spatially Discordant Repolarization Alternans in the Absence of Conduction Velocity Restitution. Biophys J. 2020;118:2574–87. 10.1016/j.bpj.2020.02.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Panfilov AV, Keldermann RH, Nash MP. Self-Organized Pacemakers in a Coupled Reaction-Diffusion-Mechanics System. Phys Rev Lett. 2005;95(25):258104 10.1103/PhysRevLett.95.258104 [DOI] [PubMed] [Google Scholar]
- 68.Keldermann RH, Nash MP, Panfilov AV. Modeling cardiac mechano-electrical feedback using reaction-diffusion-mechanics systems. Physica D: Nonlinear Phenomena. 2009;238(11):1000–7. 10.1016/j.physd.2008.08.017. [DOI] [Google Scholar]
- 69.Weise LD, Panfilov AV. Mechanism for Mechanical Wave Break in the Heart Muscle. Phys Rev Lett. 2017;119(10):108101 10.1103/PhysRevLett.119.108101 [DOI] [PubMed] [Google Scholar]
- 70.Prechtl JC, Cohen LB, Pesaran B, Mitra PP, Kleinfeld D. Visual stimuli induce waves of electrical activity in turtle cortex. Proc Natl Acad Sci U S A. 1997;94(14):7621–6. 10.1073/pnas.94.14.7621 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Huang X, Troy WC, Yang Q, Ma H, Laing CR, Schiff SJ, et al. Spiral waves in disinhibited mammalian neocortex. J Neurosci. 2004;24(44):9897–902. 10.1523/JNEUROSCI.2705-04.2004 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Schiff SJ, Huang X, Wu JY. Dynamical evolution of spatiotemporal patterns in mammalian middle cortex. Phys Rev Lett. 2007;98(17):178102 10.1103/PhysRevLett.98.178102 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Dombeck DA, Graziano MS, Tank DW. Functional Clustering of Neurons in Motor Cortex Determined by Cellular Resolution Imaging in Awake Behaving Mice. The Journal of Neuroscience. 2009;29(44):13751–60. 10.1523/JNEUROSCI.2985-09.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Restrepo JG, Weiss JN, Karma A. Calsequestrin-mediated mechanism for cellular calcium transient alternans. Biophys J. 2008;95(8):3767–89. 10.1529/biophysj.108.130419 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Tao T, O'Neill SC, Diaz ME, Li YT, Eisner DA, Zhang H. Alternans of cardiac calcium cycling in a cluster of ryanodine receptors: a simulation study. Am J Physiol Heart Circ Physiol. 2008;295(2):H598–609. 10.1152/ajpheart.01086.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Rovetti R, Cui X, Garfinkel A, Weiss JN, Qu Z. Spark-Induced Sparks As a Mechanism of Intracellular Calcium Alternans in Cardiac Myocytes. Circ Res. 2010;106:1582–91. 10.1161/CIRCRESAHA.109.213975 PubMed Central PMCID: PMC2893409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Nivala M, de Lange E, Rovetti R, Qu Z. Computational modeling and numerical methods for spatiotemporal calcium cycling in ventricular myocytes. Front Physiol. 2012;3:114 Epub 2012/05/16. 10.3389/fphys.2012.00114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Colman MA, Pinali C, Trafford AW, Zhang H, Kitmitto A. A computational model of spatio-temporal cardiac intracellular calcium handling with realistic structure and spatial flux distribution from sarcoplasmic reticulum and t-tubule reconstructions. PLOS Computational Biology. 2017;13(8):e1005714 10.1371/journal.pcbi.1005714 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Komendantov AO, Komendantova OG, Johnson SW, Canavier CC. A Modeling Study Suggests Complementary Roles for GABAA and NMDA Receptors and the SK Channel in Regulating the Firing Pattern in Midbrain Dopamine Neurons. J Neurophysiol. 2004;91(1):346–57. 10.1152/jn.00062.2003 . [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The online supporting information includes: A. AP clamp and free running protocols. B. Stability analysis of the CML model. C. Automatic detection algorithms for spatiotemporal excitation patterns. D. Boundary between discordant P2 and uniform P2 in the CML model.
(DOCX)
a). Data from Roome et al.[1] showing a spatiotemporal map of spontaneous dendritic voltage signal obtained from 5 s of linescan recording. Filled triangles indicate dendritic complex spikes (DCS). Subthreshold dendritic voltage modulation is also visible in the spatiotemporal voltage map. Red trace shows spatially averaged voltage, recorded at 2 kHz resolution. Corresponding spatiotemporal map for dendritic Ca2+ is also recorded. Green trace shows spatially averaged Ca2+. b). Data from Diaz et al.[2] showing spatiotemporal Ca2+ signals under control and ryanodine receptor blocker tetracaine with a voltage clamp protocol. Linescan recordings reveal out-of-phase spatial patterns of intracellular Ca2+ transient from beat to beat. Bottom two traces show fluorescence measured as a function of time at the regions indicated by arrows (i and ii).
(EPS)
a). Bifurcation diagram showing c vs. T for the single-element FHN model. b). Bifurcation diagram showing the peak values of the whole-cell average Ca2+ transient, vs. T for the detailed ventricular myocyte model. c). Bifurcation diagram showing c vs. γ for the single-element CML model.
(EPS)
The voltage trace is the last action potential recorded in the simulation of the physiologically detailed myocyte model. The model was paced for 100 beats to reach the steady state at the pacing period T = 450 ms. This voltage trace was used in the AP clamp simulations.
(EPS)
λk vs. k for α = 0.2 (black), 0 (red) and -0.2 (blue) are numerically computed based on Eq 7 in the main text. γ = 1.057, which is the bifurcation point in S2C Fig.
(EPS)
a). Top shows an example of discordant P2 patterns for the 1D FHN model. Bottom shows the relationship of Δcn+1(j) vs. j where the domain size l determined by the pattern recognition algorithm is marked by the double-arrow red line. b). Same as a), but for the 1D CML model. c). Same as a), but for the detailed myocyte model. Note that the gray and black traces are for m = 1 and 50 in S10 Eq, respectively. We used m = 50 to extract the domain size for the detailed myocyte model in our study.
(EPS)
Data Availability Statement
All relevant data are within the manuscript and its Supporting Information files.