Analyzing the impact of the media campaign and rapid testing for COVID-19 as an optimal control problem in East Java, Indonesia

Highlights

• •We propose a model to describe the spread of COVID-19.
• •The model consider media campaign to increase population awareness and rapid testing to trace undetected cases.
• •The parameters estimated using COVID-19 incidence data from East Java, Indonesia.
• •A sensitivity analysis on the basic reproduction number suggest media campaign is more crucial in reducing the spread of COVID-19.
• •An optimal control simulation conducted to determine the effect of media campaign and rapid testing to fights COVID-19.

Abstract

Without any vaccine or medical intervention to cure the infected individual from COVID-19, the non-pharmaceutical intervention become the most reasonable intervention against the spread of COVID-19. In this paper, we proposed a deterministic model governed by a system of nonlinear differential equations which consider the intervention of media campaign to increase human awareness, and rapid testing to track the undetected cases in the field. Analysis of the autonomous model shows the existence of transcritical bifurcation at a basic reproduction number equal to one. We estimate our parameter using the incidence data from East Java, Indonesia. Using these parameters, we analyze the sensitivity of the parameters in determining the size of the basic reproduction number. An optimal control problem which transforms media campaign and rapid testing as a time-dependent control was conducted also in this article. Cost-effectiveness analysis using the Infection averted ratio (IAR) and the Average cost-effectiveness ratio (ACER) conducted to analyze the best strategies to eradicate COVID-19 spread. We observe that the combination of the media campaign and rapid testing as time-dependent interventions reduces the number of an infected individual significantly and also minimizes the economic burden due to these strategies in East Java.

1. Introduction

The world has been shocked by an attack of new Coronavirus, which initially founded at the end of December 2019, which now known as COVID-19 [1]. As of July 13, 2020, total cases in all countries in the world have been reaching more than 13 million cases, with the number of deaths is about 570 thousand cases [2], and still increasing. Indonesia has the highest COVID-19 incidence in South East Asia, with a total of positive cases is about 76 thousand [2]. The first documented cases in Indonesia were recorded on March 3, 2020, in Jakarta [3]. Since then, COVID-19 spread to another province, including East Java, which now becomes one of the provinces with the highest incidence in Indonesia. As per July 13, 2020, total cases in East Java is 16 682 cases, which contribute to 22% from total cases in Indonesia [4].

Covid-19 is transmitted from human-to-human through direct contact with infected individuals or objects that had been contaminated with the viruses on the surfaces [5]. The incubation period of COVID-19 is approximately 2–14 days [6]. The symptoms of COVID-19 are varying, from fever, coughing, difficulty in breathing, and pneumonia for severe cases [7]. There is no vaccine available in the market until now, which forces the policymaker to use another intervention to suppress the spread of COVID-19, such as physical/social distancing, use of face-masks, quarantine, hospitalization, rapid testing, etc. Media campaigns have been conducted by policymakers to develop the awareness of the community to the danger of COVID-19. More aware of the community, more easy the policymaker to implement mass action to reduce the spread of COVID-19, for example, by conducting physical distancing even for the susceptible individuals, using medical masks, etc. Another popular intervention is the rapid testing which conducted to trace the undetected cases in the field and then isolating or hospitalizing them if they have been infected by COVID-19.

A mathematical model plays an important role in helping the community to understand the epidemic behavior of COVID-19, and furthermore, will help policymakers to develop a better intervention strategy to eradicate COVID-19. Various approaches have been conducted by many authors, such as with ordinary differential equations [3], [8], [9], [10], fractional derivatives [11], [12], [13], [14], artificial intelligence [15], [16], and many more [17], [18], [19], [20]. The aim of the mentioned paper is to understand the behavior of the data of COVID-19 using their proposed model, predicting the future dynamic, and proposed scenarios that might be implemented in the field to reduce the spread of COVID-19. However, only a few articles which discuss COVID-19 in Indonesia using a mathematical model. Author in [3] discuss the spread of COVID-19 in Jakarta, Indonesia. Their result was suggesting massive rapid testing to compromise the relaxing of physical distancing. Another research who use incidence data in Indonesia can be seen in [10] which consider human awareness on the transmission term. The author in [21] using deterministic and stochastic models to describe the dynamic of COVID-19 in the early take-off period.

Different from the mentioned references, we are focusing this article on understanding the dynamic of COVID-19 in East Java, Indonesia. We develop a S_uS_aEAIR model, which considering two susceptible compartments to accommodate the aware and unaware subpopulation. Furthermore, rapid testing also involved in the model to trace undetected cases in the community. The infection parameters then fitted using the incidence data from East Java and used in optimal control simulations to determine the best strategies to eradicate COVID-19 in East Java.

This paper is organized as follows. We carefully construct our model in Section 2, and analyze the existence and the stability criteria of all equilibrium point, which depending on the basic reproduction number. In Section 3, the optimal control problem was characterized using the Pontryagin’s Maximum Principle. Some numerical simulations regarding the parameter estimation for COVID-19 incidence data in East Java, sensitivity analysis of the basic reproduction number, autonomous simulation, and the optimal control problem were conducted in Section 4. Some conclusions are given in the last section of this article.

2. Model construction and analytical results

This section presents the new model proposed to understand the spread of COVID-19 under the effect of rapid testing and media campaign. This section contain model construction and mathematical analysis regarding the qualitative behavior of the model.

2.1. The model

The model was based on a nonlinear system of ordinary differential equations. The model takes into account the intervention by the policymaker, which promote the “self-isolation” for all individuals to avoid infection of COVID-19, and also the implementation of rapid testing to trace the undetected cases in the field.

Let us consider that the total of the human population can be separated into susceptible unaware, susceptible aware, exposed, undetected infected cases, detected infected cases, and recovered, which denoted by S_u, S_a, E, A, I, and R, respectively. We assume that the aware subpopulation conducts a health protocol to reduce the probability of getting infected by COVID-19, such as self-isolation, using medical masks, conduct physical distancing, and so on. We assume that all newborn Λ are unaware susceptible individual. Hence, we have that $\frac{d{S}_u}{dt}=\Lambda$. The S_u compartment then will decreasing due to infection caused by contact with I and A compartment, with the infection rate of β ₁. Since A is the class for undetected individuals, we assume that the infection rate from A individual is larger than with I, which has a multiplication factor σ > 1. Hence, the number of new infection from S_u is ${\beta }_{1}S(I+\sigma A)$. This compartment also decreases due to the effect of the media campaign by the government to avoid infection with an infected individual. This campaign is given at the rate of u ₁, which will transfer S_u individual into S_a. The individuals in S_a are assumed to always conduct a careful social interaction, like using a medical mask, reducing contact by conducting a self-isolation at home, using disinfectant after touching suspicious surfaces, and many more. Hence, the infection rate for S_a is lesser than with S_u, which we denote with β ₂, where β ₂ < β ₁. It is assumed that it exists a drop-out rate from S_a to S_u due to the awareness vanishing, which we denote with α.

We now describe the dynamic in the compartment of E. This compartment increases due to new infection from S_u and S_a, and decreases due to transition to be infectious individual after the incubation period of ${\delta }^{-1}$. The individual from E then transferred into A and I compartment, with a proportion of p ad $1-p,$ respectively. Since A compartment is the undetected case, we assume that this compartment will progress to I caused by two reasons. First is caused by the disease’s progression from asymptomatic to a symptomatic individual with a rate of ξ which made this individuals volunteer to go to the hospital, and the second is caused by rapid testing intervention with the rate of u ₂. We assume that only I individual who can die due to disease, with a constant rate of ϕ. Using the natural recovery rate from A and I compartment as γ ₁ and γ ₂, where γ ₂ > γ ₁, the dynamic of COVID-19 under the effect of the media campaign and rapid testing is given as follows.

$$\begin{array}{ccc}\hfill \frac{d{S}_u}{dt}& =& \Lambda -{\beta }_1{S}_u(I+\sigma A)-u_1{S}_u+\alpha S_a-\mu S_u,\hfill \\ \hfill \frac{d{S}_a}{dt}& =& u_1{S}_u-\alpha S_a-{\beta }_2{S}_a(I+\sigma A)-\mu S_a,\hfill \\ \hfill \frac{dE}{dt}& =& ({\beta }_1{S}_u+{\beta }_2{S}_a)(I+\sigma A)-\delta E-\mu E,\hfill \\ \hfill \frac{dA}{dt}& =& p\delta E-(\xi +u_2)A-\mu A-{\gamma }_{1}A,\hfill \\ \hfill \frac{dI}{dt}& =& (1-p)\delta E+(\xi +u_2)A-{\gamma }_{2}I-\varphi I-\mu I,\hfill \\ \hfill \frac{dR}{dt}& =& {\gamma }_{1}A+{\gamma }_{2}I-\mu R,\hfill \end{array}$$ (1)

where μ is the natural death rate. Please note that system (1) is supplemented with a non-negative initial condition

$$S_u\left(0\right)>0,S_a\left(0\right)\ge 0,E\left(0\right)\ge 0,A\left(0\right)\ge 0,I\left(0\right)\ge 0,R\left(0\right)\ge 0.$$ (2)

All parameters are non-negative and described in Table 1 .

Table 1.

Definitions and value ranges for the parameters in the system (1).

Param.	Description	Value/Interval	Source
Λ	Human recruitment rate	$\frac{49316712}{70\times 365}$	Assumed
μ	Natural death rate	$\frac{1}{70\times 365}$	[22]
ϕ	Death rate induced by COVID-19	0.015	[23]
β1	Effective contact rate of Su	$1.2644\times {10}^{-8}$	Fitted
β2	Effective contact rate of Sa	$2.253\times {10}^{-9}$	Fitted
σ	Correction factor of β for A	2	Assumption
δ	Rate due to incubation period of exposed individuals	$\frac{1}{5.1}$	[6], [24], [25], [26]
p	Proportion of exposed individuals who become symptomatic individuals	0.4	[27], [28]
γ1	Recovery rate of undetected individuals	0.1	[29]
γ2	Recovery rate of detected individuals	0.13978	[23]
ξ	Progression from asymptomatic to symptomatic individual	0.01	Assumed
α	drop out rate due to loose of awareness	0.1	Assumed
u1	Transition rate from Su to Sa due to media campaign	0.398	fitted
u2	The rate of rapid testing	0.306	fitted

2.2. Basic properties of the model

The population can not be negative for all time t ≥ 0. Hence it is crucial to show that the solution of system (1) for each variables is non-negative. The following theorem state this properties.

Theorem 1

Any solution (S_u, S_a, E, A, I, R) of system (1) with non-negative initial conditions (2) is positive for all time t > 0.

Proof

Please see Appendix A. □ □

Next, we analyze how the solution of system (1) is bounded. The following theorem confirm this properties.

Theorem 2

The solution of (S_u, S_a, E, A, I, R) of system (1) is bounded in the region

$$\Omega =\{(S_u,S_a,E,A,I,R)\in {\mathbb{R}}_{+}^6:S_u+S_a+E+A+I+R\le \frac{\Lambda }{\mu }\}.$$ (3)

Proof

Please see Appendix B. □ □

2.3. Analytical results on the equilibrium and the basic reproduction number

System (1) always had a trivial COVID-19 free equilibrium which given by

$$E_0=(S_u,S_a,E,A,I,R)=(\frac{\Lambda (\alpha +\mu )}{\mu (\alpha +\mu +u_1)},\frac{\Lambda u_1}{\mu (\alpha +\mu +u_1)},0,0,0,0),$$ (4)

and the basic reproduction number is given by (See Appendix C for the derivation of ${\mathcal{R}}_0$)

$${\mathcal{R}}_0={\mathcal{R}}_{\text{undetected}}+{\mathcal{R}}_{\text{detected-1}}+{\mathcal{R}}_{\text{detected-2}},$$ (5)

where

$${\mathcal{R}}_{\text{undetected}}=\frac{\sigma \Lambda ({\beta }_1\alpha +{\beta }_1\mu +u_1{\beta }_2)\delta p}{\mu (\alpha +\mu +u_1)(\mu +\xi +{\gamma }_1+u_2)(\delta +\mu )},$$ (6)

$${\mathcal{R}}_{\text{detected-1}}=\frac{\Lambda (\alpha {\beta }_1+{\beta }_1\mu +u_1{\beta }_2)\delta (\mu +{\gamma }_1)(1-p)}{\mu (\mu +\xi +{\gamma }_1+u_2)({\gamma }_2+\mu +\varphi )(\delta +\mu )(\alpha +\mu +u_1)},$$ (7)

$${\mathcal{R}}_{\text{detected-2}}=\frac{\Lambda (\alpha {\beta }_1+{\beta }_1\mu +u_1{\beta }_2)\delta (\xi +u_2)}{\mu (\mu +\xi +{\gamma }_1+u_2)({\gamma }_2+\mu +\varphi )(\delta +\mu )(\alpha +\mu +u_1)}.$$ (8)

It can be seen that ${\mathcal{R}}_0$ in (5) were constructed by three component. The first component is ${\mathcal{R}}_{\text{undetected}}$ which describe the infection in S_u and S_a due to contact with undetected individuals. The ${\mathcal{R}}_{\text{detected-1}}$ describe an infection from detected individual which directly coming from the path of E → I, while ${\mathcal{R}}_{\text{detected-2}}$ is coming from the path of E → A → I. Since the infection rate from undetected individual is larger than from detected individual (σ > 1), increasing u ₂ will reduce ${\mathcal{R}}_{\text{detected-2}}$. Furthermore, it also can be seen that increasing u ₁ will reduce ${\mathcal{R}}_0$.

Using Theorem 2 in [31], an important results regarding local stability of E ₀ stated as follows.

Theorem 3

COVID-19 model in (1) is locally asymptotically stable if ${\mathcal{R}}_0<1,$ and unstable when ${\mathcal{R}}_0>1$ .

This theorem has been reviewed by the author in [31]. Hence, we do not show it in this article. The theorem implies that it is possible to eradicate COVID-19 if this threshold is less than unity. The basic reproduction number is defined as an expected number of secondary cases due to infection from one primary case during its infection period in a completely susceptible population [32]. Many epidemiological models generate the same results (see [33], [34], [35] for some examples). However, not always ${\mathcal{R}}_0<1$ indicates the disease may not persist. When backward bifurcation appears, another stable equilibrium, which in this case is the endemic equilibrium, is locally stable. Please refer to [3], [36], [37], [38] for examples. Hence, it is important to understand the bifurcation type of our proposed model in (1).

The next equilibrium is the endemic equilibrium, which is given as follows.

$$E_1=(S_u,S_a,E,A,I,R)=(S_u^{†},S_a^{†},E^{†},A^{†},I^{†},R^{†})$$ (9)

where

$$\begin{array}{ccc}\hfill S_u^{†}& =& \frac{\Lambda (A^{†}\sigma {\beta }_2+\alpha +\mu )}{(A^{†}\sigma {\beta }_2+\alpha +\mu )(A^{†}\sigma +{\mathit{In}}^{†}){\beta }_1+A^{†}\mu \sigma {\beta }_2+A^{†}\sigma {\beta }_2{u}_1+{\mathit{In}}^{†}\alpha {\beta }_2+\alpha \mu +{\mu }^2+\mu u_1},\hfill \\ \hfill S_a^{†}& =& \frac{\Lambda (u_1-{\beta }_2{I}^{†})}{(A^{†}\sigma {\beta }_2+\alpha +\mu )(A^{†}\sigma +{\mathit{In}}^{†}){\beta }_1+A^{†}\mu \sigma {\beta }_2+A^{†}\sigma {\beta }_2{u}_1+{\mathit{In}}^{†}\alpha {\beta }_2+\alpha \mu +{\mu }^2+\mu u_1},\hfill \\ \hfill E^{†}& =& \frac{p{A}^{†}(\mu +\xi +{\gamma }_1+u_2)}{\delta p},\hfill \\ \hfill I^{†}& =& \frac{((1-p)({\gamma }_1+\mu )+\xi +u_2)A^{†}}{p(\varphi +{\gamma }_2+\mu )},\hfill \\ \hfill R^{†}& =& \frac{A^{†}(p{\gamma }_1(\mu +\varphi )+(1-p)\mu {\gamma }_2+\xi {\gamma }_2+{\gamma }_1{\gamma }_2+{\gamma }_2{u}_2)}{p\mu ({\gamma }_2+\mu +\varphi )}.\hfill \end{array}$$

A† is taken from the positive roots of the following polynomial

$$\mathcal{P}\left(A\right)=a_2{A}^2+a_{1}A+a_0=0,$$ (10)

where

$$\begin{array}{ccc}\hfill a_2& =& -{\beta }_1{\beta }_2(\mu +\xi +{\gamma }_1+u_2)(\mu p\sigma +p\varphi \sigma +p\sigma {\gamma }_2\hfill \\ & & {+(1-p)(\mu +{\gamma }_1)+\xi +u_2)}^2(\delta +\mu ),\hfill \\ \hfill a_1& =& p\delta {\beta }_1{\beta }_2\Lambda (\mu p\sigma +p\varphi \sigma +p\sigma {\gamma }_2+(1-p)(\mu +{\gamma }_1)\hfill \\ & & {+\xi +u_2)}^2\cdots -p(\mu p\sigma +p\varphi \sigma +p\sigma {\gamma }_2+(1-p)(\mu +{\gamma }_1)\hfill \\ & & +\xi +u_2)(\mu +\xi +{\gamma }_1+u_2)\cdots \hfill \\ & & ({\gamma }_2+\mu +\varphi )(\delta +\mu )({\beta }_1(\alpha +\mu )+{\beta }_2(\mu +u_1),\hfill \\ \hfill a_0& =& p^2({\gamma }_2+\mu +\varphi )\mu (\alpha +\mu +u_1)(\mu +\xi +{\gamma }_1+u_2)(\delta +\mu )({\mathcal{R}}_0-1).\hfill \end{array}$$

From the expression of $\mathcal{P}\left(A\right),$ it can be seen that a ₂ always negative, while $a_0>0\iff {\mathcal{R}}_0>1$. Hence, we have the following theorem regarding the existence of the endemic equilibrium when ${\mathcal{R}}_0>1$.

Theorem 4

COVID-19 model in (1) is always has a unique COVID-19 endemic equilibrium given by (9) whenever ${\mathcal{R}}_0>1$ .

Since $\mathcal{P}\left(A\right)$ is a two degree polynomial, we have a possibility to have two COVID-19 endemic equilibrium when ${\mathcal{R}}_0<1$. $\mathcal{P}\left(A\right)$ have two positive roots if $a_0>0\iff {\mathcal{R}}_0>1,$ a ₁ < 0 and $a_1^2-4a_2{a}_0>0$. However, this condition never fulfilled, which we state in the following lemma.

Lemma 1

Polynomial $\mathcal{P}\left(A\right)$ never has a positive roots when ${\mathcal{R}}_0<1$ .

Proof

Please see Appendix D for the proof. □

Since we always have a stable COVID-19 free equilibrium without any exist COVID-19 endemic equilibrium when ${\mathcal{R}}_0<1,$ and it always exist a unique COVID-19 endemic equilibrium when ${\mathcal{R}}_0>1,$ our system (1) indicate a transcritical bifurcation occurrence at ${\mathcal{R}}_0=1$.

3. Numerical experiments

3.1. Parameter estimation

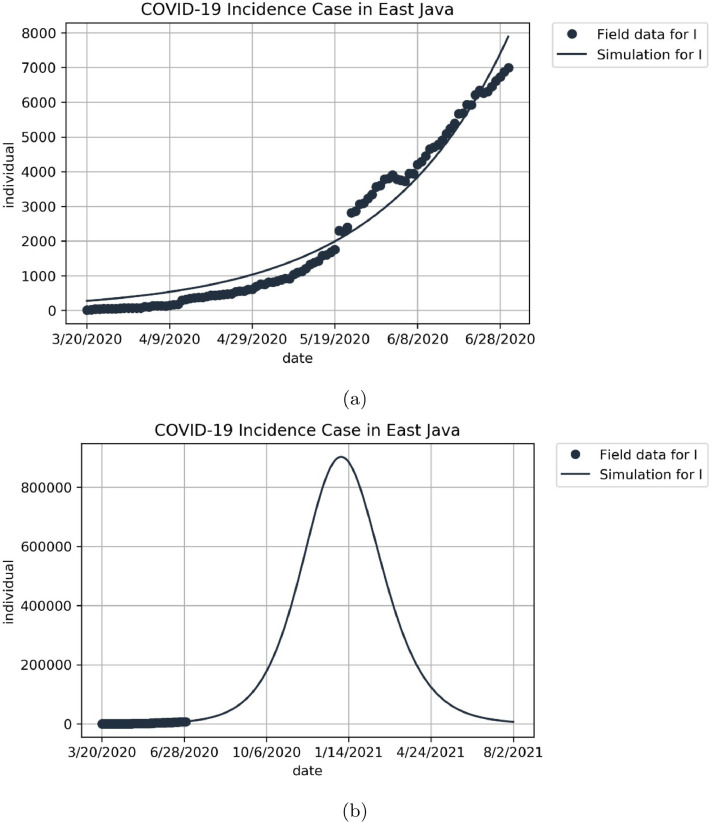
To conduct a simulation in this article, we use parameters value as shown in Table 1, while the effective contact rate β ₁ and β ₂, and the media campaign rate u ₁ and rapid testing rate u ₂ were estimated from incidence data. The incidence data of East Java are taken from [4] from Mei 20 to June 30, 2020. Total of population in East Java is 49 316 712. The result of parameter estimation is shown in Fig. 1 with the best fit parameter is ${\beta }_1=1.2644\times {10}^{-8},{\beta }_2=2.253\times {10}^{-9},u_1=0.398,$ and $u_2=0.306$. With this parameter values, the basic reproduction number in East Java is 1.66 which indicates the existence of the endemic equilibrium of COVID-19. The endemic equilibrium is given by

$$E_1=(S_u,S_a,E,A,I,R)=(5.96\times {10}^6,2.37\times {10}^7,4217,795,4827,1.789\times {10}^7).$$

Fig. 1.

Time series plot showing the performance of least square method for system (1) for East Java in a short-period (a), and long period (b). The black dots represent the incidence data, and the solid lines represent the prediction of total infected cases.

3.2. Discussion on the effect of constant control on ${\mathcal{R}}_0$ and the autonomous system

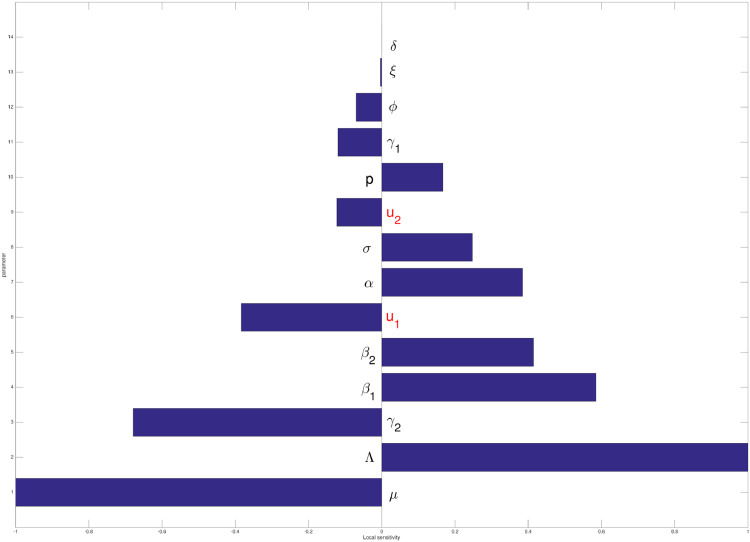
From the previous analysis, we can see that the basic reproduction number determines the qualitative behavior of our COVID-19 model. Hence, it is important to analyze the most significant parameter that can change the value of ${\mathcal{R}}_0$. To conduct this, we use the local sensitivity analysis respect to ${\mathcal{R}}_0$ using the best-fitted parameter for East Java incidence data.

Definition 1

(See [39]). The normalized forward sensitivity index of ${\mathcal{R}}_0,$ with respect to a given parameter θ, is defined by

$${\mathcal{E}}_{\theta }^{{\mathcal{R}}_0}=\frac{\partial {\mathcal{R}}_0}{\partial \theta }\times \frac{\theta }{{\mathcal{R}}_0}.$$

Since $\frac{\partial {\mathcal{R}}_0}{\partial {\beta }_1}=\frac{\delta (\mu p\sigma +p\varphi \sigma +p\sigma {\gamma }_2-p\mu -{\gamma }_{1}p+\mu +\xi +{\gamma }_1+u_2)(\alpha +\mu )\Lambda }{\mu (\mu +\xi +{\gamma }_1+u_2)({\gamma }_2+\mu +\varphi )(\delta +\mu )(\alpha +\mu +u_1)},$ then we have that

$${\mathcal{E}}_{{\beta }_1}^{{\mathcal{R}}_0}=\frac{\partial {\mathcal{R}}_0}{\partial {\beta }_1}\times \frac{{\beta }_1}{{\mathcal{R}}_0}=\frac{(\alpha +\mu ){\beta }_1}{\alpha {\beta }_1+{\beta }_1\mu +u_1{\beta }_2}.$$

Substituting parameter values on Table 1, we have that ${\mathcal{E}}_{{\beta }_1}^{{\mathcal{R}}_0}=0.5851$. This means that increasing β ₁ for 10% will increase ${\mathcal{R}}_0$ for 5.851%. We calculate the local sensitivity of all parameters value in ${\mathcal{R}}_0$ in a similar way with β ₁, and the result is given in Fig. 2 . We can see that the most significant parameter in ${\mathcal{R}}_0$ is μ, followed with Λ, Γ₂, β ₁, β ₂, u ₁, α, σ, u ₂, p, γ ₁, ϕ, ξ, and δ, respectively. This results indicates that u ₁ is more sensitive than u ₂ in determining ${\mathcal{R}}_0$.

Fig. 2.

Local sensitivity analysis of ${\mathcal{R}}_0$.

Based on Theorem 4 and 6, we notice that ${\mathcal{R}}_0$ holds an important role in determining the existence and type of stability of each equilibrium points. We have that COVID-19 dies out whenever ${\mathcal{R}}_0<1,$ and exist whenever ${\mathcal{R}}_0>1$. Hence, it is important to reduce the magnitude of ${\mathcal{R}}_0$ as small as possible until it is less than one. Since

$$\frac{\partial {\mathcal{R}}_0}{\partial u_1}=-\frac{\delta (\mu p\sigma +p\varphi \sigma +p\sigma {\gamma }_2+(1-p)(\mu +{\gamma }_1)+\xi +u_2)\Lambda ({\beta }_1-{\beta }_2)(\alpha +\mu )}{\mu (\mu +\xi +{\gamma }_1+u_2)({\gamma }_2+\mu +\varphi )(\delta +\mu ){(\alpha +\mu +u_1)}^2}<0,$$

and

$$\frac{\partial {\mathcal{R}}_0}{\partial u_2}=-\frac{\delta \Lambda (\alpha {\beta }_1+{\beta }_1\mu +u_1{\beta }_2)p(\mu (\sigma -1)+\varphi \sigma +\sigma {\gamma }_2-{\gamma }_1)}{\mu {(\mu +\xi +{\gamma }_1+u_2)}^2({\gamma }_2+\mu +\varphi )(\delta +\mu )(\alpha +\mu +u_1)}<0,$$

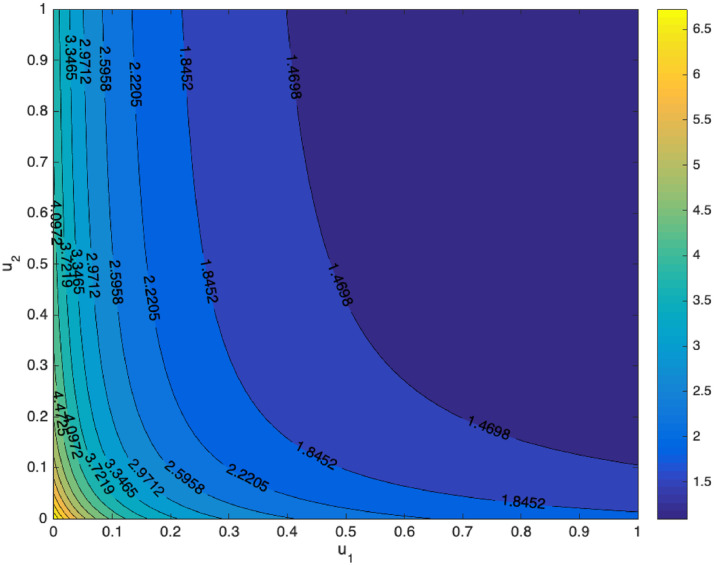
we can conclude that increasing the implementation of the media campaign and rapid testing will reduce the chance of COVID-19 to exist in the population. Increasing the media campaign for 10% will reduce ${\mathcal{R}}_0$ 3.843%. On the other hand, increasing the rapid testing rate for 10% will reduce ${\mathcal{R}}_0$ for 1.23%. Using parameters value as shown in Table 1, the contour plot of u ₁ and u ₂ respect to ${\mathcal{R}}_0$ is given in Fig. 3 . It can be seen that u ₁ and u ₂ is inversely proportional to ${\mathcal{R}}_0$. It means that increasing media campaigns and/or rapid testing will increase the chance to eradicate COVID-19 from the community.

Fig. 3.

Contour plot of the basic reproduction number respect to media campaign u₁ and rapid testing u₂.

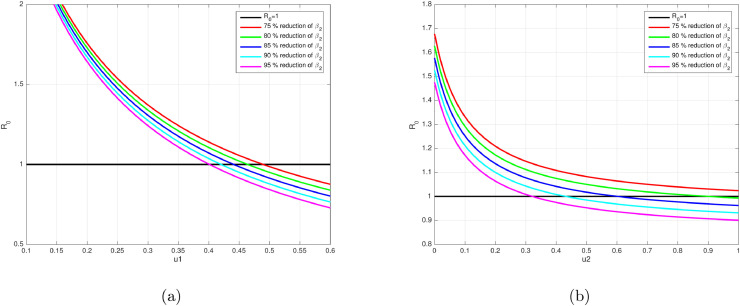
The sensitivity of ${\mathcal{R}}_0$ respect to u ₁ and u ₂ when β ₂ is varying is given in Fig. 4 . We conduct the sensitivity of u ₁ and u ₂ by reducing β ₂ 75%, 80%, 85%, 90%, and 95%. It can be seen that larger the value of β ₂ will requires more intense of media campaign and rapid test that should be implemented to achieve a condition of COVID-19 free equilibrium.

Fig. 4.

Profile of the reproduction number as a function of u₁ (a) and u₂ (b) respect to the change of β₂.

From all sensitivity analysis that had been conducted in Fig. 2, Fig. 3, Fig. 4, we can see that there is a big chance to eradicate COVID-19 from East Java, where using the media campaign could give better result rather than only depending on rapid testing. Increasing community awareness through a media campaign in our model will reduce the infection rate of the aware population. This can be done when this aware population is encouraged to do a physical distancing, using medical masks, and any other intervention which in our model will reduce the value of β ₂.

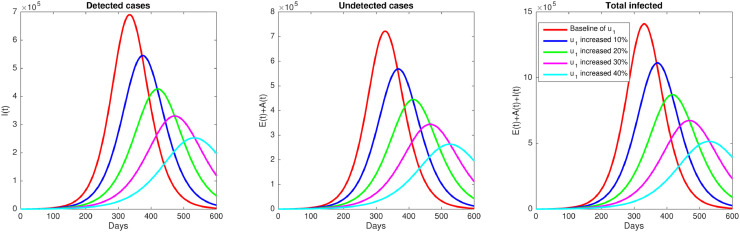
Next, we simulate our proposed COVID-19 model in (1) using parameters value in Table 1, except it stated differently, to assess the impact of various possible control strategies against COVID-19 in East Java. First, we simulate the impact of the media campaign by the government to increase the number of aware population. Hence, we use 5 different value for u ₁, where $u_1=0.398$ as the baseline value, while the other four values are 10%, 20%, 30%, and 40% increased. The results are given in Fig. 5 . It can be seen that intervention of media campaign show a dramatic decrease in the number of infected individuals in East Java.

Fig. 5.

Effect of media campaign (u₁). Simulation of the model (1) shows how number of infected individuals decreases when media campaign rate increasing.

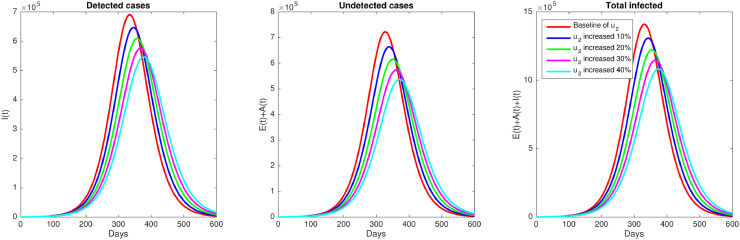
Second autonomous simulation is conducted to see the impact of rapid testing against the spread of COVID-19 in East Java. We set all parameters value similar to the baseline parameter used in the previous simulation, except we use five different values of u ₂. The baseline value of u ₂ is 0.306, while the other values are increased 10%, 20%, 30%, and 40%. The results are given in Fig. 6 . Our simulation indicates how rapid testing could suppress the outbreak of COVID-19 in East Java, even though not dramatic as the implementation of a massive media campaign. This is because u ₁ is more sensitive to ${\mathcal{R}}_0$ rather than u ₂, as already explained in Fig. 2.

Fig. 6.

Effect of rapid testing (u₂). Simulation of the model (1) shows how number of infected individuals decreases when rapid testing rate increasing.

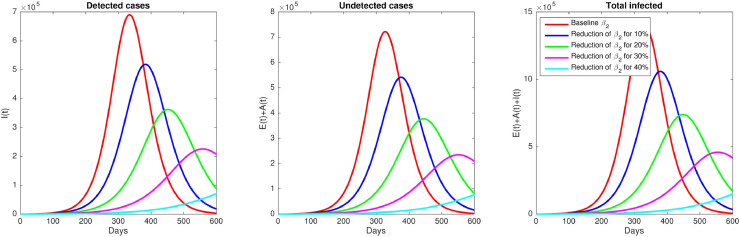
A simulation was further to see the impact of the media campaign’s effectiveness to reduce the infection rate of the aware population. To conduct this simulation, we use the same parameter values as in the previous simulation, while β ₂ will be varying for five values. The first value is $2.253\times {10}^{-9},$ while the other four values are reduced for 10%, 20%, 30%, and 40%. The result is given in Fig. 7 . It can be seen that reducing the value of β ₂ success to reduce the infected population massively. The result of this simulation shows how the peak of the outbreak reduced significantly, and the time for the occurrence of the outbreak also delayed.

Fig. 7.

Effect of reducing β₂. Simulation of the model (1) shows how number of infected individuals decreases when aware population increases their awareness to reduce the infection rate.

4. Optimal control problem

4.1. Optimal control characterization

We seek to minimize the number of infected individual E, A, and I in COVID-19 model (1) and the cost for applying media campaign u ₁ and rapid testing u ₂ controls. Hence, we consider our control parameters to be dependent on time, $u_1=u_1\left(t\right)$ and $u_2=u_2\left(t\right)$. Therefore, we have model (1) now becomes

$$\begin{array}{ccc}\hfill \frac{d{S}_u}{dt}& =& \Lambda -{\beta }_1{S}_u(I+\sigma A)-u_1\left(t\right)S_u+\alpha S_a-\mu S_u,\hfill \\ \hfill \frac{d{S}_a}{dt}& =& u_1\left(t\right)S_u-\alpha S_a-{\beta }_2{S}_a(I+\sigma A)-\mu S_a,\hfill \\ \hfill \frac{dE}{dt}& =& ({\beta }_1{S}_u+{\beta }_2{S}_a)(I+\sigma A)-\delta E-\mu E,\hfill \\ \hfill \frac{dA}{dt}& =& p\delta E-(\xi +u_2\left(t\right))A-\mu A-{\gamma }_{1}A,\hfill \\ \hfill \frac{dI}{dt}& =& (1-p)\delta E+(\xi +u_2\left(t\right))A-{\gamma }_{2}I-\varphi I-\mu I,\hfill \\ \hfill \frac{dR}{dt}& =& {\gamma }_{1}A+{\gamma }_{2}I-\mu R.\hfill \end{array}$$ (11)

We consider the objective function that describe our aim previously in the following function.

$$\mathcal{J}(u_1,u_2)={\int }_0^{t_f}(E+A+I+\frac{c_1}{2}{u}_1^2+\frac{c_2}{2}{u}_2^2)dt,$$ (12)

where c ₁ and c ₂ is the weight parameters for media campaign and rapid testing, respectively, and t_f is the final time of the simulation. We assume that the cost for media campaign and rapid testing is nonlinear, hence we choose it as a quadratic function. Please see [40], [41], [42], [43], [44] for another examples for an implementation of a quadratic cost function in an optimal control problem for epidemiological models. The term of ${\int }_0^{t_f}(E+A+I)dt$ describe the cost related to a consequences of a high number of infected individual, for an example cost due to economic condition during pandemic. On the other hand, ${\int }_0^{t_f}(\frac{c_1}{2}{u}_1^2+\frac{c_2}{2}{u}_2^2)dt,$ represent the cost for control implementation. Our task is to seek an optimal control trajectories of $u_1^{*}$ and $u_2^{*}$ such that

$$\mathcal{J}(u_1^{*},u_2^{*})=\underset{\Gamma }{\min }\mathcal{J}(u_1,u_2),$$ (13)

where Γ is the set of admissible control

$$\Gamma =\{(u_1,u_2)\in {\left(L^{\infty }(0,t_f)\right)}^2|0\le u_i\left(t\right)\le 1\text{for}i=1,2\}.$$

Before we characterize the optimal control problem, we show the existence of such optimal control function which fulfilled above task. For this purposes, we follow the results given in [45], [46].

Theorem 5

There exists an optimal control pair $u_1^{*}$ and $u_2^{*}$ in Γ such that $\mathcal{J}(u_1^{*},u_2^{*})={\min }_{\Gamma }\mathcal{J}(u_1,u_2),$ which correspond to COVID-19 model in (11) .

Proof

Please see Appendix E for the proof. □

The Pontryagin’s Maximum principle [49] provides the necessary condition for the existence of the optimal control pair $(u_1^{*},u_2^{*})$ of the model (11). The idea of this method is to convert the state system (11) and the cost function (12) with (13) into a problem of minimizing the Hamiltonian $\mathcal{H}$ with respect to u ₁ and u ₂ as follows

$$\begin{array}{ccc}\hfill \mathcal{H}& =& E+A+I+\frac{c_1}{2}{u}_1^2+\frac{c_2}{2}{u}_2^2+{\lambda }_1\frac{d{S}_u}{dt}+{\lambda }_2\frac{d{S}_a}{dt}+{\lambda }_3\frac{dE}{dt}\hfill \\ & & +{\lambda }_4\frac{dA}{dt}+{\lambda }_5\frac{dI}{dt}+{\lambda }_6\frac{dR}{dt},\hfill \end{array}$$ (14)

where λ_i for $i=1,2,3,4,5,6$ is the adjoint variables respect to S_u, S_a, E, A, I, and R, respectively. The necessary conditions for the existence of these adjoint variables and the control characterizations is given in the following theorem.

Theorem 6

Given an optimal control pairs $(u_1^{*},u_2^{*})$ which minimize the cost function (12) over Γ subject to the state system (11) , then there exist an adjoint variables λ_i for $i=1,2,\cdots ,6$ satisfying the following system

$$\begin{array}{ccc}\hfill \frac{d{\lambda }_1}{dt}& =& {\beta }_1(I+\sigma A)({\lambda }_1-{\lambda }_3)+u_1({\lambda }_1-{\lambda }_2)+\mu {\lambda }_1,\hfill \\ \hfill \frac{d{\lambda }_2}{dt}& =& \alpha ({\lambda }_2-{\lambda }_1)+{\beta }_2(I+\sigma A)({\lambda }_2-{\lambda }_3)+\mu {\lambda }_2\hfill \\ \hfill \frac{d{\lambda }_3}{dt}& =& -1+p\delta ({\lambda }_3-{\lambda }_4)+(1-p)\delta ({\lambda }_3-{\lambda }_5)+\mu {\lambda }_3,\hfill \\ \hfill \frac{d{\lambda }_4}{dt}& =& -1+\sigma {\beta }_1{S}_u({\lambda }_1-{\lambda }_3)+\sigma {\beta }_2{S}_a({\lambda }_2-{\lambda }_3)\hfill \\ & & +(\xi +u_2)({\lambda }_4-{\lambda }_5)+{\gamma }_1({\lambda }_4-{\lambda }_6)+\mu {\lambda }_4,\hfill \\ \hfill \frac{d{\lambda }_5}{dt}& =& -1+{\beta }_1{S}_u({\lambda }_1-{\lambda }_3)+{\beta }_2{S}_a({\lambda }_2-{\lambda }_3)+{\gamma }_2({\lambda }_5-{\lambda }_6)\hfill \\ & & +(\mu +\varphi ){\lambda }_5,\hfill \\ \hfill \frac{d{\lambda }_6}{dt}& =& \mu {\lambda }_6.\hfill \end{array}$$ (15)

with a transversality condition ${\lambda }_i\left(t_f\right)=0$ for $i=1,2,\cdots ,6,$ and

$$\begin{array}{ccc}\hfill u_1^{*}& =& \max \{0,\min \{1,\frac{S_u({\lambda }_1-{\lambda }_2)}{c_1}\}\},\hfill \\ \hfill u_2^{*}& =& \max \{0,\min \{1,\frac{A({\lambda }_4-{\lambda }_5)}{c_2}\}\}.\hfill \end{array}$$ (16)

Proof

Please see Appendix F for the proof. □

4.2. Simulation for the optimal control problem

In this section, we shall conduct a numerical simulation for the optimal control problem which already discussed in previous section. For this purposes, we define the following three strategies : (1) Execution only with media campaign $(u_1\left(t\right)\ge 0,u_2\left(t\right)=0),$ (2) Implementation of rapid testing only $(u_1\left(t\right)=0,u_2\left(t\right)\ge 0),$ and (3) Implementation of both intervention (u ₁(t) ≥ 0, u ₂(t) ≥ 0).

For numerical implementation, we solve the optimality system (11) and (15) together with the control characterization (16) using numerical iterative scheme. We use the forward-backward sweep method to solve our problem. The algorithm start with an initial guess for control variable, and solve the state system (11) forward in time. After that, we solve the adjoint system (15) backward in time. Both this numerical calculation are using ode45 in MATLAB. Then, the optimal control (16) should be updated using these state and adjoint variables. This process repeated until a convergence criteria is met (see [50] for detail, and [34], [35], [43] for some examples). For our numerical experiments, we consider a set of parameter given in Table 1 and the time period for simulations is 100 days along with the initial condition $S_u\left(0\right)=7924040,S_a\left(0\right)=31517500,E=8557,A=1496,R=38071$ which is the final state of curve fitting of model (1) in Fig. 1. We choose the positive weight constant $c_1=3\times {10}^7$ and $c_2=3\times {10}^5$.

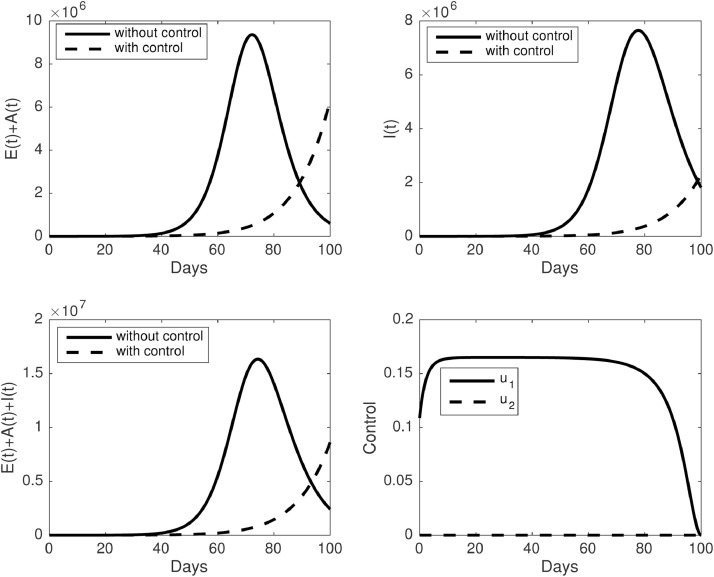
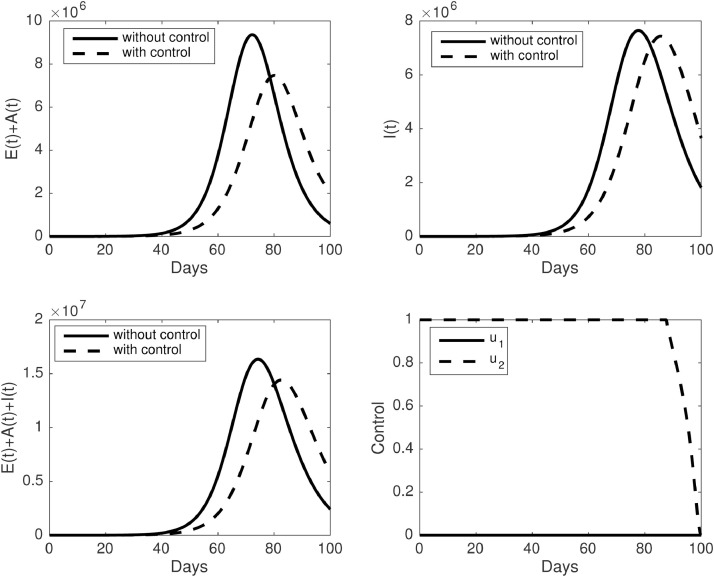
For the first scenario, when we only execute the media campaign as a single intervention, the corresponding results obtained are plotted in Fig. 8 . We noticed that the media campaign should be given at a high rate from the beginning of the simulation, remain constant at around $u=0.16$ for a long time period, and start to decrease when the time is getting closer to the final time of the simulation. As a consequence of the high rate of the media campaign, the number of infected can be suppressed for a long time, but it starts to increase when the media campaign starts to decrease.

Fig. 8.

The dynamic of infected individuals and control trajectories for the first scenario $(u_1\ge 0,u_2=0)$. Upper panel : (left) dynamic of $E\left(t\right)+A\left(t\right)$ and (right) I(t). The lower panel : (left) dynamic of $E\left(t\right)+A\left(t\right)+I\left(t\right)$ and (right) control trajectories.

The results corresponding to strategy two ($u_1=0,u_2\ge 0$) are shown in Fig. 9 . We observed that the implementation of rapid testing is always larger than the implementation of u ₁ only in the first scenario. The control trajectories of u ₂ are almost always should be given at its highest rate $(u_2=1)$ and then start to decrease when it is approaching the final time of the simulation. As a result, the reduction of infected cases achieved, even though not as good as in the first scenario.

Fig. 9.

The dynamic of infected individuals and control trajectories for the second scenario $(u_1=0,u_2\ge 0)$. Upper panel : (left) dynamic of $E\left(t\right)+A\left(t\right)$ and (right) I(t). The lower panel : (left) dynamic of $E\left(t\right)+A\left(t\right)+I\left(t\right)$ and (right) control trajectories.

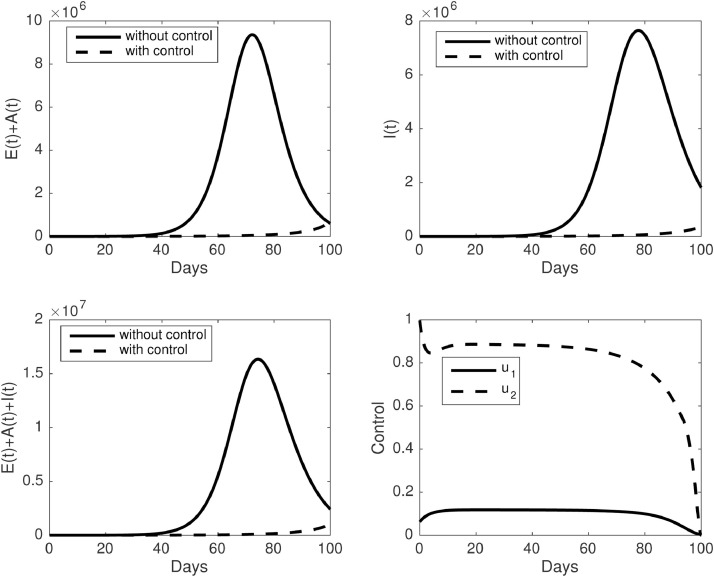
The last simulation conducted for the third scenario, when all controls executed. The results obtained in Fig. 10 . One can easily see from Fig. 10 is that the infective population can be suppressed during the simulation period. As a consequence of both interventions should be executed, it can be seen that the rate of rapid testing should be reduced as a compromise for the implementation of the media campaign.

Fig. 10.

The dynamic of infected individuals and control trajectories for the third scenario (u₁ ≥ 0, u₂ ≥ 0). Upper panel : (left) dynamic of $E\left(t\right)+A\left(t\right)$ and (right) I(t). The lower panel : (left) dynamic of $E\left(t\right)+A\left(t\right)+I\left(t\right)$ and (right) control trajectories.

4.3. Cost-effectiveness analysis

Arising from optimal control simulation in the previous section, we need to determine the best strategy, which in this case, is the most cost-effective intervention strategy to eradicate COVID-19. To do this, we conduct two cost-effectiveness analysis, namely the IAR (Infected Averted Ratio) and the ACER (Average Cost-Effectiveness Analysis). The IAR formula is given by

$$\text{IAR}=\frac{\text{Total}\text{number}\text{of}\text{infections}\text{averted}}{\text{Total}\text{number}\text{of}\text{recovered}},$$ (17)

where the total number of infections averted is given by

$${\mathcal{A}}^{inf}={\int }_0^T(E\left(t\right)-E^{*}\left(t\right))+(A\left(t\right)-A^{*}\left(t\right))+(I\left(t\right)-I^{*}\left(t\right))dt,$$ (18)

where E*, A*, and I* denote the numbers of exposed, undetected cases and detected cases individuals due to control strategies. The strategy exhibiting the highest IAR is considered to be the most effective strategy. The results for the control scenario in the previous section are given in Table 2 . From Table 2, it can be seen that strategy-3 is the most effective strategy, followed with strategy-1 and strategy-2, respectively. These results show that to minimize the number of an infected individuals, the best strategy that should be considered ia the implementation of the massive media campaign and rapid testing. However, if the policymaker should choose a single intervention that should be implemented, then the media campaign is the better option rather than rapid testing.

Table 2.

Numerical results for each prevention scenario.

Strategy	Scenario	${\int }_0^T(\frac{c_1}{2}{u}_1^2+\frac{c_2}{2}{u}^2)dt$	${\mathcal{A}}^{inf}$	IAR	ACER
1	$u_1\ge 0,u_2=0$	1.159 × 108	3.417 × 108	1.69 × 103	0.339
2	$u_1=0,u_2\ge 0$	2.77 × 107	5.03 × 107	3.53 × 102	0.552
3	u1 ≥ 0, u2 ≥ 0	6.113 × 107	4.198 × 108	3.305 × 104	0.145

The second cost-effectiveness analysis is the ACER with the formula as follows.

$$\text{ACER}=\frac{{\int }_0^T(\frac{c_1}{2}{u}_1^2+\frac{c_2}{2}{u}^2)dt}{{\mathcal{A}}^{inf}}.$$ (19)

Smaller values of ACER correspond to better performances. Again, it can be seen from Table 2 that the most cost-effective strategy is to implement media campaign and rapid testing simultaneously, rather than implement them as a single interventions.

5. Conclusions

In this work, mathematical analysis of the COVID-19 transmission model with a media campaign and rapid testing has been presented. The model constructed as a system of ordinary differential equations, which separate the human population based on their health status and also their awareness. The model accommodates the media campaign to develop the community awareness on COVID-19, such that this aware population can avoid infection from COVID-19 by conducting a health protocol, such as self-isolation, social distancing, medical mask and any other intervention that can reduce the transmission rate.

From the mathematical analysis on the model, we find that the COVID-19 free equilibrium is always locally asymptotically stable whenever the basic reproduction number is smaller than one. On the other hand, the COVID-19 endemic equilibrium always exists uniquely whenever the basic reproduction number is larger than unity. In any other case, the COVID-19 endemic equilibrium does not exist. Hence, a transcritical bifurcation occurs at basic reproduction number equal to one.

To estimate the parameter value, the model then tested with the incidence data from East Java, Indonesia. We find that the basic reproduction number in East Java is larger than one, which in this case has a high chance to reach an endemic COVID-19 situation if the intervention does not improve. To analyze the intervention strategies, we conduct our simulation as an optimal control problem. From the numerical results and cost-effectiveness analysis on the optimal control problem, we found that implementing both media campaigns and rapid testing simultaneously could give the best result compared to a single intervention. However, if the implementation should be conducted as a single intervention, then a media campaign should be implemented as a choice.

CRediT authorship contribution statement

Dipo Aldila: Conceptualization, Methodology, Formal analysis, Software, Investigation, Validation, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Proof of Theorem 1

From COVID-19 model in system (1), we have

$$\begin{array}{ccc}\hfill \frac{d{S}_u}{dt}{|}_{S_u=0,S_a\ge 0,E\ge 0,A\ge 0,I\ge 0,R\ge 0}& =& \Lambda +\alpha S_a>0,\hfill \\ \hfill \frac{d{S}_a}{dt}{|}_{S_u>0,S_a=0,E\ge 0,A\ge 0,I\ge 0,R\ge 0}& =& u_1{S}_u>0,\hfill \\ \hfill \frac{dE}{dt}{|}_{S_u>0,S_a\ge 0,E=0,A\ge 0,I\ge 0,R\ge 0}& =& ({\beta }_1{S}_u+{\beta }_2{S}_a)(I+\sigma A)\ge 0,\hfill \\ \hfill \frac{dA}{dt}{|}_{S_u>0,S_a\ge 0,E\ge 0,A=0,I\ge 0,R\ge 0}& =& p\delta E\ge 0,\hfill \\ \hfill \frac{dI}{dt}{|}_{S_u>0,S_a\ge 0,E\ge 0,A\ge 0,I=0,R\ge 0}& =& (1-p)\delta E+(\xi +u_2)A\ge 0,\hfill \\ \hfill \frac{dR}{dt}{|}_{S_u>0,S_a\ge 0,E\ge 0,A\ge 0,I\ge 0,R=0}& =& {\gamma }_{1}A+{\gamma }_{2}I\ge 0.\hfill \end{array}$$

It can be seen from the above calculation, all the rates are non-negative on the boundary planes of the non-negative of ${\mathbb{R}}_{+}^6$. Therefore, we can conclude that all the vector field direction is inward from the boundary planes. Hence, whenever the system starts in a non-negative ${\mathbb{R}}_{+}^6,$ all the solutions remain in the positive region only. Here the proof is completed. □

Appendix B. Proof of Theorem 2

Adding all equations in system (1) gives

$$\frac{dN}{dt}=\Lambda -\mu N-\varphi I\le \Lambda -\mu N.$$

Using the integrating factor technique, we have that N(t) fulfill

$$0\le N\le \frac{\Lambda }{\mu }+N\left(0\right)\exp (-\mu t).$$

Therefore, whenever the initial condition starts inside the region of Ω, then it will stay in this region. On the other hand, if the initial condition starts outside of Ω, then the solution will enter Ω and approach $\frac{\Lambda }{\mu }$ for t → ∞. Hence, we have that for t → ∞, we have $0\le N\le \frac{\Lambda }{\mu }$. Hence, we have the theorem. □

Appendix C. Derivation of ${\mathcal{R}}_0$

We use the formula introduced by author in [30] for the derivation of the basic reproduction number $\left({\mathcal{R}}_0\right)$ in this article. The sub-system of model (1) which involve only infected compartment is given by

$$J=\left[\begin{array}{ccc}-\delta -\mu & \sigma S_1{\beta }_1+\sigma S_2{\beta }_2& S_1{\beta }_1+S_1{\beta }_2\\ \delta p& -\mu -\xi -{\gamma }_1-u_2& 0\\ (1-p)\delta & \xi +u_2& -{\gamma }_2-\mu -\varphi \end{array}\right].$$

Note that J can be expressed as a summation between transition Σ and transmission T matrices, where

$$\begin{array}{ccc}\hfill \Sigma & =& \left[\begin{array}{ccc}-\delta -\mu & 0& 0\\ \delta p& -\mu -\xi -{\gamma }_1-u_2& 0\\ (1-p)\delta & \xi +u_2& -{\gamma }_2-\mu -\varphi \end{array}\right],\hfill \\ \hfill T& =& \left[\begin{array}{ccc}0& \sigma S_1{\beta }_1+\sigma S_2{\beta }_2& S_1{\beta }_1+S_2{\beta }_2\\ 0& 0& 0\\ 0& 0& 0\end{array}\right].\hfill \end{array}$$

Since T has two zero rows in the $2\text{nd}$ and $3\text{rd}$ row, the next generation matrix of system (1) is given by

$$\begin{array}{ccc}\hfill \mathbf{K}& =& -{\mathbf{E}}^{\prime }\mathbf{T}{\Sigma }^{-\mathbf{1}}\mathbf{E}=[\frac{(\sigma S_1^{*}{\beta }_1+\sigma S_2^{*}{\beta }_2)\delta p}{(\mu +\xi +{\gamma }_1+u_2)(\delta +\mu )}\hfill \\ & & +\frac{(S_1^{*}{\beta }_1+S_2^{*}{\beta }_2)\delta (1-p(\mu +{\gamma }_1)+\xi +u_2)}{(\delta +\mu )(\mu +\xi +{\gamma }_1+u_2)({\gamma }_2+\mu +\varphi )}],\hfill \end{array}$$ (C.1)

where $E=\left[100\right],$ while $S_u^{*}$ and $S_a^{*}$ is given in E ₀. Hence, the basic reproduction number of system (1) is given by the spectral radius of K. □

Appendix D. Proof of Lemma 1

To analyze the non-existence of positive roots of $\mathcal{P}\left(A\right)$ when ${\mathcal{R}}_0<1,$ we will use approach of the sign of $\frac{\partial A}{\partial {\mathcal{R}}_0}$ at $A=0$ and ${\mathcal{R}}_0=1$. Let ${\beta }_1^{*}$ as the bifurcation parameter which is taken from the solution of ${\mathcal{R}}_0=1$ respect to β ₁. Substituting ${\beta }_1^{*}$ into a ₂ and a ₁ will give us a ₂ and a ₁ as a function of ${\mathcal{R}}_0$. By implicit derivation to $\mathcal{P}\left(A\right),$ we have $\frac{\partial A}{\partial {\mathcal{R}}_0}$ evaluated at $A=0$ and ${\mathcal{R}}_0=1$ as follows :

$$\frac{\partial A}{\partial {\mathcal{R}}_0}=\frac{p\mu (\alpha +\mu +u_1)(\mu +\xi +{\gamma }_1+u_2)(\delta +\mu )}{a_1\left({\mathcal{R}}_0\right)},$$ (D.1)

where $a_1\left({\mathcal{R}}_0\right)=k_2{\beta }_2^2+k_1{\beta }_2$ with

$$\begin{array}{ccc}\hfill k_2& =& \delta {\beta }_2^2{u}_1\Lambda (\delta +\mu )(\mu +\xi +{\gamma }_1+u_2)(\mu p\sigma +p\varphi \sigma +p\sigma {\gamma }_2\hfill \\ & & {+(1-p)(\mu +{\gamma }_1)+\xi +u_2)}^2>0\hfill \\ \hfill k_1& =& -p^2{({\gamma }_2+\mu +\varphi )}^2\mu (\mu +\xi +{\gamma }_1+u_2)(\delta +\mu )(\alpha +\mu +u_1)<0.\hfill \end{array}$$

Since the discriminant of $a_1\left({\mathcal{R}}_0\right)$ which given by $k_1^2-4k_{2}0=k_1^2>0$ when ${\mathcal{R}}_0=1,$ then we always have that $a_1\left({\mathcal{R}}_0\right)$ is always positive. Hence, we have that $\frac{\partial A}{\partial {\mathcal{R}}_0}$ is always positive at $A=0,{\mathcal{R}}_0=1$. Hence, combine this results and Theorem 4, we have no positive roots of polynomial $\mathcal{P}\left(A\right)$ when ${\mathcal{R}}_0<1$. Hence, the proof is complete. □

Appendix E. Proof of Theorem (5)

Based on [46], our optimal control problem should satisfy the following conditions :

• 1.The solutions of system (11) which equipped with time-dependent control u ₁ and u ₂ is non empty.
• 2.Γ should be closed and convex and the state system can be written as a linear function of control variables u ₁ and u ₂, where the coefficients depending on state variables and time t.
• 3.
  Integrand of

  $$\mathcal{L}=E+A+I+\frac{c_1}{2}{u}_1^2+\frac{c_2}{2}{u}_2^2$$

  is convex on Γ and $\mathcal{L}\ge f(u_1,u_2)$. Note that f is a continuous function and

  $$\underset{\left|\right(u_1,u_2\left)\right|\to \infty }{lim}\frac{f(u_1,u_2)}{\left|\right(u_1,u_2\left)\right|}=\infty .$$

  Note that | · | represent the norm.

First of all, from Theorem (2), we have that S_u(t), S_a(t), E(t), A(t), I(t), and R(t) are bounded by Λ/μ. Hence, the solutions of system (11) is always bounded whenever u ₁ and u ₂ bounded in Γ. The right hand side of the time-dependent control COVID-19 model in (11) satisfies the Lipschitz condition with respect to S_u, S_a, E, A, I and R. Hence, we fulfilled (1) based on Picard-Lindelö theorem [47].

By definition, given the control set Γ, where u_i ∈ [0, 1]² for $i=1,2,$ then we have Γ is closed. Using the definition of convex set (Proposition 2.4 in [48]), for any arbitrary points y and z in Γ, where $y=(y_1,y_2),z=(z_1,z_2),$ we have that

$$\zeta y_i+(1-\zeta )z_i\in {[0,1]}^2,\forall \zeta \in [0,1],i=1,2.$$

Thus, $\zeta y+(1-\zeta )z\in \Gamma$ implying Γ is convex. The time-dependent control model in (11) is linear in control variables u ₁ and u ₂ with coefficients depending on the state variables S_u and A. Therefore, we have condition (2).

The integrand $\mathcal{L}$ is convex due to the quadratic form of u ₁ and u ₂. Furthermore,

$$\mathcal{L}=E+A+I+\frac{c_1}{2}{u}_1^2+\frac{c_2}{2}{u}_2^2\ge \frac{c_1}{2}{u}_1^2+\frac{c_2}{2}{u}_2^2.$$

By choosing $c_3=\min \{c_1,c_2\}>0,$ and $f(u_1,u_2):=c_3(u_1^2+u_2^2),$ yields

$$\mathcal{L}=E+A+I+\frac{c_1}{2}{u}_1^2+\frac{c_2}{2}{u}_2^2\ge f(u_1,u_2).$$

It is clear that f(u ₁, u ₂) is continuous and satisfy $\underset{\left|\right(u_1,u_2\left)\right|\to \infty }{lim}\frac{f(u_1,u_2)}{\left|\right(u_1,u_2\left)\right|}=\infty .$ Thus, condition (3) fulfilled. Based on [45], [46], the proof is completed. □

Appendix F. Proof of Theorem (6)

The adjoint system in (15) is taken from the derivative of $\mathcal{H}$ respect to each state variable as follows

$$\begin{array}{ccc}& & \frac{d{\lambda }_1}{dt}=-\frac{\partial \mathcal{H}}{\partial S_u},\frac{d{\lambda }_2}{dt}=-\frac{\partial \mathcal{H}}{\partial S_a},\frac{\partial {\lambda }_3}{\partial t}=-\frac{\partial \mathcal{H}}{\partial E},\hfill \\ & & \frac{d{\lambda }_4}{dt}=-\frac{\partial \mathcal{H}}{\partial A},\frac{d{\lambda }_5}{dt}=-\frac{\partial \mathcal{H}}{\partial I},\frac{d{\lambda }_6}{dt}=-\frac{\partial \mathcal{H}}{\partial R},\hfill \end{array}$$

with the transversality condition

$${\lambda }_1\left(t_f\right)={\lambda }_2\left(t_f\right)={\lambda }_3\left(t_f\right)={\lambda }_4\left(t_f\right)={\lambda }_5\left(t_f\right)={\lambda }_6\left(t_f\right)=0.$$

Furthermore, taking the first derivative of $\mathcal{H}$ respect to u ₁ and u ₂ gives

$$\frac{\partial \mathcal{H}}{\partial u_1}=c_1{u}_1-S_u({\lambda }_1-{\lambda }_2),\frac{\partial \mathcal{H}}{\partial u_2}=c_2{u}_2-A({\lambda }_4-{\lambda }_5).$$

Solving $\frac{\partial \mathcal{H}}{\partial u_i}=0$ respect to $i=1,2$ gives

$$u_1^{†}=\frac{S_u({\lambda }_1-{\lambda }_2)}{c_1},u_2^{†}=\frac{A({\lambda }_4-{\lambda }_5)}{c_2}.$$

By standard control arguments involving the lower bound $u_i^{\min }=0$ and upper bound $u_i^{\max }=1,$ it follows that

$$\begin{array}{ccc}\hfill u_1^{*}& =& \max \{0,\min \{1,\frac{S_u({\lambda }_1-{\lambda }_2)}{c_1}\}\},\hfill \\ \hfill u_2^{*}& =& \max \{0,\min \{1,\frac{A({\lambda }_4-{\lambda }_5)}{c_2}\}\}.\hfill \end{array}$$

Hence, the proof is complete. □