Atomic-Level Characterization of the Methadone-Stabilized Active Conformation of µ-Opioid Receptor

Abstract

Methadone is a synthetic opioid agonist with notoriously unique properties, such as lower abuse liability and induced relief of withdrawal symptoms and drug cravings, despite acting on the same opioid receptors triggered by classic opioids—in particular the µ-opioid receptor (MOR). Its distinct pharmacologic properties, which have recently been attributed to the preferential activation of β-arrestin over G proteins, make methadone a standard-of-care maintenance medication for opioid addiction. Although a recent biophysical study suggests that methadone stabilizes different MOR active conformations from those stabilized by classic opioid drugs or G protein–biased agonists, how this drug modulates the conformational equilibrium of MOR and what specific active conformation of the receptor it stabilizes are unknown. Here, we report the results of submillisecond adaptive sampling molecular dynamics simulations of a predicted methadone-bound MOR complex and compare them with analogous data obtained for the classic opioid morphine and the G protein–biased ligand TRV130. The model, which is supported by existing experimental data, is analyzed using Markov state models and transfer entropy analysis to provide testable hypotheses of methadone-specific conformational dynamics and activation kinetics of MOR.

SIGNIFICANCE STATEMENT

Opioid addiction has reached epidemic proportions in both industrialized and developing countries. Although methadone maintenance treatment represents an effective therapeutic approach for opioid addiction, it is not as widely used as needed. In this study, we contribute an atomic-level understanding of how methadone exerts its unique function in pursuit of more accessible treatments for opioid addiction. In particular, we present details of a methadone-specific active conformation of the µ-opioid receptor that has thus far eluded experimental structural characterization.

Introduction

Opioid addiction is the most severe form of opioid use disorders (OUDs), and together, OUDs represent a major public health concern worldwide [results from the 2018 National Survey on Drug Use and Health (Substance Abuse and Mental Health Services Administration, 2018)] owing to the high mortality from respiratory depression induced by high doses of opioids activating brainstem µ-opioid receptors (MORs) (Contet et al., 2004; Dahan et al., 2010). This so-called “opioid crisis” has been declared a national public health emergency in the United States under federal law (https://www.whitehouse.gov/opioids/) and has spearheaded aggressive initiatives to accelerate scientific solutions to this national disaster, including the development of novel medications for the treatment of opioid overdose and OUDs (Rasmussen et al., 2019). The reason for this is that in spite of demonstrably useful treatments for addiction and other OUDs, these are impaired by residual symptoms and high discontinuation rates (Morgan et al., 2019).

One of the most widely used effective treatments for opioid addiction (Kreek et al., 2019) involves the prolonged prescription of methadone as an alternative to the abused opioid. Methadone is a synthetic opioid with a different chemical structure compared with other clinically prescribed opioids (e.g., morphine, oxycodone, fentanyl, etc.) as well as a unique and distinct pharmacological profile. A MOR agonist like morphine and heroin, methadone has less abuse potential than these classic opioid drugs (Kreek, 2000) and is an effective antinociceptive agent in patients with pain that do not respond to other analgesics (Weschules and Bain, 2008). Although approximately 20%–40% of individuals drop out of methadone maintenance treatment (Kreek et al., 2019), this treatment still has greater retention than buprenorphine maintenance, making one wonder what makes methadone so special.

The underlying mechanism by which methadone exerts its unique pharmacological effects compared with other clinically used opioid agonists is not fully understood. Recent studies suggest that the unique pharmacological profile of methadone might be due to its ability to induce potent MOR internalization accompanied by strong β-arrestin-2 recruitment, similar to fentanyl but different from morphine (Doi et al., 2016). The concept whereby a ligand may exert different pharmacological profiles by preferentially activating a signaling pathway over another has gained increasing popularity in the field of G protein–coupled receptors (GPCRs), although this has been recently challenged (Gillis et al., 2020; Kliewer et al., 2020). At the atomic level of detail, one simple explanation for the suggested β-arrestin–biased MOR agonism of methadone is that this molecule is capable of stabilizing a different set of conformations of MOR compared with those stabilized by morphine or a G protein–biased ligand. As predicted, recent interferometry experiments quantifying methadone efficacy by measuring the binding of an active MOR-specific biosensor (nanobody-39) to a purified receptor suggest that this drug stabilizes an active conformation of MOR with decreased affinity for nanobody-39 as compared with other ligands (Livingston et al., 2018). However, the resolution of these experiments precluded visualization of the methadone-bound MOR complex stucture, and the question remains about the molecular determinants that are responsible for the unique pharmacological effects of methadone.

In the absence of experimental structures of the methadone-bound MOR complex, computational methods, particularly molecular dynamics (MD) simulations, can provide useful insights into the methadone-induced MOR activation mechanism. To shed light on the atomic details of the unique MOR conformation stabilized by methadone, we carried out submillisecond adaptive-sampling MD simulations of a predicted methadone-bound MOR complex and analyzed their results using Markov state models (MSMs) and transfer entropy analysis. In addition to verifying inferences from published low-resolution experiments, this study provides new testable hypotheses of methadone-specific conformational dynamics and activation kinetics of MOR.

Materials and Methods

System Setups for Molecular Docking and Simulations.

The crystal structure of the active mouse MOR corresponding to Protein Data Bank identification (PDB id) code 5C1M was prepared for automated ligand docking using the default Protein Prep Wizard protocol in the Schrödinger 2018-1 suite (Schrödinger Release, 2018). Missing residues in helix 8 (Arg345–Ile352) were added with MODELER (Eswar et al., 2007) using the corresponding region of the inactive MOR crystal structure (PDB id: 4DKL) as a template for homology modeling. A total of 50 models were generated, and the structure with the top Discrete Optimized Protein Energy (Shen and Sali, 2006) score was selected. A docking grid centered at the center of mass of the crystallized ligand (BU72) was generated using the Schrödinger Receptor Grid generation tool. L-methadone was docked to the orthosteric pocket of the active MOR using the default induced-fit docking protocol of Schrödinger 2018-1 suite, which uses Glide for docking and scoring. Since the resulting top-scoring docked poses of methadone had very similar energy scores, we used an established metadynamics-based strategy (Clark et al., 2016) to identify the most stable binding mode among them. Thus, the five top-scoring docked poses of methadone were embedded in a 1-palmitoyl-2-oleoyl phosphatidyl choline/10% cholesterol bilayer, solvated with the TIP3P water model, and neutralized using NaCl counterions (0.15 M) to enable their metadynamics rescoring (Clark et al., 2016) in a natural lipid environment. The systems were embedded in the lipid bilayer with the Membrane Builder functionality of the CHARMM-GUI webserver (Jo et al., 2008; Lee et al., 2016), which yielded systems containing MOR (residues Ser64–Ile352) bound to both methadone and the crystallized nanobody, 144 1-palmitoyl-2-oleoyl phosphatidyl choline molecules, 16 cholesterol molecules, ∼11,360 water molecules, 31 sodium ions, and 43 chloride ions, totaling ∼61,220 atoms.

Equilibration was carried out with Gromacs 2016.3 (Abraham et al., 2015) using the CHARMM36 force field (MacKerell et al., 1998; Best et al., 2012) for protein, lipids, and solvent and validated CHARMM General Force Field (Vanommeslaeghe et al., 2010) parameters for L-methadone. Each of the five systems was first minimized using the steepest descent energy minimization method for 5000 steps and then equilibrated for 100 picoseconds in the constant number, volume, temperature ensemble with positional restraints on all protein, ligand, and lipid heavy atoms and for an additional 15 nanoseconds in the constant number, pressure, temperature (NPT) ensemble. The NPT equilibration run was performed in 13 steps, the first 12 of which employed gradually decreasing positional restraints on the heavy atoms of lipids, protein sidechains, protein backbone, and, lastly, the ligand. The last step consisted of a 3-nanosecond unrestrained equilibration run in the NPT ensemble. During equilibration, system temperature and pressure were kept at 300 K and 1 bar, respectively, using velocity rescale (Bussi et al., 2007) for temperature coupling and the Parrinello-Rahman barostat (Parrinello and Rahman, 1981) for semi-isotropic pressure coupling. All bonds involving hydrogen atoms were constrained using the LINear Constraint Solver algorithm. Short-range nonbonded interactions were cut off at 12 Å, and long-range electrostatic interactions were computed using the particle mesh Ewald summation with a Fourier grid spacing of 1.2 Å. All production MD simulations reported in this study (see summary in Supplemental Table 1) were carried out using the same parameters as described above but with the thermostat switched to Nose-Hoover (Hoover, 1985) and simulation timestep switched to 4 fs with a mass repartition scheme (Feenstra et al., 1999).

Ten metadynamics simulations were run for each of the five equilibrated methadone-MOR systems using the Plumed 2.3.1 plugin (Tribello et al., 2014) and, as collective variable, the root-mean-square deviation (RMSD) of the methadone-heavy atoms plus the heavy backbone atoms of a distant, stable segment of the protein (residues 75–78) away from the binding pocket, relative to the equilibrated input structure. The heavy backbone atoms included in the RMSD calculation, hereafter referred to as “anchor atoms,” were not used as restraints in these simulations but rather to provide a frame of reference for RMSD values. Each metadynamics simulation was run for 10 nanoseconds with Gaussian hills of height 0.21 kJ/mol and width 0.02 nm deposited every 4 picoseconds. Methadone-binding pose stability was assessed based on the lowest average RMSD of the ligand heavy atoms plus the anchor atoms, calculated after averaging over the 10 independent metadynamics runs as follows:

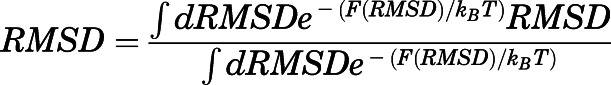where

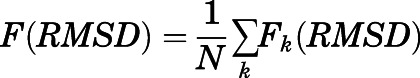is the free energy as a function of the RMSD collective variable, 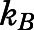is Boltzmann’s constant, and 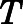is the temperature. The induced-fit docking pose (IFDP) with the lowest average RMSD (IFDP2; see Supplemental Fig. 1) was simulated for additional 100 nanoseconds using unbiased MD, and a representative conformation from the simulation was used as the starting point for adaptive sampling simulations aimed at exploring receptor activation/deactivation pathways induced by methadone (see below). A simulation setup starting from the inactive mouse MOR (PDB id: 4DKL) was also prepared. Missing residues of the intracellular loop (ICL) 3 in the inactive crystal structure were added with MODELER (Eswar et al., 2007) using the corresponding region of the active MOR crystal structure (PDB id: 5C1M) as a template for homology modeling. The methadone pose in the inactive MOR structure was obtained by substituting the crystal ligand with L-methadone after aligning the crystal inactive structure with the most stable active L-methadone–MOR complex obtained by metadynamics rescoring (IFDP2), which was followed by minimization of the binding pocket residues. This L-methadone–MOR inactive complex was prepared for adaptive sampling MD simulations using the same protocol as described for the active MOR system.

Adaptive Sampling Strategy.

The equilibrated active methadone-MOR complex from metadynamics rescoring (IFDP2) was prepared for adaptive sampling simulations (Doerr and De Fabritiis, 2014) after removing the nanobody and resolvating the system with TIP3P water. Removal of the nanobody was necessary to allow seamless conformational transitions between inactive and active states of the receptor. Na⁺ and Cl^– ions were added to neutralize the overall charge and achieve a 0.15-M physiologic concentration. Two independent equilibrations (differing only in the randomization of the initial velocities) of 50 and 500 nanoseconds, respectively, were performed for this system, and the last frame of the two simulations was used to start independent adaptive simulations of the methadone-bound MOR complex on multiple computational resources (see Acknowledgments) but using the same topology and force field. Specifically, the strategy consisted of running sequential rounds of simulations, starting new simulations from undersampled regions of the system’s conformational space identified using MSMs obtained from the simulations of previous rounds.

Three different batches of simulation (I-III) of ∼0.23 milliseconds, ∼0.02 milliseconds, and ∼0.07 milliseconds, respectively, for a total of ∼0.32 milliseconds (Supplemental Table 1), were generated to maximally use the computational resources at our disposal. The first batch (I) was run on Anton2 under NPT conditions using the multigrator framework with a REference System Propogator Algorithm scheme (Tuckerman et al., 1992). Trajectory frames were saved every 240 picoseconds. The first six adaptive sampling rounds of batch I were started from the active MOR conformation and respawned using the least populated microstates identified from MSMs built using 1) the transmembrane (TM) TM3-TM6 distance, defined by the distance between C_α-atoms of residues Arg165^3.50 and Thr279^6.34 and 2) the RMSD of the so-called NPxxY motif (specifically, residues Asn332^7.49, Pro333^7.50, Val334^7.51, Leu335^7.52, Tyr336^7.53, and Ala337^7.54) from the corresponding region in the MOR inactive crystal structure (PDB id: 4DKL). To further speed up the conformational sampling, an additional adaptive round was initiated from 10 replicas of the inactive MOR crystal structure with each system independently equilibrated for 10 nanoseconds and differing only in the randomization of the initial velocities. This was followed by six additional rounds of simulations in batch I, and two additional batches of simulations were run using Gromacs 2016.3. In particular, batch II, which consisted of 12 rounds of adaptive simulations (∼17 microseconds), used as an exploration metric the RMSD from the MOR active and inactive crystal structures, whereas batch III, which consisted of 67 rounds (∼67 microseconds), used as an exploration metric distances between the protein C_α atoms (one every three between residues Ser64 and Ile352 to reduce computational cost).

Markov State Models.

MSMs provide a mathematical framework to combine the data from several different MD simulation runs into one statistical model that can then be used to derive the thermodynamic, kinetic, and structural properties of the system under study (Husic and Pande, 2018). The time-lagged independent component analysis (tICA) (Pérez-Hernández et al., 2013) was used here to identify optimal reaction coordinates to build MSMs that describe MOR conformations as well as methadone-MOR interactions sampled during simulations. Specifically, protein conformations were encoded into the following structural descriptors: 1) 4656 C_α-C_α distance pairs calculated for 97 uniformly spaced MOR residues (one every three to reduce computational cost) and 2) 2396 sidechain-sidechain contact maps (using a cut-off of 7 Å on the minimum distance between sidechain-heavy atoms) for all pairs that had a contact in either the active or inactive MOR crystal structures. Likewise, methadone-MOR contacts were described using 289 residue–ligand pair contact maps, with contacts between the ligand and each of the MOR residues defined using a cut-off of 7 Å on the minimum distance between residue and ligand-heavy atoms. Overall, a total of 7341 structural descriptors per trajectory frame were combined with tICA to obtain reaction coordinates. Reasonably converged MSMs were obtained by finely discretizing the conformational space defined by six dominant tICA components into 1000 microstates using the k-means clustering algorithm. The MSM transition matrix was derived from the normalized counts of transitions occurring in a lag time (τ) between the microstates using maximum likelihood estimation under the constraint of detailed balance. A lag time τ of 9.6 nanoseconds was chosen by inspecting the convergence of the implied timescales of the model over increasing lag times τ (see Supplemental Fig. 2a), and the Chapman-Kolmogorov test (see Supplemental Fig. 3) was used to assess the consistency between the MSMs and the MD simulations. To enable a fair comparison with the results of previously reported adaptive sampling simulations we carried out on morphine-bound and TRV130-bound MOR systems (Kapoor et al., 2017), we recalculated the MSMs for these systems using the same number of six tICA components used to build the MSM model of the methadone-MOR system reported herein. Supplemental Tables 2–7 list the top ∼1% structural descriptors involved in the slowest conformational degrees of freedom accessible to methadone-bound MOR identified by tICA dimensions 1–6, respectively. The convergence of the implied timescales of the models calculated for the morphine-MOR and TRV130-MOR systems over increasing lag times τ is shown in Supplemental Fig. 2, b and c, respectively, whereas results of the Chapman-Kolmogorov tests carried out on the morphine-MOR and TRV130-MOR systems are shown in Supplemental Figs. 4 and 5, respectively.

Sixteen kinetic macrostates (metastable states) were identified for each of the three ligand-bound MOR systems by lumping the microstates of each system together based on their kinetic similarity, using spectral clustering of the transition matrix with the robust Perron cluster analysis algorithm (Röblitz and Weber, 2013). The equilibrium probabilities of these metastable states were calculated as the sum of the probabilities of microstates assigned to a given macrostate and are shown in Supplemental Fig. 6, a–c for MOR bound to methadone, morphine, and TRV130, respectively.

Averages of different order parameters reported in the Results section for a given macrostate 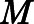were calculated as weighted averages over the microstates 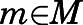assigned to that macrostate:

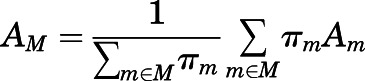where A is a structural property, the weights π_m are the steady-state probabilities of the microstates, and A_m is the frame average for microstate m.

A macrostate was assigned to the inactive region of the conformational space if the average distances 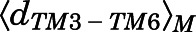between C_α atoms of residues Arg165^3.50 and Thr279^6.34 and the average C_α atom RMSD 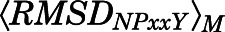of the NPxxYA region (residues Asn332^7.49–Ala337^7.54) were below 10 and 2.5 Å, respectively. Conversely, a macrostate was assigned to the MOR active region if 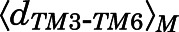≥ 10Åand 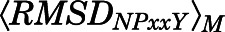≥ 2.5 Å. Macrostates characterized by 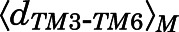≥ 10 Å and 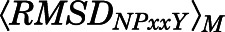< 2.5 Å or 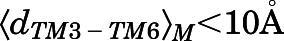and 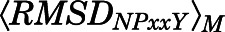≥ 2.5 Å were assigned to intermediate I or II regions, respectively. The total number of macrostates was chosen such that the intrastate fluctuations of d_TM3–TM6 and RMSD_NPxxY would be less than a few angstroms. The HTMD (Doerr et al., 2016) and PyEMMA (Scherer et al., 2015) libraries were used to perform tICA and MSM analyses.

To more clearly compare the activation kinetics of methadone-, morphine-, and TRV130-bound MOR systems, MSM MFPTs were calculated for coarse-grained versions of their dimensional MSM transition matrices. These coarse-grained matrices were obtained by aggregating the Perron cluster analysis–derived kinetic macrostates within each of the aforementioned conformational regions (active, inactive, intermediate I, and intermediate II) one by one, starting from the most probable state in a given region (Supplemental Table 8). The aggregation of macrostates continued until the time-dependent correlation functions of the occupancy of the states in the coarse-grained model matched the correlation functions of the full system, following the strategy reported in (Hummer and Szabo, 2015).

Calculation of RMSD between Representative Conformations of Aggregated Kinetic Macrostates within Conformational Regions.

To more easily compare ligand-specific conformational states that are kinetically different, 200 representatives were extracted from each aggregated kinetic macrostate with probability proportional to the equilibrium distribution. Pairwise RMSD was calculated as:

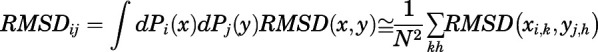where P_i(x) and P_j(y) are the distributions of receptor conformations in states 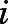and 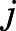, respectively, x_i,k and y_j,h are sampled conformational states, and 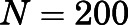is the sample size. The RMSD was calculated on the C_α atoms of TM2-7 and helix 8 (H8) after optimal alignment. When 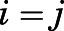, the sum was restricted to the terms 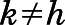so that the values of 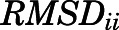reflect the average difference between conformations in state 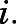The RMSD between different states of methadone-, morphine-, and TRV130-bound systems are reported in Supplemental Fig. 7.

Transfer Entropy Analysis.

The transfer entropy between two structural descriptors X and Y is defined as the conditional mutual information:

This quantity captures the causality of correlated motions, thus allowing a systematic identification of the structural determinants of allosteric communication in proteins (Hacisuleyman and Erman, 2017). Similar concepts have also been applied to GPCRs (Bhattacharya and Vaidehi, 2014; Bhattacharya et al., 2016; Vaidehi and Bhattacharya, 2016; Nivedha et al., 2018). Here, the MDEntropy package (http://msmbuilder.org/mdentropy/0.3.0/) was used to calculate pairwise transfer entropy values between 2741 residue-residue contact pairs and 289 residue-ligand contacts so that a total of 3030 structural descriptors for each trajectory frame were used to obtain the transfer entropy matrix. The receptor-receptor contacts were selected with a cut-off of 7 Å on the minimum distance between heavy atoms in either the active or inactive MOR crystal structures. To reduce the computational cost, for each ligand-bound system, three independent transfer entropy calculations were performed on a randomly selected set of 30% of the trajectories, and the average of these three runs was used as the final transfer entropy matrix for subsequent analysis. The resulting transfer entropy matrix for each of the ligand-bound MOR systems was used in the NetworkX python library (Hagberg et al., 2008) to calculate a directed graph, with each node in the graph representing a contact (either residue-residue or residue-ligand) and the directed edge between two nodes indicating the transfer entropy between them.

The information flow from the ligand to the intracellular region of the receptor undergoing the largest conformational change associated with receptor activation, specifically the TM6 outward movement, was characterized by calculating the set of paths 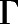connecting the set of ligand-protein nodes to the residue-residue nodes capturing the TM3-TM6 movement (Arg165^3.50-Thr279^6.34 contact), wherein the “length” of each edge is the negative logarithm of the transfer entropy value of that edge. The importance of each node (i.e., of each contact) in regulating MOR deactivation (E.N. Feinberg et al., preprint, DOI: https://doi.org/10.1101/170886) was assessed by computing the overall normalized flux contributed by a node in the shortest 1000 paths in 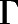. Specifically, the contribution of a given contact 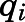to the allosteric communication between the ligand and the TM3-TM6 distance was calculated as:

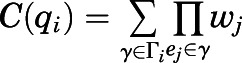where q_i is one of the contact descriptors, Γ_i is the set of paths connecting the ligand-residue nodes to residue-residue nodes capturing the TM3-TM6 movement, γ is one path in this set, e_j is an edge between two structural descriptors in path γ, and w_j is the transfer entropy value of that edge. Structural descriptors that are most significantly contributing to the transfer entropy between the ligand-binding pocket and the TM6 outward movement exemplifying receptor activation (>1% flux) are listed in Supplemental Table 9.

Ligand-Receptor Interaction Fingerprints.

Ligand-MOR interaction fingerprints were calculated over the entire conformational space sampled by the methadone-bound MOR system during the transition between inactive and active states achieved by adaptive sampling simulations and compared with those calculated for analogous explorations of morphine-bound and TRV130-bound MOR systems from previously published simulations (Kapoor et al., 2017). Specifically, ligand-receptor interaction fingerprints were calculated for a total of 1000 conformations selected based on microstate probability within each of the identified 16 macrostates of methadone-, morphine-, or TRV130-bound MOR systems, and an overall fingerprint for each residue and ligand moiety (see details in Supplemental Fig. 8) was obtained as a weighted average of the interactions in the 16 macrostates of each system using an in-house python script. For each MOR residue, interactions with each of the ligand moieties were calculated as a seven-bit representation based on the following seven types of interactions: apolar interactions (carbon-carbon atoms in contact), face-to-face and edge-to-face aromatic interactions, hydrogen-bond interactions with the protein as hydrogen-bond donor or hydrogen-bond acceptor, and electrostatic interactions with positively or negatively charged residues. A distance cut-off of 4.5 Å was used to define apolar interactions, whereas a cut-off of 4 Å was used to describe aromatic and electrostatic interactions. Interactions were calculated for residue sidechain atoms only. The average probabilities and errors for each interaction were estimated using a two-state Markov model sampling the transition matrix posterior distribution using standard Dirichlet priors for the transition probabilities as described in (Trendelkamp-Schroer et al., 2015).

Results

Predicted Binding Mode of Methadone to MOR.

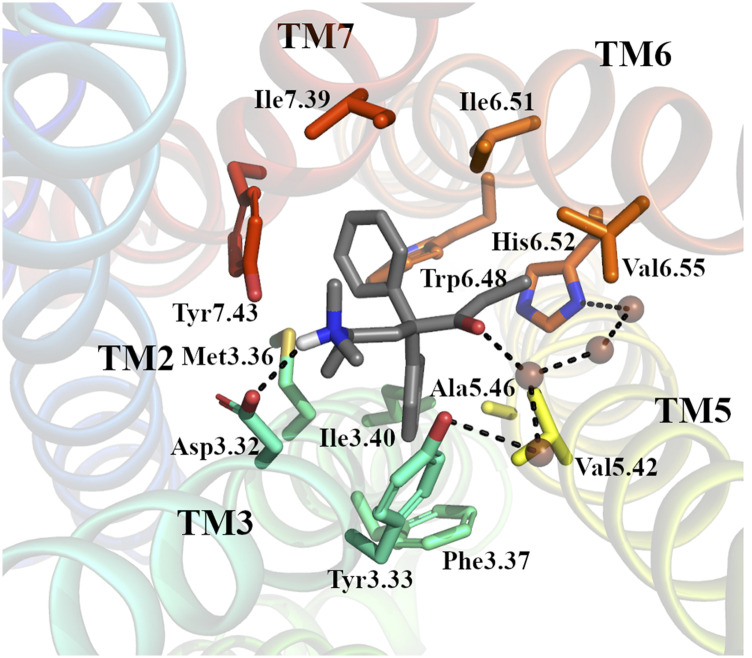
Initial binding of L-methadone to the orthosteric binding pocket of the active MOR crystal structure 5C1M was predicted using an established induced-fit docking protocol that uses metadynamics for rescoring of docking poses (Clark et al., 2016). The strategy, which is described in detail in the Materials and Methods section, led to the identification of IFDP2 as the preferred binding pose of methadone given its lowest average RMSD from the equilibrated docking pose (see Supplemental Fig. 1). In this pose (Fig. 1 and Supplemental Fig. 1_IFDP2.pdb in Supplemental Information), similarly to the two crystal structures of MOR bound to morphinan ligands, L-methadone forms a stable (>70% of simulation frames) ionic interaction between its protonated tertiary amine and Asp147^3.32 as well as water-mediated interactions between its carbonyl group and both His297^6.52 and Tyr148^3.33. Stable (>70% of simulation frames) hydrophobic/aromatic ligand-receptor interactions are also formed between methadone and residues on TM3, TM5, TM6, and TM7. Although one of the two phenyl groups at position 4 on methadone points toward TM3 and TM5 and forms an aromatic interaction with residue Phe152^3.37 and hydrophobic interactions with residues Tyr148^3.33, Met151^3.36, Val236^5.42, and Ala240^5.46, the other one points toward TM6 and TM7, forming an aromatic interaction with Trp293^6.48 and hydrophobic interactions with Ile296^6.51, Ile322^7.39, and Tyr326^7.43. The methadone’s ethyl group points toward TM6 and engages in hydrophobic interactions with Ile296^6.51, His297^6.52, and Val300^6.55. In contrast, the methadone’s chiral methyl and the dimethylamino group at position 6 are located between TM3 and TM7 and are involved in hydrophobic interactions with residues Tyr148^3.33, Met151^3.36, and Tyr326^7.43 (see Fig. 1). Superscripts on these residues and throughout the text refer to the Ballesteros-Weinstein generic numbering sheme (Ballesteros and Weinstein, 1995), in which the first number corresponds to the helix, and the second number is the position relative to the most conserved residue in that helix, which is assigned a value of 50.

Fig. 1.

The binding pose of methadone to active MOR. Representative pose from 100-nanosecond simulation of the top-ranked IFDP2 by metadynamics. MOR is shown in cartoon representation with helices colored from blue (TM1) to red (TM7). Methadone (in gray) and residue side chains forming interactions in more than 70% simulation frames (see Supplemental Fig. 8) are shown as sticks. Water molecules are shown as brown spheres. Dotted lines illustrate hydrogen bond interactions.

The equilibrated methadone-MOR complex shown in Fig. 1 was simulated for ∼0.3 milliseconds in an explicit lipid-water environment using an adaptive sampling protocol (see Materials and Methods for details of the system setup and simulations) that enabled full exploration of the conformational transition between the active and inactive crystallographic states of MOR. This thorough exploration was verified by projecting the trajectory frames of the methadone-MOR simulation onto established order parameters that describe receptor activation (see below) as well as by inspecting the RMSD from the active or inactive crystal structures of MOR (Supplemental Fig. 9). Although the methadone mode of binding in the active conformation of MOR remained similar, in average, to the originally predicted one, different binding poses (e.g., see Fig. 5 and Supplemental Fig. 5_Macrostate16.pdb in Supplemental Information) were acquired by the ligand during the conformational transition between inactive and active states of the receptor. Comparison of the ligand-receptor interaction fingerprints calculated for methadone, morphine, and TRV130 over the entire conformational transition between inactive and active conformations sampled by MOR during adaptive sampling simulations (Supplemental Fig. 8) draws attention to three residues that uniquely interact with the carboxyethyl moiety of methadone, specifically Leu121^2.57, Gln124^2.60, and Tyr128^2.64. Notably, two MOR residues that interact with both morphine and TRV130 either do not form interaction with methadone (residue Lys233^5.39) or interact with methadone with a less than 10% probability (residue Tyr148^3.33).

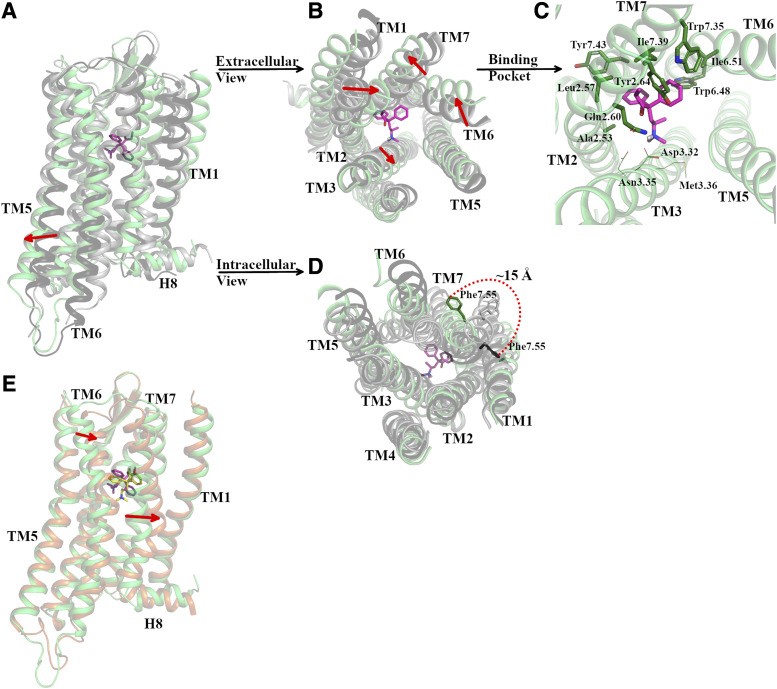
Fig. 5.

Representative conformation of the most probable macrostate (#16, I2₁) of the methadone-MOR system compared with active and inactive MOR crystal structures as well as to the second most probable macrostate (#15, I2₂). Cartoon representations of the receptor are in green, orange, dark gray, and light gray colors for macrostate #16, macrostate #15, active MOR crystal structures, and inactive MOR crystal structures, respectively. The ligand bound to the representative MOR conformation of macrostate #16 is shown in magenta sticks, whereas the ligand bound to the representative MOR conformation of macrostate #15 is shown in yellow sticks. (A) Vertical view of the MOR, (B) extracellular view of MOR, (C) methadone binding pose with MOR residues shown as sticks if forming interactions with the ligand in >70% of simulation frames or lines if interacting with the ligand in 40%–60% of frames. (D) Intracellular view of MOR. (E) Vertical view of the representative conformation of macrostate #16 (green cartoon) superimposed onto macrostate #15 (orange cartoon) with bound methadone shown in magenta and yellow sticks, respectively. The direction of red arrows in (A, B, and E) indicates the outward or inward movements of the TM segments, whereas the red-dotted curve in (D) indicates the change in orientation of Phe338^7.55 in macrostate #16 with respect to its position in the active MOR crystal structure.

The Conformational Landscape of Methadone-Bound MOR.

The dynamics of the methadone-bound MOR complex were analyzed via MSMs and compared with the dynamics of MOR bound to morphine or the G protein–biased agonist TRV130 from our previously published high-throughput MD simulations (Kapoor et al., 2017), reanalyzed in this study with similarly constructed MSMs. Briefly (see Materials and Methods section for details), we used tICA dimensionality reduction to compare the conformational space of the three ligand-receptor systems in terms of structural descriptors of protein conformation and protein-ligand interactions. The significantly different tICA components obtained for the methadone-bound MOR systems compared with morphine-bound and TRV130-bound receptors [see (Kapoor et al., 2017)] prevented the selection of the same microstates to build the MSMs for the three systems. Thus, we used each system’s tICA components to build validated MSMs of the three ligand-bound systems (see implied timescales in Supplemental Fig. 2 and Chapman-Kolmogorov tests in Supplemental Figs. 3–5). Comparison of the slowest relaxation timescales of the three ligand-bound systems (Supplemental Fig. 2) suggests that the methadone-MOR system undergoes significantly slower activation dynamics (by ∼2 orders of magnitude) compared with the morphine-MOR and TRV130-MOR systems.

To further investigate possible conformational and kinetic uniquenesses of the methadone-MOR system compared with MOR bound to morphine or TRV130, we defined and characterized 16 macrostates based on kinetic similarity. Supplemental Fig. 6 reports the equilibrium probabilities of these macrostates for each of the three ligand-bound MOR systems. Projection of the trajectory frames of each ligand-bound MOR complex onto two order parameters capturing the most pronounced conformational changes associated with receptor activation, namely, 1) the TM6 outward displacement (measured by the distance between the C_α atoms of residues Arg165^3.50 and Thr279^6.34, herein termed 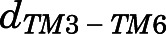) and 2) the backbone distortion of the NPxxY motif at the cytoplasmic end of TM7 (measured by the RMSD of the Asn332^7.49-Ala337^7.54 segment from the corresponding region in the inactive MOR crystal structure, herein termed 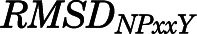), revealed a different distribution of kinetic macrostates across the different regions of the conformational phase space sampled by the three ligand-bound MOR systems, suggesting different activation kinetics of MOR when bound to methadone, morphine, or TRV130.

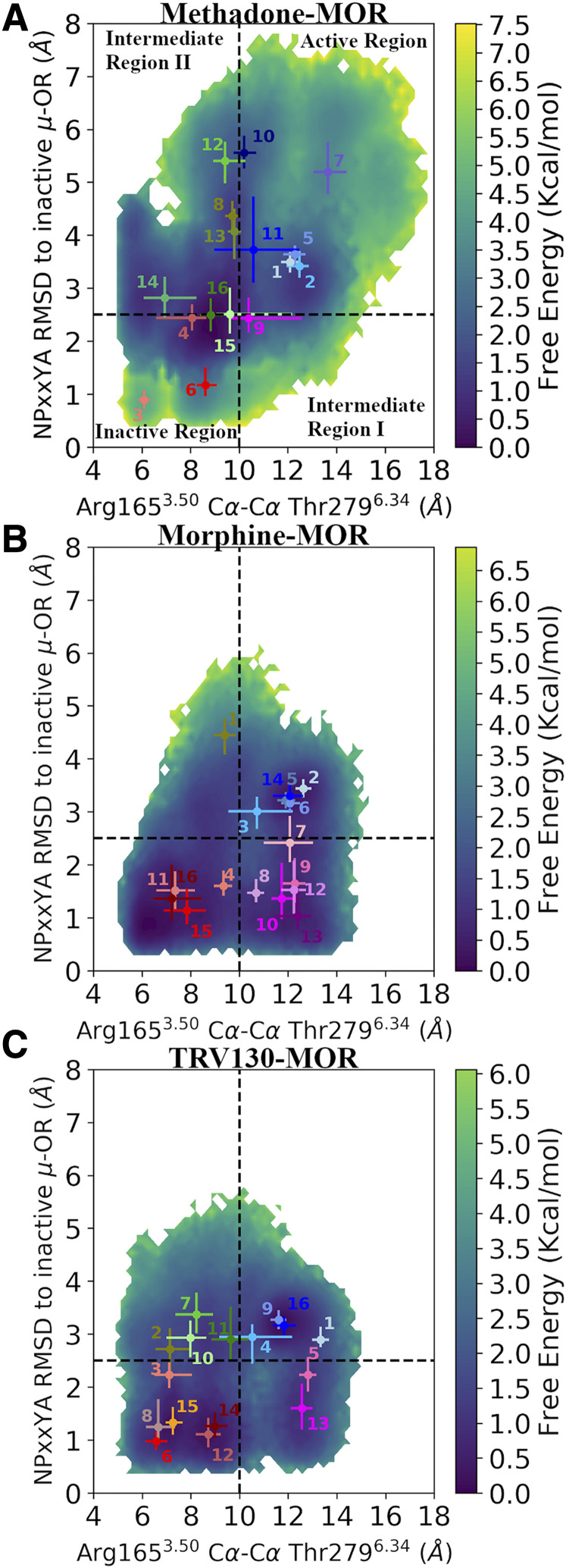
Figure 2 shows the two-dimensional free-energy surfaces of the methadone-bound, morphine-bound, and TRV130-bound MOR systems as a function of the two aforementioned order parameters epitomizing receptor activation and with the 16 kinetic macrostates depicted in different colors. As previously observed in the morphine-bound and TRV130-bound MOR systems (Kapoor et al., 2017), two intermediate conformational regions (referred to as “Intermediate I” and “Intermediate II” regions) are sampled by the methadone-MOR system in addition to regions containing active-like and inactive-like experimental conformations of the receptor. However, the conformational landscape of the methadone-MOR complex (Fig. 2a) is substantially different from those sampled by the other two ligand-MOR complexes (Fig. 2, b and c). Although for both the morphine-MOR and the TRV130-MOR systems, the inactive region of the MOR conformational space is the most probable one (the sums of the microstate probabilities are 51% and 49%, respectively; see Supplemental Table 10) and also contains the most probable kinetic macrostates (#16 and #12, respectively; see Fig. 2; Supplemental Fig. 6), intermediate II is the most probable region in the methadone-MOR system (47%), with the most probable state (#16) falling within this region, albeit at the boundary with the inactive region. Notably, although both intermediate regions are equally populated in the TRV130-MOR system (Supplemental Table 10), intermediate I and intermediate II regions are the least probable in the methadone-MOR and morphine-MOR systems, respectively. As observed in the representative structures of the most probable macrostates of the intermediate region I in the three ligand-bound MOR systems (Supplemental Fig. 10, A–C), TM6 in these states assumes an active-like conformation, whereas the backbone of the TM7 NPxxY region is in an inactive-like state, with its Tyr336^7.53 sidechain adopting a conformation similar to the one observed in the inactive MOR crystal structure. In contrast, representative structures of intermediate region II are characterized by a distorted NPxxY motif similar to that of active MOR conformations but with TM6 only partially swung out toward the active conformation of the receptor (Supplemental Fig. 10, D–F).

Fig. 2.

Free energy surfaces of A) methadone-, B) morphine-, and C) TRV130-bound MOR systems as a function of two-order parameters associated with receptor activation. Specifically, the two-order parameters refer to the TM6 outward movement captured by the Arg165^3.50-Thr279^6.34 C_α distance and the backbone distortion of the NPxxY motif measured as RMSD of the NPxxYA segment from the corresponding region in the inactive MOR crystal structure. Dotted black lines define the boundaries of the four identified conformational regions (Active, Inactive, Intermediate I, and Intermediate II). Dots represent reweighted averages of the two-order parameters in the identified 16 kinetic macrostates for each ligand-bound MOR system. The 16 kinetic macrostates are numbered as in Supplemental Fig. 6 and are colored based on the region they fall within. Specifically, macrostates in the “Active region,” “Inactive region,” “Intermediate region I,” and “Intermediate region II” are colored in shades of blue, red, magenta, and green, respectively. Error bar refers to first and third quartiles of the distribution of two order parameters in each macrostate. OR, opioid receptor.

Methadone-Induced Slowest Motions in MOR.

Figure 2 clearly shows the difference in the conformational landscape of methadone-MOR compared with morphine-MOR and TRV130-MOR when plotted as a function of the order parameters that are typically used to describe receptor activation. However, these order parameters do not necessarily correspond to the slowest reaction coordinates, which are hypothesized to capture the functionally relevant dynamic degrees of freedom of the system.

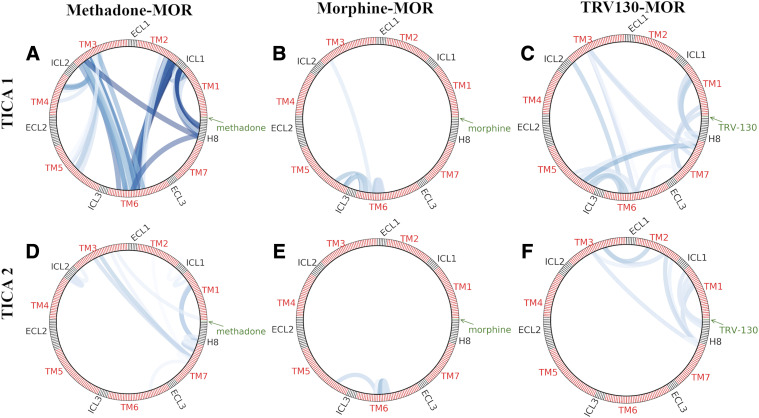
To further characterize the dynamics of the methadone-MOR system, we identified the structural descriptors that most contributed to the receptor’s slow dynamics using tICA (Supplemental Tables 2–7) and compared them with corresponding data we previously obtained for the morphine-MOR and TRV130-MOR systems (Kapoor et al., 2017). Although for all three ligand-bound MOR systems the majority of top-ranked correlated motions identified by tICA components 1–6 suggests that the slowest motions occur at the receptor’s intracellular side, important differences were observed. In particular, the top two slowest tICA components differed significantly between the three ligand-bound MOR systems, as shown by the projection of the simulation data onto the first two tICA components in Supplemental Fig. 11. Although methadone-induced slowest motions in MOR primarily involve specific residues in helices TM2-TM7, ICL1, and H8, the most significant morphine-induced slowest motions are exclusively localized within TM6, whereas residues in TM1, TM3, TM5, TM6, TM7, and H8 are mostly involved in the MOR slowest motions induced by TRV130 (Fig. 3). Among the most significant motions identified in the methadone-MOR system by the first tICA component are some capturing the TM6 movement associated with receptor activation, in particular Thr103^2.39-Val282^6.37. Additionally, the first tICA component calculated for the methadone-MOR system captures important conformational changes in ICL1 (e.g., Val92^1.56-Met99^ICL1). Although most kinetic macrostates of the methadone-MOR complex adopt the same conformation of ICL1, as seen in the active MOR crystal structure, active-like macrostate 5 exhibits a substantially different conformation characterized by a loose coupling between residue Met99^ICL1 and residues in TM1 and TM2 (e.g., Ile93^1.57 and Ile105^2.41, as seen in MOR active crystal structure), whereas other ICL1 residues, in particular Lys98^ICL1 and Lys100^ICL1, become more exposed to the cytosol (Supplemental Fig. 12A). In contrast, in the active-like macrostate 10, ICL1 on average assumes a conformation similar to those seen in the inactive crystal structure of MOR, with the residue Met99^ICL1 sidechain pointing toward H8 (Supplemental Fig. 12B). The second tICA component calculated for the methadone-MOR system primarily captures the movement of TM7 (Fig. 3), as exemplified by residue pairs Leu88^1.52-Phe338^7.55 and Ser154^3.39-Asn328^7.45 (see Supplemental Table 3).

Fig. 3.

Residue sidechain-sidechain pairs with greater than 0.6 correlation with the top two tICA components in (A, D) methadone-, (B, E) morphine-, and (C, F) TRV130-bound MOR systems. Low-to-high correlation values are color-coded from light to dark blue. ECL, extracellular loop.

Activation Kinetics and Structural Characterization of the Most Probable Kinetic Macrostate of the Methadone-MOR Complex.

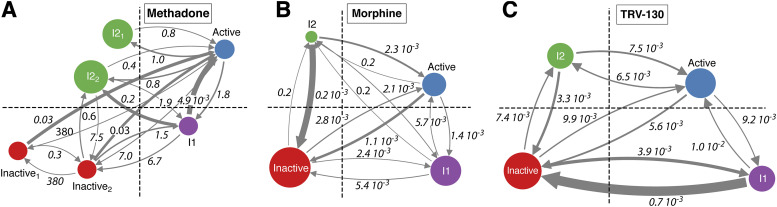
The activation kinetics of the methadone-bound MOR system were assessed and compared with those of morphine-bound and TRV130-bound MOR systems by MSM analysis. Technical details of this comparison are provided in the Materials and Methods section. For the methadone-MOR system, the MSM analysis identified two kinetically distinct inactive states (see Inactive₁ and Inactive₂ in Fig. 4A) and two kinetically distinct states in the intermediate II region (I2₁ and I2₂ in Fig. 4A), whereas the macrostates of the active conformational region could be grouped into a single state. The transition timescales between these states are also shown in Fig. 4A and compared with those obtained for the morphine-bound and TRV130-bound systems. Unlike the methadone-MOR system, the macrostates of the morphine-bound and the TRV130-bound systems (Fig. 4, B and C, respectively) only formed single kinetic states in each conformational region.

Fig. 4.

Mean first-passage times between states within the four conformational regions (active: blue, inactive: red, intermediate I: magenta, and intermediate II: green) marked by black dotted lines as shown in Fig. 1 for (A) the methadone-bound MOR, (B) the morphine-bound MOR, and (C) the TRV130-bound MOR systems. The timescales are reported in milliseconds. Arrow thickness connecting the different states is proportional to the corresponding transition probabilities. The circle area is proportional to the total equilibrium probability of the different states. The macrostates that form part of each of the states depicted in the four regions are listed in Supplemental Table 8.

Notably, the overall activation kinetics of the methadone-bound MOR system are significantly slower than those of the morphine-bound and TRV130-bound MOR systems with different states of the methadone-MOR complex; in particular, its most probable states (I2₁ and I2₂) exchange on a millisecond timescale compared with microsecond timescales among the different states of the morphine-MOR and TRV130-MOR systems (Fig. 4). Because the methadone-bound I2₁ state is not kinetically connected to the inactive state, it is tempting to speculate that this intermediate state acts as a kinetic trap.

To compare and contrast the structural properties of kinetically distinct conformations stabilized by methadone versus morphine and TRV130, we calculated the average pairwise RMSD between the different ligand-stabilized aggregated kinetic macrostates of the receptor (Supplemental Fig. 7). Notably, the RMSD between methadone-bound MOR conformations and either the morphine-bound or the TRV130-bound MOR systems is larger than the RMSD between morphine-bound and TRV130-bound MOR, indicating that the methadone stabilizes kinetically distinct conformations that are overall markedly different from those stabilized by the other two ligands. In particular, the two most probable aggregated kinetic macrostates of the methadone-bound system, states I2₁ and I2₂, show large deviations (RMSD > 2.6 Å) from the MOR states bound to morphine or TRV130.

The conformations of methadone-bound MOR states I2₁ and I2₂ differ significantly from the metastable states of the morphine-bound or TRV130-bound systems as well as from the active and inactive crystal structures of MOR in several aspects. Both I2₁ and I2₂ are characterized by different rearrangements of helices TM6, TM7, and the extracellular end of TM2 in addition to differences in TM3 and H8 when compared with the two crystal structures of MOR. For instance, in the most probable macrostate of the methadone-bound MOR system (#16; Supplemental Fig. 6) that is part of the I2₁ state (Supplemental Table 8), the extracellular side of the receptor is characterized by an outward movement of TM6 and TM7 and an inward movement of TM2 (Fig. 5B). At the intracellular side, TM5 moves toward its conformation in the inactive state while TM6 assumes an intermediate position between the two MOR crystal structures (Fig. 5D). In addition, a change in the overall tilt of the intraceullar end of TM7 produces a ∼15-Å reorientation of the Phe338^7.55 sidechain away from its position in the two crystallographic states of MOR and toward TM6 (Fig. 5D). In this state, methadone adopts a binding mode that is different from the initial metadynamics-ranked top docking pose (IFDP2). In this pose, methadone forms stable (>70% simulation frames) hydrophobic/aromatic interactions with residues on TM2, TM6, and TM7 (Fig. 5C). While one of the two phenyl groups of methadone at position 4 points toward TM6 and TM7, forming an aromatic interaction with Trp293^6.48 and hydrophobic interactions with residues Ile296^6.51, Trp318^7.35, and Ile322^7.39, the other one is positioned between TM2 and TM7, forming hydrophobic inteactions with residues Ala117^2.53, Leu121^2.57, and Tyr326^7.43. The carbonyl moiety and the ethyl group on methadone also interact with TM2 and TM7 residues, specifically Leu121^2.57, Gln124^2.60, Tyr128^2.64, and Ile322^7.39. The methadone’s tertiary amine, along with the dimethylamino group at position 6, points toward TM3, forming direct polar or hydrophobic interactions with residues Asp147^3.32, Asn150^3.35, and Met151^3.36, although this occurs in less than 60% of simulation frames. The most pronounced difference between the I2₁ and I2₂ states stems from the orientations of TM6, TM7, and H8, which can be discriminated by the structural features identified by tICA components 3 and 4 (see Supplemetal Tables 4 and 5, respectively). Figure 5E shows a comparison between representative conformations of the most probable macrostates that are part of I2₁ and I2₂ (#16 and #15, respectively).

Distinct Structural Features Contribute to Methadone-Induced MOR Activation.

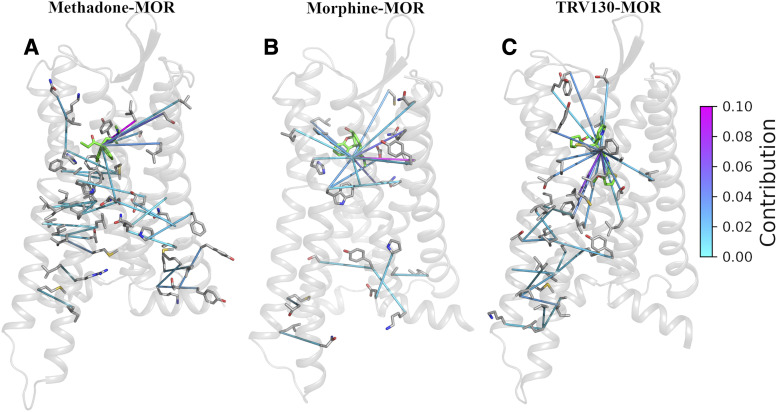
To identify structural features that allosterically link the ligand-binding pocket to the intracellular side of the receptor that binds to the G protein, we computed the transfer entropy between residue-residue or residue-ligand contacts for the methadone-bound MOR system and compared it with equivalent results obtained for MOR simulated in the presence of morphine or TRV130. The resulting transfer entropy matrix was used to calculate the contribution of each ligand-receptor or receptor-receptor contact to the TM6 movement associated with receptor activation and characterized by 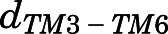measurements as described in Materials and Methods. Supplemental Table 9 lists the top structural features that contribute to the allosteric coupling between the TM6 movement and the ligand in methadone-, morphine-, and TRV130-bound MOR systems. The top structural features that are specific to each ligand-bound MOR system are depicted in Fig. 6. Only five contacts (in green in Supplemental Table 9) between the ligands and residues Asp114^2.50, Ile146^3.31, Tyr149^3.34, Phe152^3.37, and Ala240^5.46 are common to the three ligand-MOR systems. Unlike the TRV130-MOR system in which the individual contact contributions were similar (Supplemental Table 9) and spread across the receptor (Fig. 6C), the transfer entropy in the methadone-MOR system (Fig. 6A) involved just a few residues, as was also verified in morphine-MOR (Fig. 6B).

Fig. 6.

System-specific contacts that contribute more than 1% of flux to the TM6 movement in A) methadone-, B) morphine-, and C) TRV130-bound MOR systems. Contacts (depicted as lines) that are common among all three systems or between any two systems (as highlighted in Supplemental Table 9) are not shown. Low-to-high contribution values (0, 0.25) are color-coded from light cyan to magenta.

Different contributions among the three ligand-MOR complexes were also identified at the intracellular side of the receptor, with no contact shared between the three systems (Supplemental Table 9). Although several residues that have often been reported to undergo conformational changes upon receptor activation [e.g., the so-called toggle switch Trp293^6.48 and the conserved core triad Ile155^3.40, Pro244^5.50, and Phe289^6.44 (Huang et al., 2015)], are identified among those contributing to the coupling between the TM6 movement and residues in the ligand pocket, the specific contacts and their contributions (Supplemental Table 9) differ for the methadone-bound MOR system compared with the morphine-bound and TRV130-bound systems. For instance, the following contacts involving known residues are specific to the methadone-MOR system (Supplemental Table 9): Phe156^3.41-Pro244^5.50, Asp114^2.50-Trp293^6.48, and Ile155^3.40-Val245^5.51. Novel contacts that are specific to the methadone-induced activation of the receptor are: Met161^3.46-Val286^6.41, Tyr91^1.55-Thr97^ICL1, and Tyr96^ICL1-Lys100^ICL1 (see Supplemental Table 9 for complete list).

Discussion

High-resolution experimental structures of ligand-bound GPCRs, including opioid receptors, have greatly enhanced our understanding of how ligands bind to their receptors and offered hypotheses of how they might activate or inactivate them. However, there are only three high-resolution experimental structures of the MOR: a crystal structure of the inactive receptor bound to the irreversible morphinan antagonist β-funaltrexamine, the crystal structure of the active MOR bound to the morphinan agonist BU72, and the cryo-electron microscopy structure of the active MOR bound to the synthetic opioid peptide agonist DAMGO (H-Tyr-D-Ala-Gly-N-MePhe-Gly-ol). This information is not only limited to the chemotypes of the specific bound ligands but also to the receptor conformational states obtained under conditions used for the sole purpose of structural determination, which may or may not be physiologically relevant. Most importantly, these structures are single snapshots along activation pathways that need to be characterized both thermodynamically and kinetically to understand how a drug may exert its action.

Computational methods, and particular MD simulations, can help achieve this goal, and have been used here to characterize, at an atomic level of detail, the conformational ensemble of MOR when bound to its unique agonist methadone. To the best of our knowledge, this is the first time that a complete conformational characterization of the methadone-bound MOR complex is attempted and compared with that of a classic opioid drug (morphine) and a G protein–biased ligand (TRV130). Confidence in the metadynamics top-ranked initial docking pose of methadone at the orthosteric binding site of MOR is given by the several ligand-receptor interactions that are also observed in available experimental structures of MOR. Not only do these interactions include the direct ionic contact between methadone’s protonated tertiary amine and Asp147^3.32 but also the water-mediated interactions between the ligand and both His297^6.52 and Tyr148^3.33 as well as hydropobic interactions with residues Tyr148^3.33, Met151^3.36, Val236^5.42, Ile296^6.51, Trp293^6.48, His297^6.52, Val300^6.55, Ile322^7.39, and Tyr326^7.43. Notably, this binding pose, which is stable in the active conformation of MOR determined experimentally, changes during the transition between inactive and active conformations of MOR, adopting a different pose in the identified most probable kinetic macrostate of the methadone-bound MOR complex, with most ligand interactions formed with residues on TM2, TM6, and TM7. Although a direct ionic interaction is still formed between the ligand’s tertiary amine and residue Asp147^3.32, the methadone’s pose in the most probable kinetic macrostate differs from the pose adopted in the crystal-like active conformation of MOR primarily in the orientation of one of the two phenyl groups at position 4 (pointing toward TM3,TM5 in the most stable methadone’s pose in the crystal-like active conformation of MOR or TM2,TM7 in the most probable kinetic macrostate of the methadone-bound MOR complex) and the ethyl group (pointing toward TM6 in the most stable methadone’s pose in the crystal-like active conformation of MOR or TM2,TM7 in the most probable kinetic macrostate of the methadone-bound MOR complex).

One of the most important findings from MSM analysis of the large (0.3-millisecond) MD simulation data set presented herein is that although the methadone-MOR complex samples four distinct conformational regions, as we had previously reported for TRV130-bound and morphine-bound MOR systems (Kapoor et al., 2017), the corresponding conformational landscapes are substantially different. The most striking difference lies in intermediate II being the most probable region sampled by the methadone-MOR system, as opposed to the most probable inactive regions sampled by the morphine-bound and TRV130-bound MOR complexes. Representative structures of intermediate region II have TM6 only partially swung out toward the active conformation of the receptor but a NPxxY motif that is very similar to that of active MOR conformations that have been solved experimentally. Notably, our simulations reveal a very low probability of visiting the MOR active conformation observed experimentally for all of the simulated systems, which is in line with NMR results suggesting that both the agonist and the G protein are required to stabilize that conformation (Sounier et al., 2015). The MOR dynamics induced by methadone are substantially different from those induced by morphine and TRV130, as indicated by the structural descriptors that most contributed to the receptor slow dynamics identified by tICA. These dynamics mostly involve residues in helices TM2-TM7 (e.g., Thr103^2.39-Val282^6.37), ICL1 (e.g., Val92^1.56-Met99^ICL1), and H8, as opposed to an exclusive slow-motion localization within TM6 in the morphine-MOR complex and specific residues in TM1, TM3, TM5, TM6, TM7, and H8 in the TRV130-MOR complex.

Another interesting finding of this study is that activation of the methadone-bound MOR system occurs over significantly slower timescales (milliseconds) than MOR activation induced by morphine or TRV130 (microseconds). Notably, methadone stabilizes kinetically distinct conformations that are markedly different from those stabilized by morphine or TRV130 as well as from the active and inactive crystal structures of MOR. For instance, the most probable aggregated kinetic macrostates I2₁ and I2₂ present unique arrangements of helices TM6, TM7, the extracellular end of TM2, TM3, and H8 in comparison with inactive and active experimental structures of MOR. These macrostates also differ among themselves given their different orientations of TM6, TM7, and H8. One of these states, I2₁, is not linked to the inactive state of MOR, and it is possibly acting as a kinetic trap. We speculate that this slower conformational transition of the methadone-bound MOR system might have a direct effect on its signaling profile. This can eventually be tested experimentally by site-directed mutagenesis of residues that are likely to contribute to the stability of the I2₁ state (e.g., Phe338^7.55) or disrupt ligand-receptor interactions that are specific to this state (e.g., those involving Ala117^2.53, Leu121^2.57, Gln124^2.60, and Tyr128^2.64).

Finally, our study allowed us to confirm inferences from published interferometry experiments hinting at a different active conformation of MOR stabilized by methadone and to contribute the specific structural features underlying methadone-induced MOR activation. In particular, measurements of transfer entropy between residue-residue or residue-ligand contacts allowed us to identify top structural features that contribute to the allosteric coupling between methadone and the TM6 outward movement associated with receptor activation and to compare and contrast them with those identified in the morphine- or TRV130-bound complexes. Although a handful of residues were identified by transfer entropy as unique to the methadone-MOR system, contacts between ligands and residues Asp114^2.50, Ile146^3.31, Tyr149^3.34, Phe152^3.37, and Ala240^5.46 were identified in all three ligand-MOR systems, suggesting that these residues may be contributing to a common mechanism of MOR activation. Other residues that have often been reported to undergo conformational changes upon receptor activation in various GPCR sytems [e.g., the so-called toggle switch Trp293^6.48 and conserved core triad residues Ile155^3.40, Pro244^5.50, and Phe289^6.44 (Hulme, 2013; Huang et al., 2015; Sun et al., 2017; Weis and Kobilka, 2018)] were indeed found among the top contributors to the coupling between the TM6 movement and residues in the ligand pocket in the methadone-bound complex. However, the specific contacts formed by these residues (i.e., Phe156^3.41-Pro244^5.50, Asp114^2.50-Trp293^6.48, and Ile155^3.40-Val245^5.51) are unique to the methadone-MOR system, as are a number of others (e.g., Met161^3.46-Val286^6.41, Tyr91^1.55-Thr97^ICL1, and Tyr96^ICL1-Lys100^ICL1). The presence of well-known residues in many of these testable hypotheses (Hulme, 2013; Huang et al., 2015; Sun et al., 2017; Weis and Kobilka, 2018) instills confidence that they may be worthy of experimental testing.

Abbreviations

GPCR

G protein–coupled receptor

H8

helix 8

ICL

intracellular loop

IFDP

induced-fit docking pose

MD

molecular dynamics

MOR

µ-opioid receptor

MSM

Markov state model

NPT

number

pressure

temperature

OUD

opioid use disorder

PDB id

Protein Data Bank identification

RMSD

root-mean-square deviation

tICA

time-lagged independent component analysis

TM

transmembrane

Authorship Contributions

Participated in research design: Kapoor, Provasi, Filizola.

Conducted experiments: Kapoor.

Performed data analysis: Kapoor, Provasi.

Wrote or contributed to the writing of the manuscript: Kapoor, Provasi, Filizola.