RhoA Mediates Epithelial Cell Shape Changes via Mechanosensitive Endocytosis

SUMMARY

Epithelial remodeling involves ratcheting behavior whereby periodic contractility produces transient changes in cell-cell contact lengths, which stabilize to produce lasting morphogenetic changes. Pulsatile RhoA activity is thought to underlie morphogenetic ratchets, but how RhoA governs transient changes in junction length, and how these changes are rectified to produce irreversible deformation, remains poorly understood. Here, we use optogenetics to characterize responses to pulsatile RhoA in model epithelium. Short RhoA pulses drive reversible junction contractions, while longer pulses produce irreversible junction length changes that saturate with prolonged pulse durations. Using an enhanced vertex model, we show this is explained by two effects: thresholded tension remodeling and continuous strain relaxation. Our model predicts that structuring RhoA into multiple pulses overcomes the saturation of contractility and confirms this experimentally. Junction remodeling also requires formin-mediated E-cadherin clustering and dynamin-dependent endocytosis. Thus, irreversible junction deformations are regulated by RhoA-mediated contractility, membrane trafficking, and adhesion receptor remodeling.

In Brief

Cavanaugh et al. use optogenetic control of RhoA to discover a mechanosensitive endocytic pathway that stabilizes cell-cell junction lengths in model epithelia. This pathway likely represents a homeostatic mechanism to regulate junction lengths, where small fluctuations in exogenous RhoA are buffered but longer patterned RhoA activity directs morphogenetic change.

INTRODUCTION

Epithelial cell sheets dynamically remodel themselves to sculpt higher-order assemblies of tissues and organs (Heisenberg and Bellaïche, 2013; Lecuit et al., 2011; Siedlik and Nelson, 2015). Individual cells execute complex shape changes to alter cell-cell junction lengths, cell surface area, and overall cell shape that, when coordinated, drive tissue morphogenesis (Heer and Martin, 2017; Martin et al., 2010). Underlying cell and tissue mechanics is the dynamic interplay of cell force generation and adhesion (Choi et al., 2016; Lecuit et al., 2011; Pinheiro and Bellaïche, 2018). Such mechanics underlie the capability of epithelial sheets to variably maintain or dramatically change shapes during morphogenesis. To enable such varied and adaptive mechanical behaviors, the actin cytoskeleton harnesses mechanochemical feedbacks (Choi et al., 2016; Martin et al., 2010). The structures of these mechanochemical systems, and how they regulate cell physiological processes, remains largely unknown.

A primary regulator of cell shape changes in epithelia is the small GTPase RhoA, which acts through downstream effectors to control actomyosin assembly and contractility (Coravos et al.,2017; Lessey et al., 2012). Morphogenetic processes often involve highly dynamic RhoA activity, with pulses of active RhoA preceding the shortening of cell-cell junctions (Martin et al., 2009; Rauzi et al., 2010; Simões et al., 2014). Transient junction contractions are incrementally stabilized to direct irreversible morphogenetic change (Fernandez-Gonzalez et al., 2009; Kasza et al., 2014). This process of transient contraction and relaxation plus incremental stabilization is commonly referred to as an oscillatory ratchet (Fernandez-Gonzalez and Zallen, 2011; Gorfinkiel and Blanchard, 2011; Rauzi et al., 2010; Solon et al., 2009). By spatiotemporally coordinating these pulsatile contractions within and between cells, incremental changes in individual cell shapes can collectively drive large-scale tissue deformations required for invagination (Blanchard et al., 2018; Martin et al., 2009) or convergent extension (Bertet et al., 2004; Simões et al., 2014). While pulsatile RhoA activity is observed in diverse contexts (Kerridge et al., 2016; Maître et al., 2015; Mason et al., 2016; Michaux et al., 2018; Munjal et al., 2015), the significance of this temporal structure and what role it may have in junctional shortening is unknown.

Adherens junction remodeling at cell-cell contacts is essential for the maintenance of cell shapes in a variety of developmental contexts (Pinheiro and Bellaïche, 2018; Roeth et al., 2009; Xie et al., 2018). In both the Drosophila ectoderm and amnioserosa, the Rab membrane trafficking pathway is essential in the maintenance of adherens junctions and their trafficking during morphogenesis (Roeth et al., 2009). During dorsal closure in Drosophila, tension-dependent membrane removal helps to maintain a constant junctional straightness, documenting feedback between junctional tension and these Rab regulators (Sumi et al., 2018). Similarly, during germband extension in Drosophila, the dynamic interplay of actomyosin contractility and Rab-dependent membrane internalization contributes to the incremental stabilization of junction contractions that underlies the oscillatory ratchet (Jewett et al., 2017). In this context, membrane tubules emanating from adherens junctions require actomyosin forces to complete vesiculation and enforce progressive junctional shortening (Jewett et al., 2017). Shear forces have also been shown to regulate junctional E-cadherin levels, whose clustering and subsequent internalization is also facilitated by formin and myosin activity during germband extension (Kale et al., 2018; Levayer et al., 2011). These data highlight the importance of coupling between actomyosin contractility, junction tension, and membrane remodeling during junctional shortening, but the underlying mechanisms remain unknown.

Here, we study the response to dynamic changes in junctional tension induced by optogenetic activation of RhoA in a model epithelium. We find that RhoA activation along the junction length leads to a rapid contraction that occurs primarily through the shortening of a few distinct microdomains. For short activation times, this shortening is reversible such that junctions return to their original lengths after removal of the exogenous RhoA. However, as the activation time is increased, the extent of permanent junctional shortening is limited for a single activation pulse. To capture these data, we introduce modifications to the existing vertex-based models for epithelial tissues to include strain-dependent remodeling of junction tension and rest length. To account for our experimental data, our model must include junctional tension remodeling that occurs only above a critical junctional deformation, or strain. We show that temporally structuring the exogenous RhoA activity into distinct pulses overcomes the limited shortening, highlighting an essential role for pulsatile activation of RhoA. Finally, live-cell imaging reveals that membrane remodeling and vesicular internalization occur during this RhoA-dependent junction contraction, whose stabilization at shorter lengths requires dynamin and formin activities. Altogether, these data provide new insights into the molecular and biophysical feedback mechanisms between RhoA activity and membrane remodeling that underlie junctional length changes in epithelia.

RESULTS

Optogenetic Activation of RhoA Induces Cell-Cell Junction Shortening

To spatiotemporally control RhoA activity in model epithelia, we generated a stable Caco-2 cell line expressing the TULIP optogenetic system (Oakes et al., 2017; Strickland et al., 2012; Wagner and Glotzer, 2016). TULIPs utilize the photosensitive LOVpep domain attached to a GFP-tagged transmembrane protein, Stargazin. The LOVpep’s binding partner is the prGEF complex that contains 3 components: a photorecruitable engineered tandem PDZ domain, the catalytic DH domain of the RhoA-specific guanine nucleotide exchange factor (GEF) LARG, and an mCherry fluorescent tag (Figure 1A). Blue light increases the binding affinity of the two protein complexes, recruiting the prGEF complex to the membrane where it locally activates RhoA (Figures 1A and 1B) (Oakes et al., 2017; Wagner and Glotzer, 2016).

Figure 1. RhoA-Mediated Tension Determines Junction Length at Short Timescales.

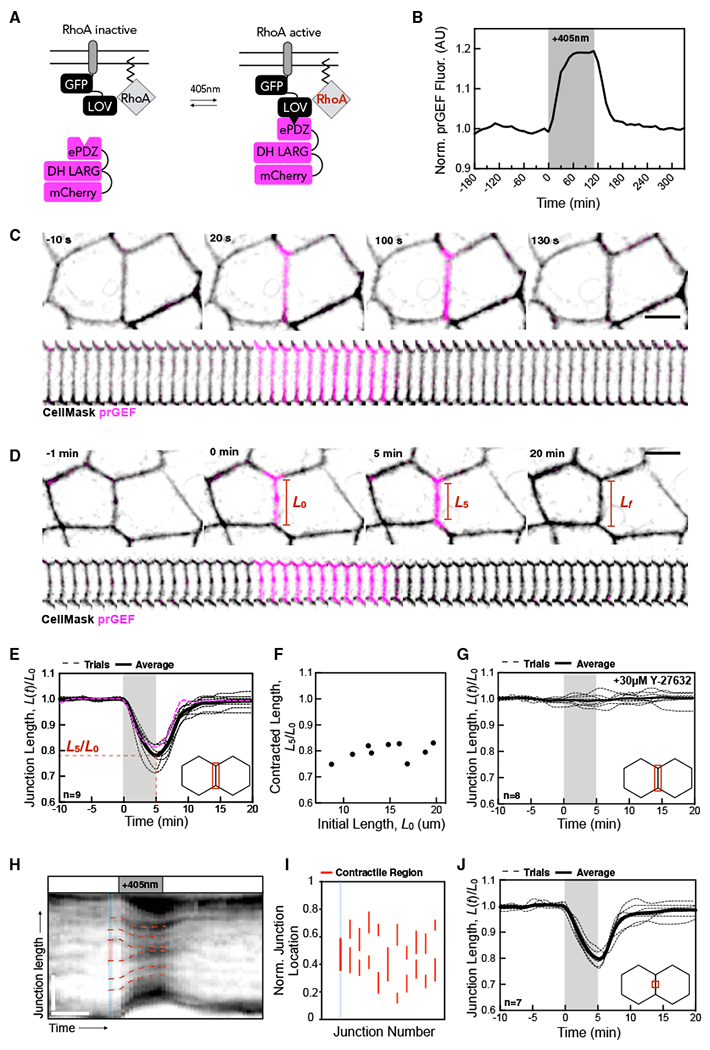
(A) Schematic of TULIP optogenetic system. Blue light activation causes recruitment of prGEF to the plasma membrane.

(B) Quantification of the local intensity increase of mCherry-prGEF in the junctional activation region shown in (C) (magenta). Activation period is indicated by the gray box.

(C) Representative images of cells undergoing junctional prGEF (magenta) recruitment. prGEF rapidly accumulates at the junction and dissociates upon light inactivation. Scale bar, 10 μm.

(D) Representative images of a junction undergoing a 5-min activation. Junctions undergo rapid contraction upon prGEF recruitment that is reversible upon its removal. Red lines denote positions and lengths between the two junction vertices. Scale bar, 10 μm.

(E) Normalized junction length over time with a 5-min activation shows junction contraction during activation (gray). Individual trials are in a dashed line with the average in a solid line. The magenta line represents data shown in (D).

(F) Plot of the fractional contracted length after a 5-min activation, L₅/L₀, as a function of the initial junction length.

(G) Normalized junction length over time of cells treated with Y-27632.

(H) Representative kymograph of a junction (visualized by Cell Mask) prior to, during, and after a 5-min activation. The red dashed lines denote fiduciary marks within a junction. The blue region denotes the junction length; the red portion indicates a region that contracts. Horizontal scale bar, 6 min and vertical scale bar, 5 μm.

(I) The location of the contractile regions for 11 distinct junctions, indicated by a unique junction number. The junction length is normalized such that the top vertex is denoted by 1, with the bottom vertex denoted by 0. The junction in 1H is depicted by the blue line.

(J) Normalized junction length over time of junctions in a 5-min activation with light targeted only to the junction center.

Cell morphologies and junction lengths in Caco-2 monolayers are incredibly stable; over 1 h, the junction lengths change less than 3%. The remarkably static nature of the monolayer makes it particularly well suited to study junctional responses to acute optogenetic stimulation. Targeting light to a desired cell-cell junction (Figure 1C; CellMask, black) induces rapid prGEF (magenta) association (20 s) and dissociation (30–50 s) when the light is turned on and off, respectively (Figures 1B and 1C; Video S1). Consistent with previous studies, prGEF recruitment is tightly localized to the targeted region (Oakes et al., 2017; Wagner and Glotzer, 2016). The targeted junction rapidly contracts upon continuous light activation over a period of 5 min, shortening from 13.1 to 10.3 μm, and then returning to its original length once light is removed (Figures 1D and 1E, pink line; Video S2).

To quantify junction contraction over time, we measured the fractional junction length L(t)/L₀, where L(t) is junction length at time t, and L₀ = L(t = 0) is the length at the activation onset at t = 0. The shortening is measured by (L₀−L(t))/L₀. Strikingly, we find that the rate and extent of junction shortening is remarkably consistent across junctions with varying initial lengths and geometries. During a 5-min activation, junctions consistently contract to 75%–80% of their initial length at an average contraction rate of 0.047 min⁻¹ (Figure 1E). The fractional junction length at 5 min after the activation onset (L₅/L₀), or contracted length, was largely independent of initial length L₀ (Figure 1F). Treating monolayers with the Rho-kinase inhibitor Y-27632 completely abolished light-induced junction shortening (Figure 1G), confirming that light-induced junction contraction is mediated by a downstream response to local activation of RhoA.

Junction shortening could involve uniform contraction of the entire junction or heterogeneous contraction of individual sub-junctional segments. To distinguish between these possibilities, we used variations in membrane fluorescence intensity as fiduciary markers to examine local variations in deformation along individual junctions. Kymographs made from line scans along individual junctions, observed over time, reveal how different segments along a junction move prior to, during, and after light-mediated shortening (Figure 1H). For a contraction that occurs uniformly along the junction length, we expect the speed of fiduciary marks to vary linearly from one end of the junction to the other. Strikingly, the kymograph data indicate that junctions do not contract uniformly in response to uniform activation of RhoA. Rather, we observed distinct regions that contract, indicated by converging fiduciary marks (Figure 1H, red region between red the dashed lines), separated by non-contractile regions, indicated by neighboring fiduciary marks that remain parallel (Figure 1H, blue region).

To quantify and compare the location, size, and deformation of contracting segments in different activated junctions, we located fiduciary marks that define the endpoints of each contracting region (bottom vertex = 0 and top vertex = 1) just before the onset of activation (Figure 1H, red line). We then measured the initial locations and normalized lengths, divided by the junction length, of contracting regions (Figure 1I). We found that junctions typically contain 1–2 contracting regions with an average length of several micrometers. The average fraction of the junction that contracts in response to stimulation is 26%, and these regions contract to 76% of their original length, accounting for 83% of the observed junction contraction. Plotting a histogram of these contracting regions’ lengths and localization with respect to normalized junction position reveals that contracting regions typically lie within the central portion of the junction with average normalized junctional position at 0.45 (Figure 1I). Interestingly, illuminating only the central third of junctions induced contraction rates similar to those produced by full-length activation (Figure 1J). These data indicate that junction contraction is largely accomplished by a few distinct contractile units that are concentrated near the centers of junctions and somehow predisposed to undergo rapid and complete shortening in response to uniform activation of RhoA.

Extent of Junction Contraction Saturates for a Single Rho Activation

We exploited optogenetic control to study systematically how junction deformation depends on the duration, intensity, and location of exogenous activation. To determine how junction shortening depends on the duration of prGEF junctional localization, we varied the duration of the activation pulse from 2.5 to 40 min, and measured the final junction length L_f, defined to be the junction the length measured 15 min after the end of the pulse. For all activation periods less than 5 min, junction shortening is reversible with the ratio of the final length, L_f, to initial length, L₀, being equal to 1 (Figure 2E). However, when we increase the activation time to 10 min, we observe a striking biphasic response (Figure 2A). A fast-initial contraction lasting for approximately 5 min is followed by a slower contraction phase over which junction length decreases to ~65% of its original length. After light removal, the junction does not return to its original length. Instead, the final junction length is ~20% shorter than its initial length. We observed similar kinetics for 20-min activations (Figures 2B and 2C; Video S3) with the slow phase showing clear saturation with a 40-min activation time (Figure 2D).

Figure 2. Contraction Saturates at Longer Timescales to Limit Junction Length Changes.

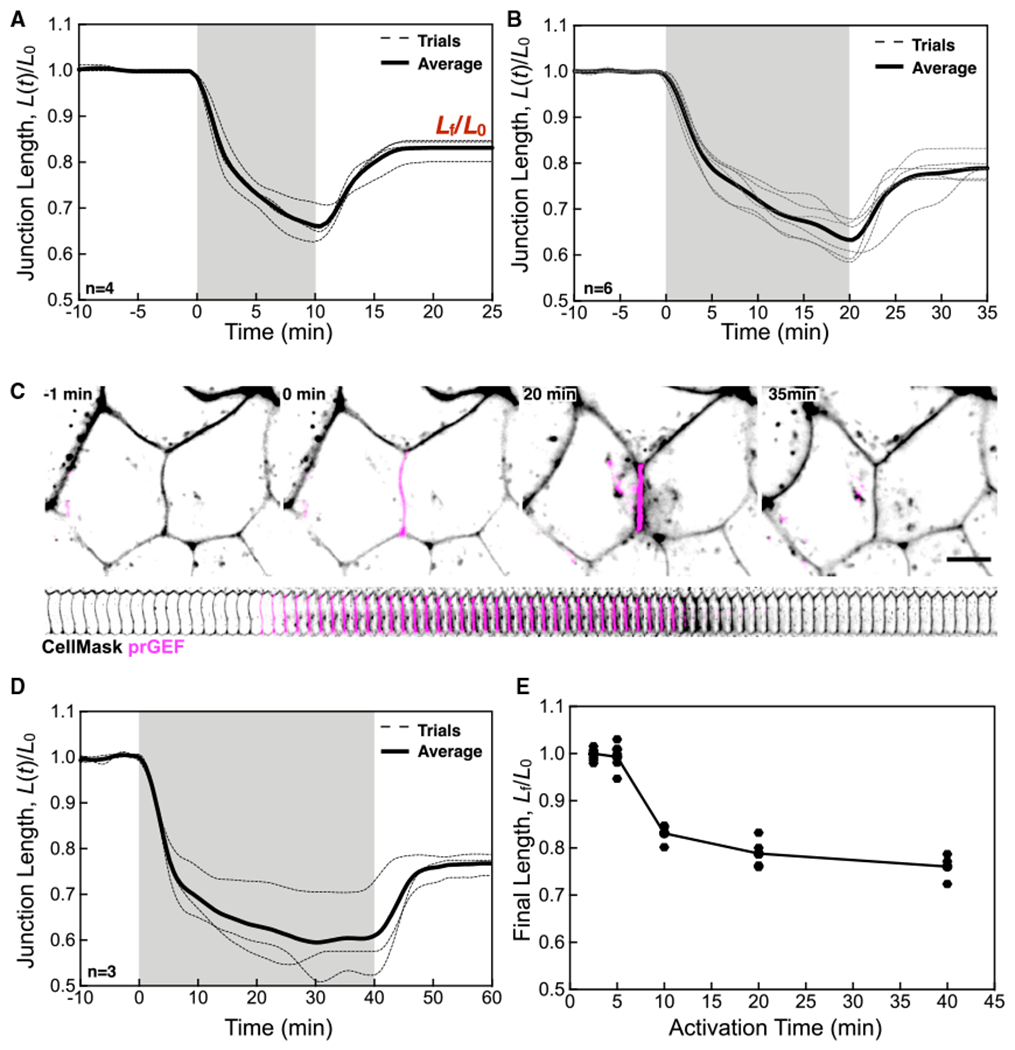
(A) Normalized junction length over time for a 10-min activation.

(B) Normalized junction length over time for a 20-min activation.

(C) Representative image of a junction in a 20-min activation. Red lines denote positions and lengths between the two junction vertices. Scale bar, 10 μm.

(D) Normalized junction length over time for a 40-min activation. (E) The fractional final junction length, L_f/L₀ as a function of the activation time. Data for individual junctions are shown, with the line as a guide for the eye.

For (A), (B), and (C) the individual traces for n junctions are shown (dashed lines) as well as the average (solid line).

To explore how the activation time controls the extent of junction length remodeling, we measured L_f/L₀ as a function of activation time (Figure 2E) and found that a rapid transition to permanent junction shortening occurs for activation times longer than 5 min. Furthermore, the junction shortening saturates to a 20% length reduction, even for activation times up to 40 min (Figure 2E). We believe that this limited remodeling behavior is restricted to the activated junctions, as analysis of the deformations of adjacent junctions show a wide distribution of strains, including positive, negative, and no strain (Figure S1). This suggests that the strain on adjacent junctions does not limit the target junctional response; instead, the contractile limit appears to arise within the activated junction. These data are consistent with only ~26% of the junction fully contracting (Figures 1H and 1I) and raises the possibility that only a portion of the junction is remodeling upon sustained activation. Collectively, these data reveal two distinct regimens of junction response to RhoA activation: reversible shortening on short timescales and irreversible shortening on longer timescales. However, the maximum extent of shortening in response to sustained activation appears to be limited.

Strain-Dependent Tension Remodeling Captures Adaptive Junctional Length Changes

To better understand the mechanistic basis for junctional length regulation in response to induced contractions, we turned to physical models of epithelial monolayers. Traditional vertex-based models represent an epithelial monolayer as a network of vertices, connected by straight junctions to form cells (Farhadifar et al., 2007). These models assume that junction lengths, L, are determined by the balance of two forces: junction contractility quantified by a tension Λ and elastic resistance to changes in cell area, set by an area compressibility modulus, K(Figure 3A). To model an optogenetic pulse of RhoA activation, we apply a transient step increase in junctional tension, ΔΛ. The simple vertex model can reproduce the reversible junction shortening response that we observe for short-duration optogenetic pulses (Figure 3B, solid gray). However, regardless of input pulse duration, the vertex model fails to capture the biphasic response and irreversible shortening observed for longer activations (Figure S2), as do other existing variants of the vertex model (Fletcher et al., 2014) and other mechanical models of cell junction rheology (Clément et al., 2017; Muñoz and Albo, 2013; Noll et al., 2017; Odell et al., 1981). Thus, our experimental data are inconsistent with existing mechanical models of epithelial tissues.

Figure 3. Enhanced Vertex Model for Mechanosensitive Junction Remodeling.

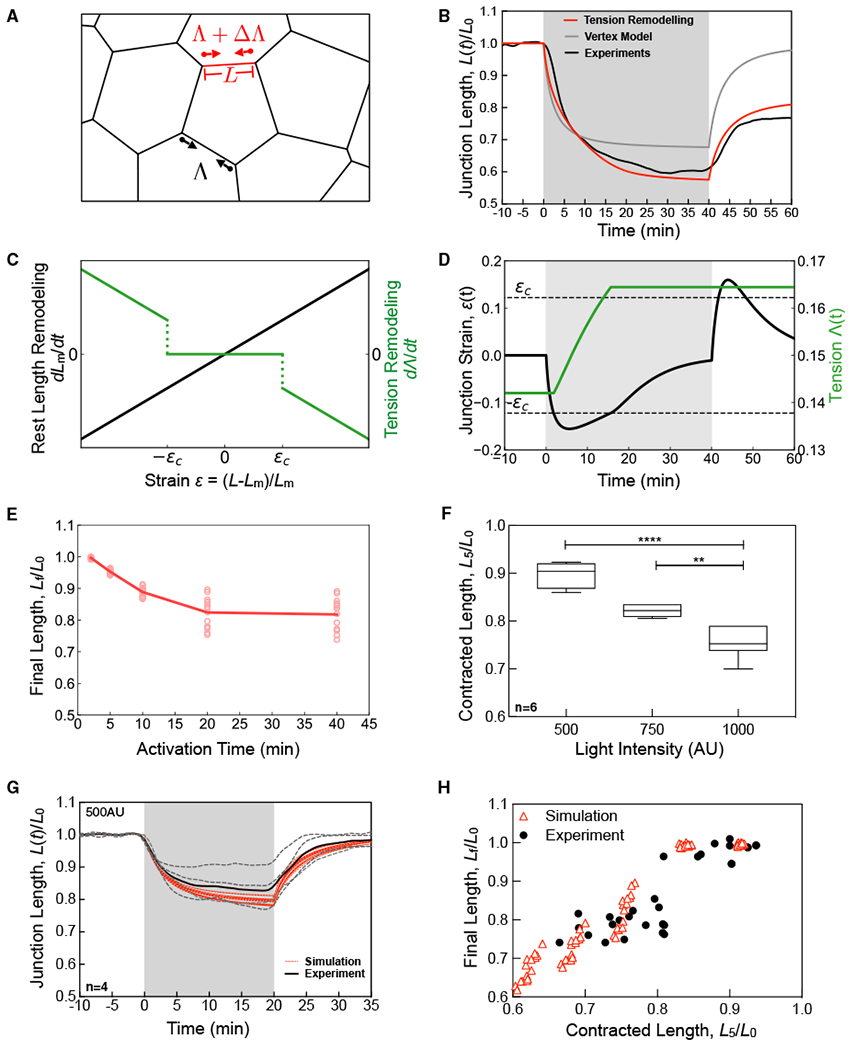
(A) Schematic of the vertex model. Cell edges (black lines) are characterized by a length, L, and contractile tension, Λ. During an optogenetic activation, the red edge has an increased line tension, characterized by ΔΛ.

(B) Normalized junction length over time for a 40-min activation, using the vertex model without (gray) and with (red) tension remodeling, as compared to experimental data (black).

(C) Rest length remodeling rate (left, black) and tension remodeling rate (right, green) as a function of junctional deformation, or strain.

(D) The junction strain and tension over time during a 40-min activation corresponding to (B).

(E) Final normalized junction length as a function activation time determined from simulations.

(F) The fractional contracted junction length for a 5-min activation for varying light intensity determined experimentally for n = 6 junctions. Boxes indicate SD; whiskers are min/max; ** = p < 0.05; **** = p > 0.0001.

(G) Normalized junction length over time for reduced light intensity (500 AU) (black dashed lights). Simulation results obtained with ΔΛ reduced 2-fold (red lines).

(H) Final normalized junction length as a function of the contracted length after 5 min of activation, L₅/L₀. Experimental data (black circles) are pooled from experiments of varying light intensity and duration and simulation data (open red triangles) are pooled from simulations with varying duration and magnitude of ΔΛ.

In a companion theoretical study (Staddon et al., 2019), we used a computational approach to explore what additional ingredients might allow vertex-based models to explain our experimental observations. In particular, we considered junctions as elastic materials that can undergo remodeling over time. For a strand of elastic material, the natural measure of deformation is the strain ϵ, defined as ϵ = (L−L_m)/L_m, where L_m is the “rest length” of the material in the absence of force. In a simple elastic material, the rest length is fixed and the strain can only change through changes in material length. However, for a junction whose components (e.g., F-actin) undergo turnover, replacing strained material with new unstrained material, rest length L_m will tend to approach the current length and the strain will tend to approach 0, a mechanism we term strain relaxation and has been previously considered (Khalilgharibi et al., 2019). We model strain relaxation by proposing that the junction rest length remodels at a rate proportional to the junction strain (Figure 3C, black solid line). Second, we introduced the concept of strain-dependent tension remodeling, where junction tension undergoes a permanent change only when strain crosses a critical magnitude, ϵ_c, at a rate proportional to the strain (Figure 3C, green line). We refer to the vertex model incorporating strain relaxation and strain-dependent tension remodeling as an enhanced vertex model.

Strikingly, we found that using a single set of model parameters (Figures 3A, 3B, and S2), the enhanced vertex model reproduces experimental data for the junction length as a function of time, over a wide range of activation periods (2.5–40 min), including the changes in the final junction lengths as a function of activation time (Figures 3B and 3E). The underlying mechanism can be understood as follows: for a short optogenetic pulse, the critical strain threshold is not reached, junctional tension remains constant, and the junction length recovers to its original value. However, for longer pulses, and for sufficiently strong ΔΛ, junctional strain crosses the critical threshold and tension remodeling results in a permanent increase in junctional tension and a permanent shortening of junction length (Figure 3B, red and black lines, 3D) (see Staddon et al., 2019 for further details).

A key assumption of the enhanced vertex model is that deformation beyond a critical strain is necessary to initiate junctional tension remodeling to enable irreversible shortening. To test this assumption, we reduced the initial contraction amount by reducing the prGEF recruitment, controlled by the light intensity (Figure 3F). When the light intensity is 1000 AU, the average junction shortens by 20%–25% of its original length after 5 min, with an average contracted length, L₅/L₀, equal to 0.77 (Figure 3F). Reducing the activation light intensity by 25% (750 AU) and 50% (500 AU) reduced the amount of initial contracted length, increasing L₅/L₀ to 0.81 and 0.89, respectively (Figure 3F). When L₅/L₀ < 0.8, we find that the final length, L_f/L₀, is proportional to the amount of initial contraction (Figure 3H). However, when the initial contraction is less than 20% (L₅/L₀ > 0.8), we find that no junctional shortening occurs (L_f/L₀ ≈ 1) (Figures 3G and 3H; Video S4). These experimental results agree remarkably well with those predicted by the model when ΔΛ is varied to modify the initial contraction (Figures 3G and 3H). Together, these findings demonstrate that a mechanosensitive junctional remodeling pathway, involving strain-dependent tension remodeling, stabilizes junction lengths in response to a temporal pulse of RhoA activity.

A Pulsatile Pattern of RhoA Activation Allows Multiple Rounds of Junctional Ratcheting

Our experimental and modeling data show that junction shortening in response to a single prolonged pulse of RhoA activity saturates at a ~20% reduction, even for longer activation times (Figure 3E). In the enhanced vertex model, this saturation arises because strain relaxation opposes the effects of tension remodeling to stabilize junction length (Figure 3C). For a step increase in applied tension ΔΛ that drives the junction strain below the threshold −ϵ_c (Figure 3C), the junction tension remodels until strain relaxation causes junctional strain again to rise above −ϵ_c (Figure 3D). Thus, for a single activation, junctional shortening is limited by the amount of tension remodeling that occurs during the initial phase of rapid contraction. Moreover, following termination of a single pulse, the rapid increase in junction length induces a rapid increase in positive strain that subsequently relaxes overtime (Figure 3D), defining an interval in which the junction is refractory to further input.

These simulation results suggest that temporally separated activation pulses can overcome the limit on irreversible junction shortening observed in response to a single pulse, provided the time between pulses is sufficiently long to relax the residual positive strain. To explore this possibility, we perform simulations with two activation pulses, with identical strength ΔΛ and durations ½t_act separated by varying amounts of “rest” time t_rest (Figure 4A). During this rest period, the tension removal results in junction length extension (Figure 4A) and increased strain that relaxes over time (Figure 4B). Consequently, the second exogenous tension pulse results in a sufficient contractile strain to drive a second period of tension remodeling (Figure 4B). The extent of tension remodeling that occurs in the second pulse depends on the residual strain ϵ_rthat remains at the end of the relaxation time (Figure 4C). Consequently, the amount of additional length contraction that occurs between the second and first pulse (Figure 4A) is proportional to ϵ_r (Figure 4C).

Figure 4. Pulsatile RhoA Enables Junctional Ratcheting.

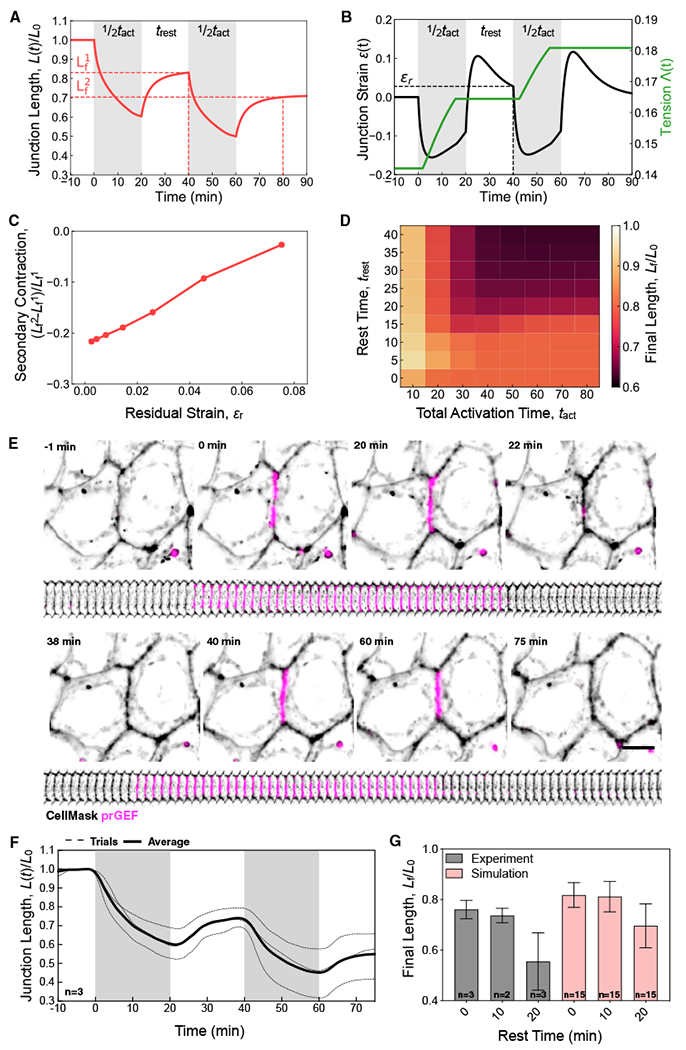
(A and B) Normalized junction length (A) and junction strain ([B] left, black) and tension ([B] right, green), during two 20-min activations with a 20-min rest period, t_rest. The residual strain, ϵ_r, is the junction strain at the end of the rest period.

(C) The average additional contraction that occurs after the second pulse as a function of residual strain obtained from n = 15 simulations.

(D) Final junction length (heat scale) as a function of rest time and total activation time, for pulsed activation scheme in (A) and (B).

(E and F) Representative image (E) and normalized junction length over time (F) of a junction in an experiment with a two 20-min activation with a 20-min rest period. Scale bar, 10 μm.

(G) Final normalized junction length for varying rest times in experiments (gray, n = 2 or 3) and simulations (pink, n = 15 for each condition). Error bars indicate the standard deviation of the number of experiments and simulations indicated within each bar.

We then examined how the junction shortening varies when the total activation time, t_act, is temporally sculpted into two shorter pulses, of duration ½t_act, separated by a rest time, t_rest, (Figure 4A). When the rest time is short, the final junction length is limited to 80% of the initial value for all activation times longer than 15 min and rest time ranging from 0 to 10–15 min (Figure 4D). However, for longer rest times, temporally structuring the contraction into two distinct pulses enables further junction shortening for the same activation time (Figure S3A–S3D). For instance, for a constant t_act of 25 min, increasing the rest time from 15 to 40 min decreases the final normalized length from 0.80 to 0.60 (Figure 4D). Thus, our model for mechanosensitive dynamics junction remodeling predicts that frequency modulation of Rho GTPase activity will have a significant impact on junction shortening.

To test these predictions, we modify the temporal pattern of exogenous RhoA activation and compared the total length change induced by a single 40-min light activation to that of two 20-min pulses separated by either 10 or 20 min rest. As described previously, a single 40-min pulse shortens the junction length by 20%. Dual pulses separated by <10 min induce a similar extent of contraction (Figures 4G and S3). However, when the rest time is increased to 20 min, the junction shortens to 40%-50% of the original length (Figures 4E–4G; Video S5), in agreement with our model predictions.

RhoA-Induced Junction Contraction Initiates Membrane Coalescence and Internalization

To gain insight into the cell biological mechanisms underlying junctional tension and length remodeling, we examine changes in the cell membrane that occur during Rho-mediated junctional shortening. We measure membrane intensity profiles perpendicular to the junction, averaged along the junction length at several times, t = 0, 5, and 20 min, during activation (Figure 5A). Initially, the line scans reveal a narrow intensity profile of the membrane, with a full width at a half max of 0.75 μm (Figures 5B and 5C) that reflect membrane localization at the cell-cell interface. During stimulated junction contraction, both the peak and width of the membrane intensity profile increases (Figures 5B and 5C), reflecting the accumulation and coalescence of the membrane during contraction. To measure the change in membrane intensity proximal to the activated junction, we measure the average intensity in a region a distance of 1.5 μm away from the peak intensity and observe a dramatic increase during both the fast and slow contraction phases (Figure 5D). Close examination of these regions reveals vesicles emanating from the junction during the slow contractile phase of activation (Figure 5E, red arrow). Notably, we see these vesicles emanating from concentrated membrane regions that span a few microns along the junction proper (Figure 5E, yellow arrows), similar in size to the regions that undergo local contraction (Figures 1H and 1I).

Figure 5. Compressive Strain Induces the Remodeling of Slackened Membrane.

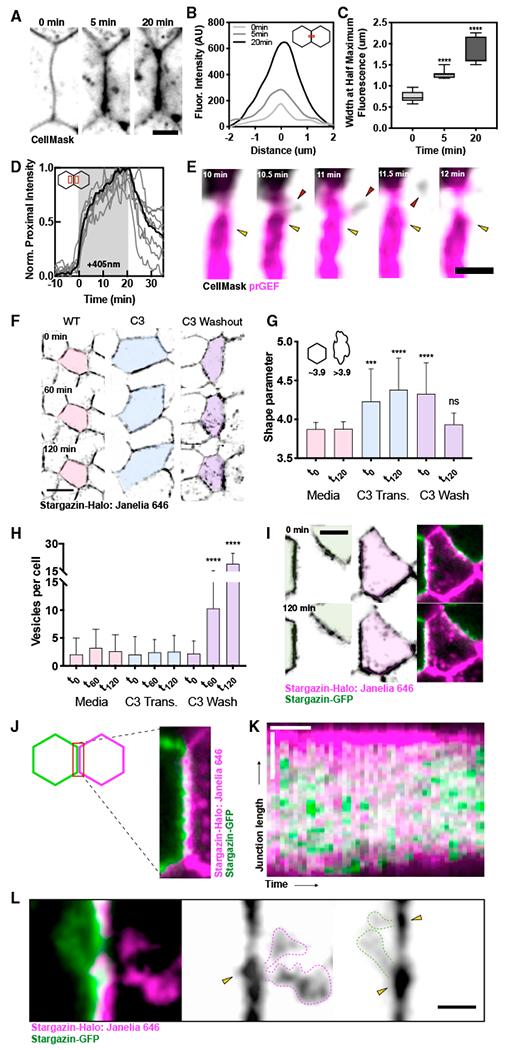
(A) Representative images of a junction at t = 0, 5, and 20 min after activation. Scale bar, 5 μm.

(B) CellMask intensities along a line perpendicular to the times in (A).

(C) The full width at half maximum fluorescence from data in (B). Each box is an average of n = 8 regions, **** = p < 0.0001 compared to t = 0 data.

(D) Normalized fluorescence intensity for the region proximal to the activated junction during an optogenetic experiment. Data for 8 regions is shown, with the average indicated by a bold line.

(E) Representative image of a junction between 10 and 12 min after activation showing membrane vesiculation and internalization. Scale bar, 2 μm.

(F) Stargazin images at 0, 60, and 120 min of wild-type cells, with C3 transferase treatment or immediately after a C3 transferase wash out at t = 0 min. Scale bar, 10 μm.

(G) Quantification of cell shape parameters from (F). Each bar is the average and/or SD of n = 30 cells for each condition.

(H) The number of vesicles observed within the cell interior in images from (F). Each bar is the average/SD of n = 30 cells for each condition.

(I) Representative images of a mosaically labeled cell (pink) undergoing self-internalization from 0 to 120 min.

(J) Representative image of a mosaically labeled cell-cell junction showing heterogeneous distribution of membrane.

(K) Kymograph of a junction undergoing shortening in (I) shows distinct membrane regions appearing during contraction. Horizontal scale bar, 20 min and vertical scale bar, 5 μm.

(L) Representative image showing tubular vesicles emanating from membrane regions during junction contraction. Scale bar, 2 μm.

To further interrogate the relationship between changes in junction length and membrane internalization, we developed an assay to monitor the response of cell sheets to a uniform increase in RhoA activity induced by washing out its inhibitor, C3 transferase. Our goal with this washout assay was to examine the tissue-level response to acute RhoA activation, recapitulating our optogenetic activations. In control conditions, time-lapse imaging of monolayers expressing a Stargazin-Halo membrane marker show little cellular movement over the course of 2 h (Figure 5F; Video S6, left). We quantify cell shape using a dimensionless shape parameter, defined as the ratio of the cell perimeter to the square root of the cell area (Bi et al., 2015). This shape parameter is a reliable measure of junction perimeters and cell shapes in response to varying cortical tension. In control conditions, the shape parameter is 3.9, indicating a compact, hexagonal shape (Figure 5G), and the average number of fluorescently labeled vesicles per cell remains low (< 4) over 2 h, consistent with a low rate of membrane internalization during this time (Figure 5H).

To globally inhibit Rho activity, we incubated the monolayers in media containing C3 transferase for 4 h (Figure 5F). Rho inhibitor treatment induces an increase in the cell shape parameter to 4.5, reflecting a more elongated shape and induces increased cell motion (Figure 5G; Video S6, middle). The mean number of vesicles per cell remained low (~2) over 2 h (Figure 5H). Thus, global RhoA inhibition induces changes in overall cell shape, and increases junction length, but does not modify the amount of membrane internalization that occurs over several hours.

To explore how a global increase in Rho activity modulates cell shape and surface membrane reorganization, we visualize changes in cell shape upon washing out C3 transferase (Figure 5F). After C3 transferase washout, the cell shape parameter decreased from 4.3 to 3.9, consistent with the increased contractility driving the transition from a more elongated to hexagonal shape with decreased perimeter and therefore junction lengths (Figure 5G; Video S6, right). Strikingly, this change in junction length is accompanied by a significant increase in cytoplasmic vesicles, increasing to a mean of 10–19 vesicles per cell 2 h after C3 washout (Figures 5F and 5H). Thus, we observe a significant increase in internalized membrane that occurs during Rho-mediated changes in junction length. Consistent with our optogenetic data, increased RhoA activity causes a decrease in junction length and induces vesicle internalization and membrane remodeling response.

To further examine Rho-mediated membrane remodeling, we generate mosaic monolayers of cell lines expressing spectrally distinct membrane tags, Stargazin-Halo:Janelia-646 and Stargazin-GFP (Figure 5J). This mosaic labeling allows us to determine which cells contribute membrane during individual internalization events. The internalized vesicles within a given cell 2 h after C3 washout have the same fluorescence as that of the cell’s plasma membrane, indicating that during junction shortening, cells internalize their own membranes but not that of their neighbors. (Figure 5I). When we examine junctions between differently labeled cells at high resolution, we could resolve a heterogeneous distribution of labeled membranes, characterized by patchy variation in both label’s intensities along the junction’s length (Figure 5J). Kymographs of junctions during Rho-mediated shortening show that this patchy distribution of membrane labels persists but varies over time (Figure 5K). This indicates that, along the adherens junction, membrane materials from the two cells disappear abruptly and asynchronously over time. Examining regions proximal to the adherens junction at these time points reveals that membrane internalization occurs via extended, tubule-like structures from concentrated membranous regions (Figure 5L, yellow arrows), consistent with our optogenetic data (Figure 5E). Together, these data indicate that during Rho-mediated junction shortening, membrane at the adherens junction remodels and is internalized within micrometer-sized domains.

Permanent Junction Shortening Requires Formin-Dependent Clustering and Dynamin-Mediated Endocytosis of E-Cadherin

During morphogenic processes in Drosophila development, adherens junction remodeling is mediated by the internalization of junctional components, including E-cadherin (Levayer et al., 2011). We therefore sought to determine the relationship between RhoA-mediated membrane remodeling and junctional components. To determine how E-cadherin puncta are impacted by optogenetic RhoA activation, we visualize E-cadherin in live cells by incubation with fluorescent conjugates of HECD1 antibody to preserve trans-cadherin interactions while labeling endogenous E-cadherins (Brouxhon et al., 2013). Notably, this labeling reveals a punctate pattern of E-cadherin along cell junctions (Figures 6A and 6B), and this treatment did not induce any junction length changes or endocytic events prior to light activation and optogenetically induced junction contraction was similar to control cells. Consistent with the heterogenous shortening of junction segments, we observe heterogeneity in the remodeling of E-Cadherin, involving local events in which groups of E-cadherin puncta at the center of the junction coalesce together, intensify, and are then internalized within the slow remodeling phase of RhoA stimulation (Figure 6A, yellow arrows; Video S7). Thus, internalization of E-cadherin clusters occurs during junctional shortening triggered by optogenetic activation of RhoA.

Figure 6. Form in-Mediated E-Cadherin Clusters and Their Endocytosis Are Necessary for Junction Length Changes.

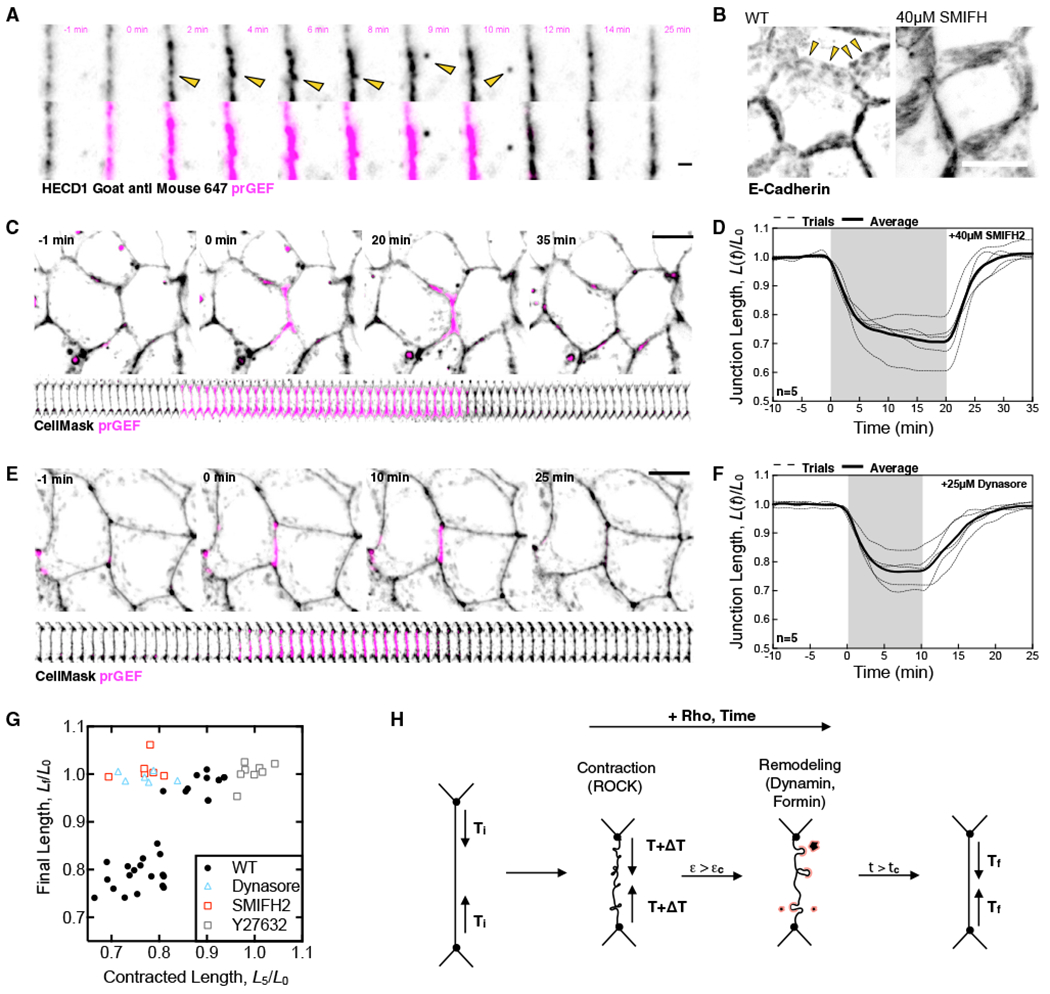
(A) Representative image of cells treated with HECD1 primary and GaM 647 secondary antibodies showing internalization of E-cadherin-positive clusters. Scale bar, 2 μm.

(B) Representative z stack projection of a cell stained for E-cadherin and a representative z stack projection of a cell treated with SMIFH2 and stained for E-cadherin. Scale bar, 10 μm. Arrows indicate regions of E-cadherin-rich junctional puncta.

(C) Representative images of cells treated with SMIFH2 and undergoing a 20-min activation. Scale bar, 10 μm.

(D) The normalized junction lengths over time in SMIFH-treated cells from (C) for n = 5 junctions.

(E) Representative images of cells treated with Dynasore and undergoing a 10-min activation. Scale bar, 10 μm.

(F) Quantification of normalized junction length over time in Dynasore-treated cells from (E) for n = 5 junctions.

(G) The final junction length, L_f/L₀, as a function of the initial contracted length after 5 min of activation L₅/L₀ for various perturbations shown in this manuscript.

(H) Graphical summary of the Rho-mediated junctional remodeling described here. The initial tension of a junction is T_i. A stepwise increase in tension, ΔT drives ROCK-mediated contraction. If the junction is deformed above a critical strain, ϵ > ϵ_c, dynamin and formin-dependent junction remodeling occur. After sufficient time, the junction remodels to a new length with a new base tension, T_f.

We next sought to elucidate the molecular regulation of observed membrane remodeling and internalization. Immunolocalized E-cadherin exists as distinct puncta along lateral junctions of epithelial monolayers (Figure 6B, yellow arrows). Consistent with previous work (Levayer et al., 2011), we find this clustering is formin-dependent, as treatment with the panformin inhibitor SMIFH2 abolishes E-cadherin punctae (Figure 6B). To test if formin-mediated E-cadherin clustering is important for junction remodeling in response to optogenetic activation of RhoA, we treat monolayers with SMIFH2 and stimulate the junction for 20 min (Figures 5C and 5D). SMIFH2 treatment has no impact on the initial junction contraction relative to controls (Figures 6D and 6G). However, in contrast to controls, upon removal of light, SMIFH2-treated junctions return to their original length and no permanent length reduction is observed (Figures 6D and 6G; Video S8).

If internalization of E-cadherin clusters by endocytosis is important for junction remodeling, then blocking vesicle internalization should also prevent irreversible changes in junction length in response to optogenetic activation of RhoA. To test this prediction, we treat monolayers with Dynasore, a pharmacological inhibitor of dynamin-mediated vesicle scission (Macia et al., 2006). Indeed, treating monolayers with Dynasore does not alter the initial contractile phase in response to optogenetic activation of RhoA (Figures 6E–6G), but the slower remodeling is abolished, and junctions return to their original lengths following the end of an activation (Figures 6F and 6G; Video S9). Thus, dynamin is required for junctional remodeling. Together, these data suggest that the permanent junction shortening that occurs after a pulse of increased RhoA activity requires formin-mediated E-cadherin clustering and dynamin-mediated endocytosis (Figure 6H).

DISCUSSION

In this study, we utilized optogenetics to investigate how transient activation of RhoA can induce longer lasting irreversible changes in cell shape in model epithelia. Exploiting optogenetic control, we identified how changes in the strength and temporal structure of RhoA activation can access qualitatively different regimens of junctional remodeling. We find that small changes in junction length are completely reversible. In contrast, sufficiently strong or prolonged activation of RhoA can drive junctions across a deformation threshold to trigger junctional tension remodeling that drives irreversible junction shortening. Furthermore, episodic pulses of RhoA activity, separated by periods of quiescence, can induce a greater degree of irreversible change than a prolonged pulse of the same strength. These results provide a basis for understanding how the strength and pattern of RhoA activity can encode fine-tuned instructions for epithelial morphogenesis.

Our data have significant implications for the use of simple vertex models to describe morphogenetic remodeling of epithelial tissues (Fletcher et al., 2014). In traditional vertex models, junction lengths evolve solely in response to junction tension and cell elasticity. These models and their existing variants capture reversible changes in junction length in response to small contractions, but they are inadequate to describe the time-dependent junction shortening dynamics we observe in response to sustained or multiple pulses of RhoA activation. To describe these responses, we find that it is necessary and sufficient to consider two additional properties: continuous relaxation of junctional strain and local remodeling of active junction tension above a critical strain threshold (see also Staddon et al., 2019). Threshold-dependent remodeling of active tension encodes the trigger for irreversible deformation. Continuous relaxation of junction strain sets a limit on the amount of irreversible deformation produced by a single pulse of activation and sets the timescale on which the system is refractory to further input, allowing for frequency-dependent modulation of morphogenetic change. This combination of strain threshold and frequency dependence provides a way to balance dual requirements for epithelial tissue homeostasis and large-scale remodeling. A strain threshold maintains architectural homeostasis against small fluctuations in contractile activity, while higher amplitude patterned activity can direct major morphogenetic movements in epithelial tissues.

The exact mechanisms underlying junctional strain relaxation remain unknown. However, the tendency to relax internal strain is a property of any material whose load-bearing elements undergo turnover in such a way as to replace strained elements with new unstrained elements. For example, turnover of actin filaments is thought to underlie strain relaxation in cortical actin networks, endowing those networks with effectively viscous behaviors (Kim et al., 2014; McFadden et al., 2017). At the filament scale, mechanical strains accelerate severing and turnover of F-actin (Wilson et al., 2010), providing a putative force-sensitive fluidization of actin networks. In addition, turnover of structural elements of adherens and/or tight junctions, through exocytosis and/or endocytosis or other mechanisms, may also contribute to strain relaxation (Choi et al., 2016). Strain relaxation in epithelial junctions could arise from mechanosensitive mechanisms either within the actin cortex itself or via turnover of adherens and/or other junctional adhesions. Understanding the mechanisms that govern and tune junctional remodeling to account for both length changes and strain relaxation will be an important target for future work.

Our experiments strongly support the idea that junctional tension remodeling is strain thresholded. However, the origins of this strain threshold, and the mechanisms underlying changes in local junctional tension, remain unclear. Because there is no clear relationship between the strains on activated junctions and neighboring junctions during the response to activation (Figure S1), we think it likely that the mechanism for strain-dependent tension remodeling is intrinsic to individual junctions. Our observations highlight a few key features of junction contraction induced by exogenous RhoA activation. First, contraction is heterogeneous, mediated by a few contractile regions, occupying ~26% of the junction’ length, which shorten rapidly and completely during exogenous RhoA activation (Figures 1I, 5J, 5K, and 6A). Second, contraction of these regions appears to be sufficient to account for the extent of fast junction contraction (~20%) and the expected strain threshold (~20%) to triggering tension remodeling. Third, contraction is associated with local accumulation of membrane within contractile regions, consistent with local membrane buckling (Figure 6H). Fourth, local clustering and coalescence of E-cadherin puncta also occur during contraction (Figure 6A). Finally, local endocytosis of junctional membrane, E-cadherin, and other junctional components correlates with, and is critical for, irreversible junctional shortening driven by super-threshold pulses of RhoA activity.

This model is in line with recent work documenting roles for the Rab trafficking pathway in promoting irreversible changes in junction length during epithelial morphogenesis (Jewett et al., 2017; Levayer et al., 2011; Mateus et al., 2011; Roeth et al., 2009; Sumi et al., 2018). Internalization of slackened membrane has been described during dorsal closure (Sumi et al., 2018) and germ band elongation (Jewett et al., 2017) in Drosophila embryos. Thus, our and other data point toward a more general model in which strain induces membrane buckles that either initiate or control the rate of endocytosis to control junction length (Figure 6H). In principle, such mechanisms could act either to stabilize cell shapes or promote irreversible change in cell shape, depending upon the nature of feedback in the system. Indeed, it will be of interest to explore any feedback mechanisms between RhoA and the general endocytic machinery. Already it has been shown that Dia signaling, downstream of RhoGEF2, can induce ectopic clathrin recruitment at junctions (Levayer et al., 2011).

The possibility that local clustering, coalescence, and internalization of E-cadherin could play a role in junction remodeling is consistent with recent work reporting how differences in the subcellular origin of contractile forces affects junctional E-cadherin endocytosis (Kale et al., 2018). Polarized junctional nonmuscle myosin II (NMII) generates shear stress that destabilizes and dissociates E-cadherin trans-interactions for their subsequent internalization via heterogeneous load distribution (Kale et al., 2018). Our data similarly document punctate patterns of local E-cadherins that heterogeneously contract upon RhoA activation (Figure 6A). Formin activity is required for the formation and coalescence of these puncta. Thus, formin-mediated actin assembly and E-cadherin clustering may help to organize the distinct contractile units that drive heterogenous junction contraction. In addition, coalescence of E-cadherin puncta may help to stabilize regions of slackened membrane, which act as endocytic hubs and assist in packaging buckled regions of membrane and/or cortex for dynamin-mediated internalization. It will be of interest to further dissect the molecular basis of this formin-mediated E-cadherin endocytosis.

Cells in developmental systems are tuned to undergo dynamic processes such as intercalation events and undergo fast contractions to reach what we propose to be a threshold strain. In vivo, junctions contract at a strain rate of 0.5 min⁻¹ (Rauzi et al., 2010) with cycles of pulsatility being significantly shorter. Here, junction contractions range from 90–120 s and rest periods range from 2–7 min (Jewett et al., 2017; Rauzi et al., 2010). We do not produce any significant length changes post-activation when using optogenetic activation schemes that are more characteristic of developmental systems (Figure S3E). We also find that the Caco-2 junction contraction rate (0.047 min⁻¹) is slower than developing tissues. This difference in tissue deformability may arise from subcellular or tissue-scale effects. For instance, in vivo, multiple junctions are shrinking in the face of tension (Fernandez-Gonzalez et al., 2009). Neighboring pulses also occur in antiphase with junctional contractions; such an oscillatory contractile structure may further shorten the junctions or stabilize cell shapes (Xie and Martin, 2015). Additionally, our system lacks any basolateral protrusions that coordinate with apicojunctional vertex formation to facilitate tissue fluidity (Sun et al., 2017). Despite these differences, our simplified system and approach present a means to isolate how temporal regulation of junctional Rho activity sculpts junctional length and provide insights into in vivo junctional ratcheting.

STAR★METHODS

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources and reagents should be directed to the Lead Contact, Margaret Gardel (gardel@uchicago.edu). All unique/stable reagents generated in this study are available from the Lead Contact upon request.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Male Colorectal adenocarcinoma (Caco-2) and HEK293T cells were cultured in a humidified incubator at 37C with 5% CO2 using Dulbecco’s minimal essential medium (Corning) supplemented with 5% FBS (Corning), 2mM l-glutamine, and penicillin-streptomycin (Corning).

METHOD DETAILS

Plasmids and Generation of Cell Lines

Lentiviral vectors described here were generated with the aid of SnapGene Software (GSL Biotech LLC). The optogenetic membrane tether consisting of Stargazin-GFP-LOVpep and prGEF constructs were constructed by PCR amplification of the region of interest and inserting it into a lentiviral vector, pWPT-GFP (12255; Addgene) using restriction sites BamHI and Sall. This created the lentiviral constructs WPT-Stargazin-GFP-LOVpep and WPT-mCherry-prGEF. pWPT-Stargazin-Halo was constructed by inserted a PCR amplified a Halo tag region into the the pWPT-Stargazin-GFP-LOVpep backbone isolated by PCR amplification.

Lentivirus was produced using 293T cells (a gift from G. Green, University of Chicago, Chicago, IL) using Fugene 6 transfection reagent (Promega) to transfect the lentiviral vectors, a pHR1-8.2-delta-R packaging plasmid, and VSV-G pseudo typing plasmid (gifts from M. Rosner, University of Chicago). Viral supernatant was collected, filtered, and incubated with target Caco-2 cells for 24hr in the presence of 8 μg/ml polybrene (EMD Millipore). After viral transfection, cells were sorted by fluorescence (UChicago Flow Cytometry Core) and screened for optimal expression of constructs by fluorescence microscopy.

Collagen Gel Preparation

Collagen gels were prepared by mixing Rat tail collagen 1 (Corning) with collagen polymerizing reagents to a final concentration of 2mg/ml. Collagen polymerizing agents were prepared with media mixed with 1M Hepes and 7.5% NaHCO₃forafinal ratio of 1:50 and 1:23.5, respectively. Four-well chambers (Ibidi) were coated with 30 μl of 2mg/ml collagen solution and polymerized in the incubator for 10min before plating cells.

Microscopy

Cells were imaged on an inverted Nikon Ti-E (Nikon, Melville, NY) with a Yokogawa CSU-X confocal scanning head (Yokogawa Electric, Tokyo, Japan) and laser merge model with 491, 561, and 642nm laser lines (Spectral Applied Research, Ontario, Canada). Images were collected on a Zyla 4.2 sCMOS Camera (Andor, Belfast, UK). Optogenetic recruitment utilized a Mosaic digital micromirror device (Andor) coupled to a 405-nm laser. A 60× 1.49 NA ApoTIRF oil immersion objective (Nikon) or a 60× 1.2 Plan Apo water (Nikon) objective was used to collect images. MetaMorph Automation and Image Analysis Software (Molecular Devices, Sunnvyale, CA) controlled all hardware.

Live-Cell Imaging

To ensure a mature and polarized epithelial monolayer, Caco-2 cells were plated at a confluent density on a collagen gel within an IbidI chamber and cultured for two days prior to any experiments. Ibidi chambers were then placed in culture media supplemented with 10mM Hepes and maintained at 37°C or maintained with a stage incubator for temperature, humidity, and CO2 control (Chamlide TC and FC-5N; Quorum Technologies). For the stage incubator, the stage adapter, stage cover, and objective were maintained at 37C, whereas humidified 5% CO2 was maintained at 50°C at its source to prevent condensation within its tubing.

For optogenetic experiments, cell-cell junctions were labeled with CellMask Deep Red plasma membrane stain (Molecular Probes, Life Technologies). Cells were imaged in the 561 and 647 channel every 35 s. The first 10min was used document average junction length fluctuations and the last 15 minutes to document junction recovery. For analysis of the timescales of RhoA activation, the activation period was 2.5, 5, 10, 20, or 40 minutes. During the stated activation period, a local region was drawn around the cell-cell junction in MetaMorph and illuminated by the 405-nm laser for 1000ms immediately before the acquisition of each image. Activated regions were adjusted in real time to isolate the prGEF at contracting junctions. Unless otherwise stated, laser power was set at 1000AU. For determining junction strain rates as a function of laser intensity analysis, laser power was reduced to 750 or 500AU.

Mosaic labeling of cells was performed by mixing the two cell lines, Stargazin-Halo and Stargazin-GFP, at least a day before imaging and grown to ensure a confluent and polarized monolayer. For visualization, Stargazin-Halo cells were conjugated with the Halo ligand, JaneliaFluor 646 (a kind gift from Luke Lavis, HHMI Janelia Research Campus, Ashburn, VA).

Drug Treatments

For optogenetic experiments, cells were treated with stated drug for at least one hour before any optogenetic activations and imaging. Treatments here were 30uM Y-27632 (Sigma), 25uM Dynasore (Tocris), 40uM SMIFH2 (a gift from D. Kovar, University of Chicago, Chicago IL), or 1:1500 dilution of HECD1 antibody (Abcam) and Alexa Fluor Goat anti Mouse 647 (Invitrogen). For C3 transferase washout experiments, cells were incubated with 1ug/ul C3 transferase (Cytoskeleton, Inc.) diluted in serum-free media for 4 hours, washed with PBS, and then replaced with fresh media.

Image Analysis

For junction length analysis, junction lengths were measured manually in each frame using the free hand line tool in FIJI software (Schneider et al., 2012). Strain and strain rates were calculated from this data using custom R scripts. Junction width analysis was done by taking a junctional region of 3μm by 3μm and measuring fluorescence intensities with the FIJI intensity analysis tool. Full width by half maximum was calculated by hand in Excel. Proximal fluorescence intensity analysis was done by taking a region proximal to the junction outside of the junctional regions and also measured using the FIJI intensity analysis tool. Localization of microdomains was calculated by measuring the distance of concentrated membrane regions from each vertex using the FIJI line tool. Vesicle number was calculated using FIJI by thresholding and segmenting the image to create a mask of vesicles within the cell perimeter, which was overlaid onto the channel for segmentation and measurement analysis in FIJI. Cell perimeter and area was calculated manually by tracing cell junctions with the line tool in FIJI. Shape parameter was then calculated in Excel.

Immunofluorescence

Cells were seeded onto collagen gels in LabTek II Chamber Slides (Thermo Fisher Scientific) and allowed to form a polarized, mature monolayer before fixing. Cells were fixed in a solution of 4% paraformaldehyde with 0.1% Triton X-100 in PBS solution (Corning). Cells were permeabilized in 0.5% Triton X-100 for 10 min and blocked with 2.5% BSA and 0.1% Triton X-100 in PBS for 1 hr. Cells were incubated with mouse HECD1 antibody (Abcam) at 1:300 in blocking solution overnight at 4°C and washed three times in 0.1% Triton X-100 for 20 min each, and then placed in secondary antibody Alexa Fluor Goat anti Mouse 647 (Invitrogen) in blocking solution for 1 hr. After another three 20-min washes with 0.1% Triton X-100, slide chambers were removed. Samples were prepared with 20 μl ProLong Gold (Thermo Fisher Scientific) per well and sealed with glass coverslips. Slides were allowed to dry, sealed with nail polish, and stored at 4°C.

Model Implementation

The vertex model is implemented using Surface Evolver (Brakke, 1992). A tissue of 50 cells is generated and relaxed, without junctional remodeling, to a stable energy minimum. 15 different edges within the tissue are selected for activation, with the tissue reset to its stable state after activation. A time step of Δt = 0.058 s is used to numerically simulate the dynamics.

Cell-Based Model for Epithelium with Variable Tension and Junctional Remodeling

Vertex Model for Epithelial Mechanics

Each cell is modeled by a two-dimensional polygon, with edges representing cell-cell junctions, and vertices three-way junctions. The mechanical energy for the tissue is given by(Farhadifar et al., 2007):

$$E={\sum }_{\alpha }\frac{1}{2}K{(A_{\alpha }-A_0)}^2+{\sum }_{ij}{\Lambda }_{ij}{L}_{ij},$$ (Equation 1)

where the first term represents the area elasticity of each cell, A_α is the area of cell α, A₀ is the preferred area, and K is the areal elastic modulus. The second term is the interfacial energy resulting from cortical tension and cell-cell adhesion, where L_ij is the length of edge ij connecting vertices i and j, and Λ_ij is the tension on that edge.

The net mechanical force acting on vertex i with position x_i is given by F_i = −∂E/∂x_i. Assuming overdamped dynamics, the equation of motion for the vertex i is:

$$\mu \frac{d{\mathit{x}}_i}{dt}={\mathit{F}}_i,$$ (Equation 2)

where μ is an effective friction coefficient. Prior to RhoA induced contractions, all cell-cell junctions are assumed to carry uniform tension, Λ. Under applied mechanical strain both tension and junctional lengths can remodel as described below.

Modeling RhoA Induced Contractions

To model the mechanical effect of optogenetic activation of RhoA on cell junctions, we increase the tension on the activated edge ij, by an amount ΔΛ = Γ_optL_ij, where Γ_opt is applied contractile force per unit length, and L_ij is the length of the edge. The increase in tension is assumed to be proportional to the edge length, so as to produce a strain that is independent of the initial edge length (Figure S2D), as observed in our experiments. Having a constant strain, ΔΛ = Λ_opt, applies a higher strain on shorter edges.

Mechanosensitive Junctional Remodeling

Each cell-cell junction has a rest length, $L_{\mathit{ij}}^m$, which is the length at which the junctional elastic strain is zero and the tension is constant. Prior to RhoA induced contraction of edge ij, $L_{\mathit{ij}}^m=L_{\mathit{ij}}$. As the junctional edges contract or expand due to applied forces, the rest length remodels overtime to adjust to the current length of the edge (Muñoz and Albo, 2013):

$$\frac{d{L}_{ij}^m}{dt}=k_l(L_{ij}-L_{ij}^m),$$ (Equation 3)

where k_l is the rate of rest length remodeling. When the edge is stretched, or compressed, above a critical strain, ϵ_c, the edge tension begins to remodel:

$$\frac{d{\Lambda }_{\mathit{ij}}}{dt}=\{\begin{array}{c}-k_e(L_{\mathit{ij}}-L_{\mathit{ij}}^m),\mathit{if}{ϵ}_{\mathrm{ij}}<{ϵ}_c\\ -k_c(L_{ij}-L_{ij}^m),\mathit{if}{ϵ}_{\text{ij}}<-{ϵ}_c,\\ 0,\mathit{otherwise}\end{array}$$ (Equation 4)

where k_e is the rate of tension remodeling during extension, k_c the rate of tension remodeling during compression, and ${ϵ}_{\mathit{ij}}=(L_{\mathit{ij}}-L_{\mathit{ij}}^m)/L_{\mathit{ij}}^m$ is the strain on the edge. Since cell membrane can buckle easily under compression, and stiffen under extension, we allow the remodeling rates to be different during extension and compression.

Short timescale contraction – if the contraction is induced for a short period such that ϵ> – ϵ_c, then the edge tension does not remodel and remains constant at Λ (Equation 4). The edge length contracts by an amount proportional to Γ_opt, and the rest length remodels at a rate k_l to approach the current length (Equation 3). As the applied contraction is turned off, Γ_opt = 0, the edge length fully recovers to its initial value (Figure 3) determined by the balance between tension (Λ) and elasticity.

Long Timescale Contraction

During long timescale contraction of an edge, the edge gains a permanent increase in tension due to tension remodeling (ϵ< – ϵ_c). As a result, the balance between edge tension and elasticity is altered, leading to a shorter final length in the steady state after the contraction is turned off (Figure 3).

Ratcheting –

Since we observe that the strain on an edge is independent of the initial edge length, applying a second activation to an already-shortened junction should lead to further contraction, even in the case of a long, saturated contraction. During the first contraction, at long times the strain rate slows down and the rest length remodels and the strain falls below the critical strain, stopping tension remodeling and eventually leading to a saturation of the contraction. After activation the edge recoils to a new length. A second activation leads to a fast contraction, which strains the edge above the critical strain, and so the tension continues to increase, leading to a further decrease in junction length. Thus, applying repeated contractions can repeatedly shorten the junction.

Different Model Limits

1. Vertex model with constant tension and constant rest length $(\frac{d{L}_{\mathit{ij}}^m}{\mathit{dt}}=0;\frac{d{\Lambda }_{\mathit{ij}}}{\mathit{dt}}=0)$ - Using the traditional vertex model, we find that, regardless on contraction time, junctions always return to their initial length after contraction. Other common variants on the vertex model also fail to capture the change in length of the edges, such as including an energy term proportional to square of the perimeter) (Figure S2A). The stable state of the junction is such that forces balance. Since forces don’t change during a contraction, the stable state remains unchanged and the junction returns to its initial length. This model is equivalent to setting tension remodeling to zero.

2. Vertex model with constant rest length and tension remodeling $(\frac{d{L}_{\mathit{ij}}^m}{\mathit{dt}}=0)$ – With no rest length remodeling, an activation would shorten the edge and increase the edge tension. After the activation, the new steady state length is shorter than the rest length, leading to a further increase in tension and an even shorter rest length. This positive feedback loop would lead to the collapse of any junction after an activation (Figure S2B).

3. No critical strain for tension remodeling (ϵ_c = 0) - With ϵ_c = 0, after activations the edges slowly recover to their original length. With no critical strain, the tension increases during and activation, but immediately after activation it begins to decrease. As a result, the junction extends, further decreasing the tension until it returns to its original length. In particular, the recoil continues for a long time when compared to experiments (Figure S2C). With a critical strain, the tension stops decreasing and a new steady state is reached.

4. Constant applied tension – Increasing the tension by a constant amount during an activation, Λ_opt instead of Γ_optL, shrinks edges at a constant speed, independent of initial length, and so shorter edges experience a much higher strain rate than longer edges (Figure S2D). In contrast, using a tension proportional to the edge length leads to a strain rate independent of edge length, as in experiments.

Model Parameters

Model parameters are fit to the experimental data by minimizing the error between simulated and experimental data, for 2, 5,10, 20, and 40-min activations. We minimize the mean square error between individual simulated lengths and mean experimental lengths during an activation during and after the activation, averaged over the different activation times:

$$Error=\frac{1}{5}\sum _a\sum _{ij}\frac{1}{T_a}{\int }_0^{T_a}{\left(\langle \frac{L_{\mathit{exp}}^a(t)}{L_{\mathit{exp}}^a(0)}\rangle -\frac{L_{ij}^a(t)}{L_{ij}^a(0)}\right)}^{2}dt$$

where a = 2, 5, 10, 20, 40 indicates the activation time, ij, indicates the simulated edge being activated, T_a is the total time recorded in experiments for activation a, and $\langle \frac{L_{\mathit{exp}}^a(t)}{L_{\mathit{exp}}^a(0)}\rangle$ is the normalized length in experiments averaged over all activations. We then use the Nelder-Mead algorithm implemented in scipy to minimize the error, giving the parameters in the table below.

We nondimensionalize our parameters byrescaling length by $A_0^{1/2}$ and force by ${\mathit{KA}}_0^{3/2}$, so that the nondimensional energy becomes

$$E=\sum _{\alpha }\frac{1}{2}{(A_{\alpha }-1)}^2+\sum _{ij}{\Lambda }_{ij}{L}_{ij}$$

Parameter	Symbol	Value
Default edge tension	Λ	0.142
Rest length remodeling rate	kl	0.159 / min
Contraction tension remodeling rate	kc	0.0203/min
Extension tension remodeling rate	ke	0.000/min
Critical strain	ϵc	0.122
Optogenetic contractility	Γopt	0.0846
Viscosity	μ	1.132 mins

QUANTIFICATION AND STATISTICAL ANALYSIS

Statistical significance was determined under specific experimental conditions and was established during a two-tailed Student t-test in Prism (Graphpad, La Jolla, California). n represents the number of junctions activated and used in each experiment, as indicated in the figures. For analysis of shape parameters and vesicle internalization, 30 cells were used for each condition.

DATA AND CODE AVAILABILITY

The data and code that support the findings in this paper are available from the Lead contact upon request.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Anti-E-Cadherin HECD1	Abcam	ab1416
Alexa Fluor Goat anti Mouse 647	Invitrogen	Cat#A-21235
Chemicals, Peptides, and Recombinant Proteins
Y-27632	Sigma	CAS#129830-38-2
SMIFH2	David Kovar Laboratory	N/A
C3 Transferase	Cytoskeleton, inc.	Cat#CT04
Dynasore	Tocris	Cat#2897
Fugene 6 Transfection Reagent	Promega	Cat#E2691
Polybrene	EMD Millipore	Cat#TR-1003-G
Experimental Models: Cell lines
Human: Caco-2	ATCC	HTB-37
Human: 293T	ATCC	CRL-3216
DNA
Stargazin-GFP-LOVpep	Wagner and Glotzer, 2016	Addgene #80406
2XPDZ-mCherry-LARG	Wagner and Glotzer, 2016	Addgene #80407
WPT-GFP	Didier Trono Laboratory	Addgene#12255
WPT-Stargazin-GFP-LOVpep	This paper	To be deposited
WPT-2XPDZ-mCherry-LARG	This paper	To be deposited
WPT-Stargazin-Halo	This paper	To be deposited
pHR1-8.2-delta-R	Marsha Rosner Laboratory	Addgene #12263
VSV-G pseudo typing plasmid	Marsha Rosner Laboratory	Addgene #8454
Software and Algorithms
Snapgene Software	GSL Biotech LLC	Snapgene.com
FIJI	Schneider et al., 2012	Fiji.sc
Metamorph	Molecular Devices	Moleculardevices.com
Prism	GraphPad Sofware	Graphpad.com
Surface Evolver	Brakke, 1992	N/A
R Studio	R Foundation	R-project.org
Other
Nunc Lab Tek II Chamber Slides	ThermoFisher	Cat#154453PK
Ibidi Chamber	Ibidi	Cat#80426
Rat Tail Collagen I	Corning	Cat#354236
CellMask Deep Red Plasma membrane stain	Molecular Probes, Life technologies	Cat#C10046
JaneliaFluor 646	A kind gift from Luke Lavis, Janelia HHMI Research Campus	N/A
ProLong Gold	ThermoFisher	Cat#10144
Oligonucleotides
WPT Stargazin Halo insert FWD: CCA CGC CCG TAG GAT CCA TGG CAG AAA TCG GTA CTG G	This paper	N/A
WPT Stargazin Halo insert REV: AGG GCC CTC TAG ATT ATC TAG AGC CGG AAA TCT CGA GCG T	This paper	N/A
WPT Stargazin GFP LOVpep insert FWD: CCGGACTCTAGCGTTTAAACTTAAGATGGGGCTGTTTGATCGAGGTG	This paper	N/A
WPT Stargazin GFP LOVpep insert REV: CTCATGCACCAGAGTTTCGAACGAACCTAGGTTACACCCAGgTATCCA	This paper	N/A
WPT 2xPDZ mCherry LARG insert FWD: GTC GTG ACG CGG ATC ATC GAT ACC GTC GAC ATG GC	This paper	N/A
WPT 2xPDZ mCherry LARG insert REV: TTC CCT CGA GGT CGA TTA GCG CTG CTT GTT TTC TG	This paper	N/A

Highlights.

• Short RhoA pulses reversibly shorten junction length, and long pulses stabilize shortening

• Threshold-dependent tension remodeling and strain relaxation explain length changes

• Endocytosis stabilizes junction length remodeling

• Ratcheting RhoA produces more junction length change than one equivalent pulse