A Systematic Review of Estimating Breast Cancer Recurrence at the Population Level With Administrative Data

Abstract

Background

Exact numbers of breast cancer recurrences are currently unknown at the population level, because they are challenging to actively collect. Previously, real-world data such as administrative claims have been used within expert- or data-driven (machine learning) algorithms for estimating cancer recurrence. We present the first systematic review and meta-analysis, to our knowledge, of publications estimating breast cancer recurrence at the population level using algorithms based on administrative data.

Methods

The systematic literature search followed Preferred Reporting Items for Systematic Reviews and Meta-Analysis guidelines. We evaluated and compared sensitivity, specificity, positive predictive value, negative predictive value, and overall accuracy of algorithms. A random-effects meta-analysis was performed using a generalized linear mixed model to obtain a pooled estimate of accuracy.

Results

Seventeen articles met the inclusion criteria. Most articles used information from medical files as the gold standard, defined as any recurrence. Two studies included bone metastases only in the definition of recurrence. Fewer studies used a model-based approach (decision trees or logistic regression) (41.2%) compared with studies using detection rules without specified model (58.8%). The generalized linear mixed model for all recurrence types reported an accuracy of 92.2% (95% confidence interval = 88.4% to 94.8%).

Conclusions

Publications reporting algorithms for detecting breast cancer recurrence are limited in number and heterogeneous. A thorough analysis of the existing algorithms demonstrated the need for more standardization and validation. The meta-analysis reported a high accuracy overall, which indicates algorithms as promising tools to identify breast cancer recurrence at the population level. The rule-based approach combined with emerging machine learning algorithms could be interesting to explore in the future.

In many countries, cancer incidence is captured by cancer registries (1). However, population-wide registration of cancer recurrence is lacking, apart from a limited number of developed countries, including the Netherlands and Denmark. These countries register cancer recurrence but only for certain cancers on a project-based manner. To the best of our knowledge, registries of breast cancer recurrence at the population level do not exist.

Experts in the field advocate for more complete and reliable cancer recurrence data at the population level, because recurrence is an important cancer outcome metric (2–4). Also, it would be possible to measure the burden of cancer recurrence and evaluate efficacy of cancer treatment modalities (chemotherapy regimen, radiotherapy, surgery, etc.) outside a conventional clinical trial setting. This could eventually lead to improvements in quality of cancer care (4).

Administrative data from health insurance companies or health-care providers on medical treatments and procedures often referred to as “claims data” represent an alternative or proxy for follow-up of patients. Cancer recurrence is described as the reoccurrence of the disease after a period of undetectable disease. Algorithms based on administrative claims data have been used to detect cancer recurrence at the population level and, more frequently, for breast (5–21), lung (8–11,14,20–27), or colorectal cancer (8,9,11,14,20,21,23,24,28–31) compared with other cancers (7,8,10,14,21–24,32–40).

This systematic review and meta-analysis gives an overview of studies using administrative claims data to estimate cancer recurrence in breast cancer patients (including local, regional, or distant recurrences and second primary or contralateral breast cancers) and evaluates the accuracy of the algorithms.

Methods

Literature Search and Eligibility Criteria

This systematic review followed the Preferred Reporting Items for Systematic Reviews and Meta-Analysis guidelines (41). A systematic literature search was conducted in the databases of Pubmed (including MEDLINE), EMBASE, and the Web of Science Core collection with the search concepts cancer recurrence, registries, administrative claims, and algorithm-based (see Supplementary Material, available online, for full search strategy). The concepts algorithm-based and registries are combined, because the concept algorithm-based alone rather refers to predictive algorithms for cancer recurrence (eg, clinical or pathological factors predicting recurrence).

All citations obtained from the search strategy were merged into 1 set using EndNote X9 (Clarivate Analytics, Philadelphia, PA). After removal of duplicates, eligible citations were reviewed and screened using RAYYAN QCRI, the Systematic Reviews Web App (42), and divided into 3 groups based on title and/or abstract: eligible, potentially eligible, or not eligible (41). The full texts of potentially eligible or eligible articles were then screened and assessed for eligibility.

Although the search strategy detected articles on all cancer types, only articles describing breast cancer were retained in the qualitative analysis. Studies were included if they reported on algorithms to detect breast cancer recurrence based on administrative data, using information from medical files or clinical or patient registries for verification (gold standard). Articles were only considered if they were peer-reviewed primary research articles in which an algorithm is developed. Only articles written in English were eligible for inclusion.

Data Extraction and Statistical Analysis

Data extraction was conducted independently by 2 review authors (H.Izci and V.Depoorter). Information on data sources to develop the algorithm, patient selection and sample size, and data sources for the gold standard was extracted for each study (Table 1). Extra attention was given to algorithm development rules and modeling of the algorithm.

Table 1.

Study characteristics

Reference	Country	Cancer type	Data source for development of algorithm	Format of data	No. of BC patients for training set	Median follow-up period, mo	Period of patient inclusion, incidence	Clinical definition of recurrences used for gold standard
Xu, 2019 (7)	Canada	Breast	Alberta provincial administrative registry	—	598	48	2007–2010 and 2012–2014	All recurrences (local, regional, and distant) or second breast primary
Rasmussen, 2019 (15)	Denmark	Breast	Danish National Patient Register	ICD-10	471	90	2003–2007	Recurrence or second breast primary
Cronin-Fenton, 2018 (12)	Denmark	Breast	Danish National Patient Register	ICD-10	155	—	1991–2011	Bone metastases, visceral metastases, and breast cancer recurrence (included local, regional, and distant)
Ritzwoller, 2018 (16)	United States	Breast	Kaiser Permanente regions of Colorado and Northwest	ICD-9 and ICD-10	3370	52	2000–2011	Recurrence
Chubak, 2012 (17), Chubak, 2017 (18)	United States	Breast	Group Health Research Institute	ICD-9	1892	74.4	1993–2006	All recurrences (local, regional, and distant) or second breast primary
Kroenke, 2016 (5)	United States	Breast	Kaiser Permanente Northern California	ICD-9	LACEb: 1535	—	1997–2000	All recurrences (local, regional, and distant) or second breast primary
					WHIb: 225
Haque, 2015 (13)	United States	Breast	Kaiser Permanente regions of southern and northern California	ICD-9	175	72	1996–2007	All recurrences (local, regional, and distant) or contralateral breast cancer recurrence (incl. DCIS)
Liede, 2015 (6)a	United States	Breast	Flatiron Health electronic health records	ICD-9	8796	21.2	—	Bone metastases
Lamont, 2006 (1)a	United States	Breast	Medicare	ICD-9	45	71	1995–1997	Recurrence or death
Nordstrom, 2012 (8)	United States	Breast and others	Oncology Services Comprehensive Electronic Records from Amgen	ICD-9	1385	—	2004–2010	Metastases
Nordstrom, 2015 (9)	United States	Breast and others	Geisinger Health system	ICD-9	502	35.7	2004–2011	Metastases
Whyte, 2015 (11)	United States	Breast and others	Optum Research Database	ICD-9	4631	—	2007–2010	Metastases
Chawla, 2014 (20)a	United States	Breast and others	Medicare	ICD-9	27 143	—	2005–2007	Metastases
Hassett, 2014 (21)a	United States	Breast and others	Medicare and Kaiser Permanente Colorado and Kaiser Permanente Northwest	ICD-9	2590	—	2000–2005	Recurrence
Sathiakumar, 2017 (10)a	United States	Breast and others	Medicare	ICD-9	240	—	2005–2006	Bone metastases
McClish, 2003 (14)	United States	Breast and others	Medicare	ICD-9	—(15 043 all cancers)	—	1994–1996	Recurrence or second breast primary

^aStudies not excluding breast cancer patients with another primary cancer diagnosis from other cancer types.

^bLACE = Life After Cancer Epidemioogy; WHI = Women's Health Initiative; BC = breast cancer; DCIS = Ductal Carcinoma In Situ; ICD = International Classification of Diseases.

Performance measures such as sensitivity, specificity, positive predictive value (PPV), and negative predictive value (NPV) (43) as well as (internal or external) validation methods were extracted from all studies to evaluate and compare the algorithms (Table 2) (44). True positives, true negatives, false positives, and false negatives were also extracted for every algorithm to calculate accuracy. If multiple algorithms were reported within a study, an algorithm was selected based on high sensitivity, high PPV, or a combination of both. Algorithms were grouped into model-based algorithms if supervised learning models were used to develop their algorithm and compared with rule-based algorithms that did not use models.

Table 2.

Algorithm outcome and validation

Reference	Model type	Sensitivity, % (95% CI)	Specificity, % (95% CI)	PPV, % (95% CI)	NPV, % (95% CI)	Calculated performance measures, accuracy, % (95% CI)	Internal validation (size and performance)	External validation (size and performance)	Distribution of development and validation set
Xu, 2019 (7)	CART	94.2 (90.1 to 98.4)	98.3 (97.2 to 99.5)	93.4 (89.1 to 97.8)	98.5 (97.4 to 99.6)	97.5 (95.8 to 98.5)a	Yes (—)	—	60-40
Rasmussen, 2019 (15)	Rules	97.3 (93 to 99)	97.2 (95 to 99)	94.2	98.7	97.2 (95.3 to 98.4)a	—	—	—
Cronin-Fenton, 2018 (12)	Rules	88.1 (75.9 to 95.3)	87.6 (80.6 to 92.7)	72.5 (59.3 to 83.3)	95.2 (89.8 to 98.1)	87.7 (81.6 to 92.1)a	—	—	—
Ritzwoller, 2018 (16)	Logistic regression	80.5 (77.5 to 87.7)	97.3 (91.9 to 98.1)	70.0 (44.2 to 77.7)	98.5 (98.2 to 99.0)	96.1 (95.4 to 96.7)	Yes (3370; AUROC of validation set: 0.96 [0.94 to 0.97])	Yes (3961; AUROC of validation set: 0.90 [0.87 to 0.93])	50-50
Chubak, 2012 (17),	CART	94 (90 to 97)	92 (91 to 94)	58 (52 to 63)	99 (99 to 100)	92.2 (90.9 to 93.3)	Yes (—)	—	60-40
Chubak, 2017 (18)	CART	94 (90 to 97)	92 (91 to 94)	58 (52 to 63)	99 (99 to 100)	92.2 (90.9 to 93.3)	—	—	—
Kroenke, 2016 (5)	CART	LACE cohort: 88.5	LACE cohort: 94.6	LACE cohort: 76.4	LACE cohort: 97.7	93.6 (92.3 to 94.7)	—	Validates algorithms for a previous dataset published by Chubak et al. (18)	—
		WHI cohort: 86.7	WHI cohort: 92.3	WHI cohort: 63.4	WHI cohort: 97.8	91.6 (87.1 to 94.6)
Haque, 2015 (13)	Rules	96.8 (87.6 to 99.4)	93.0 (85.1 to 96.1)	88.2 (75.9 to 93.4)	98.1 (92.8 to 99.7)	94.3 (89.7 to 97.0)	Yes 500; sensitivity: 96.9% (88.4% to 99.5%); specificity: 92.4% (89.4% to 94.6%); PPV: 65.6% (55.2% to 74.8%); NPV: 99.5% (98.0% to 99.9%)	—	—
Liede, 2015 (6)	Rules	77.5 (73.9 to 81.1)	98.1 (97.8 to 98.4)	72.1 (68.4 to 75.8)	98.6 (98.3 to 98.8)	96.9 (96.5 to 97.2)	—	—	—
Lamont, 2006 (19)	Rules	92 (66 to 100)	94 (82 to 99)	—	—	93.3 (81.5 to 98.4)	—	—	—
Nordstrom, 2012 (8)	CART and random forestsb	62	97	75	95	92.6 (91.1 to 93.9)a	Yes (—)	—	60-40
Nordstrom, 2015 (9)	Random forestsb	47.1	95.9	28.6	98.1	94.2 (91.8 to 96.0)	Yes (—)	—	—
Whyte, 2015 (11)	Rules	77.19	79.54	30.91	97.71	79.3 (78.1 to 80.5)a	—	Validates 28 different algorithms used to identify metastatic cancers (algorithms not published)	—
Chawla, 2014 (20)	Rules	43.9	98.6	93.8	78.5	80.8 (80.3 to 81.3)	—	—	—
Hassett, 2014 (21)	Rules	81 (67 to 90)	78 (76 to 80)	20	—	78.1 (76.4 to 79.6)	—	—	—
Sathiakumar, 2017 (10)	Rules	96.8 (83.8 to 99.4)	98.6 (95.9 to 99.5)	90.9 (76.4 to 96.9)	99.5 (97.3 to 99.9)	98.3 (95.6 to 99.5)a	—	—	—
McClish, 2003 (14)	Logistic regression	—	—	—	—	—a	Yes (—)	—	—

^aStudies reporting performance measures: Xu et al. (2019): accuracy = 97.5% (96.2%–98.7%); Ritzwoller et al. (2019): AUROC = 0.96 (0.94–0.97); Rasmussen et al. (2019): kappa = 0.94 (0.90–0.97); Nordstrom et al. (2012): AUROC = 0.82; Whyte et al. (2015): accuracy: 79.3%; Sathiakumar et al. (2017): kappa = 0.93 (0.80–1.05); McClish et al. (2003): AUROC = 0.90; — = not reported. AUROC = area under the receiver-operator characteristics curve; CART = classification, regression and decision tree; CI = confidence interval; LACE = Life After Cancer Epidemiology; NPV = negative predictive value; PPV = positive predictive value; WHI = Women's Health Initiative.

^bCART is a decision tree built on a dataset, whereas random forests are a collection of decision trees which randomly selects variables. CART and random trees are categorized together as model-based approaches.

Accuracy of algorithms in individual studies was quantified by means of a binomial proportion with 95% confidence intervals. A single pooled estimate of accuracy over the studies was obtained by a random-effects meta-analysis using a generalized linear mixed model. The choice for a random-effects approach was motivated by the fact that different tools were used in all studies. A random-effects meta-analysis assumes intrinsic variability in detection performance (accuracy) between studies. The pooled estimate quantifies the accuracy of the “average” study. Median values and ranges of performance measures were also calculated to compare subgroups of algorithms. Analyses were performed using SAS software (version 9.4 of the SAS System for Windows).

Results

Study Selection

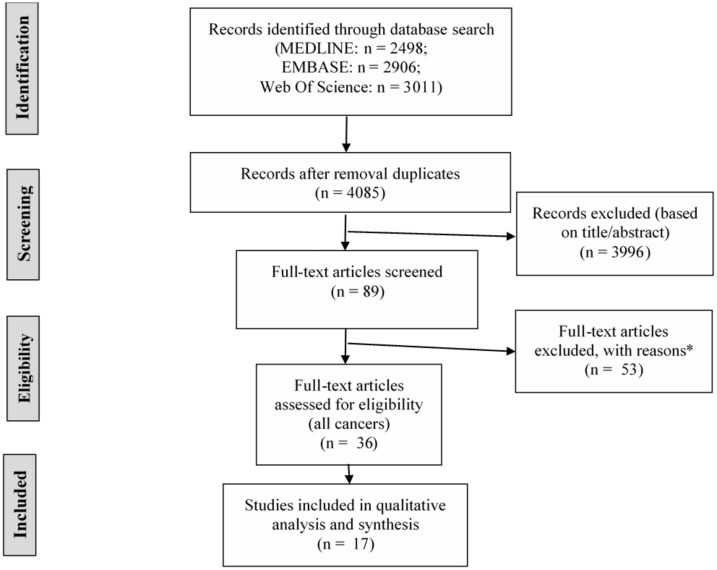
A total of 4085 studies were identified through Pubmed (including MEDLINE), EMBASE, and the Web of Science Core collection after removal of duplicates (Figure 1). After screening titles and/or abstracts, 89 records were retained for screening full-text articles. Finally, 17 of 36 relevant studies were breast cancer specific and therefore included for qualitative analysis.

Figure 1.

PRISMA or Preferred Reporting Items for Systematic Reviews and Meta-Analyses flow diagram for the identification, screening, and inclusion of research articles for the systematic review. Last search conducted on July 16, 2019. *Wrong publication type (meeting abstract, book): n = 23; wrong outcome (prediction of breast cancer recurrence, detection of incident breast cancer or treatment outcome): n = 23; no performance measures: n = 3; no administrative claims: n = 3; foreign language (non-English): n = 1.

General Characteristics of Included Studies

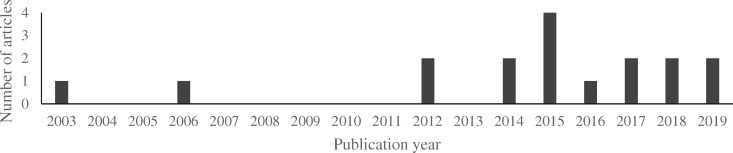
The final list of 17 studies was used for the detailed data extraction and analysis. Most studies (64.7% or 11 of 17) were published in the last 5 years (2015-2019) and all but 2 in the last decade (Figure 2). It is noted that all studies were conducted in a limited number of countries (Table 1).

Figure 2.

Distribution of included studies by publication year. In the last 10 years, more articles were published on the topic of detection of breast cancer recurrence using administrative data.

With regard to the US studies (14 of 17), sources of administrative data for the development of the algorithms were obtained from either health-care providers (5,6,8,9,11,13,16–18), health-insurance providers (10,14,19,20), or a combination of both (21).

Two Danish studies, by Rasmussen et al. and Cronin-Fenton et al., were able to use extensive nationwide population-based registries to develop a recurrence algorithm (12,15). A study conducted in Canada by Xu et al. used a regional population-based registry as an administrative data source, which covers the whole population in the province of Alberta (7).

Regarding the obtained datasets of each study, it is observed that all of the included studies were multicentric. The range of inclusion years per study varied from 2 (10) to 21 years (12). Median follow-up in years to detect recurrence obtained from these individual studies ranged from 21.1 months (6) to 90 months (15). The sample size to develop the algorithm in breast studies varied from 45 (14) to 27 143 patients (20).

Across all the studies, different approaches were used to define the gold standard. Most of them (88.2% or 15 of 17) used data from medical files (5–14,16–19,21,45) or cancer registers (15,20) as the gold standard to validate recurrence. The definition of recurrence varied among publications and included distant metastases (8,9,11,20,21), second primary breast cancers or contralateral breast cancers (5,7,13,14,17,18,37), or only bone metastases (6,10). The gold standard of recurrence status in medical files was often (94.1% or 16 of 17) reviewed manually by trained medical abstractors.

Different approaches can be applied to develop algorithms to identify cancer recurrences with administrative data. The approach can be rule based (58.8%) (6,10–13,15,19–21) or constructed using models (41.2%) (Table 2). The rule-based approach focuses on expert-driven rules, whereas the model-based approach essentially includes data-driven models but can simultaneously include expert-driven rules. Supervised machine learning algorithms such as decision trees (classification, regression and decision tree [CART] models or random forests) were used in 6 studies to identify recurrences (5,7–9,17,18). McClish et al. (14) and Ritzwoller et al. (16) also incorporated logistic regression models to identify recurrence through administrative data (14,16).

The final selection of variables or data used to construct the algorithm comprised diagnosis codes (6,11,12,19,20), treatment procedure codes (ie, chemotherapy, surgery, radiotherapy) (7,13), or a combination of both (5,8–10,14–18,21).

Performance of Algorithms

Performance of algorithms was reported using measures for sensitivity, specificity, PPV, or NPV. Median values for these measures were calculated for all models reported on one hand (n  = 17) and for all models excluding those developed for only bone metastases on the other hand (n = 15) (Table 3 and Figure 3). When considering the algorithms of the included studies altogether, the median values were 87.4% for sensitivity, 94.3% for specificity, 72.6% for PPV, and 98.3% for NPV.

Table 3.

Median and range of performance measures across subgroups and all algorithms

	Median (range)
Model type	Sensitivity, % (95%CI)	Specificity, % (95%CI)	PPV, % (95%CI)	NPV, % (95%CI)	Calculated accuracy, %(95%CI)
Model based (n = 7)	86.7(62.0–94.2)	94.6(86.0–98.3)	70.0(13.9–93.4)	98.5(95.0–99.0)	93.6(91.6–97.5)
Rule baseda (n = 7)	81.0 (43.9–97.3)	93.0 (78.0–98.6)	72.3 (20.0–94.2)	98.1 (78.5–100.0)	93.3 (78.1–98.3)
All modelsa (n = 14)	87.4 (43.9–97.3)	93.5 (78.0–98.6)	72.6 (13.9–94.2)	98.0 (78.5–99.0)	93.0 (78.1–97.5)
All models (n = 16)	87.4 (43.9–97.3)	94.3 (78.0–98.6)	72.6 (13.9–94.2)	98.3 (78.5–99.5)	93.0 (78.1–97.5)

^aExcluding Liede et al. (6) and Sathiakumar et al. (10), which investigated only bone metastases. NPV = negative predictive value; PPV = positive predictive value.

Figure 3.

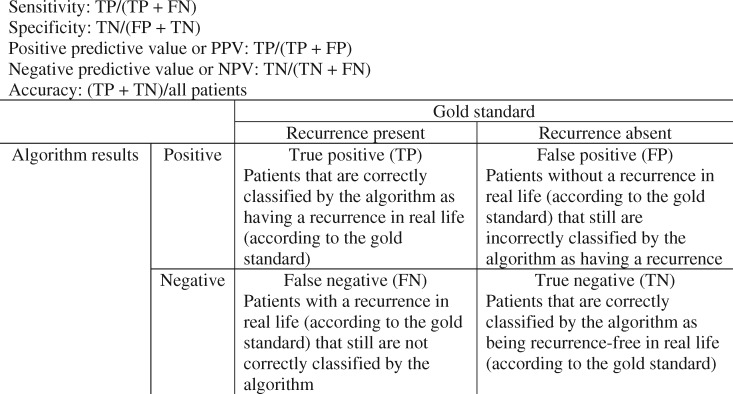
Definitions of sensitivity, specificity, negative predictive value (NPV), positive predictive value (PPV), and accuracy in the context of algorithms for detection of recurrences. FN = false negative; FP = false positive; TN = true negative; TP = true positive.

Performance measures for algorithms such as area under the receiver-operator characteristics curve (AUROC), classification accuracy, or Cohen’s kappa coefficient can be used for evaluating performance of an algorithm (44). Three of the included articles reported the AUROC curve value to measure the performance of their algorithm: 0.96 (95% confidence interval [CI] = 0.94 to 0.97) (16), 0.82 (8), and 0.90 (14); 2 studies reported the classification accuracy measure: 97.5% (95% CI = 96.2% to 98.7%) (7) and 79.3% (11); and 2 other studies the Cohen’s kappa coefficient: 0.94% (95% CI = 0.90% to 0.97%) (37) and 0.93% (95% CI = 0.80% to 1.05%) (10). The accuracy calculated for this review for individual studies varied from 78.1% to 98.3% (Table 2).

The calculated pooled random-effects meta-analysis quantified an accuracy of 92.2% (95% CI = 88.4% to 94.8%), which excluded studies by Liede et al. (6) and Sathiakumar et al. (10) because they investigated only bone metastases in breast cancer patients.

In a sensitivity analysis excluding studies that incorporated second primary or contralateral breast cancer in the definition of recurrence, the calculated accuracy was 90.5% (95% CI = 83.0% to 94.9%) (1,5,7,11,13–15,17,18).

There were fewer algorithms reported using decision trees or logistic regression models (model based) compared with algorithms without any specified model (rule based). For the studies using a model-based approach (5,8,9,14,17,18,24), the reported median values were 86.7% for sensitivity, 94.6% for specificity, 70.0% for PPV, and 98.5% for NPV (Table 3). The calculated median accuracy for the model-based approach was 93.6%.

Of all model-based algorithms, the study with highest sensitivity, specificity, PPV, and accuracy was by Xu et al. (7) with an accuracy of 97.5% (95% CI = 96.2 to 98.7%), which also used additional chart review (Table 2).

For all rule-based algorithms (excluding those detecting only bone metastases) (6,10–13,15,19–21), the median value was 81.0% for sensitivity, 93.0% for specificity, 72.3% for PPV, and 98.1% for NPV, respectively. Of all rule-based algorithms (not including those only detecting bone metastases), the highest sensitivity, specificity, PPV, NPV, and accuracy were by Rasmussen et al. (15) with an accuracy of 97.2% (95% CI = 95.3% to 98.4%) (Table 2).

The highest calculated accuracy overall for all included articles was reported for an algorithm without a specified model by Sathiakumar et al. (10) but was specifically constructed for bone metastases. Excluding 2 studies that reported only bone metastases (6,10), the highest accuracy for studies reporting local or distant recurrences was a CART model by Xu et al. (7) with 97.5% (95% CI = 95.8% to 98.5%). When comparing the median accuracy per group based on model type, the results for model-based and rule-based approaches were similar.

Detection rules for identifying breast cancer recurrence timing were included in only 4 studies (15,16,18,19). The range in median difference with the gold standard for the timing of recurrence varied from 0 days (18) to 3.3 months (16).

Evaluation of Studies

Internal and external validation is possible to evaluate reported algorithms. Internal validation can be done by a split sample validation, which is a method that uses a random sample for algorithm development and the remaining patients for validation of the algorithm, or cross-validation and bootstrap resampling, which uses patient data from the development sample.

A few studies (29.4% or 5 of 17) used an internal validation cohort to test reproducibility of the algorithm by performing a split sample validation (eg, 60-40 distribution of data for development-validation set) (7,8,13,16,17) (Table 2). The studies by Nordstrom et al. (8,9) and Ritzwoller et al. (16) used some type of cross-validation (eg, random forests) in their validation process.

An external validation set was only reported by Ritzwoller et al. (16) to see if the developed algorithms were usable in different settings and thus generalizable. Kroenke et al. (5) validated an algorithm previously published by Chubak et al. (17), which are reported in this review. The included study by Whyte et al. (11) validated different algorithms that were previously used but are not published.

Performance of validation sets was reported only in studies by Ritzwoller et al. (16) and Haque et al. (13), where the performances of the validation sets were similar (Table 2).

Discussion

To our knowledge, this is the first systematic review and meta-analysis on algorithms using administrative data to identify breast cancer recurrences at the population level. After thorough analysis of the limited number of publications, we acknowledge a need for standardization and validation of these diverse algorithms detecting breast cancer recurrences. Most included studies were published in the last 5 years (from 2013 onwards) (Figure 2).

Data sources used to develop these algorithms varied across all included countries. Next to variations between countries, variations in data sources within countries such as the United States were also noted. Most of the data sources used in studies to develop and validate the algorithms, except for 2 studies (12,15), did not cover a whole country but encompassed a well-defined population. The ideal setting would be to develop and validate an algorithm nationwide to have real-world data of recurrences of cancer patients within a country. However, this is challenging because it would require nationwide standardized and readily available administrative data.

These algorithms can only be developed in countries where administrative claims data are precise, reliable, complete, and available (3,46). Some registries (eg, the Netherlands) have the advantage of receiving registrations based on international diagnosis codes, such as diagnosis codes of a secondary malignant neoplasm for breast cancer or distant metastases, that can be used in the algorithms. This is, however, not established in most registries and would only be possible if registration of this code is reliable and the patient is followed up. The study by Chawla et al. (20) used Medicare claims to identify recurrences in a relatively large set. Nonetheless, it is important to note that Medicare claims only cover patients aged 65 years or older in the United States (47).

A few studies also included information about comorbidities in the study population, which was often noted in older patients (12,15,20,21). Because these patients may be contraindicated to receive further treatment and this could impede the performance of algorithms, future researchers should consider taking into account comorbid diseases.

More specifically, next to the data sources used, the selection of variables was heterogeneous across studies. Variables or administrative codes such as diagnosis codes, treatment codes, or a combination of both are often employed, which often originate from different types of databases. On one hand, if reliable, metastases-specific diagnosis codes could give a direct indication of a cancer recurrence for a patient. On the other hand, treatment codes in the follow-up of patients could pick up signals of a subsequent admission in a hospital or administration of medication for a recurrence of the cancer. Advantages of combining both types of codes are that it would make use of various sources and thus result in robust algorithms. Drawbacks of combining both types of codes are that it would be harder to standardize and validate the algorithms. If algorithms are developed only by making use of international classification codes, these algorithms could be applied and validated in other countries that follow international coding guidelines (48). However, most algorithms in this review utilize codes from multiple, often country-specific administrative data sources.

When developing an algorithm, recurrence status should be collected from a reliable data source to test the algorithm (49). To confirm the presence of cancer recurrences and have a valuable reference, an extensive review was conducted for the gold standard sources used. One study had a relatively small gold standard sample (19), and the confidence intervals of the performance measures were rather large. This might impede the usability of these algorithms in other populations and make it less reliable. The algorithm should be based on a large sample for which a gold standard is available, if one would want to develop such algorithms in the future.

Importantly, future researchers who are interested in developing such algorithms should determine the definition of recurrence for their gold standard. This definition of recurrence varied across the included articles, resulting in diverse algorithm development processes (eg, selection of codes). Four articles explored only distant breast cancer recurrences (8,9,11,20), whereas most of the studies included any recurrence (local, regional, or distant). Interestingly, a few studies also included second primary or contralateral breast cancer recurrence (5,7,11,13–15,17,18), although this is not always considered a recurrence of a primary breast cancer. Performing a sensitivity analysis excluding the studies that included second primary or contralateral breast cancer recurrence resulted in a somewhat lower accuracy. Obtained results should be evaluated based on what type of recurrence you are interested in, for example, solely the recurrence of the initial primary breast cancer and not including other second primary breast cancers.

Two studies had only bone metastases as their definition of recurrence (6,10) and thus were not representative of all sorts of cancer recurrences and were excluded from the pooled random-effects meta-analysis. The disadvantages of using a single algorithm that only utilizes bone metastases-specific codes is that it is not comparable with or generalizable to other local or distant breast cancer recurrence algorithms. An algorithm developed for all types of recurrences is more complex than one that can detect bone metastases only. This is because the disease timing and pattern will vary and requires more specific codes when detecting bone metastases only.

All of the included studies used either a rule-based or a model-based approach to construct the algorithm. Although algorithms to identify cancer recurrences are often rule based, the use of model-based algorithms has increased.

Within the model-based approach, decision trees such as CART models (or random forests) and logistic regression models have been used. In more recent years, there has been a growing interest in CART models to identify recurrences (50). On the other hand, conventional logistic regression models have been used by only 2 studies in the past to ascertain breast cancer recurrences. Ritzwoller et al. (16) used logistic regression models to generate a smooth continuous probability of having recurrence for each patient rather than a dichotomous variable of recurrence status (present or not).

Model-based algorithms or machine learning models such as CART models and logistic models were previously compared in the literature (51,52). Generally, publications point out that logistic regression models are more accurate than CART models but are not capable of investigating interactions or relationships between used variables. Decision trees like CART models investigate subsequent relationships between predictors, which makes it easier to interpret (51,52).

Complementing expert-driven algorithms with data-driven models is likely to improve the performance of algorithms, because it will take into consideration the data source and its reach. By taking into consideration all available codes and their combinations and selecting those that are clinically relevant, a robust algorithm can be developed.

These developed algorithms can be evaluated with sensitivity, specificity, PPV, and NPV values (Figure 3). This was investigated for all studies together on one hand, and based on a rule-based or model-based approach on the other hand (Table 3).

Overall, studies using algorithms to identify breast cancer recurrence at the population level using administrative data were able to correctly identify recurrence with high sensitivity and specificity. In general, there were lower values observed for the PPV measure than for the other measures, meaning that there are more false positives and low true positives (fewer patients with recurrence) (Table 3 and Figure 3). This could be because recurrences are not so common in breast cancer patients in general, which influences the PPV of a test. The more common a disease is in a test, the better the test will be at predicting the disease (or recurrence).

Over the years, a shift can be noted from rule-based algorithms to model-based algorithms. Algorithms with a model-based approach were reported more recently in the literature and often combined with expert opinion in the model-based approach. Rule-based algorithms achieved overall similar results compared with model-based algorithms. Machine learning techniques are emerging and could be utilized in the future when developing an algorithm.

When comparing decision trees with logistic regression models, the highest sensitivity was reported in decision tree models, whereas the logistic regression models recently published by Ritzwoller et al. (16) reported high specificity, PPV, and NPV. This can be due to the low number of studies (McClish et al. (14) and Ritzwoller et al. (16)) reporting performance values in logistic regression models, with only Ritzwoller et al. (16) reporting performance measures. It should be noted that the CART model reporting the highest accuracy by Xu et al. (7) used additional chart review to enhance its algorithm accuracy. Decision trees are used in studies reporting a different gold standard definition of recurrence (including either all recurrences or only metastases) and datasets, which may hamper the comparability of outcome measures. This means that various algorithms for different purposes have been developed using decision trees over the years, which leads to variable results.

Accuracy is a performance measure of the algorithm, which was calculated in this review for each individual algorithm. Generally, performance measures for algorithms such as AUROC (53), classification accuracy, or Cohen’s kappa coefficient are reported to evaluate these individual models (44). There are more general guidelines stating that an AUROC of 0.75 is seen as not clinically useful, but an AUROC of 0.97 has high clinical value (53). This systematic review quantified accuracy and conducted a random-effects meta-analysis to obtain the “average” accuracy measure for all studies (Table 2). The pooled estimate for accuracy for all studies (excluding 2 studies reporting bone metastases) (6,10) was 92.2%, thus yielding a high discriminatory power and high quality. This means that research groups that would like to conduct a study to develop an algorithm to detect recurrences such as the studies reported might expect results similar to this average value.

Despite the high quality of these algorithms, it is imperative to stress that the data used do not have the primary purpose to detect recurrences but are rather administratively collected data of treatment and procedures of cancer patients (47). There are currently no guidelines or a cut-off value for the best performance measure in algorithms developed to identify recurrences.

However, 2 of the major setbacks of using administrative codes are data errors and quality of codes (46,54). Therefore, the algorithm performance measures used should always be interpreted in the specific context of the developed algorithm (Figure 3). Thus, depending on the final goal of the investigator and the real setting in which the algorithm would be used, the final algorithms should be selected based on one or a combination of the defined performance measures.

Finally, internal or external validation of detection algorithms is important, because the algorithm should ideally be developed in a robust way to make it reproducible and generalizable to the whole population (44). Treatment and diagnosis codes and the use of these codes can change over time within the same setting. This change would additionally require an update and monitoring of the used codes, which is why validation of the algorithm in time is important (55).

For both studies by Ritzwoller et al. (16) and Haque et al. (13), reported performance results for validation sets were similar. The majority of the studies that did perform internal validation used split sample resampling. This validation method is not as effective as cross-validation or bootstrapping (44). The 2 studies by Nordstrom et al. (8,9)  used random forests to validate their findings. Random forests are models that use cross-validation inherently.

External validation was only performed by Ritzwoller et al. (16), which is preferable and can make the algorithm applicable in external cohorts. The asset of external validation comprises transportability of the algorithms and is a much stronger approach than internal validation. The studies by Kroenke et al. (5) and Whyte et al. (11) validated algorithms from previous studies, which have proven their generalizability.

Detecting timing of recurrence would be the next step after recurrence status is obtained. From the few studies that investigated timing of recurrence, the least difference between the predicted recurrence time and gold standard clinical definition for date of recurrence was found in the study by Chubak et al. (18). Timing of recurrence or disease-free survival can be an important outcome measure. The potency of a new treatment can be evaluated based on the disease-free survival, because overall survival can be less affected. Nonetheless, defining the clinical timing of recurrence is often difficult to pinpoint, because the cancer can be growing days or weeks before the pathological confirmation or confirmation by imaging of the recurrence. In clinical trials, recurrence or progression as a response to treatment is often defined with response evaluation criteria in solid tumors (RECIST) guidelines and can be an example in other types of studies (56).

These algorithms are essential tools to detect recurrences, which can be useful to eventually compare and confirm already available data from Early Breast Cancer Trialists’ Collaborative Group, where clinical data and recurrence prediction are evaluated in populations outside these trials (57–60). Only 1 study by Cronin-Fenton et al. (12) correlated the recurrence detection they obtained from the algorithm with clinicopathological factors to investigate prediction of recurrence. According to the results from the algorithm of this study, predictors of recurrence were in particular age, hormone receptor status, stage at diagnosis, and treatment receipt (chemotherapy, endocrine therapy, and radiotherapy).

Examples from countries such as Denmark and the Netherlands have shown the value of active registration of recurrences. Prospective registration of recurrence would be of great value alongside retrospective algorithms to obtain information on recurrence at the population level and over an extensive time frame.

International research groups should standardize the approaches for developing and, more importantly, validating such algorithms by setting up more collaboration. This would allow making better comparisons between different algorithms for detection of breast cancer recurrence (eg, comparison between different countries).

The limitations of the study and outcome level were that only a few studies had internal and/or external validation of their algorithms. These algorithms made use of country-specific administrative claims data and thus could only be applied within their own or similar datasets. Major setbacks of these studies were that they used various datasets, where some development datasets only included older patients, for example. The majority of the studies were from the United States (except for 2 other countries), which makes it especially difficult to compare with other countries. Other setbacks of some studies were relatively small sample sizes, which was also linked to larger confidence intervals of outcome measures.

The limitations on the review level were that it was difficult to quantitatively compare different performance heterogeneous measures, and AUROC, accuracy coefficient, or Cohen’s kappa coefficient were barely reported. Research groups working on this topic should agree on using similar outcome measures to be able to learn from and compare results. We did, however, individually calculate accuracy and could select the best performing algorithm. Another limitation was the variability of model types or variables used in different studies, which made it more difficult to compare.

Algorithms constructed with administrative claims codes can be valuable tools to identify breast cancer recurrences at the population level, as our random-effects meta-analysis reported an overall high quality. In recent years, these algorithms (more often constructed with models) make use of real-world data from the follow-up of patient treatments, procedure codes, or diagnosis codes. More recent model-based algorithms reported similar accuracy as rule-based algorithms. Advantages of these algorithms are that they do not require active registration of recurrence, which would be labor intensive and costly, but make use of readily available claims data.

In general, there is a need for comparable definition of recurrence and standardization of the gold standard, the validation samples, and reporting of demographic information for the population in question (eg, age) for these types of studies. More internal and external validation of these algorithms should be conducted in the future to verify if the algorithms have potential in other settings ranging from various nationwide settings to populations in other countries.

Funding

This work was supported by VZW THINK-PINK (Belgium).

Notes

Disclosures: All authors have declared no conflict of interest.