Neural Correlates of Evidence and Urgency During Human Perceptual Decision-Making in Dynamically Changing Conditions

Abstract

Current models of decision-making assume that the brain gradually accumulates evidence and drifts toward a threshold that, once crossed, results in a choice selection. These models have been especially successful in primate research; however, transposing them to human fMRI paradigms has proved it to be challenging. Here, we exploit the face-selective visual system and test whether decoded emotional facial features from multivariate fMRI signals during a dynamic perceptual decision-making task are related to the parameters of computational models of decision-making. We show that trial-by-trial variations in the pattern of neural activity in the fusiform gyrus reflect facial emotional information and modulate drift rates during deliberation. We also observed an inverse-urgency signal based in the caudate nucleus that was independent of sensory information but appeared to slow decisions, particularly when information in the task was ambiguous. Taken together, our results characterize how decision parameters from a computational model (i.e., drift rate and urgency signal) are involved in perceptual decision-making and reflected in the activity of the human brain.

Introduction

Decisions are often made based on noisy or changing information. A prominent theory in decision neuroscience, referred to as the evidence accumulation or drift diffusion model (Smith and Ratcliff 2004), posits that deliberation is an integrative mechanism in which sensory information supporting different options accumulates over time until a boundary is reached, at which point the decision is made (Gold and Shadlen 2007; Yang and Shadlen 2007; Glaze et al. 2015). Neuroscientific support for the drift diffusion model comes principally from single-unit recordings in non-human primates. “Accumulator regions”—where neurons exhibit ramp-like increases or drift in their firing toward a decision threshold—have been located in several brain areas in a widely studied dot motion perceptual decision paradigm (Shadlen and Newsome 1996, 2001; Roitman and Shadlen 2002; Gold and Shadlen 2007; Hanks et al. 2015; Scott et al. 2017). This work suggests that different pools of selectively tuned, lower-level sensory neurons could feed information to higher-level cortical regions to compute perceptual decisions. However, single-unit recordings provide a spatially narrow view of the brain mechanisms underlying decision-making. Functional magnetic resonance imaging (fMRI) studies, though comparatively limited in spatial resolution, have begun to explore the neural substrates of evidence accumulation during perceptual decision-making in humans in an attempt to provide a more holistic view (Heekeren et al. 2004; Ploran et al. 2007; Tremel and Wheeler 2015).

Also, some decisions need to be made promptly despite incomplete or changing evidence. Simple drift diffusion models have difficulty accounting for these situations. A recent theoretical approach suggests that decision-making incorporates an “urgency” signal, independent of the sensory evidence, which grows over time to bring neural activity closer to a decision threshold (Cisek et al. 2009; Mormann et al. 2010; Thura et al. 2012; Murphy et al. 2016). Single-unit recordings in monkeys have implicated the basal ganglia as the neural driver of this postulated urgency signal (Thura and Cisek 2017). Urgency signals are of interest in human behavior as they may relate to the trait of impulsivity (Thura and Cisek 2014, 2016; Carland et al. 2019). However, the few studies to date that have employed fMRI to differentiate evidence accumulation and urgency parameters are limited by relatively small sample sizes (Mulder et al. 2014). Moreover, the univariate blood oxygenation level-dependent (BOLD) response analysis typically employed may fail to differentiate relevant neuronal populations that encode stimulus features used for making the decision as they ignore the possibility that information may be represented in a distributed manner across voxels (Gluth et al. 2012; Braunlich and Seger 2016). Multivariate analysis overcomes this limitation by searching for the optimal combination of (distributed) voxels and assessing their contribution to stimulus discriminability (Kriegeskorte et al. 2006; Davis et al. 2014).

We designed a novel fMRI task to identify neural substrates of the time-dependent processes that occur during deliberation in a simple sensory decision-making task. We took advantage of the fact that it is possible to reliably decode brain activity related to facial emotion detection. Subjects decided whether a short video of a face presented on screen was transitioning to a happy or sad emotion. Previous work suggests that not only is it possible to decode representation of faces from fMRI signal in extrastriate visual areas (Haxby et al. 2001) but also distinct emotional facial features are uniquely represented in the brain and can be decoded (Kassam et al. 2013; Wager et al. 2015). Our task allowed identification of multivariate patterns indicative of happy or sad faces, which we took to represent the sensory evidence upon which the decision was made. According to evidence accumulator models, information on the upcoming choice decoded from the population of neurons participating in facial processing should increase toward a decision threshold, reflecting the gradual accumulation of evidence in support of the upcoming choice. Analogous to results from single-unit recording studies in non-human primates, we hypothesize that decision-making parameters will covary with decoded fMRI activity related to detection of facial emotion. To test the urgency-gating model (Cisek et al. 2009), we included ambiguous trials in the study design. We examined the extent to which neural representation of evidence accumulation contributed to decisions in ambiguous conditions and whether an urgency parameter improved model fit.

Materials and Methods

Participants

Fifty-three right-handed young, healthy adults (23 males; age mean ± standard deviation [SD], 24.02 ± 5.49 years) participated in the present study. Exclusion criteria included current or past diagnosis of a psychiatric disorder, neurological disorder, or concussion, and moderate to severe depression (score >5 on the Beck Depression Inventory; Beck et al. 1961). All participants gave written informed consent prior to data acquisition and received monetary compensation for their participation. The study was approved by the Montreal Neurological Institute Research Ethics Board.

Task Design

Face stimuli were derived from the NimStim database (Tottenham et al. 2009). Photographs of 6 (3 males) out of 43 models with closed-mouth happy and sad expressions were selected as stimuli for the task because they had the highest identification accuracy in both Tottenham et al.’s (2009) initial validation of the data set and in our piloting. Face stimuli were made achromatic in MATLAB and presented on a gray background. In order to manipulate the intensity of the emotional expressions, 18 intermediate face stimuli were also generated from the NimStim faces using STOIK MorphMan software (http://www.stoik.com/) to create different emotion levels that gradually transitioned between a model’s neutral and happy or sad face. Thus, emotion levels varied from 0 to 19 in both directions. Two independent tasks were conducted using these stimuli: 1) a training task and 2) a dynamic task.

The static training task (Fig. 1A) served to localize patterns of brain activity related to happy and sad faces. Subjects viewed a face with an emotional level >15 for 2.5 s; this fixed time of display ensured that we eclipsed at least one full repetition time (TR) of fMRI acquisition to allow for accurate parameter estimation. After this, a question mark appeared with a maximum time of 1 s, during which the subject was instructed to respond with their evaluation of whether the face was happy or sad; if no response was made, “Too Slow” was displayed on the screen for 1 s.

Figure 1.

Experiment overview. (A) Training task was used to decode BOLD activity in response to viewing of static happy or sad faces. One classifier was generated for each of seven bilateral regions of interest, per subject. The classifiers were then used to determine support vector machine learning (SVM) weights, or distance from hyperplane, which were in turn projected to the BOLD effect size values while viewing faces in the (B) dynamic task. This yielded a neural “code” per trial, per region. Two trial types were used in the dynamic task: (i) easy trials where facial expression gradually morphed toward one of the two emotions and (ii) ambiguous trials where facial expression varied around neutral until two-thirds into the trial after which point emotion rapidly ramped up toward happy or sad. * refers to the dot product operator.

In the dynamic task (Fig. 1B), subjects viewed stimuli of faces “morphing” between expressions. In these trials, a maximum of 60 frames were presented over 6 s (i.e., 10 frames/s), plus a final image of the correct emotion (with the emotion level >15) for 1 s either after a response was made or at the end of a trial if the subject had not yet made a response. Participants were instructed to predict whether the face would be happy or sad by the end of the trial and to respond whenever they felt confident enough to do so. Subjects were asked to respond both as quickly and as accurately as possible. Within the dynamic task, there were two types of trials, namely, “easy” and “ambiguous,” which were modeled after previous work (Thura et al. 2012). In both trial types, the first image presented was the model’s neutral face.

In easy trials, all faces presented were of the correct emotion (e.g., in a trial in which the correct answer is happy, no sad images are ever presented). Each successive frame had a 65% chance of being one level higher than the previous frame in the direction of the correct emotion. By the final frame, all trials had an emotion level >16. The final frame was presented for 1 s as soon as the subject made a response, or it was presented as a 1 s long additional frame if they had not yet responded. Subjects could respond during this final frame only if they had not yet done so.

In ambiguous trials, the probability of each frame during the first two-thirds of the trials (i.e., up to the 40th frame) had a 50% chance of being one level higher than the previous in the direction of the correct emotion, such that the images generally hovered around a neutral valence. To prevent, for example, many slightly happy images and a few very sad images being presented, the maximum levels presented in the correct and incorrect direction before the 40th frame were kept within two levels of each other. Furthermore, the maximum level reached in either direction before the 40th frame was limited to 7. In the final third of the trial, there was a steep increase of level in favor of the correct emotion, with a 95% chance that a given frame would be exactly one level higher in favor of the correction emotion than the previous frame. All trials had a final emotion level > 16. As with the easy trials, this final frame was presented for a duration of 1 s as soon as a response was made or as a 1 s long 61st frame during which subjects could respond if they had not yet done so.

In both tasks (i.e., static training and dynamic), a pause followed by a time-jittered fixation cross preceded each trial. The trials were evenly split between happy and sad (determined by the emotion at the final frame for the dynamic task), with the order of trials randomized in every block. Participants took part in four runs for the localizer task and three runs for the dynamic task. Both tasks had a total of 120 trials each, divided equally among the runs.

MRI Acquisition

Neuroimaging was carried out with a Siemens Magnetom Prisma 3 T MRI scanner equipped with a 64-channel head coil at the Montreal Neurological Institute (MNI). High-resolution MPRAGE T1-weighted structural images were first obtained for anatomical localization (TR = 2.3 s; TE = 2.3 ms; FOV = 240 mm; scan matrix = 192 × 256 × 256; voxel size = 0.9 mm isotropic). Functional data were then acquired with an echo-planar T2^*weighted sequence for BOLD contrast (TR = 0.719 s; TE = 30 ms; scan matrix = 104 × 108 × 72; flip angle = 44°; FOV = 208 mm; voxel size = 2 mm isotropic, multiband acceleration factor = 8). Here, we capitalized on multiband acquisition to help improve temporal resolution, allowing for the potential of multiple data points per trial to better characterize signal change during the decision process.

MRI Preprocessing

Preprocessing and beta extraction were performed using SPM12 (http://www.fil.ion.ucl.ac.uk/spm/) and MATLAB. Signals with >4% intensity change were despiked and corrected using ArtRepair Toolbox (Mazaika et al. 2007). Images were corrected for motion, realigned, normalized to the MNI ICBM152 template (Fonov et al. 2009), and minimally smoothed (6 mm FWHM Gaussian kernel). Spatial filtering techniques (such as Gaussian smoothing) have been shown to increase the signal-to-noise ratio (Brants et al. 2011; Hendriks et al. 2017), as well as classification performance in multivariate pattern analysis (MVPA) (Op de Beeck 2010). One subject was excluded from further analysis after quality control due to excessive motion.

Generation of Regions of Interest

We generated bilateral region of interest masks for seven brain areas previously shown to be involved in the detection of facial expression (Haxby et al. 2000; Wegrzyn et al. 2015) and one for the caudate thought to play a role in urgency. An association test (FDR-corrected, <0.01) for the terms “amygdala,” “anterior temporal,” “fusiform gyrus,” “inferior occipital,” “insula,” “intraparietal,” “superior temporal,” and “caudate” on the Neurosynth meta-analytical database was conducted yielding one brain map per term indicating the probability of that term being used in a study given the reported activation (i.e., P(Term|Activation)) (Yarkoni et al. 2011). To avoid overlaps between our regional masks, voxels in overlapping regions were assigned to the region with the greatest z-score from the reverse inference map derived from the Neurosynth search terms. These spatially unique maps were then binarized.

Multivariate Pattern Analysis and Fusiform Code

Preprocessed functional data were used as input for run-wise GLM first-level designs yielding one regressor for the event of interest, a second for all other events, and six motion regressors (Mumford et al. 2012), creating one GLM per event. This approach is thought to lead to more representative trial-by-trial estimates of the true activation magnitude. Only the beta value (i.e., parameter estimate or coefficient representing effect size from the linear regression) for the event of interest was used for all further analysis in generating a classifier in the localizer task. For the dynamic task, fMRI signal extracted through the canonical GLM (i.e., one GLM per run with regressors for the duration of face presentation, intertrial interval, button press, six additional motion regressors as nuisance regressors, and a constant) implemented by SPM was used for statistical analysis.

A linear support vector machine learning (SVM) algorithm (C = 1.0, L2 penalty, square hinged loss, tolerance = 0.0001, max iterations = 1000) was implemented using the scikit-learn package in Python (Pedregosa et al. 2011) to classify happy and sad stimuli from the preprocessed beta images after data normalization. Features were extracted within each of the seven regional masks, without additional voxel selection. A feature’s distance away from hyperplane determined the SVM weight. A k-fold cross validation (k = 10) was conducted to test the accuracy of the classifier and reveal voxels where local patterns of activation reliably discriminated between happy and sad faces. After subtracting the activity in the preceding intertrial period and normalization, the SVM weights from the classifier derived from the localizer task were then projected to each trial’s BOLD effect size in the dynamic task to calculate the regional “code” during viewing of the morphing video.

Statistical significance of the decoder’s accuracy was tested using permutation of the original data per subject with randomly shuffled class labels of the training and testing data sets before supplying them to the classifier (Pereira and Botvinick 2011; Mahmoudi et al. 2012). This procedure was done 1000 times in order to generate a null distribution and was used to test how likely a certain classifier accuracy was to occur by pure chance. Due to exchangeability issues between run—that is, the risk of predicting runs rather than class label—labels were only permuted within, rather than across data splits (i.e., within each subject, within each run). P values were calculated as the proportion of instances where permutated data had equal or higher accuracy than the original decoder accuracy divided by the number of all permutations. Eight subjects with classifiers that did not perform better than chance in any of the regions investigated were excluded from further analysis.

Fitting the Hierarchical Drift Diffusion Model (HDDM)

The drift diffusion model (DDM), an established dynamic model of two-choice decision processes (Ratcliff et al. 2016), was fitted to subjects’ reaction time (RT) distributions. The DDM simulates two-alternative forced choices as a noisy process of evidence accumulation through time. The model implies a single accumulator integrating the sample evidence according to a stochastic diffusion process until the evidence accumulated reaches one of two decision bounds, here for “happy” or “sad.” The model decomposes behavioral data into four parameters mapped onto the latent psychological process: drift rate (v) for speed of accumulation, starting point (z) for a response bias toward one choice, non-decision time (t) for stimulus encoding and response execution latencies, and critical decision threshold (a).

Here we used a hierarchical extension of the DDM (HDDM) (Wiecki et al. 2013) to estimate decision parameters. This method assumes that parameters for individual participants are random samples drawn from group-level distributions and uses Bayesian statistical methods to optimize all parameters at both the group and subject level. In other words, fits for individual subjects are constrained by the group distribution but can vary from this distribution. This Bayesian approach for parameter estimation has distinct advantages over other methods in robustly recovering model parameter estimates for both individual and group levels, particularly when the number of trials is relatively small. Moreover, HDDM has been shown to reliably estimate DDM parameters, including regressing effects of trial-by-trial variations of neural signals on decision parameters (Matzke and Wagenmakers 2009; Wiecki et al. 2013). Bayesian estimates allow for quantification of parameter estimates and uncertainty in the form of joint posterior distribution, given the observed experimental data (Gelman et al. 2013). To account for outliers in behavior that cannot be captured by HDDM (e.g., slow responses due to inattention or fast erroneous responses due to action slips), we removed 5% of the trials at each tail of the RT distribution. Markov chain Monte Carlo sample methods were used to accurately approximate the posterior distribution of the estimated parameters. Five thousand samples were drawn from the posterior to obtain smooth parameter estimates, the first 100 samples were discarded as burn-in. Convergence of Markov chains were assessed by inspecting traces of model parameters, their autocorrelation, and computing the Gelman-Ruben statistic (Gelman and Rubin 1992) to ensure that the models had properly converged.

Two models were used: one without inclusion of any fMRI data and a second that allowed for trial-by-trial variations in neural activity to modulate decision parameters. To test our hypotheses relating neural activity to model parameters, we estimated posterior distributions not only for basic model parameters, but the degree to which these parameters are altered by variations in neural measures (i.e., facial emotion code from each region of interest and caudate BOLD activity—see below). In these regressions, the coefficient weighs the slope of the parameters (defined by drift rate v and threshold a) by the value of the neural measure on this trial, with an intercept, for example: v(t) = β₀ + β₁condition + β₂fusiform code(t) + β₃condition(t)^*fusiform code(t). This regression across trials allows us to infer the degree to which drift rate changes with neural activity. Changes in drift rate relate to RT and accuracy.

Modulators, in this case the fMRI-derived neural parameters, were iteratively added into our model to test whether successive additions improved model fit. Model fit was assessed by comparing each models’ deviance information criterion (DIC) value (Spiegelhalter et al. 2002), with a lower value for a given model (for the whole group) indicating higher likelihood for that model compared with an alternative model, taking into account model complexity (degrees of freedom). A DIC difference of 10 is considered significant (Zhang and Rowe 2014). DIC is widely used for comparisons of hierarchical models where other measures (e.g., Bayesian information criterion) are not appropriate (Frank et al. 2015; Ratcliff et al. 2016). Parameters of the best model were analyzed by Bayesian hypothesis testing, which examines the probability mass of the parameter region in question (i.e., percentage of posterior samples greater than zero). Posterior probabilities ≥95% were considered significant. Note, this value is not equivalent to P values estimated by frequentist methods but can be interpreted in a similar manner.

Psychophysiological Interaction (PPI)

Generalized psychophysiological interaction (gPPI) analysis (McLaren et al. 2012) was used to identify brain regions with activity that covaried with the activity of the fusiform “seed” voxels as parametrically modulated by the fusiform code. Two 6 mm spheres centered at the peak voxel from the z-score map of the “fusiform gyrus” search term from Neurosynth—identical to the aforementioned search in the Generation of Regions of Interest section—in each hemisphere were used as seeds (left center: x = −42, y = −48, z = −20; right center: x = 44, y = −48, z = −16). Our GLM included regressors accounting for periods corresponding to trials for each emotion (i.e., happy and sad) each parametrically modulated by the fusiform code, with intertrial interval duration, button press, six additional motion regressors as nuisance regressors, and a constant. gPPI regressors were created by deconvolving the seed to obtain an estimated neural signal during perceptual decisions using SPM’s deconvolution algorithm, calculating the interaction with the task in the neural domain, and then re-convolved to create the final regressor. Participant effects were then used in a group-level analysis, treating participants as a random effect, using a one-sample t-test against a contrast value of zero at each voxel.

Fitting the Urgency Gating Model (UGM)

A filtered evidence variable 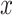was derived using the following differential equation:

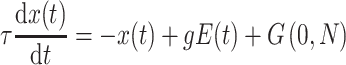(1)

whereby at a given time t, the evidence E, which denotes the amount of information (i.e., facial emotion level), is multiplied by an attentional fixed gain term . Further, an intra-trial Gaussian noise variable G(0,N) with a mean of 0 and a SD of N was added. Here we chose N = 6, because it gave a range of simulated RTs with similar variability as the observed data (but see Supplementary Table 4 for evidence that the model is robust to the choice of N). How far back in time sensory information is considered by the model is determined by the time constant 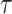. We next computed the estimated neural activity :

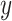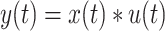(2)

This was determined by multiplying the filtered evidence with an urgency parameter 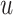. A decision is made when the variable 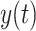reaches threshold T. A non-decision time of 200 ms was added to yield the predicted RT.

Implementation of the non-hierarchical DDM (nDDM) and the urgency-gating model (UGM) differed in two key ways. First, there was no urgency parameter added to the nDDM. In other words, the nDDM assumes that once the variable 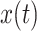reach the threshold T, a decision is made. Second, in the UGM, a low-pass filter of the sensory information in the first-order linear differential equation was applied. The time constant 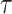was set to 200 ms for the UGM, whereas the maximum trial duration of 6000 ms was used as time constant for the nDDM. We assumed a time constant of 200 ms for the UGM on the basis of previous behavioral and physiological studies (Cisek et al. 2009; Thura et al. 2012; Thura and Cisek 2014). Evidence (E), gain (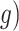, and noise (N) parameters were the same in both models.

In the nDDM, the T parameter was adjusted using an exhaustive search to find the variable that minimized the mean squared error between the model’s predicted RT and the real RT across all trials for each subject. In the UGM, the 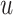parameter was similarly searched for using this criterion. Note that for each model, one parameter was adjusted to fit the data; both T and influence the means of RT distributions. The models were used to simulate 5000 trials, the mean of which was used to compare against the real RT distributions.

Statistical Analysis of Behavioral Data

Statistics for this study were conducted in R (R Core Team 2015) and MATLABR2018b (MATLAB 2018). Due to low sample size, which may increase vulnerability to spurious outliers, non-parametric tests were used to assess the following subject-level data. Mean RTs and accuracy were evaluated by a Friedman’s test to compare the effect of trial type and emotion while accounting for runs in each instance. Spearman correlations were used to test for all correlations between task performance (i.e., accuracy and RT) and other metrics of interest (e.g., HDDM decision threshold, UGM urgency signal, questionnaires). To test a possible two-way interaction effect of accuracy (i.e., correct and incorrect) and condition (i.e., easy and ambiguous) on neural activity, we ran a two-away analysis of variance as the non-parametric equivalent (i.e., Friedman’s test) does not consider interaction effects. Wilcoxon signed-ranks tests were then used to compare neural activity between incorrect and correct trials, whereas Wilcoxon rank-sum tests were used to compare between groups (i.e., early vs. late responders—see below). In both cases, z-values refer to Wilcoxon’s z (approximation).

Neural Correlates of Urgency

To look for neural correlates of urgency gating, we compared individuals who tended to wait for information in ambiguous trials to those who tended to respond early (n = 24 and 21 participants, respectively, see below). We compared BOLD activity during stimulus presentation in early versus late responders, using the fusiform MVPA code as a parametric modulator (see equation 2). Because there were no significant differences in the whole-brain analysis, we focused on the caudate nucleus as the region of interest, based on previous work identifying this structure as a likely source of urgency signals (Ding and Gold 2012; Nagano-Saito et al. 2012; Thura and Cisek 2017).

Results

Multivariate Pattern Analysis of Facial Emotion Detection

First, the static task was used to localize patterns of brain activity related to the two facial emotions using linear SVM classifiers (Fig. 1). MVPA was applied to the beta values derived from a first-level GLM of the BOLD response from each trial (Mumford et al. 2012) for each of the seven a priori face-processing regions of interest (Haxby et al. 2000; Wegrzyn et al. 2015), resulting in seven classifiers per participant. Subjects who failed quality control or had classifiers that did not significantly decode above chance level were removed from further analysis (n = 8). In the remaining group, above-chance classification was possible in all seven regions of interest (Fig. 2).

Figure 2.

Decoding performance. Mean decoding accuracy (n = 45) from each region of interest. Error bars depict standard error of the mean. Brain slices show SVM weights from a sample subject with warm and cold colors representing weighting toward happy and sad, respectively.

Decision-Making Task: Behavioral Results

Participants then engaged in the dynamic task, with easy and ambiguous trials. RTs on easy trials (with gradually increasing information) were significantly faster (χ²_F(1,52) = 138.77, P < 0.0001) and responses more accurate (χ²_F(1,52) = 197.32, P < 0.0001) relative to ambiguous trials (Fig. 3). RTs on ambiguous trials were bimodally distributed with responses tending to either be early or late. Overall, subjects also responded faster (χ²_F(1,52) = 46.30, P < 0.0001) and more accurately (χ²_F(1,52) = 31.42, P < 0.0001) to trials that were heading toward the happy than the sad direction.

Figure 3.

Reaction time distributions. Histogram of reaction time for (A) easy and (B) ambiguous trials. Solid lines reflect the Gaussian kernel density estimation. ER, early responders (n = 21); LR, late responders (n = 24).

Fusiform Code Modulates Drift Rate on a Trial-By-Trial Level

SVM weights from the classifiers derived from the static task were projected to the BOLD effect size maps in each trial of the dynamic task to determine the regional MVPA “code” while viewing the morphing video. Two central hypotheses were tested using HDDM (Wiecki et al. 2013).

First, we assessed basic assumptions of the model without inclusion of any fMRI data. This involved modulating drift rate by differences in the information available as determined by trial type (analogous to motion coherence in random dot motion tasks (Ratcliff and McKoon 2008)). High (absolute) drift rates result in faster responses and fewer errors, whereas a drift around zero indicates chance performance with long RT. The drift rate parameter calculated using this basic model was correlated with participants’ overall accuracy in predicting the correct emotion at the end of a trial (r = 0.3331, P = 0.0271), even when RT was used as a covariate in a partial correlation (r = 0.302, P = 0.0463), suggesting that drift rate was a better reflection of behavioral performance than RT alone. Consistent with the behavioral data (above), there was a bias toward the happy decision threshold (z, mean = 0.5606 ± 0.0019).

Second, we tested whether drift rate reflected the regional fMRI MVPA code from our seven regions of interest on a trial-by-trial level (Fig. 4A). We estimated posterior distributions not only for basic model parameters, but the degree to which these parameters are altered by variations in neural measures. Compared with a base model, allowing fusiform MVPA code to modulate drift rate yielded an improved model fit (difference in DIC = 26.29), whereas MVPA codes from the other six regions did not improve model fit (Fig. 4C). Thus, model selection provided strong evidence that trial-by-trial variations in drift rate are modulated by fusiform code as a measure of the evidence for facial emotion. Moreover, while facial emotion is reflected in the entire set of a priori regions, only information in the fusiform gyrus appeared to influence the decision.

Figure 4.

Hierarchical drift diffusion model (HDDM). (A) Illustration of the model with trial-wise neural regressors. Decision parameters including drift rate (v), decision threshold (a), non-decision time (t), bias (z), and SD of drift rate (sv) were estimated for the group (circles outside the plates with group mean (μ) and variance (σ)) and subjects (s) (circles in outer plate). Blue nodes represent observed data, including trial-wise behavioral data (accuracy, RT) and neural measures (neural MVPA code from a region as determined by projected SVM weights). Trial-wise variations in v were modulated by neural measures as well as trial type (easy or ambiguous trials). (B) Schematic of the drift diffusion model and estimated decision parameters. Evidence is accumulated over time until one of two decision thresholds is reached at which point a response is made. (C) Model comparison of the seven neural HDDMs. Inverse function of DIC values relative to DIC of the HDDM not containing any neural data is shown (raw DIC values can be found in Supplementary Table 1).

Neural Circuitry Interacting with Fusiform Code

We were interested in exploring the broader neural circuits that interact with the fusiform face area during perceptual decisions. We used a generalized psychophysiological interaction (gPPI) analysis (McLaren et al. 2012) to identify brain regions with activity that covaried with the activity of fusiform “seed” voxels as parametrically modulated by the fusiform code. This allows us to identify putative downstream areas that receive the information decoded in the fusiform gyrus in the dynamic task. Two gPPI analyses were conducted with two 6 mm spherical seeds: one in the left fusiform (center: x = −42, y = −48, z = 20) and one in the right fusiform (center: x = 44, y = −48, z = −16). We found significant increases in connectivity within the entire ventral face processing stream posterior and anterior to the fusiform seed, including multiple areas along the lateral occipital cortex and superior temporal sulcus (Fig. 5, Supplementary Table 2). There was also connectivity with several portions of the dorsal visual stream, namely, the superior parietal lobule, inferior parietal sulcus, and supramarginal gyrus, moving anteriorly to premotor areas that encompass the frontal eye fields. In addition, for the left fusiform seed alone, there was also connectivity with inferior frontal gyrus and dorsolateral prefrontal and orbitofrontal cortex.

Figure 5.

Information flow. Group psychophysiological interaction (gPPI) from a left (top row) and right (bottom row) fusiform seed as parametrically modulated by the multivariate fusiform code for emotion. Color bar represents t-values.

Individual Differences in the Tendency to Wait

To further probe the role of fusiform MVPA code, we tested whether the magnitude of this code may differ in easy versus ambiguous trials. In easy trials, the absolute fusiform code significantly differed between correct and incorrect trials (z = 2.212, P = 0.0269). This was the not the case in ambiguous trials with no difference in fusiform code observed between correct and incorrect trials (z = −0.103, P = 0.9179). Analysis of variance revealed a significant interaction effect (F(1,43) = 4.381, P = 0.042) but no main effect for either accuracy (P = 0.241) or condition (P = 0.086) on fusiform code. However, a proportion of participants tended to respond rapidly during ambiguous trials, before there was enough information to arrive at a decision (Fig. 3B). To disentangle these individual differences, we conducted a post hoc analysis comparing subjects who tended to respond when no information was present in an ambiguous trial versus those who tended to wait for information to be available before responding. Subjects were split into two groups: 1) early responders who, on ≥80% of ambiguous trials, responded during the first two-thirds of the trial before information ramped toward one direction (N = 21) and 2) the rest, who were categorized as late responders (N = 24). Across the three runs, early responders demonstrated no significant changes in RT (F(2,46) = 0.433, P = 0.651), suggesting no learning effect (average RT for run 1 = 1.819 s, run 2 = 1.835 s, run 3 = 1.773 s). Conversely, late responders seemingly learned to slow down over time (average RT for run 1 = 3.690 s, run 2 = 4.019 s, run 3 = 4.156 s) (F(2,40) = 5.920, P = 0.006). As expected, early responders had significantly lower decision thresholds (mean = 2.671 ± 0.724) than late responders (mean = 5.067 ± 0.1.114) in the non-neural HDDM model (t(43) = −8.661, P < 0.0001). Early responders were significantly less accurate in predicting trial outcome (mean = 53.17%, SD = 0.05) than late responders (mean = 77.22%, SD = 13.12) (z = −5.604, P < 0.0001) in ambiguous trials. Early responders had accuracy close to chance in ambiguous trials, suggesting that they were guessing based on partial information.

We next examined the regression coefficients to determine the relationship between trial-by-trial variations in fusiform code and drift rate in a post hoc analysis (see methods). Our data was split in three ways to generate separate models in HDDM: 1) easy trials across all subjects, 2) ambiguous trials among late responders, and 3) ambiguous trials among early responders. This allowed us to compare drift rates of decisions made during periods of low versus high information. Greater fusiform code increased drift rates in easy trials (95.61% of posterior probability >0) and in ambiguous trials among late responders (97.86% of posterior probability >0). However, this effect was not observed in ambiguous trials among early responders (73.96% of posterior probability >0) (Fig. 6). A post hoc independent samples Kolmogorov–Smirnov test indicates that the distributions of the posterior probability in early and late responders significantly differed from one another (D = 0.688, P < 0.0001). Taken together, our results suggest that fusiform code does not simply drive increases in drift rate, but that this relationship depends on the quality of information as well as individual differences. Early responses during ambiguous trials are made before information is available; therefore the fusiform code cannot affect the response or the modeled drift rate. This further supports the interpretation that the fusiform code is a measure of the evidence that drives the response.

Figure 6.

Posterior probability density for modulation of drift rate. (A) easy trials, (B) ambiguous trials split by early (ER) and late (LR) responders. Peaks reflect the best estimates, while width represents uncertainty.

Caudate BOLD Signal May Reflect Inhibition

We then tried to determine what neural signals differed between late and early responders. A whole-brain group-level GLM of late, versus early, responders revealed no significant differences. However, there was higher caudate activation in two clusters (1) t = 4.45; x = −8, y = 4, z = 18; 2) t = 3.97; x = −8, y = 18, z = 2) after small volume correction using a structural caudate mask (alpha = 0.05) as an a priori region of interest (Ding and Gold 2012; Thura and Cisek 2017) when comparing ambiguous versus easy trails, taking into account the parametric modulation of the fusiform (Fig. 7B). This suggests that caudate activity plays a role and may serve to slow down the decision in favor of better accuracy. Conversely, lower caudate BOLD activity among early responders potentially reflects disinhibition, resulting in response prior to having accrued enough evidence.

Figure 7.

Urgency gating. (A) Predicted neural activity 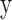for a sample trial as estimated per the urgency gating model (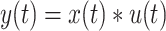) across time 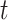. This is determined by multiplying a filtered evidence variable 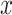with no (mirroring the drift diffusion model), low, or high urgency 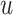. Both 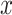and 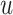change across time, with 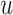growing as a linear function of time. Once 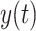crosses the decision threshold, a decision is made. (B) A whole-brain group-level general linear model (GLM) revealed that early, versus late, responders had lower caudate activation in two clusters (1) t = 4.45; x = −8, y = 4, z = 18; 2) t = 3.97; x = −8, y = 18, z = 2), highlighted in red, after small volume correction using a structural caudate mask (alpha = 0.05) when comparing BOLD activity, which was parametrically modulated by the fusiform code, between ambiguous and easy trials. An estimated urgency parameter was negatively correlated with (C) performance accuracy among ambiguous trials (r = −0.80, P < .0001) and (D) mean beta of caudate BOLD signal from within the two significant clusters from our GLM analysis (r = −0.28, P = 0.06).

Testing the Caudate Signal with the Urgency-Gating Model

The caudate is not typically implicated in facial processing (Haxby et al. 2000). Therefore, we sought to test whether its involvement here reflected a not previously described role in facial emotion processing or whether it may be involved in another aspect of decision-making that is independent of the sensory information content, as hypothesized by the urgency-gating model. We ran an SVM classifier per participant restricted to the caudate to decode happy and sad faces in the training task. We found that, as opposed to the fusiform and other face processing areas, caudate activity did not decode facial emotions better than chance (mean = 50.08% ± 0.06). Furthermore, we found that adding the trial-by-trial caudate BOLD signal extracted from the aforementioned clusters to the HDDM model did not improve model fit nor did it significantly modulate the drift rate (Supplementary Fig. 1). Taken together, this suggests that the caudate did not decode facial information in this task, but rather, perhaps reflects another decision variable untested by the HDDM.

Given the growing literature in support of an “urgency”-gating signal (Cisek et al. 2009) (Fig. 7A) and the hypothesized role for the basal ganglia in this gating, we tested whether the caudate BOLD may reflect this decision parameter. We used a second model (see methods) that directly tested whether an additional urgency parameter may multiplicatively add to the evidence accumulated, driving it toward a decision threshold, as described by Thura et al. (2012). First, we validated that parameter fits by a non-hierarchical DDM (nDDM) model without urgency corroborated the non-neural basic HDDM results. The estimated decision threshold parameter per participant generated from these two models was highly correlated (r = 0.9461, P < 0.0001). Next, we tested whether a fitted urgency parameter added to this nDDM model may relate to the caudate BOLD signal from our clusters. We found that the mean caudate BOLD activity per subject negatively correlated with participants’ urgency parameter with marginal significance (r = −0.2789, P = 0.0636) (Fig. 7D). Urgency was strongly related to decreased accuracy in ambiguous trials (r = −0.7995, P ≤ 0.0001) (Fig. 7C). We did not find any significant correlation between urgency and any of our questionnaire measures of impulsivity (i.e., BIS-11, BIS/BAS) (P > 0.05) (Supplementary Table 3).

Discussion

Much research on decision-making has used simple choice paradigms based on visual evidence, such as dot motion tasks. When used in non-human primates, these tasks allow accurate characterization of the properties of sensory inputs, fitting of computational models to behavior, and identification of neural activity that reflects the underlying sensory evidence or decision variables (Gold and Shadlen 2007). However, these paradigms are difficult to use in human participants, where trial numbers are usually smaller, and the ability to accurately measure neural activity is limited. Here, we took advantage of the large body of knowledge on face processing studied with fMRI, combined with MVPA and hierarchical Bayesian modeling, to overcome these limitations.

We used a dynamic task in which participants had to identify the correct emotion from face pictures that gradually transitioned from neutral to happy or sad. Applying machine learning to fMRI data from a training task, we identified patterns of neural activity that encode facial emotion information. We then applied the individual decoders to the dynamic task and showed that the MVPA code in the fusiform gyrus reflected the evidence used to make a choice, as suggested by its relation to computational modeling parameters (drift rate) and by connectivity patterns to areas implicated in sensory decoding, decision-making, and motor control. This suggests that the neural MVPA code was driving decision in our task.

Multivariate encoding of sensory information was found to reflect adjustments of decision parameters in our evidence accumulation model. We confirmed previous MVPA studies by showing that facial emotion can be decoded from each of seven brain regions hypothesized to form a distributed system for facial emotion processing (Haxby et al. 2000; Wegrzyn et al. 2015). However, only the MVPA code from the fusiform gyrus contributed to the drift diffusion model. There was a clear distinction between it and the other six regions in terms of DIC (Fig. 4C). This suggests that, while emotional facial features lead to recoverable neuronal activity in the entire face processing network, the fusiform gyrus is central to decoding and feeding the information forward in this decision-making task. These results are in keeping with recent evidence that the fusiform gyrus is especially involved in emotion processing (Harry et al. 2013; Wegrzyn et al. 2015). On the other hand, the amygdala, sometimes postulated to specifically decode facial emotion (Haxby et al. 2000), did not influence evidence accumulation in our model. Further support for the role of the fusiform comes from the fact that the strength of the emotional code derived from MVPA was correlated with the estimated drift rate. Single-cell recordings in monkeys have shown that drift rate is proportional to the signal-to-noise or coherence of the stimulus (Gold and Shadlen 2007), implying that better sensory evidence is associated with faster accumulation. Note that the relationship between fusiform code and drift rate was contingent on the trial type and on individual differences in participants’ tendency to wait for more information before deliberation: it only influenced drift rate in easy trials and for late responders on ambiguous trials. In early responders on ambiguous trials, fusiform code did not contribute to evidence accumulation; this is expected, as there is insufficient evidence in the early portion of ambiguous trials. In sum, our results point to the fusiform gyrus as the key node in decoding facial information and accumulating evidence for the purpose of decision-making in this experiment.

The fusiform gyrus decodes the sensory information, but does it feed this information forward for the purpose of computing a decision variable (Gold and Shadlen 2007)? We used generalized PPI to identify brain regions where functional connectivity with a seed in the fusiform gyrus was modulated by the fusiform MVPA code. This approach attempts to go beyond simple connectivity to map the actual flow of information used in the task. It has a similar goal to other multivariate pattern covariance methods proposed previously sometimes referred to as informational connectivity (Coutanche and Thompson-Schill 2013; Anzellotti et al. 2017). While these analyses do not reveal directionality, they suggest possible pathways by which information flows to a series of regions belonging to the ventral and dorsal visual streams as well as premotor and cerebellar regions. Informational connectivity with fusiform was found along several more posterior areas of the visual system, likely representing visual information streaming from occipital cortex to fusiform. In the forward direction, the observed connectivity pattern suggests that face information flows to ventral stream regions implicated in object identification (Mishkin et al. 1983), such as the superior temporal sulcus, and dorsal stream areas involved in action specification (Goodale and Milner 1992). The latter regions included the inferior parietal sulcus, superior parietal lobule, supramarginal gyrus, and frontal eye fields. All of these regions have been previously implicated in sensory evidence accumulation in monkeys and humans (Gold and Shadlen 2007; Mulder et al. 2014). The inferior parietal sulcus, which corresponds to the lateral intraparietal area in monkeys, is thought to receive sensory evidence information from relevant sensory areas (motion sensitive areas in the case of moving-dot tasks, the fusiform in the current study) and to convert this into a decision variable that is then passed on to premotor areas (Hanks et al. 2006; Gold and Shadlen 2007). Our results support this model, by demonstrating 1) that sensory evidence is computed in the fusiform and 2) that the fusiform exhibits informational connectivity with inferior parietal sulcus and premotor areas. This informational connectivity pattern can be interpreted in the light of the affordance competition model (Cisek 2007), in which information related to sensory representations and action selection constantly interacts as it moves from occipital to motor areas and where decisions emerge from a competition between relevant motor outputs. This model predicts that sensory decoding should feed information forward to the medial temporal, parietal, and premotor areas involved in converting sensory information into action, as shown here.

Previous fMRI studies have attempted to image regions involved in evidence accumulation (reviewed in: Mulder et al. 2014). Typically, researchers look for correlations between BOLD signal and fitted values of drift rate or computed evidence variables. However, in studies to date, it has not been possible to use fMRI to discriminate between neural representations of sensory evidence as opposed to decision variables. For example, Wheeler et al. (2015) designed a paradigm in which shapes appeared successively to indicate cumulative probability in favor of a left or right hand response. Thus, at each time point it was possible to relate BOLD to an evidence variable. They were able to identify brain regions involved in evidence accumulation independent of action preparation, but because the visual stimuli were similar, sensory evidence accumulation could not be imaged. Braunlich and Seger (2016), using a similar paradigm, found that evidence thus defined correlated with BOLD in motor regions (contralateral motor cortex and putamen, ipsilateral cerebellum), suggesting that a motor decision rather than a sensory evidence correlate was being imaged. Using a stock-picking paradigm with sequential probabilistic information, Gluth et al. (2012) found that a calculated decision variable was reflected in value-coding brain areas (ventromedial prefrontal cortex and ventral striatum), while a response variable was tracked in motor areas. Another study using a moving-dot paradigm identified correlates of the accumulation rate in the inferior parietal sulcus, but once again this likely reflected a decision variable rather than sensory evidence (Nagano-Saito et al. 2012). In sum, previous fMRI studies imaged decision variables or value signals related to different choice options rather than the accumulating sensory evidence that guides these choices. By using MVPA, we were able to distinguish neural responses to the two choice stimuli used here and show that this response reflected evidence accumulation since it modulated the drift rate in our Bayesian model.

The basal ganglia did not display PPI connectivity to fusiform, nor did they appear to encode face information; however, they did emerge in our analysis of group differences, albeit only after small volume correction. Specifically, there was greater caudate activation during ambiguous stimulus viewing in late versus early responders. In the affordance competition model, the basal ganglia are thought to bias decisions via cortico-striatal connections (Cisek 2007; Thura and Cisek 2017). One type of response bias is to slow down in ambiguous situations, which one could call “negative urgency.” Indeed, Cisek et al. (2009) have suggested that the pure evidence accumulation models do not fully account for observed behavior when speed–accuracy trade-offs are present or information is ambiguous. They suggest the presence of an additional model parameter, termed urgency, that is independent of the sensory evidence but multiplies the drift rate to hasten or slow down decisions when the context demands it. Fortuitously, approximately half of our subjects slowed down during ambiguous trials, waiting for the stimuli to morph toward the final emotion, and the others did not. One way for race models to accommodate slower responses is to raise the decision threshold, but because easy and ambiguous trials were intermixed, participants did not have a priori knowledge of which type of stimulus would be displayed in any given trial. Another way to account for slower responses on ambiguous trials is lower urgency. Our findings implicate the caudate in slowing down decisions when the evidence is ambiguous. Moreover, there was a weak negative correlation between caudate BOLD effect size during ambiguous trials and the fitted urgency parameter; therefore, caudate BOLD may reflect negative urgency. These results are consistent with microelectrode recordings in the basal ganglia of monkeys in which neuronal firing was insensitive to evolving sensory evidence but could influence the response speed by modulating activity in sensory processing regions (Thura and Cisek 2017). The observed caudate activity in our study may reflect the indirect pathway of the basal ganglia—originating from a striatal population of projection neurons thought to generate a net inhibition resulting in a “stopping signal” (Frank and Claus 2006). For example, in a fMRI study with a dot-motion task, we found that participants slowed their responses when offered the possibility of monetary reward and that caudate activation during these trials correlated with a raising of the decision threshold (Nagano-Saito et al. 2012). Dopamine signaling was shown to underpin this effect. It should be noted that evidence-independent urgency signals could end up being modeled as drift rate or threshold in pure evidence accumulation models; to disambiguate urgency from pure evidence accumulation, one needs to dynamically manipulate the amount of information presented, as in the present study (Cisek et al. 2009). It must be noted however that the caudate effect only emerged after small volume correction of the neuroimaging data, meaning that it should be confirmed in future studies.

Findings from our study should be considered in light of its limitations. First, both the evidence accumulation and urgency signal are hypothesized to grow in time. Though we used multiband fMRI acquisition to reduce repetition time below 1 s, without the ability to record at millisecond resolution, the estimated neural parameters of each model may lack in precision. Second, we used facial emotion as an exemplar of sensory information for perceptual decision-making. Future studies should test whether MVPA decoding can also be applied to other forms of sensory information and whether the relationship to decision parameters holds. Third, though we observed caudate activity thought to reflect a dopaminergic stopping signal, our study does not measure dopamine nor the indirect pathway per se. The implications of this pathway in human decision-making in ambiguous environments merit further research.

Conclusion

By combining model-driven multivariate fMRI analysis, psychophysics, and computational modeling, we characterized two decision parameters underlying human perceptual decision-making processes (drift rate and urgency signal) in the setting of dynamic, changing environments. Our results reveal how these decision parameters are encoded in the human brain and indicate that MVPA techniques can be used to probe and disentangle the biological underpinnings of the decision process. This may be of particular relevance to characterizing brain phenotypes related to disorders of decision-making (e.g., addictions, impulse control disorders, and obsessive–compulsive disorder).

Funding

Canadian Institutes of Health Research and the Natural Sciences and Engineering Research Council of Canada (CIHR grant FDN-143242, NSERC grant 436259-13 to A.D.); Canadian Institute of Health Research Vanier scholarship (to Y.Y.).

Notes

We would like to thank Gaël Varoquaux for advice on multivariate decoding and Michael J. Frank for advice on using the hierarchical drift diffusion model. Y.Y., P.C., and A.D. designed research; Y.Y. and M.T. collected the data; Y.Y., M.D., and Y.Z. analyzed the data and contributed methods; and Y.Y., A.D., L.F., and P.C. contributed to result interpretation. Y.Y. drafted the initial manuscript; all authors contributed to the writing of this manuscript.

Conflict of Interest: The authors declare no competing financial interests.

Data and Software Availability

Classifier weights from SVM and statistical maps are available for download from Neurovault (https://identifiers.org/neurovault.collection:6025 and https://identifiers.org/neurovault.collection:6026). Raw data and code used to carry out our analysis can be found at https://github.com/yvonnio/face-decoding-fmri. Further information and data requests should be directed to and will be fulfilled by the corresponding author, Alain Dagher (alain.dagher@mcgill.ca).