Relating N–H Bond Strengths to the Overpotential for Catalytic Nitrogen Fixation

Abstract

Nitrogen (N₂) fixation to produce bio-available ammonia (NH₃) is essential to all life but is a challenging transformation to catalyse owing to the chemical inertness of N₂. Transition metals can, however, bind N₂ and activate it for functionalization. Significant opportunities remain in developing robust and efficient transition metal catalysts for the N₂ reduction reaction (N₂RR). One opportunity to target in catalyst design concerns the stabilization of transition metal diazenido species (M-NNH) that result from the first N₂ functionalization step. Well-characterized M-NNH species remain very rare, likely a consequence of their low N–H bond dissociation free energies (BDFEs). In this essay, we discuss the relationship between the BDFE_N–H of a given M-NNH species to the observed overpotential and selectivity for N₂RR catalysis with that catalyst system. We note that developing strategies to either increase the N–H BDFEs of M-NNH species, or to avoid M-NNH intermediates altogether, are potential routes to improved N₂RR efficiency.

Graphical Abstract

The reduction of N₂ to NH₃ (N₂RR) is a globally significant reaction that is challenging due to the inertness of N₂. Transition metals can activate N₂ and mediate catalytic N₂RR but challenges remain with respect to catalytic efficiency in terms of overpotential and selectivity. We discuss the role of the N–H bond dissociation free energy (BDFE) of metal diazenidos (M-NNH), the first intermediates of N₂RR, plays in determining N₂RR efficiency.

1. Introduction

Despite the abundance of nitrogen (N₂) in the atmosphere, its bioavailability limits growth in many environments.^[1] Thus, the fixation of N₂ into its most common bioavailable form, ammonia (NH₃), is essential to all life and is among the most important (and fascinating) chemical transformations on the planet. N₂-to-NH₃ conversion (commonly called the nitrogen reduction reaction and abbreviated as N₂RR) is challenging owing to the chemical inertness of N₂ with respect to proton transfer (PT), electron transfer (ET), and hydrogen atom transfer (Figure 1).

Figure 1:

(A) Properties of free N₂ highlighting its recalcitrance to initial functionalization (e⁻, H⁺, and H• affinity), which are similar to those of the noble gases, and its strong N≡N triple bond (BDE = bond dissociation enthalpy).^[2,8,9] (B) N₂ terminally binds transition metals via σ-donation of its lone and acceptance of π-backdonation from the metal center. Binding induces a dipole on N₂ and weakens the N≡N bond, priming it for conversion to NNH. Subsequent reductive protonation steps lead to the formation of NH₃. (C) Comparison of the standard (1 M or 1 atm, 298 K, 0 V vs NHE) free energy for the formation of NH₃ from both H₂ (ΔG°_f) and H⁺/e⁻ (ΔG°(N₂RR)).^[10]

Its high stability is due to a very strong N≡N triple bond and the absence of a dipole (distinct from isoelectronic CO).^[2] N₂ can be rendered far more chemically reactive by binding to a transition metal. The σ-lone pair donation from N₂ to the metal and corresponding π-backdonation from the metal into the empty π* orbitals of N₂ can weaken the N≡N bond and induce a dipole, priming the N₂ ligand for functionalization.^[3] Nonetheless, the first functionalization step to form a metal diazenido (M-NNH) intermediate remains a significant challenge in catalytic N₂RR. In accord with their highly reactive nature, very few M-NNH species have been reliably characterized.^[4–7] In this short perspective, we draw attention to the significance of the M-NNH intermediate in terms of overall catalytic N₂RR efficiency with respect to overpotential and likely also selectivity. We formulate a semi-quantitative relationship between the stability of the M-NNH species, assessed via its N–H bond dissociation free energy (BDFE_N-H), and the net overpotential required for catalytic N₂RR (Figure 1).

2. Bonding in M-N₂H_y Species

Chatt and coworkers were the first to synthesize well-defined M-N_xH_y coordination complexes and to demonstrate stoichiometric ammonia generation via the protonation of N₂ complexes, with particular emphasis on bis(phosphine)-supported N₂ complexes of the group 6 metals Mo and W (e.g., (depe)₂W(N₂)₂, depe = diethylphosphinoethane; Figure 2).^[4,11] Later, other groups established that such systems could serve as precursors for electrosynthetic (but not electrocatalytic) NH₃ formation.^[12,13] Most recently, catalytic N₂RR in the presence of SmI₂ and H₂O or ethylene glycol has been established using these types of phosphine-supported Mo complexes.^[14]

Figure 2:

(left) Force constants for the W–N and N–N normal modes in a PT series derived from (depe)₂W(N₂)₂ ([W] ≡ (depe)₂W). (right) Force constants for the N–N bond in free N₂, NNH₂, and N₂H₄ provided as standards for N–N triple, double, and single bonds respectively.^[15,17]

Detailed vibrational spectroscopy and analysis by Tuczek and coworkers mapped the evolution of the W–N and N–N bonding as a function of the protonation state (e.g., N₂ vs NNH vs NNH₂ vs NNH₃) in a family of these foundational group 6 systems. Their studies underscore the challenge of stabilizing a M-NNH intermediate.^[15–17] To summarize their findings, the N≡N bond in free N₂ is characterized by a force constant (f) of 22.4 mdyn•Å⁻¹. The formal reduction to isodiazene (NNH₂) generates a double bond (f = 11.7) and, ultimately, reduction to hydrazine (N₂H₄) yields a single bond (f = 4.3, Figure 2). To compare, in (depe)₂W(N₂)₂, backdonation from the zerovalent W center reduces the N–N bond order, evinced by the reduction of f_N–N to 16.4 mdyn•Å⁻¹ and an increase in W–N bond character (f_W–N = 2.9 mdyn•Å⁻¹). Monoprotonation to form (depe)₂W(F)(NNH) significantly attenuates the N–N π-bonding (f_N–N = 8.3 mdyn•Å⁻¹), with W–N bonding increasing only slightly (f_W–N = 4.5 mdyn•Å⁻¹). Further protonation to yield [(depe)₂W(F)(NNH₂)]⁺ decreases the N–N bonding only negligibly (Δf_N–N = −1 mdyn•Å⁻¹), which is compensated for by a further increase in the W–N bonding (Δf_W–N = +1.5 mdyn•Å⁻¹).^[15] Lastly, in [(depe)₂W(F)(NNH₃)]²⁺, its formal W–N triple bond has a f_W–N = 7.3 mdyn•Å⁻¹, and its formal N–N single bond has a f_N–N = 6.0 mdyn•Å⁻¹ (Figure 2).^[17]

If we compare the first, second, and third PT steps, the first PT causes a much more significant reduction in the N–N bonding then the next two. Indeed, after the first step the N–N force constant is already significantly less than that of the N=N double bond in free isodiazene (NNH₂). However, the increase in the W–N force constant for each PT is qualitatively similar. Thus, there is a relatively uncompensated loss of N–N π-bonding following the first PT step to generate the M-NNH, and, hence, we can expect the resultant N–H bond in the resulting diazenido species to be homolytically weak. Indeed, whereas N–H bonds in amines typically have BDFEs between 90 and 100 kcal•mol⁻¹,^[8] density functional theory (DFT) studies on the BDFE_N–H of several diazenido species have consistently predicted values less than 50 kcal•mol⁻¹.^[18–21] This is an important value to keep in mind, because below 50 kcal•mol⁻¹ N–H (and other X-H) bonds are thermodynamically prone to bimolecular reactions that release H₂ (BDFE(H₂) = 102.3 kcal•mol⁻¹ in MeCN).^[8]

Thus, although a transition metal can significantly stabilize an NNH species via coordination compared to its free state (calculated gas-phase BDE_N–H(NNH) = −4 kcal•mol⁻¹),^[8] M-NNH species remain susceptible to the hydrogen evolution reaction (HER, vide infra). DFT calculations^[19–21] and fundamental chemical intuition suggest that reductive protonation steps that occur after N–N bond cleavage are comparatively easier. Therefore, in N₂RR reactions proceeding from terminal N₂ complexes, the most challenging functionalization step is likely to be formation of the M-NNH intermediate. What is more, we suggest that the necessary overpotential for catalytic N₂RR with a particular catalyst can be roughly estimated from the BDFE_N–H of the catalytically relevant diazenido intermediate. To explore this idea further, we test here the validity of this approach for two cases of N₂RR catalysts (Mo and Fe) that proceed through an M-NNH intermediate.

3. M-NNH Intermediates and Catalytic N₂RR

In 2003, Schrock and coworkers published the first example of a well-defined, organometallic N₂RR catalyst.^[22] Their triamidoamine Mo system, (HIPTN₃N)Mo(N₂) ([HIPTN₃N]³⁻ = [HIPTNCH₂CH₂)₃N]³⁻, HIPT = 3,5-(2,4,6-ⁱPr₃C₆H₂)₂C₆H₃)), is capable of forming NH₃ catalytically (63%) concomitant with H₂ formation (33%) in the presence of excess Cp*₂Cr (−1.45 V vs Fc^+/0 in MeCN) and [Lut-H]⁺ ([Lut-H]⁺ = 2,6-dimethylpyridinium, pK_a = 14.13 in MeCN).^[22,23] Later, Schrock and coworkers established that lower but still catalytic yields of NH₃ (3.6 equiv NH₃ per Mo) could be obtained using the same acid and the weaker reductant Cp₂Co (−1.33 V vs Fc^+/0 in MeCN, Figure 3).^[24] As articulated by Mayer and coworkers,^[8,25] the equation (Eq 1), in which C_G is a solvent dependent constant (C_G = 54.9 kcal•mol⁻¹ in MeCN), that is typically used to determine BDFEs can also be used to predict an effective BDFE (BDFE_eff) for any acid/reductant pair.^[8] Such estimates are inherently limited by the lack of available data with respect to E°, pK_a, and C_G values in the types of non-polar solvents typically used in N₂RR catalysis. However, since net H• transfer reactions do not change the overall charge of an intermediate, solvent-dependence is anticipated to be moderate and likely does not significantly affect the estimates presented here.

$${\text{BDFE}}_{\text{eff}}=1.37\times \text{p}{K}_{\text{a}}\left(\text{acid}\right)+23.06\times E°\left(\text{reductant}\right)+{\text{ C}}_{\text{G}}$$ (1)

Figure 3:

(A) Lowest established overpotential catalytic conditions, using [LutH]⁺ and Cp₂Co as the acid/reductant pair, for N₂RR by a (HIPTN₃N)Mo species ([Mo]).^[24] (B) Hess’s law scheme showing the thermodynamic equivalence between pK_a and E° for the separated acid/reductant pair and the BDFE_eff.^[8,25] (C) Protonation equilibrium between [(HIPTN₃N)Mo(N₂)]⁻/(HIPTN₃N)Mo(NNH) and [DBU-H]⁺/DBU in THF, which allows the pK_a to be estimated.^[5] (D) The redox couple for [(HIPTN₃N)Mo(N₂)]^0/− in THF.^[23] (E) Decay pathway^[5] and estimated BDFE of (HIPTN₃N)Mo(NNH).

By comparing the BDFE_eff value of the Cp₂Co/[LutH]⁺ pair (43.6 kcal•mol⁻¹) to the strength of an H• derived from H₂,^[8] one can derive the excess energy used relative to the Gibbs free energy of formation for NH₃ (ΔΔG_f(NH₃), Eq 2) in this reaction. Since the reduction of N₂ with H₂ to form NH₃ is nearly thermoneutral (i.e., ΔG_f(NH₃) ~ 0 kcal•mol⁻¹, Figure 1), this analysis provides a good estimate of the net overpotential needed to drive N₂RR.^{[18,19,26,27]} For the present case, the deduced ΔΔG_f(NH₃) of 23 kcal•mol⁻¹ provides an experimental lower limit for N₂RR by the Schrock Mo catalyst; in accord with this notion, their efforts to perform catalysis using weaker acids, such as [Et₃NH]⁺ (pK_a = 18.82 in MeCN),^[23] proved unsuccessful.^[22]

$$\Delta \Delta G_{\text{f}}\left({\text{NH}}_3\right)=3\times \left(\text{BDFE}\left({\text{H}}_2\right)/2–{\text{ BDFE}}_{\text{eff}}\right)$$ (2)

An estimate of the BDFE_N–H of the parent diazenido species in this same system, (HIPTN₃N)Mo(NNH), can be ascertained from experimental data previously reported by Schrock and coworkers (Figure 3).^[5,18,23] In particular, [(HIPTN₃N)Mo(N₂)]⁻/(HIPTN₃)Mo(NNH) were shown to be in a PT equilibrium with [DBU-H]⁺/DBU (DBU = 1,8-diazaobicyclo[5.4.]undec-7-ene) in THF (pK_a([DBU-H]⁺) = 18.5 in THF).^[28,29] The [(HIPTN₃N)Mo(N₂)]^0/− redox couple is −1.81 V vs Fc^+/0 in THF.^[23] From these observations, the BDFE_N–H(Mo-NNH) can be approximated as 45 kcal•mol⁻¹ (C_G in THF ~ 61 kcal•mol⁻¹).^[30] This value accords both with computational studies^[18,19] and its solution instability; (HIPTN₃N)Mo(NNH) slowly decays via formal β-hydride elimination to release N₂ and form (HIPTN₃N)Mo(H) (Figure 3).²⁷ One can then predict a ΔΔG_f(NH₃) for N₂RR catalysis by (HIPTN₃N)Mo, using as a basis the BDFE_N–H((HIPTN₃N)Mo(NNH)) and comparing this to BDFE(H₂) (Eq 3). This analysis leads to the prediction of a minimum ΔΔG_f(NH₃) for (HIPTN₃N)Mo to be 20 kcal•mol⁻¹, which compares quite well with the 23 kcal•mol⁻¹ value deduced above using the BDFE_eff for Cp₂Co/[LutH]⁺.

$$\Delta \Delta G_{\text{f}}{\left({\text{NH}}_3\right)}_{\text{predicted}}=3\times \left(\text{BDFE}\left({\text{H}}_2\right)/2-{\text{ BDFE}}_{\text{N}–\text{H}}\left(\text{M-NNH}\right)\right)$$ (3)

In 2013, our lab at Caltech reported the first example of a molecular iron catalyst for N₂RR, (^iPrP₃^B)Fe (^iPrP₃^B = tris(o-diisopropylphosphinophenyl)-borane). This was the first non-Mo system to be identified for catalytic N₂RR and was initially shown to be active using HBAr^F₄ and KC₈ at low temperature in diethyl ether.^[31,32] It was later shown that this same catalyst was competent for N₂RR with Cp*₂Co (E° = −1.91 V vs Fc^+/0 in MeCN) and substituted anilinium acids (Figure 4).^[18] A comparison of the N₂RR efficacy versus the strength of the acid revealed that the weakest anilinium acid for which catalysis could be observed (7.3 equiv NH₃ per Fe at the loading tested) was [PhNH₃]⁺ (pK_a = 10.62 in MeCN).^[33] Efforts to achieve catalysis with milder reductants, such as Cp*₂Cr or Cp₂Co, were unsuccessful.^[18] Using the above E° and pK_a values for Cp*₂Co and [PhNH₃]⁺, respectively, and Eqs 1 and 2, allows one to deduce a BDFE_eff = 25.4 kcal•mol⁻¹, and hence an experimental ΔΔG_f(NH₃) of 75 kcal•mol⁻¹ for this acid/reductant pair.

Figure 4:

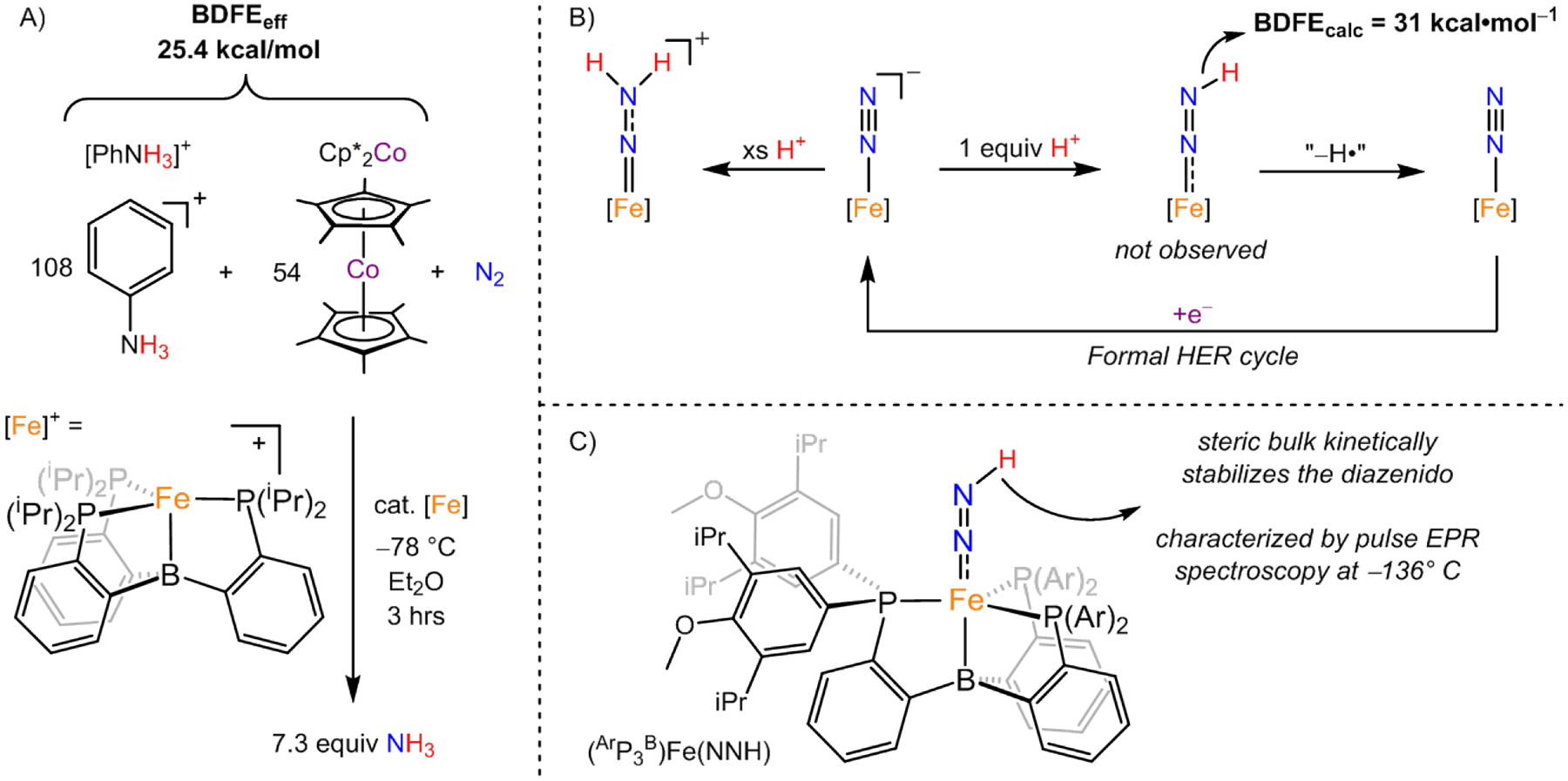
(A) Lowest established overpotential conditions, using [PhNH₃]⁺ and Cp*₂Co as the acid/reducant pair, for N₂RR catalysis observed with (^iPrP₃^B)Fe.^[18,33] (B) Double protonation of [(^iPrP₃^B)Fe(N₂)]⁻ leads to formation of the cationic isodiazene complex.^[34,35] Efforts to form the Fe-NNH diazenido via single protonation lead to formal H• loss (observed as 0.5 equiv H₂), consistent with its low BDFE_N–H.^[18,20,34] Reduction of the resultant (^iPrP₃^B)Fe(N₂) closes a cycle for HER. (C) Bulkier (^ArP₃^B)Fe platform allows for kinetic stabilization (at −136 °C) of an Fe-NNH diazenido species, as elucidated by pulse electron paramagnetic resonance (EPR) spectroscopy.^[7]

Efforts to synthesize (^iPrP₃^B)Fe(NNH) from [(^iPrP₃^B)Fe(N₂)]⁻ via monoprotonation lead instead to the instantaneous formation of H₂ and oxidation at Fe, even at very low temperature,^[34] highlighting that the Fe-NNH species is a potential source of H₂ formation during catalytic N₂RR. However, the intermediacy of (^iPrP₃^B)Fe(NNH) in N₂RR is supported by the double protonation of [(^iPrP₃^B)Fe(N₂)]⁻ in the presence of excess acid to afford the isodiazene intermediate, [(^iPrP₃^B)Fe(NNH₂)]⁺.^[33,34] Additionally, direct spectroscopic characterization of a related diazenido species, (^ArP₃^B)Fe(NNH) (^ArP₃^B = tris(o-di-(3,5-diisopropyl-4-methoxy)phenylphosphinophenyl)-borane), was accomplished at cryogenic temperatures (−136 °C) with a ligand featuring bulkier phosphine substituents.^[7] While the solution instability of (^RP₃^B)Fe(NNH) species has to date precluded the experimental determination of a BDFE_N–H, DFT calculations predict a BDFE_N–H of ~31 kcal•mol⁻¹. This theoretical approach has been calibrated with experimentally derived BDFE values derived from similar iron complexes.^[18,20] Using this BDFE_N–H in Eq 3 leads to a predicted minimum ΔΔG_f(NH₃) of 60 kcal•mol⁻¹ for the (^iPrP₃^B)Fe-catalyst system.

4. Conclusion

Note that in both of the case studies presented here, the experimentally observed minimum ΔΔG_f(N₂RR) is higher than that estimated from the BDFE_N–H of the M-NNH species. This “extra” driving force might be necessary because steps that are not related to N₂ functionalization, such as NH₃/N₂ exchange, are instead thermodynamically limiting. Alternatively, as most N₂RR catalysts are also HER catalysts,^{[23,32,33,36]} this excess driving force may be necessary to form (and consume) reactive intermediates at a sufficient rate to prevent their decay to H₂.^[20,21] For our iron catalyst system, it may remain to be discovered that a modestly weaker acid (or reductant) is compatible with N₂RR, such that an overpotential closer to the predicted ΔΔG_f(NH₃) of 60 kcal•mol⁻¹ can be achieved. Our view is that strategies to improve not only the thermodynamic stability but also the kinetic stability of the key M-NNH intermediate will offer a means of achieving N₂RR catalysis at lower overpotentials and with higher selectivities. These efforts should be complemented by further development of N₂RR catalysts that can circumvent such an M-NNH intermediate, such as those recently proposed for Mo by Nishibayashi and coworkers^[27,37] and for Ti by Liddle and coworkers.^[38] Given the global importance of nitrogen fixation, and the rich catalytic landscapes that are at play in the growing number of synthetic catalyst systems, there are exciting opportunities to improve mechanistic understanding and develop more robust and efficient catalyst systems.^[39]