Design and Characterization of a Novel Series of Geometrically Complex Intravaginal Rings with Digital Light Synthesis

Abstract

Intravaginal rings (IVRs) represent a sustained-release approach to drug delivery and have long been used and investigated for hormones and microbicides delivery. For decades, IVRs have been manufactured by injection molding and hot-melt extrusion with very limited design and material capabilities. Additive manufacturing (AM), specifically digital light synthesis (DLS), represents an opportunity to harness the freedom of design to expand control and tunability of drug release properties from IVRs. We report a novel approach to IVR design and manufacturing that results in geometrically complex internal architectures through the incorporation of distinct unit cells using computationally-aided design (CAD) software. We developed a systematic approach to design through the generation of an IVR library and investigated the effects of these parameters on ring properties. We demonstrate the ability to precisely and predictably control the compressive properties of the IVR independent of the internal architecture with which control of drug release kinetics can be achieved, thus opening the door for a ‘plug-and-play’ platform approach to IVR fabrication.

1. Introduction

Intravaginal rings (IVRs) are a toroidal medical device fabricated from a polymeric material containing a dispersed active pharmaceutical ingredient (API) for delivery via the vaginal tract.¹ For commercially available IVRs, drug delivery is enabled by API diffusion from the device, through the stratified vaginal mucosal epithelium, and systemically distributed through the highly vascularized vaginal cavity.² This method of delivery is advantageous for several reasons, including avoidance of gastrointestinal absorption, hepatic first-pass metabolism and increase in bioavailability. Extensive patient compliance studies of IVRs have shown strong acceptability among users.^3–5 IVRs are well tolerated by women, and are established as contraceptive devices (NuvaRing®)^6–9 and hormone replacement therapy (Estring®, Femring®)¹⁰. More recently, IVRs have been extensively investigated for microbicide delivery to prevent against sexually transmitted infections (STIs)^8,9 and human immunodeficiency virus (HIV)^8,10–12.

IVRs are conventionally mass-produced with hot-melt extrusion or injection molding (IM) in which thermoplastic (ethylene vinyl acetate, EVA) or thermoset (silicone) polymer pellets are melted in the presence of API. In the IM process, the heated material is conveyed by a series of temperature controlled screws, and under pressure, pushed and injected into a mold.¹⁶ Commercially available rings are either matrix, in which the API is dispersed homogenously throughout the polymer matrix (Progerin®, Fertiring®) or reservoir, in which a drug-loaded core surrounded by a thin membrane to control diffusion rate and achieve therapeutic delivery within the targeted release window (NuvaRing, Estring, Femring®). Because IM utilizes such high temperatures and pressures, it is inherently therapeutic restrictive. Additionally, the solid cross-section of the IVR means that the release kinetics of APIs is determined by the diffusion rate of drug from the solid polymer matrix. Often, to achieve targeted kinetics, the API must be significantly ‘overloaded’ resulting in a device that contains >50% residual API post IVR use and is considerably more expensive to produce given the increased cost of incorporated drug.¹⁷ Methods have been developed to counter these limitations however have resulted in increased number of fabrication steps^11,18–22, thus detracting from the main advantage of IM, namely high throughput. Therefore, while the IVR as a drug delivery vehicle has the potential to address numerous indications, its concept, design, and manufacturing have been restricting IVRs to indications with therapeutics and configurations that are compatible with the fabrication process.

Additive manufacturing (AM), or more commonly 3D-printing, represents an attractive alternative to the limited kinetic release profiles associated with IM.²⁰ AM is the selective layering of material in a specified manner, usually dictated by a computationally-aided design (CAD) file. The advantages of AM over IM for the fabrication of IVRs include the generation of complex geometries not beholden to a mold, expansion of material choice, and a larger pool of compatible APIs. Collectively, AM has the potential to enlarge the IVR design space thereby enabling targeted release profiles of therapeutics previously excluded from the vaginal delivery route. There are many commercially available 3D-printing platforms such as fused-deposition modeling (FDM), selective laser sintering (SLS), and stereolithography (SL).^24,25 The difference among these platforms centers on the method of CAD reconstruction, namely how material is additively layered to generate the desired part. For instance, FDM utilizes a heated thermoplastic to selectively deposit material in a layer-wise fashion. Alternatively, SLS utilizes either metal or plastic particles that are fused via a rastering laser. AM, however, is not without its drawbacks which are almost exclusively related to how the CAD file is reconstructed. For example, the platforms are material restrictive²⁶, reconstruct CAD files at a pace too slow for mass production^27,28, and result in rough structures with poor mechanical properties^26,29,30. Therefore, while 3D printing has the potential to address the main drawbacks to implementing IVRs^31,32 (and other intrauterine devices^33–35) over a wider range of indications, the currently available technology is lacking.

A novel approach to 3D printing was recently developed by Carbon, called continuous liquid interface production (CLIP™)³⁶ or digital light synthesis (DLS™). DLS utilizes a photosensitive resin that solidifies upon ultra-violet (UV) illumination. The apparatus incorporates an oxygen (O₂) permeable window to harness a known phenomenon of O₂ inhibition of the solidification, or polymerization, process, forming a region of unpolymerized resin called the dead zone.³⁶ The dead zone prevents the growing part from solidifying to the window as it is constructed. This enables continuous fabrication of the part, which translates to smooth, non-layered structures with highly resolved features that are produced with rapid build rates of upwards of 100 mm/hr.; these speeds are amenable to large scale manufacturing.^36–39

Herein, we report a novel platform approach to the design and fabrication of geometrically complex intravaginal rings using DLS. We propose utilizing geometric complexity, within the IVR as an avenue to achieve a range of targeted API-release profiles³⁹. Briefly, the platform combines the capacity of CAD to generate structures with specific dimensional metrics, such as diffusion distances (strut thicknesses), surface area and volume with the ability of DLS to fabricate structures layerlessly, with minimal surface roughness, and at production-relevant speeds in a biocompatible silicone-based resin. This approach was intended to address the fundamental drawbacks associated with current IVR manufacturing and to harness the inherent design advantages of AM to reengineer IVRs. For example, the IM process requires that the biocompatible polymer exhibits properties (e.g. molecular weight, viscosity, melt index) that are compatible with IM manufacturing parameters. Digital light synthesis provides the flexibility to design and manufacture the final polymer to fit specific device properties in a controlled process that combines both the starting liquid resin material and the 3D printing parameters. Here we report on the first portion of this proposed platform for development, fabrication, and characterization of a geometrically complex IVR design library. We hypothesized that the introduction of geometric complexity within the cross-section of the IVR would implement greater control over diffusion distance, opening the door to a wider range of drug-release properties. We found our design and fabrication method results in rings with controlled mechanical properties in a silicone-based resin independent of the internal lattice design. This unique distinction between decoupling of parameters that control compressive properties and parameters that have the potential to control drug release properties enables the first step of a novel platform approach to IVR fabrication.

2. Results

2.1. Design and Fabrication of Geometrically Complex Intravaginal Rings

The performance and drug release properties of intravaginal rings (IVRs) are, in part, dependent on the interplay between material and ring geometry (outer diameter, OD, and cross-sectional diameter, CS). For matrix IVRs, the rate of drug diffusion from the polymer is driven in part, both by the drug loading as well as the diffusion distance of the IVR cross-section. We hypothesized that the introduction of geometric complexity to the cross-section of the IVR would enhance the available design space, opening the door to a wider range of drug-release properties. We developed a method outlined in Fig. 1A to systematically impart internal architectures to the IVRs using computationally-aided design (CAD) software. The geometric complexity emerges from the arraying of a unit cell into a torus template resulting in an architecture containing specified strut thickness. A unit cell describes the simplest repeating structure within a lattice and is contained within the volume, such as a cube, encompassing both solid struts and void pores. In CAD, the internal architecture can then be encased with a band to both seal the structure and provide mechanical support. The combination of the internal architecture and the band in CAD results in the final, geometrically complex IVR.

Figure 1. Design and fabrication approach for geometrically complex intravaginal rings.

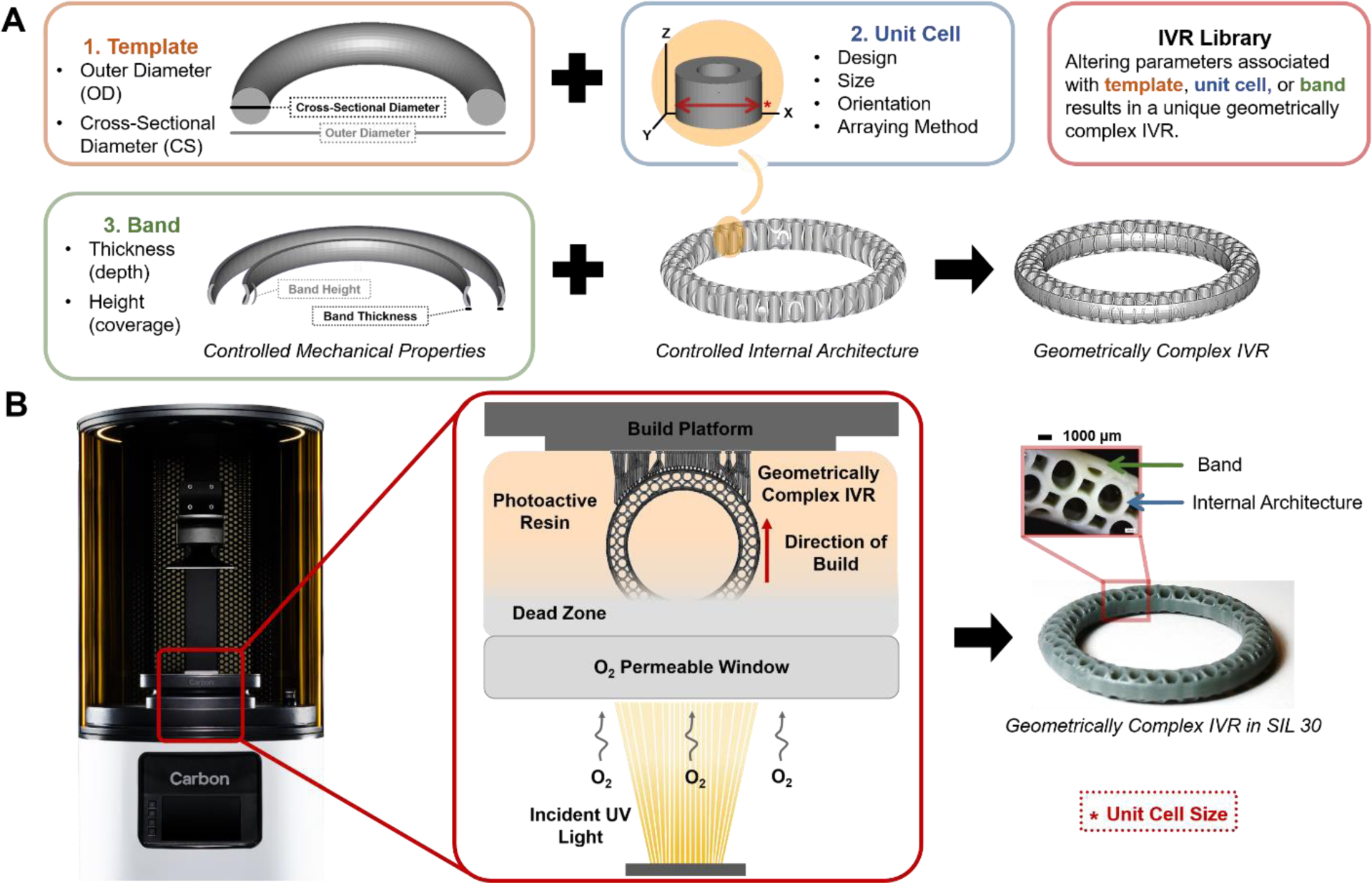
(A) Design method for geometrically complex IVRs in CAD software. Illustration of template, unit cell and band parameters. The unit cell is arrayed into the template and encased in the band material resulting in the finalized IVR in CAD. (B) Fabrication method of IVRs with DLS with illustration of print orientation and formation of the “dead zone” from oxygen inhibition during part reconstruction. Finalized example ring in silicone-based resin (SIL 30) with stereo microscopy inset illustrating internal architecture.

Geometrically complex IVRs were fabricated with Digital Light Synthesis (DLS, Carbon), previously described as Continuous Liquid Interface Production (CLIP). DLS is a method of 3D printing that utilizes the interplay between light and oxygen to selectively solidify a photo-active resin. To meet the performance requirements of an IVR, rings were fabricated in a silicone-based resin, SIL 30, which is noted for its potential for life science applications, particularly wearable devices.⁴⁰ The resin contains a photoinitiator that generates free radicals upon illumination from the light source. In the absence of oxygen, these radicals interact with the (meth)acrylate functional groups in the SIL 30 resin to form a solid. In the presence of oxygen, the free radicals are inhibited from propagating, resulting in a region of uncured resin, called the ‘dead zone’.³⁶ The extent of the dead zone formation and subsequent solidification is a product of the light exposure and the inherent reactivity of the resin. Therefore, longer or shorter exposure durations, increased or decreased number of photons introduced to the resin, respectively, can alter the final cured dimensions. Fabrication parameters associated with this exposure are optimized for each resin, however a range of parameters often exists in which the DLS process can operate. For SIL 30, the final mechanical properties of the part are driven by a post-fabrication thermal cure, in which a secondary polymerization is initiated by heat to further solidify the part.⁴¹ An example of a geometrically complex IVR fabricated from DLS in SIL 30 is shown in Fig. 1B, highlighting both the ring and the internal architecture.

2.2. Developing IVR Design Library

The method developed to generate geometrically complex IVRs allows for multiple design iterations at each of the steps, resulting in rings that could range in performance. Therefore, an IVR library was developed to systematically investigate the effects of these design options on ring properties. The library features designs classified by experimental designation, shown in Table 1. The initial outer-diameter and cross-sectional diameters of the blank template rings were chosen to mimic those of the Estring and NuvaRing. These solid IVRs were denoted under experimental designation (1) and served as material benchmarks to commercially available rings. All internal architectures generated were evaluated in the absence and presence of a band, denoted as (2). For banded rings, a standard set of parameters was established as a height (H) of 4.0 mm and thickness (T) of 0.6 mm. To determine if the unit cell contributed significantly to the mechanical properties of the ring, several unit cell designs (nodal, cylinder, dode, and honeycomb) were investigated at a single unit cell size, 3.80 mm (3). The internal architecture was further probed as a function of unit cell size for the cylinder and honeycomb rings (4). Sizes were selected as a ratio integer for the cross-sectional diameter, 7.60 mm, of 1:2 (3.80 mm), 1:3 (2.53 mm) and 1:4 (1.90 mm). To further explore the effect of the band, IVRs were designed as a function of increasing band thickness for the cylinder unit cell, (5). Band height was held constant at 4.0 mm and thickness of 0.0 (unbanded), 0.3, 0.6, 0.9, and 1.2 mm were explored. The honeycomb unit cell was used to explore the effect of band height (coverage) where band thickness was held constant at 0.6 mm and band height was varied from 3.0, 4.0, 5.0, and 6.0 mm, (6). All generated designs yielded a theoretical volume (mm³) and surface area (mm²). These values were used to calculate theoretical specific surface area (SSA, SA/V, mm⁻¹). The final experimental designation (7) is for rings generated to have the same SSA, 5.8 mm⁻¹, for all unit cell types. Table 1 represents the design parameters and theoretical values associated with each design in the IVR library. Strut thickness (μm) is the thickness of the features within the internal architecture of the design as designated in CAD.

Table 1. Design parameters and theoretical values associated with the IVR library.

Rings are classified by experimental designation and vary by unit cell design and size and band thickness and height (coverage). Theoretical values of volume and surface area were obtained from CAD and used to calculate specific surface area (SSA).

Template Ring Parameters		Unit Cell Parameters				Band Parameters		Theoretical Values			Experimental Designation†
OD (mm)	CS (mm)	Unit Cell Design	Unit Cell Image	Unit Cell Size (mm) *	Strut Thickness (μm)	Thickness (T) (mm)	Height (H) (mm)	Volume (mm3)	Surface Area (mm2)	SSA (mm−1)
54	4.0	---	---	---	---	---	---	1962.2	1970.4	1.0	1
54	7.6	---	---	---	---	---	---	6573.6	3474.1	0.5	1
54	7.6	Nodal		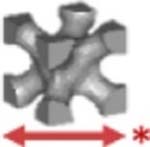3.80	1100	---	---	3037.6	8067.1	2.7	2,3
54	7.6			3.80	1100	0.6	4.0	3450.3	8694.3	2.5	2,3
54	7.6			1.52	1300	---	---	3281.6	18995.2	5.8	2,
54	7.6			1.52	1300	0.6	4.0	3932.6	22056.5	5.6	2,7
54	7.6	Cylinder		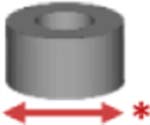3.80	350	---	---	1831.0	10724.9	5.9	2,3,4,5
54	7.6			3.80	350	0.3	4.0	2097.3	12062.2	5.8	2,3,4,5,7
54	7.6			3.80	350	0.6	4.0	2357.5	11593.1	4.9	2,5
54	7.6			3.80	350	0.9	4.0	2436.3	11192.6	4.6	5
54	7.6			380	350	1,2	4.0	2913.3	10920.4	3.7	5
54	7.6			2.53	250	---	---	1823.8	14790.5	8.1	2,4
54	7.6			2,53	250	0.6	4.0	2372.2	15352.4	6.5	2,4
54	7.6			1.90	160	---	---	1827.8	20447.6	11.2	2,4
54	7.6			1.90	160	0.6	4.0	2374.7	20353.9	8.6	2,4
54	7.6	Dode		3.80	760	---	---	1615.1	10900.1	67	2.3
54	7.6			380	760	0.6	4.0	2193.9	12125.8	5.5	2,3
54	7.6			3.63	740	---	---	823.1	6924.1	8.4	2,
54	7.6			3.63	740	0.6	4.0	1479.8	8578.6	5.8	2,7
54	7.6	Honeycomb		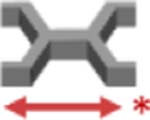3.80	350	---	---	1983.3	11070.1	5.6	2.3,4
54	7.6			3.80	350	0.6	4.0	2506.9	11971.3	48	2,3,4
54	7.6			3.12	310	---	---	1980.8	13250.4	6.7	2,
54	7.6			3.12	310	0.6	4.0	2403.4	13913.6	5.8	2,7
54	7.6			2.53	250	---	---	1981.5	15298.7	7.7	2,4,6
54	7.6			2.53	250	0.6	3.0	2360.7	15665.9	6.6	6
54	7.6			2.53	250	0.6	4.0	2503.3	15725.5	6.3	2,4,6
54	7.6			2.53	250	0.6	50	2664.2	15825.7	5.9	6
54	7.6			2.53	250	0.6	6.0	2873.9	16079.8	5.6	6
54	7.6			1.90	150	---	---	1981.4	21080.4	10.6	2,4
54	7.6			1.90	150	0.6	4.0	2503.4	20866.5	8.3	2,4

^†Experimental Designations: 1.) SIL 30 solid reference rings 2.) Presence/absence of band 3.) Unit cell design 4.) Unit cell size 5.) Thickness of band 6.) Height (coverage) of band 7.) Specific surface area equivalence

2.3. Characterization of Solid IVRs

A noted drawback of 3D printing is the poor mechanical properties of the final part, which are often brittle and weak.^26,42,43 For an application such as IVRs, where compressive strength is a key performance metric^44,45, it was necessary to compare DLS fabricated SIL 30 rings against commercially available counterparts, namely Estring (silicone) and NuvaRing (EVA). Therefore, solid IVRs from experimental designation (1) were fabricated with DLS in both urethane-methacrylated resin (UMA) prototyping resin and SIL 30 and evaluated for dimensional, material and mechanical properties. The dimensions of outer and cross-sectional diameter are shown in Fig. 2A. Percent deviation was calculated as deviation form theoretical values (shown in italics). All rings considered demonstrated minimal deviation from design for both outer and cross-sectional diameters. No significant dimensional deviation was observed in DLS rings between prototyping UMA resin and SIL 30 resin.

Figure 2. Characterization of solid rings as a function of fabrication method and material type.

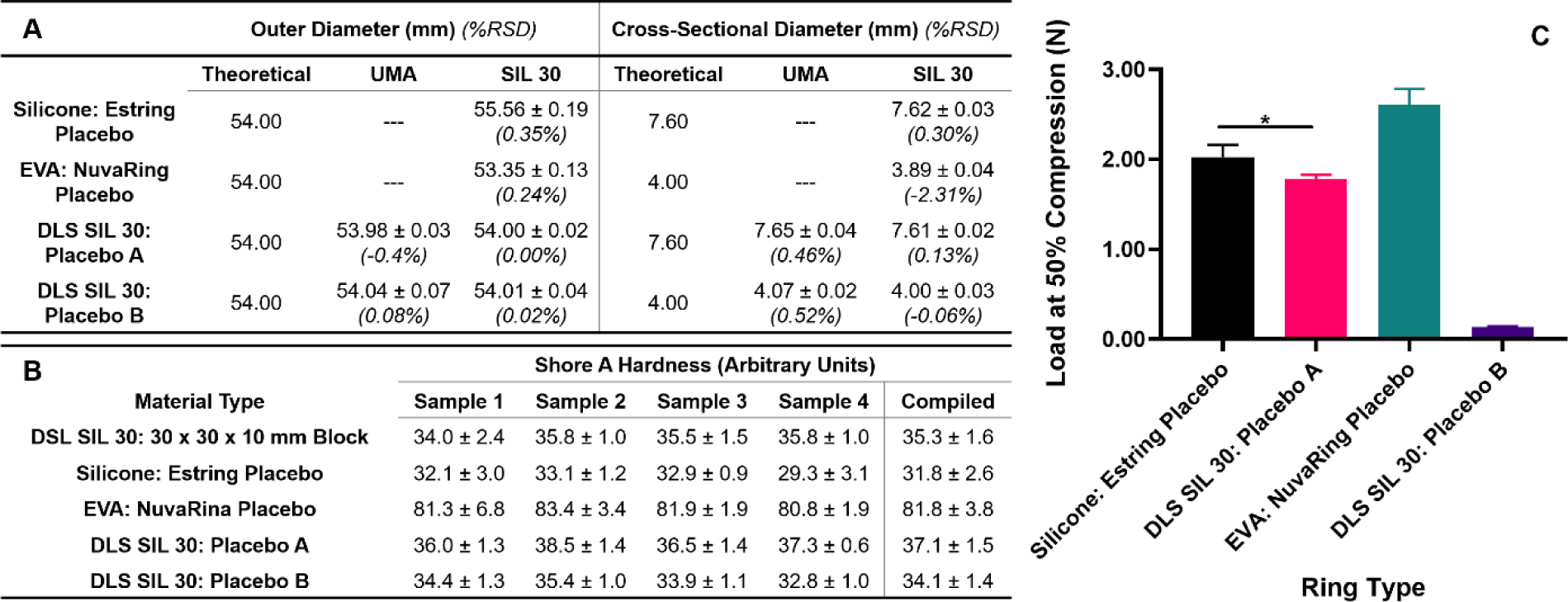
DLS SIL 30 rings were fabricated to mimic dimensions of placebo Estring (silicone) and NuvaRing (EVA) (A) Dimensional characterization of solid rings by outer and cross-sectional diameter. Average and standard deviations represent n=4 samples per ring type. Italicized percentages represent percent deviation from theoretical values. (B) Shore A hardness testing of materials by sample number (n=4 measurements) and compiled (n=4 samples). (C) Load at 50% compression by solid ring type. Data were assessed via one-way ANOVA for statistical significance. Silicone Estring Placebo and DLS SIL 30: Placebo A were assessed via a two-tailed unpaired t-test where p<0.05 was considered statistically significant (*).

The ring material of both commercial placebos and DLS rings was evaluated with a durometer on a Shore A hardness scale. The SIL 30 material was evaluated first as a 30 × 30 × 10 mm (l × w × h) block, independent of the torus shape of the ring. Durometer testing was conducted four times per sample for four samples and the values compiled in Fig. 2B. The compiled average value of the SIL 30 block was found to be 35.3 ± 1.6, compared to the published value of 35.⁴⁰ The silicone, EVA, and solid DLS SIL 30 rings were evaluated in a similar manner. The silicone placebo and the DLS SIL 30 Placebo A rings yielded a compiled Shore A hardness of 31.8 ± 2.6 and 37.1 ± 1.5, respectively. This suggests the preliminary compatibility of the SIL 30 resin for an IVR application. The EVA placebo yielded a substantially higher Shore A hardness value but because these rings were from a different material class, the values could not be directly compared.

The mechanical properties of the rings were evaluated by compression testing.⁴⁶ Rings were compressed to 50% of their initial outer diameter (Supporting Fig. 1) and the associated load reported is shown in Fig. 2C. The compressive loads of the silicone placebo and the DLS SIL 30 Placebo A were directly compared and while within the same range, were statistically different. The compression force of EVA placebo ring (2.61 ± 0.17 N) was substantially higher than the silicone Estring (2.03 ± 0.13 N), and the dimensionally equivalent DLS SIL 30 Placebo B (0.13 ± 0.01 N). As with the durometer testing, the EVA placebo could not be directly compared to the silicone rings however instead served as an upper limit describing the possible compression values of insertable IVRs. These values do suggest that the cross-sectional diameter plays a considerable role in compressive properties for the SIL 30 rings.

2.4. Effect of Unit Cell Design

Final part properties of lattice containing structures are determined, in part, by the lattice design and strut thickness.^47,48 To assess the ability of DLS to produce a variety of geometrically complex structures, IVRs from group (3) (Table 1) were generated using four unit cell designs at the same unit cell size (3.80 mm) both with and without a band. Rings were fabricated in prototyping resin (UMA) and SIL 30, shown in Fig. 3A, and evaluated for dimensional accuracy to the original CAD design (outer-diameter, cross-sectional diameter, and strut thickness), as described in Fig. 3B. For rings fabricated in UMA, minimal deviation from CAD was observed for all dimensions assessed. This was irrespective of band presence or unit cell design. For rings fabricated in SIL 30, the macro dimensions of outer-diameter and cross-sectional diameter universally deviated slightly negative compared to the initial CAD dimensions. Conversely, the strut thickness deviated positively, most dramatically with the cylinder unit cell. It should be noted that the fabrication parameters for SIL 30 (as described in section 2.1) have been optimized by Carbon and are not validated for structures below 1.5 mm in thickness⁴⁰. Nearly all of the strut thicknesses for the geometrically complex IVRs fall below this minimum distance. Therefore, deviation from CAD is to be expected. Further, this deviation is a function of the fabrication parameters. To illustrate this, the honeycomb unit cell rings were fabricated with modified parameters that resulted in a slightly lower UV exposure (thus limiting the extent of polymerization)³⁹. As a result, the strut thickness deviation is significantly less when compared to the other unit cell designs.

Figure 3. Fabrication and characterization of IVRs by unit cell design and band presence.

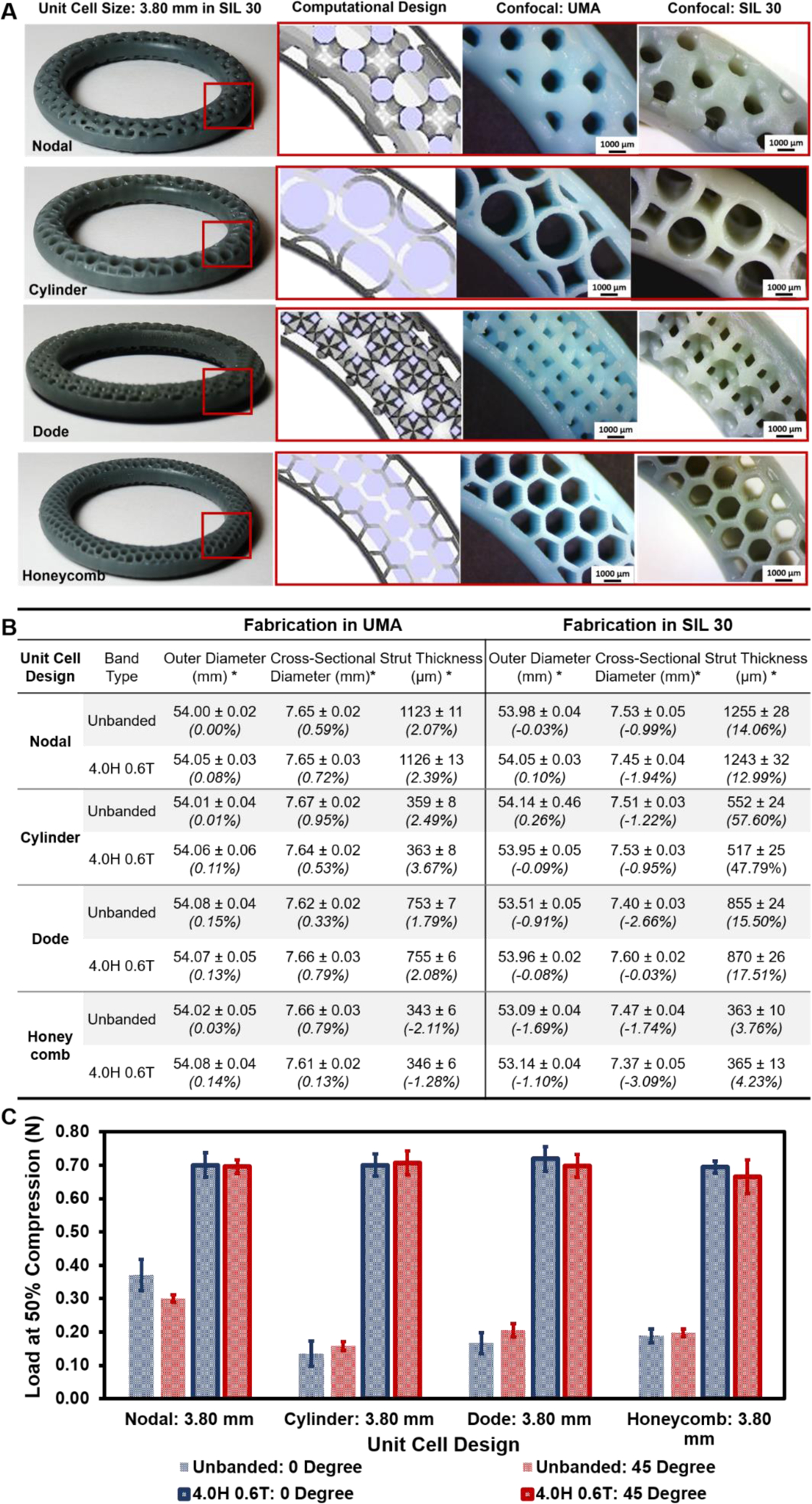
IVRs from group (3) were designed by varying unit cell design, holding unit cell size constant at 3.80 mm with band parameters of 4.0 mm height (H) and 0.6 mm thickness (T). (A) Whole banded DLS fabricated rings are shown in SIL 30 with inlays of internal architecture by CAD, in UMA, and in SIL 30. Fabricated rings were imaged with stereo microscopy. (B) Dimensional analysis of outer diameter, cross-sectional diameter and wall thickness. Outer and cross-sectional diameter measurements represent average and standard deviations of n=4 per ring type. Wall thickness values represent average and standard deviation of n=4 per sample and n=4 per ring type (total of 16). Percent deviation from theoretical values is shown italicized. (C) Load at 50% compression (N) as a function of unit cell type, band presence and force orientation. Values represent average and standard deviation of n=4 per ring type.

The IVRs generated as a function of unit cell design contain structures with varying surface area and volume, resulting in a distribution of solid material in lattice structures, which is well understood to impact the final mechanical properties. To investigate the effect of design on these properties, rings fabricated in SIL 30 were compressed at 50% of the outer diameter both with and without a band, as shown in Fig. 3C. Additionally, orientation of the lattice relative to the applied force can impact final properties^47,49, and therefore rings were evaluated a 0° and 45° relative to the linear array of the unit cell (Supporting Fig. 2). Unbanded (no band) rings were found to vary by both unit cell design and force orientation. The unbanded nodal ring, with comparatively higher theoretical volume and lower specific surface area relative to the other rings, exhibited the highest compressive force. Additionally, this value was found to be force orientation dependent with the 45° angle yielded a lower value. The three other unit cells were found to have comparable values and were not found to be force orientation dependent. Banded rings exhibited significantly higher compressive forces than their unbanded counterparts. Banded nodal, cylinder, dode and honeycomb rings demonstrated an average increase of compressive force of 88.7, 331.1, 417.4, and 268.1%, respectively compared to their unbanded analogues. No statistical different (p<0.05) between banded rings was observed as a function of unit cell design or force orientation.

2.5. Effect of Unit Cell Size

Surface area (SA) is a known factor in the diffusion of drug from a device^39,50,51 and modifications in lattice SA are often coupled with changes in structure volume that can result in downstream changes in other properties, such as mechanical.⁵⁰ The method developed to generate geometrically complex IVRs allows for changes in SA by altering the unit cell size. Both the cylinder and honeycomb unit cells were generated at three unit cell sizes, shown in Table 1 (4). Unit cell sizes were selected to be integer ratios of the cross-sectional diameter (7.60 mm) of 3.80 mm (1:2), 2.53 mm (1:3) and 1.90 mm (1:4). The resulting banded (4.0 mm height (H) and 0.6 mm thickness (T)) and unbanded rings yielded similar theoretical volumes but inversely proportional theoretical surface areas, enabling the isolated evaluation of SA on ring properties. Rings were fabricated with DLS in both UMA and SIL 30 (cylinders with standard parameters and honeycombs with modified lower exposure parameters), shown in Fig. 4A–B.

Figure 4. Fabrication and characterization of IVRs by unit cell size and band presence for cylinder and honeycomb unit cells.

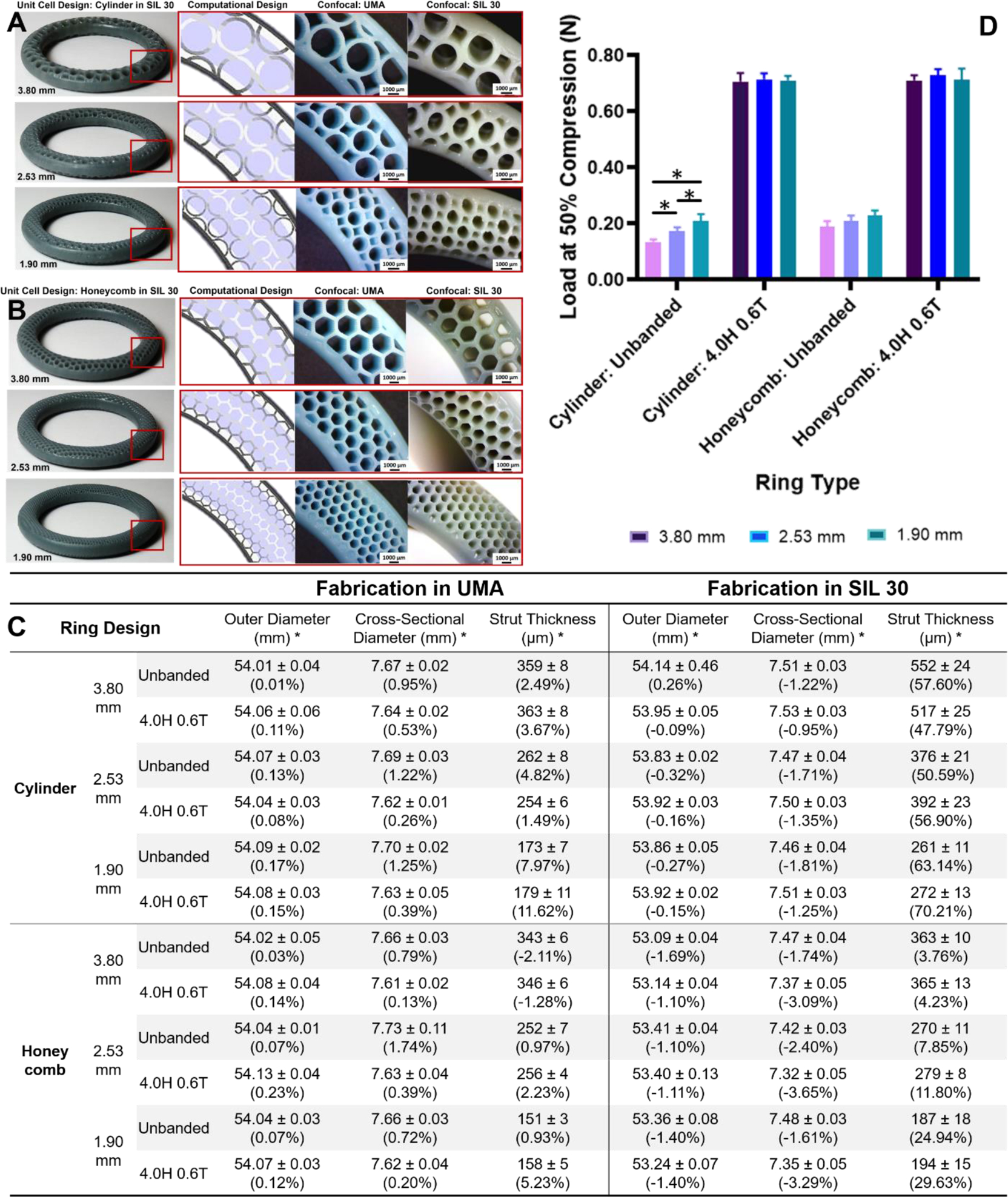
IVRs from group (4) were designed by varying unit cell size by integer ratio to the cross-sectional diameter of the template ring. Rings were designed in the absence and presence of a band (4.0 mm H and 0.6 mm T). Whole banded DLS fabricated rings are shown in SIL 30 with inlays of internal architecture by CAD, in UMA, and in SIL 30, by decreasing unit cell size for (A) cylinder and (B) honeycomb. Fabricated rings were imaged with stereo microscopy. (C) Dimensional analysis of outer diameter, cross-sectional diameter and wall thickness. Outer and cross-sectional diameter measurements represent average and standard deviations of n=4 per ring type. Wall thickness values represent average and standard deviation of n=4 per sample and n=4 per ring type (total of 16). Percent deviation from theoretical values is shown italicized. (D) Load at 50% compression (N) as a function of unit cell type, unit cell size and band presence. Values represent average and standard deviation of n=4 per ring type. Data were assessed via one-way ANOVA for statistical significance. The Unbanded Cylinder f(unit cell size) were further assessed via multiple two-tailed unpaired t-tests where p<0.05 was considered statistically significant (*).

The effect of increasing SA by decreasing unit cell design was investigated by assessing both the dimensional and mechanical properties of the rings. As described in Section 2.4, dimensional accuracy was assessed for both UMA and SIL 30 rings relative to the original CAD dimensions (Fig. 4C). A similar trend was observed in which rings fabricated in UMA were dimensionally accurate for all metrics, independent of unit cell design. Rings fabricated in SIL 30 with standard parameters (cylinder) yielded larger, and more deviating strut thicknesses than rings fabricated with modified parameters (honeycomb). Additionally, this deviation in strut thickness was observed to be dependent on the unit cell size, with smaller strut thicknesses yielding a higher deviation. As strut thickness decreases, it approaches the inherent limit of resolution of the DLS printer (75 × 75 μm)^36,37.

Mechanical properties of the rings fabricated as a function of unit cell size were evaluated. Rings were tested for compressive load and compared to unbanded rings, shown in Fig. 4D. For both cylinder and honeycomb rings, a slight increase in compressive load was observed to correlate with decreasing unit cell size. This was a statistically significant trend for the cylinder unit cell but not the honeycomb. The presence of the band both increased the compressive load and equalized the observed unit cell size dependency. The resulting values were not found to be statistically different with respect to unit cell size, unit cell design, or fabrication parameters.

2.6. Effect of Band Parameters

As demonstrated above, the band contributed significantly to the mechanical properties of the geometrically complex IVRs. The method developed to generate these IVRs contains avenues to modify the dimensions of the band, in terms of height and thickness, which could alter the final properties of the rings. Therefore, IVRs were generated and fabricated by varying band parameters as described by designation (5, thickness) and (6, height) in Table 1, and evaluated for dimensional and mechanical properties. To more fully investigate the library and the interchangeability of the interior architecture, two unit cell designs were selected. The honeycomb unit cell, arrayed at 2.53 mm (1:3) and fabricated using modified SIL 30 parameters, was utilized to investigate the effect of band height (H) where the thickness was maintained at 0.6 mm and the height varied between 3.0 – 6.0 mm, Fig. 5A. The cylinder unit cell, arrayed at 3.80 mm (1:2) and fabricated using standard SIL 30 parameters, was utilized to investigate the effect of band thickness (T) where height was maintained at 4.0 mm and thickness was varied from 0.0 to 1.2 mm.

Figure 5. Fabrication and characterization of geometrically complex IVRs as a function of band parameters.

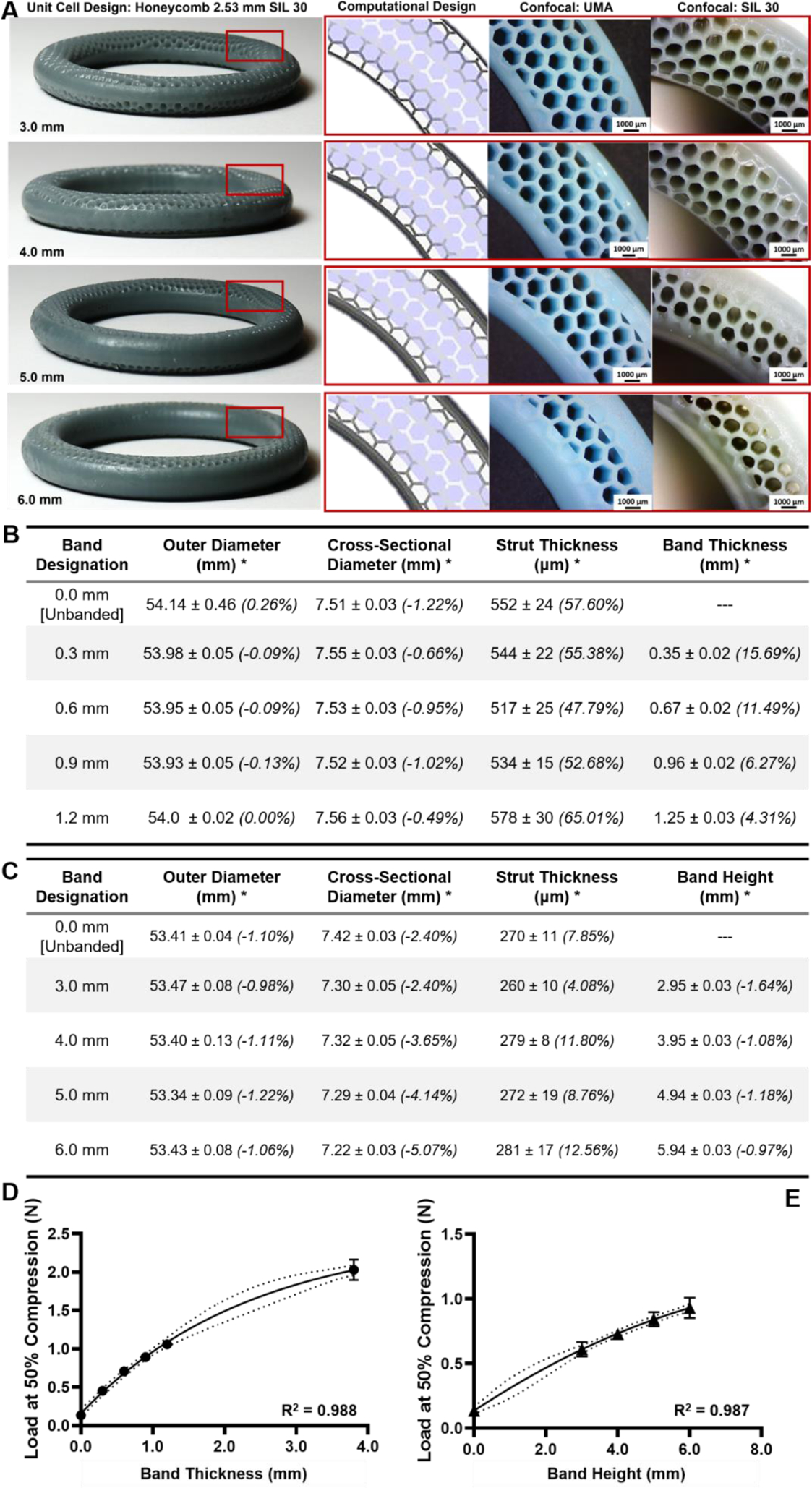
(A) Images of the honeycomb unit cell arrayed at 2.53 mm shown with increasing band height (coverage) from 3.0 to 6.0 mm. Inlays indicate the internal architecture and the increased band height (coverage) observed in CAD, in UMA, and in SIL 30. (B) Confocal dimensional analysis of rings generated as a function of band coverage in SIL 30. Values represent average and standard deviation of n=4 samples for outer and cross-sectional diameters. Values represent average and standard deviation of n=4 measurements of n=4 samples (total of 16) for wall thickness and band height (coverage). Percent deviation from CAD is shown in italics. (C) Dimensional analysis of rings generated as a function of band height (coverage) in SIL 30. Values represent average and standard deviation of n=4 samples for outer and cross-sectional diameters. Values represent average and standard deviation of n=4 measurements of n=4 samples (total of 16) for wall thickness and band height (coverage). Percent deviation from CAD is shown in italics. (D) Load at 50% compression for cylinder rings fabricated with increasing band thickness. Data fitted with log regression with dashed lines indicated 95% confidence intervals. (E) Load at 50% compression for cylinder rings fabricated with increasing band height (coverage). Data fitted with log regression with dashed lines indicated 95% confidence intervals. Values represent average and standard deviation of n=4 samples per ring type.

Rings generated to investigate the effects of band parameters were fabricated in SIL 30 and evaluated for dimensional accuracy (outer-diameter, cross-sectional, band accuracy) via stereo microscopy imaging (Fig. 5B–C). For honeycomb rings fabricated with lower exposure (Fig. 5B), all values measured slightly deviated from CAD, as previously observed. For cylinder rings fabricated with standard exposure (Fig. 5C), the strut thickness deviated significantly from CAD (as previously observed). The band thickness yielded an inverse relationship between thickness and accuracy, as the thickness approached the prescribed minimum threshold of 1.5 mm.

The effect of band parameters on compression properties was evaluated and shown in Fig. 5D–E. For band thickness (Fig. 5D), the minimum thickness is 0.0 mm (unbanded) and the maximum 3.80 mm (midpoint of a solid ring). For band height, the minimum height is 0.0 mm (unbanded) and the maximum tested was 6.0 mm. The solid ring was not included as a reference because complete band height (coverage) would result in encased internal architecture rather than solid cross-section. Both series were fitted to a log curve and yielded coefficients of variation above 0.98, suggesting an appropriate fit.

2.7. Effect of IVR Specific Surface Area for Equivalence and Allometric Scaling

An essential aspect of IVR development is the testing of the ring in various animal models to demonstrate efficacy.⁵² Therefore, to demonstrate the utility of the method developed to incorporate geometric complexity, IVRs were allometrically scaled to macaque dimensions (25 mm outer diameter (OD), 6.0 mm cross-sectional diameter). This was done by determining equivalent specific surface areas (SSAs, ratio of SA/V), as described in Table 1 (7). Theoretical SSA was calculated for honeycomb unit cells fabricated as a function of decreasing size, both banded (4.0H 0.6T) and unbanded (Fig. 6A). An exponential fit was determined and an equation derived for banded rings only. The target SSA value was 5.8 mm⁻¹ determined from the 3.80 mm cylinder banded (4.0H 0.6T) ring. Therefore, solving for the exponential equation resulted in a macaque honeycomb unit cell size of 2.85 mm. This approach was carried out for human-sized IVRs, also equated to a SSA of 5.8 mm⁻¹. The resulting unit cell values were 1.52 mm (Nodal), 3.63 mm (Dode) and 3.12 mm (Honeycomb).

Figure 6. Design, fabrication and characterization of geometrically complex IVRs by specific surface area equivalence for allometric scaling to macaque.

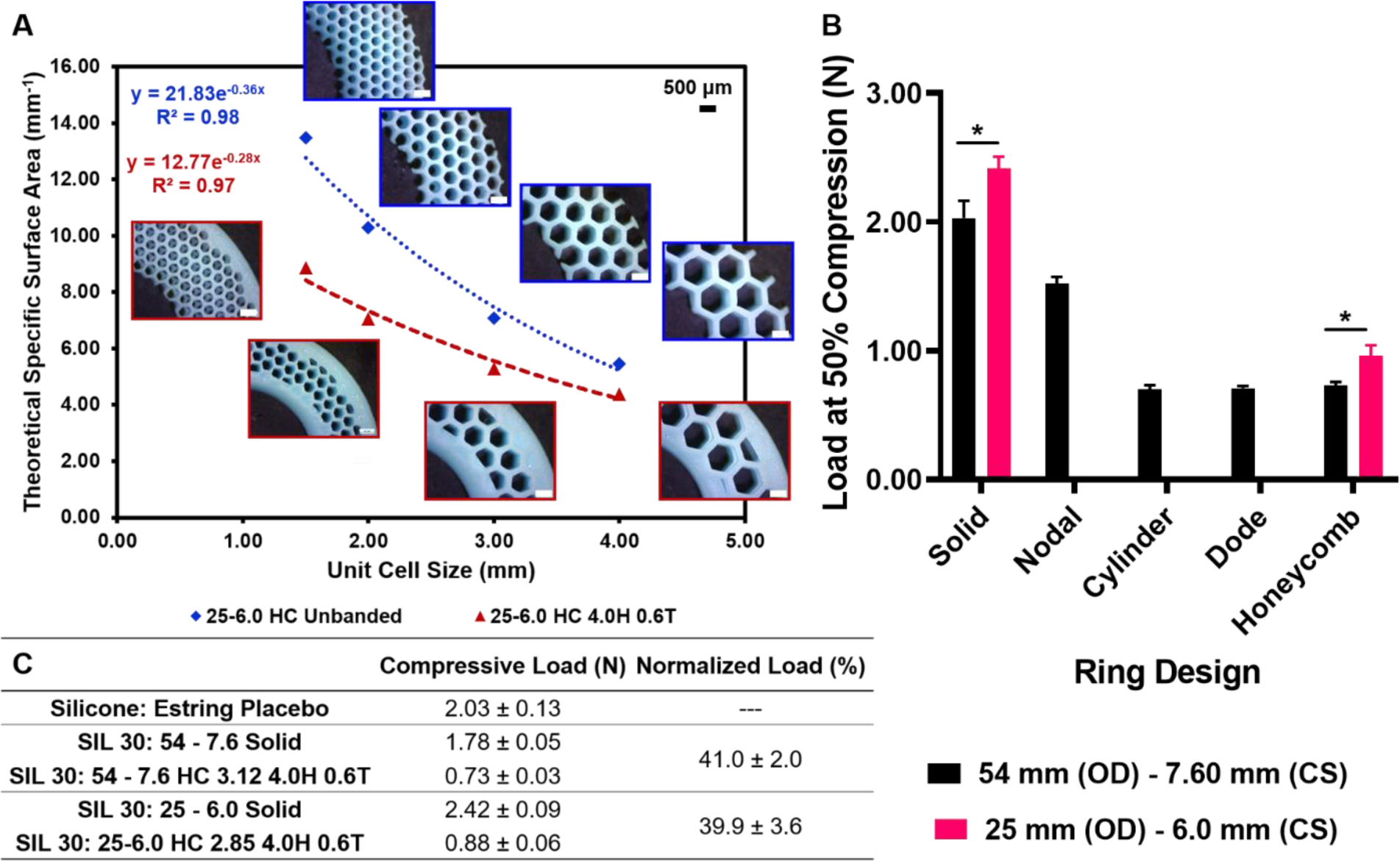
(A) Theoretical specific surface area (mm⁻¹) as a function of honeycomb (HC) unit cell size for banded and unbanded macaque-size rings (25 mm outer diameter and 6.0 mm cross sectional diameter). Inlays represent obtained from stereo microscopy of macaque rings fabricated in UMA. Exponential fit for banded rings was used to determine (B) Load at 50% compression for two template ring sizes: 54–7.6 (human) and 25–6.0 (macaque) rings fabricated in SIL 30. Specific surface area equivalence was 5.8 mm⁻¹ yielded unit cell sizes of 1.52 mm (Nodal), 3.80 mm (Cylinder), 3.63 mm (Dode) and 3.12 mm (Honeycomb) for human rings and 2.85 mm (Honeycomb) for macaque rings. Values represent average and standard deviation of n=4 samples per ring type. (C) Compressive load at 50% by ring type for n=4 samples per condition with normalized load relative to the solid template equivalent. Data were assessed via one-way ANOVA for statistical significance. Two groups, the solid human and macaque rings and the honeycomb human and macaque rings were further assessed via two-tailed unpaired t-tests where p<0.05 was considered statistically significant (*).

IVR rings generated for SSA equivalence and allometric scaling were fabricated in SIL 30 and evaluated for compression properties. Load at 50% compression is shown in Fig. 6B for both human and macaque-sized rings. In both ring sizes, the solid ring predictably generated the highest compressive force. Within the human-size rings, the dode, cylinder and honeycomb unit cells demonstrated comparable compressive forces. The nodal unit cell with SSA equivalent at 1.52 mm exhibited a higher compressive value than the other geometrically complex rings within the group. Macaque-sized IVRs were fabricated as solid and with honeycomb unit cell arrayed at 2.85 mm (Supporting Fig. 3). Macaque-sized IVRs yielded a similar compressive trend however could not be compared to human-sized IVRs for compression direction due to the differences in the original template dimensions. To enable comparison, compressive values obtained were normalized to the solid ring counterpart, shown in Fig. 6C. It can be observed that while the absolute values of the equivalent honeycomb (HC) unit cells were different. These data can be further assessed by normalizing the compressive performance of the honeycomb ring to the compressive performance of the solid ring of the same outer diameter. Expression of this normalized load as a percent found that both human and macaque IVRs exhibited the same trend. That is, at 5.8 mm⁻¹ SSA, both rings, regardless of size, demonstrated a compressive force approximately 40% that of the solid ring.

2.8. IVR Library by Volume Fraction

The mechanical properties of the IVR library were compiled based on volume fraction of the ring. Volume fraction is a measure that indicates geometric complexity. Solid rings, such as the commercially available placebos (Estring and NuvaRing) and their DLS SIL 30 counterparts, have a volume fraction of 1. Geometric complexity introduces void volumes, which result in volume fractions ranging between 0 and 1. The IVR library utilizes theoretical values obtained from CAD to describe volume. To calculate volume fraction experimentally, the density of the resin was determined from the solid SIL 30 Placebo A IVR. The ratio of this density to the post fabrication mass of the ring yielded the experimental volume. The ratio of the geometrically complex volume to the solid volume yielded volume fraction. Compressive values were plotted as a function of the volume value, shown in Fig. 7 by unit cell design. Reference values of commercially available placebo rings are shown at the upper extreme of volume fraction, with values of 1. Geometrically complex IVRs were observed to cluster between volume fractions of 0.25 and 0.75, indicating the significant presence of void volumes, imparted by the arrayed unit cells.

Figure 7. Compiled load at 50% compression of IVR library by volume fraction.

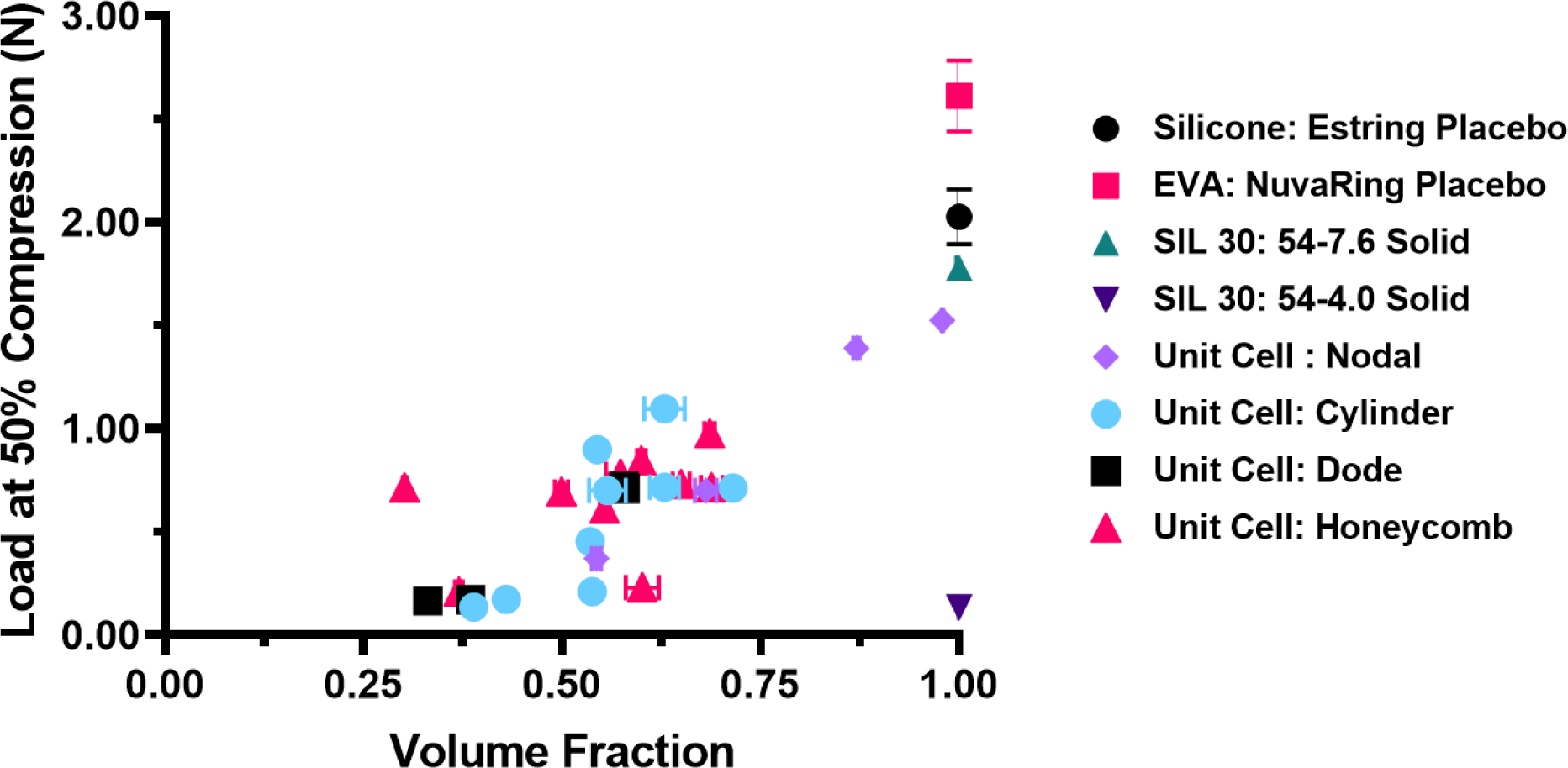
Volume fraction for commercially available rings of Estring and NuvaRing placebos is shown as 1. Volume fraction of geometrically complex SIL 30 rings by unit cell type were relative to SIL 30: 54–7.6 solid ring. X-axis error was calculated as compounded error from density and mass measurements. Y-axis error represents standard deviation of n=4 samples per ring type.

3. Discussion

IVRs have demonstrated enormous potential as a drug delivery device however their true potential may not be fully realized due to the limitations of device fabrication, namely the inability to utilize design to intentionally drive performance properties. We have shown a systematic approach to imparting geometric complexity within an IVR through the incorporation of distinct unit cells using CAD software. Our design approach utilized two main components: an internal architecture, governed by the unit cell and a surrounding band. We systematically investigated the parameters associated with these components through the development of an IVR library and the fabrication of these designs with DLS, a 3D-printing platform compatible with scalability that yields smooth, elastic parts. The dimensional and mechanical characterization of these rings enabled a holistic understanding to the effects of each of these design parameters on the final properties of the rings.

We first evaluated the resin for preliminary compatibility to the IVR design by comparing dimensional, material, and mechanical properties to those of known, commercially available rings. The DLS rings were fabricated in both UMA (prototyping) and SIL 30 (application) resins. The SIL 30 resin demonstrated compatible Shore A hardness to that of the silicone Estring placebo. Mechanical testing demonstrated that at 50% compression, the Estring placebo required slightly, but statistically significant, more force than the DLS counterpart. The compressive value of the EVA NuvaRing placebo was significantly higher than the compressive forces of both the placebo Estring and DLS rings. Given that the compressive properties of the commercial placebo rings are dictated by the ring size and material used, these values were viewed as reference points but not ultimate benchmarks. The injection molding process does not allow for tuned mechanical properties, therefore, the properties observed were not explicitly targeted but rather the result of the fabrication method. Comparing the two DLS solid rings (4 mm versus 7.6 mm cross-sectional diameter, CS) indicates the substantial contribution of the cross-sectional diameter to the final compressive properties of the ring. Collectively, these data indicate that commercially relevant properties were achieved with the DLS SIL 30 54–7.6 ring in terms of dimensional, material, and compressive properties. The IVR library was largely centered on the outer and cross-sectional diameters of the Estring mimic as a result.

The purpose of the IVR library was three fold. First to explore the available internal architectures afforded by the unit cell arraying approach. Second, to evaluate the effect of interchanging unit cells on dimensional and mechanical properties. Finally, third, to determine if the mechanical properties could be influenced independently by the band, irrespective of the internal architecture. This is a critical aspect toward developing a platform approach of this next generation IVR technology for drug delivery and therefore, the design parameters were independently and collectively evaluated.

The effect of interchanging unit cells on dimensional and mechanical properties was determined through the characterization of IVRs fabricated as a function of unit cell design and size. The fabrication in UMA and subsequent dimensional analysis indicated the capacity of the DLS printer to fabricate intricate internal architectures slightly above the theoretical resolution of 75 × 75 μm (as determined by the projected pixel size from the digital light processing (DLP) unit). Rings fabricated in SIL 30, which were observed to have macro dimensional accuracy for the outer and cross-sectional diameters, yielded substantial positive deviation from CAD when fabricated using standard exposure parameters, suggesting over-curing of the internal structure. These parameters were optimized for SIL 30 for structures with thicknesses greater than 1.5 mm. Because DLS is a dynamic process, a range of exposure values can yield dead zone formation and solidification. To demonstrate this, all honeycomb unit cells were fabricated using slightly lower exposure parameters, effectively lowering the total number of incident photons and reducing the extent of curing. As a result, these rings yielded strut thicknesses that only slightly deviated from CAD, suggesting the capacity of DLS to achieve dimensional accuracy with fabrication parameters dependent on geometry. For all rings from experimental designations (2), (3), and (4) fabricated in either UMA or SIL 30, the macro-dimensional properties were nearly identical to the input CAD values.

The characterization of compressive properties as a function of unit cell design and size demonstrated the interchangeability of the internal architecture. The greatest determining factor for compressive load was found to be attributed to the presence of a band. Rings fabricated with the same band parameters (thickness and height) yielded similar compressive results, irrespective of the unit cell design or size within the internal architecture. Unbanded rings demonstrated slight trends as a function of either unit cell design or size however, these trends were no longer apparent upon incorporation of a band. Collectively, these data demonstrate that mechanical properties of the rings are dominated by the band parameters, and are independent of the unit cell.

The effect of band parameters on the dimensional and mechanical properties of geometrically complex IVRs was evaluated within the IVR library. Band parameters investigated were band coverage and band height (coverage), associated with experimental designations (5) and (6), respectively. An increasing, non-linear dependence of compressive load on band parameters was observed, as the rings became more solid-like. This suggests there exists an optimized middle ground between dominant band parameters and maximized volume of internal architecture.

Drug delivery using a medical device is highly dependent on drug-device interaction. Understanding the design parameters that control the diffusion distance within geometrically complex rings was a key aspect of this development process. It was therefore necessary to further demonstrate the interchangeability of the unit cell approach as well as the utility of the IVR library as a drug delivery platform. In the design process, theoretical values associated with design such as part volume and surface area can be determined. As such, theoretical specific surface area (SSA), a metric describing volume distribution of the part, can be calculated. Parts with large SSA values have a higher degree of exposed surface area than parts with low SSA values. It has been demonstrated that SSA can play a role in drug-release properties.^51,53 For reference, the SSA of the placebo rings was calculated to be 1 for both the Estring and NuvaRing. The unit cells utilized within the library have different volume distributions and as a result, rings generated with the same unit cell sizes have varying theoretical SSA values. Additionally, the IVR library was constructed based on the template of a human-sized IVR. To generate IVRs compatible with testing necessary to validate a medical device in relevant animal models, namely efficacy in non-human primates, macaque-sized IVRs were designed to be equivalent by SSA to a human-sized IVR (3.80 mm cylinder banded). This method is outlined in Fig. 6A using theoretical SSA values to generate an equation to solve for unit cell size. This method was also applied to human-sized IVRs as a function of unit cell design. The compressive properties indicate that for the human-sized IVRs, the dode, cylinder and honeycomb unit cells generated comparable values. Both macaque solid IVR and the macaque SSA honeycomb equivalent generated higher compressive values compared to their human-sized counterparts. This increase further bolsters the notion that template and band dimensions play a critical role in compressive properties. When the loads were normalized, both the human and macaque-sized rings yielded similar values, demonstrating the ability to allometrically scale the IVR library both by release properties (SSA) and mechanical properties (compressive force).

The compressive data of the IVR library expressed by volume fraction, shown in Fig. 7, enables further insight into the relationship of geometric complexity and mechanical properties. IVRs with volume fractions of 1 (solid) yielded the highest compressive values and unbanded geometrically complex IVRs, yielded the lowest values. The IVR library is shown to largely cluster between volume fractions 0.25 and 0.75 with the nodal unit cell showing the highest volume fractions (Supporting Table 1) of the geometrically complex IVRs. Collectively with compressive properties, these data indicate that while the band is the predominant and overarching factor determining compressive force, this relationship only truly holds within a certain volume fraction. As shown with the effect of band thickness, as the ring gets progressively more solid, it will behave more similarly to the solid ring. For example, the nodal unit cell 1.52 mm, (SSA equivalent to cylinder 3.80 mm) resulted in a dense structure and a volume fraction of 0.97. Therefore, it is expected to behave more similarly to a solid SIL 30 IVR, as was shown by the compressive force data shown in Fig. 7.

4. Outlook

Herein we demonstrate a novel approach for design and fabrication of geometrically complex IVRs. We developed a library of IVR designs that enabled the systematic investigation of aspects of the process that influence mechanical properties. We determined that the compressive properties of the ring were largely independent of the internal architecture. Our goal was to lay the foundation for a platform approach to IVR design and fabrication with 3D printing. This represents the first step toward the development of a platform IVR technology for drug delivery. While more extensive compressive testing would be required for future devices, there is not, to the authors knowledge, an established protocol to systematically investigate the mechanical properties of IVRs. Future studies will include additional testing such as cyclic compression and recovery rate, particularly in the presence of vaginal fluid, to add to the understanding of the IVR library. To our knowledge this is the first report on 3D-printed intravaginal rings using digital light synthesis (DLS) with a comprehensive design library to establish a foundation for a platform technology as a customized drug delivery device.

5. Methods

5.1. Design of Geometrically Complex IVRs

Geometrically complex intravaginal rings (IVRs) were generated with computationally-aided design (CAD) software in a multi-step process. A template ring of given outer and cross-sectional diameter was generated in SolidWorks (Dassault Systèmes). The template was converted into standard tessellation language (.STL, binary). Rings generated to mimic commercially available placebo dimensions were denoted as ‘solid’ and not modified beyond this point. To impart geometric complexity, the .STL template was imported into Magics (Materialise), also a CAD software primarily used in correction of tessellation error. A unit cell of given type and size was linearly arrayed into the template using the Scaffolds feature. The Nodal and Dode unit cells were used unmodified from the pre-existing scaffolds unit cell collection. Additional unit cells of Cylinder and Honeycomb were generated in OpenSCAD and Solidworks, respectively, and then imported into the unit cell collection as a .STL. The Cylinder unit cell was generated to have a 5:4 outer to inner diameter ratio and rendered with resolution ($fn) of 20 to reduce complexity, enabling compatibility with Magics arraying. Arrayed rings in Magics were denoted as ‘unbanded’ and refer to the internal architecture of the IVR; theoretical values of volume and surface area were noted.

Banded rings were generated by modifying unbanded rings. A band of given thickness and height (coverage) was generated in SolidWorks and exported as a .STL. Both the internal architecture and band were imported into MeshMixer (AutoDesk). Files were first centered on the absolute origin, combined, and exported as a unified .STL design. Banded rings were then imported into the Magics and a ‘tessellation fixing’ procedure was conducted following the ‘Fix Wizard’ function within the software. Files were deemed ‘fixed’ once the shell number was reduced to 1. Banded rings following this fix were noted for theoretical volume and surface area and exported as a .STL for fabrication.

5.2. Fabrication of IVRs with Digital Light Synthesis (DLS)

Printer.

Parts were fabricated on an M1 DLS printer (Carbon, Inc.). Banded rings were fabricated vertically at 16 rings per print (Supporting Fig. 4). Unbanded rings were fabricated horizontally at 2 rings per print. Vertically fabricated rings were supported by manually adding supports above the build platform with the support feature in the Carbon user interface. Approximately 40 supports were used per ring extending from the center to the approximate midpoint of the outer diameter.

Prototyped Rings.

IVRs were prototyped in urethane-methacrylated (UMA) resin generously supplied by Carbon, Inc. Resin contained 3.0 g UMA cyan and 99.0 g white and was mixed in a Thinky ARE310 mixer for 5 min at 2000 rpm immediately prior to ring fabrication. Standard UMA fabrication parameters were used, characterized as viscosity (2400 cP), dosage to cure (7), alpha (0.003899 μm⁻¹), exposure compensation (2.5) and base exposure multiplier (3). Parts were sliced using a standard thickness, 100 μm.

Rings in SIL 30.

Rings were fabricated in SIL 30 generously supplied by Carbon, Inc. (Redwood, CA.). SIL 30 is a methacrylated silicone-poly(urethane) resin. The two-part resin was mixed immediately prior to use on the M1 printer using the provided static mixer. Approximately 100 mL of SIL 30 resin was dispensed at a time to ensure the appropriate part ratio was obtained during the dispensing of the SIL 30 resin. For vertical fabrication, 130 mL of resin was dispensed immediately prior to the start of the print. It should be noted the resin was nearly entirely consumed during the fabrication of 16 vertical rings. Resin was not used beyond the 12 hr. pot life, as recommended by Carbon.

Solid and banded geometrically complex rings were fabricated vertically using standard SIL 30 parameters. Fabrication was conducted with 16 rings loaded on to the build platform resulting in a total fabrication time of 3 hr and 1 min or 18 min per ring. Banded rings containing the honeycomb unit cell were fabricated using modified SIL 30 parameters to obtain geometric complexity. Parameter modification included lowering the dose to cure from 19 to 18 and lowering the exposure compensation factor from 2.5 to 2.35. It should be noted that the modified parameters were optimized and not chosen at random. There is a lower limit to the input dosage (number of photons per unit area per time) to the resin, below which the part does not cure, in part from the lack on energy to initiate the polymerization and the lack of propagating radicals to effectively consume the O₂ at the interface of the window. Additionally, the part integrity needs to be maintained throughout the fabrication process. SIL 30 is noted as having a green Young’s modulus of 7 MPa and a green yield strength of 0.6 MPa. These values are fairly low compared to the known suction forces that are applied on the part as the build platform moves upward.⁵⁴ Therefore, there was only a small window for parameter modification to fabricate the honeycomb banded rings with a resulting fabrication time of 2 hr and 48 min or 16.8 min per ring. Unbanded rings containing the unit cells nodal, cylinder or dode were fabricated using standard SIL 30 parameters with 2 rings loaded on the build platform. The resulting fabrication time was 26 min or 13 min per ring. Unbanded honeycomb rings were fabricated with the modified SIL 30 parameters with a total fabrication time of 24.5 min or 12.25 min per ring.

Durometer Parts.

A solid block measuring 30 × 30 × 10 mm³ (length × width × height) was generated in SolidWorks and exported as a .STL. Parts were fabricated in SIL 30 using standard parameters (n=4).

5.3. Post-Fabrication Treatment

UMA Parts.

Parts fabricated in UMA were removed from the build platform upon completion of fabrication. Parts were washed in a sealed container with 200 mL of isopropyl alcohol (IPA) on a shaker table for two min, removed, and allowed to partially air-dry. Parts were then fully dried using compressed air until all visual residual resin was removed. Parts were treated to a UV post-cure with a FireJet Fj800 Controller (Phaseon Technology) in a chamber purged with N₂ for 30 s prior to a 2 min exposure of 20 mW/cm² 385 nm light per side.

SIL 30 Parts.

Parts fabricated in SIL 30 were treated post-fabrication to a modified version of the recommended procedure provided by Carbon. Briefly, parts were removed from the build platform and patted down with a Kimwipe to remove excess residual resin. Parts were subsequently placed in a sealed container with 200 mL IPA on a shaker table for 30 s. Parts were removed from IPA. Supports from vertically fabricated rings were removed and the band smoothed with a razor. Parts were wrapped in a WipeAll towel and then in aluminum foil. Parts were transferred to a manual spinner and spun for 30 s clockwise followed by 30 s counter clockwise. The washing and spinning step were repeated a second time. Parts were then placed on a WipeAll towel between two Teflon plates for approximately 45 min to compress any residual resin out from internal architecture. Dried parts were treated to a UV post-cure with a FireJet Fj800 Controller (Phaseon Technology) in a chamber purged with N₂ for 30 s prior to a 2 min exposure of 20 mW/cm² 385 nm light per side. Finally, parts were placed in a programmable oven to initiate a secondary thermal post cure. The program followed recommended curing, beginning at 31°C and ramping up to 120°C over 15 min, holding at 120°C for 8 hr and finishing by ramping down to 31°C in 15 min. Parts were removed from the oven for immediate further testing or stored at −4°C.

5.5. IVR Measurements

Macro-dimensional measurements of the outer and cross-section diameters for UMA and SIL 30 rings were conducted with calipers. Rings were laid on a hard, flat surface for testing. Reported values represent average and standard deviations of n=4 samples per ring type.

5.6. Durometer

A Sauter HBA 100–1 graduated dial durometer (Shore A scale) was utilized for hardness testing. Material (10 × 10 × 30 mm³ blocks or solid rings) were placed on a hard, flat surface prior to testing. The durometer was placed on the ring until resistance was met. Each sample was measured four times to account for variability in the testing method. Rings were measured in the 12, 3, 6, and 9 o’clock positions. Each material type (silicone, EVA, and SIL 30) contained four samples. Values obtained were averaged within the sample and compiled and averaged within the material type. Values represented were average and standard deviation of Shore A hardness (arbitrary units). The SIL 30 resin was noted as having a Shore A hardness of 35.

5.7. Stereo microscopy Imaging

DLS IVRs fabricated were imaged with a Zeiss Stemi 508 Stereo Microscope Labscope. Images were captured and dimensional analysis conducted with Zeiss Labscope software. Strut thickness and band thickness measurements were conducted using ImageJ. Measurements were n=4 for each ring for n=4 samples resulting in 16 total measurements per design. Average and standard deviations were reported. Percent deviation of the thickness measurements was calculated relative to the input specifications of the CAD file.

5.8. Mechanical Testing

The force at 50% radial compression was measured using an Instron 5566 Universal test system and a 100N load cell. Tensile grips fitted with spacers to surround and support the upper and lower portion of an IVR without applying pressure to the ring seated in the fixtures were used for the testing (Supporting Fig. 1). Spacers were custom designed in SolidWorks and fabricated with DLS in UMA (black). Once seated in the fixture, compression was applied to the IVR in the Z direction at 1 mm/s until the IVR was compressed to a distance of 50% of its outer diameter. The load at 50% compression in Newtons (N) was reported. Radial compressions were reported as an average and standard deviation of n=4 samples.

Rings fabricated as a function of unit cell design and band presence were tested for radial compression in two orientations: 0° and 45°. Orientation was determined by the direction of force relative to the linear array of the unit cell within the rings, as shown in Supporting Fig. 2. Radial compressions by orientation were reported as an average and standard deviation of n=4 samples.

5.9. Statistical Analysis

Statistical analysis was done using Prism 8 (GraphPad). In general, data were expressed as mean ± standard deviation with the number of samples (n) included in each analysis specified specifically. Differences in data was assessed first with one-way ANOVA to determine if significance existed within the set. If so, data was assessed via unpaired two-way t test. The values p < 0.05 were considered statistically significant.