Dynamics of respiratory droplets carrying SARS-CoV-2 virus in closed atmosphere

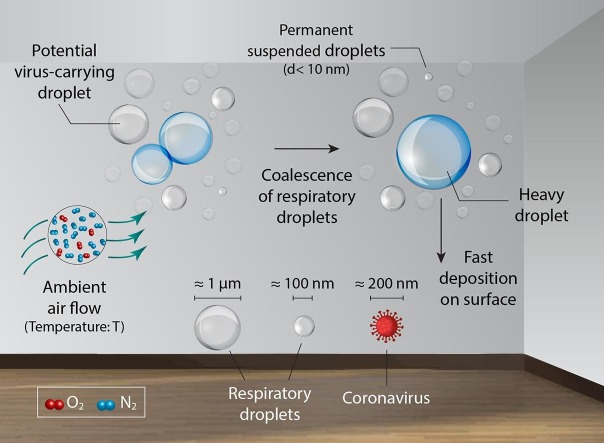
Graphical abstract

Abstract

From the epidemiological point of view, the lifetime of cough and sneeze droplets in the ambient atmosphere plays a significant role in the transmission rate of Coronavirus. The lifetime of indoor respiratory droplets, per se, is a function of droplet size, ambient temperature, and humidity. In the attempt to explore the effective factors of droplet lifetime, sufficient knowledge of atomic-scale interactions and dynamics of the droplet with themselves, as well as the airflow molecules in the room space, is necessary. In this study, the vertical traveling of a wide range (100 nm–10 μm) of representative carrier droplets is studied in three ambient temperatures of 258, 298, and 318 K using all-atom molecular dynamics simulation. Our obtained results confirm that by increasing the room temperature, the suspending time of aerosol (suspended droplets carrying virus particles) increases due to the higher dynamics of air and evaporated water molecules in room space. In fact, by increasing the indoor temperature, the collision rate of aerosol and ambient atmosphere molecules increases significantly. Our result shows this higher rate of collision could have a dual effect on the lifetime of aerosol considering the fact of faster deposition of larger (heavier) droplet due to the gravitational force. On one hand, in higher temperatures, the higher collision can split the droplets to smaller ones with a semi-permanent suspension period. On the other hand, the higher dynamics of ambient molecules can lead to meet and coalesce of smaller cough/sneeze droplets making larger (heavier) droplets with faster sediment times. So, the role of indoor humidity to fuel the probability of coalescence phenomenon and lifetime of droplets becomes more determinant in the warmer spaces.

Introduction

The coronavirus discovered firstly in 1966 and isolated from the sick with common cold [1]. In 2019, the spread of new coronavirus (SARS-CoV-2) increased the attention worldwide. On 11 March 2020, the World Health Organization (WHO) notified this virus as a pandemic based on its high spreading rate. SARS-CoV-2 is now known as a new microorganism from the subfamily orthocoronavirinae that causes olfaction failure, respiratory and gastrointestinal infection in hosts. As yet, no effective vaccine has been discovered, thus precautionary measures such as social distancing and home isolation is the best way to minimize the spread of Coronavirus. During the last decade, some epidemiological model for the propagation of viruses has been developed for a verity of virus classes from computer viruses [2], [3] to Coronavirus (2019-nCov) [4] using different mathematical approaches.

In case of SARS-CoV-2 virus, specialists believe that this virus spreads mainly from person to person by (i): airborne transmission, (ii): droplets or aerosols transmission, and (iii): surface transmission. Among all of these mechanisms, airborne and droplets transmission is more perilous due to the deprivation of the applicable way to disinfection of the air molecules. When infected people sneeze, cough or, even talk, the droplets or small particles carry the coronavirus into the air and in these modes, the ambient becomes infected by SARS-CoV-2. In 1995 Wells [5] showed that the droplet nuclei (dried-out residual of droplets containing infectious pathogens) are the conveyance for airborne respiratory disease transmission. Therefore, people who are in such an ambient could breathe the droplets into their lungs. This is the major issue faced by governments and the public around the world. Therefore, one of the main concerns related to COVID-19 is the longevity of droplets in the environment. On the other hand, the longevity of droplets in coastal cities or in cold regions could be different from the room condition. Therefore, analyzing the behavior of droplets with different sizes in such conditions could release a new perspective in order to confront COVID-19.

Much literature accomplished to study the horizontal spread of droplets. Zhu et al [6] by employing the particle image velocimetry (PIV) method showed that during each coughing, the droplet with a size of 30 μm affect more than 2 m away from the source. Xie et al [7] by using numerical simulation indicated that expelled large droplets (>60 μm) can travel more than 6 m. Parienta et al [8] employed the mathematical modeling and released that the droplets with a diameter of 16 μm and a coughing velocity of 11.7 m/s, could pass a distance of 7 m. In the mathematical modeling of Bourouiba et al [9], it has been calculated that droplets with 30 μm diameter, during coughing within a turbulent gas could travel a horizontal distance in range of 2.5 m. Wei and Li [10] with using mathematical modeling released that with mouth opening of 2 cm, large droplets in range of 96 μm could pass a distance up to 1.4 m. Lee et all [11] used optical particle spectrometer to calculate the cough particle concentration of 10 patients. They indicated that transition could spread more than 3 m from the person. In the mathematical study of Chen [12], a one-dimensional droplet evaporation model was invoked to estimate the droplet lifetime from evaporation in air. He showed that the ambient temperature and ambient relative humidity have the potential effects on virus-carrying drops. Asadi et al. [13]; Jones and Brosseau [14] indicated that the competing influences of gravity, evaporation, and inertia specify the commendation of the expelled droplets.

Although previous studies have released efficacious data in the context of coronavirus and droplets, we believe that studying the longevity and vertical traveling of droplets could be served in precautionary measures which have not been studied clearly hitherto. In this study, molecular dynamics (MD) simulation has been employed to investigate the behavior of water droplets in a room environment. The main finding of this study is to predict the vertical traveling and lifetime of aerosol at different thermodynamics conditions. Different sizes of water droplets were considered to assess the effect of air temperature on the behavior of hovering droplets. We anticipate our study could lead to a better understanding of expelled droplets as a significant factor in the transmission of SARS-CoV-2.

Problem geometry

In this study, an infinite silicon surface is considered as the floor and some water droplets with wide-range sizes are placed on the above of the surface. The droplets are located in the different coordinates of the surface. Fig. 1 shows the schematic configuration of geometry simulated in this study. In Fig. 1, the silicon surface is indicated and the droplets which solved in the bulk air box, are put on tho above the silicon surface. The dimension of the simulation box is 43.4 × 43.4 × 120 nm.

Fig. 1.

The simulation box of respiratory droplets, air and suspended water molecules, and floor surface.

Computational method

In this study, the large scale atomic/molecular massively parallel simulator (LAMMPS) [15] was employed to accomplish the atomistic studies. In order to visualize the atomistic output data, we employed OVITO [16].

In MD simulation the classical equations of motion were solved, which for a simple atomic simulation could be written as:

$$m_i{\ddot{r}}_i=f_i{f}_i=-\frac{\partial U}{\partial r_i}$$ (1)

where $m_i$, ${\ddot{r}}_i$ and are the mass acceleration of molecule i respectively. In order to determine the $U$, many literature has been reported the governing equation of intermolecular potential. Among all of the potential, Lennard-Jones 6–12 $(U^{\mathit{LJ}})$ is used extensively as follow:

$$U^{\mathit{LJ}}(r)=4\epsilon \lceil {\left(\frac{\sigma }{{\mathrm{r}}_{\mathit{ij}}}\right)}^{12}-{\left(\frac{\sigma }{{\mathrm{r}}_{\mathit{ij}}}\right)}^6\rceil$$ (2)

where $r_{\mathit{ij}}$ is the distance between two atoms of the system. $\sigma$ and $\epsilon$ are the molecular diameter and well depth of potential function, respectively which known as the Lennard-Jones parameters. The Verlet-velocity algorithm is carried out to integrate the equation of motion. To describe the intermolecular potential for all atoms in this study, such as water molecules, air molecules, and silicon atoms the Lennard–Jones (12–6) potential has been employed. Also, a Lennard–Jones potential with modified parameters of ${\epsilon }^{\text{'}}$ and ${\sigma }^{\text{'}}$ is implemented for interactions between various molecules. The parameters ${\epsilon }^{\text{'}}$ and ${\sigma }^{\text{'}}$ are obtained by Lorentz–Berthelot [17] combination rules. The wall (floor of the room) consists of different layers of silicon atoms. The silicon wall atoms are kept fixed and a Nose-Hoover thermostat scheme is used to keep the water and air in the desired temperature. Periodic boundary conditions are applied along with all directions. In this study, the SPCE model of water is employed. All the Lennard–Jones parameters and partial charge values of the SPCE model [18], air molecules, and silicon atoms are listed in Table 1 .

Table 1.

The parameters of Lennard–Jones and partial charges for all the molecules in the study.

Label	Site	$\sigma \left(\mathrm{\AA }\right)$	$\epsilon (kcal{\mathit{mol}}^{-1})$	Mass ($\mathit{gr}{\mathit{mol}}^{-1}$)	q$\left(e\right)$	reference
Wall	Si	3.8264	0.4023	28	0	[19]
Water	O	3.166	0.1553	15.9994	0.8476	[19]
	H	2.058	0	1.008	0.4238	[19]
Air	N	3.31	0.0715	14.0067	0.4238	[20]
	O	3.02	0.0973	15.9994	0.482	[20]

Results and discussion

In the initial configuration of our system, we consider 22 boxes of water molecules and also air molecules including $N_2$ and $O_2$ molecules with a density of $1.225\times {10}^{-3}gr/{\mathit{cm}}^3$. The air molecules consist of 4570 $N_2$ and 1290 $O_2$ molecules. At first, we performed $5$ ns in order to relax and equilibrate the air molecules at the desired temperature. In the next step, we allow 22 boxes of water molecules to reach the equilibrate state. In this part of the simulation, some small droplets stick together to form larger droplets (see Fig. 2 ). As we discussed later, the formation of the large droplets (coalescence phenomenon) in an indoor environment could lead to the faster sediment of droplets.

Fig. 2.

The coalescence of adjacent small droplets forming larger droplet. A) Two approaching droplets. B) The new merged droplet during the simulation time.

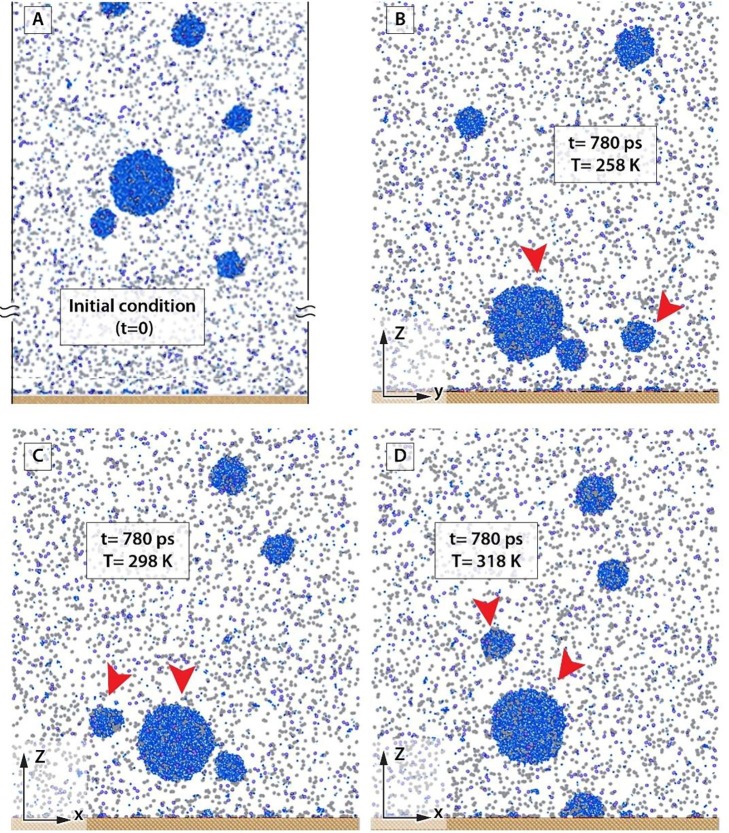
After the equilibration state, the gravitational force is applied to the representative virus-carrying droplets of various sizes. Fig. 3 shows the system in different conditions including droplets, air molecules, and evaporated water molecules (room humidity molecules). Fig. 3A shows a snapshot of the equilibration state considered as the initial condition ($t=0$) and Fig. 3B-D indicate the system topology after $780ps$, for $T=258$, $298$and $318\mathrm{K}$ respectively. In order to start the nonequilibrium simulation, we exerted the external force of 143E⁻⁶ kcal/mol to each water molecule. This force is equivalent to the weight of a drop with a diameter of 10 µm. For a better understanding of temperature effect on vertical traveling of droplets, the biggest droplet and, one of the small droplets are considered as the basis of our simulation. These two droplets are marked with red arrows. As shown in Fig. 3, at $t=0$ the big droplet is located at a higher height, while it reaches to ground sooner than the small one. This issue is more significant in higher values of temperature. For $T=258K$ two droplets reach the ground almost simultaneously while by increasing the air temperature to $298K$ and $318K$ the big droplet is more interesting to reach the ground. On the other hand, as Fig. 2 shows, at the low temperature of $T=258K$ both the droplets like to hit the surface sooner in comparison to higher temperatures of $298K$ and $318K$.

Fig. 3.

The configuration of simulated cases in different temperature.

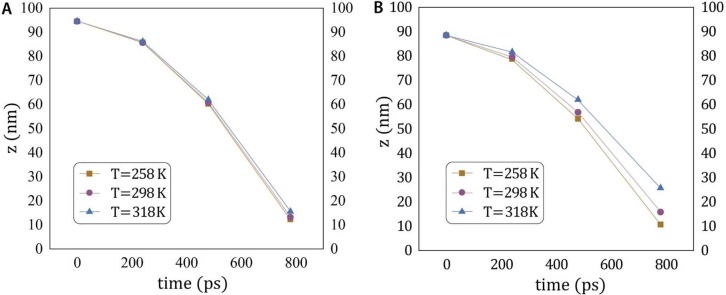
In Fig. 4 , the time-dependent vertical movement of two targeted droplet are plotted for three different temperature of $T=258$, $298$, and $318K$. The results show that throughout the traveling, the droplets in higher indoor temperature tend to stay suspended more than those in the lower ambient temperature and this issue becomes more significant by decreasing the droplet size. As shown in Fig. 4A, the difference in the traveling distance for small droplets is more considerable than the bigger one (see Fig. 4B). The observed effect of ambient temperature on the vertical traveling distance of droplets reveals that the deposition speed of virus-carrying droplets on the floor increases in higher indoor temperature, especially for smaller droplets (less than10 μm). This matter implies that the lifetime of aerosol in the ambient atmosphere of closed space is longer for warmer places.

Fig. 4.

The time-dependent vertical traveling distance of two targeted droplet (A: small and B: big droplet) for three different indoor temperature of T = 258, 298, and 318 K.

Although Jahangiri et al [21] and Yao et al [22] show that the ambient temperature is no a transmissibility factor for coronavirus in both Iran and China, our MD simulation shows that the indoor temperature could be a significant factor in the transmission of SARS-CoV-2 through inhaling the infected air in closed ambiance. The main reason for this contradiction is that the transmissibility rate of the virus in fact can be affected by several direct and indirect factors including but not limited to the difference of the population density in warmer and moderate climates of countries, the level of undermining adherence to physical distancing measures and movement restrictions, and inappropriate use of essential supplies and equipment.

According to the official report of the Minister of Health, Treatment and Medical Education of Iran, the number of newly infected cases in June-July 2020 in the warmest states of Iran, Khuzestan and Hormozgan, increased rapidly. Based on our result of the effect of the dynamics of air and water molecules on the suspension time periods of virus-carrying droplets, using air conditioner systems in indoor space of warm regions, could enhance the dynamics of air molecules and prolong the lifetime of aerosols in closed spaces. This pretension is completely in agreement with the recent study [12]. It has been reported that the lifetime of the droplet does not decrease by increasing the temperature when the ambient relative humidity is set below 37%. The results indicate beyond a critical ambient relative humidity, increasing the ambient temperature can increase the droplet lifetime exponentially [12].

The role of ambient relative humidity can be incorporated to increasing the rate of collision of air/water molecules with droplets as well as the coalescence phenomenon in which, the smaller droplets stick together and form a larger (heavier) droplet with a higher sediment speed. Due to the observation of permanently suspended droplets with 1 µm diameter in our simulation, more studies are invoked to investigate the disinfecting efficiency of large indoor space with fogging machines considering the higher probability of coalescence of droplets and faster deposition rate of larger aerosols.

Conclusion

In this study, molecular dynamics simulation has been carried out to analyze the dynamics and lifetime of the virus-carrying water droplets. Our simulation performed for various sizes of droplets and three different ambient temperatures have been considered to assess the vertical traveling of droplets. The major obtained results from the following study are:

• 1.Although the droplets with a size of less than 10 µm could suspend in an indoor environment for a long time, these small droplets could cohere to each other and form the bigger droplets. This phenomenon could lead to the deposition of expelled small droplets.
• 2.Droplets could be suspended more time in a warm ambient atmosphere compared to the cold one. Therefore the transmission rate by inhaling the infected aerosols in warm indoor space can be higher than the cold one.
• 3.Rising the dynamics of ambient air molecules with increasing the temperature or air conditioner, has a more significant effect on small droplets than the bigger one.
• 4.Increasing the ambient relative humidity can facilitate the coalescence of the smaller droplets and therefore, reduce the suspension time of these droplets.

CRediT authorship contribution statement

Alireza Shadloo-Jahromi: Conceptualization, Methodology, Software, Investigation, Validation. Omid Bavi: Supervision, Writing - original draft, Software, Investigation, Validation. Mohammad Hossein Heydari: Investigation, Validation, Methodology, Software. Masoud Kharati-Koopaee: Software, Supervision, Investigation, Validation. Zakieh Avazzadeh: Visualization, Funding acquisition, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.