A numerical simulation method of natural fragment formation and injury to human thorax

Abstract

Objective

Fragment injury is a type of blast injury that is becoming more and more common in military campaigns and terrorist attacks. Numerical simulation methods investigating the formation of natural fragments and injuries to biological targets are expected to be developed.

Methods

A cylindrical warhead model was established and the formation process of natural fragments was simulated using the approach of tied nodes with failure through the explicit finite element (FE) software of LS-DYNA. The interaction between the detonation product and the warhead shell was simulated using the fluid–structure interaction algorithm. A method to simulate the injury of natural fragments to a biological target was presented by transforming Lagrange elements into smooth particle hydrodynamics (SPH) particles after the natural fragments were successfully formed. A computational model of the human thorax was established to simulate the injury induced by natural fragments by the node-to-surface contact algorithm with erosion.

Results

The discontinuous velocities of the warhead shell at different locations resulted in the formation of natural fragments with different sizes. The velocities of natural fragments increased rapidly at the initial stage and slowly after the warhead shell fractured. The initial velocities of natural fragments at the central part of the warhead shell were the largest, whereas those at both ends of the warhead shell were the smallest. The natural fragments resulted in bullet holes that were of the same shape as that of the fragments but slightly larger in size than the fragments in the human thorax after they penetrated through. Stress waves propagated in the ribs and enhanced the injury to soft tissues; additionally, ballistic pressure waves ahead of the natural fragments were also an injury factor to the soft tissues.

Conclusion

The proposed method is effective in simulating the formation of natural fragments and their injury to biological targets. Moreover, this method will be beneficial for simulating the combined injuries of natural fragments and shock waves to biological targets.

Introduction

Owing to military campaigns and terrorist attacks in some regions and changes in war patterns and combat weapons, blast injury has become the main type of combat wound.^1,2 The main injury factors of explosive weapons are fragments and shock waves, which result in fragment injury and shock injury, respectively. According to data from several modern local wars, the incidence of fragment injury is 53%–81% and that of shock injury is approximately 50%.^3,4 Therefore, fragment injury is an important type of injury compared with shock injury.5, 6, 7

Animals have traditionally been used as substitutes for humans to study fragment injury. The porcine tissue is most used owing to both its availability and the belief that the retardation of bullets in porcine muscles is comparable to that in humans.^8,9 Xu et al.,¹⁰ Albreht et al.,¹¹ and Tikka et al.¹² conducted experimental studies regarding gunshot wounds to pig head or hind legs. The animal experiments have understandable ethical implications and are costly. Therefore, the investigation of fragment injury by numerical simulation is desired. Xu et al.¹⁰ and Karimi et al.¹³ investigated gunshot injury to human head by finite element (FE) simulation. Tang et al.¹⁴ conducted a dynamic simulation and preliminary FE analysis of gunshot wounds to human mandible. However, numerical simulations regarding the injury of natural fragments to human thorax are relatively rare.

A numerical simulation of the formation of natural fragments and its injury to biological targets is presented herein. The computational model of human thorax was established, and the injury induced by natural fragments was analyzed. Success of the method will be beneficial for simulating the combined injury of natural fragments and shock waves to biological targets.

Methods

Computational model

A cylindrical warhead was used in the simulation, and the warhead comprised two steel covers, a steel shell, and a trinitrotoluene (TNT) charge, as shown in Fig. 1A. The diameter, length, and shell thickness of the warhead were 122 mm, 144 mm, and 6 mm, respectively. An explosive was detonated at the center point of the warhead. Fig. 1B shows the natural fragment warhead and the spherical air domain. The diameter of the air domain was set to be 330 mm. The warhead located at the center of the air domain, in which the TNT charge was filled by using the keyword ∗INITIAL_ VOLUME_ FRACTION_ GEOMETRY. Geometric information from the visible human project was used as a guide for determining the profile of each part of the human thorax.^15,16 The geometry instance and computational model of the human thorax was established using the software HyperMesh (State Key Laboratory of Explosion Science and Technology, Beijing, China), as shown in Fig. 1C. The human thorax measured approximately 350 mm in width, 250 mm in depth and 98 mm in height.

Fig. 1.

Computational model. (A) Natural fragment warhead displayed without trinitrotoluene charge; (B) Natural fragment warhead and air domain; (C) Human thorax.

The computational model was meshed by using the software HyperMesh. The two covers and the shell of the warhead were meshed with hexahedral Lagrange elements. The element size of the warhead shell was 2 mm. The air was meshed with hexahedral Euler elements. For computation accuracy and efficiency, the element size increased gradually from the center of the air domain to the outside. The minimum element size was 1.2 mm and maximum 12 mm. The human thorax was meshed with hexahedral Lagrange elements, in which the element size was 2.5 mm. Table 1 shows the number of elements and nodes in each part of the computational model.

Table 1.

Number of elements and nodes in each part of the computational model.

Part	Element number	Node number
Warhead	115200	376178
Air	364800	361091
Thorax	295876	311606

Numerical simulation

The software LS-DYNA 970 and LS-PrePost 4.5 (Livermore Software Technology Corporation, USA) was used to perform the numerical simulation and result analysis, respectively. The approach of tied nodes with failure was used to simulate the formation process of natural fragments. Each node of the warhead shell element was separated into eight coincident nodes, which were tied together with a constraint relation, followed by a failure criterion of plastic strain set using the keyword ∗CONSTRAINED_ TIED_ NODES_ FAILURE to decide whether the constraint had failed. The fluid-structure interaction algorithm was used to simulate the interaction between the detonation product and the warhead shell, achieved by using the keyword ∗Constrained_ Lagrange_ in_ Solid. To simulate the injury of natural fragments to human thorax, the Lagrange elements were transformed into smooth particle hydrodynamics (SPH) particles after the natural fragments were formed finally. The node-to-surface contact algorithm with erosion was used to simulate the interaction between natural fragments and the human thorax using the keyword ∗Contact_ Eroding_ Nodes_ to_ Surface. The failure strains were set to determine the injury of human thorax during the penetration of natural fragments.

Material model and parameters

The constitutive model and equation of state for each material used in the numerical simulation are described as follows.

The MAT_HIGH_EXPLOSIVE_BURN constitutive model and Jones–Wilkins–Lee equation of state were employed to describe the explosiveness of TNT.¹⁷ The pressure was expressed as follows:

$$p=A\left(1-\frac{\omega }{R_{1}V}\right)e^{-R_{1}V}+B\left(1-\frac{\omega }{R_{2}V}\right)e^{-R_{2}V}+\frac{\omega e_0}{V},$$ (1)

where A, B, R₁, R₂ and ω are constants, V is the relative volume, and e₀ is the initial internal energy per unit reference specific volume.

The air was described by the MAT_NULL constitutive model and EOS_ LINEAR_POLYNOMIAL equation of state.¹⁸ The pressure was expressed as

$$p=C_0+C_1\mu +C_2{\mu }^2+C_3{\mu }^3+\left(C_4+C_5\mu +C_6{\mu }^2\right)e_0,$$ (2)

where μ = 1/V - 1, V is the relative volume, C₀–C₆ are polynomial equation coefficients, and e₀ is the initial internal energy per unit reference specific volume.

The steel was adopted as the warhead covers and shell. The dynamic yield stress was described by the constitutive model of MAT_PLASTIC_KINEMATIC, and the strain rate effect was investigated using the Cowper–Symonds model.¹⁹

$${\sigma }_d=\left({\sigma }_0+\frac{E{E}_t}{E-E_t}{\epsilon }_p\right)\left[1+{\left(\frac{\dot{\epsilon }}{C}\right)}^{1/p}\right],$$ (3)

where σ_d is the dynamic yield strength, σ₀ the static yield strength, E the Young's modulus, E_t the hardening modulus, ε_p the effective plastic strain, and $\dot{\epsilon }$ the equivalent plastic strain rate; C and p are constants.

The human thorax, sternum, costal cartilage, rib, and vertebrae were described by the linear elastic model, whereas the muscle, heart, lung, inner tissue, and intercostal tissue were described by the constitutive model of MAT_VISCOELASTIC.²⁰ The shear relaxation behavior was expressed as

$$G\left(t\right)=G_{\infty }+\left(G_0-G_{\infty }\right)e^{-\beta t},$$ (4)

where $G_0$ is the initial shear modulus, $G_{\infty }$ the long-time shear modulus, and $\beta$ the viscoelastic decay constant.

The specific parameters of each material are listed in Table 2.

Table 2.

Specific material parameters.17, 18, 19, 20

Material name	Density (g/cm3)	Material parameters
Trinitrotoluene	1.63	A = 374 GPa, B = 3.74 GPa, R1 = 4.15, R2 = 0.9, ω = 0.35, e0 = 7 GPa vCJ = 6930 m/s, pCJ = 21 GPa.17
Air	1.293E-3	C0 = C1 = C2 = C3 = C6 = 0, C4 = C5 = 0.4 MPa, e0 = 0.25 MPa.18
Steel	7.86	E = 210 GPa, ν = 0.28, σ0 = 1.08 GPa, Et = 0, C = 40.4 s−1, p = 5.19
Muscle	1.20	G0 = 200 kPa, G∞ = 195 kPa, K = 2.9 GPa, β = 0.1.20
Lung	0.60	G0 = 67 kPa, G∞ = 65 kPa, K = 0.744 GPa, β = 0.1.20
Heart	1.00	G0 = 67 kPa, G∞ = 65 kPa, K = 0.744 GPa, β = 0.1.20
Sternum	1.25	E = 9.5 GPa, ν = 0.25.20
Rib	1.08	E = 9.5 GPa, ν = 0.20.20
Vertebrae	1.33	E = 0.355 GPa, ν = 0.26.20

Note: v_CJ and p_CJ are the detonation velocity and Chapman–Jouget pressure, respectively; E is the Young's modulus, ν the Poisson's ratio and K the bulk modulus.

Results

Formation process of natural fragments

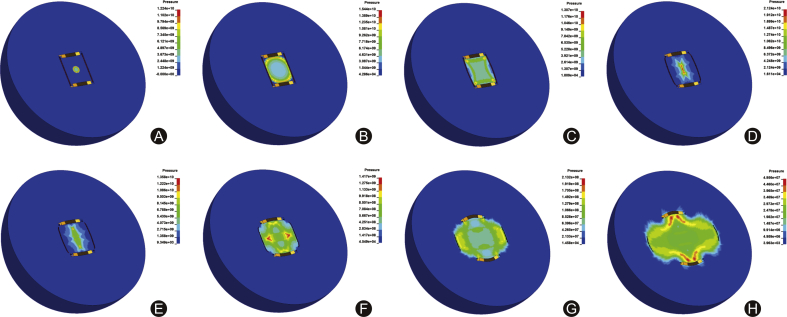
Fig. 2 shows the interaction process of detonation product and warhead shell. A detonation product with high temperature and pressure was developed, and the detonation wave propagated inside the explosive at t = 2.5 μs after the warhead was detonated. The detonation wave arrived at the inner surface of the warhead shell at approximately t = 10 μs; subsequently, it was reflected at about t = 15 μs, producing a high pressure around the two ends of the warhead shell. At t = 22.5 μs, the reflected detonation waves converged at the warhead center and the warhead shell expanded under the action of the detonation product. The two ends of the warhead shell fractured first at approximately t = 25 μs. The warhead shell continued to expand outward and fractured to form natural fragments at t = 35 μs. After the warhead shell fractured, the detonation product entered the air, forming blast shock waves at t = 60 μs.

Fig. 2.

Interaction between detonation product and warhead shell. (A) t = 2.5 μs; (B) t = 10 μs; (C) t = 15 μs; (D) t = 22.5 μs; (E) t = 25 μs; (F) t = 35 μs; (G) t = 60 μs; (H) t = 90 μs.

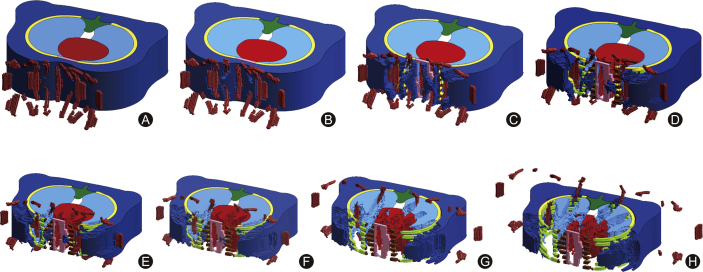
Fig. 3 shows the formation process of natural fragments. The warhead shell began to expand under the action of the detonation product at t = 20 μs. The warhead shell fractured first at both ends at approximately t = 25 μs. At approximately t = 35 μs, the fragment began to form at the central part of the warhead shell. Subsequently, the warhead shell further expanded under the interaction of the detonation product, and the natural fragments formed eventually at about t = 80 μs.

Fig. 3.

Formation of natural fragments. (A) t = 20 μs; (B) t = 25 μs; (C) t = 35 μs; (D) t = 50 μs; (E) t = 60 μs; (F) t = 70 μs, (G) t = 80 μs; (H) t = 90 μs.

Characteristic parameters of natural fragments

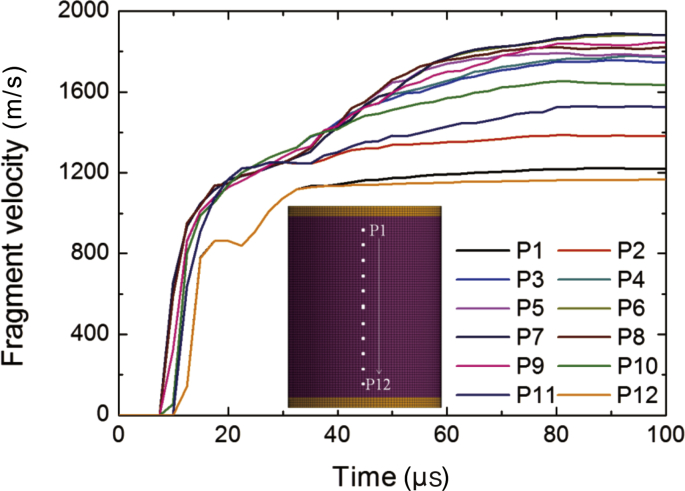
Fig. 4 shows the velocity histories of fragments at typical positions of the warhead shell. The velocities of the natural fragments increased sharply owing to the acceleration of the detonation product at the first 20 μs; subsequently, the velocities increased slowly. At approximately t = 80 μs, the fragment velocities tended to be stable. The initial velocity of the natural fragments was defined as the maximum velocity during the fragment flying under the driving force of the detonation product. The initial velocity of the natural fragment can be estimated according to the Gurney formula,²¹ which is expressed as

$$v_0=\sqrt{2E}\sqrt{\frac{C/M}{1+0.5C/M}},$$

where C is the total charge mass and M the total mass of warhead shell; $\sqrt{2E}$ is the Gurney constant, which depends on the characteristic of the explosive and is approximately 2460.4 m/s for TNT.

Fig. 4.

Velocity histories of natural fragments at typical positions of warhead shell.

The average fragment velocity of 1487 m/s from the numerical simulation was close to the result of 1388 m/s obtained from the empirical formula, with an error less than 10%.

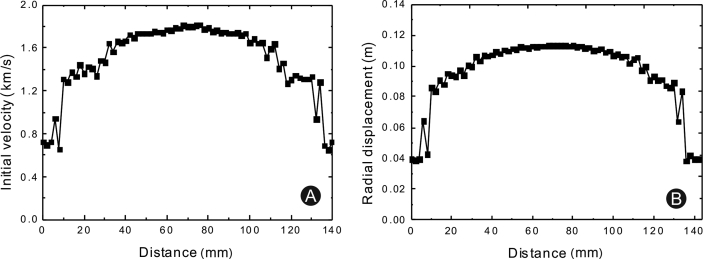
Fig. 5 shows the distribution of the initial velocity and the radial displacement of natural fragments along the axial direction of the warhead shell. The initial velocity and radial displacement at both ends of the warhead shell were the smallest, whereas those at the central part were the largest. The maximum initial velocity of the fragment at the central part of the warhead shell reached approximately 1800 km/s, and the corresponding radial displacement was approximately 0.11 m, which was approximately twice the initial diameter of the warhead.

Fig. 5.

Characteristic parameters of natural fragments along the axial direction of warhead shell. (A) Initial velocity; (B) Radial displacement.

Translation of Lagrange elements to SPH particles

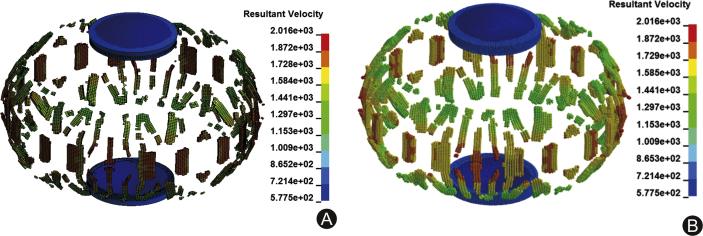
Fig. 6 shows the velocity distribution of the natural fragments in the form of Lagrange elements and SPH particles, separately. Both the spatial and velocity distributions of the natural fragments were consistent after the fragments were transformed from Lagrange elements to SPH particles. The number of SPH particles of the natural fragments after the transformation was approximately 130,000.

Fig. 6.

Velocity distribution of natural fragments in different forms. (A) Lagrange elements; (B) Smooth particle hydrodynamics particles.

Injury of natural fragments to human thorax

Fig. 7 shows the relative location of the natural fragments and human thorax. The distance between the center of the warhead and the surface of the human thorax was approximately 200 mm, and the natural fragments (indicated in purple) penetrated the human thorax as they dispersed outside.

Fig. 7.

Relative locations of natural fragments and human thorax.

Fig. 8, Fig. 9 show the injury process and effective strain distribution of human thorax during the penetration of natural fragments. Three natural fragments almost reached the thorax surface simultaneously at approximately t = 12.5 μs and deformed the muscle. Subsequently, the muscle, sternum, and rib were penetrated through by the fragments as the continuing movement at approximately t = 40 μs. The fragments penetrated into the heart and lung at approximately t = 60 μs. Several bullet holes were produced in the thorax after the fragments penetrated through. Stress waves in the ribs and ballistic pressure waves were observed during the penetration.

Fig. 8.

Penetration process of natural fragments into the human thorax. (A) t = 12.5 μs; (B) t = 20 μs; (C) t = 40 μs; (D) t = 60 μs; (E) t = 80 μs; (F) t = 100 μs; (G) t = 150 μs; (H) t = 200 μs.

Fig. 9.

Strain distribution of human thorax during penetration process of natural fragments. (A) t = 12.5 μs; (B) t = 20 μs; (C) t = 40 μs; (D) t = 60 μs; (E) t = 80 μs; (F) t = 100 μs; (G) t = 150 μs; (H) t = 200 μs.

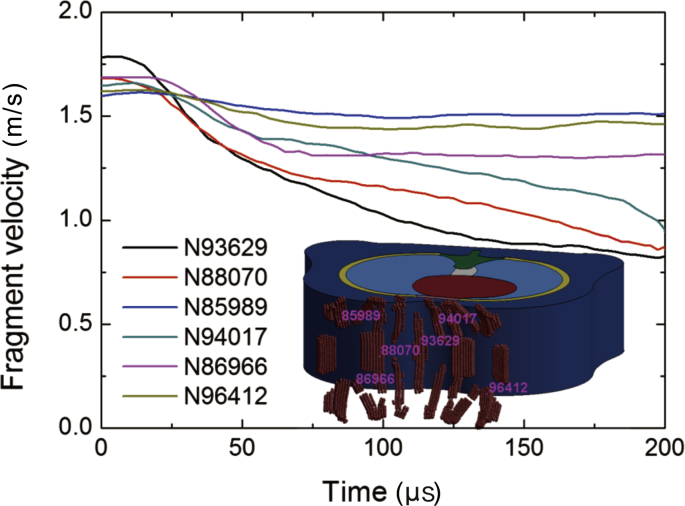
Fig. 10 shows the velocity histories of nodes located at typical fragments. The velocities decreased gradually during the penetration. The velocity attenuations of nodes N93629, N88070, and N94017 were more obvious than those of nodes N85989, N96412, and N86966. The fragment associated with node N93629 penetrated through the sternum and vertebra during the penetration; therefore, it was subject to the greatest resistance. The node N88070 penetrated the ribs twice, and the node N94017 penetrated through the sternum and ribs; therefore, the velocities decreased significantly. The fragments associated with nodes N85989, N96412, and N86966 did not interact with the bone during the penetration but only the soft tissues, such as muscles and the heart and lung, with a small attenuation in velocity.

Fig. 10.

Velocity histories of nodes located at typical fragments.

Discussion

FE simulations have been widely used in investigating biological injuries induced by blast shock waves or fragments because of its advantages compared with traditional animal experiments.22, 23, 24 First, an FE simulation can provide reliable results in a shorter time and with lower cost. Next, it can present and predict detailed information regarding the biomechanical response of a biological target. Finally, it enables the easy control of experimental conditions. Fragment injury is as important as shock injury because the incidence of the former is even higher than that of the latter.5, 6, 7 Some studies performed using FE simulations have been conducted to analyze fragment injury. Karimi et al.¹³ investigated a gunshot injury to human head protected by a polyvinyl alcohol sponge. The severity of injury to the human skull was assessed through stress analysis, and the injury competence of the projectiles was compared with that of the forehead protected by the polyvinyl alcohol sponge. Tang et al.¹⁴ simulated gunshot wounds to the human mandible using two projectiles, three impact velocities, and three entry angles. The results indicated that the injury severity of the mandible and the injury efficiency of the projectiles varied under different injury conditions. Duan et al.²⁵ and Li et al.²⁶ investigated the combined damage of shock waves and fragments driven by explosives to a clamped square steel plate and sandwich panels, respectively. In their simulations, each fragment was preformed into hexahedrons and only assembled seamlessly according to their geometric shapes. However, these simulation methods cannot reflect the actual physical process of natural fragments interacting with the target. Up to date, numerical simulations of natural fragments to biological targets are not common. The current study simulates the formation of natural fragments and its injury to human thorax by using the explicit FE software LS-DYNA.

Element erosion and tied nodes with failure were two main approaches used to simulate the formation of natural fragments. The element erosion approach realized the formation of natural fragments by deleting the element when it reaches the failure criterion of yield stress or plastic strain under the action of detonation product.^27,28 In the present study, the tied nodes with failure approach was adopted to simulate the formation of natural fragments. Each node of the warhead shell element was separated into eight coincident nodes, which were tied together with a constraint relation and then a failure criterion of plastic strain was set to decide whether the constraint failed.^29,30 The formation process of natural fragments of a cylindrical warhead was successfully simulated by using this method. It was difficult to simulate the injury of natural fragments to the target because the natural fragments were in the form of Lagrange elements that had deformed severely and were extremely vulnerable to failure as soon as interaction with the target began in the subsequent penetration. The injury of natural fragments to biological targets was successfully simulated by transforming the natural fragments in the form of Lagrange elements into SPH particles after the natural fragments were successfully formed. The SPH method was a meshless Lagrange method. It overcame the disadvantages of the Euler method, i.e., difficulty in tracing the material deformation and recognizing the interface of different materials, and avoided the problem of grid distortion occurring in large deformation simulations in the Lagrange method.^31,32

The formation process of natural fragments was simulated, and the characteristic parameters of the natural fragments were obtained. The discontinuous velocities of different locations on the warhead shell were the main reasons behind the formation of natural fragments. The fast expansion of the warhead shell had an obvious inertia effect, and the discontinuous velocities resulted in the formation of natural fragments of different sizes. At the initial stage of fragment formation, the detonation product accelerated the warhead shell and hence the velocity of the fragments increased rapidly. After the warhead shell fractured, the detonation product entered the air and partial energy was converted to form blast shock waves; therefore, the velocity of the fragments increased slowly. The propagation velocity of the detonation product used to accelerate the warhead shell decreased and separated from the warhead shell, and the natural fragment reached its maximum velocity, which was called the initial velocity. The initial velocities at the central part of the warhead shell were the largest, whereas those at both ends were the smallest. This was because the acceleration time of the detonation product on the warhead shell at both ends was the shortest, and the obtained kinetic energy was the smallest; the opposite situation occurred at the central part of the warhead shell.

A computational model of the human thorax was established, and the injury of natural fragments penetrating against the human thorax was analyzed. The fragment resulted in a serious penetration injury in a local area because of its large initial velocity exceeding 1000 m/s, which differed significantly from the injury induced by shock waves, where a relatively larger scale of injury is typically yielded.³³ Several bullet holes, which were of the same shape as the fragments but slightly larger, were produced in the thorax after the fragments penetrated through. Stress waves were produced in the ribs when the fragments penetrated through, consistent with the findings of a previous study.³⁴ Owing to the high wave impedance of bones compared with that of soft tissues, the stress waves propagated quickly in the ribs. The stress waves deformed areas surrounding the heart, lung, and muscle and enhanced their injury. In addition, ballistic pressure waves were produced ahead of the fragment during the penetration process. The ballistic pressure waves traveled near or above the speed of sound and might reduce remote effects, such as the cerebral injury resulting from the penetration of projectiles to the thorax.³⁵

Two main limitations exist in the current study. One was that the human thorax model established was quasi two-dimensional, and the other was that the materials in each part of thorax were considered isotropic. These two aspects differed from the reality. Therefore, the simulated injury data of natural fragments to the human thorax might differ from the experimental data. Nonetheless, the simulation of the formation of natural fragments and its injury to the human thorax proposed herein was effective. In addition, the simulation suggested that the injury mechanism of natural fragments to the human thorax include mainly fragment penetration and interactions between stress waves and ballistic pressure waves.

In conclusions, the approach of tied nodes with failure was effective in simulating the formation of natural fragments of a cylindrical warhead. The method of transforming Lagrange elements into SPH particles after the formation of natural fragments can be used to successfully simulate the injury of natural fragments to biological targets. The injury of natural fragments penetrating against human thorax mainly included three mechanisms of penetration and interactions between stress waves and ballistic pressure waves. The present method will be beneficial for simulating the combined injury of natural fragments and shock waves to biological targets.

Funding

The work was funded by the National Science Foundation for Young Scientists of China (11902356), China Postdoctoral Science Foundation (2018M633715), Innovation and Cultivation Fund of the Sixth Medical Center of PLA General Hospital (No. CXPY201825) and the Army Scientific Research (LB20182D040012).

Ethical Statement

This study is a numerical simulation and thus ethical approval is not required.

Declaration of Competing Interest

The authors declared no competing interest.