X-Ray Structural Analysis of Single Adult Cardiomyocytes: Tomographic Imaging and Microdiffraction

Abstract

We present a multiscale imaging approach to characterize the structure of isolated adult murine cardiomyocytes based on a combination of full-field three-dimensional coherent x-ray imaging and scanning x-ray diffraction. Using these modalities, we probe the structure from the molecular to the cellular scale. Holographic projection images on freeze-dried cells have been recorded using highly coherent and divergent x-ray waveguide radiation. Phase retrieval and tomographic reconstruction then yield the three-dimensional electron density distribution with a voxel size below 50 nm. In the reconstruction volume, myofibrils, sarcomeric organization, and mitochondria can be visualized and quantified within a single cell without sectioning. Next, we use microfocusing optics by compound refractive lenses to probe the diffraction signal of the actomyosin lattice. Comparison between recordings of chemically fixed and untreated, living cells indicate that the characteristic lattice distances shrink by ∼10% upon fixation.

Significance

Diffraction with synchrotron radiation has played an important role in deciphering the molecular structure underlying force generation in muscle. In this work, the diffraction signal of the actomyosin contractile unit has for the first time, to our knowledge, been recorded from living cardiomyocytes, bringing muscle diffraction to the scale of single cells. In addition to scanning diffraction, we use coherent optics at the same synchrotron endstation to perform holographic imaging and tomography on a single cardiomyocyte. By this hard x-ray microscopy modality, we extend the length scales covered by scanning diffraction and reconstruct the electron density of an entire freeze-dried cardiomyocyte, visualizing the three-dimensional architecture of myofibrils, sarcomeres, and mitochondria with a voxel size below 50 nm.

Introduction

Force generation in heart muscle relies on a hierarchically ordered structural organization, reaching from the actomyosin assembly in the sarcomere to the entire structural organization of cardiomyocytes (CMs). The latter includes, for example, the dense packing of myofibrils, the high number of mitochondria, and the structural and dynamical properties underlying excitability. Classical x-ray diffraction studies of skeletal (1) and heart muscle (2) have helped to shape our understanding of the average structure of the sarcomere. In contrast to electron microscopy, muscle structure analysis by x-ray diffraction is compatible with in situ mechanical loading, physiological parameters, and simultaneous measurements of the contractile force. Many molecular details of the myosin head dynamics, binding, and stroke have been revealed by third-generation synchrotron radiation (3, 4, 5, 6). In these experiments, however, structural information is averaged over macroscopically large volumes of the muscle tissue, without sensitivity to the cellular organization or cell-to-cell variations. Electron microscopy, on the other hand can unravel the molecular and subcellular organization of myocytes (7,8) but requires invasive staining and sectioning, whereas confocal fluorescence microscopy is compatible with in vivo recordings of contracting cells (9) but lacks the resolution for the molecular scale and also contrast for unlabeled structure.

With recent progress in x-ray focusing optics, as reviewed in (10), it has become possible to perform diffraction experiments with spot sizes in the micron and nanometer range. This enables recordings of the small-angle x-ray scattering (SAXS) while scanning the sample in real space, as initially introduced for biomaterials (11,12) and more recently also for soft matter (13), as well as for three-dimensional (3D) vector SAXS (14). Scanning diffraction from biological cells with spot sizes smaller than a single organelle are still more challenging in terms of signal-to-noise (15, 16, 17, 18, 19, 20), as well as radiation damage (21). Recently, we have used this approach to study the cytoskeletal structure of single CMs to compare the signal level for different preparation states (22). For freeze-dried heart muscle cells (20,23), we have observed anisotropic diffraction patterns, and by correlating the x-ray signal to fluorescence data obtained by in situ stimulated emission depletion (STED) microscopy recordings, we have linked the signal to the actin portion of the cell (24). A diffraction signature of a sarcomeric complex was observed for the first time, to our knowledge, for hydrated and chemically fixed cardiomyocytes (22). Hence, by this technique, variations of structural parameters in single isolated cells or in muscle tissue have now become accessible, unaffected by macroscopic averaging. However, it cannot be expected that the signal level and amount of structural details can compete with macroscopic muscle diffraction.

Regarding subcellular and cellular organization, a second line of development, not in x-ray diffraction but in coherent imaging with hard x-rays, has also matured (25, 26, 27, 28), providing 3D electron density maps for unstained cells reconstructed by coherent diffractive imaging (29), ptychography (19,30,31), or x-ray holography (32, 33, 34, 35). Although the resolution is still lower than in x-ray microscopy with Fresnel zone plate lenses (36), the size of adult CMs is too large to be penetrated by soft x-rays in the water window.

In this work, we now combine full-field 3D imaging of the electron density by holographic x-ray tomography (holotomography) and scanning x-ray diffraction to study the structure of isolated murine adult CMs on the molecular and cellular scale. As illustrated in Fig. 1, this multimodal x-ray approach has been implemented at the same synchrotron endstation, where both modalities can be realized by a simple rearrangement of its modular compound optics (37). The purpose of this work is threefold. First, this study is a benchmark of current x-ray method development geared toward cellular biophysics and cell biology. Second, it can contribute to computational modeling of the contractile functions of CMs. Third, it illustrates the capability and limitations of how x-ray imaging methods can contribute to future multimodal correlative imaging approaches. Such efforts will most certainly comprise visible light, electron microscopy, and fluorescence microscopy and hopefully also cover structural dynamics. To this end, the “x-ray contrast,” offering quantitative electron density as well as actomyosin lattice parameters without slicing or staining, will be complementary to the other, more established microscopy methods. The following achievements highlight the progress that has been made with respect to prior work: 1) the first, to our knowledge, demonstration of diffraction analysis for (initially) living cells that shows a proper exploitable actomyosin signal; 2) the demonstration of how the actomyosin lattice spacing changes when the CMs are chemically fixed; and 3) the first, to our knowledge, 3D electron density reconstruction by phase-contrast x-ray tomography, albeit at this time only for a freeze-dried cell.

Figure 1.

(a) Sample preparation. CMs were isolated by dissociation of healthy mouse hearts. One part (top row) of the cells was chemically fixed and mounted on a silicon nitride window, and actin was stained with a fluorescent dye (Atto633-Ph). Afterwards, the samples were plunge frozen and freeze dried. For experiments in hydrated conditions (middle rows), the cells were either analyzed in buffer solution or chemically fixed. They were placed in liquid chambers made of SiN (chemically fixed cells) or polypropylene windows (living cells). For tomography, fixed cells were mixed and embedded in agarose and mounted in a polyimide tube with a diameter of 1 mm (bottom row). (b) Microscopy image of freshly isolated CMs is shown. Healthy, contracting cells and apoptotic cells can be identified. (c) Schematic overview of the cellular structures of a CM is given. The nucleus, mitochondria, and myofibrils are sketched. The red circle marks a sarcomeric unit, which is magnified in the scheme on the right. A cross section of the sarcomere and the definition of the sarcomeric lattice spacing is shown below. (d) Experimental setup for x-ray phase-contrast tomography at the GINIX endstation of the P10 beamline at the PETRAIII storage ring (Deutsches Elektronen-Synchrotron) is shown. The x-ray beam is focused by a pair of KB mirrors and coupled into a waveguide channel for further reduction of the beam size and for coherence filtering. The sample is placed on a fully motorized tomography stage at distance x₀₁ ≈ 0.35 m, and the detector is placed at x₁₂ ≈ 5 m behind the sample. The resulting cone beam geometry of the highly coherent wavefront is used to acquire projections at high geometric magnification M ≫ 1 and low Fresnel number F ≪ 1. (e) The same endstation can also be used for scanning diffraction experiments. In this mode, the beam is focused by CRLs, and the sample is moved into the focus. Diffraction patterns are acquired by an EIGER 4M detector at distance x₀₂ ≈ 5 m. The primary beam is blocked by beam stops to protect the detector. To see this figure in color, go online.

Beyond the technical focus, this work also reports structural insight regarding adult cardiomyocytes. Specifically, we can quantify the distribution of the actomyosin lattice spacing within a single adult cardiomyocyte. We also show that fixation, which is ubiquitous in cellular biophysics and cellular biology, results in shrinkage of the actomyosin lattice. Finally, regarding tomography, we provide data on the 3D distribution of mitochondria in the cell, which is valuable information for modeling energy supply.

The manuscript is organized as follows. After this introduction, we describe methods of sample preparation, instrumentation, optics, reconstruction, and analysis. We then present the holotomography results for single CMs, followed by the x-ray microdiffraction results for living CMs, before closing with a brief summary and outlook.

Materials and Methods

Preparation of CMs for x-ray analysis

The workflow of the sample preparation is sketched in Fig. 1 a. After the dissociation of the hearts, single CMs were prepared for the x-ray analysis. The structure of CMs, as sketched in Fig. 1 c, was analyzed using the two modalities of the beam line setup. For the investigation of subcellular structures such as the nucleus and mitochondria, full-field holographic x-ray tomography was used, whereas the molecular actomyosin structure (sketched in the magnification of Fig. 1 c) was probed by scanning x-ray diffraction. For diffraction measurements, the CMs were mounted in liquid chambers, whereas for tomographic scans, the cells were either freeze dried or embedded in agarose to increase stability. A detailed description of the preparation steps is given below.

Isolation of CMs

The isolation of adult CMs followed the procedure described in (38). Before sacrifice, the wild-type mice (C57BL/6) were anesthetized with isoflurane. The hearts were explanted and put in an ice-cold tyrode solution to wash out remaining blood. After this, a canula was placed in the aorta, and the heart was washed with the tyrode solution. The hearts with the canula were mounted in a Langendorff perfusion system containing a liberase solution that was preheated to 36.5°C. The hearts were perfused by this solution, starting the digestion of the heart tissue. After 5 min, the hearts were transferred to a petri dish also containing the enzyme solution. The hearts were cut into smaller pieces and resuspended in the same medium using a 10 mL pipette with a cutoff tip. The resuspended cells were mixed with a stop solution (containing bovine calf serum and CaCl₂) in a Falcon tube. The remaining tissue sinks to the bottom, the supernatant is transferred to another Falcon tube, and the cells sediment and form pellets. Afterwards, the cells were washed twice with tyrode solution. Directly after the isolation, the extracted cells were observed in the microscope. The success of the isolation was evaluated by the vitality of the cells. Fig. 1 b shows a microscopy image of freshly extracted CMs. The healthy, contracting cells can be distinguished from apoptotic cells. Only isolations with a vitality rate above 50% were used for further analysis.

Preparation of CMs for diffraction

For the diffraction experiments, the isolated CMs were transferred to liquid sample chambers (see middle row of Fig. 1 a). Part of the cells were chemically fixed right after the extraction. Karlsson-Schultz fixation solution (39) containing 4% formaldehyde and 2.5% glutaraldehyde was used as a fixative. The cells were incubated in the solution for 15 min and stored in phosphate-buffered saline at 4°C for 2 weeks before the experiment started. For the x-ray diffraction measurement, a chamber from Silson (Warwickshire, United Kingdom) was used. The chamber consists of two 1-μm-thick silicon nitride membranes in silicon frames. One of the frames has a 70 μm polymer spacer keeping the frames apart to protect the CMs from squeezing. The cells, with a diameter of ∼10–25 μm and a length of 50–100 μm, are carefully sandwiched between the two silicon nitride frames. To seal the chamber, the silicon nitride frames are placed in a metal frame, which is sealed with two gaskets and screwed together. The metal frame is then inserted into a sample holding pin. The investigation of living CMs required a higher effort in the planning of the experiments. Right after the extraction, the living CMs were transported from Göttingen to the beamline in a mobile incubator (37°C). The cells were stored in tyrode buffer during transport and measurement. At the beamline, the living cells were sandwiched between two polypropylene membranes. To keep the membranes apart, a gasket of the Silson chambers with a thickness of 300μm were used. The polypropylene membranes were sealed tightly by applying nail polish to the edges. The chamber was then inserted into a sample holding pin for the measurement. Additionally, plunge-frozen and freeze-dried CMs mounted on SiN windows were analyzed. Because this preparation was primarily used for holographic and tomographic imaging, the procedure is described in the next paragraph.

Preparation of CMs for x-ray holography and tomography

For the tomographic scans, CMs were coated to SiN windows and plunge frozen and freeze dried (top row of Fig. 1 a) or embedded and hydrated in 1% agarose gel (bottom row of Fig. 1 a) to increase stability. To reduce absorption for the agarose embedded cells and to allow for a rotation of the sample, the cells were transferred into a capillary using a 1 mm biopsy punch. The protocol of the preparation for freeze-dried samples closely followed (20,22,23). CMs were pipetted onto SiN windows coated with a 1% fibronectin coating and incubated for 15 min. Afterwards, the cells were chemically fixed (15 min in 7% formaldehyde). Additionally, the actin skeleton of the CMs was stained with a fluorescent dye (Atto633-phalloidin; ATTO-TEC, Siegen, Germany). Plunge freezing of CMs was performed with a grid plunger (Leica EM GP; Leica, Wetzlar, Germany). Afterwards, the cells were freeze dried. The stained samples were stored in a light-protected desiccator until the measurements were performed. As an alternative to freeze-dried preparations, which compromise the structural preservation of the ultrastructure, we also used embedding in a gel to prevent dehydration while at the same time increasing positional stability for the tomographic scan. Because the native electron density contrast in hydrated CMs was found insufficient, contrast enhancement by staining, namely by 1% OsO₄ and phosphotungstic acid (40,41), was used.

Inspection of CMs by STED

Before x-ray holography and tomography experiments were performed, the freeze-dried CMs were imaged with a custom-built STED microscope (Abberior Instruments, Göttingen, Germany) (24). This setup is compatible with the GINIX endstation of the P10 beamline. For the beamtime block of this work, however, the STED microscope was only available in “offline mode” at the institute for x-ray physics in Göttingen. It allowed us to precharacterize the freeze-dried samples before the beamtime. In this way, cells that did not show any ruptures from the procedure of plunge freezing and freeze drying were selected for x-ray imaging. First, the cells were analyzed in confocal mode and raster scanned with a step size of 200 nm in the lateral and 400 nm in the axial direction. Additionally, one slice was acquired in STED mode and with a step size of 50 nm.

Synchrotron beamline and instrumentation

The x-ray experiments were carried out at the undulator beamline P10 at Deutsches Elektronen-Synchrotron in Hamburg, Germany, using the GINIX (“Göttingen instrument for nanoscale imaging with x-rays”) endstation (37). The modular design of the GINIX endstation enables rapid switching between the two modalities used here: holotomography based on a Kirkpatrick-Baez (KB) and x-ray waveguide compound optics (32,42,43) and scanning diffraction based on microfocusing by a beryllium compound refractive lens (CRL) transfocator system. Both settings are sketched in Fig. 1 d. Experimental parameters concerning the instrumentation and optics are tabulated in Table 1 and described in more detail below.

Table 1.

Beamline Specifications of the Setups for Scanning SAXS and Tomography of the GINIX Endstation

	Scanning SAXS	Tomography
Energy (keV)	8	7.5
Monochromator	Si(111) channel-cut	Si(111) channel-cut
Detector	Eiger 4M	sCMOS (15 μm Gadox scintillator)
Source-to-detector distance x02 (cm)	507.5	501.14
Pixel size px (μm)	75	6.5
Focus (horizontal × vertical)	2 × 3 μm2	<50 nm
I0 (photons/s)	2.5 × 1010	1.1 × 109

For x-ray diffraction, the undulator beam was monochromatized by an Si(111) channel-cut crystal to an energy of E_ph = 8 keV. The beam was focused by a set of beryllium CRLs to a size of 2 × 3 μm². The total photon flux was 2.5 × 10¹⁰ photons/s. The sample was placed in the focal plane and moved by a fully motorized sample stage using a piezo motor. To protect the detector, the primary beam was blocked using two beamstops. The diffraction signal was recorded by a single-photon-counting detector with a pixel size of px = 75 μm (Eiger 4M; Dectris, Baden, Switzerland) located ∼5 m behind the sample.

For the holographic and tomographic scans, the photon energy was set to E_ph = 8 and 7.5 keV in two subsequent beamtimes. The beam was focused by a set of KB mirrors to a focal spot size with a full width at half maximum of about FWHM_{y, z} = 300 × 300 nm² in horizontal (y) and vertical (z) direction. The photon flux was I₀ ≈ 1.1 × 10¹¹ photons/s. The KB-focused beam was then coupled into a lithographic x-ray waveguide channel (44,45) that is placed in the focal plane. The waveguide serves the purposes of further beam confinement as well as spatial and coherence filtering, providing a clean wavefront for inline holography (32). At the detector plane, a photon flux of I₀ ≈ 1.1 × 10⁹ photons/s was detected. The sample was moved by a fully motorized sample stage to a defocus plane and probed by the highly coherent exit wave field emanating from the waveguide. Small phase shifts of the wavefront after interaction with the object transform into a measurable intensity pattern by free space propagation of the beam and self-interference of the divergent wave field. The geometrically magnified hologram was recorded by a detector placed ∼5 m behind the sample. The hologram encodes the local phase shift or equivalently the projected electron density distribution of the object. By choice of the focus-to-sample distance x₀₁, which is typically a few millimeters to centimeters, the geometrical magnification M = $\left(x_{01}+x_{12}/x_{01}\right)$ with sample-detector distance x₁₂ and the effective pixel size px_eff = $p/M$ are adjusted, as well as the field of view.

Data acquisition and image analysis

Scanning SAXS measurements

For the scanning SAXS experiments, the samples are continuously scanned by a piezo motor. Positioning of the sample in the focal spot is facilitated by an on-axis microscope. In view of radiation damage, a “diffract before damage” strategy is adopted (21):

• 1.Position a pristine cell or pristine cellular region in the focal spot.
• 2.Record a diffraction pattern with an exposure time, for which the signal is unaffected by structural damage.
• 3.Move to a new cell/spot.

Regarding (2), the critical dose for damage is estimated from a test involving a variation of accumulation time or from fractionating the dose over several subframes. This strategy is based on the tested assumption that the signal is stable up to a critical time depending on dose, dose rate, and resolution. This is the case for a pristine spot. Because previous exposures of neighboring scan points can induce a “bystander effect,” the step size is a further important parameter and has to be chosen sufficiently large (21). Therefore, this scheme results in rather coarse-grained real-space maps of the cells. Table 2 presents the data acquisition parameters for the three different sample preparations. Data analysis was performed using the MATLAB (The MathWorks, Natick, MA) nanodiffraction toolbox developed in our institute (46).

Table 2.

Data Acquisition Parameters of the SAXS Experiments

	Living	Fixed	Freeze-dried
Fixative	–	Karlsson-Schultz	formaldehyde
Step size (μm)	5	10	2
Scan size (μm2)	200 × 200	180 × 180	200 × 200
Stitching	1	5 × 5	1
Acquisition time	0.1 s	0.1 s	0.05 s

X-ray holography

As a full-field technique, x-ray holography does not require any lateral scanning of the sample, which makes it ideally suited for tomography. However, before any tomographic scan, the signal level, i.e., the contrast of the hologram, has to be evaluated, and the geometry and detector configuration has to be optimized. An overview of the different configurations of the beamline setup and the sample preparation tested in this work is summarized in Table 3. Because contrast depends on the variations in electron density, freeze-dried cells result in much higher contrast than cells in solution. For CM recordings, we compared different detectors. We performed scans with a single-photon counting pixel detector (Eiger 4M; Dectris, Baden-Daettwil, Switzerland), offering the highest dose efficiency because of photon counting. However, the large pixel size px = 75 μm requires the sample to be moved very close to waveguide to reach high magnification, impeding tomographic rotations at high magnification. We therefore then turned to indirect, detection-based, scintillator-based fiber-coupled sCMOS detectors. To this end, we used a single-crystal scintillator (LuAG, thickness 20 μm) with an sCMOS (Hamamatsu Photonics K.K., Hamamatsu, Japan) coupled by a 1:1 fiber optic plate, as well as another 1:1 fiber-coupled scintillator-based sCMOS camera (2048 × 2048 pixels; Photonic Science, Sussex, UK) with a custom 15-μm-thick Gadox scintillator with pixel size of px = 6.5 μm. This configuration was favored because the whole cardiomyocyte fitted into the FOV and, at the same time, the effective pixel size was sufficiently small, namely px_eff = 45 nm at M = 143. The sample preparation and environment were also tested in view of compatibility with holographic tomography (holotomography). As described above, we tested hydrated unstained CMs as well as CMs with 1% OsO₄ or phosphotungstic acid staining embedded in agarose. All cases resulted in a rather weak signal. For unstained cells embedded in agarose, almost no signal could be detected at the given photon energy. Sample mounting was another concern. Because isolated CMs are not attaching to a substrate, one easily encounters drift during scan. For these reasons, we decided in this work to perform tomography scans only on freeze-dried CMs mounted on thin foils made from silicon nitride (Silson). It is necessary to mention that for these experiments, the size and shape of the SiN frames is a compromise between the missing wedge, the tolerable tilt angle, and the window’s stability: thick and broad frameworks lead to a rather stable window at the cost of a large missing wedge. Windows with large edge lengths diminish the maximum tolerable tilt angle of the sample in horizontal and vertical direction because of the small x₀₁ distance as required for high-resolution cone beam recordings. Also, the cell density must be chosen relatively low; otherwise, neighboring cells will enter the field of view upon rotation and disturb the reconstruction of the target cell.

Table 3.

Acquisition Parameters of the X-Ray Holography Experiments

Preparation	I	II	III	IV
	Freeze-Dried	Freeze-Dried	Freeze-Dried	Hydrated, Stained
Detector	Eiger 4M	sCMOS (20 μm LuAG)	sCMOS (15 μm Gadox)	sCMOS (15 μm Gadox)
px (μm)	75	6.5	6.5	6.5
x01 (mm)	20.8	20.8	35	35
x02 (mm)	5413	5413	5011	5011
pxeff (nm)	300	24	45	45
Photon energy (keV)	8	8	7.5	7.5
Acquisition time (s)	10 × 0.1	1	1	1

X-ray tomography

The configuration of the tomography setup as well as the sample preparation was chosen after the evaluation of the two-dimensional (2D) holographic data sets. To avoid lack of contrast and motion artifacts, which would influence the quality of reconstructions, we focused on freeze-dried cells for tomographic recordings. At the same time, the size of single CMs (typically around 150 μm) prompted us to choose a moderate magnification, resulting in a pixel size of px_eff = 45 nm. To perform a proper phase reconstruction, projections were taken for four slightly different propagation distances (see Table 4) for each angular position. For each distance, 720 equidistant angular positions were recorded over 180°. At the beginning and the end of the tomographic recording, a set of 50 empty beam images were recorded to characterize the probing wave front. After the scan, 20 images of the camera dark current were acquired. The acquisition parameters of the experiment are summarized in Table 4.

Table 4.

Acquisition Parameters of the X-Ray Tomography Experiments

Parameter	value
Photon energy E (keV)	7.5
Source-detector-distance x02 (mm)	5011.4
Source-sample-distance x01 (mm)	{35, 36, 39, 45}
Magnification M	{143, 139, 128, 111}
Pixel size px (μm)	6.5
Effective pixel size dxeff (nm)	{45.40, 46.69, 50.58, 58.37}
Number of projections over 180°	720
Number of empty beam projections	50
Number of darks	20
Acquisition time (s)	1

Phase retrieval and tomographic reconstruction. The phase and amplitude of the exit wave is reconstructed from the recorded holograms by phase retrieval, either based on iterative projection algorithms or in some cases direct Fourier filtering, which enables us to obtain a phase or projected electron density map of the cell. Note that for a biological cell at the given photon energy, absorption can be neglected, and the cell can essentially be regarded as a pure phase object. In this study, a nonlinear approach of the contrast transfer function (CTF) was used for phase retrieval (47,48). The phase distribution in the object plane $\varphi \left({\mathbf{r}}_{\perp }\right)$ retrieved by the linear form of the CTF is given by

$$\varphi \left({\mathbf{r}}_{\perp }\right)=F^{-1}\left[\frac{{\sum }_N\left(\text{sin}\left(\chi \right)+\frac{\beta }{\delta }\text{cos}\left(\chi \right)\right)\cdot F\left[I^{\left(exp,N\right)}\left({\mathbf{r}}_{\perp }\right)-1\right]}{{\sum }_{N}2{\left(\text{sin}\left(\chi \right)+\frac{\beta }{\delta }\text{cos}\left(\chi \right)\right)}^2+\alpha \left({\mathbf{k}}_{\perp }\right)}\right],$$ (1)

with natural units χ = $\left(\lambda x{k}_x^2/4\pi \right)$ for the (squared) spatial frequencies, measured intensities in the detector plane $I^{\left(\text{exp}\right)\left({\mathbf{r}}_{\perp }\right)}$, β/δ ratio of imaginary and real part of the refractive index n, N indicating the index of the respective distance, and a frequency-dependent regularization parameter $\alpha \left({\mathbf{k}}_{\perp }\right)$ (lim₁ for high and lim₂ for low spatial frequencies). The nonlinear approach uses the solution of the CTF as input for an iterative phase retrieval based on a minimization of the Tikhonov functional (47). Thus, the accuracy of the reconstructed phase is not less than the results of the CTF. The parameters of the phase retrieval are given in Table 5.

Table 5.

Phase Retrieval Parameters for the Nonlinear Tikhonov Approach of the CTF for the X-Ray Tomography Experiments

Parameter	Value
Maximum phase shift	0
β/δ ratio	1/40
lim1	0.09
lim2	0

Before tomographic reconstruction, an alignment of the single projections based on the linogram was performed to correct for a vertical movement of the sample. A ring removal was not necessary because artifacts from oversensitive pixels were reduced from the previous shifting based in the alignment of the linogram. For tomographic reconstruction, the ASTRA toolbox was used (49,50). Projections in the range in which the frame of the SiN window enters the FOV were excluded.

After tomographic reconstruction, the local electron density can be computed from the phase shift induced by each voxel length v as

$${\rho }_e\left(\mathbf{r}\right)=\frac{{\phi }_v\left(\mathbf{r}\right)}{v\lambda \cdot r_0},$$ (2)

with wavelength λ and r₀ the classical electron radius.

Dose calculation

The dose was calculated using (51,52)

$$D=\frac{I_0\tau E_{ph}}{l\rho \Delta x\Delta y},$$ (3)

with the total photon flux I₀, the exposure time τ, the energy E_ph, and the size of the illuminated area ΔxΔy as listed in Table 1. Cellular samples are commonly described by H₅₀C₃₀N₉O₁₀S. For the experimental parameters used here, this yields a mass density ρ = 1.35 g/cm³ and a mass attenuation length l = 7.46 × 10⁻⁴ m (51,52). The choice of image acquisition parameters for diffraction experiments was guided by our previous investigation and simulation of radiation damage (21). The average dose per shot in the diffraction experiments was D = 5.3 × 10⁵ Gy. For the holotomography, the total dose for a tomography scan with 720 projections an acquisition time of 1 s was estimated to be D = 1.1 × 10⁵ Gy, where the illuminated area ΔxΔy is given by the effective area (FOV) covered by the detector. This shows that the dose of a complete tomographic scan is still lower than a single shot of the diffraction measurements.

Results and Discussion

2D holography of isolated CMs

Fig. 2 shows single projections for different sample preparations, detectors, and magnifications, which were acquired to test contrast and stability imaging conditions. Table 3 summarizes the parameters tested for the different sample preparations and beamline configurations. Additionally, an intensity profile highlights the interference fringes originating from phase effects caused by the interface of the cell and the surrounding medium is marked by the red lines in the image. Noise was reduced by averaging the intensities from pixels perpendicular to the lines corresponding to a linewidth of 1 μm. The fringes originating from changes in electron density indicate the holographic nature of image formation and contain structural information. In Fig. 2 a, a projection of a freeze-dried CM recorded with a single-photon-counting detector (Eiger 4M) at an effective pixel size of px_eff = 300 nm is shown. In this projection, the interface between cell and surrounding air dominates the contrast. Besides that, the position of the nucleus can be determined, and the signal of the sarcomeric structure starts to appear. For this configuration, the field of view (FOV) is not limited by the detector size (FOV = px_eff × N_pixel) but by the illuminated area of the waveguide. Only 351 × 351 pixels of the detector are shown in the image. To reach higher magnifications, the sample-detector distance has to be increased. Because the detector distance cannot exceed the length of the experimental hutch, the sample has to be moved closer to the wave guide. This would be possible for 2D holographic measurements, but because it is the goal to image the 3D structure, and therefore the sample has to be rotated, the minimal source-to-sample x₀₁ distance is limited by the size of the SiN frame on which the CMs are mounted.

Figure 2.

Exemplary projections of the 2D holography measurements. To optimize the imaging conditions, different detectors, magnifications, and sample preparations were tested. The red lines mark the area of the intensity profiles shown below each projection. (a) Projection of a freeze-dried CM using a single-photon-counting detector (Eiger 4M) resulting in an effective pixel size of px_eff = 300 nm is shown. (b) Projection of the same CM using a fiber-coupled sCMOS Camera (20 μm LuAG) with px_eff = 24 nm is shown. (c) Projection of a freeze-dried CM at an effective pixel size of px_eff = 45 nm (15 μm Gadox) is shown. (d) Projection of a CM stained with 1% OsO₄, embedded in agarose, and mounted in a polyimide tube with a diameter of 1 mm is shown. To see this figure in color, go online.

Fig. 2 b shows a projection of the same cell acquired with a fiber-coupled sCMOS Camera (LuAG) at an effective pixel size of px_eff = 24 nm. In this case, the entire detector is illuminated, and smaller effective pixel sizes can be achieved. The signal from the cellular membrane and also sarcomeric structure is much stronger than in the projection at lower effective pixel size. The fringes around the CM are very clear, as also indicated by the profile shown below the projection. At this high magnification, only a part of the cell can be imaged because of the relatively small FOV. Furthermore, thermal drift of the sample and vibrations of the setup in the range of a few manometers led to artifacts in the tomographic reconstruction. Fig. 2 c shows that a projection of a freeze-dried CM was acquired at moderate effective pixel size of 45 nm using the sCMOS camera with a 15 μm Gadox scintillator. In this case, an entire CM could be imaged within a single projection, and the signal emerging from the cell-air interface as well as from the sarcomeric structure can be identified. Because the goal was to image an entire CM, we decided to use this beamline configuration for the x-ray tomography.

In the next step, the CM in hydrated condition were investigated. Fig. 2 d shows a projection of a CM stained with 1% OsO₄, embedded in agarose, and mounted in a polyimide tube with a diameter of 1 mm. The image was acquired with the same beamline configuration as for the freeze-dried cell shown in Fig. 2 c. In this case, the signal from the cell is very weak. Note that the quality of the signal is also diminished by the strong absorption from the agarose in the 1 mm tube. In view of the above, tomographic scans were recorded for the freeze-dried sample with the sCMOS (15 μm Gadox) camera at an effective pixel size of 45 nm.

3D structure of a single cardiomyocyte

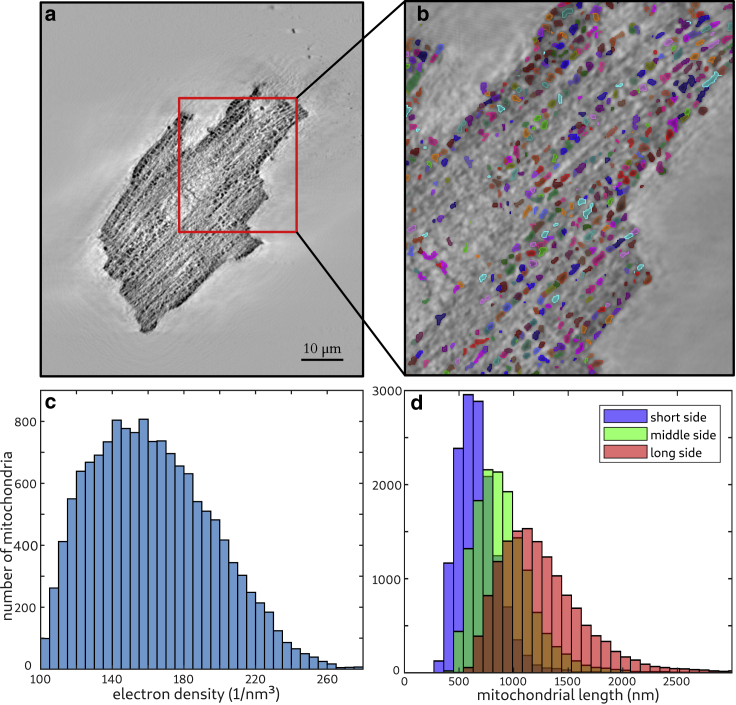
The 3D structure of the cardiomyocyte was reconstructed by propagation-based phase-contrast tomography in the holographic regime. Fig. 3 shows the results of the 3D cellular structure. For all projections, phase retrieval was performed by the nonlinear Tikhonov approach of the CTF as explained above. An example for a projection and the corresponding reconstruction by phase retrieval is shown in Fig. 3 a. The sarcomeric structure is clearly visible. The brighter stripes with a lower phase shift, perpendicular to the orientation of the cell correspond to cellular structures with a lower electron density and probably indicate the M-line of the sarcomere. Based on the phase-retrieved projections, tomographic reconstruction was performed. Fig. 3 b shows a volume rendering of the entire CM. The total volume of the cell was determined to ∼16,200 μm³. A slice of the reconstructed 3D electron density is shown in Fig. 3 c. Subcellular structures of the CM are resolved. In the case of this cell, we have two nuclei instead of just one nucleus (see white arrows in Fig. 3 c). Both are located in the center of the cell. Further, the myofibrils and the sarcomeric structure can be identified. Between the elongated myofibrils, small dense organelles with a diameter of roughly 500 nm are visible. As justified further below, these structures can be attributed to mitochondria, which are known to be abundant in CMs, providing the required energy for force generation and contraction. They are arranged in chains next to the myofibrils. Within the range of one sarcomere, the mitochondria frequently appear in pairs of two elongated blobs. Fig. 3 d shows a maximum projection of the 3D confocal microscopy stack. The actin skeleton was fluorescently labeled, and the orientation and position of the elongated actin structures indicate that fibers of 3D electron density correspond to the actomyosin filaments (myofibrils) of the CM.

Figure 3.

Phase retrieval and reconstruction. For each of the 720 angular positions, phase retrieval was performed based on the projections acquired at different Fresnel numbers. An exemplary projection and the corresponding phase retrieval are shown in (a). The 3D structure was reconstructed by the inverse radon transform. A volume rendering of the CM is shown in (b). A 2D slice though the reconstructed volume is shown in (c). White arrows indicate nuclei. Subcellular structures such as the nuclei, mitochondria, and myofibrils can be identified. Furthermore, the fluorescently labeled actin skeleton of the same cell was imaged by a confocal scan. A maximum projection of the microscopy stack is shown in (d). To see this figure in color, go online.

Segmentation of mitochondria

The dense structures observed in the electron density can be attributed to mitochondria for several reasons. First, mitochondria exhibit a high electron density close to that of a protein crystal (53) and therefore appear as dark structures compared to the surrounding actomyosin in the reconstruction. Second, they are of elliptical shape with a diameter in the range of 0.5–1 μm (54). Third, they are located next to the elongated myofibrils, as is already known from histological observations and 2D electron microscopy images of healthy cardiomyocytes (55). Most importantly, apart from the actomyosin, which appears in the form of the expected sarcomeric and myofibrillar structure in the reconstruction, there is no equally abundant organelle in CMs that could explain this additional structure.

The segmentation of the mitochondria was performed using a software designed for the analysis of 3D (fluorescence) microscopy and tomography data sets (Vision 4D; arivis AG, Munich, Germany). To this end, the 3D volume from the x-ray tomography analysis was converted to an eight-bit .tif stack and loaded into the program. Using a “blobfinder” tool, roundish structures can be identified. For this data set, a characteristic size of 12 px $\widehat{=}$ 520 nm was chosen, which fits well to the size of murine mitochondria. After this step, more than 45,000 blobs that could be associated with mitochondria, parts of the sarcomeres, membrane residues, and other subcellular compartments were tracked. Next, false-positive blobs were removed by thresholding the minimal volume to a minimal voxel count of 500 voxels per detected volume. This volume corresponds to a perfect sphere with a radius of 5 px (225 nm). Further selection of the mitochondria was done by a threshold in density. Only blobs containing voxels with at least 100 electrons/nm³ were included. As a result of this analysis pipeline, 14,334 blobs matching the size and position of the mitochondria remained, which corresponds to an estimated average density of ∼0.88 mitochondria per μm³.

Fig. 4 shows the results of the segmentation. The mitochondria appear as small dark spots in the slice of the reconstructed electron density shown in Fig. 4 a. The red box marks an area for which the quality of the segmentation is shown in Fig. 4 b. The segmented mitochondria of this slice are shown in random color to facilitate distinguishing between neighbors. In the area at the bottom of the slice, two mitochondria can be assigned for each sarcomere (from M-line to M-line). Based on this segmentation of the entire 3D volume, the electron density of all mitochondria was analyzed. A histogram of the extracted electron density is shown in Fig. 4 c. From this distribution, a mean electron density of freeze-dried mitochondria was determined to 162 electrons/nm³. Further, the size of the mitochondria can be quantified by the length of the segmented volumes along its main axis. The short, middle, and long sides of segmented blobs are shown in Fig. 4 d. From this distribution, the diameter and length of the ellipsoid-shaped mitochondria can be extracted. The peak in the histogram of the short axis (blue) corresponds to a diameter of 585 nm, whereas the long side (red) has a peak for a length of 1125 nm. For the short side, a small increase can also be seen at ∼1200 nm, and for the medium and long axis, an increase in the range of the double length of the peak can be identified. This increase can be explained by a pooling of neighboring mitochondria as one selection. Thus, we conclude that the total number of mitochondria is underrated. The mean volume of a mitochondrion was determined to be 0.23 μm³. The smaller size of the mitochondria may result from a volume change at the mitochondrial level during the sample preparation. The volume fraction was determined to ∼20% by comparing the sum of mitochondria volume to the total cell volume. Considering the shrinking of the mitochondrial level by a factor of ∼2, these results are consistent with a volume fraction between 29 and 36% in the literature. Besides analysis of density, size, and shape of mitochondria, this analysis yields the location of the mitochondria in the cell.

Figure 4.

Mitochondria were segmented based on the reconstructed 3D electron density of the CM. We used an image processing software (Vision 4D) developed for microscopy data. The dense roundish mitochondria were identified by a “blobfinder” algorithm and a threshold in size and density. In (a), one slice from the tomographic reconstruction is shown. To visualize the quality of the data analysis, a magnification of the area marked with a red box and the corresponding segmentation are shown in (b). The segmentation is colorized in a random color to distinguish neighboring mitochondria. Based on the segmented data from the entire volume, further analysis can be performed. In (c), a histogram of the maximum electron density of the segmented mitochondria is shown. (d) Distribution of the short (blue), medium (green), and long (red) axis of the segmentation is shown. From this information, the diameter and length of an average mitochondrion can be calculated. To see this figure in color, go online.

Characterization of the actomyosin lattice

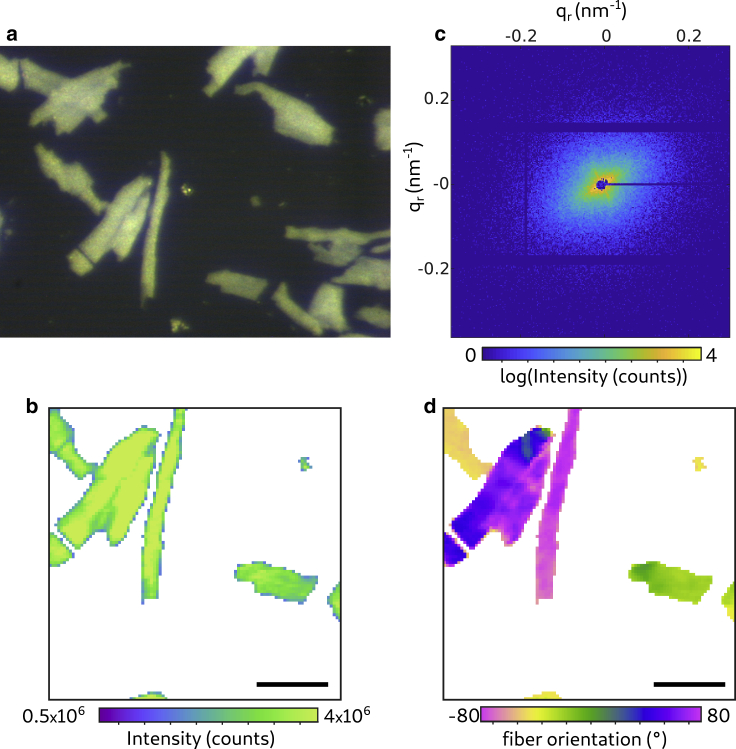
The molecular structure of heart tissue cells was analyzed by scanning x-ray diffraction. Fig. 5 shows a typical result for scanning diffraction from freeze-dried CMs using a microfocus beam. We include this example for comparison with the live recordings below. As becomes immediately evident, the x-ray darkfield signal is particularly strong in this case. Furthermore, freeze-dried CMs can be imaged with relatively high sampling in real space because fewer free radicals are produced in the absence of water or buffer. More importantly, free radicals do not spread by diffusion as in hydrated environments (21). In Fig. 5 a, an optical micrograph of (fluorescently labeled) freeze-dried CMs taken by the beamline on-axis video microscope is shown. The cells are clearly visible in brightfield contrast. Using the live images of the on-axis video microscope, the samples were aligned for the x-ray diffraction measurements. An example for an x-ray darkfield image from the analysis of freeze-dried cells is shown in Fig. 5 b. Pixels with an intensity below 1.5 × 10⁶ counts were masked in white. The step size was 2 μm, and the acquisition time was 0.05 s. In Fig. 5 c, an isolated diffraction pattern is shown, representing a single shot from the freeze-dried cells. There are no actomyosin reflections visible in the diffraction pattern, indicating that the structure of the cells is damaged by freeze drying. The diffraction pattern shows an anisotropy that nevertheless makes it possible to determine the local actomyosin fibril orientation. The fiber orientation and anisotropy, shown in Fig. 5 d, is obtained from an automatized principal components analysis in the same way as in (20,46). To improve the quality of the diffraction data, we turn to recordings of hydrated and living cells using a polypropylene chamber. In view of radiation damage, a “diffract before damage” strategy is adopted (21).

Figure 5.

Scanning diffraction from freeze-dried CMs. (a) Micrograph recorded with the beamline on-axis optical microscope (brightfield) is shown. (b) X-ray darkfield image is given. The image is formed by integration of all detector counts (outside the beamstop), i.e., the integrated scattering signal. Pixels with an intensity below 1.5 × 10⁶ counts are masked in white. Scale bars, 50 μm. (c) Isolated diffraction pattern of a single shot on a freeze-dried cell (0.05 s accumulation time) is shown. (d) Orientation of the actomyosin fibrils is shown. To see this figure in color, go online.

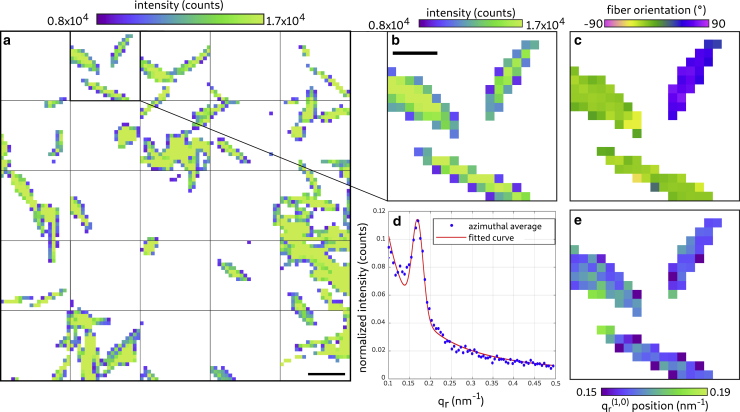
Fig. 6 illustrates the data collection and processing, which closely followed (22) but was now applied to living cells. We also took into account the constraints of sparse sampling and reduced dose to collect a signal that was not spoiled by radiation damage (21). For data analysis, the nanodiffraction toolbox (46) was used. In Fig. 6 a, the liquid chamber used for the measurement of living CMs is shown. Fig. 6 b shows the example of an isolated diffraction pattern recorded by a single shot. The acquisition time was 0.1 s. In contrast to the freeze-dried CMs, the signal of the living CM shows clearly both the (1,0) and the (1,1) reflection in the diffraction pattern. The cells were raster scanned with a step size of 5 μm, yielding a coarse darkfield map of the scanned CMs. An example for such a map can be seen in Fig. 6 d. Note that the background in the map is colored in white based on a threshold of minimal photon counts. Next, each diffraction pattern above this threshold was azimuthally averaged, and a mean background was subtracted to obtain a local SAXS curve. The model function

$$I\left(q_r\right)=A{q}_r^{-B}+C\text{exp}\left({\left(\frac{q_r-q^{\left(\mathrm{1,0}\right)}}{\sigma }\right)}^2\right)+D\text{exp}\left({\left(\frac{q_r-\sqrt{3}{q}^{\left(\mathrm{1,0}\right)}}{\sigma }\right)}^2\right)+E$$ (4)

was fitted to these data, where A–E and q^(1,0) are fit parameters. Whereas A × $q_r^{-B}$ describes a monotonous SAXS contribution, the actomyosin reflections are modeled as Gaussians with amplitudes C and D and positions q^(1,0) and q^(1,1). Note that the relation $q_r^{\left(\mathrm{1,1}\right)}=\sqrt{3}{q}_r^{\left(\mathrm{1,0}\right)}$ was used to obtain the position of the (1,1) reflection. The reflection width was set to σ = 0.0184 nm⁻¹. An example of this fit for the isolated shot can be seen in Fig. 6 c. This fit yields the position of the (1,0) position. In Fig. 6 f, the q^(1,0) reflection positions of the sample are plotted. Using principal component analysis, the fiber orientation was determined for the diffraction pattern for all scan points. An example for the fiber orientation is shown in Fig. 6 e.

Figure 6.

Signal processing of scanning diffraction data: living CMs. (a) Photograph of the sample chamber used for measuring living CMs is shown. (b) Diffraction pattern of a living muscle cell is shown. The (1,0) and the (1,1) reflections are visible in the pattern. (c) One-dimensional azimuthal average of the diffraction pattern on the left is shown. The fitted curve was obtained using the fitting function introduced in Eq. 4. (d) Darkfield map of a cluster of living cells is given. Scale bars, 50 μm. (e) Orientation of the myosin fibers obtained by performing a principal component analysis is shown. (f) Position of the (1,0) reflection obtained from the fitted curves is shown. In (c–e), all pixels with a darkfield intensity below 2 × 10⁴ counts were masked in white. To see this figure in color, go online.

For comparison to the living CM, we also investigated chemically fixed, hydrated cardiac tissue cells. Fig. 7 a shows an example for a darkfield map of such a recording. Multiple scan areas covered by continuous piezo scanning, each with a size of 200 × 200 μm² and an acquisition time of 0.05 s per scan point, were stitched using a stepper motor below the piezo. The entire composite with 5 × 5 piezo scans results in the darkfield map in Fig. 7 a. The different scans areas are indicated by boxes. The acquisition time for each scan point was 0.05 s. In Fig. 7 b, a zoom of the marked box in (Fig. 7 a) is shown. In Fig. 7 c, the calculated fiber orientation of this region is plotted. The data show that the fiber orientation throughout a cell is roughly constant. An example for an azimuthal average of a single diffraction pattern of a chemically fixed cell is shown in Fig. 7 d. Only the first peak representing the (1,0) reflection is visible. This was the case for all shots recorded from all chemically fixed cells. Therefore, the signal of the (1,1) reflection was excluded for the fit of the fixed cells. The results for the ${\text{q}}_{\text{r}}^{\left(\mathrm{1,0}\right)}$ position for one region of the map are shown in Fig. 7 e.

Figure 7.

Scanning diffraction: hydrated and chemically fixed CMs. (a and b) Darkfield maps of isolated, fixed cardiomyocytes are given. Scale bar, (a) 100 μm, (b) 50 μm. (c) Orientation map of the actomyosin fibrils is shown. (d) One-dimensional azimuthal average of a single shot from a fixed cardiomyocyte is given. In contrast to Fig. 6c, only the (1,0) reflection is visible. (e) Position of the (1,0) reflection is shown. All pixels with a darkfield intensity below 0.8 × 10⁴ counts were masked in white. To see this figure in color, go online.

Next, we turn to the recordings of living cells, which are displayed in Fig. 8. These cells were in an initially living state, as one could derive from their contraction inside the sample chamber before the measurement. However, one has to keep in mind the challenging issue of radiation damage arising during data acquisition, which will have a considerable effect on cellular structures. Thus, we can only claim that the cells are living initially at the beginning of the scan or when recording shots from a new cell. In Fig. 8 a, a darkfield map of a cluster of living CMs is depicted, the same that was already shown before when explaining the workflow. The boxes marked in in the map of the darkfield signal are represented in detailed view in Fig. 8, b–d. For the three areas, the amplitude of the first peak representing the (1,0) reflection is shown in (Fig. 8 b.1). The first peak was visible in all observed boxes. On the contrary, this is not the case for the amplitude of the second peak representing the (1,1) reflection, which is shown in (Fig. 8 b.2). The harmful effect of radiation damage can be observed by the loss of the (1,1) reflection signal that is visible in the first few lines of the first area (Fig. 8 b.2). In this region, the signal of the (1,1) reflection is clearly visible in the first scan points, but then vanished. This observation is consistent with previous observations on muscle tissue, in which the intensity of the second peak vanished when tissue was affected by radiation damage (21). Here, we also observe that the intensity of the second peak decreases, indicating that living cells are strongly affected by radiation damage. This signal decrease is plausible because the scan points were acquired row by row from top left to bottom right, and free radicals spread easily during the scan. Hence, for the first region, the concentration of free radicals was lower, and less time was available for their diffusion or for an apoptotic reaction of the cells. The map of the (1,1) peak amplitude also shows that the intensity decreases line by line.

Figure 8.

Scanning diffraction: living CMs. (a) Darkfield image showing three CM clusters magnified in (b) and (d). Scale bars, 50 μm, colorbar: linear range 2 × 10⁴–4.5 × 10⁴ counts. In all figures, pixels with a darkfield intensity below 2 × 10⁴ counts were masked in white. The structural parameters of the actomyosin lattice were calculated, namely 1) amplitude of the (1,0) reflection, 2) amplitude of the (1,1) reflection, 3) ${\text{q}}_{\text{r}}^{\left(\mathrm{1,0}\right)}$ lattice spacing, and 4) histogram of the ${\text{q}}_{\text{r}}^{\left(\mathrm{1,0}\right)}$ position (b.1). Scale bars, 25 μm, colorbar: linear range 0–0.1 counts/pixel (b.2). Colorbar: linear range 0.5 × 10⁻³–4 × 10⁻³ counts/pixel (b.3). Colorbar: linear range 0.14 nm–0.18 nm⁻¹ (b.4). In area (b), only shots in which two peaks are visible contributed to the histogram. To see this figure in color, go online.

The q-spacing of the the actomyosin lattice was evaluated for the entire data set. The subfigures with index (Fig. 8 b.3) show the map for the q-spacing of the different areas. Boxes with index (Fig. 8 b.4) show the distribution of the q-spacing (histogram). In Fig. 8 b.4, only shots with two visible peaks were selected for the histogram. In Fig. 8 c.4 and Fig. 8 d.4, only shots with one peak contributed to the histogram. A Gaussian was fitted to every histogram to obtain the mean and standard deviation. The analysis of the histograms shows that the q-spacing for the first box (q = 0.149 ± 0.007 nm⁻¹) is smaller than the q-spacing in Fig. 8 c (q = 0.157 ± 0.011 nm⁻¹) and Fig. 8 d (q = 0.159 ± 0.009 nm⁻¹). This leads us to conclude that the q-spacing increases when the cells are affected by radiation damage. Because the presented scans were also partly affected by damage as inferred from the decrease of the (1,1) peak, we adapted our measurement strategy and, in addition to the scans, also took the diffraction pattern from isolated points within the CMs, moving to new cells for each shot.

Finally, the violin plot in Fig. 9 compares the distribution of the q-spacing for (initially) living, hydrated CMs and CMs that were chemically fixed. In fixed CMs, only the (1,0) reflection was visible in the diffraction pattern. For the characterization of living cells, the diffraction patterns from the data already seen in Fig. 8, as well as additional single shots, from freshly prepared samples were used. Only patterns with two visible peaks were used for the calculation of the lattice spacing of living CMs. The q-spacing determined for fixed cells is larger than the one found for the living cells. To quantify the mean and standard deviation, Gaussians were fitted to the distributions. The horizontal lines in the violin plot indicate the mean value. For living CMs, a q-spacing of q = 0.148 ± 0.006 nm⁻¹ was obtained, and for chemically fixed CMs, q = 0.167 ± 0.006 nm⁻¹ was obtained. The corresponding actomyosin lattice spacing d^(1,0) = $\left(2\pi /q^{\left(\mathrm{1,0}\right)}\right)$ was 37.6 and 42.5 nm for the fixed and living cells, respectively.

Figure 9.

Actomyosin lattice spacings. Distribution of the lattice spacing obtained by the position of the ${\text{q}}_{\text{r}}^{\left(\mathrm{1,0}\right)}$ reflection for living and chemically fixed CMs is shown. The horizontal lines in the violin plot indicate the mean value of the q-spacing. The corresponding actomyosin lattice spacing was determined to be 37.6 nm for chemically fixed CMs and 42.5 nm for living cells. To see this figure in color, go online.

Conclusions

In this work, we have combined full-field 3D coherent x-ray imaging and scanning x-ray diffraction to analyze the cellular and molecular structure of isolated adult CMs of wild-type mice. The 3D electron density distribution of a single CM was reconstructed from propagation-based x-ray phase-contrast tomography with a voxel size smaller than 50 nm. Single myofibrils, the sarcomeric organization, and location of mitochondria were visualized within a single cell without sectioning. The molecular structure of the actomyosin lattice was probed by scanning x-ray diffraction using CRLs for microfocusing.

For the first time, to our knowledge, the diffraction signal of the actomyosin contractile unit could be observed for living cells. Importantly, whereas previous recordings of living cells only showed a monotonous decay of the SAXS signal (16), the diffraction signal of CMs shows characteristic peaks that can be fitted to determine the actomyosin lattice spacing. A comparison between living cell and chemically fixed cell recordings indicates that the characteristic lattice distances (d₁₀) shrink by ∼10% upon fixation, namely from 42.5 nm to 37.6 nm in the (1,0) lattice planes. The values fall into the range reported in the literature for rodent cardiac muscle (rat trabecula), i.e., 42.5–44.5 nm and 34–36 nm reported in (56) for relaxed (skinned) and intact (unskinned) trabecula, respectively, and 38 nm reported in (5).

Despite its merit in extending diffraction analysis to living CMs, this study also indicated limitations of this approach, imposed by radiation damage and low signal/noise. For future work, it would be desirable to probe different states of contraction, eventually in combination with well-controlled forces acting on the cell. To this end, only isolated shots in fresh spots should be collected, guided by online light microscopy and correlated with the contraction state. Continuous replenishment of samples and washing out of free radicals could be achieved by suitable microfluidic devices. Finally, high-throughput lattice parameter determination at the single cell level, eventually in the form of “diffraction flow cytometry,” could be used as a diagnostic tool for dissociated tissue. To this end, genes regulating actomyosin structure in patient-derived stem cells would be targets of particular interest (57). Concerning the tomography, investigations of hydrated or even living cells seem very challenging based on our results. Frozen hydrated (vitrified) cells after plunge freezing (18,29,58, 59, 60), however, could be a suitable approach to probe the native structure in 3D. In this study, we could, for example, determine an average density of ∼0.88 mitochondria per μm³ as well as the average size of a mitochondrion in such a CM. A number of technical improvements can also be foreseen; a small glass tube with thin walls and a hydrogel could provide stability for single cells and minimize absorption. The sample could be moved closer to source spot for higher magnification, and single-photon-counting pixel detectors with higher quantum efficiency could be used.

Concerning the sequence of correlative imaging of the same cell, it is important to first perform optical fluorescence microscopy, second holotomography, and finally diffraction, in view of mitigating the radiation damage. The final state could then be probed again by optical microscopy to evaluate damage.

Author Contributions

T.S. and M.R. designed research. K.T. developed adult cardiomyocyte protocols and contributed expertise. M.R. and T.S. carried out the x-ray holography experiments. M.R., C.N., T.S., and J.-D.N., carried out the diffraction experiments. J.-D.N. wrote analysis software. M.R. carried out the phase retrieval and tomographic reconstruction. C.N. and J.-D.N. carried out the SAXS analysis, supervised by T.S. M.B., and M.R. prepared the freeze-dried cells and recorded the florescent microscopy data. M.R., T.S., and C.N. wrote the article; all authors read final data.

Editor: Bridget Carragher.