Mechanisms of Local Stress Amplification in Axons near the Gray-White Matter Interface

Abstract

Diffuse axonal injury is a primary neuropathological feature of concussion and is thought to greatly contribute to the classical symptoms of decreased processing speed and memory dysfunction. Although previous studies have investigated the injury biomechanics at the micro- and mesoscale of concussion, few have addressed the multiscale transmission of mechanical loading at thresholds that can induce diffuse axonal injury. Because it has been recognized that axonal pathology is commonly found at anatomic interfaces across all severities of traumatic brain injury, we combined computational, analytical, and experimental approaches to investigate the potential mechanical vulnerability of axons that span the gray-white tissue interface. Our computational models predict that material heterogeneities at the gray-white interface lead to a highly nonuniform distribution of stress in axons, which was most amplified in axonal regions near the interface. This mechanism was confirmed using an analytical model of an individual fiber in a strained bimaterial interface. Comparisons of these collective data with histopathological evaluation of a swine model of concussion demonstrated a notably similar pattern of axonal damage adjacent to the gray-white interface. The results suggest that the tissue property mismatch at the gray-white matter interface places axons crossing this region at greater risk of mechanical damage during brain tissue deformation from traumatic brain injury.

Significance

Although diffuse axonal injury has been identified as a major mechanism of the impairment of brain function after mild traumatic brain injuries, a thorough understanding of the transmission of loads from the scale of tissues to axons is lacking. Here, we studied the transmission of stress in axons at the gray-white matter interface, where we observed overt axonal injury in in vivo experiments. In agreement with our experiments, our theoretical model predicted the amplification of stress in axons near the gray-white matter interface, implying that axonal injury can occur at the interface even in the subthreshold loading of tissues. Our results contribute to the understanding of the mechanisms of axonal injury and guide the future development of multiscale models of mild traumatic brain injury.

Introduction

Although most patients with a concussion quickly recover, 20–30% suffer persistent neurocognitive dysfunction after this so-called “mild” traumatic brain injury (TBI). Recent evidence suggests that persisting symptoms of concussion, including decreased processing speed and memory dysfunction, are a consequence of degenerative diffuse axonal injury (DAI) (1,2). Selective damage to axons in the white matter resulting from concussion occurs during head rotational acceleration, in turn causing dynamic deformation of brain tissue. It is thought that the very long and thin architecture of axons, in combination with their arrangement in highly organized white matter tracts and their viscoelastic nature, renders them particularly susceptible to damage from shear and tensile forces as the brain is rapidly deformed (3). The rate of strain is particularly important in DAI. At slow strain rates, axons are able to withstand substantial strains, whereas axonal damage occurs at high strain rates for the same magnitude of strain (4, 5, 6, 7). We have previously shown that microtubules, the stiffest components of axons, can mechanically break at the moment of injury (8,9). We then found that the viscoelastic properties of the microtubule-stabilizing protein, τ, plays a key role in this process (10,11). Specifically, at high rates of axon stretch, τ proteins induce high stress at their microtubule-binding sites as parallel microtubules slide past each other. Past a failure threshold, this causes rupture of the microtubules, which results in interruption of the transport. In turn, accumulation of transported proteins causes regional swelling of the axons leading to degeneration (3,12). The gold standard in assessing axonal pathology is observing the buildup in amyloid precursor protein (APP) that occurs in areas of transport interruption in the forms of varicosities and bulbs (3,13,14).

Swollen axonal profiles are commonly found in the deep gyri at the interface between the gray and white matter of the cortex after TBI (3,15,16). The gray-white matter interface represents an area where mechanical mismatch of adjoining tissues occurs. The gray matter is composed of an isotropic mixture of neuronal soma, neurites, and glia, while the white matter is composed of an anisotropic tract organization of axons, myelin, and oligodendrocytes and other glia (17,18). Although some studies suggest that white matter is stiffer than gray matter (19), there remains debate regarding the specific elastic modulus for each tissue type. Nonetheless, previous works show that differences in material properties of organization and/or elastic modulus of tissues sharing an interface may lead to amplification of mechanical stresses and concentration of injury (20).

This work investigates the amplification of tissue-level stresses in axons near the gray-white matter interface. Our experimental results from a clinically relevant large animal model of concussion demonstrate the overt presence of axonal pathology, selectively near the gray-white matter interface. A computational analysis, including a detailed geometric model, is presented that shows the nonuniform distribution of stress in axons near the interface, and a simplified computational approach elucidates the mechanism of the amplification of stress near the interface. Furthermore, an analytical model closely reproduces the computational results by considering a fiber adhered to a strained interface. Finally, the effect of varying levels of adhesion between the axon and the surrounding tissue was examined, as was the influence of a gradual change in material properties at the interface.

Materials and Methods

Experimental design, procedures, and analysis

Rotational acceleration model of TBI

All experiments were conducted in accordance with protocols approved by The University of Pennsylvania Institutional Animal Care and Use Committee and in accordance with the National Institutes of Health (NIH) Guide for the Care and Use of Laboratory Animals. Tissue was examined from 6-month old female Hanford miniature swine that previously underwent the rotational acceleration model of TBI under general anesthesia and survived for 72 h (n = 4) and was compared with shams (n = 3). This established model induces injury via forces caused by rotational acceleration and deceleration due to pure impulsive centroidal head rotation (5,7,12,21, 22, 23). For TBI in humans, the size of the brain is critical because mass effects between regions of tissue can create high strains during dynamic brain deformation and rapid accelerations (24, 25, 26). Accordingly, injury parameters were scaled up relative to brain mass to create the mechanical loading of brain tissue relevant to that which occurs in human TBI (5,24, 25, 26). Notably, there is an absence of any head impact or forces arising from linear acceleration or deceleration.

After induction of anesthesia using 0.4 mg/kg midazolam intra muscular and 5% inhaled isoflurane, animals were intubated, and anesthesia was maintained via 2.5% inhaled isoflurane. The HYGE pneumatic actuator device (HYGE, Kittanning, PA) was used to induce rapid head rotation. Specifically, the HYGE actuator generates linear motion via the triggered release of pressurized nitrogen. This linear motion is then converted to angular motion via custom-designed linkage assemblies to induce rotation over ∼20 ms. Rotational kinematics were recorded using angular velocity transducers (Applied Technology Associates, Albuquerque, NM) mounted to the linkage sidearm coupled to a National Instruments data acquisition system (Austin, TX) running custom LabView software (10 kHz sampling rate). In this fashion, pure impulsive centroidal head rotation of up to 110° was produced in the coronal plane with a peak angular velocity of 225–250 rad/s. Animals were recovered from anesthesia and returned to the housing facility. Although the procedure is nonsurgical, preemptive analgesia was provided postinjury in the form of 0.1–3 mg of Buprenex (slow-release preparation) subcutaneous and acetaminophen 50 mg/kg per rectum. Sham animals were euthanized 72 h after being subjected to identical procedures absent head rotation.

At the study endpoint, all animals were deeply anesthetized and transcardially perfused using chilled heparinized saline (2 L) followed by 10% neutral buffered formalin (8 L). Brains were subsequently postfixed for 7 days in 10% neutral buffered formalin, sectioned into 5 mm blocks in the coronal plane, and processed to paraffin using standard techniques. Whole-brain coronal, 8-μm-thick tissue sections were cut from each block, and standard hematoxylin and eosin staining was performed.

Immunohistochemistry

For examination of axonal pathology, whole-brain coronal tissue sections were selected from four regions spanning the rostrocaudal extent of the brain, including at the levels of 1) the frontal cortex at 5 mm from the frontal pole, including prefrontal cortex; 2) the basal ganglia at the level of the head of caudate nucleus; 3) the anterior hippocampus; and 4) the posterior hippocampus at the level of the posterior commissure.

After deparaffinization and rehydration, tissue sections were immersed in aqueous hydrogen peroxide (15 min) to quench endogenous peroxidase activity. Antigen retrieval was performed in a microwave pressure-cooker with immersion in preheated Tris-EDTA buffer. Subsequent blocking was achieved using 1% normal horse serum (Vector Labs, Burlingame, CA) in Optimax buffer (BioGenex, San Ramon, CA) for 30 min. Incubation with the primary antibodies was performed overnight at 4°C. Specifically, sections were labeled with an antibody reactive for the N-terminal amino acids 66–81 of the APP (Millipore, Billerica, MA) at 1:80 k, permitting visualization of APP accumulating within transport-interrupted axonal bulbs or swollen varicosities along the length of damaged axons. After rinsing, sections were incubated with the relevant species-specific biotinylated secondary antibody for 30 min (Vector Labs), followed by avidin-biotin complex (Vectastain Universal Elite kit; Vector Labs). Finally, visualization was achieved using 3,3′-diaminobenzidine (Vector Labs), and counterstaining with hematoxylin was performed.

Positive control tissue for APP immunohistochemistry included sections of swine tissue with previously established axonal pathology. Omission of the primary antibody was performed on the same material to control for nonspecific binding. Slides were digitally scanned at 20× using the Aperio slide scanner (Leica Biosystems, Wetzlar, Germany) and viewed using the associated ImageScope software (Leica Biosystems). Results were presented in Fig. 1.

Figure 1.

Representative examples of axonal pathology as identified using APP immunohistochemistry after the rotational acceleration model of TBI at 72 h postinjury. (a) A map generated from a high-resolution digital scan of histology shows the dorsomedial frontal cortex with APP immunoreactive axonal pathology that has been manually annotated (blue). The gray-white interface is outlined in green. Note the predominant pathology at the gray-white interface at the gyral crest at the dorsal surface, a feature observed in all animals. (b) A representative example of multiple varicose axonal swellings immunoreactive for APP at the gray-white interface of the gyral crest in the frontal cortex is shown. (c) Example of a single axonal swelling within the gray-white boundary in the parahippocampal cortex showing multiple points of transport interruption and APP accumulation is given. (d) An absence of APP immunoreactivity in a sham animal is shown. (e) Extensive axonal pathology along the gray-white interface in the fusiform gyrus is shown. Scale bars, 50 μm long. All dotted lines represent the approximate region of the gray-white interface. GM, gray matter; WM, white matter. To see this figure in color, go online.

A three-dimensional computational model with a detailed geometry

To assess the transfer of tissue-level loads between the gray and white matter and neurons, a finite element model with the detailed geometry of an axon was prepared using a computationally reconstructed geometric model. The initial three-dimensional geometric model was prepared using the Neuronize software package (27). The three-dimensional geometry of a neuron was generated based on previously processed, two-dimensional images of neurons obtained using microscopy. The result was a geometric model, consisting of triangular elements that covered the surface of an axon, cell body, and dendrites. Next, the nonmanifold feature detection functions in the Blender (28) and MeshLab (29) software packages were used to remove the intersecting elements of the geometric model. The geometric model was then smoothed using a Laplacian filter (30).

The surface mesh was next imported to the COMSOL Multiphysics finite element software package (31). An unstructured volumetric mesh, consisting of second-order tetrahedral elements, was generated to model the neuron (Fig. 2 f). The neuron was embedded in a cylindrical geometry of relatively larger dimensions that represented the gray and white matter. The cylinder was oriented such that the axon ran roughly parallel to the axis of the cylinder. To study the mechanism of load transfer, a pseudoelastic model was used with isotropic linear elastic materials, including varying elastic moduli for the gray and white matter, and the neuron (Table 1). The soma and dendrites were modeled using elastic moduli 1/3 of the modulus of the axon (32). Loading of the tissue was modeled by prescribing the nodal displacements at the flat surfaces of the cylindrical domain. Nominal strains of 20%, close to the values observed in experiments of axonal injury, were prescribed to the model (33,34). The normal stress in the axon in the orientation parallel to the axon was analyzed.

Figure 2.

A three-dimensional computational model of the transfer of loads to an axon near the gray-white matter interface, showing a nonuniform distribution of stress over the length of the axon. (a) Computational results of the stretch of a neuron in a gray-white continuum background, representing the effective properties of the surrounding tissue, are shown. The colors display normal stress in the direction of stretch, shown by the white arrows, normalized by the mean axial stress σ_mean. (b) Schematic of an axon, shown in green, passing from the gray matter, plotted in pink, to the white matter, plotted in white, is given. (c) Normal stress at various points through the length of the axon is shown. A nonuniform distribution of stress is exhibited within the gray matter, close to the gray-white matter interface. The vertical dashed line (pink) marks the boundary between the gray and white matter. (d) Unlike (c), in which material heterogeneity induces amplification of stresses close to the gray-white matter interface, stress amplification is not observed in axons embedded within a homogeneous environment (E_g = E_w = 1.4 kPa). (e) Similar to the stress distribution in (c), the normal strain ε_a also exhibits a nonuniform distribution close to the gray-white matter interface. (f) Second-order tetrahedral elements are used to mesh the neuron. (g) Stress amplification at the interface increases with increasing material heterogeneity. (h) Refining the mesh size does not noticeably change the stress amplification in (c) because the maximal and mean stresses change less than 3% with reducing mesh size. The normalized difference is defined as (σ_max − ${\hat{\sigma }}_{\text{max}}$)/σ_max and (σ_mean − ${\hat{\sigma }}_{\text{mean}}$)/σ_mean, where σ_max and σ_mean are, respectively, the maximal and the mean axial stresses calculated with the normal mesh size, and ${\hat{\sigma }}_{\text{max}}$ and ${\hat{\sigma }}_{\text{mean}}$ are, respectively, the maximal and the mean axial stresses calculated with finer mesh sizes. To refine the mesh size, we increased the number of elements by factors of 1.5, 2, and 4. (i) The normalized least-squares ${\left[\sum _{i=1}^n{\left({\sigma }_i-{\hat{\sigma }}_i\right)}^2\right]}^{1/2}/{\left[\sum _{i=1}^n{{\sigma }_i}^2\right]}^{1/2}$ also does not change more than 5% with reducing mesh size or using hyperelastic models (${\hat{\sigma }}_i$ is the axial stress at different points through the length of the axon using a finer mesh or a hyperelastic model). (j) θ is defined as the angle between the axon orientation and the interface. (k) Because axons may not be always perpendicular to the interface, the effect of θ on the stress distribution in axons was studied, and it is shown that axons experience the highest stress amplification when they are perpendicular to the gray-white matter interface (θ= 90). To see this figure in color, go online.

Table 1.

Parameters Used in the Axially Symmetric Computational and Theoretical Models

Parameter	Value	Description	Reference
Ew	2.5 kPa	Elastic modulus of white matter	(18,19)
Eg	1.4 kPa	Elastic modulus of gray matter	(18,19)
ν	0.4	Poisson’s ratio	(63,64)
Ea	30 kPa	Elastic modulus of axons	(65)
ta	1.0 μm	Thickness of axons	(35,63)

A simplified axially symmetric computational model

A simplified axially symmetric model was prepared to investigate the effect of adhesion between axons and the tissue and to explain the mechanism of the load transfer between the white and gray matter and the axon. The model consisted of a cylindrical domain, representing the axon, two larger cylinders, modeling the gray and white matter, and a thin layer between the axon and the surrounding tissue, modeling the level of adhesion. Typically, the adhesion layer was modeled using an elastic modulus, E_h, 1/10 of the modulus of the axon (35). The effect of the level of adhesion was investigated by varying the elastic modulus of the adhesion layer. Furthermore, the effect of the gradual change in the stiffness of the tissue at the interface of the gray and white matter was modeled by a linear gradient of the elastic modulus of the medium surrounding the axon over a distance l_i. The axially symmetric three-dimensional model was represented using an unstructured mesh, consisting of two-dimensional triangular elements. The same material properties used in the detailed model were used in the simplified model. The right surface of the model domain, white matter, was fixed whereas the left surface, gray matter, was moved to prescribe 20% axial tissue strain.

The material properties used in the models are given in Table 1. Our study treats material properties as time independent, as commonly practiced in pseudoelastic analyses of biological tissues (36,37). Previous studies, however, showed that the apparent stiffness of brain tissue increases at higher rates of strain (19). Therefore, to model deformation at higher speeds and accelerations, corresponding to shorter durations of impact in sports-related injuries, the tissue behavior may be modeled by higher elastic moduli in future studies. At higher strain rates, up to 100 s⁻¹, we expect a moderate change in the ratio of the stiffness of the gray and white matter. However, the stiffness of both gray and white matter will remain smaller compared with the elastic stiffness of the axon. Therefore, the results should hold over the range of strain rates 20–100 s⁻¹. In this work, we carry out quasistatic analyses because the timescale of the equilibration of elastic waves in the brain tissue is orders of magnitude smaller than the timescale of the application of loads. The speed of sound in the brain tissue is on the order of 10³ m/s (38), and the characteristic lengths of the studied problem are of the order of 10³ μm, resulting in timescales of equilibration of the order of 1 μs. The strain of ∼0.2 is applied to the tissue in ∼10⁻² s, indicating that the duration of loading is ∼4 orders of magnitude larger than the timescale of the transmission of elastic waves, confirming the validity of these quasistatic analyses.

Results

Axonal injury at the gray-white matter interface

Clinical presentation after the rotational acceleration model of TBI was as previously reported in detail (23,39). Briefly, normal mobilization, feeding, and drinking behavior resumed upon recovery from anesthesia. In all animals, neurological examination was grossly normal with respect to mental status, posture, tone, gait, power, sensation, proprioception, and cranial nerve examination when possible to examine. On gross examination, brains appeared normal at 72 h after rotational injury, without evidence of focal pathologies including hemorrhage, and were indistinguishable from shams. There was no evidence of brain swelling or raised intracranial pressure, and the cerebral hemispheres were symmetrical. Hematoxylin and eosin staining confirmed an absence of hemorrhagic, ischemic, or focal pathologies.

As shown in Fig. 1, immunohistochemistry revealed widespread axonal injury across all brain levels comprising of axons that were morphologically swollen, with abnormal accumulations of APP secondary to axon transport interruption (identical to that observed in human DAI (13,14,40, 41, 42, 43, 44)). As reported previously in this model (23,39), DAI was observed in all brain levels in a stereotyped distribution that included hemispheric differences consistent with a biomechanical etiology in the coronal plane. Upon a more detailed review of the gray-white boundary and consistent with predictions from our theoretical model in Fig. 2, multiple foci of injured axons were observed close to the gray-white interface in all injured animals (Fig. 1 a–c and e). Interestingly, although not directly quantified, this was commonly observed in the frontoparietal cortex at the gyral crests within the gyri orientating toward the dorsal surface of the brain (Fig. 1, a and b). No axonal pathology was observed in sham animals.

Nonuniform distribution of stresses in axons

A three-dimensional computational model with a detailed geometry of a neuron was used to study the transfer of loads between the gray and white matter and a neuron close to the gray-white matter interface (Fig. 2, a and b). As the tissue was loaded at the boundaries, highly nonuniform normal stresses parallel to the orientation of the axon developed in the axon. The normal stress, averaged over cross sections of the axon, exhibited a peak within the gray matter, close to the gray-white matter interface (Fig. 2 c), which in turn generates a significantly higher tensile strain at this region (Fig. 2 e). The peak stress was 40% larger than the mean stress in the axon in the white matter (Fig. 2 c). The stress amplification further increased with increasing the difference between the gray and white matter stiffness (Fig. 2 g), whereas the stress amplification was not observed when the axon was embedded within a homogeneous environment (Fig. 2 d). Also, our simulations showed that the stress amplification observed in Fig. 2 c is independent of element mesh size and material constitutive model (Fig. 2, h and i). Furthermore, because axons may not be always perpendicular to the gray-white matter interface, we studied how the stress amplification changes with axon orientation (Fig. 2 j), and we found that axons experience the highest stress amplification when they are perpendicular to the gray-white matter interface (Fig. 2 k).

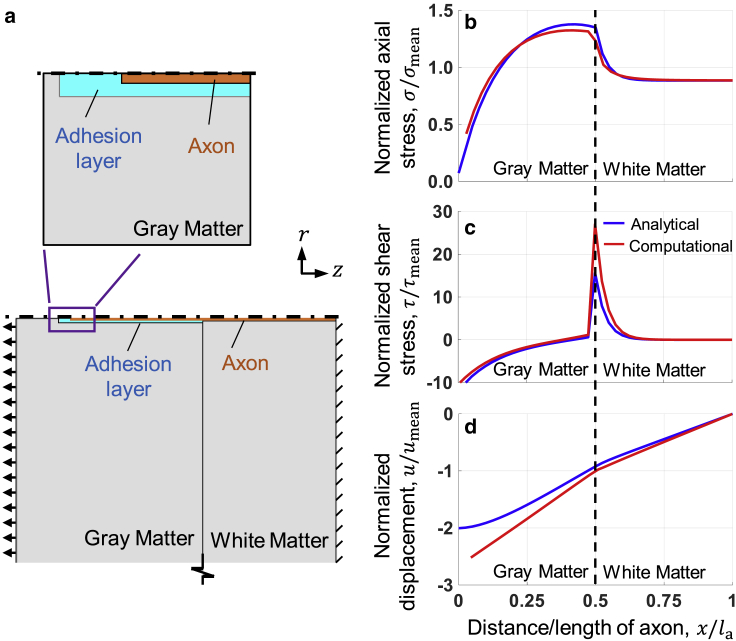
We then used a model with a simplified, axially symmetric geometry (Fig. 3 a) to investigate the mechanism of the nonuniform distribution of stress in axons close to the gray-white matter interface. In this model, the axon is constrained at the end in the white matter because the part of the axon in white matter is commonly much longer than the part in the gray matter because axons may travel deep into white matter and beyond. Similar to the model presented in Fig. 2, the simplified model shows a peak in the axial stress σ close to the gray-white matter interface within the gray matter (red curve in Fig. 3 b). Starting from the gray matter and going to the white matter, the axial stress σ increases through the length of the axon until reaching a maximum close to the gray-white matter interface. After that, within the white matter, σ decreases until reaching a plateau. The axonal shear stress τ also exhibits different trends in gray and white matter (red curve in Fig. 3 c). At the interface, it is singular but has a different slope on the different sides of the interface. In the gray matter, there is a rapid increase in τ peaking at the interface, whereas in the white matter, it starts from a high value and rapidly decreases to plateau at zero. As expected, the mean displacement of the axon u is also different at the two sides of the gray-white matter interface (red curve in Fig. 3 d).

Figure 3.

Results of the analytical model of a fiber adhered to a strained bimaterial interface closely agree with the computational results. (a) The simplified, axially symmetric computational model of the axon near the gray-white matter interface is given. Bottom panel: the axon is modeled as a cylinder, shown in orange, adhered to the surrounding tissue, shown in gray, by an adhesion layer, shown in blue. The surrounding medium is modeled as a background continuum much larger than the axon and the adhesion layer. The arrows demonstrate the direction of loading, whereas the diagonal lines indicate constrained motion of the domain. The horizontal black dashed-dotted line marks the axis of symmetry. Top panel: the zoomed-in view of the axon and the adhesion layer marked by the purple box in the bottom panel. (b) Normalized axial stress in the axon is shown as a function of the distance through the length of the axon; amplification of stresses is exhibited close to the gray-white matter interface. (c) Normalized shear stress in the axon is shown; shear stress changes sign close to the bimaterial interface. (d) Normalized displacement in the axon is shown. The vertical black dashed line indicates the gray-white matter boundary. All values were normalized by the mean of the respective parameters. To see this figure in color, go online.

The model indicates that as the tissue is subjected to loads, the relatively softer gray matter deforms by a larger mean strain ε_g, whereas the stiffer white matter deforms by a relatively smaller mean strain ε_w (Fig. 4 a). Because the gray and white matter domains are much larger compared with the axon, the mean strains ε_g and ε_w are roughly equal to the mean tissue stress in the entire domain divided by the respective elastic moduli of the gray E_g and white E_w matter. As the tissue is deformed, the softer gray matter domain, being strained relatively more, pulls the axon along. At the same time, the stiffer white matter, deforming at a relatively smaller amount, prevents the deformation of the axon. This state of loading suggests a “tug-of-war” mechanism of selectively high shear and tensile stress imparted at the interface between the gray and white matter during head rotational acceleration (Fig. 3 b). As a result, axons experience higher tensile strains at the interface, which in turn places axons at greater risk of damage at the interface. The gray and white matter pull on the axon predominantly by shear stresses causing greater tensile elongation than occurs at other regions of the axon. To quantitatively express the mechanism of load transfer, we developed an analytical model of a fiber adhered to a strained bimaterial interface that closely reproduces the computational results.

Figure 4.

Schematic of the model of a fiber adhered to a strained bimaterial interface. (a) View of the stretching of an axon adhered to a bimaterial continuum modeling the surrounding tissue is given. At the same applied load, the gray and white matter are strained by different amounts ε_g and ε_w. Gray matter, which is softer, is strained more and pulls the axon to the left, whereas white matter is strained less and acts to prevent the pulling of the axon. (b) A tug-of-war-like mechanism forms near the interface, with the white and gray matter pulling the axon in opposite directions. The displacement field of the gray and white matter tissues are denoted by u_{b − w} and u_{b − g}, respectively. (c) The free-body diagram of a section of the axon is shown. k_b denotes a constant that relates the relative displacement of the axon and the surrounding tissue to the reaction force of the surrounding media. τ denotes the shear stress acting between the axon and the surrounding tissue, and the axial stress in the axon is denoted by σ. To see this figure in color, go online.

An analytical model of an individual fiber in a strained bimaterial interface for the tug-of-war mechanism of load transfer at the interface

Based on our computational observations, we explain the nonuniform distribution of stresses through the length of the axon using an analytical model of a fiber attached to a strained bimaterial interface (Fig. 4). We begin by expressing the displacement field of the surrounding medium or the background, u_b, associated with the strains in the gray ε_g and white ε_w matter. The displacement of the white matter increases linearly from the fixed end with slope ε_w until reaching the interface at a distance equal to half of the axon length, x = l_a/2 (see also Fig. 3 a). At the interface, u_b = ε_w(l_a/2). Within the gray matter, u_b starts from ε_w(l_a/2) and increases with a slope ε_g. Note that u_b approximately describes the deformation of the medium surrounding the axon (Fig. 4 b). The shear force exerted on the axon by the surrounding tissue depends on the difference of displacement between the axon and the surrounding tissue, which can be expressed using a linear relation as

$$\tau =k_{\text{b}}\left(u-u_{\text{b}}\right),$$ (1)

where u is the displacement field of the axon and k_b is a material constant similar to a Winkler foundation coefficient (45), describing the shear force resulting from a unit change of displacement. The constant k_b in the gray and white matter is proportional to the elastic moduli of the gray and white matter, respectively (46).

The variation of the displacement through the length of the axon results in variations of axial stress, σ, that are balanced by the shear stress τ exerted on the axon by the surrounding tissue (Fig. 4 c). The free-body diagram of an axon element of length dx includes σ and $\sigma +d\sigma$ on its two cross sections and τ at its interface with the medium. The balance of forces, therefore, is expressed as dσ = τ. The stress in the axon, σ, can be expressed as E_aε_a, where ε_a is the axial strain of the axon. Also, note that ε_a = u_,x, where the comma in the subscript denotes differentiation. The variation of stress is therefore expressed as dσ = E_au_,xxdx. Combining the relation defining dσ with the balance of forces and Eq. 1 results in

$$E_{\text{a}}{t}_{\text{a}}{u}_{,\text{xx}}=k_{\text{b}}\left(u-u_{\text{b}}\right).$$ (2)

The solution of Eq. 2 in each domain is

$$u=c_1{e}^{x/a}+c_2{e}^{-x/a}+u_{\text{b}},$$ (3)

where a = (E_at_a/k_b)^1/2 is a characteristic length scale, t_a is the thickness of axons, and the constants c₁ and c₂ are independent of x and can be evaluated in gray and white matter by considering the following four boundary conditions: first, the constrained boundary displacement at the tip of the axon in white matter; second, the equality of $u$ at the interface from the solution in the white and gray matter; third, the equality of σ at the interface from the solutions in the white and gray matter; and finally, setting the stress at the tip of the axon in gray matter equal to the mean stress in the tissue. The last condition represents an approximation because nonuniform stresses may be present at the tip of the axon in gray matter. The obtained displacement, shear, and axial stresses predicted using the analytical model, Eq. 3, agree with the computational results (Fig. 3, b–d). The agreement of the models confirms the validity of the tug-of-war mechanism of load transfer between the tissue and the axon near the gray-white matter interface.

Effect of the level of adhesion of the axon and the surrounding tissue

The computational and analytical models indicated that the transmission of forces by the shear stresses between the axon and the surrounding tissue depends on the level of adhesion between the axon and the surrounding medium. The level of adhesion may depend on factors such as the different strength of the connections between a neuron and neighboring neurons (47,48), the pericellular matrix (49,50), and the degree of myelination (51,52). To investigate the effect of the adhesion, we performed computational tests, including various levels of adhesion strength. Adhesion was varied by changing the elastic modulus of the adhesion layer between the axon and the gray matter, E_h. We used E_h/E_g values of 1, 0.1, 10⁻², and 10⁻⁴ to test the behavior of axons in a broad range of conditions.

The results indicated that the amplification effect is present in the cases representing mild to high adhesion strength, E_h/E_g values of 0.1 and 1 (Fig. 5 a). In the case in which E_h/E_g was 1 (Fig. 5 a, black curve), a broader peak of stress was observed. In this case, stress from the gray matter was transmitted to the axon at a shorter distance, farther from the interface and closer to the soma. Also, a longer portion of the axon experienced amplified stresses, a segment starting from the cell body and ending close to the interface. In the cases representing low adhesion strength, E_h/E_g values of 10⁻² (Fig. 5 a, red curve) and 10⁻⁴ (Fig. 5, green curve), however, amplification of stress was not observed. In these cases, because of the low adhesion, stress was not fully transmitted from gray matter to the axon. This response resembles the sliding of the axon with respect to gray matter.

Figure 5.

Effects of adhesion level, tissue viscosity, and tissue stiffness on the transmission of loads between the surrounding tissues and the axon. (a) Results obtained for E_h/E_g values of 1, 0.1, 10⁻², and 10⁻⁴ are plotted using black, blue, red, and green curves, respectively. In the case of the highest adhesion, the maximal stress is present in the axon within the gray matter. As adhesion decreases, at E_h/E_g of 0.1, the maximal stress occurs at the interface. At lower levels of adhesion, the stress in the gray matter is not entirely transmitted to the axon, and the maximal stress is carried by the axon in the white matter. The vertical dashed black line marks the boundary between the gray and white matter. (b) Increasing the surrounding tissue stiffness while keeping the E_w/E_g ratio constant increases the stress magnitudes almost equally in both gray and white matter. As, a result, the stress amplification (the difference between the stress levels in the gray and white matter) remains almost unchanged. (c) The stress amplification in axons increased with increasing viscosity of the surrounding tissue. To see this figure in color, go online.

Next, we studied the effect of viscous properties of the surrounding tissue on the transmission of forces to the axon. Previous studies have shown that both gray and white matter exhibit time-dependent behavior under mechanical loads (19). As a result, the apparent stiffness of brain tissue may change with strain rate. Therefore, we first changed the stiffness of gray E_g and white matter E_w (while keeping the E_w/E_g ratio constant) and studied how the stress amplification is influenced by changing the brain tissue stiffness. Our simulations in Fig. 5 b showed that the stress magnitudes in both gray and white matter changed with changing tissue stiffness. These changes in the stress levels are almost equal in the gray and white matter and, as a result, the stress amplification (the difference between the stress levels in the gray and white matter) remained almost unchanged. These simulations showed that material heterogeneities, represented by the E_w/E_g ratio, regulate the stress amplification at the gray-white interface. We next studied how the E_w/E_g ratio, and subsequently the stress amplification, changes with the surrounding tissue viscosity. To this end, we assumed that both gray and white matter exhibit the same time-dependent viscous behavior, and we used the Zener model (standard model), as well as the Maxwell model, to model them. Our simulations in Fig. 5 c showed that the E_w/E_g ratio increased with tissue viscosity, which in turn led to higher stress amplification at the gray-white matter interface. These results again showed that the stress amplification in axons is caused by material heterogeneities at the gray-white matter, which can change with different factors, including tissue viscosity.

Effect of a gradual change in material properties close to the interface

The model described in the previous section includes a sharp interface between the gray and white matter, where material properties change suddenly over a short distance across the interface. In brain tissues, however, the tissue stiffness and the related level of myelination change gradually across the interface (51). To study the effect of the gradual change in tissue stiffness, we prepared a model with a gradual change in elastic modulus at the gray-white matter interface and compared its mechanical behavior with the original model (Fig. 6, a and b). In the model with a graded interface, the elastic modulus of the tissue linearly varied from E_g to E_w over a distance l_i (Fig. 6 b). The value used for l_i was selected to be 10 times larger than the thickness of the axon. The same stretch test, using the described axially symmetric model, was performed with a graded gray-white matter interface.

Figure 6.

Stress amplification in the presence of a gradient of stiffness near the interface. (a and b) Spatial maps of the elastic modulus of the computational models with (a) a sharp interface and (b) an interface with a gradual change of stiffness between the gray and white matter are given. The horizontal dashed-dotted lines are the axis of symmetry. Normalized (c) axial and (d) shear stresses in the models with the sharp interface, solid red curve, and graded interface, dotted black curve, are shown. The vertical purple dashed lines represent the boundary between gray and white matter. To see this figure in color, go online.

The computational results indicated that the amplification of axial stress close to the interface persisted in the presence of a gradient of material properties (Fig. 6 c). The shear stress, however, showed a marked difference in the graded case. The singularity of the shear stress was absent in the case with the graded interface (Fig. 6 d). The gradual change in material properties led to a gradual change in shear stress. This indicates that the thickness over which mechanical properties gradually change (interface thickness) can significantly affect the distribution of shear stress. It is notable that the sign of the shear stress changed in the middle of the graded region, consistent with the tug-of-war mechanism of load transfer observed in tests with the sharp interface.

Discussion

The predicted amplification of stresses in axons close to the gray-white matter interface can be combined with previous findings on the thresholds of axonal injury (6,10,53,54) to inform tissue-scale models of DAI. Specifically, our model of load transfer relates the mean tissue stress to the stress experienced by the axons close to the gray-white matter interface. The model indicates that axonal injury may be observed because of the amplification effect even when the mean tissue stress is below the threshold of axonal injury.

In this study, the tissue material properties were treated as time independent as commonly assumed in pseudoelastic analyses of biological tissues (36,37). However, it is known that both gray and white matter show time-dependent behavior under mechanical loads (19). As a result, the apparent stiffness of gray (E_g) and white (E_w) matter under high strain rates may be different from the ones under low strain rates. Our simulations showed that the E_w/E_g ratio regulates the stress amplification at the gray-white interface. Furthermore, we found that time-dependent properties of gray and white matter can change the E_w/E_g ratio and can subsequently impact the stress amplification at the interface. Extracting the time-dependent behavior of gray and white matter and incorporating these viscous properties into the model will be the subject of our future work.

The theoretical results indicated that the development of different strains in the tissues with different stiffness across an interface leads to the amplification of stress close to the material interface. Similar mechanisms can lead to the amplification of stress in other bimaterial interfaces in the brain, as well as in other modes of loading of the cortex. For example, amplification of stresses is expected in areas around the blood vessels and the ventricles, where overt axonal damage has been reported (39,55). Also, it is expected that axons are damaged close to the gray-white matter interface when the brain tissue experiences shear strains (56). Because of the different stiffness of the gray and white matter, in the case of shear deformation, the gray and white matter would deform by different amounts. This effect leads to a sudden variation of the displacement of the axon in the plane of the interface causing the kinking of the axon and higher stresses at the interface. Notably, however, even with the high shear strain, axons rarely disconnect at the moment of injury, but the damage to their ultrastructure leads to swelling and secondary disconnection.

This work can be expanded to include representations of the different regions of the brain tissue at a coarser scale, as well as axons at a finer scale, in multiscale models. Such models may also account for the anisotropy of the white matter as resolved by methods such as diffusion tensor imaging (57). Future studies on the junction between neurons and the pericellular matrix (35) and the neuronal synapses will assist in the determination of the level of adhesion between neurons (58) and the surrounding tissue and improve the presented model. Our simulations showed that the interface thickness can considerably affect the distribution of shear stress in the axon, and therefore accurate experimental measurements of the interface thickness at different regions of the brain are required for the development of future multiscale models. Furthermore, cells are known to sense and respond to changes in the physical properties of their surrounding environment by adjusting their cytoskeletal structures (59,60). Also, drug-induced disruption of cytoskeletal tension has been shown to impact the microtubule structure and subsequently the cell physical properties (61,62). How these matrix-induced and drug-induced changes in the physical properties of cells impact axonal injuries can be the subject of future work.

In conclusion, we studied the transmission of stresses from the tissue scale to axons near the gray-white matter interface. Computational models showed the amplification of tissue-level stresses in axons near the interface, indicating that axons may experience damage even when tissue-level stresses are below the threshold of axonal injury. A tug-of-war mechanism was observed at the interface between gray and white matter that leads to the amplification of stress in the axon close to the interface. An analytical model of a fiber adhered to a strained bimaterial interface was developed that closely reproduced the computational results. Our results explain the propensity for injury of axons at the gray-white matter interface in subthreshold loading of tissues and help the future development of multiscale models of mild TBI.

Author Contributions

F.A., Z.G., and V.B.S. designed and implemented the theoretical models. V.E.J., J.-P.D., and D.H.S. designed and conducted the experiments. F.A., Z.G., V.E.J., J.-P.D., D.H.S., and V.B.S. wrote the manuscript.

Editor: Guy Genin.