Analysis of barotactic and chemotactic guidance cues on directional decision-making of Dictyostelium discoideum cells in confined environments

Significance

Cells confined in complex environments use a combination of chemical and mechanical cues for robust pathfinding and effective migration. Analysis of directional “decision-making” of Dictyostelium discoideum cells migrating within microchannels harboring asymmetric bifurcations shows that unlike neutrophils and immature dendritic cells Dictyostelium cells use chemical rather than barotactic guidance cues. Cells in steeper adenosine 3′,5′-cyclic monophosphate gradients migrating at higher speeds split their leading edges more readily when confronted with a bifurcation in the channel. The point at which one of the competing pseudopods starts to retract appears to be dependent on a relative force imbalance between two competing pseudopods, showing that cellular mechanics plays a major role in leading-edge dynamics, including front splitting, polarization, and retraction in D. discoideum.

Abstract

Neutrophils and dendritic cells when migrating in confined environments have been shown to actuate a directional choice toward paths of least hydraulic resistance (barotaxis), in some cases overriding chemotactic responses. Here, we investigate whether this barotactic response is conserved in the more primitive model organism Dictyostelium discoideum using a microfluidic chip design. This design allowed us to monitor the behavior of single cells via live imaging when confronted with bifurcating microchannels, presenting different combinations of hydraulic and chemical stimuli. Under the conditions employed we find no evidence in support of a barotactic response; the cells base their directional choices on the chemotactic cues. When the cells are confronted by a microchannel bifurcation, they often split their leading edge and start moving into both channels, before a decision is made to move into one and retract from the other channel. Analysis of this decision-making process has shown that cells in steeper nonhydrolyzable adenosine- 3', 5'- cyclic monophosphorothioate, Sp- isomer (cAMPS) gradients move faster and split more readily. Furthermore, there exists a highly significant strong correlation between the velocity of the pseudopod moving up the cAMPS gradient to the total velocity of the pseudopods moving up and down the gradient over a large range of velocities. This suggests a role for a critical cortical tension gradient in the directional decision-making process.

Cell migration plays a key role in several different biological processes, such as embryonic morphogenesis, immune responses, and wound healing (1, 2). Various animal cells exhibit extensive migratory capabilities; for instance, macrophages and neutrophils crawl toward invaders and engulf and destroy them, osteoclasts and osteoblasts ensure the continuous remodeling of bones, and fibroblasts migrate to damaged sites of tissue helping to rebuild them (3). Cell movement is also a key driver of some pathological processes such as osteoporosis, chronic inflammatory diseases, and tumor metastasis (1). Insights into the mechanisms that control and execute migration will be required for more effective medical treatments and facilitate new approaches in regenerative medicine and tissue engineering.

One of the most important questions in understanding cell movement is how the cell interprets external cues and actuates the internal cytoskeletal machinery to achieve the motion (4). A variety of biochemical and physical cues have been shown to trigger cellular responses (5–11). Chemical concentration gradients are one of the environmental signals which can instruct the migration of certain cell types. This kind of response is known as chemotaxis and involves a directed migration as a consequence of directional sensing, and has been extensively investigated using in vitro systems (12). However, in their physiological environment cells are exposed to a combination of a variety of chemical and mechanical stimuli and it is still largely unresolved how responses are prioritized and coordinated. The advent of microfluidic techniques has enabled the investigation of cell migration in more detail by providing better control over the mechanical and chemical complexity of the microenvironment that surrounds each individual cell (13). Microfluidics provides good control over the dynamics of signaling, as well as over spatial complexity of the cellular environment. For instance, maze-like microfluidic networks (14) have been developed to analyze the mechanisms that amoeboid cells such as neutrophils and Dictyostelium discoideum (Dd) cells use to effectively navigate through these complex environments (15, 16).

Dd is a well-established model for the study of eukaryotic chemotaxis (17, 18). Research conducted on the mechanism of chemotaxis in this organism has greatly contributed to our basic understanding of chemotaxis and also led to the establishment of novel experimental methods to study chemotaxis now successfully used in other systems (19–24). The signal transduction pathways involved in chemical gradient sensing and transduction to the organization of the actin–myosin cytoskeleton resulting in directed motion are highly conserved between Dictyostelium and neutrophils reviewed in ref. 25. Most of the insights into the mechanisms governing cell migration arose from investigations on planar surfaces, but recent studies showed that this classical picture of cell locomotion is inadequate to recapitulate the properties of cell migration within tissues and other complex environments (26). During in vivo cell migration, a number of physical parameters such as mechanical properties, geometry, adhesion, and degree of confinement imposed by the microenvironment in which cells move affect how cells respond to chemical cues (27–29). Interestingly, Prentice-Mott et al. (30, 31) first showed that human promyelocytic leukemia cells, also known as HL60 cells, can interpret small differences in hydraulic resistance when confronted with asymmetric bifurcating channels of varying resistance and called this “barotaxis.” The authors developed a microfluidic-based migration assay where HL60 cells were forced to move through asymmetric microchannels and observed that cells migrated toward the path of least hydraulic resistance, both in the presence and in the absence of a chemoattractant, showing that the mechanical stimulus seemed to override the chemotactic response.

Here we design and use a microfluidic device harboring microchannels that allow us to decouple the chemical and hydraulic stimuli. The particular topology consists of bifurcating microchannels where only one arm is connected to the source of chemoattractant and this arm has a hundred times higher hydraulic resistance than the other arm. In this way, cells are subjected to a dual choice: one direction corresponds to an increasing chemical gradient and the other to a significantly lower hydraulic resistance. This approach showed that cells always migrate up the chemical gradient despite the hundred-times-higher hydraulic resistance and chemotaxis. Furthermore, we show that Dictyostelium cells readily migrate into dead-end channels. These observations make the existence of a barotactic response in Dictyostelium highly unlikely. We take advantage of the finding that cells confronted by a bifurcating microchannel often partially split their leading edge and start moving into both paths to investigate this process in more detail. Cells migrating through steeper chemoattractant (cAMPS) gradients tend to move faster and have a higher tendency to split at the bifurcation. Interestingly, the decision to retract the pseudopod moving away from the cAMPS source is made when the velocity of the pseudopod moving up the cAMPS gradient is 20% higher than the average velocity of the pseudopod moving down the gradient. Surprisingly, this decision threshold is largely independent of the steepness of the cAMPS gradient and speed of movement. This suggests the existence of a relative force imbalance threshold that underlies the cytoskeletal repolarization and ultimately the direction of cell migration.

Results

First, we sought to determine whether Dictyostelium cells could detect small pressure differences and show a barotactic response as reported for HL60 cells. We developed a ladder-like microfluidic device (Fig. 1A) where cells and chemoattractant could simply be added and controlled by adjusting the volume of the media in each loading reservoir, without the use of syringe or pressure pumps. Applying the definition of hydraulic resistance (Eq. 2), we designed the microchannel topologies shown in Fig. 1C.

Fig. 1.

Microfluidic chip designs to test barotactic responses. (A) Three-dimensional structure of the chip; the two symmetric sides are arranged in a "ladder-like" structure. Each side comprises an inlet and an outlet, connected by a loading channel. The two symmetric halves are bridged by a number of small-diameter migration channels. (B) Picture of an actual PDMS chip compared to a one-pound coin. (C) Schematics of the various geometries of the migration channels used to test the role of barotaxis in the directional bias. The length and width of the channels are designed following the definition of hydraulic resistance of a duct (Eq. 2), whereas the height is set to 2.5 μm. For each design, the upper arm corresponds to the arm of least hydraulic resistance. For each geometry, the ratio between the higher and lower resistance is stated. (D) The directional bias, that is, the percentage of cells migrating toward the arm of least hydraulic resistance as a function of the ratio in hydraulic resistance between the two bifurcating arms, for each of the designs shown in C. To test the statistical significance of any difference in cell behavior in different geometries 2 × 2 and 2 × 3 Fisher tests were used.

During the initial phase of an experiment diffusion sets up a cAMPS gradient from the cAMPS loading channel to the cell loading channel. Upon detection of the chemoattractant, cells start migrating up the chemical gradient across the “migration channels” and while doing so effectively plug the channels (Movie S1). Since the diffusion of small molecules is fast on the small length scales of these channels, the concentration of chemoattractant is essentially uniform and high at the front of the cells and low at the back of the cell, resulting in a steep chemoattractant gradient over the length of the cell (SI Appendix, Fig. S1 and Movie S2).

In the migration channel the cells are confronted with a bifurcation of the channel in two arms, characterized by a specific ratio in hydraulic resistance. When cells migrate through the asymmetric bifurcating microchannels they tend to protrude two pseudopods, one into each arm of the bifurcation and after a “tug of war” one pseudopod “wins” while the other starts retracting, similarly to what has been reported by Prentice-Mott et al. (31) (SI Appendix, Fig. S1C and Movies S3 and S4). The bifurcating branches harbor asymmetric features 10 µm downstream of the bifurcation so that no geometrical factors would influence cellular curvature before the decision-making process occurred.

In Fig. 1D we show how the directional bias (i.e., the percentage of cells migrating toward the arm of least hydraulic resistance) changes as a function of the ratio in hydraulic resistance between the two bifurcating arms, for each of the designs shown in Fig. 1C. Although there are possible indications of very small biases, no statistically significant differences were found in directional bias among geometries with different hydraulic resistance ratios between their competing arms (geometries 1 and 2: P = 0.87; geometries 2, 3, and 4: P = 0.19; geometries 2, 3, and 5: P = 0.5; geometries 1 and 5: P = 0.17). Moreover, no evidence for a “directional memory” (30) was found in our experiments as shown in SI Appendix, Fig. S2; rather, each cell explores both bifurcating paths at every consecutive bifurcation (Movie S5).

Cells Protrude inside Dead-End Channels.

To further test whether Dd cells responded to hydraulic resistance we designed a migration channel where one of the arms of the asymmetric bifurcations is a dead-end microchannel and hence, in theory, has infinite hydraulic resistance. Many cells exhibited the ability to partially or fully penetrate these dead-end branches (Fig. 2 A and B and SI Appendix, Fig. S3 and Movie S6). In the case of total or partial penetration, the cells appear smaller than the cross-section of the channel and therefore the fluid in front of them can be displaced around the cell through the imperfect seal between the cell and the channel wall. In the cases where cells do not invade blind channels, the leading edges seem to plug the channel completely and cannot invade the dead-end branches (SI Appendix, Fig. S3). To further investigate this aspect we added a fluorescent dye, fluorescein isothiocyanate–dextran (FITC dextran, 70 kDa), into the loading channel at the right-hand side of the chip, together with the chemoattractant. We observed that as the cell protruded into the blind channels the fluid was displaced around the leading edge, while there was no evidence for micropinocytosis as has been reported for immature dendritic cells (DCs) recently (32). These results appear to indicate that cells are only able to migrate into dead-end channels under conditions where they can deform sufficiently to shunt some fluid between the wall and membrane to generate space to move into. However, even under these likely high hydraulic pressures the cells will still explore these channels. These observations also do not support the idea that barotaxis is a key driver in the decision to extend a pseudopod or not and argue against barotaxis as a dominant mechanism governing Dd cells’ directional choice.

Fig. 2.

Decoupling barotactic and chemotactic response. (A and B) Examples of cells actively protruding into dead-end channels. Actin filaments are labeled with RFP-LifeAct in A and myosin II with GFP in B. (C) Microchannel design aimed at decoupling the barotactic and chemotactic response: only the narrower arm joins the cAMPS loading channel (on the right-hand side, not visible), whereas the wider and longer arm goes back into the loading channel where cells are seeded. The cAMPS distribution across the system is calculated using Comsol. We assume pure diffusion with a concentration of 1 μM at the right side of the channel and 0 µM at the left-hand side, which in the chip is connected to the cell loading channel.

Opposing Chemical Signal and Hydraulic Resistance Gradients.

Although it was statistically not significant the observed small directional bias shown in Fig. 1D could indicate a very weak barotactic response. However, in all of the designs in Fig. 1C the upper channels of lower hydraulic resistance are also characterized by a larger channel volume. This larger reservoir of cAMPS could result in a small cAMPS gradient across the bifurcation under some conditions, with the higher cAMPS concentration coinciding with the low hydraulic resistance channel, possibly explaining the small directional bias. To better separate the chemotactic and barotactic signal, we designed a migration channel shown in Fig. 2C. In this geometry, the bifurcating channel of high hydraulic resistance is connected to the chemoattractant source, while the other arm with low hydraulic resistance feeds back into the “cell loading” channel that does not contain chemoattractant. This geometry allows the generation of true opposing directions of the chemotactic and barotactic gradients (i.e., “up” the chemical gradient in one channel or “down” the hydraulic resistance gradient in the other channel). We observed the behavior of migrating cells in this chip design, and the resulting response was unambiguous: 100% of cells (N = 77), analyzed over seven independent experiments, migrated up the chemical gradient, despite the hundred-times-higher resistance of the upper narrow path (Movie S5). This remained true when the chemotactic gradient of cAMPS was varied 50-fold (20 nM, 100 nM, and 1μM). These experiments show that the behavior of the cells is completely controlled by the chemotactic signal and not by the large hydraulic cue.

Analysis of Cell Bifurcation and Polarization Behaviors.

When a cell encounters a bifurcation it often extends a pseudopod in both channels; however, after a while the cell always decides to move into one channel and retract from the other. These extension–retraction processes are characterized by typical changes in the organization of the actin–myosin cytoskeleton. Labeling of the actin cytoskeleton with Lifeact shows that these leading pseudopods are, as expected, enriched in filamentous actin (Fig. 2A), while myosin II-GFP (green fluorescent protein) strongly localizes at the uropod and at retracting ends (Fig. 2B and Movies S1–S3).

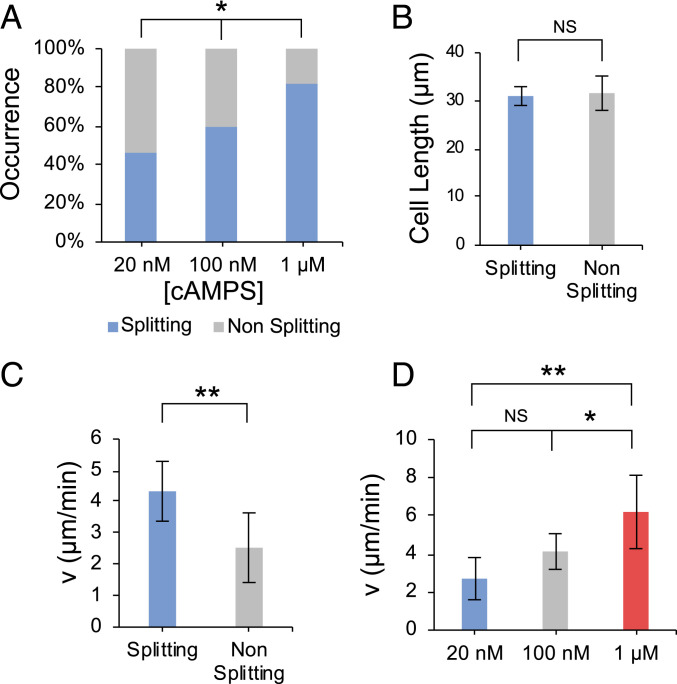
As shown above, we have designed a microfluidic chip where cells in 100% of the cases move up a cAMPS gradient when confronted with a bifurcation. Some cells did split in two pseudopodia at the bifurcation, while others instead were able to directly move into the channel connected to the cAMPS source. The splitting occurrence increased with the cAMPS concentration; at the highest cAMPS concentration tested 80% of the cells split (Fig. 3A). This poses two questions: 1) Why do the cells extend a pseudopod in the wrong direction and 2) when and how do they make the decision to retract?

Fig. 3.

Relationship between cell properties and splitting behavior at the asymmetric bifurcation in Fig. 2C. (A) Relationship between the cAMPS concentration and cell splitting. (P = 0.039, using 2 × 3 Fisher exact test). (B) Relationship between cell length and splitting behavior. P = 0.008. (C) Relationship between splitting behavior and the velocity of the cells in the straight channel upstream of the bifurcation. (D) Relationship between the cell speed and the cAMPS concentration for the splitting subgroup. NS, P > 0.05, *P = 0.06, **P = 0.02. Kruskal–Wallis test was performed in B–D. Median values are shown. Error bars represent 95% confidence interval.

We sought to better understand which parameters affected these behaviors. We found that splitting did not depend on cell size (Fig. 3B), but we did notice a significant correlation between the speed of cell before entering the channel and the frequency of splitting (Fig. 3C). We also determined that cell speed increased with the cAMPS concentration in these conditions (Fig. 3D), similar to previous reports that showed that cells under unconfined conditions exhibited a dependence of migration speed on cAMP concentration (33). Thus, the dependence of migration speed on cAMPS concentration recorded here likely underlies the observed dependence of splitting on cAMPS concentration (Fig. 3A). It is well established that the formation of new pseudopods during normal and chemotactic motion requires localized actin polymerization at the leading edge and that this contributes to the driving force necessary for extension and migration. We observed that cells migrating in long, straight channels tended to exhibit a persistent localization of polymerized actin at the leading edge and to a lesser extent at the trailing edge (Fig. 4A). Within a given cell population there was a considerable individual variation in the amount of polymerized actin at the front, which was expected to reflect the observed variations in migration speed. Measurement of the linear extent of the actin polymerization zone at the leading edge for each cell showed that this correlated well with the speed of the cells (Fig. 4B). Since faster-moving cells also split more readily, this suggests that cell-specific differences in internal actin dynamics may determine whether splitting occurs (Fig. 4 D–F).

Fig. 4.

Relationship between the size of the actin-rich leading edge and the splitting behavior at the asymmetric bifurcation in Fig. 2C. (A) Example of cells migrating in straight channels characterized by a cross-section of 5 × 2 μm². Actin filaments, labeled with RFP-LifeAct, primarily localizes at the leading edge and, in a lower amount, at the uropod. (Scale bar, 10 μm). (B) Relationship between the length of the actin-rich leading edge and the velocity of 37 cells migrating in straight channels with cross-section 3 × 2 μm². (C) Relationship between the speed of the leading edge along the path of the positive cAMPS gradient (V_left) and the sum of the average speeds of the pseudopodia protruding in both bifurcating channels (V_left + V_right). Data are pooled from two to four experiments at different cAMPS gradients (20 nM, 100 nM, and 1 μM). The correlation is highly significant (F = 250, degrees of freedom = 44, P < 10⁻¹²). See SI Appendix, Fig. S4 for data at the individual concentrations. (D) Schematic representation of the actin distribution of migrating cells confined in microchannels. (E) Schematic representation a fast-moving cell with large leading edge, which tends to split. (F) Schematic representation of a slow-moving cell with a small leading edge, which tends to migrate straight toward the source of chemoattractant.

Then, to better understand when and how cells make the decision to retract the pseudopods along the developing negative cAMPS gradient we performed the following analysis. We measured the length and speed of extension of the pseudopods protruding inside the bifurcating arms up to the point where the pseudopod moving down the cAMPS gradient stopped moving and started to retract. We found that there exists a very strong positive linear correlation between the average speed of extension of the pseudopod up the gradient and the sum of the average speeds of extensions up and down the cAMPS gradient (Fig. 4C). The slope of this dependency is ∼0.55. Interestingly the slope does not depend significantly on the steepness of the cAMPS gradient across the cell, as shown in SI Appendix, Fig. S4. Since during cell migration there is no significant inertia, average pseudopod expansion speed is proportional to the net local driving force. These data therefore strongly suggest that a pseudopod is retracted when a critical imbalance in the driving forces in the competing pseudopods is reached.

Discussion

Here we have tested whether Dd cells would respond to asymmetric hydraulic resistance conditions by confronting them with a variety of microfluidic channels of different topologies as has been reported for neutrophils (31). Dd requires a cAMP gradient in order to move directionally into the microchannel. Once the cells enter the channel, they effectively plug the channel due to its small size. Since the channels are short and diffusion is fast, the cell will rapidly experience a binary cAMPS gradient over the length of the cell. The front of the cell sees the cAMPS concentration of the chemoattractant loading channel (20, 100, or 1,000 nM cAMPS) and the back the concentration of the cell loading compartment (∼0 M cAMPS). When cells migrate through the asymmetric bifurcating microchannels presented in Fig. 1C they tend to protrude two pseudopods, one into each arm and after a “tug of war” one pseudopod “wins” and keeps extending, while the other starts retracting, similarly to what has been reported by Prentice-Mott et al. (31).

Although we assume that there are only small differences in chemoattractant concentration between the two channels coming from the bifurcation, we cannot rule out the residual differences in chemoattractant concentration that exist at the time of decision-making. In our chip design, the higher concentrations would be expected in the channels with a larger reservoir of cAMPS molecules which correspond with the channels of lowest hydraulic resistance. Therefore, it is formally impossible to say whether the cells preferentially respond to a residual chemoattractant concentration difference or a difference in hydraulic resistance or possibly a combination of both using these geometries.

To better understand the directional bias exhibited by cells moving through asymmetric bifurcations, we developed a microchannel possessing an asymmetric bifurcation aiming to decouple the two main environmental stimuli competing in the system: the chemical gradient and the hydraulic resistance. This topology allowed us to show that all cells analyzed migrated toward the positive chemical gradient, rather than moving into the arm of hundred-times-lower hydraulic resistance. Our results, therefore, showed that chemotaxis completely determines cell polarization and movement and we found no evidence for barotaxis in Dd in the different experimental conditions tested here.

These findings are also supported by the observation that many cells were able to move into dead-end channels, despite the theoretical infinite hydraulic resistance of these channels. It has recently been demonstrated that tumor cells confined in microchannels display a polarized distribution of ion pumps (Na⁺/H⁺) and aquaporins in the cell membrane. This is assumed to create a net influx of water at the leading edge and a net outflow at the uropod driving the motion of the cells and represents an alternative to the actin-driven motion [osmotic engine model (34)]. Further studies are required to elucidate the role of the osmotic engine in the mode of movement and the directional decision-making process in Dd. Recent work by Moreau et al. (32) suggested that immature DCs could cope with high hydraulic resistance via a high level of macropinocytosis that allows fluid transport across the cell and thereby exploration of dead-end channels (35). Mature DCs down-regulate macropinocytosis and lose the ability to penetrate dead-end channels. Although growing Dd cells show a high level of macropinocytosis, nouptake of labeled dextran from the fluid via macropinocytosis was observed during our experiments with starving Dd cells, making the latter mechanism an unlikely explanation (SI Appendix, Fig. S2). The ability of Dd cells to move into the dead-end channels is likely due to the fact that the fluid confined inside the blind channels in front of the protruding leading edge of the cell manages to leak between the cell and the channel wall, as the cell protrusion advances into the dead-end branch (SI Appendix, Fig. S2). It can be estimated that to be barotactic Dd cells should be able to measure very small differences in pressure at their leading edges to respond to the local differences in hydraulic resistance. In fact, the force necessary to push a column of water through a microchannel is given by the capillary force (36):

$$F=\mathrm{\Delta }pA=vR{A}^2,$$ [1]

where $v$ is the cell velocity, R is the hydraulic resistance of the channel and A is the cross-section. Using the definition of R given in Eq. 2 and the values L = 250 µm, w = 3 µm, $v=8$ µm/min, µ = 1 mPa⋅s, and h = 2.5 µm the estimated force is in the order of 0.5 pN. These forces are very small, even smaller than that generated by a single actin filament that polymerizes at the leading edge, which are in the range of a few piconewtons (37, 38) and it remains unresolved how they would be measured. Taken together, we consider it unlikely that starving Dd cells exhibit a significant barotactic response.

Directed and conditional pseudopod extension and retraction is key to the chemotactic mechanism. The compass-based model predicts that a cell first senses the direction of the attractant gradient polarizes followed by the extension of a new pseudopod in the direction of the gradient (39). Movement in steep gradients can be explained as the persistent extension of pseudopods in the correct direction, largely alleviating the need for pseudopod retraction. However, previous work by Insall and coworkers (40, 41) has shown that Dd cells migrating in shallow gradients of cAMP move via a mechanism that involves the generation of bifurcating pseudopods at the leading edge of the cell. The pseudopods appear to be generated in random directions, but the pseudopod pointing toward the higher concentration of chemoattractant is stabilized, while the pseudopod pointing in other directions is retracted. This results in a slow but reproducible turning of the cell in the direction of the gradient. Although this decision to extend or retract is clearly dependent on the gradient of cAMP, it remains unresolved at which stage and by what mechanism the cell decides to retract a pseudopod pointing in a less favorable direction.

Our experiments have shed some light on the decision-making process in pseudopod extension and retraction. We found that fast-moving cells split in two when reaching a bifurcation and the pseudopod protruded inside the arm of low cAMPS extended for a short time before stopping and retracting, a process that involved the recruitment of myosin II. Slower-moving cells did not split and moved straight into the correct channel. We also found a clear relationship between the extent of the zone of filamentous actin at the leading edge and the speed of movement, faster cells having a larger filamentous actin-rich zone. We also confirmed that under our conditions of high confinement cells experiencing higher cAMPS gradients migrate faster than cells experiencing smaller cAMPS gradients. Therefore, it seems likely that high levels of cAMPS-dependent actin polymerization result in a more active and larger actin polymerization zone at the leading edge, which may increase the probability of splitting at a bifurcation.

We also demonstrated that the velocities of the pseudopodia protruding up the cAMPS gradient in different cells are linearly proportional to the sum of the velocities of the competing pseudopodia protruding up and down the cAMPS gradient of these cells over a wide range of velocities. The slope of this relationship (threshold) is surprisingly independent of the magnitude of the cAMPS gradient over the cells. Since speed in this overdamped system is proportional to the local driving force, this implies that the decision to retract is independent of the absolute difference in driving forces between the two ends but only depends on the steepness of the gradient between the two ends. It has been argued that during neutrophil migration a cortical tension gradient along the cell might be responsible for maintenance of cell polarization, as well as preventing initiation of new pseudopods through inhibition of actin polymerization, but it has been difficult to estimate how large this tension gradients would be (42, 43). Our results suggest that this tension gradient has to be 20% (or larger) to be able to suppress a secondary leading pseudopod. The mechanism underlying tension dependence will have to be addressed in future experiments.

Materials and Methods

Microfluidic Device.

The structure of the microfluidic device is similar to that used in other studies on neuronal cultures (44) and tumor cell invasiveness and migration (28) and is characterized by the presence of two main loading channels, each of which connects two cylindrical reservoirs that act as infinite source and as the sink, respectively. The two “loading channels” are bridged by “migration channels” having a cross-sectional area that is much smaller than that of the loading channels. The three-dimensional (3D) schematics of the device are shown in Fig. 1A. The cell suspension is loaded in one side of the chip, whereas the other symmetric half is loaded with the chemoattractant (cAMPS).

The hydraulic resistance of a duct can be defined as R_h = ΔP/Q, where ΔP is the pressure drop and Q the flow rate (45). This formula can be considered the hydrodynamic analogous to Ohm’s law R = ΔV/I, where ΔV is the voltage and I the current through a wire. In the case of microchannel with a rectangular cross-section the hydraulic resistance can be expressed as

$$R_h=\frac{12\mu L}{w{h}^3\left(1-0.63h/w\right)},$$ [2]

where w is the width of the channel, L is its length, h is its height, and μ is the fluid dynamic viscosity (45). The migration channels in Fig. 1C have been designed using Eq. 2 by varying the length and cross-sectional diameter of the channels. In all cases, the height of the channels was fixed at 2.5 μm.

Device Fabrication.

The design of the mold is carried out in QCAD professional (version 3.9.8.0). The molds of the microfluidic chip were developed using standard photolithographic techniques (46). First, a 2.5-µm-high film of the photopolymer SU-8 2002 was spread onto a 6-in silicon wafer (IDB Technologies) via spin coating to produce the first layer of the mold. A first high-resolution photomask was used to transfer the features of the migration channels through ultraviolet (UV) illumination. A second 80-µm-high layer of SU-8 2075 was then spun on the wafer and the features of the bigger loading channels were aligned with those of the first layer through alignment marks and transferred to the second layer via UV illumination. All of the areas that were not exposed to the UV light were then etched using an SU-8 developer. Replicas of the patterned mold were obtained by soft lithography using polydimethylsiloxane (PDMS) (Sylgard 184 Silicone Elastomer Kit; Dow Corning Corporation). The PDMS base and curing agent were mixed at 10:1 ratio, degassed in a vacuum desiccator, and poured on the mold. After baking for 6 h at 80 °C the solid PDMS was separated from the mold and ports were punched through the inlets and outlets regions using 8-mm biopsy punchers (Harris Uni-Core). Patterned PDMS was reversibly bonded to standard microscope glass slides (VWR) exploiting the Van der Waals forces that generate at the interface between the PDMS and the glass.

Cell Culture.

Dd cells (strain Ax2) were used. Cells were grown in shaken suspension in HL5 medium using glass flasks at 22 °C. Cells were harvested when the cultures reached ∼4 × 10⁶ cells/mL cells by centrifugation (400 × g for 2 min). Cells were washed twice and resuspended in KK2 buffer at the concentration of 1 × 10⁷ cells/mL and starved for 4.5 h while subjected to periodic stimulation with 10⁻⁷ M cAMP (47). To visualize actin dynamics a strain transformed with Lifeact red fluorescent protein (RFP) was used; to visualize myosin dynamics a myosin II heavy chain GFP N-terminal knock-in strain was used. The GPF knock-in strain was made using established homologous recombination techniques, using a five-amino-acid linker (GALVG) resulting in the GFP-myosin fusion sequence MDELYKGALVGNPIHDRT.

Cell Loading.

After starvation, cells were washed twice and suspended in KK2 at a final concentration of 1 × 10⁷ cells/mL. An aliquot of 200-μL cell suspension was loaded inside one of the two inlets of the microfluidic device using a pipette. The opposite inlet was filled with 200 μL of nonhydrolyzable cAMP analog cAMPS at increasing concentration: 20 nM, 100 nM, and 1 μM. After loading the system with the cell and chemoattractant solutions, it becomes subject to a transient flow directed from the source to the sink reservoirs. The flow lasts until the hydrostatic pressure at these two ends of the loading channels is balanced. At the equilibrium, a linear spatial gradient of chemoattractant establishes inside the bridging channels (SI Appendix, Fig. S1), mainly by diffusion, as previously shown by Abhyankar et al. (48). The symmetry guaranteed by the microfluidic device allows for a very good equilibration of the system. Cells adhere to the substrate and those that sit in the proximity of the entrance of the migration microchannels readily sense the cAMPS and move up the gradient while undergoing a drastic shape modification to adapt to the mechanical confinement. The choice of using the nonhydrolyzable cAMP analog cAMPS was based on the fact that upon exposure to the cAMP gradient each Dd cell secretes intracellular cAMP at a concentration comparable to that imposed by the system (1 μM) (49), which would have affected our analysis. Moreover, Dictyostelium cells express and secrete phosphodiesterase, which degrades cAMP into 5′-adenosine monophosphate (50). This means that the local concentration around the single cell would have been the result of these two competing effects and cells that migrate close to each other could interact. The use of cAMPS simplifies the chemical landscape cells are exposed to. At the end of each experiment, the glass coverslip was separated from the PDMS chip and both surfaces were cleaned with 70% ethanol and stored for following experiments. Additionally, to maintain the chemical gradient steady, the four reservoirs were covered using small pieces of PDMS.

Imaging, Image Analysis, and Statistical Analysis.

The cell motion was recorded at room temperature on a Leica SP8 confocal microscope equipped with a 10×, 0.3 numerial aperture plan apochromat objective lens. The length of the splitting pseudopodia was quantified manually using ImageJ by measuring the distance of the extent of each pseudopod in both bifurcating arms, relative to the center of the bifurcation. Similarly, the length of each cell and the actin polymerization zone was estimated manually using ImageJ. The speed of the cells and pseudopodia was measured using ImageJ, via kymograph analysis. The inclusion criteria for our analysis were that cells had to travel directionally toward the higher end of the chemical gradient. In the case when multiple consecutive cells were migrating inside a channel only the first cell was considered. To characterize how cells interacted with the surrounding fluid, FITC dextran (FD-70; Sigma-Aldrich) was loaded into the right-hand side reservoirs along with cAMPS. Data analysis was conducted in Excel for Mac 2011, MATLAB R2018b, and Python.

Numerical Simulation.

To estimate the local concentrations of cAMPS cells were exposed to at the bifurcating microchannels we simulate the transport of cAMPS through the migration channels using the software Comsol Multiphysics 5.2b (Comsol, Inc.). The transport of cAMPS was assumed to be driven by diffusion. We calculated the equilibrium solution of the two-dimensional diffusion equations for the actual topology of the bifurcating channels using the module “Transport of Diluted Species.” Constant-concentration boundary conditions were imposed at the two ends of the channel; the values at these positions were set to be c = 1 μM and c = 0 μM, respectively, as in the actual experiments. The boundary conditions were set as “no-flux” at the edges of the channel. The initial conditions were 0 μM throughout the channel. The value of the cAMP diffusion coefficient, D, in water is 4.44 × 10⁻⁶ cm²/s (51).

Data Availability.

All study data are included in the paper and SI Appendix. Selected time-lapse image sequences of the hundreds of experiments performed are included as Movies S1–S6. Raw image data will be made available upon request.