The 17-y spatiotemporal trend of PM_2.5 and its mortality burden in China

Significance

Estimation of the chronic health effects of PM_2.5 exposure has been hindered by the lack of long-term PM_2.5 data in China. To support this, high-performance machine-learning models were developed to estimate PM_2.5 concentrations at 1-km resolution in China from 2000 to 2016, based on satellite data, meteorological conditions, land cover information, road networks, and air pollution emission indicators. By adopting imputation techniques, relatively unbiased spatiotemporally continuous exposure estimates were generated. Annual mortality burdens attributable to long-term PM_2.5 exposure were estimated at the provincial scale, and the national total adult premature deaths were estimated at 30.8 million over the 17-y period in China.

Abstract

Investigations on the chronic health effects of fine particulate matter (PM_2.5) exposure in China are limited due to the lack of long-term exposure data. Using satellite-driven models to generate spatiotemporally resolved PM_2.5 levels, we aimed to estimate high-resolution, long-term PM_2.5 and associated mortality burden in China. The multiangle implementation of atmospheric correction (MAIAC) aerosol optical depth (AOD) at 1-km resolution was employed as a primary predictor to estimate PM_2.5 concentrations. Imputation techniques were adopted to fill in the missing AOD retrievals and provide accurate long-term AOD aggregations. Monthly PM_2.5 concentrations in China from 2000 to 2016 were estimated using machine-learning approaches and used to analyze spatiotemporal trends of adult mortality attributable to PM_2.5 exposure. Mean coverage of AOD increased from 56 to 100% over the 17-y period, with the accuracy of long-term averages enhanced after gap filling. Machine-learning models performed well with a random cross-validation R² of 0.93 at the monthly level. For the time period outside the model training window, prediction R² values were estimated to be 0.67 and 0.80 at the monthly and annual levels. Across the adult population in China, long-term PM_2.5 exposures accounted for a total number of 30.8 (95% confidence interval [CI]: 28.6, 33.2) million premature deaths over the 17-y period, with an annual burden ranging from 1.5 (95% CI: 1.3, 1.6) to 2.2 (95% CI: 2.1, 2.4) million. Our satellite-based techniques provide reliable long-term PM_2.5 estimates at a high spatial resolution, enhancing the assessment of adverse health effects and disease burden in China.

Exposure to ambient fine particulate matter (PM_2.5, or particulate matter with aerodynamic diameter ≤2.5 µm) is known to be a harmful environmental factor that impacts human health (1, 2), contributing to 4.2 million deaths globally in 2015, with 1.1 million deaths in China alone (3). Ambient PM_2.5 levels in China greatly exceed World Health Organization (WHO) guidelines on a regular basis, as well as the levels in most postindustrial countries (e.g., the United States). However, due to the lack of PM_2.5 monitoring data before 2013, research focusing on chronic health effects and disease burden of PM_2.5 exposure is very limited in China.

One emerging solution to this challenge is spatial modeling driven by remotely sensed data. This approach employs satellite aerosol optical depth (AOD) and both meteorological and geographical factors to estimate spatially resolved PM_2.5 levels. Due to advances in long-term stability of satellite AOD retrievals, PM_2.5 concentrations during periods without ground monitoring may be predicted under the assumption that the relationships between ground-level PM_2.5 concentrations and these predictors are relatively constant across a given time period (4, 5). With its broad coverage, satellite data can provide spatial surfaces of PM_2.5 as well. For example, Ma et al. (4) predicted PM_2.5 concentrations in China from 2004 to 2013 using AOD retrieved by the moderate resolution imaging spectroradiometer (MODIS) at 10-km resolution and a two-stage spatial statistical model. Using a similar model structure, Liang et al. (6) estimated the PM_2.5 concentrations in Beijing and its surrounding areas from 2004 to 2014 with the multiangle implementation of atmospheric correction (MAIAC) AOD at 1-km resolution. Satellite-based spatial estimates can fill in the gaps of ground observations and capture local-scale PM_2.5 variability. The applications of satellite data are especially valuable in less developed regions of the world with few monitors. In addition to these methods, machine-learning techniques are increasingly employed to improve prediction accuracy and hindcast performance (5, 7). For example, Xiao et al. (5) predicted PM_2.5 concentrations across China in 2008 at 10-km spatial resolution using ground observations between 2013 and 2016 and multiple machine-learning algorithms, which demonstrated better performance compared with traditional statistical models.

Accurately estimating PM_2.5 levels is a crucial step toward characterizing long-term population exposure. Although both national and regional PM_2.5 models have previously performed well in China (5, 6), key challenges remain that limit their applications in epidemiological studies and mortality burden estimation. First, cloud cover and high surface reflectance lead to nonrandom missingness in AOD, especially during winter or in regions covered by snow or desert. Consequently, aggregated long-term PM_2.5 estimates with missing values tend to be biased due to the nonrandom samples. For example, Xiao et al. (8) were able to improve the predictive accuracy of annual mean PM_2.5 estimates by filling the AOD gaps as indicated by cross-validation (CV) R² of 0.87 to 0.94 compared to 0.76 without gap filling. However, most previous studies in China have assessed exposure levels using satellite-based PM_2.5 estimations without accounting for this missingness in AOD or PM_2.5 data (9, 10). Second, most national long-term estimations of PM_2.5 have been at relatively coarse resolutions in China (e.g., 10 km) (4, 11). Although global PM_2.5 concentrations at 1-km resolution have been reported (12), they were predicted at the annual level. Due to the large population size and a highly complex air pollution emissions profile in China, high-resolution data at both spatial and temporal levels are essential to distinguish the exposure levels for populations who live in neighboring areas but are affected by different emission sources. Although regional-scale MAIAC-driven PM_2.5 models have been reported in China (6, 8, 13), high-resolution national PM_2.5 surfaces are still needed to support large-scale epidemiological studies focusing on chronic health effects of PM_2.5 exposure.

The aim of this work is to develop high-performance prediction models to assess long-term PM_2.5 exposure levels in China at 1-km resolution using machine-learning algorithms and to estimate the spatial and temporal characteristics of all-cause excess mortality attributable to PM_2.5 exposure in each province of China.

Results

Performances of Machine-Learning Models.

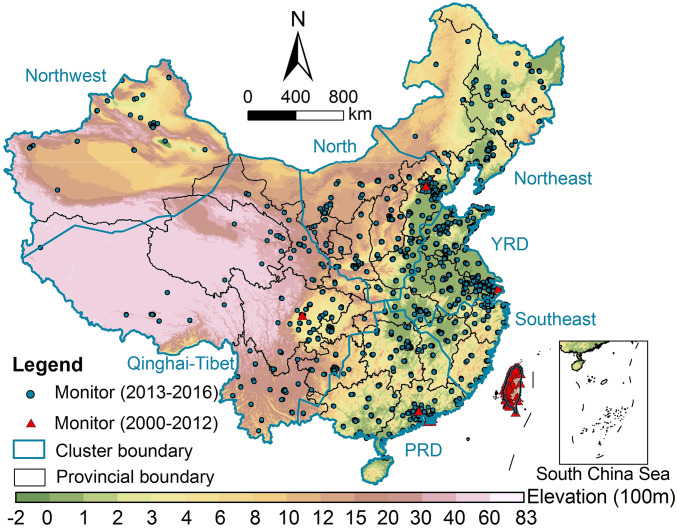
Our study domain is presented in Fig. 1. Summary statistics of model CV performances and performance in each subregion are shown in Table 1. Our machine-learning models performed well in all regions of China. Monthly predicted PM_2.5 concentrations were in overall agreement with ground measurements. Random 10-fold CV R² was 0.93 with a root-mean-squared prediction error (RMSE) of 8.90 μg/m³ at the monthly level. Our models performed best in the southeast region, with a CV R² of 0.93 and a RMSE of 6.18 μg/m³, and worst in the northwest region (R² of 0.87 and RMSE of 16.29 μg/m³). During the historical period (i.e., 2000–2012), a moderate agreement was observed between the available measurements and predicted PM_2.5 concentrations at the monthly level (R² = 0.67, RMSE = 10.61 μg/m³), and the agreement improved significantly at the annual level with a R² of 0.80 and a RMSE of 8.90 μg/m³.

Fig. 1.

Study domain and spatial distributions of ground monitors and elevation.

Table 1.

Model CV performances in each subregion of China at the monthly level

Cluster	Slope	Intercept	R2	RMSE
Overall	1.02	−1.36	0.93	8.90
Southeast	1.03	−1.29	0.93	6.18
Qinghai-Tibet	1.04	−2.08	0.91	8.12
North	1.02	−1.61	0.92	11.53
Northeast	1.04	−2.27	0.91	9.06
Northwest	1.04	−3.07	0.87	16.29
PRD	1.03	−1.22	0.93	6.23
YRD	1.02	−1.27	0.93	8.88

PRD, Pearl River Delta; R², coefficient of determination; RMSE, root-mean-squared prediction error; YRD, Yangtze River Delta.

Performance of Gap-Filling Approaches.

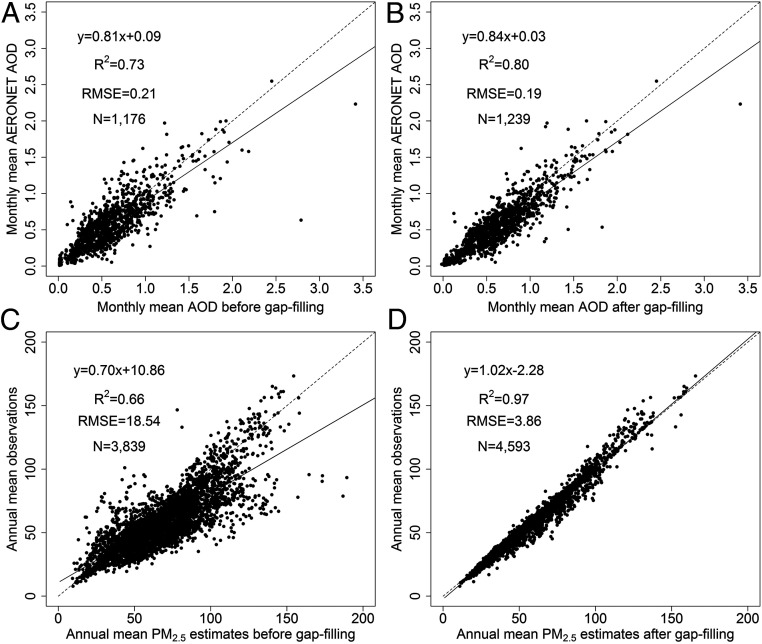
The original 17-y temporal coverage (percentage) of daily MAIAC AOD across the study domain was 56%, which was higher in north China (∼70%) and lower in the southwest (<50%) (SI Appendix, Fig. S1). After filling the missing AOD values, temporal coverage in all grid cells increased to 100%. The linear regression R² value between monthly aggregated ground aerosol robotic network (AERONET) AOD observations and gap-filled AOD was 0.80 (Fig. 2B), which was higher than that with missingness (R² = 0.73; Fig. 2A). Similarly, the annual mean PM_2.5 after filling missing AOD showed higher accuracy than those without gap filling as estimated by comparing with the annual mean observations from 2013 to 2016 (Fig. 2 C and D). The R² values increased from 0.66 to 0.97, with RMSE decreased from 18.54 to 3.86 μg/m³.

Fig. 2.

Performances of gap-filling approaches on AOD and PM_2.5 estimates. A and B are comparisons of monthly mean MAIAC AOD and AERONET AOD before and after gap filling (2000–2016), respectively. C and D are comparisons of annual mean PM_2.5 estimates and ground observations before and after gap filling (2013–2016), respectively.

Long-Term Spatiotemporal Trends of PM_2.5 Concentrations.

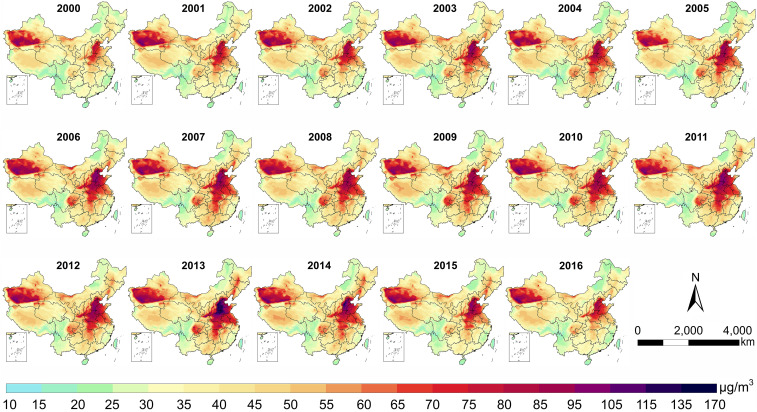
Fig. 3 shows the spatial distribution of annual mean PM_2.5 concentrations at 1-km resolution from 2000 to 2016. Spatial trends of PM_2.5 concentrations across the domain were comparable in all years, with high concentrations occurring at Beijing, Tianjin, and southern Hebei (70 to 170 μg/m³). PM_2.5 levels were lower in the rural areas of northern Inner Mongolia, southeastern Tibet, and western Sichuan (10 to 30 μg/m³). Temporally, annual mean PM_2.5 concentrations across China fluctuated between 39.5 and 47.0 μg/m³ from 2000 to 2016, with the lowest level observed in 2000. The national PM_2.5 level peaked in 2013, followed by a gradual decline from 2013 (47.0 μg/m³) to 2016 (41.5 μg/m³). Regionally speaking, all provinces suffered the most severe pollution during 2013 and 2014 except Hunan, Hubei, Chongqing, and Shaanxi, which saw annual mean PM_2.5 concentrations peak in 2011 followed by a downward trend from 2012 to 2016 (SI Appendix, Fig. S2). The lowest PM_2.5 level was observed in either 2000 or 2016 in all provinces.

Fig. 3.

Annual mean spatial distribution of PM_2.5 concentrations in China from 2000 to 2016 at 1-km spatial resolution.

Mortality Burden Attributable to PM_2.5 Exposure.

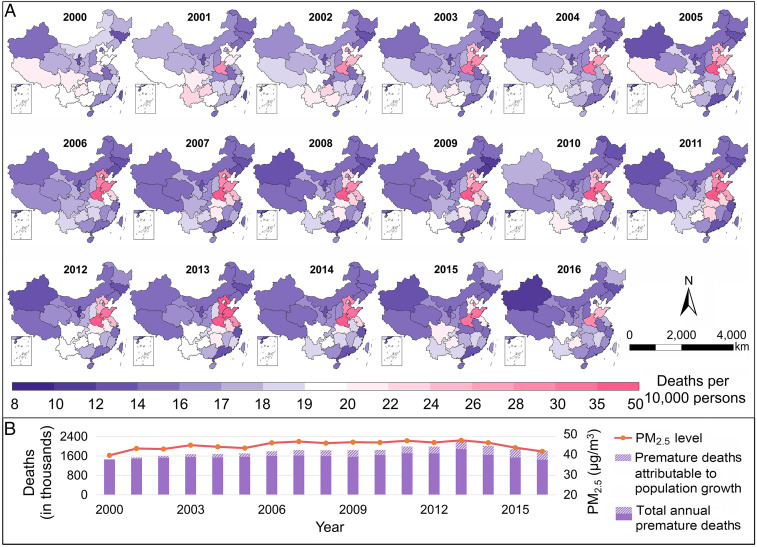
Fig. 4 shows the estimated premature deaths per 10,000 persons among adults (i.e., ≥25 y old) in each province (Fig. 4A) and the total number of adult premature deaths attributable to long-term PM_2.5 exposure from 2000 to 2016 (Fig. 4B). Estimated per-capita deaths were higher in Henan, Shandong, Tianjin, and Hebei (19.0 to 49.4 per 10,000 persons) and relatively lower in Macao, Taiwan, and Hainan (8.0 to 17.9 per 10,000 persons). Annual premature deaths of adults in China ranged from 1.5 [95% confidence interval (CI): 1.3, 1.6] million (2000) to 2.2 (95% CI: 2.1, 2.4) million (2013), with a total number of 30.8 (95% CI: 28.6, 33.2) million across the 17 y. A downward trend of annual mortality burden due to PM_2.5 exposure was also observed from 2013 to 2016 [2.2 (95% CI: 2.1, 2.4) million to 1.8 (95% CI: 1.7, 2.0) million]. After subtracting the annual burden caused by population growth, temporal variations of total mortality burden attributable to long-term PM_2.5 exposure were still consistent with the variations of annual mean PM_2.5 concentrations, with a peak observed in 2013 (1.9 million; 95% CI: 1.7 million, 2.1 million). The provincial distributions of the annual absolute number of PM_2.5-associated premature deaths from 2000 to 2016 are shown in SI Appendix, Fig. S3, and county-level burdens in 2000 and 2010 are shown in SI Appendix, Fig. S4. Although a similar spatial distribution pattern was observed, detailed features were better captured by the county-level estimates compared with those at the provincial level.

Fig. 4.

Premature deaths attributable to long-term PM_2.5 exposures from 2000 to 2016. A shows the annual premature deaths per 10,000 persons attributable to long-term PM_2.5 exposure in each province of China. B shows annual mean PM_2.5 concentrations and their corresponding total mortality burdens across China.

Discussion

Comparison with National-Scale PM_2.5 Models.

Various spatial models have been adopted previously to estimate the spatiotemporal patterns of PM_2.5 in China. Interpolation methods such as Kriging have been used traditionally to generate PM_2.5 surfaces. Although interpolation demonstrates high accuracy near ground monitors, they often fail to provide estimates with comparable accuracy in areas further from the monitors. Additionally, interpolation often produces overly smooth estimates (14), especially when robust spatial predictors are absent. Moreover, since interpolation methods rely heavily on ground measurements, using them to estimate historical PM_2.5 levels before 2013 in China is difficult. Various forms of land use regression models have been used for exposure estimation given their ability to capture fine-scale PM_2.5 gradients near roads. However, limited by the temporal resolution of source data (i.e., land cover type and road networks), these methods detect fewer variations of PM_2.5 over time (15). Chemical transport models (CTMs) may also provide PM_2.5 simulations with complete coverage in space and time (16). However, without detailed emission inventories, large discrepancies are usually reported when compared with ground observations. As a result, CTM simulations have rarely been used directly in epidemiological studies (17). Thus, satellite-driven techniques are preferred methods to predict long-term PM_2.5 concentrations in China given their high accuracy and extensive temporal coverage. Compared with previous PM_2.5 estimates using satellite data and machine-learning models (7, 11), we provide PM_2.5 values at a finer spatial resolution (1 km vs. 3 or 10 km) and higher accuracy (monthly CV R² of 0.93 vs. 0.71 and 0.86).

High-Resolution PM_2.5 Estimates.

High-resolution PM_2.5 concentration estimates are necessary to resolve more accurate exposure gradients within population clusters. As a result, both the health effects of air pollution between clusters and within clusters may be detected in large-scale studies (18). PM_2.5 estimates at the monthly level help to distinguish long-term exposure levels for individuals who reside in the same grid cell, but have different time points regarding the occurrence of health outcomes (e.g., the beginning and end of a year). They are especially helpful in regions where air pollution levels vary significantly by season. Moreover, our estimates showed higher consistency with ground observations when compared with a previously reported global dataset of annual PM_2.5 levels by van Donkelaar et al. (12) (CV R² of 0.93 vs. 0.81). For example, in the North China Plain region, van Donkelaar et al.’s model tended to overestimate the PM_2.5 concentrations in 2016 in the relatively clean regions (e.g., Shanxi province; SI Appendix, Fig. S5B) and underestimated the PM_2.5 concentrations in the more polluted regions (e.g., downtown Beijing; SI Appendix, Fig. S5D). Although van Donkelaar et al.’s annual mean estimates showed similar patterns from 2000 to 2016, the estimated absolute PM_2.5 levels are much lower than our model in many parts of China (e.g., Beijing; SI Appendix, Fig. S5E). This is likely because our model was specifically trained in China, resulting in better capability of capturing fine-scale PM_2.5 variations as compared to a global model.

Effect of Gap-Filling Approaches.

Spatiotemporally continuous PM_2.5 data are crucial to assess long-term exposures in epidemiological research. Nonrandom missingness in satellite AOD due to high surface reflectance and/or cloud cover can cause substantial data losses (19). If not properly addressed, time-averaged PM_2.5 levels will be heavily biased toward sunny days, snow/ice-free regions or seasons, and densely vegetated areas. This, in turn, will affect the magnitude and spatial distribution of estimated health effects and disease burdens (20). In this study, substantial efforts were dedicated to the multiple imputation procedure to fill missing AOD retrievals in order to reduce the sampling bias. The accuracy of long-term PM_2.5 averages was greatly enhanced after filling the AOD gaps (Fig. 2). Without gap-filling approaches, the 17-y mean PM_2.5 concentrations were underestimated by 5 to 43 μg/m³ in northeastern and northwestern China, and overestimated by 5 to 65 μg/m³ in central and southern China (SI Appendix, Fig. S6).

Accuracy of Historical Exposure Estimates.

Due to the lack of routine ground PM_2.5 monitoring data before 2013 in China, historical estimates were generated using our machine-learning algorithms trained with data since 2013. This hindcasting approach is likely to introduce errors to historical estimates at a relatively high temporal resolution. Ma et al. (4) developed a two-stage model to estimate PM_2.5 levels in China (10-km resolution) from 2004 to 2013 and reported an annual prediction R² of 0.73. Xiao et al. (5) imputed missing AOD and used machine-learning models to predict daily PM_2.5 levels in Beijing in 2008 with a hindcasting R² of 0.58. Geng et al. (16) predicted PM_2.5 concentrations between 2006 and 2012 with CTM simulations calibrated by satellite data, and reported a R² of 0.55 at the monthly or annual level when compared with limited ground observations. By averaging the predictions of two machine-learning algorithms, our predictions in the historical period at 1-km resolution showed excellent predictive power with a R² of 0.80 at the annual level.

Spatial and Temporal Trends of PM_2.5 and Its Mortality Burden.

A comprehensive control policy, named the Air Pollution Prevention and Control Action Plan, was issued by the China State Council in 2013 to control severe air pollution and improve public health (21). It has resulted in improved air quality with decreasing PM_2.5 levels nationwide. Using measurements from over 1,000 ground monitors, the China National Environmental Monitoring Center (CNEMC) reported that the annual mean PM_2.5 concentrations were 72, 62, 55, and 47 μg/m³ in China from 2013 to 2016, respectively (http://www.cnemc.cn/jcbg/zghjzkgb/). A similar trend during the same time period can be seen in our PM_2.5 estimates with all grid cells of China included (Fig. 4B). However, our spatially aggregated estimates are lower than the averages from only the ground monitors. Similar to the regulatory monitoring network in the United States, the Chinese national monitoring network is mostly concentrated in densely populated regions in central and eastern China (Fig. 1). Since rural areas and less developed provinces are scarcely monitored (e.g., Tibet, Qinghai, and Inner Mongolia), using averages obtained from the monitors tends to overestimate actual national mean PM_2.5 concentrations.

Several studies have reported the mortality burden attributable to long-term PM_2.5 exposure in China. For example, a study of county-level mortality burden in 2010 estimated a total burden of 1.27 million (22). Liu et al. (23) estimated the PM_2.5 impact on mortality defined as the sum of deaths caused by lung cancer, ischemic heart disease, and stroke from 2004 (0.8 million) to 2012 (1.2 million). Xie et al. (24) reported 1.26 million excess deaths in 2010 across China, which was 42% higher than their PM_2.5-associated mortality burden estimation in 2000. Although similar spatial distributions were observed between our estimation and previous researches (22, 24), our annual mortality burdens are higher than the aforementioned studies. The discrepancy may partly be explained by our exposure estimates. Most previous studies adopted satellite-based PM_2.5 estimates at 0.1-degree resolution without accounting for the AOD missingness or an elaborate gap-filing approach (4, 25). Our study indicates that the biases in mortality burden estimation need to be corrected in most regions of China with gap-filled PM_2.5 estimates (SI Appendix, Fig. S6), and substantial underestimation of premature deaths in Xinjiang province and overestimation in central and eastern China may be introduced if biased PM_2.5 exposure was adopted. In addition, previous studies have estimated the mortality burden based on the integrated exposure–response functions (IERs), which simulated the health impacts of PM_2.5 using estimated hazard effects of household air pollution, active and second-hand smoking, assuming equal toxicity without considering compositional difference (3, 26). By including more causes of death and additional cohort studies, Burnett et al. (27) reported a 120% larger mortality burden using the Global Exposure Mortality Model (GEMM) than the IER-based estimates. Our estimated annual mortality burden based on a Chinese cohort study and the GEMM was also higher than those predicted by the IERs (3, 22, 23). Our results are overall 20% lower than direct GEMM estimates (SI Appendix, Fig. S7), suggesting that uncertainties may still exist when applying global models directly in China.

In the current analysis, provincial adult disease burdens of long-term PM_2.5 exposure in China were also estimated. In a country with about 1.4 billion people and a vast territory, air pollution levels, population density, age structure, and economic development in China vary substantially in space and time. Greater resources need to be devoted to the provinces with severe air pollution to meet WHO guidelines (28), compared with the relatively clean regions. Therefore, a comprehensive analysis of provincial mortality burden would support targeted planning for air quality improvement and health promotion. Despite continuous population growth, adult mortality burden caused by PM_2.5 exposure increased by 29% from 2000 to 2013, then gradually decreased to the level of 2000 until 2016 (Fig. 4B), demonstrating the effectiveness of aggressive emission control measures taken by the Chinese government. A similar finding was reported by Huang et al. (29), where a yearly reduction in mortality burden in 74 major Chinese cities was observed from 2013 to 2017.

Strengths.

Taking advantage of satellite-retrieved AOD at 1-km resolution and spatiotemporally resolved environmental and geographical data from multiple sources, we generated a 17-y time series of high-quality PM_2.5 estimates. Unlike many previous studies (4, 11), gap-filling techniques were used to minimize the bias in monthly PM_2.5 estimates caused by the nonrandom missingness in AOD. Combining two machine-learning algorithms helped improve prediction accuracy and stability. This study characterizes the long-term trend of PM_2.5-associated mortality burden in China with high-resolution, full-coverage, and unbiased PM_2.5 exposure estimates, as well as an exposure–response relationship derived from a nationally representative Chinese cohort study supplemented by the GEMM.

Limitations.

While our method demonstrated significant strengths in estimating long-term PM_2.5 exposure in China, several limitations remain. First, despite our effort to use all available observations to validate model predictions, historical PM_2.5 trends cannot be assessed equally well in every region of China. Second, although our machine-learning models performed well overall, their performance varied regionally. A slightly lower accuracy was noted in northwestern China, which could result from both sparse ground monitors and challenging conditions for AOD retrieval. Third, although the concentration–response (C–R) relationship between PM_2.5 and mortality in our study was adopted from a Chinese cohort study, the section of this curve at PM_2.5 levels below 31.2 μg/m³ [minimum PM_2.5 concentrations in Yang et al. (30)] was modeled using the GEMM approach, which mainly involves studies from developed countries. Given different PM_2.5 composition, population susceptibility among countries, and modeling methodology, this integrated C–R relationship may still differ from the true causal effect in China at low exposure levels. Additional investigations in relatively clean regions of China are still needed. Finally, limited by the availability of detailed annual population and mortality rate data, the PM_2.5 mortality burden at a finer scale cannot be estimated every year. However, the spatial patterns of our provincial-level estimates are consistent with county-level estimates in 2000 and 2010 when detailed population and mortality rate data are available (SI Appendix, Fig. S4). Nonetheless, more research on the spatiotemporal distribution of mortality burden at finer scales is still needed, especially in the western regions of China.

Perspectives for Future Applications.

Using spatiotemporal exposure estimates from this analysis, additional epidemiological studies focusing on the chronic health effects of PM_2.5 exposure among the Chinese population can be conducted in the future. Consequently, the health burden of other diseases attributable to PM_2.5 exposure in China could be generated. Furthermore, this massive outdoor PM_2.5 database may be applied in combination with indoor source information to better characterize the adverse effect of personal air pollution exposure.

Conclusion.

We reported a high-performance modeling technique to estimate reliable PM_2.5 concentrations at 1-km resolution. These long-term PM_2.5 estimates will greatly enhance environmental epidemiological studies relating to air pollution exposure in China. Comprehensive assessments of the health effects attributable to air pollution in highly polluted regions such as China are urgently needed to illustrate the full shape of the global exposure–response relationship.

Materials and Methods

Study Setting.

Our study domain includes Chinese mainland, Hong Kong, Macao, and Taiwan (Fig. 1). In this study, provinces refer to all provinces, municipalities, autonomous regions, and special administrative regions of China. A 1 × 1-km² grid was designed to cover the entire study domain plus a 100-km buffer zone for data collection and spatial alignment. A total of 9,507,413 grid cells were within the border of China. Monthly mean PM_2.5 concentrations from 2000 to 2016 in each grid cell were estimated, and the corresponding annual mortality burden in each province was calculated.

Ground PM_2.5 Measurements.

Daily mean PM_2.5 concentrations from 1,530 ground monitors during 2013 and 2016 were collected from the CNEMC (http://www.cnemc.cn), Hong Kong Environmental Protection Department (https://www.epd.gov.hk/epd/english/top.html), and Taiwan Environmental Protection Agency (http://taqm.epa.gov.tw) (Fig. 1). Daily PM_2.5 concentrations from each monitor with no less than 15 d in any given month were aggregated to the monthly mean. These data were used for model training and CV. The validation of historical PM_2.5 predictions from 2000 to 2012 used available PM_2.5 measurements from Hong Kong, Taiwan, the US Embassy and Consulates in Beijing, Shanghai, and Guangzhou (https://china.usembassy-china.org.cn), as well as experimental campaigns operated by Tsinghua University (31). Locations of these PM_2.5 monitors from 2000 to 2012 are shown in Fig. 1, and detailed information about them is presented in SI Appendix, Table S1. Each monitor was matched to the grid cell where it is located. Monthly mean PM_2.5 concentrations were calculated using all daily measurements in the same grid cell.

AOD Data.

MAIAC AOD at 1-km spatial resolution was produced by the MAIAC team at the National Aeronautics and Space Administration (NASA) Goddard Space Flight Center (32). Derived using MODIS observations, MAIAC AOD has higher spatial coverage and better accuracy than the standard MODIS AOD products (33). AERONET AOD measurements (Version 3) at 440 and 675 nm in China were extracted and interpolated to 550 nm using the Angstrom exponent to evaluate the accuracy of MAIAC AOD. MAIAC AOD was highly correlated with AERONET observations with correlation coefficients over 0.92 (34). MAIAC AOD data from the Terra satellite (overpass at 10:30 AM local time) were available since the 56th day of the year 2000, and from the Aqua satellite (overpass at 1:30 PM local time) since the 185th day of 2002. We extracted all AOD values at 550 nm from their available dates until the end of 2016.

Meteorological Data.

Meteorological variables at 12.5-km spatial resolution were extracted from the European Center for Medium-Range Weather Forecast (ECMWF) Reanalysis Interim (ERA-Interim) (35). An inverse distance weighting (IDW) approach was used to interpolate all meteorological variables to 1-km grid cells. Data during the overpass times of Terra and Aqua satellites in each day were then averaged and used for filling daily AOD gaps. Monthly data with all daily hours included were used for PM_2.5 estimation. To investigate the impact of different interpolation approaches on the ECMWF data, we performed a 10-fold CV for IDW and Ordinary Kriging results at the monthly level separately, and compared interpolated temperature and relative humidity at 1-km resolution with observations from over 3,600 weather stations in China between 2000 and 2016. Satisfactory and highly comparable model performances were shown for both approaches with CV R² values of 0.96 and 0.75 at the monthly level for temperature and relative humidity, respectively (SI Appendix, Fig. S8).

Cloud Fraction.

Collection 6 level 2 MODIS daytime Cloud fraction was obtained from NASA (https://ladsweb.modaps.eosdis.nasa.gov/). We resampled the daily data of Aqua and Terra cloud fraction at 5-km resolution to the 1-km grid cells by a nearest-neighbor approach, separately, and then the values in each grid cell were averaged and used as a predictor to fill missing AOD.

Reanalysis AOD and PM_2.5 Data.

Daily AOD and monthly PM_2.5 components simulations at 0.5° × 0.625° (latitude × longitude) resolution were extracted from the modern-era retrospective analysis for research and applications (MERRA, Version 2) (36). Major PM_2.5 components, including organic carbon, black carbon, sulfate, dust, and sea salt, were assigned weights of 2.100, 1.375, 1.000, 1.000, and 1.000, respectively, then summed to estimate PM_2.5 mass concentration. Details on the weighting method of these four components can be found elsewhere (5).

Emissions Inventory of PM_2.5.

Monthly inventories of total emissions of PM_2.5 at 0.1-degree resolution from 2000 to 2014 were obtained from Peking University (37) and matched to the 1-km grid cells by a nearest-neighbor approach to maintain a consistent spatial resolution with MAIAC AOD. Since inventories were unavailable after 2014, data on the corresponding months in 2014 were used in 2015 and 2016.

Other Variables for PM_2.5 Estimation.

Normalized difference vegetation index (NDVI) data at 500-m resolution (16-d interval) were extracted from the Global MODIS vegetation indices (VI) level-3 product. The beginning dates of Terra and Aqua AOD for each year were staggered with an 8-d difference. By combining Terra and Aqua NDVI, 8-d composite NDVI was calculated (6) and then averaged to the monthly level. Road network, including highways and city expressways in 2002, 2006, 2010, 2014, and land use information (at 1-km resolution every 5 y, starting in 2000) were obtained from the Institute of Geographic Sciences and Natural Resources Research of the Chinese Academy of Sciences. Highway length and major types of land surfaces in each grid cell were calculated. Elevation at 30-m resolution was extracted from the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) Global Digital Elevation Model, Version 2 (GDEM V2) (https://asterweb.jpl.nasa.gov/gdem.asp). Population density at 1-km resolution in 2010 was downloaded from LandScan website.

AOD Gap-Filling Techniques.

A two-step approach was used to fill AOD missingness and produce an AOD field with complete coverage in space and time. In the first step, we performed a daily simple linear regression to impute the missing values for Aqua or Terra AOD (38, 39). Then daily average of Terra and Aqua AOD in each grid cell was used. In the second step, a multiple-imputation technique was employed to fill in the remaining missing AOD values at the daily level. An additive model was adopted with predictors including MERRA AOD, MODIS cloud fraction, temperature, relative humidity, boundary layer height, albedo, total column water, and elevation. Each missing value was imputed five times, and then averaged to address the extra variability introduced by traditional imputation models (38). A bootstrap method was used for repeated sampling in order to vary the random error (8). The assumption behind our gap-filling approach is that the AOD field is continuous in space and time, and this spatiotemporal autocorrelation is mediated by various meteorological and land surface conditions represented by the covariates included in the multiple imputation model. The smooth terms of geographic coordinates of grid cell centroids were included to address the spatial continuity of gap-filled AOD. Since previous research suggested that the temporal autocorrelation of fine particles drops significantly after 3 d (31), we fitted the multiple-imputation model (Eq. 1) in a 5-d rolling window (i.e., 2 d before and 2 d after the target date). The model structure is as follows:

$$AO{D}_{gt}={\beta }_{1}MERRAAO{D}_{gt}+{\beta }_{2}C{F}_{gt}+{\beta }_{3}Tem{p}_{gt}+{\beta }_{4}R{H}_{gt}+{\beta }_{5}PBL{H}_{gt}+{\beta }_{6}A{l}_{gt}+{\beta }_{7}TC{W}_{gt}+{\beta }_{8}Ele{v}_g+{\text{D}}_t+s\left({\text{X}}_g\right)+s\left({\text{Y}}_g\right)+s\left(X_g^2\right)+s\left(Y_g^2\right)+s\left({\text{X}}_g\times {\text{Y}}_g\right)+{\epsilon }_{gt},$$ [1]

where $AO{D}_{gt}$ is the combined AOD in grid cell g on DOY t; ${\beta }_1-{\beta }_8$ are slopes for the predictors; $MERRAAO{D}_{gt}$ is MERRA simulated AOD in grid cell g on DOY t; $C{F}_{gt}$ is the MODIS cloud fraction in grid cell g on DOY t; $Tem{p}_{gt}$, $R{H}_{gt},\hspace{0.17em}PBL{H}_{gt}$, $A{l}_{gt},\hspace{0.17em}\mathrm{and}\hspace{0.17em}TC{W}_{gt}$ are mean temperature, mean relative humidity, boundary layer height, surface albedo, and total column water in grid cell g on DOY t, respectively; $Ele{v}_g$ is the elevation in grid cell g; $D_t$ is the dummy variable of day across the 5-d period; ${\text{X}}_g\hspace{0.17em}\mathrm{and}\hspace{0.17em}{\text{Y}}_g$ are the projected longitude and latitude coordinates of the centroid of grid cell g; and ${\epsilon }_{gt}$ is the error term in grid cell g on DOY t.

Machine-Learning Algorithms to Estimate PM_2.5 Levels.

Two machine-learning algorithms, random forest (RF) and extreme gradient boosting (XGBoost), were employed to generate monthly mean PM_2.5 concentrations between 2000 and 2016. Data from 2013 to 2016 were used for model training. The final model was constructed with predictors that are correlated with the distribution of PM_2.5 in space and time and collectively ensured best model CV R² and RMSE values. Finally, in addition to gap-filled AOD, model predictors included MERRA PM_2.5, temperature, relative humidity, surface pressure, total precipitation, snowfall, UV B, cloud cover, boundary layer height, evaporation, albedo, surface net solar radiation, wind speed at 10-m height, population density, NDVI, highway length, total PM_2.5 emission, and elevation.

Given that the relationship between PM_2.5 and AOD varies in space, our RF and XGBoost models were trained separately in seven subregions, including the North, Northwest, Northeast, Qinghai-Tibet, Pearl River Delta (PRD), Yangtze River Delta (YRD), and Southeast (Fig. 1). These subregions were identified by a K-means clustering algorithm using geographically weighted regression (5). We took the average of the RF and XGBoost predictions in each grid cell as the final exposure estimate in order to improve the overall predictive accuracy (SI Appendix, Table S2). Additionally, we compared these arithmetic means with weighted averages using a Bayesian model averaging method (40) on model fitting, model CV, and prediction accuracy. Although Bayesian model averaging performed better on model fitting (R² of 0.99 vs. 0.97 at the monthly level), similar or slightly worse performances were observed for model CV and historical prediction compared with the arithmetic means (SI Appendix, Fig. S9).

Model Validation.

Tenfold CV was used to evaluate model performance and potential overfitting. The dataset with all data records at the monthly level during 2013–2016 was randomly split into ten subsets. Nine subsets were used to train a model, which was then employed to predict the withheld one. This process was repeated 10 times to generate CV PM_2.5 concentrations corresponding to each monthly mean observation used for model training. Simple linear regression was performed for CV-generated PM_2.5 estimates and observations to evaluate model performance using statistical indicators, such as R² and RMSE. Model predictive power during the historical period was also calculated.

In order to assess the effect of gap-filling approaches on the long-term PM_2.5 estimation, we reran the machine-learning models using AOD data before filling the missingness, and then monthly mean PM_2.5 concentrations were estimated by adopting the same model structure and factors as the main estimation, except the AOD type. Here, we removed grid cells with fewer than 15 d of AOD when calculating monthly mean AOD values.

Estimation of the Mortality Burden of PM_2.5 Exposure.

Limited by the availability of spatially resolved population mortality data, the annual burden of deaths attributable to long-term PM_2.5 exposure was calculated at the provincial level from 2000 to 2016, following methods from the Global Burden of Disease project (41). Annual age-specific population and all-cause mortality rates in each province from 2000 to 2016 were collected from the National Bureau of Statistics of China (http://data.stats.gov.cn/), China Population and Employment Statistics Yearbooks, and Census and Statistics Department of the Hong Kong and Macao Special Administrative Regions, and Taiwan province (https://www.censtatd.gov.hk/home/index.jsp, https://www.dsec.gov.mo/zh-MO/, https://www.stat.gov.tw/). Age-specific mortality data in 2010 were obtained from demographic census statistics (http://data.stats.gov.cn/) and those in other years were calculated using the province-specific proportion of adult deaths (no less than 25 y old) among all ages.

A C–R function between long-term PM_2.5 exposure and nonaccidental mortality for Chinese adults was adopted (30). Involving 116,821 participants in 15 provinces of China, Yang et al.’s C–R function was fitted across an exposure range of 31.2 to 97.0 μg/m³. In their study, the effect sizes of the fitted curve were reported with the lowest exposure level as the reference (i.e., hazard ratio = 1.00 at PM_2.5 concentration = 31.2 μg/m³). However, it has been previously reported that even exposure to extremely low levels of PM_2.5 may still adversely impact human health (2) and no threshold of PM_2.5 exposure has been observed (42). Therefore, we incorporated a function modeled after the GEMM (27) to account for the health effect of PM_2.5 exposure below 31.2 μg/m³. The GEMM was fitted using data from 41 cohorts, 3 of which are from Chinese mainland, Hong Kong, and Taiwan. From the GEMM function, the hazard ratio at the reference exposure level (i.e., 31.2 μg/m³) in Yang et al.’s study was obtained and used as the reference value to calibrate the relative effect sizes (i.e., hazard ratio) of Yang et al.’s C–R function above 31.2 μg/m³ in China. Since annual exposure levels in Fujian, Hainan, Yunnan, and Taiwan (∼8.3% of the total population) can be lower than the floor level of Yang et al.’s curve, the health effects in these years/regions were estimated using the GEMM directly. This C–R curve in China and the GEMM are shown in SI Appendix, Fig. S10.

The absolute number of adult deaths attributable to PM_2.5 exposure in each province was calculated annually using the following equation (Eq. 2). Province-specific per-capita mortality was presented as the absolute number of adult deaths divided by adult population size.

$$Mortalit{y}_{ij}=\left(HR\left(C_{ij}\right)-1\right)/HR\left(C_{ij}\right)\times Po{p}_{ij}\times I_{ij},$$ [2]

where $Mortalit{y}_{ij}$ is the estimated premature deaths in province $i$ at year $j$; $HR\left(C_{ij}\right)$ is the estimated hazard ratio in province $i$ at year $j$; $Po{p}_{ij}$ is the total adult population in province $i$ at year $j$; and $I_{ij}$ is the baseline mortality rate of adults in province $i$ at year $j$.

To estimate the 95% CI of the national mortality burden each year, the HRs of the 34 provinces (assuming independent normal distributions) were randomly and simultaneously sampled 10,000 times. The estimated provincial premature deaths in each iteration were summed to represent the annual total mortality burden associated with long-term PM_2.5 exposure in China (43). Finally, the 95% CIs of the national burdens were estimated as range between the 2.5th and 97.5th percentile of the 10,000 national estimates. In order to subtract the amount of premature death attributable to population growth, annual mortality burden among adults in each province was recalculated using the population in year 2000 as the reference. Taking advantage of the age-specific population and mortality data from the fifth and sixth National Census of China (http://data.stats.gov.cn/), county-level mortality burdens were calculated in 2000 and 2010 to show their spatial distribution patterns at a finer scale.

Data Availability.

Relevant data sources for modeling are provided in the paper and SI Appendix. Data and codes for the maps of this study are available from the corresponding authors on reasonable request.