Significance
Animals frequently need to choose the best alternative from a set of possibilities, whether it is which direction to swim in or which food source to favor. How long should a network of neurons take to choose the best of options? Theoretical results suggest that the optimal time grows as , if the values of each option are imperfectly perceived. However, standard self-terminating neural network models of decision-making cannot achieve this optimal behavior. We show how using certain additional nonlinear response properties in neurons, which are ignored in standard models, results in a decision-making architecture that both achieves the optimal scaling of decision time and accounts for multiple experimentally observed features of neural decision-making.
Keywords: neural circuits, optimal decision-making, speed–accuracy trade-off, noisy computation
Abstract
An elemental computation in the brain is to identify the best in a set of options and report its value. It is required for inference, decision-making, optimization, action selection, consensus, and foraging. Neural computing is considered powerful because of its parallelism; however, it is unclear whether neurons can perform this max-finding operation in a way that improves upon the prohibitively slow optimal serial max-finding computation (which takes time for noisy candidate options) by a factor of , the benchmark for parallel computation. Biologically plausible architectures for this task are winner-take-all (WTA) networks, where individual neurons inhibit each other so only those with the largest input remain active. We show that conventional WTA networks fail the parallelism benchmark and, worse, in the presence of noise, altogether fail to produce a winner when is large. We introduce the nWTA network, in which neurons are equipped with a second nonlinearity that prevents weakly active neurons from contributing inhibition. Without parameter fine-tuning or rescaling as varies, the nWTA network achieves the parallelism benchmark. The network reproduces experimentally observed phenomena like Hick’s law without needing an additional readout stage or adaptive -dependent thresholds. Our work bridges scales by linking cellular nonlinearities to circuit-level decision-making, establishes that distributed computation saturating the parallelism benchmark is possible in networks of noisy, finite-memory neurons, and shows that Hick’s law may be a symptom of near-optimal parallel decision-making with noisy input.
Finding the best of options is an elemental and ubiquitous computation in many complex biological systems. It is invoked in a wide range of tasks including inference, optimization, decision-making, action selection, consensus, and foraging (1–5). In inference and decoding, finding the best-supported alternative involves identifying the largest likelihood (), then finding the model corresponding to that likelihood (); decision-making, action selection, and foraging involve determining and selecting the most desirable alternative (option, move, or food source, respectively) according to some metric, again requiring operations. In all these cases, data arrives over time and is noisy; thus, assessing the alternatives involves integration of evidence over time.
In the brain, the operations recur across a variety of organisms, systems, and scales. Here, we focus on two distinct regimes in which it is interesting to consider how the brain computes . The first is finding the most activated neuron (or pool of neurons) across thousands of neurons (pools). An example of this large- computation is the dynamic that leads to the sparsification of Kenyon cell activity within fly mushroom bodies (5), and, potentially, to the sparse activation of hippocampal place cells (6–8). It is possible that many more areas with strong inhibition display similar dynamics, including the vertebrate olfactory bulb (9, 10) and basal ganglia (3, 11, 12). The same operation is needed in network implementations of Bayesian inference, to find the best supported hypothesis given noisy input, as well as in the decision layers of artificial neural networks that classify inputs. In this large- regime, the competition is between internal states or representations, rather than between externally presented options.
The second regime is encountered in explicit behavioral decision-making scenarios that involve choosing between a small number of externally presented alternatives. This regime is typically explored in multialternative psychophysical decision tasks (2, 13).
In this study, we seek a unified understanding of how efficiently neurons compute across these disparate regimes. That is, given a set of noisy inputs, how rapidly could a network of neurons correctly identify the input with the largest value?
The conventional strategy to find the largest of values (as would be implemented on a computer) involves running through the values sequentially, integrating each for some time . The time to carry out this procedure grows proportionally to , which is at least linear in . We will refer to such a strategy as serial since it processes values one at a time. An optimal parallel strategy should run a factor of times faster.
Neural computation is thought to be highly efficient because of the capacity for massive parallelism: The brain could distribute a task across large populations of neurons that process information simultaneously, dramatically increasing computation speed by trading (serial) computation time for number of neurons. However, neurons are hardly ideal processors: They are leaky and noisy, and their nonlinear thresholds could discard relevant information. Thus, it is unclear whether parallel processing with neurons can find the best option with high accuracy in a time comparable to an optimal parallel strategy. Because of the importance of operations, they are well-studied in neuroscience in the guise of winner-take-all (WTA) neural circuit models and phenomenological accumulate-to-bound (AB) models.
A WTA network consists of pools of leaky neurons (with one or more neurons per pool) representing different alternatives. Pools amplify their own state and interact competitively through inhibition. Self-amplification and lateral inhibition can produce a final state in which only the pool with the largest integrated input () remains active, while the rest are silenced (14–16). If the activation of the winner is proportional to the size of its input (17), the network also solves the problem. The final state of such a network serves as the completed output of the computation.
AB models (3, 18–25) consist of individual integrators. They have provided tremendous insight into the psychophysics of decision-making (26) and are closely connected to models of optimal decision-making (3, 24, 27). We focus on WTA networks rather than AB models for three reasons. First, AB models, in contrast to WTA networks, are typically developed as phenomenological descriptors without a mechanistic implementation [see Discussion and SI Appendix, section S1 for exceptions and for an exploration of a biologically plausible AB model tied to the structure of the basal ganglia (3)]. Second, unlike the self-terminating WTA dynamics, most AB models do not themselves directly answer the , questions, because they require a separate readout that decides when to terminate the process and identify the largest sum, typically done by applying a threshold [that is itself modeled as a dynamical variable that could change over time (19, 27, 28)]. Although movement initiation might impose such a threshold in behavioral decision-making tasks, there is no natural external threshold in computations like activity sparsification. Third, the relationship between optimal performance and AB models has been well characterized (3, 22–24, 27, 29), but much less has been done for WTA networks.
We seek to characterize the time complexity of WTA networks—how long it takes a network to compute and from a set of inputs, as a function of —and compare this time complexity to normative bounds derived from theoretical arguments and from AB models.
We begin by bounding the optimal scaling of decision time with the number of inputs and introduce a parallelism benchmark, defined as a speedup of a factor of over the serial strategy. We show that, in the presence of noise, conventional WTA models either have suboptimal scaling or, when is large, altogether fail to complete the WTA computation. We propose the nWTA network, in which neurons are equipped with a second nonlinearity so that weakly active neurons (pools) cannot contribute inhibition to the circuit. The nWTA network accurately identifies the largest input times faster than the serial strategy, achieving the parallelism benchmark. Unlike conventional models, this performance requires no parameter fine-tuning. Moreover, the nWTA network self-adjusts (without any parameter change) its integration time as with the number of noisy inputs, matching both Hick’s law of behavioral decision-making (30) and a normative scaling of fixed-accuracy decision-making with noisy input options.
In total, our results suggest that it is at least theoretically possible for neural circuits to optimally perform and exploit truly parallel computation in a canonical task.
Results
The Problem.
Consider finding the largest element in a set of options that are presented as time series of values with constant means , numbered in descending order of strength. In the deterministic case, the options are presented without noise. In the noisy case, the options fluctuate over time as , where is the fixed mean and are zero-mean fluctuations (see Methods), and the task is to identify the option with the largest fixed mean. We consider the computation to be completed accurately if the option with the largest mean is correctly identified, and define the accuracy of a strategy to be the probability that it identifies the correct item.
We assume that the top two options are separated by an -independent gap of size , so that . For simplicity, we also assume that the remaining are equal to each other ( and ). For a discussion of more general distributions of the (including a fully uniform distribution, , where the top gap shrinks with ); see SI Appendix, section S2.
Optimal Serial Strategy and Parallelism Benchmark.
Consider the time complexity of a serial procedure that examined each option in turn, as would be carried out on a computer. In the absence of noise, the options do not need to be integrated over time to estimate the mean, and thus it suffices to examine each for a short fixed time that does not depend on . Thus, the time to choose the largest of nonnoisy options presented serially takes a time .* We refer to this as the deterministic serial scaling of .
In the noisy case, obtaining a correct answer involves collecting information for long enough to estimate the means of the time series, then performing a operation on the estimates. Because of noisy fluctuations, any strategy with a finite decision time will sometimes identify the wrong option as having the largest mean, and thus have nonzero error probability. We expect a speed–accuracy trade-off that involves setting an acceptable error probability and finding the shortest time required to reach this accuracy (one may also make a maximally accurate decision within a set time; SI Appendix, section S1). If is the time for which each option is integrated, then the total time taken to make a decision is ; as we show next, depends on .
How long should each option be integrated to maintain a fixed high accuracy (or fixed low total error probability) as grows? Consider integrating each option for time before making a decision, and let be the integrated value of the th option. The decision will be an error if (; recall that the first option has the largest mean). The total error probability can be bounded by the sum of the probabilities that any individual incorrect option is greater than the correct option. Thus . To maintain below some small fixed for any , it is sufficient that each . For a large class of distributions, the integrated values of the options concentrate around their true values, with the probability of these error-inducing fluctuations falling off exponentially as (for some constant that depends on the distribution of the fluctuations but not on ) according to very general concentration inequalities (Fig. 1A). Choosing an integration time that grows as is thus sufficient to maintain a fixed total error probability (Fig. 1B; we make these arguments precise in SI Appendix, section S1). Consequently, the time for a serial strategy to achieve a constant decision accuracy is bounded by . We refer to this as the noisy serial scaling of .
Fig. 1.
Parallelism benchmarks and setup of the WTA circuit. (A) Schematic illustration of how integration time is sufficient to maintain fixed accuracy (here measured as number of correct trials over total number of trials). Thin lines denote sample time series from different trials for each option ( options are in different colors; here ). Thick curves denote sample histograms (distributions) after integrating for time . The tails of the distribution shrink exponentially (shown by gray shading). Thus, integrating for time means a per-option error probability of , so that the total error probability, given by times the per-option error probability, is fixed. (B) The integration time is necessary to maintain fixed accuracy when estimating the means of noisy time series with Gaussian fluctuations. Plot shows the integration time to fixed accuracy (dashed and solid lines, and accuracy, respectively) in (nonneural) simulations with Gaussian input fluctuations. Thin black lines are logarithmic fits. (C) WTA network architectures. (Top) The time series serve as input to neurons (or pools of neurons), ordered by the size of their constant mean (with gap between the top two inputs). Each neuron pool inhibits all others and excites itself. (Bottom) Mathematically equivalent network with a global inhibitory neuron pool: All neuron pools excite the inhibitory neuron pool, which inhibits them. This requires only synapses, compared to for the mutual inhibition circuit (Top). (D) Neural firing rates and synaptic activations (coloring as in C). Convergence time is the time taken for the firing rate of the winner neuron pool to reach a fraction (usually chosen as 0.8; see Methods) of its expected asymptotic activity (black line). Dashed line denotes threshold for a neuron pool to contribute inhibition in the nonlinear inhibition model (nWTA; see Methods).
The scaling time above is an upper bound, both because we bound the total error probability by the sum of the individual error probabilities and because, for some real-world distributions, the probability of errors falls off faster than exponential. For example, if the extent of the noise is smaller than the gap between the largest and second-largest options, then no integration is needed, because fluctuations will never result in an error. Indeed, our framework predicts that the factor should vanish for easy tasks.
For the case of Gaussian fluctuations, the integration time bound per option is known to be tight (24) (see SI Appendix, section S1 for a simple derivation of this scaling and for more general arguments for the bound). Gaussian fluctuations are natural both because many common noise sources are Gaussian and because the results of an integration process over non-Gaussian fluctuations are eventually Gaussian-distributed by the central limit theorem. Thus, a total scaling time of will be characteristic of many max finding processes.
A strategy that can process the options in parallel (rather than considering each in turn) should achieve a factor of speedup over the serial strategies (31), achieving times and . We will refer to these idealized parallel computation times as parallelism benchmarks. Note that these parallelism benchmarks are equivalent to perfectly integrating options in parallel to an externally determined threshold selected for that choice of to maintain high accuracy, as performed by AB models.
Specific normative strategies for decision-making can be formulated in a Bayesian framework for decision time minimization at high accuracy (the multihypothesis sequential probability ratio test [MSPRT]) (3, 24, 32, 33) or in a framework for maximization of a total reward rate (27, 34). The MSPRT, which is known to minimize decision time in the limit of vanishing error rate (33) and thus achieves scaling, tracks the log-likelihood of each option. It makes a decision when either the largest log-likelihood (“absolute MSPRT”) or the ratio between the largest and second-largest log-likelihoods (“relative MSPRT”) crosses a threshold. Both versions have similar asymptotic performance and, with an appropriate choice of bound, are AB models (3, 24).
Interestingly, the theoretical benchmark on parallel max with noisy options matches the empirical Hick’s law (3, 22, 24, 30, 35–38), an influential result in the psychophysics of human decision-making used as far afield as commercial marketing and design to improve the presentation of choices (39). Hick’s law states that, when choosing between a small number of externally presented alternatives, the time to reach an accurate decision increases with the number of alternatives, , as . While Hick’s law is usually studied in the small- psychophysical decision-making regime, the parallel with our derived parallelism benchmark for max finding suggests that the phenomenology of Hick’s law might apply beyond the small- case and reflect a general process of efficient decision-making when options are noisy.
The natural question, which we address in the rest of this study, is, what type of neural circuit can perform such efficient parallel decision-making between noisy options?
Neural Decision-Making Circuits.
The parallelism benchmarks derived above are idealizations without a neural implementation. The benchmarks require perfect integration of time series without leak, assume no loss of information from internal noise and nonlinear processing, and are also not self-terminating: They require an external observer to apply a threshold to terminate the operation and select the option on top at that time as the winner.
The natural way to model a self-terminating computation in the brain is through the WTA circuit, with a variety of circuits in the brain exhibiting WTA-like architectures. Here, we focus on a basic and canonical WTA architecture (14, 15, 17) (Fig. 1C; see SI Appendix, section S2 for a discussion of the WTA circuit in Fig. 1 C, Bottom with an additional nonzero inhibitory time constant, and see Discussion for alternative WTA circuits).
Consider neurons or neuron pools, interacting through self-excitation (strength ) and mutual inhibition (strength ) (Fig. 1C). The neural states are described by synaptic activations or firing rates , ,
| [1] |
Here, is a rectifying nonlinearity which ensures nonnegative rates. The inputs are the noisy time series with means and fluctuations . The are modeled as Ornstein–Uhlenbeck processes; see Methods and Eq. 6. The fluctuation model is quite general, and could represent randomness in the options presented by the external world, noise in perceiving the option values, variable activity within each neuron pool (reflecting synaptic failures, stochastic spiking, etc.), or any combination of these factors. In our simulations, we consider a wide spread of noise magnitudes, from approximately the gap between the largest two options to 20 times larger, thus accounting both for tasks with low signal-to-noise ratio and for stochastic Poisson-like or overdispersed neural spiking. Note that any internally contributed noise from variable neural activity should decrease with the size of the pool. When making comparisons across values of , we assume that the magnitude of the noise per neuron pool (and hence the size of the neuron pools) remains fixed, but performance will be better if the pool size can grow with . We assume initial conditions for all (see Methods for discussion of initial conditions). For appropriate parameter values (), and in the absence of noise, the network exhibits stable WTA dynamics with a unique winner with asymptotic activity , where is the input of the winning neuron (17) (Fig. 1D; see also Methods and SI Appendix, section S2). All key quantities are summarized in Table 1. These dynamics can be understood as movement downhill on an energy landscape, which drives the network to one of possible stable states, each corresponding to solo activation of a different neuron or pool (SI Appendix, Fig. S2).
Table 1.
Overview of key quantities of WTA network dynamics
| Name | Definition |
| Number of options and neurons (pools) | |
| Activation of th node; see Eq. 1 | |
| Coupling strength of self-excitation | |
| Coupling strength of lateral inhibition | |
| Expectation value of th option | |
| OU noise in the th option; Eq. 6 | |
| Initial condition for all nodes | |
| Deterministic asymptotic activity of winner | |
| with input | |
| Time at which any reaches from | |
| below, | |
| Threshold on inhibitory input, Eq. 4 |
We wish to understand how WTA dynamics behave as a function of the number of competing alternatives and, in particular, how long it takes to arrive at an accurate single estimate of a winner ().
Conventional WTA Networks Do Not Show Efficient Parallel Decision-Making
Weak Inhibition: Accurate but Slow WTA.
Total inhibition in Eq. 1 grows as . A reasonable possibility is to scale inhibitory strengths as , where is some constant. This choice ensures that the total inhibition seen by each pool does not depend on . We call this “weak” inhibition (Fig. 2A).
Fig. 2.
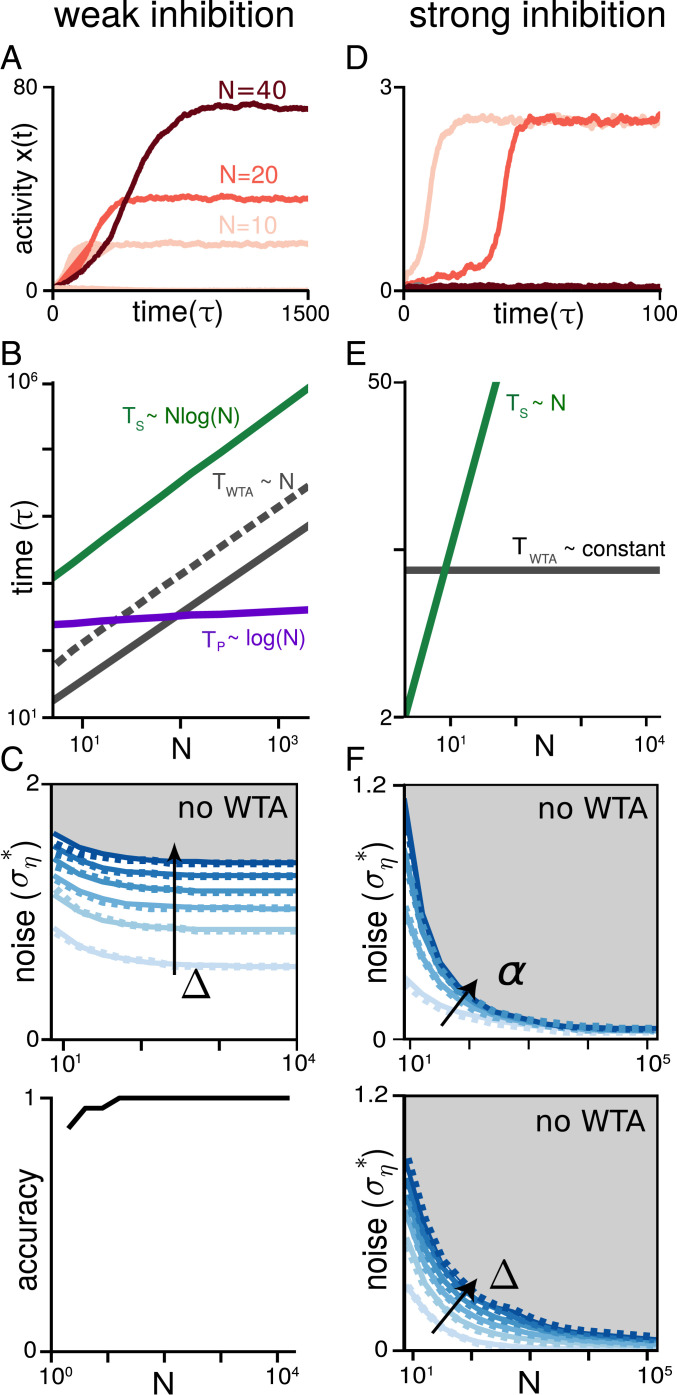
Conventional WTA networks fail the parallelism benchmark. (A–C) Results for weak inhibition. (A) Activity dynamics of the most active neuron (pool) for networks of size (light to dark red), respectively, with noisy input; , , , , . The asymptotic activity level grows with . (B) WTA simulation results on decision time without (solid gray) and with (dashed gray) noise. Also shown are noisy serial strategy (green) and noisy parallelism benchmark (purple). Note that benchmarks are shown up to an overall constant. Error bars are smaller than the line width. Deterministic serial strategy (i.e., ) is not shown, for simplicity. (C) (Top) Critical noise amplitude versus : WTA dynamics exists below a given curve and fails above it (dashed curve, numerical simulation; solid curve, analytical). Darker curves correspond to a larger gap between the top two inputs (, , ). (Bottom) Average accuracy, that is, fraction of correct trials, as a function of (simulations averaged over 150 trials). (D–F) Results for strong inhibition. (D) As in A but for strong inhibition. WTA breaks down rapidly (note absence of WTA for = 40, dark curve). (E) WTA decision time in the absence of noise (gray) along with the deterministic serial strategy (green). (F) As in C, showing critical noise amplitude versus . Darker curves denote stronger self-excitation (Top; ; ) or a widening gap (Bottom; ; ). , in all curves.
Self-excitation must be set to both maintain stability and assure a WTA state, requiring (17) (SI Appendix, section S2). The two-sided constraint is a fine-tuning condition: For large , the allowed range of self-excitation is very small and shrinks toward zero.
In the deterministic case (), the network always converges to the correct solution where the neuron with input is the winner. The equations can be analytically solved to obtain the convergence time (SI Appendix, section S2),
| [2] |
The linear growth of is the same as the serial strategy (Fig. 2B), and thus offers no parallel speedup.
Above a certain critical value of noise (predicted analytically; SI Appendix, section S2), the weak-inhibition network, moreover, fails to exhibit WTA dynamics (Fig. 2 C, Top). This failure is to be distinguished from an error: The network does not select the wrong winner, it simply fails to arrive at a winner, and multiple neurons remain active. Below the critical noise threshold, WTA dynamics persists even for (Fig. 2 C, Top). The critical noise threshold is substantially larger than , and the network exhibits WTA even when (lightest line in Fig. 2C), selecting a random neuron as the winner. The decision time with fluctuating inputs (Fig. 2B) grows linearly as for deterministic inputs (see SI Appendix, section S2 for an explanation of the linear scaling). Although this time scaling is much slower than the parallelism benchmark, it asymptotically (large ) exhibits perfect computation accuracy, given finite (Fig. 2 C, Bottom) (the above which perfect accuracy is obtained depends on and ).
In summary, the existence of WTA in a weak-inhibition circuit requires exquisite fine-tuning of excitation, which is biologically unrealistic. Moreover, the weak-inhibition circuit cannot be adjusted to provide a speed–accuracy trade-off: It favors accuracy over speed, always achieving perfect accuracy for large enough . Convergence time grows as , a modest speedup of relative to that does not approach the factor of speedup of an efficient parallel strategy.
Strong Inhibition: Optimal Parallel Speedup without Noise, but WTA Breakdown with Noise.
An alternative choice is to hold fixed as is varied. We call this “strong” inhibition (Fig. 2D). The total inhibition in the circuit then grows with . A unique WTA solution exists for any choice of in the -independent interval (no fine-tuning required, unlike weak inhibition). For noiseless inputs, we analytically obtain (SI Appendix, section S2)
| [3] |
As with the weak-inhibition case, depends on . Notably, however, is independent of (Fig. 2E, solid gray), matching the parallelism benchmark .
In the noisy case, for a given , the network can perform WTA if the noise amplitude is smaller than a threshold that depends on . If grows (while holding and noise amplitude fixed), however, the network entirely fails to reach a WTA state (Fig. 2F). Unlike with weak inhibition, strong-inhibition networks appear to fail to asymptotically exhibit WTA behavior for any nonzero noise level.
We can understand the failure as follows. Unbiased (zero mean) noise in the inputs, when thresholded, produces a biased effect: Neurons receiving below-zero mean input will nevertheless exhibit positive mean activity because of input fluctuations. Thus, even neurons with input smaller than their deterministic thresholds continue to inhibit others. Total inhibition remains over time and, for sufficiently large , prevents any neuron pool from breaking away from the rest to become a winner. We note that giving up the stability constraint by allowing (using the decision threshold for ) does not qualitatively change the result (Fig. 2F), but can produce other problems (SI Appendix, section S2). As with weak inhibition, we can analytically predict the breakdown of strong-inhibition WTA (SI Appendix, section S2). The resulting predictions can be used to determine the feasibility of WTA computation in large networks in the presence of noise.
Thus, although networks with strong inhibition can meet the parallelism benchmark when the inputs are deterministic, they are not capable of finding a winner in large networks with even slightly noisy inputs (and when they do perform WTA for sufficiently small , the scaling is suboptimal; see, e.g., SI Appendix, section S3 and Fig. S8K, where we find log () scaling only for a subset of parameters). These pessimistic results raise the question of whether neural networks can ever implement parallel computation that is efficient, fully trading serial time for space.
The nWTA Network: Fast, Robust WTA with Noisy Inputs and an Inhibitory Threshold.
We introduce a model motivated by the successes and failings of the existing models. A network with weak inhibition and fine-tuning is accurate, but too slow, because inhibition is too weak to drive a rapid separation between winner and losers. A network with strong inhibition achieves WTA with a full parallelism speedup for deterministic inputs, but entirely fails to perform WTA for large , because the nearly losing neuron pools prevent any pool from breaking away. (Simply increasing the activation threshold does not fix the failure of WTA; SI Appendix, Fig. S5E.) In addition, the residual noise-driven inhibition decreases the average asymptotic activity of the near-winner so that the true value of will be underestimated.
We hence consider a circuit with strong inhibition, in which individual neuron pools can only contribute inhibition when their activations exceed a threshold (see Methods; see Discussion for biological candidates),
| [4] |
We set (no fine-tuning) and self-excitation in the range .
In this nonlinear-inhibition WTA (nWTA) network, if the th neuron pool wins, its expected asymptotic state is , so the direct proportionality to is recovered. Every neuron pool contributes an inhibition of strength when highly active (), ensuring robust early competition. However, the inhibitory threshold will cause neuron pools with decreasing activations to effectively drop out of the circuit, allowing the top pool to take off unimpeded later in the dynamics.
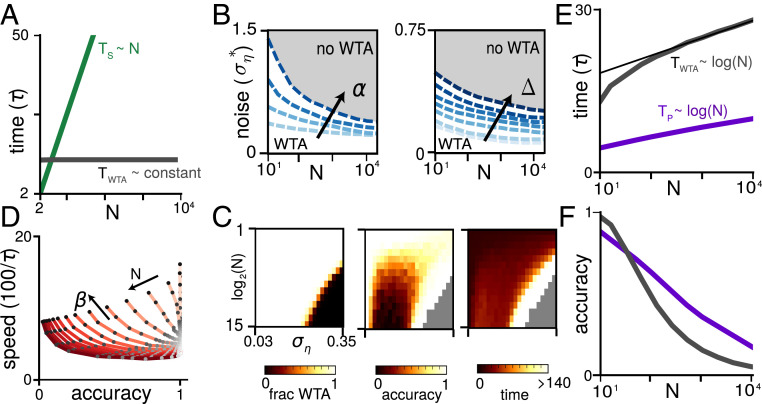
When presented with deterministic inputs, the nWTA network matches the conventional strong-inhibition network and the parallelism benchmark by converging in a time independent of (Fig. 3A).
Fig. 3.
The nWTA is robust to noise and achieves the parallelism benchmark. (A) The nWTA decision time without noise (gray) and the deterministic serial strategy (green). (B) Critical noise amplitude as a function of for varying , (Left) and , , (Right). Below each curve, WTA behavior exists, while, above, it does not. (C) Heat maps showing fraction of trials with a WTA solution (single winner; Left), accuracy of the WTA solution (Middle), and convergence time (Right) as function of network size and noise amplitude . , , and , averaged over 1,500 trials each. (D) Speed–accuracy curves for , , and for varying (light to dark red) and (light to dark gray circles): 1,500 trials, of which only trials that produced a WTA solution were included. Curves are nonmonotonic, so that certain parameters are strictly better than others for both speed and accuracy. (E) scaling of decision time to achieve fixed accuracy of 0.99 for nWTA (gray) and the parallelism benchmark (purple). Thin black line shows logarithmic fit. ; ; ; ; see SI Appendix, section S2 and Fig. S6 for similar results with different parameters and noise levels. (F) scaling of accuracy at fixed decision time. Gray denotes nWTA for integration time 12.5; purple denotes parallelism benchmark for integration time 2.
Moreover, and unlike the conventional WTA network, the diminishing inhibition in the nWTA circuit over time permits the leading neuron pool to break away and win even in the presence of noise. The losing pools continue to receive inhibitory drive from the remaining highly active pool(s), becoming less active over time (here, can increase the noise-robustness [Fig. 3B], but would necessitate some kind of saturating nonlinearity for stability; SI Appendix, section S2). The network exhibits WTA behavior well into the noisy regime, even with asymptotically many neuron pools (Fig. 3 B and C) without fine-tuning (see SI Appendix, section S2 and Fig. S5F for more discussion).
The network can also trade off speed and accuracy over a broad range. Starting at high accuracy and holding noise fixed, the accuracy of computation can be decreased, and speed increased, by increasing (Fig. 3D, for fixed , i.e., fixed expected asymptotic activity ; darker gray circles along a curve correspond to increasing ) or (SI Appendix, Fig. S6 A–F). The overall integration time is generally set by the combination of and , with high accuracy and low speed achieved as approaches 1. When is increased away from 1, the overall trend is that speed increases and accuracy decreases. Note, however, that the nWTA network exhibits an interesting nonmonotonic dependence of accuracy on both noise level and network size (as can be seen in the heat map of Fig. 3C). This improvement in performance at some intermediate noise level is a form of stochastic resonance (40) (see SI Appendix, section S2 for discussion).
Conveniently, a top-down neuromodulatory or synaptic drive can regulate where the network lies on the speed–accuracy curves, with many mechanistic knobs for control, including synaptic gain control of all (excitatory and inhibitory) synapses together (resulting in covariation of ), neural gain control of principal cells (also effective covariation of ), or a threshold control of inhibitory cells (effective modulation of ).
For fixed noise at each input or WTA circuit neuron, the decision time for the network to reach a fixed accuracy scales as (Fig. 3E; also see SI Appendix, Fig. S6 E and K). Compared to the serial time complexity of for fixed accuracy with noisy inputs, the nWTA network therefore achieves a fully efficient trade-off of space for time, matching the parallelism benchmark of .
Not only does the scaling of decision time with in the nWTA network match the functional form of the parallelism benchmark, the prefactor is not far from unity: It takes only a factor of approximately three more time steps (in units of the biophysical time constant of single neuron pools) to converge than the number of discrete time steps of the parallelism benchmark (Fig. 3E, gray vs. purple curves).
Similarly, if we compare accuracy at fixed in Fig. 3F (here at ) to the parallelism benchmark at some fixed (here, ), we see that accuracy at large is similar to that of the parallelism benchmark, again with a near-unity prefactor (Fig. 3F; note that, in order to make a direct comparison with perfect integration, we assume here that noise is coming only from the inputs and not from stochastic neural activity). Further, as we show in the following sections, for small , even the prefactor can be almost optimal.
In summary, the nWTA network can identify the input with the largest mean (i.e., perform the , operations) from noisy inputs, with accuracy comparable to the optimal serial strategy, but with a full factor- parallelism speedup, even though the constituent neuron pools are leaky. It does so with network-level integration and competition, but does not require fine-tuning of network parameters.
Self-Adjusting Dynamics: High Accuracy and Hick’s Law without Parameter Tuning.
The results above, on efficient parallel decision-making by nWTA across a wide range of , assumed that network parameters could be changed to optimize the decision time for the given value of noise or . As previously mentioned, there are many biologically plausible mechanistic ways to change effective excitation, inhibition, and thresholds in the network. Nevertheless, the assumption that the network can retune parameters for each new set of inputs may not hold in all cases. The retuning assumption may be especially unrealistic for psychophysical decision-making among small numbers of alternatives, where the number and noisiness of inputs are controlled by the external world and may change from trial to trial and without prior warning. We thus investigate the performance of nWTA when parameters do not change with .
Remarkably, nWTA networks can self-adjust to maintain high accuracy, even if increases up into the thousands, with an appropriate fixed initial parameter choice (Fig. 4A). The amount of recurrent inhibition in the network depends on the number of active options and automatically increases when the task gets harder, either because of an increase in noise, a smaller gap between the correct and incorrect input, or more options to choose from. This increase in inhibition slows network convergence, causing the network to integrate for longer when the task is harder and thus compensating for the increased difficulty. Consequently, the network is able to maintain high accuracy as increases by automatically extending its decision time (Fig. 4B). The automatic increase in is logarithmic in , thus matching the parallelism benchmark.
Fig. 4.
The nWTA network self-adjusts to maintain accuracy and exhibits Hick’s law without any parameter change. (A) Accuracy for fixed parameter values as a function of for large . Dark and light blue show (, ) = (0.5, 0.51), (0.6, 0.41), respectively (one accuracy trace not visible). Input parameters are as in Fig. 3 D–F, 5,000 trials per data point. (B) Decision time for the parameter values shown in A, along with logarithmic fits (thin black). (C) Accuracy for fixed parameter values for small . Blue symbols show nWTA network (light, dark show (, ) = (0.3, 0.71), (0.6, 0.41), respectively), while purple squares show AB model with perfect integration. , . Inset shows selected parameter values as well as average accuracy for all parameter combinations (averaged across to 10). (D) Decision time for nWTA networks and AB model shown in C. Thin black lines show logarithmic fits for nWTA and constant fit for AB.
For small , as is the case in psychophysical decision-making tasks, a logarithmic scaling of decision time with while maintaining high, fixed accuracy is known as Hick’s law, specifically, (30). The nWTA networks robustly reproduce Hick’s law across a range of (fixed) possible parameter settings (Fig. 4 C and D, blue symbols). Moreover, for every parameter combination we examined, the increase of with was better described as logarithmic than linear, regardless of whether high accuracy was maintained, unlike conventional WTA networks; see SI Appendix, Fig. S8K. Thus, Hick’s law is a generic dynamical consequence of decision-making by self-terminating WTA networks with noisy input and thresholded recurrent inhibition.
The observed increase in decision time with can be reproduced by leaky or idealized AB models of decision-making. However, the threshold applied to the integrated inputs must be hand designed and vary with (increasing as ) to produce a Hick’s law-like decision time (22, 24). When the parameters and thresholds of these models are kept fixed with , the behavior is qualitatively different from WTA networks: The decision time remains fixed with (instead of increasing logarithmically), and accuracy decreases (Fig. 4 C and D, purple squares). Thus, if is not known ahead of time and the model threshold is not appropriately retuned, typical AB models show behavior very different from Hick’s law.
We show that one AB framework, which implements the absolute form of the MSPRT in a biological circuit model (3) (henceforth, the Bogacz–Gurney model), can achieve the optimal scaling of decision time without parameter tuning as is varied across both small and large , like the nWTA (SI Appendix, Fig. S1 and section S1). Moreover, for a given level of accuracy, the Bogacz–Gurney model is slightly quicker to make a decision (nWTA is a factor of to 2.5 slower [SI Appendix, Fig. S1D; also see Fig. 5B]). The optimal decision time scaling of the Bogacz–Gurney model is due to a nonlinear (softmax) inhibition term: If is the integrated evidence with the largest value, then Bogacz–Gurney terminates when crosses a threshold, where the term is contributed by feedforward nonlinear inhibition. This term scales as when all s are similar in size, and, in the limit of one large entry, approaches the value of that entry. Thus, when many competitors are active, this feedforward nonlinear inhibition automatically raises the effective threshold by a factor of as required by AB models, thus providing the optimal scaling with fixed parameters in this setting.
Fig. 5.
Self-terminating WTA dynamics as a minimal-parameter, neural model of multi-AFC decision-making. (A) Reward rate for the fixed parameters chosen to maximize reward rate (dark blue circles, ) along with reward rate when parameters are individually optimized for each (light blue). Thin black lines show fit to . Inset shows accuracy for fixed parameters chosen to maximize reward rate. Accuracy at highest reward rate is high but not constant, reflecting a speed–accuracy trade-off. (B) Reward rate vs. accuracy for . Gray, nWTA (using best , for given accuracy); dark purple: AB model; light purple: AB implementation of relative (max-vs-next) form of MSPRT. Inset for panel shows speed–accuracy curves for that yield optimal reward rate for ; see SI Appendix, Fig. S8F [speed (100/) includes ms; dark blue: fixed, ; light blue: fixed, varied; other parameters are as follows: , , ]. (C) Example activation trajectories for nWTA networks with different () but with (i.e., integration time constant) held fixed. (Left) Lower self-excitation and higher inhibition; (Right) vice versa. (D) Example activation trajectories for network with same inhibition as C, Right, but stronger self-excitation. Trials are faster, but final activation of winner is higher. (E) Example activation trajectories for (light to dark red) with fixed parameters. Activity at the time of convergence remains constant. (F) (Top) Decision time for fixed parameters as a function of gap between largest and second largest input (related to task difficulty), showing that network self-adjusts to integrate longer for difficult tasks. Colors as in E. (Bottom) As in Top but for noise in input. Note that, in the small- regime, conventional WTA models show similar performance to nWTA for many of these results, although less robustly; see SI Appendix, section S3 and Fig. S8.
WTA as a Minimal, Flexible Model for Multialternative Forced-Choice Decision-Making.
Results thus far were primarily focused on the scaling and robustness of nWTA in the large limit, which might apply in contexts like the input sparsification by Kenyon cells in the mushroom body (5) and the readout of grid cell activity by hippocampal place cells (8). We now discuss the performance of WTA networks in the context of multialternative forced-choice (multi-AFC) decision-making behavioral tasks (2, 13), when the number of alternatives is small ().
Despite its simplicity, the nWTA model not only maintains performance comparable to idealized, perfect integrator AB models, as shown above and elaborated next, but can also reproduce a number of behavioral and physiological observations from multi-AFC studies. These include the existence of step- and ramp-like responses of individual neurons, convergence to the same activity level at decision time even though is varied, partial self-adjustment to the statistics of the input, faster decision times on correct compared to error trials (SI Appendix, Fig. S8E), and the flexibility to preferentially weight early evidence (SI Appendix, section S2 and Fig. S2C). Throughout this section, the parameters used are comparable to those that achieve high performance in the large- regime, suggesting that the same basic circuit can be reused across a variety of scales.
The nWTA circuit can achieve a broad range of speeds and accuracies by varying self-excitation and recurrent inhibition. This translates to a broad range of reward rates, that is, the product of speed and accuracy, a key quantity for psychophysics experiments (Fig. 5 A and B). Note that, for closer correspondence with psychophysical literature, we here assume an additional nondecision time ms (SI Appendix, section S3). The reward rates achieved by the self-adjusting dynamics of nWTA networks when parameters are held fixed as is varied are comparable to when they are separately optimized for each (Fig. 5A, dark versus light symbols). The self-adjustment process is thus near optimal, at least over the range of number of options considered here ().
Moreover, the reward rate achieved by nWTA networks, both when parameters are held fixed and when they are individually optimized for each , is competitive both with a perfect integrator AB model (outperforming it in the high-accuracy regime at small [Fig. 5B; see gray for network and dark purple for AB model]) and with an AB model that implements the MSPRT (Fig. 5B, light purple; see also Discussion and SI Appendix, section S1 and Fig. S8B), and is thus optimal in the limit of vanishing error rate (3, 24).
During integration, neurons vary enough from trial to trial for fixed parameter settings and across parameter settings to look variously more step-like or ramp-like (compare curves within and across Fig. 5 C–E). Different choices of modulate the neural response curves, producing diverse responses even as the network integration time ( and mean inputs are held fixed (Fig. 5C).
In WTA networks, the asymptotic activity of the winning neuron is proportional to , while speed increases with . Starting from parameters consistent with a high reward rate, a speedup can be achieved by increasing or or both (Fig. 5 C, Right vs. Fig. 5D; see SI Appendix, Fig. S8A for a complete overview). Note that increasing will also increase the asymptotic threshold, while increasing will not.
On the other hand, if parameters are held fixed, but increases, the decision threshold remains fixed in the strong-inhibition WTA models (Fig. 5E), as seen in experiments (41).
Finally, increases when the signal-to-noise ratio of the input decreases, for example, due to a smaller gap between correct and incorrect options, or an increased input noise amplitude (Fig. 5F). The bulk of this additional time is spent on averaging the inputs (SI Appendix, Fig. S7G). As with the results shown in Fig. 4, this compensatory capability is the result of recurrent inhibition, which may offer powerful computational flexibility to a decision-making circuit.
It has recently been shown, in experiment, that decision circuits can be trained to adapt their integration time to the time-varying statistics of the input (42). The present result shows how such neural circuits, if similar to the nWTA network, may be able to automatically and instantly, without plasticity, adjust to the input statistics.
Discussion
Identifying the largest option among several possibilities, or, formally, performing max, argmax operations, is pivotal in inference, optimization, decision-making, action selection, consensus, error correction, and foraging computations. We have examined the efficacy of parallel computation for finding the best option, both in the abstract and in neural circuit models with leaky neurons. We show that the nWTA neural network can accurately determine and report in the noiseless and noisy input cases, with a computation time that meets the benchmarks of optimal parallelization: constant decision time in the noiseless case and a time that grows as in the presence of noise.
When applied to psychophysical decision-making tasks () (30, 35, 41, 43, 44), the model provides an explanation for Hick’s law (22–24, 30, 35), a canonical result in the psychophysics of human decision-making. This demonstrates Hick’s law within a leaky neural network decision-making model with self-terminating dynamics. Moreover, the nWTA model reproduces Hick’s law without the need to tune or change any parameters as the number of options changes. Thus we have found both a computational (efficient normative computation that saturates the parallelism benchmark) and dynamical explanation (self-adjustment of decision time with number of options without parameter change) of Hick’s law, both based on computation in the presence of noise.
We find that recurrent inhibition enables nWTA networks to flexibly adjust computation time as the number of options is increased, noise is increased, or the gap between options is decreased, while the additional threshold on inhibition in the nWTA circuit ensures that the WTA state exists in the presence of noise, even in large networks.
Our work additionally reproduces a number of (sometimes counterintuitive) psychophysical and neural observations, including faster performance on correct than on error trials and a natural tendency to weight early information over late (however, the extent of this tendency to impulsivity is tunable; SI Appendix, section S2 and Fig. S2C).
The efficiency of accurate parallel computation by the nWTA network holds not only in the regime of psychophysical decision-making but also when the number of options ranges in the thousands, corresponding, possibly, to a microscopic circuit inference operation of finding the maximally active neuron in a large set of neurons or neuron groups that competitively interact. In this way, our work provides a single umbrella under which systems neuroscience questions about parallel computation distributed across large numbers of individual neurons, as well as psychophysics questions about explicit decision-making, can be answered.
Relationship to Past Work.
In both the normative derivation of the optimal integration time and the nWTA model, we found that the necessity to average out noise underlies a scaling of decision time. This necessity also underlies the scaling of decision time in AB models, where the threshold is increased to allow longer integration with more options (3, 24, 38). This origin of scaling is in contrast to classical explanations of Hick’s law, which attribute the scaling to the number of progressive binary classification steps needed to winnow (deterministic) options down to one, or, equivalently, to the number of bits required to specify one out of options (30, 45). These alternative explanations would predict Hick’s law-like scaling also for deterministic options, while a noise-averaging theory such as ours predicts a crossover from logarithmic scaling of decision time with number of options to a time that is independent of , once the task is sufficiently noiseless or noise is reduced through practice. This crossover prediction is consistent with some studies (36, 45), and could provide a good test of whether Hick’s law is fundamentally due to noise in the alternatives during decision-making.
Leaky competing accumulator models (22, 24, 29, 46) are more biologically plausible variants of AB in that they incorporate leak in the integration process and inhibition between alternatives. However, like classical AB models, these models use the crossing of a predetermined threshold not tied explicitly to the asymptotic states as the decision criterion. If the strength of inhibition is increased to put these networks (22) in the self-amplifying regime, and if (47), they become mathematically equivalent to the conventional WTA models.
We reimplemented an AB neural circuit model of MSPRT decision-making (3), and showed that it exhibits optimal scaling of decision time across with fixed parameters, enabled by a feedforward nonlinear inhibition. The fundamental similarity in performance between the nWTA and the Bogacz–Gurney MSPRT models is underpinned by the presence of nonlinear inhibition that discounts the contribution of weakly active neurons in decision-making when there are multiple alternatives.
A different framework for decision-making is to optimize the total reward obtained over the course of multiple trials; reward rate optimization can involve making faster but inaccurate decisions on hard or low-reward trials to move to the next, easier or high-reward trial. Tajima et al. (27) formalize the multialternative decision-making problem under this framework to derive symmetries of the optimal stopping rule, and implement it in an AB model with interacting accumulators. It will be interesting to explore the behavior of nWTA compared to this stopping rule and to examine the scaling of decision time in Tajima et al. in the large- regime.
The nWTA model is an attractor network for decision-making. WTA attractor models (14, 17, 48–55) are self-terminating (at least for small or deterministic dynamics), and, in the context of behavioral decision-making, have been shown to match multiple neural and behavioral phenomena (56, 57). However, they have typically focused on the dynamics of only a few options and not the large- regime with noise.
Biological Mechanisms for Thresholding Inhibitory Contributions.
In circuits with separate excitatory and inhibitory neurons (58), there are multiple candidate mechanisms for the inhibitory nonlinearity required by nWTA. These can be categorized by whether inhibitory interneurons are selectively tuned to particular principal cell inputs, or are nonselective because they pool inputs from many principal cells. If inhibitory neurons are selective, then a simple threshold nonlinearity in the input–output transfer function, like the type-II firing rate responses in inhibitory neurons (59), is sufficient. A similar effect could be achieved by fast-spiking inhibitory interneurons that act as coincidence detectors rather than integrators (60): These cells would respond weakly to low firing-rate inputs and reliably for high-rate inputs, thus effectively thresholding activity. Finally, if interneurons target pyramidal cell dendrites, then dendritic nonlinearities (61) could threshold inhibitory input.
If inhibitory neurons are nonselective, then the nonlinearity must be present in the excitatory-to-inhibitory synapse so that the drive from the low-activity input principal cells is specifically ignored. If the excitatory to inhibitory synapses have low release probability and are strongly facilitating, only high firing rate inputs would make it through (62).
Finally, while we have considered one particular form of the second nonlinearity (i.e., an activation threshold), it may be possible to replace the activation threshold with other nonlinearities in either the excitatory or inhibitory units.
Spatial Organization of WTA Circuit.
Neural WTA models can be viewed as principal cells or groups inhibiting each other (e.g., via interneurons private to each cell or group), which requires synapses. This connectivity is both dense and global (Fig. 1C). Alternatively, all cells can drive a common inhibitory neuron (pool) which inhibits them all, an architecture that requires only synapses, a much sparser connectivity (only synapse per neuron) that is still global (Fig. 1C). It may be possible to replace the global inhibitory neuron by local inhibitory neurons that pool smaller excitatory groups. However, local inhibition generically produces pattern formation (63), and consensus formation with local connections can be unstable (64); thus it is an interesting open question whether WTA can be implemented with purely local connectivity.
Extensions, Generalizations, and Limitations.
Our results, including the need for an inhibitory nonlinearity, apply broadly to a range of WTA and WTA-like architectures. First, our results hold for architectures with separate excitatory and inhibitory populations, for a wide range of inhibitory time constants (SI Appendix, section S2). Second, they extend to spiking neuron architectures, where each option is represented by a small pool of neurons (SI Appendix, section S4). Third, modifying the shape of the output nonlinearity in conventional WTA (rather than adding a second inhibitory nonlinearity) is unlikely to produce a scaling that matches the parallelism benchmark as long as losing neurons can contribute inhibition, because even a small contribution from losing neurons will become overwhelming for large . Fourth, with the exception of the unrealistic weak-inhibition case, both conventional and nonlinear WTA results hold for a range of synaptic coupling strengths (, ), and thus will be robust to variability in the synaptic strengths. And, finally, while we have considered competing neuron pools, the framework should naturally extend to competing patterns that are distributed across neurons, as long as there is a mechanism that prevents losing patterns from contributing inhibition (17).
In neural data obtained during small- psychophysical decision-making, varying the speed versus accuracy demands can affect baseline firing rates, which are lower for trials cued to be accurate rather than fast. However, this effect varies across subjects and neurons. The dominant modulation for speed versus accuracy appears in the gain or slope of neural responses rather than baseline activity (65–68). The WTA model we consider reproduces the slope effect, but cannot reproduce the baseline modulation effect: Starting the network closer to threshold results in higher recurrent inhibition, which counteracts the smaller distance the network needs to travel to convergence; thus higher baseline activity does not result in faster convergence. It may be possible to incorporate baseline modulation in the model by considering multiple computational stages or gated input (69), and it remains to be seen, empirically, whether baseline firing rate modulation is a robust strategy used by neural systems when making decisions across large numbers of options.
Distributed decision-making is a feature of many collective systems, including bacterial quorum sensing (70), foraging and house-hunting in ants and bees (1, 71), social and political consensus formation (72), and economic choice behaviors. The present work may also have a broader relevance to the question of efficient parallel algorithms for (73–76). While our model is based on neural dynamics, the ingredients (self-amplification; recurrent nonlinear inhibition) are simple and should have analogues in other distributed decision-making systems. When conditions are noisy, our results suggest a scaling of with the number of options, and the existence of a thresholded or otherwise nonlinear inhibition if is large.
Real-world systems are also often bandwidth limited: Neurons communicate with spikes; scout insects achieve consensus through brief interactions with subsets of others (1, 77). Here we have assumed high bandwidth communication: neurons or pools of neurons exchanging analog signals in continuous time (although see SI Appendix, section S4). Nevertheless, the principal cells in our model do not communicate their individual activation levels to all other cells; other principal cells receive information only about global activity in the network in the form of a single inhibitory signal, and there is noise, both forms of limited communication. In this sense, our results should generalize to the lower-bandwidth case. Studying the impact of low-bandwidth communication on WTA and parallel decision-making in more detail is an interesting direction for future work.
Methods
Network Model and Dynamics.
We consider coupled neurons with activations , , and dynamics given by
| [5] |
The neural nonlinearity is set to be the threshold-linear function: ; is the neural time constant, is the strength of self-excitation, and is the strength of global inhibition. Here, is the inhibitory activation function: If , the activation is fully linear, and conventional WTA dynamics, as previously studied (17), is recovered. We also consider an alternative, threshold-linear activation function with threshold , that is, if , and, otherwise, zero. We call the respective dynamical system nWTA-dynamics. The right-hand side of Eq. 5 may be viewed as the instantaneous firing rate of neuron .
Each neuron receives a constant external drive . Neurons are ordered such that , and it is assumed that each input drives exactly one neuron; see Fig. 1C. In addition, each neuron receives a private zero-mean fluctuation term , which is modeled by statistically identical Ornstein–Uhlenbeck processes, that is,
| [6] |
with Gaussian white noise , such that, . It follows that and .
A network that converges to a unique WTA state with nonnoisy inputs and internal dynamics need not do the same when driven by noise. Noise kicks the state around, and the system generally cannot remain at a single point. Nevertheless, the network state can still flow toward and remain near a fixed point of the corresponding deterministic system (SI Appendix, section S2 and Fig. S5 A–D). We will refer to such behavior in the noise-driven WTA networks as successful WTA dynamics, defined in terms of one neuron reaching a criterion distance (defined below) from the deterministic WTA high-activity attractor, while the rest are strongly suppressed.
Conditions for WTA Dynamics.
Analysis of the linear stability of the noise-free conventional dynamical system Eq. 5 with (see SI Appendix, section S2 and ref. 17) reveals one eigenvalue with uniform eigenvector , and an -fold degenerate eigenvalue whose eigenvectors are difference modes with entries that sum to zero. If , the difference modes grow through a linear instability, and the eventual (nontrivial) steady states involve only one active neuron. If and , the network will always select a unique winner for each and initial condition (17). For a discussion of more general constraints on , see SI Appendix, section S2.
After meeting the conditions for stability and uniqueness (), there is freedom in the choice of how the strength of global inhibition scales with : We may choose , which we call the strong-inhibition condition, or , the weak-inhibition condition. In the weak-inhibition regime, we set (with ; specifically, we choose throughout the paper) for stability.
For simplicity, throughout the paper, we consider the case where all neurons start at the same resting activity level . In this case, the winner is the neuron with the largest input. (For heterogeneous initial conditions, the situation is more complex, since the wrong neuron can be pushed to be the winner just by starting at large enough activity to suppress all other neurons; see also the discussion in ref. 17.) We further assume (if , there is an initial transient that scales logarithmically with but is unrelated to the actual WTA computation; SI Appendix, section S2).
In the case of noisy conventional WTA dynamics (but not for the nonlinear WTA model), the asymptotic activation of the winner depends on the number of neurons and the noise amplitude in a nontrivial manner (SI Appendix, section S2). For convenience, we thus define as the time some neuron reaches an activation level greater than or equal to with (we use ) in all simulations (noisy or deterministic). We emphasize that this convergence criterion is nonetheless set by the dynamics, and hence is inherently different from an external arbitrary threshold, and does not change the scaling of either the deterministic or noisy dynamics; see SI Appendix, section S2.
Simulations and Analysis.
All simulations and analyses were carried out using standard Python packages (Python 2.7.12, NumPy 1.11.0, SciPy 0.17.0). The dynamics Eq. 5 was solved by simple forward-Euler integration with integration time step depending on numerical requirements. For the simulation of Ornstein–Uhlenbeck noise, we made use of exact integration on a time grid with increment (78), that is,
| [7] |
Supplementary Material
Acknowledgments
We are grateful to Jon Cohen, Alexander Huk, John Murray, Carlos Brody, and Tim Hanks for helpful discussions on parts of this work. I.R.F. is an HHMI Faculty Scholar and a CIFAR senior fellow, and acknowledges funding from the Office of Naval Research and from the Simons Foundation through the International Brain Laboratory. B.K. acknowledges funding from the Norwegian Research Council (grant NFR 231495) and from the Marie Sklodowska-Curie Actions cofunding program (grant GA 609020). Part of this work was performed by R.C. and I.R.F. while in residence at the Simons Institute for the Theory of Computing at Berkeley.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
*We use the notation to mean a time that grows proportionally to for large N (i.e., in complexity theoretic notation). In all of our theoretical bounds, we ignore proportionality constants, as is common in deriving such scaling arguments.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1917551117/-/DCSupplemental.
Data Availability.
Study contains only numerical experiments. Simulation code is available in Github (https://github.com/BKriener/nWTA).
References
- 1.Franks N. R., Pratt S. C., Mallon E. B., Britton N. F., Sumpter D. J. T., Information flow, opinion polling and collective intelligence in house–hunting social insects. Philos. Trans. R. Soc. Lond. B Biol. Sci. 357, 1567–1583 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gold J. I., Shadlen M. N., The neural basis of decision making. Annu. Rev. Neurosci. 30, 535–574 (2007). [DOI] [PubMed] [Google Scholar]
- 3.Bogacz R., Gurney K., The basal ganglia and cortex implement optimal decision making between alternative actions. Neural Comput. 19, 442–477 (2007). [DOI] [PubMed] [Google Scholar]
- 4.Chittka L., Skorupski P., Raine N. E., Speed–accuracy tradeoffs in animal decision making. Trends Ecol. Evol. 24, 400–407 (2009). [DOI] [PubMed] [Google Scholar]
- 5.Stevens C. F., What the fly’s nose tells the fly’s brain. Proc. Natl. Acad. Sci. U.S.A. 112, 9460–9465 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Amaral D. G., Witter M. P., The three-dimensional organization of the hippocampal formation: A review of anatomical data. Neuroscience 31, 571–591 (1989). [DOI] [PubMed] [Google Scholar]
- 7.Freund T. F., Buzsaki G., Interneurons of the hippocampus. Hippocampus 6, 347–470 (1996). [DOI] [PubMed] [Google Scholar]
- 8.Sreenivasan S., Fiete I., Grid cells generate an analog error-correcting code for singularly precise neural computation. Nat. Neurosci. 14, 1330–1337 (2011). [DOI] [PubMed] [Google Scholar]
- 9.Shepherd G. M., Synaptic organization of the mammalian olfactory bulb. Physiol. Rev. 52, 864–917 (1972). [DOI] [PubMed] [Google Scholar]
- 10.Poo C., Isaacson J. S., Odor representations in olfactory cortex: “Sparse” coding, global inhibition, and oscillations. Neuron 62, 850–861 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mink J. W., The basal ganglia: Focused selection and inhibition of competing motor programs. Prog. Neurobiol. 50, 381–425 (1996). [DOI] [PubMed] [Google Scholar]
- 12.Redgrave P., Prescott T. J., Gurney K., The basal ganglia: A vertebrate solution to the selection problem? Neuroscience 89, 1009–1023 (1999). [DOI] [PubMed] [Google Scholar]
- 13.Churchland A. K., Ditterich J., New advances in understanding decisions among multiple alternatives. Curr. Opin. Neurobiol. 22, 920–926 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Grossberg S., Contour enhancement, short term memory, and constancies in reverberating neural networks. Stud. Appl. Math. 52, 213–257 (1973). [Google Scholar]
- 15.Coultrip R. L., Granger R. H., Lynch G., A cortical model of winner-take-all competition via lateral inhibition. Neural Network. 5, 47–54 (1992). [Google Scholar]
- 16.Maass W., On the computational power of winner-take-all. Neural Comput. 12, 2519–2535 (2000). [DOI] [PubMed] [Google Scholar]
- 17.Xie X., Hahnloser R. H. R., Seung S. H., Selectively grouping neurons in recurrent networks of lateral inhibition. Neural Comput. 14, 2627–2646 (2002). [DOI] [PubMed] [Google Scholar]
- 18.Donald R. J. L., Information Theory of Choice-Reaction Times (Wiley, New York, NY, 1968). [Google Scholar]
- 19.Douglas V., Evidence for an accumulator model of psychophysical discrimination. Ergonomics 13, 37–58 (1970). [DOI] [PubMed] [Google Scholar]
- 20.Ratcliff R., Rouder J. N., Modeling response times for two-choice decisions. Psychol. Sci. 9, 347–356 (1998). [Google Scholar]
- 21.Ratcliff R., Van Zandt T., McKoon G., Connectionist and diffusion models of reaction time. Psychol. Rev. 106, 261–300 (1999). [DOI] [PubMed] [Google Scholar]
- 22.Usher M., McClelland J. L., The time course of perceptual choice: The leaky, competing accumulator model. Psychol. Rev. 108, 550–592 (2001). [DOI] [PubMed] [Google Scholar]
- 23.Bogacz R., Brown E., Moehlis J., Holmes P., Cohen J. D., The physics of optimal decision making: A formal analysis of models of performance in two-alternative forced-choice tasks. Psychol. Rev. 113, 700–765 (2006). [DOI] [PubMed] [Google Scholar]
- 24.McMillen T., Holmes P., The dynamics of choice among multiple alternatives. J. Math. Psychol. 50, 30–57 (2006). [Google Scholar]
- 25.Ratcliff R., McKoon G., The diffusion decision model: Theory and data for two-choice decision tasks. Neural Comput. 20, 873–922 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Schall J. D., Accumulators, neurons, and response time. Trends Neurosci. 42, 848–860 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tajima S., Jan D., Patel N., Pouget A., Optimal policy for multi-alternative decisions. Nat. Neurosci. 22, 1503–1511 (2019). [DOI] [PubMed] [Google Scholar]
- 28.Ditterich J., Stochastic models of decisions about motion direction: Behavior and physiology. Neural Network. 19, 981–1012 (2006). [DOI] [PubMed] [Google Scholar]
- 29.Roxin A., Drift–diffusion models for multiple-alternative forced-choice decision making. J. Math. Neurosci. 9, 1–23 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hick W. E., On the rate of gain of information. Q. J. Exp. Psychol. 4, 11–26 (1952). [Google Scholar]
- 31.Lynch N. A., Distributed Algorithms (Elsevier, 1996). [Google Scholar]
- 32.Baum C. W., Veeravalli V. V., A sequential procedure for multihypothesis testing. IEEE Trans. Inf. Theor. 40, 1994–2007 (1994). [Google Scholar]
- 33.Dragalin V. P., Alexander G. T., Veeravalli V. V., Multihypothesis sequential probability ratio tests. I. Asymptotic optimality. IEEE Trans. Inf. Theor. 45, 2448–2461 (1999). [Google Scholar]
- 34.Gold J. I., Shadlen M. N., Banburismus and the brain: Decoding the relationship between sensory stimuli, decisions, and reward. Neuron 36, 299–308 (2002). [DOI] [PubMed] [Google Scholar]
- 35.Merkel J., Die zeitlichen verhältnisse der willensthäthigkeit. Philisophische Studien 2, 73–127 (1885). [Google Scholar]
- 36.Teichner W. H., Krebs M. J., Laws of visual choice reaction time. Psychol. Rev. 81, 75–98 (1974). [DOI] [PubMed] [Google Scholar]
- 37.Laursen A. M., Task dependence of slowing after pyramidal lesions in monkeys. J. Comp. Physiol. Psychol. 91, 897–906 (1977). [DOI] [PubMed] [Google Scholar]
- 38.Usher M., Olami Z., McClelland J. L.. Hick’s law in a stochastic race model with speed–accuracy tradeoff. J. Math. Psychol. 46, 704–715 (2002). [Google Scholar]
- 39.Lidwell W., Holden K., Butler J., Universal Principles of Design, Revised and Updated: 125 Ways to Enhance Usability, Influence Perception, Increase Appeal, Make Better Design Decisions, and Teach Through Design (Rockport, 2010). [Google Scholar]
- 40.McDonnell M. D., Ward L. M., The benefits of noise in neural systems: Bridging theory and experiment. Nat. Rev. Neurosci. 12, 415–426 (2011). [DOI] [PubMed] [Google Scholar]
- 41.Churchland A. K., Kiani R., Shadlen M. N., Decision-making with multiple alternatives. Nat. Neurosci. 11, 693–702 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Piet A., Hady A. E., Brody C. D., Rats adopt the optimal timescale for evidence integration in a dynamic environment. Nat. Commun. 9, 4265 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Salzman C. D., Newsome W. T., Neural mechanisms for forming a perceptual decision. Science 264, 231–238 (1994). [DOI] [PubMed] [Google Scholar]
- 44.Niwa M., Ditterich J., Perceptual decisions between multiple directions of visual motion. J. Neurosci. 28, 4435–4445 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Proctor R. W., Schneider D. W., Hick’s law for choice reaction time: A review. Q. J. Exp. Psychol. 71, 1281–1299 (2018). [DOI] [PubMed] [Google Scholar]
- 46.Bogacz R., Usher M., Zhang J., McClelland J. L.. Extending a biologically inspired model of choice: Multi-alternatives, nonlinearity and value-based multidimensional choice. Philos. Trans. R. Soc. B 362, 1655–1670 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Miller K., Fumarola F., Mathematical equivalence of two common forms of firing-rate models of neural networks. Neural Comput. 24, 25–31 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Jin D. Z., Seung H. S., Fast computation with spikes in a recurrent neural network. Phys. Rev. 65, 051922 (2002). [DOI] [PubMed] [Google Scholar]
- 49.Wong K.-F., Alexander H., Shadlen M., Wang X-J., Neural circuit dynamics underlying accumulation of time-varying evidence during perceptual decision making. Front. Comput. Neurosci. 1, 6 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Rutishauser U., Douglas R. J., Slotine J.-J., Collective stability of networks of winner-take-all circuits. Neural Comput. 23, 735–773 (2011). [DOI] [PubMed] [Google Scholar]
- 51.Hahnloser R. H. R., Sarpeshkar R., Mahowald M. A., Douglas R. J., Seung H. S., Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit. Nature 405, 947–951 (2000). [DOI] [PubMed] [Google Scholar]
- 52.Fukai T., Tanaka S., A simple neural network exhibiting selective activation of neuronal ensembles: From winner-take-all to winners-share-all. Neural Comput. 9, 77–97 (1997). [DOI] [PubMed] [Google Scholar]
- 53.Mao Z. H., Massaquoi S. G., Dynamics of winner-take-all competition in recurrent neural networks with lateral inhibition. IEEE Trans. Neural Network. 18, 55–69 (2007). [DOI] [PubMed] [Google Scholar]
- 54.Yuille A. L., Grzywacz N. M., A winner-take-all mechanism based on presynaptic inhibition feedback. Neural Comput. 1, 334–347 (1989). [Google Scholar]
- 55.Lippmann R. P., Gold B., Malpass M. L., Laboratory L., “A comparison of Hamming and Hopfield neural nets for pattern classification” (Tech. Rep. 769, Massachusetts Institute of Technology, 1987). [Google Scholar]
- 56.Wong K.-F., Wang X.-J., A recurrent network mechanism of time integration in perceptual decisions. J. Neurosci. 26, 1314–1328 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Moran F., Wang X.-J., Similarity effect and optimal control of multiple-choice decision making. Neuron 60, 1153–1168 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Eccles J. C., Fatt P., Koketsu K., Cholinergic and inhibitory synapses in a pathway from motor-axon collaterals to motoneurones. J. Physiol. 126, 524–562 (1954). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Hodgkin A. L., The local electric changes associated with repetitive action in a non-medullated axon. J. Physiol. 107, 165–181 (1948). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Angulo M. C., Rossier J., Audinat E., Postsynaptic glutamate receptors and integrative properties of fast-spiking interneurons in the rat neocortex. J. Neurophysiol. 82, 1295–1302 (1999). [DOI] [PubMed] [Google Scholar]
- 61.London M., Häusser M., Dendritic computation. Annu. Rev. Neurosci. 28, 503–532 (2005). [DOI] [PubMed] [Google Scholar]
- 62.Zucker R. S., Regehr W. G., Short-term synaptic plasticity. Annu. Rev. Physiol. 64, 355–405 (2002). [DOI] [PubMed] [Google Scholar]
- 63.Bard E., Neural networks as spatio-temporal pattern-forming systems. Rep. Prog. Phys. 61, 353–430 (1998). [Google Scholar]
- 64.Bamieh B., Jovanovic M. R., Mitra P., Patterson S., Coherence in large-scale networks: Dimension-dependent limitations of local feedback. IEEE Trans. Automat. Contr. 57, 2235–2249 (2012). [Google Scholar]
- 65.Heitz R. P., Schall J. D., Neural mechanisms of speed-accuracy tradeoff. Neuron 76, 616–628 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Hanks T., Kiani R., Shadlen M. N., A neural mechanism of speed-accuracy tradeoff in macaque area lip. eLife 3, e02260 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Thura D., Paul C., Modulation of premotor and primary motor cortical activity during volitional adjustments of speed-accuracy trade-offs. J. Neurosci. 36, 938–956 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Thura D., Cisek P., The basal ganglia do not select reach targets but control the urgency of commitment. Neuron 95, 1160–1170.e5 (2017). [DOI] [PubMed] [Google Scholar]
- 69.Purcell B. A., et al. , Neurally constrained modeling of perceptual decision making. Psychol. Rev. 117, 1113–1143 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Miller M. B., Bassler B. L., Quorum sensing in bacteria. Annu. Rev. Microbiol. 55, 165–199 (2001). [DOI] [PubMed] [Google Scholar]
- 71.Beckers R., Deneubourg J.-L., Goss S., Pasteels J. M., Collective decision making through food recruitment. Insectes Soc. 37, 258–267 (1990). [Google Scholar]
- 72.List C., Goodin R. E., Epistemic democracy: Generalizing the Condorcet jury theorem. J. Polit. Philos. 9, 277–306 (2001). [Google Scholar]
- 73.Assaf S., Upfal E., Fault tolerant sorting networks. SIAM J. Discrete Math. 4, 472–480 (1991). [Google Scholar]
- 74.Feige U., Raghavan P., Peleg D., Upfal E., Computing with noisy information. SIAM J. Comput. 23, 1001–1018 (1994). [Google Scholar]
- 75.Suter B. W., Kabrisky M., On a magnitude preserving iterative maxnet algorithm. Neural Comput. 4, 224–233 (1992). [Google Scholar]
- 76.Lynch N., Musco C., Parter M., Computational tradeoffs in biological neural networks: Self-stabilizing winner-take-all networks. arXiv:1610.02084 (6 October 2016). [Google Scholar]
- 77.Franks N. R., Dechaume-Moncharmont F.-X., Hanmore E., Reynolds J. K., Speed versus accuracy in decision-making ants: Expediting politics and policy implementation. Philos. Trans. R. Soc. Lond. B Biol. Sci. 364, 845–852 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Gillespie D. T., Exact numerical simulation of the Ornstein-Uhlenbeck process and its integral. Phys. Rev. E 54, 2084–2091 (1996). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Study contains only numerical experiments. Simulation code is available in Github (https://github.com/BKriener/nWTA).