Diffusioosmotic and convective flows induced by a nonelectrolyte concentration gradient

Significance

Our bodies rely on molecular transport within a complex, nonequilibrium environment incorporating gradients of charged and neutral solutes. Concentration gradients near solid surfaces are known to induce material transport via diffusioosmotic fluid flow. These are well understood for charged molecules, but less so for neutral molecules such as glucose. Glucose is an important biological energy source and is often distributed in gradients across cell membranes, vasculature, tissues, and whole organs. We measure diffusioosmotic flow due to glucose gradients and find its speed depends only weakly on concentration. Our models can reproduce this behavior by accounting for strong interactions, concentration-dependent viscosity, and heterogeneous surfaces. Understanding these flows will allow us to harness them for improved transport of targeted nanomedicines.

Abstract

Glucose is an important energy source in our bodies, and its consumption results in gradients over length scales ranging from the subcellular to entire organs. Concentration gradients can drive material transport through both diffusioosmosis and convection. Convection arises because concentration gradients are mass density gradients. Diffusioosmosis is fluid flow induced by the interaction between a solute and a solid surface. A concentration gradient parallel to a surface creates an osmotic pressure gradient near the surface, resulting in flow. Diffusioosmosis is well understood for electrolyte solutes, but is more poorly characterized for nonelectrolytes such as glucose. We measure fluid flow in glucose gradients formed in a millimeter-long thin channel and find that increasing the gradient causes a crossover from diffusioosmosis-dominated to convection-dominated flow. We cannot explain this with established theories of these phenomena which predict that both scale linearly. In our system, the convection speed is linear in the gradient, but the diffusioosmotic speed has a much weaker concentration dependence and is large even for dilute solutions. We develop existing models and show that a strong surface–solute interaction, a heterogeneous surface, and accounting for a concentration-dependent solution viscosity can explain our data. This demonstrates how sensitive nonelectrolyte diffusioosmosis is to surface and solution properties and to surface–solute interactions. A comprehensive understanding of this sensitivity is required to understand transport in biological systems on length scales from micrometers to millimeters where surfaces are invariably complex and heterogeneous.

Gradients in solution concentration are unavoidable in many areas of research, manufacturing, and materials processing (1) and are fundamental to the operation of biological systems, including our bodies (2–4). Gradients may be intentionally imposed (5–10) or else arise due to chemical reactions (11), solid dissolution (12), sedimentation (13), or evaporation (14). Microscopic objects in suspension, such as colloidal particles, vesicles, viruses, proteins, and cells, may exhibit directed motion in response to an external concentration gradient due to physico-chemical processes such as diffusiophoresis (DP) (6, 7, 9, 15, 16), osmophoresis (10, 17, 18), and chemotaxis (19–21).

Among these phenomena, the most widely studied from a physical perspective is DP: motion of a particle driven by interactions between a solute and a surface of the solid particle. A concentration gradient establishes a stress gradient at the particle surface, resulting in a fluid slip velocity and motion of the particle relative to the surrounding liquid (1, 22–24). When the surface is a stationary wall instead of the surface of a freely suspended particle, the fluid motion is called diffusisoosmosis (D_O) (24, 25), and when it is along a pore it is what Anderson and Malone (23) call osmotic flow. In a sealed, thin-channel geometry, D_O flow along the walls can set fluid into circulating motion (26, 27).

The majority of experiments investigating D_O or DP consider electrolytes (1, 28, 29), for which it is well established that the speed scales with the zeta potential and with the gradient of the logarithm of the concentration (30). Investigation into nonelectrolyte gradients is much more limited, with only a handful of studies of aqueous ethanol gradients (6, 31) or polymers (31–34). Paustian et al. (6) measured diffusiophoretic motion at speeds $\sim 0.1$ to 1 $\mathrm{\mu }\mathrm{m}$/s, comparable to those in gradients of electrolytes. Very recent simulation work of Wei et al. (35) reports speeds that decrease at high concentrations due to saturation of the interfacial region, but this remains untested experimentally. While the dependence of DP and D_O speeds on the concentration gradient is relatively well understood for electrolytes, our understanding is much poorer for neutral solutes.

But D_O is not the only motion created by concentration gradients. The mass density of a solution typically increases with concentration. Therefore, a concentration gradient is a density gradient which inevitably induces convective fluid flow (25, 36). This is analogous to natural convection driven by a temperature gradient (37, 38). In a thin channel geometry, buoyancy-driven convective flow results in fluid circulation. Therefore, whenever a concentration gradient is established in an attempt to measure diffusiophoresis, osmophoresis, or chemotaxis, it is necessary to characterize or mitigate circulating fluid flows due to both diffusioosmosis and convection to correctly interpret data.

Researchers have made great progress harnessing chemical gradients to direct the motion of colloidal-scale suspended objects and transport materials more quickly than is possible via diffusion alone (5, 7, 10, 16, 26, 36, 39). And, if human beings are exploiting this effect, it is incredibly unlikely that it is not also employed by nature to efficiently transport material within and between cells and across membranes and barriers (40–42). Glucose is one of the most important biological energy sources as it fuels numerous metabolic processes in both unicellular and multicellular organisms. It is thus expected that glucose generates gradients across cells, tissues, and whole organs (43). In humans, the brain consumes up to 50% of the body’s glucose intake; and in cancer cells, the anabolic demand for glucose often drives accumulation and the emergence of anomalous gradients (44). Delivering drugs to the brain is notoriously difficult (45, 46) and we have already demonstrated that glucose can augment blood–brain barrier crossing in vivo (19).

In this work, we measure circulating flows caused by gradients of glucose concentration in aqueous solution. In Slip Velocity and Convection-Driven Flow we briefly recapitulate textbook analytical flow profiles for slip velocity and convection-driven flows in thin channels. Experimentally Measured Velocity Profiles presents our experimental measurements revealing two qualitatively distinct fluid velocity profiles, which we compare to the analytical profiles of Slip Velocity and Convection-Driven Flow. In small concentration gradients, flow is dominated by the D_O slip velocity at the channel walls, while in large gradients it is dominated by the density contrast. The cross-over between these behaviors cannot be explained by the established theory for nonelectrolyte D_O (22, 47, 48), but requires a nonlinear scaling of D_O slip velocity with concentration. Model for Diffusioosmosis Due to Nonelectrolytes develops a simple model for nonelectrolyte D_O, building in a concentration-dependent viscosity, and we show that this additional feature is sufficient to qualitatively reproduce the experimental observations. Finally, our findings are discussed and summarized in Discussion and Conclusion. This study represents a first step in understanding the physicochemical principles governing D_O in glucose gradients and will lead to improvements in bioinspired targeted nanomedicines able to “surf” along the glucose gradients present in the body, potentially locating cancerous cells and crossing the blood–brain barrier (49–51).

Slip Velocity and Convection-Driven Flow

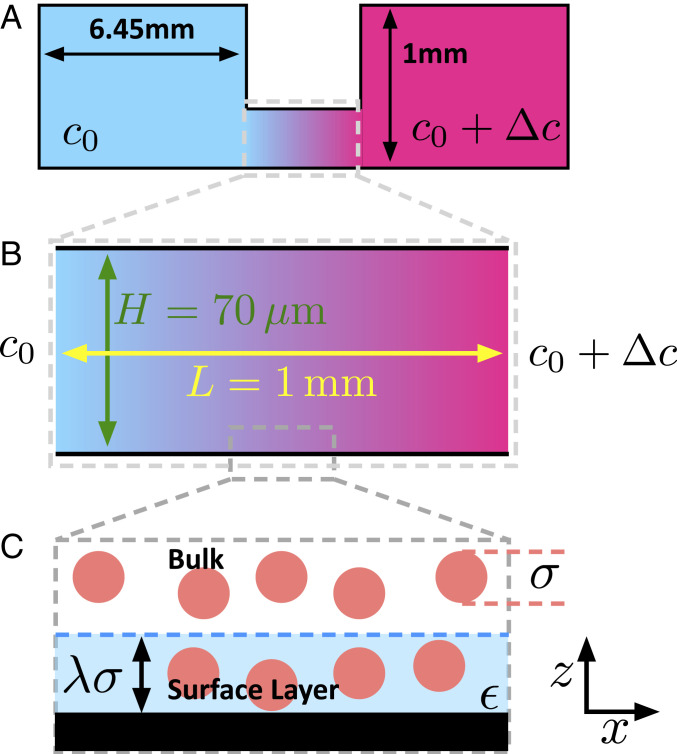
Experiments are performed in a thin channel of length $L=1\hspace{0.17em}\mathrm{m}\mathrm{m}$ and height $H=70\hspace{0.17em}\mathrm{\mu }\text{m}$, where $H\ll L$, as shown schematically in Fig. 1 A and B. This channel connects two large reservoirs containing solutions at concentrations $c_0$ and $c_0+\mathrm{\Delta }c$ such that a gradient $\mathrm{\Delta }c/L$ exists in the $x$ direction along the channel length. Importantly, the reservoirs are sealed, precluding any overall flow of material through the gradient channel. Complete details are provided in Materials and Methods. The $y$ dimension of the channel, $W\gg H$, is assumed to be unimportant and is neglected.

Fig. 1.

Schematics illustrating experimental gradient channel and key model features. (A) Side view of experimental chamber. Large sealed reservoirs containing solutions of concentration $c_0$ and $c_0+\mathrm{\Delta }c$ are connected by a thin gradient channel. (B) Detail of thin ($L\gg H$) gradient channel of height $H=70\hspace{0.17em}\mathrm{\mu }\text{m}$ and length $L=1\hspace{0.17em}\mathrm{m}\mathrm{m}$. (C) Zoomed-in schematic illustrating our model of the microscopic surface–solution interface region. The surface (black) attracts the solute (red circles), inside an interfacial region (pale blue) of thickness $\lambda \sigma$. Within this region, the surface–solute interaction is $ϵ$.

In the low Reynolds number limit and under the Boussinesq approximation, fluid flow is described by the Stokes equation,

$$-\overrightarrow{\nabla }p+\eta {\nabla }^2\overrightarrow{u}+\overrightarrow{f}=\overrightarrow{0},$$ [1]

where $p$ is the pressure, $\overrightarrow{u}=\left(u_x,u_y,u_z\right)$ is the fluid velocity, $\eta$ is its viscosity, and $\overrightarrow{f}$ is the net body force acting on the fluid. If the fluid is incompressible, its velocity also obeys $\overrightarrow{\nabla }\cdot \overrightarrow{u}=0$.

For $H\ll L$ and $H\ll W$, unidirectional fluid flow is anticipated, $\overrightarrow{u}=\left(u_x,\mathrm{0,0}\right)$, and so the incompressibility condition is ${\partial }_x{u}_x=0$. Implicit in this is the additional assumption that viscosity is uniform. In the case of a glucose solution this is not true (52), but, to obtain analytical predictions for velocity profiles we proceed here as if it were.

Diffusioosmosis and Flow Due to a Slip Velocity.

Diffusioosmosis is flow due to an externally imposed concentration gradient near a solid surface. Gradients in velocity are restricted to the microscopic interfacial region, outside of which, flow can be modeled using a slip velocity, $u_s$ (22, 30, 53, 54). The theory of Derjaguin, Anderson, and Prieve (22, 29, 30, 47, 54), as extended by Marbach et al. (48), predicts a slip velocity

$$u_s={\mathrm{\Gamma }}_{{\mathrm{D}}_{\mathrm{O}}}\left(\frac{d\mathrm{\Pi }}{dx}\right),$$ [2]

where $\mathrm{\Pi }$ is the solution osmotic pressure, and ${\mathrm{\Gamma }}_{{\mathrm{D}}_{\mathrm{O}}}$ is the diffusioosmotic coefficient given by

$${\mathrm{\Gamma }}_{{\mathrm{D}}_{\mathrm{O}}}=-\frac{1}{\eta }\hspace{0.17em}{\int }_0^{\infty }z\left[\left(\frac{c\left(x,z\right)}{c\left(x\right)}\right)-1\right]\mathrm{d}z.$$ [3]

Here $c\left(x\right)$ is the concentration far from the surface at position $x$, and $c\left(x,z\right)$ is the concentration at height $z$ above and near the surface. The slip velocity is directed toward (away from) lower concentrations for attractive (repulsive) surface–solute interactions. The original theory of Derjaguin and others (22, 30, 47) assumes a dilute solution for which ${\mathrm{\Gamma }}_{{\mathrm{D}}_{\mathrm{O}}}$ does not depend on concentration, and the bulk solution is ideal, with $\mathrm{d}\mathrm{\Pi }/\mathrm{d}x=k_{\mathrm{B}}T\left(\mathrm{d}c/\mathrm{d}x\right)$. Thus, the D_O speed is proportional to the concentration gradient. Eqs. 2 and 3 do not assume a dilute solution and are generally valid. The predicted D_O speed depends on the concentration gradient via $\mathrm{d}\mathrm{\Pi }/\mathrm{d}x$.

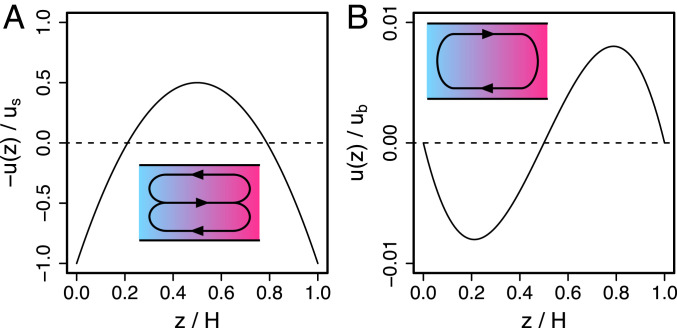
For a concentration gradient in a thin channel, in the absence of body forces, $\overrightarrow{f}=0$, and subject to slip velocity boundary conditions, $u_x=u_s$ at $z=0$ and $z=H$, Eq. 1 can be solved in the thin channel geometry, yielding

$$u_x\left(z\right)=u_s\left[6{\left(\frac{z}{H}\right)}^2-6\left(\frac{z}{H}\right)+1\right],$$ [4]

where the condition of zero net flow is imposed, ${\int }_0^H{u}_x\left(z\right)\hspace{0.17em}dz=0$. This is shown in Fig. 2A. The slip velocity directs flow in the same direction at the top and bottom walls, and the zero net transport condition requires a backflow along the channel center, resulting in a parabolic profile. We plot $-u\left(z\right)/u_s$ to facilitate comparison with experimental data in Fig. 3.

Fig. 2.

Predicted thin ($H\ll L$) channel velocity profiles. (A) Flow due to a slip velocity, $u_s$ (Eq. 4). (B) Flow due to convection (Eq. 5). Insets illustrate the circulating flow patterns.

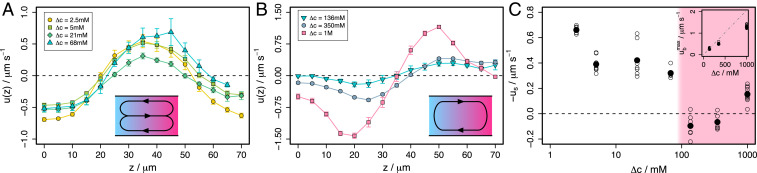
Fig. 3.

Flow in glucose gradients between reservoirs at $c_0=0$ and $c=\mathrm{\Delta }c$. (A) Velocity profiles for $\mathrm{\Delta }c<100$ mM showing the characteristic shape of slip velocity-driven flows. (B) Velocity profiles for $\mathrm{\Delta }c>100$ mM showing the characteristic shape of convection. Profiles are averages over all experiments and waiting times. Error bars represent the SEM. Insets show the shape of circulating flow in the $x$-$z$ plane. (C) Estimated slip velocities (average velocity in wall-adjacent optical sections) as a function of $\mathrm{\Delta }c$. Pink shaded region represents convection-dominated experiments. Open points are individual experiments and solid points show the average over all experiments at each $\mathrm{\Delta }c$. Inset shows peak velocity in buoyancy-driven flows in B compared to analytical prediction for peak velocity according to Eq. 5 (dashed gray line).

Convection.

Convection is flow driven by mass density gradients. The mass density of glucose solutions, $\rho$, increases linearly with glucose concentration (52). Assuming that $c$ depends only on $x$, then $\rho \left(x\right)={\rho }_s\left[1+\beta c\left(x\right)\right]$, where ${\rho }_s$ is the solvent density and $\beta$ is the solutal expansion coefficient. The body force in Eq. 1 is then a gravitational force acting on a fluid element $\overrightarrow{f}={\rho }_s\beta c\left(x\right)\overrightarrow{g}$.

Solving for the velocity profile in the presence of this gravitational body force, subject to no slip boundary conditions, $u_x\left(z=0\right)=0$ and $u_x\left(z=H\right)=0$ and the condition of zero net flow, yields

$$u_x\left(z\right)=u_b\left[\frac{1}{6}{\left(\frac{z}{H}\right)}^3-\frac{1}{4}{\left(\frac{z}{H}\right)}^2\right.+\left.\frac{1}{12}\left(\frac{z}{H}\right)\right],$$ [5]

with $u_b=\left[\left({\rho }_s\beta g{H}^3\right)/\eta \right]\left(dc/dx\right)$, which is the textbook solution for natural convection in a thin channel (25, 28, 36, 37, 55).

This profile is shown in Fig. 2B and is qualitatively distinct from that driven by a slip velocity. The horizontal density gradient drives fluid flow from high $c$ to low $c$ in the bottom half of the channel and in the opposite direction in the top half of the channel, resulting in a circulating flow. The minimum and maximum occur at $z/H\approx 0.21$ and $z/H\approx 0.79$, respectively, and both have magnitude $u_b^{max}\approx 8\times 10^{-3}{u}_b$. Therefore, the speed of convective flow scales linearly with concentration gradient and depends on the third power of $H$.

Experimentally Measured Velocity Profiles

Glucose gradients are established in thin channels between two large reservoirs, as illustrated in Fig. 1A, following the protocol described in Materials and Methods. Fluid flow near $x=L/2$ is measured by tracking the motion of tracer particles in micrograph series acquired using laser scanning confocal microscopy. Velocity profiles $u_x\left(z\right)$ are constructed from the average tracer velocity in two-dimensional (2D) videos acquired at different heights, $z$, in the channel. Velocity profiles do not depend on the waiting time between gradient initiation and data acquisition for waiting times between 5 and 40 min (SI Appendix), suggesting that gradients are quasi-static on this timescale. Unlike some conceptually similar experiments (6, 9, 39), reservoir concentrations are not maintained. Equilibrium in our experiments is uniform concentration throughout both reservoirs and the gradient channel. However, equilibration occurs over a much longer timescale than our experimental duration.

Tracer motion is expected to have contributions from Brownian motion, fluid flow, and diffusiophoresis. However, our measurements suggest that tracer DP is sufficiently slow that it cannot be unambiguously distinguished from the experimental uncertainty (SI Appendix). By contrast, tracer DP is easily observed in a salt gradient (SI Appendix). Therefore, we proceed assuming that the dominant contribution to directed tracer motion is fluid flow.

Experiments with Zero Background Concentration.

Initially, the low concentration reservoir is fixed at $c_0=0$ and the high concentration reservoir is varied. Concentration drops between $\mathrm{\Delta }c=2.5\hspace{0.17em}\mathrm{m}\mathrm{M}$ and $\mathrm{\Delta }c=1\hspace{0.17em}\mathrm{M}$ are applied across the $L=1\hspace{0.17em}\mathrm{m}\mathrm{m}$ channel. The key experimental finding is that, for small concentration gradients ($\mathrm{\Delta }c\lesssim 100\hspace{0.17em}\mathrm{m}\mathrm{M}$), the velocity profiles have very different shapes from those measured in large gradients ($\mathrm{\Delta }c\gtrsim 100\hspace{0.17em}\mathrm{m}\mathrm{M}$). Plots of velocity as a function of height are compared in Fig. 3A (small gradients) and Fig. 3B (large gradients).

For $\mathrm{\Delta }c\lesssim 100\hspace{0.17em}\mathrm{m}\mathrm{M}$ (Fig. 3A) velocities are largest and codirectional at the top and bottom walls and are reversed in the center of the channel. Positive velocity indicates flow toward high glucose concentration. So the flow adjacent to walls is directed away from high glucose concentrations.

For $\mathrm{\Delta }c\gtrsim 100\hspace{0.17em}\mathrm{m}\mathrm{M}$ (Fig. 3B), fluid flows away from high glucose concentration in the bottom half of the channel and toward high glucose concentration in the top half. Any slip velocities are at most a small fraction of the maximum velocities.

In the smaller gradients, the profile shape is close to that predicted for slip velocity-driven flow (Eq. 4 and Fig. 2A), while in the larger gradients the profile has the form predicted for convection (Eq. 5 and Fig. 2B). Judging by the profile shapes, slip velocity-driven flow dominates in small glucose gradients, and convection dominates in larger gradients. We postulate that the slip velocities are due to D_O induced by the glucose–wall interaction, which must be attractive based on the direction of the slip velocity. This implies that the surface free energy is lower at high glucose concentration. However, despite the small gradient experiments exhibiting the qualitative features of a slip velocity-driven flow, the profiles in Fig. 3A differ from the analytical profile in Fig. 2A. The experimental profiles flatten in the vicinity of the walls, while the analytical profile approaches the walls as a steep parabola.

The particles experience the same gradient as the channel walls so why might we observe D_O at the walls but find that particle DP is too slow to measure? First, the existence of D_O at the wall is inferred from the shape of the entire velocity profile, which makes it easier to distinguish than DP, which would manifest only as an offset in the velocity profile. But, perhaps more importantly, the particles are amine functionalized polystyrene, while the channel walls are coated with ibiTreat, giving a different surface chemistry. Since nonelectrolyte D_O and DP depend on the solute–surface interaction, a stronger interaction between glucose and the channel walls than between glucose and the particle surface could explain these observations. We do not yet have a good understanding of these interactions, but clearly the differences between the channel walls and the particles are sufficient to create very different fluid flows in the same gradient.

The qualitative difference in the flow profiles at low and at high glucose concentrations is not predicted by conventional theory. Models for diffusioosmosis and convection predict speeds that increase linearly with the gradient. Approximating the slip velocity, $u_s$, by the average tracer velocity in the wall-adjacent optical sections, we see that $u_s$ is between $0.3$ and $0.7\hspace{0.17em}\mathrm{\mu }\mathrm{m}\cdot {\mathrm{s}}^{-\mathrm{1}}$ over nearly two decades in $\mathrm{\Delta }c$ and that $u_s$ decreases as $\mathrm{\Delta }c$ increases. This is shown in Fig. 3C. Slip velocities are absent without a glucose gradient so must ultimately tend to zero for sufficiently low $\mathrm{\Delta }c$.

The measured scaling of D_O speed with concentration gradient is surprising. However, our convective speeds are consistent with the work of Gu et al. (25) and (mostly) with the model shown in Fig. 3 C, Inset. The gray dashed line shows the peak velocities predicted by Eq. 5, using the solutal expansion coefficient, $\beta =6.8\times 10^{-5}\hspace{0.17em}{\mathrm{m}}^3/\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{e}$, and the kinematic viscosity of water, $\nu =\eta /\rho =8.9\times 10^{-7}\hspace{0.17em}{\mathrm{m}}^2\cdot {\mathrm{s}}^{-1}$ (25). These are parameter-free predictions and capture the scale of the measurements accurately. However, as $\mathrm{\Delta }c$ increases, the analytical prediction increasingly overestimates the peak velocity. This is attributed to effects that are neglected in the theory, including the increase in solution viscosity with concentration.

Experiments with a Background Concentration.

In their studies of polystyrene colloids in aqueous ethanol gradients, Paustian et al. (6) measured diffusiophoretic velocities that varied as $u_{\mathrm{D}\mathrm{P}}\propto \nabla \ln X$, with $X$ the ethanol mole fraction. This amounts to a nonlinear dependence of slip velocity on concentration gradient. In the experiments described in Experiments with Zero Background Concentration, $\nabla \ln X=\nabla X/X$ is independent of $\mathrm{\Delta }c$ and is always $\nabla \ln X=2/L$ at the observation location, assuming a linear gradient. This predicts a D_O slip velocity independent of $\mathrm{\Delta }c$, which should be measurable even in the experiments exhibiting convection, contrary to our observations.

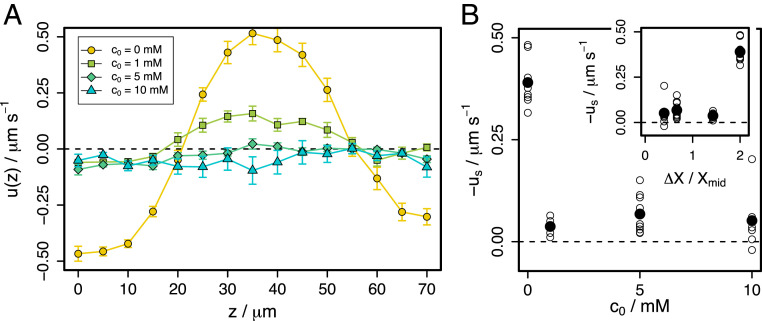
Although the scaling of Paustian et al. (6) seems incompatible with our observations, it is prudent to test this with a second set of experiments in which the concentration difference between the reservoirs is fixed at $\mathrm{\Delta }c=5\hspace{0.17em}\mathrm{m}\mathrm{M}$, and the background concentration is varied between $c_0=0$ and $c_0=10\hspace{0.17em}\mathrm{m}\mathrm{M}$. The results are shown in Fig. 4.

Fig. 4.

Flow in glucose gradients between reservoirs at $c_0$ and $c=c_0+5\hspace{0.17em}\mathrm{m}\mathrm{M}$. (A) Velocity profiles averaged over all experiments and waiting times. Error bars represent the SEM. (B) Estimated slip velocities (average velocity in wall-adjacent optical sections) as a function of $c_0$. Inset shows same data as a function of $\mathrm{\Delta }X/X_{\mathrm{m}\mathrm{i}\mathrm{d}}$, where $\mathrm{\Delta }X$ is the difference in glucose mole fraction between the reservoirs and $X_{\mathrm{m}\mathrm{i}\mathrm{d}}$ is mole fraction at the channel center. Open points are individual experiments and solid points show the average over all experiments at each $c_0$.

The $\nabla \ln X$ scaling predicts that maintaining $\mathrm{\Delta }c$ while increasing $c_0$ should decrease $u_s$. The data show that even at $c_0=1\hspace{0.17em}\mathrm{m}\mathrm{M}$, the slip velocity is greatly reduced compared to $c_0=0$. The profile shape is preserved, with backflow along the channel center, but its scale is reduced. Further increasing $c_0$ to $5$ or $10\hspace{0.17em}\mathrm{m}\mathrm{M}$ gives a flat profile indicative of complete suppression of circulating flow. Estimated slip velocities are shown in Fig. 4B as a function of $c_0$ (main panel) and $\mathrm{\Delta }X/X_{\mathrm{m}\mathrm{i}\mathrm{d}}$ (Inset), where $\mathrm{\Delta }X$ is the difference in glucose mole fraction between the reservoirs and $X_{\mathrm{m}\mathrm{i}\mathrm{d}}$ is the mole fraction at the observation location. If $u_s\propto \nabla \ln X$ describes our system, the Inset plot would show a linear increase in $u_s$ with $\mathrm{\Delta }X/X_{\mathrm{m}\mathrm{i}\mathrm{d}}$, which it clearly does not. Therefore, while we measure qualitatively similar behavior to that in Paustian et al. (6), their $\nabla \ln X$ dependence does not describe our D_O slip velocities. Although both sets of experiments reveal a decrease in speed on increasing concentration, the physical origin of these effects may differ between glucose and ethanol gradients.

In the remainder of this article, we seek to understand the concentration dependence of the D_O slip velocity and present a plausible physical mechanism for its origin, capable of explaining the cross-over to convection-dominated flow in large gradients.

Model for Diffusioosmosis due to Nonelectrolytes

In this section we develop a simple model for diffusioosmosis and qualitatively compare its predictions to experimental measurements. First, we account for a concentration-dependent solution viscosity, and subsequently we provide a simple description of a heterogeneous surface. Many models of D_O conceptually separate the system into an interfacial region and the bulk, as illustrated in Fig. 1C. We follow this convention and define an interfacial region of width $\lambda \sigma$, where $\sigma$ is an estimate of the solute molecular size, and $\lambda$ controls the width of the interface. Within the interfacial region, a solute molecule experiences an effective attractive interaction $ϵ<0$. All properties of the solution within the interfacial region are assumed to be uniform across its width.

Diffusioosmosis with a Concentration-Dependent Viscosity in the Surface Region.

The model for D_O as written in Eqs. 2 and 3 assumes the same viscosity in both interfacial and bulk regions, equal to that of the solvent. However, the viscosity of a glucose solution increases with $c$ and there is an upper limit to glucose solubility. The concentration dependence of viscosity can be incorporated into Eq. 3 by noting that $\eta =\eta \left(c\right)$ means $\eta =\eta \left(x,z\right)$ and moving the viscosity inside the integral.

We assume that the solution is ideal up to the solubility limit. Osmotic pressure measurements (56) of glucose solutions show that this is an acceptable approximation. Then $d\mathrm{\Pi }/dx=k_{\mathrm{B}}Tdc/dx$. Ideality also means that the concentration in the interfacial layer is enhanced by a Boltzmann factor compared to the bulk, $c_{\mathrm{S}\mathrm{L}}\left(x\right)/c\left(x\right)=\exp \left(-ϵ/k_{\mathrm{B}}T\right)$. When the surface layer concentration exceeds the bulk glucose solubility limit, $c_{max}=3.2$ M (52, 57), we assume that the interface solidifies, and the slip velocity becomes zero. We also assume that the viscosity in the interfacial region is the viscosity of a bulk glucose solution, but at the interfacial region concentration.

With these modifications, Eq. 3 becomes

$${\mathrm{\Gamma }}_{{\mathrm{D}}_{\mathrm{O}}}=\frac{f_{\mathrm{M}\mathrm{N}}\left[\exp \left(-ϵ/k_{\mathrm{B}}T\right)-1\right]{\left(\lambda \sigma \right)}^2}{2{\eta }_{\mathrm{g}}\left(c_{\mathrm{S}\mathrm{L}}\right)}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{c}_{\mathrm{S}\mathrm{L}}<c_{max}$$ [6]

and ${\mathrm{\Gamma }}_{{\mathrm{D}}_{\mathrm{O}}}=0$ for $c_{\mathrm{S}\mathrm{L}}>c_{max}$. The factor $f_{\mathrm{M}\mathrm{N}}=10^3{N}_{\mathrm{A}}$ converts between molar concentrations and number densities. This is equivalent to Eq. 3 calculated using a square-well solute–wall attraction of depth $-ϵ$ and range $\lambda \sigma$ and using the concentration-dependent bulk viscosity of glucose solutions, ${\eta }_{\mathrm{g}}$ given in Materials and Methods.

We assume a linear gradient, $\mathrm{\Delta }c/L$, at the midpoint glucose concentration, $c_{\mathrm{m}\mathrm{i}\mathrm{d}}=c_0+\mathrm{\Delta }c/2$. Thus, for a given $\mathrm{\Delta }c$, we use the solute chemical potential equilibrium between the surface layer and the bulk to determine $c_{\mathrm{S}\mathrm{L}}$ and hence the viscosity, osmotic pressure gradient, and slip velocity.

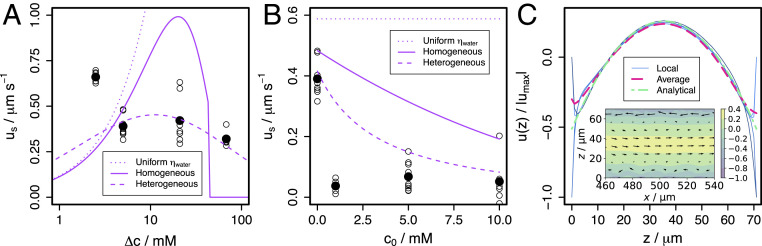
Slip velocities predicted by this model are compared with experimental data in Fig. 5 A and B where they appear as solid lines. We do not expect this model to be truly quantitative so we do not fit it to the data, but we do compare trends by setting $\lambda =1$ and $ϵ=-5\hspace{0.17em}{k}_{\mathrm{B}}T$. The characteristic size of a glucose molecule is estimated to be $\sigma =0.8\hspace{0.17em}\mathrm{n}\mathrm{m}$. For reference, the dotted lines show the prediction when viscosity is independent of concentration and equal to that of water.

Fig. 5.

Comparison of experimental estimates of slip velocity (points) with model predictions. (A) In glucose gradients between reservoirs at $c_0=0$ and $\mathrm{\Delta }c$. (B) In gradients between reservoirs at $c_0$ and $c_0+5\hspace{0.17em}\mathrm{m}\mathrm{M}$. Solid black point is average over repeated experiments, open circles are individual experiments. Solid line shows model prediction for $ϵ=-5\hspace{0.17em}{k}_{\mathrm{B}}T$. Dashed line shows heterogeneous model predictions with mean $\overline{ϵ}=-5\hspace{0.17em}{k}_{\mathrm{B}}T$ and SD ${\sigma }_{ϵ}=\overline{ϵ}/3$. Dotted line is prediction for $ϵ=5\hspace{0.17em}{k}_{\mathrm{B}}T$, according to Eqs. 2 and 3 neglecting the concentration-dependent viscosity. (C) Velocity profiles calculated in Navier–Stokes simulations with heterogeneous patchy slip velocities at the top and bottom walls. Patch size is $1\hspace{0.17em}\mathrm{\mu }\mathrm{m}$. Thin blue lines show local velocity profiles at $x=480$, $490$, $510$, and $520\hspace{0.17em}\mathrm{\mu }\mathrm{m}$. Dashed magenta line shows velocity profile averaged over $10\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ in $x$ (10 patches). Dotted-dashed green line shows analytical profile from Eq. 4 using the patch-averaged slip velocity. Inset shows velocity field in the vicinity of the channel center.

From Fig. 5A, it is clear that the increase in viscosity in the surface layer reduces the slip velocity compared to the conventional model with uniform viscosity. Glucose solution viscosity increases nonlinearly with concentration and this is sufficient to create a nonlinear dependence of $u_s$ on $\mathrm{\Delta }c$. The result is a broad peak in the slip velocity, with maximum speeds in the range 0.1 to $1\hspace{0.17em}\mathrm{\mu }\mathrm{m}$/s—the same as in experiment. The speed goes to zero both as $\mathrm{\Delta }c$ goes to zero and at large $\mathrm{\Delta }c$. The peak spans two orders of magnitude and is centered around a $\mathrm{\Delta }c$ that scales as $\exp \left(-ϵ/kT\right)$; i.e., strong surface–glucose interactions give rise to strong D_O at lower bulk concentration gradients. SI Appendix explores the $ϵ$ and $\lambda$ dependence of the model predictions and the viscosity dependence of the uniform viscosity model of Eqs. 2 and 3.

Fig. 5B compares the second set of experiments with model predictions when the background glucose concentration is increased. The model predicts that the slip velocity decreases with increasing $c_0$, but this effect is weaker than is measured in experiment. The model correctly predicts that the maximum speed is of order $kT{\sigma }^2/\eta$ multiplied by the gradient in number density. However, when compared to our measurements, the predicted slip velocity varies more strongly with the gradient and more weakly with the background concentration. Importantly, simply augmenting the conventional D_O model with a concentration-dependent solution viscosity in the interfacial layer is sufficient to give slip velocities that decrease as concentration gradient increases for concentration gradients larger than the peak in Fig. 5A. This allows the experimentally observed cross-over between D_O-driven flow and convection at some finite gradient.

Diffusioosmosis at Heterogeneous Surfaces.

So far, we have perfect uniformity in the plane of the interface, down to the nanometer length scale of glucose molecules. This is certainly unrealistic. So, in our final development, we introduce a laterally heterogeneous surface. Surface heterogeneity will cause variations in slip velocity over a characteristic, small length scale. As the glucose molecule is about a nanometer across, D_O will be sensitive to nanoscale heterogeneity. To understand the effect of a spatially varying slip velocity, we perform (2D, incompressible) Navier–Stokes simulations with nonuniform slip velocities. We use a modified version of the cavity flow code of Hau and Ohl (58), which is in turn based on that of Barba and Forsyth (59). Full simulation details are provided in SI Appendix.

Example velocity profiles obtained from these simulations are shown in Fig. 5C. If the slip velocity varies over a length scale ${\lambda }_{\mathrm{P}}$, flow is perturbed within a comparable range from the wall. Over longer length scales, flow appears as if it were driven by a uniform average slip velocity. With heterogeneity on the scale ${\lambda }_{\mathrm{P}}=1\hspace{0.17em}\mathrm{\mu }\mathrm{m}$, local velocity profiles (thin blue lines) relax to the average profile (dashed magenta line) over a few micrometers. This profile is the average of individual profiles over a length of 10 times ${\lambda }_{\mathrm{P}}$ and is virtually indistinguishable from the analytical profile (green) obtained according to Eq. 4 using a uniform slip velocity equal to the average slip velocity.

Therefore, our micrometer-sized tracer particles are insensitive to nanometric heterogeneities in slip velocity and sensitive only to the spatially averaged slip velocity. Within our model, the surface–solute interaction is characterized by $ϵ$. We model nanometric heterogeneity by assuming a distribution of $ϵ$ and average the resulting distribution of slip velocities, assuming our experiments measure the average slip velocity.

The average slip velocities for heterogeneous surfaces are shown as dashed curves in Fig. 5 A and B. The mean interaction strength is $\overline{ϵ}=-5k_{\mathrm{B}}T$ and the SD ${\sigma }_{ϵ}=\left|\overline{ϵ}\right|/3$. This is described in Materials and Methods. The heterogeneous model predictions are closer to the experimental data for both the variations with gradient (Fig. 5A) and with background concentration (Fig. 5B). They reproduce the qualitative features of our experiments, but still disagree quantitatively for low $\mathrm{\Delta }c$ and intermediate $c_0$.

This suggests that surface heterogeneity might play an important role in determining D_O flows in gradients of nonelectrolytes, a conclusion supported by computer simulation (60). The majority of research into D_O and DP assumes flat surfaces, simple interactions, and electrolyte gradients, assuming surface uniformity may be a much better approximation for electrolytes than for nonelectrolytes. Resolving this question is crucial to understand and exploit DP or D_O in living systems where surfaces are invariably highly heterogeneous (61).

Discussion and Conclusion

Our results show that concentration gradients of nonelectrolytes can drive flows as fast as those of electrolytes ($\sim 0.1$ to $1\hspace{0.17em}\mathrm{\mu }\mathrm{m}$/s). This is in agreement with previous results (6, 31). Our model predicts the correct flow velocities, and we obtain the best reproduction of concentration dependence by assuming a strong, several $k_{\mathrm{B}}T$, surface–solute attraction and a heterogeneous surface. Both assumptions are physically reasonable but systematic experiments varying surface chemistry and heterogeneity will be needed to definitively test these two assumptions.

For charged surfaces and electrolyte gradients, modeling the surface via a zeta potential gives good agreement between experiment and theory (6, 28). Experiments confirm DP speeds are proportional to $\nabla \ln c$ (6) which is well understood and follows from the concentration dependence of the interfacial width, the Debye length. Studies of D_O and DP due to nonelectrolytes are much less frequent and these phenomena are less well understood. However, nonelectrolyte D_O along nanoscale membrane pores (referred to as osmotic flow) was described theoretically in a pioneering study by Anderson and Malone (23). They considered long pores only nanometers across. This is much smaller than our channels, but the physics of slip velocities were shown to be relevant at these length scales, and thus our results may prove relevant to transport through nanoscale pores. Experimental (24, 62) and modeling (63) studies have investigated electrolyte-driven flows in nanoscale pores where the solute is much closer in size to the channel dimension. We speculate that the effects of surface heterogeneity will be much more prominent in these geometries.

For glucose, we find only a weak dependence of the D_O speed on the gradient, but this may be specific to our system. It seems likely that the concentration dependence of D_O flows is not universal as it is for electrotytes. However, our experiments and model, and the simulations of Wei et al. (35), all find a speed that decreases at sufficiently high concentrations and strong attractions. As the speed must tend to zero as the concentration tends to zero, a maximum in speed at some concentration may be common for nonelectrolytes. With strong attractions, the concentration in the interfacial region is much larger than in the bulk, and this region may become very viscous. Therefore, D_O flow speeds depend sensitively on both the solute–surface interaction [in the manner described by the theory of Derjaguin, Anderson, Marbach, and others (22, 47, 48)] and on any changes in solution properties as a consequence of this interaction. Indeed, Lee et al. (31) found that even understanding the direction of D_O flows in ethanol and polymer gradients requires carefully accounting for the structure and solute mobility in the interfacial region. This means that D_O slip velocities and velocity profiles depend on both the concentration gradient and the concentration, suggesting that we may expect to measure position-dependent velocity profiles. However, within the limits of our data, acquired close to the channel center, we discern no such dependence (SI Appendix).

Predicting the D_O speed for a given combination of nonelectrolyte solute and surface is difficult, but this problem can be inverted. A readily observable property (flow) is a sensitive probe of the surface–solute interactions. The concentrations at which flow speeds increase and/or saturate should scale with the surface–solute attraction strength and allow the interaction to be estimated. In our case it appears to be ∼$5k_{B}T$. This approach has already been employed using electrolyte D_O and DP to measure zeta potential (8).

In contrast to D_O, the convective flow profiles are accurately described by the standard, parameter-free, theory. In $70\hspace{0.17em}\mathrm{\mu }\mathrm{m}$-high channels, switching between D_O-dominated and convection-dominated flow is achieved simply by varying the concentration gradient. A consequence of these two competing effects is that experimentalists must proceed with caution when generating gradients in channels of height $\sim 100\hspace{0.17em}\mathrm{\mu }\mathrm{m}$, as flows may arise due to a combination of factors. Convective speeds vary as the cube of the height, while diffusioosmotic speeds are independent of height. Thus, convection will always dominate in deep channels, while for shallower channels, diffusioosmosis will dominate.

Concentration gradients are ubiquitous in living systems (4, 64), and we expect them to drive transport in our bodies (41). Living organisms rely on transport over many length scales, including those in the 10- to 100-μm range where phoretic transport can be faster than both diffusion (41) and fluid flow. Biological surfaces and particles are complex, heterogeneous, and dynamic (61, 65–67). We have shown that for nonelectrolyte D_O, even simple properties like the concentration dependence of viscosity can surprise. We expect many more surprises as we develop our understanding of diffusioosmosis in living systems.

Materials and Methods

Experimental Samples.

Solutions of glucose (Sigma-Aldrich) are prepared in deionized water (milliQ) at concentrations between 0 (pure water) and $1\hspace{0.17em}\mathrm{M}$. Fluorescently labeled amine-modified polystyrene spheres of diameter $\sigma =1\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ are obtained from Sigma-Aldrich in aqueous suspension at $\sim 2.5\%$ solids, and $4\hspace{0.17em}\mathrm{\mu }\mathrm{L}$ of this stock suspension is added for each milliliter of glucose solution or pure water.

Gradient Generation.

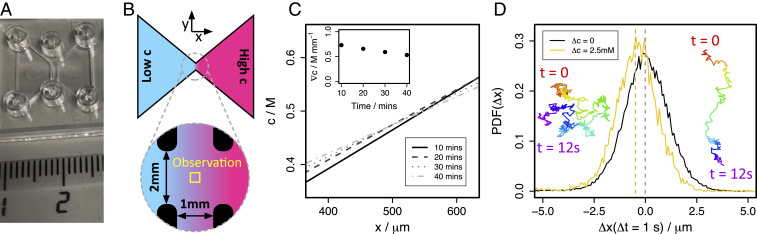
Glucose gradients are established in commercially available ibidi $\mathrm{\mu }$slide chemotaxis chambers (photograph in Fig. 6A), which consist of two $1\hspace{0.17em}\mathrm{m}\mathrm{m}$-deep triangular reservoirs connected by a $H=70\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ deep gradient channel, as illustrated in Figs. 1A and 6B. The length, $L$, of the gradient channel (the distance between the reservoirs) is $L=1\hspace{0.17em}\mathrm{m}\mathrm{m}$, and the reservoir openings have width $W=2\hspace{0.17em}\mathrm{m}\mathrm{m}$, as shown in the close-up detail in Fig. 6B. The channel walls are polymer coated with ibiTreat, rendering them hydrophilic. Six inlets allow loading and unloading of the reservoirs and gradient channel using a micropipette and provide outlets for air, so no bubbles are trapped in the device during experiments. These inlets may be sealed with plastic stoppers.

Fig. 6.

Experimental details. (A) Photograph of experimental device and centimeter ruler scale. Circular inlets allow loading of reservoirs and the gradient channel and provide outlets for air. Inlets are sealed with plastic stoppers after loading. (B) Top view schematic of sample chamber and close-up detail of central gradient channel. Yellow box indicates observation region. (C) Concentration gradient at $z=35\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ in the center of the gradient channel, at 10-min intervals after initiation as extracted from 2D COMSOL model of the experimental geometry. Inset shows $\nabla c$ as a function of time. (D) Probability distribution for tracer displacement $\mathrm{\Delta }x$ in interval $\mathrm{\Delta }t=1\hspace{0.17em}\mathrm{s}$ in experiment with no gradient (black) and glucose gradient $2.5\hspace{0.17em}\mathrm{m}\mathrm{M}/\mathrm{m}\mathrm{m}$ (gold). Insets show examples of single-particle trajectories without a gradient (left) and with a gradient (right).

The $x$ direction is defined along $L$, between the reservoirs from low to high concentration, and gravity acts in the negative $z$ direction. Experiments are initialized by first filling and sealing the low concentration reservoir and then filling and sealing the high concentration reservoir. We allow 5 min for the concentration gradient to establish itself before observing at the center of the channel (yellow box in Fig. 6B). Diffusive mixing in this setup will eventually lead to a uniform concentration throughout the device. However, the reservoirs are sufficiently large and the gradient channel is sufficiently small that this occurs over a timescale much longer than the experimental duration. This is conceptually distinct from experimental protocols using flushed microfluidic channels as reservoirs in which a true steady-state gradient is established (6, 9). To estimate the concentration gradient, we simulate a 2D model of the chamber in COMSOL Multiphysics. This neglects convective flow and concentration-dependent viscosity and simply considers the diffusive transport of glucose from the high concentration reservoir across the channel. Simulated concentration profiles in the midplane of the channel ($z=35\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ above the bottom) as a function of time after initiation with $c=1\hspace{0.17em}\mathrm{M}$ in the high concentration reservoir are shown in Fig. 6C. These data are calculated using a glucose diffusion constant $D=0.67\times 10^{-9}\hspace{0.17em}{\mathrm{m}}^2\cdot {\mathrm{s}}^{-1}$ (25). This modeling suggests that the concentration gradient is quickly established and is linear over the central observation region. Furthermore, the gradient is fairly stable with time. Fig. 6 C, Insets show linear fits to the gradient as a function of time.

Data Acquisition.

Measurements are made using an inverted laser scanning confocal microscope (Leica TCS SP8). Data are acquired following an $xytz$ protocol, whereby a 2D video is recorded at 15 different heights separated by $\mathrm{\Delta }z=5\hspace{0.17em}\mathrm{\mu }\mathrm{m}$, spanning the $70-\mathrm{\mu }\mathrm{m}$ deep gradient channel, working from the bottom to the top. At each height, $z$, a 200-frame video is acquired in resonant scanning mode at a rate of $\sim 14$ frames per second. We image using a $10\times$ objective, giving a 2D image size of $258\times 258\hspace{0.17em}\mathrm{\mu }\mathrm{m}$. Acquisition of the whole stack of 15 videos takes $\sim 3.5$ min, and so in a given experiment, there is a time delay between data acquired at the bottom and the top of the channel.

Since there is a density contrast between the polystyrene tracers and the glucose solutions, the tracer particles sediment. One hour after initiating the experiment, the top half of the channel is typically depleted of tracers, and so the full velocity profile cannot be measured beyond this time.

Data Analysis.

Particle trajectories are obtained in each 2D video using standard particle-tracking algorithms (68) implemented in the R programming language (69). From particle trajectories, displacements over 10 frame intervals are calculated. Probability histograms for displacements in the $x$ direction are shown in Fig. 6D for an experiment with no concentration gradient (black line) and an experiment with $\mathrm{\Delta }c=2.5\hspace{0.17em}\mathrm{m}\mathrm{M}$ (gold line). In the no gradient case, the histogram is symmetric about zero, indicating no preferred displacement direction; i.e., motion is Brownian. With a gradient, the histogram shape is preserved, but it is no longer centered at zero. Brownian motion remains a significant contribution to tracer particle motion, but it is superposed over a directed drift velocity, which is interpreted as the underlying fluid velocity. Example particle trajectories are shown in Fig. 6 D, Insets when there is no gradient (left) and in the $\mathrm{\Delta }c=2.5\hspace{0.17em}\mathrm{m}\mathrm{M}$ gradient (right). In the gradient case, directional drift is clearly evident.

Velocity profiles are constructed by finding the mean of the $x$ displacement distribution in each of the 15 2D videos acquired in each experiment. Therefore each point in the velocity profiles represents a spatial average over the $258-\mathrm{\mu }\mathrm{m}$ square at the center of the gradient channel and a time average over the $\sim 14$ s of video acquisition at each height. Each of the average profiles in Figs. 3 and 4 is the average over at least three independently prepared experiments and multiple observations after different waiting times.

Physical Properties of Aqueous Glucose Solutions.

Osmotic and activity coefficients of aqueous glucose solutions have been measured by Miyajima et al. (56). These data are shown in SI Appendix and show that the solution is close to ideal, i.e., that the osmotic pressure is close to $\mathrm{\Pi }=\rho kT$, with $\rho =c{N}_{\mathrm{A}}/10^{-3}$, the glucose number density. Lewis (70) gives $\mathrm{\Pi }=23.6$ atmospheres or $2.4\times 10^6$ Pa as the osmotic pressure of 1 M glucose. An ideal solution at 1 M has an osmotic pressure of $2.5\times 10^6$ Pa.

The CRC Handbook of Chemistry and Physics (52) has data for glucose solutions at 293 K. We fit these data and obtain

$${\eta }_{\mathrm{g}}=\eta {\left(1-c/6.2586\right)}^{-3.1828},$$ [7]

where $\eta =1.0002$ mPa (52) is the viscosity of water at 293 K. This fit is shown in SI Appendix.

Surface Heterogeneity.

Based on the findings of cavity flow Navier–Stokes simulations, we model surface heterogeneity in a simple way by assuming that the measured slip velocity is an average over a D_O velocity that varies over the surface due a spatially nonuniform surface–solute interaction. Fixing the width of the surface layer to be $\lambda \sigma$ everywhere, the surface can only vary through changes in $ϵ$. Thus, we implement surface heterogeneity via

$$u_s=\int P\left(ϵ\right)\hspace{0.17em}{u}_{{\mathrm{D}}_{\mathrm{O}}}\left(ϵ\right)\hspace{0.17em}\mathrm{d}ϵ,$$ [8]

where $P\left(ϵ\right)$ is the probability density that a part of the surface attracts solute with a strength $ϵ$. We choose a Gaussian $P\left(ϵ\right)$, with mean $\overline{ϵ}$ and SD ${\sigma }_{ϵ}$.

Data Availability.

Data for this article are available online in Figshare at https://doi.org/10.6084/m9.figshare.12643205.v2 (71).