Quantum approximate optimization of the long-range Ising model with a trapped-ion quantum simulator

Significance

Variational quantum algorithms combine quantum resources with classical optimization methods, providing a promising approach to solve both quantum many-body and classical optimization problems. A crucial question is how variational algorithms perform as a function of qubit number. Here, we address this question by applying a variational quantum algorithm (QAOA) to approximate the ground-state energy of a long-range Ising model, both quantum and classical, and investigating the algorithm performance on a trapped-ion quantum simulator with up to 40 qubits. A negligible performance degradation and almost constant runtime scaling is observed as a function of the number of qubits. By modeling the error sources, we explain the experimental performance, marking a stepping stone toward more general realizations of hybrid quantum–classical algorithms.

Abstract

Quantum computers and simulators may offer significant advantages over their classical counterparts, providing insights into quantum many-body systems and possibly improving performance for solving exponentially hard problems, such as optimization and satisfiability. Here, we report the implementation of a low-depth Quantum Approximate Optimization Algorithm (QAOA) using an analog quantum simulator. We estimate the ground-state energy of the Transverse Field Ising Model with long-range interactions with tunable range, and we optimize the corresponding combinatorial classical problem by sampling the QAOA output with high-fidelity, single-shot, individual qubit measurements. We execute the algorithm with both an exhaustive search and closed-loop optimization of the variational parameters, approximating the ground-state energy with up to 40 trapped-ion qubits. We benchmark the experiment with bootstrapping heuristic methods scaling polynomially with the system size. We observe, in agreement with numerics, that the QAOA performance does not degrade significantly as we scale up the system size and that the runtime is approximately independent from the number of qubits. We finally give a comprehensive analysis of the errors occurring in our system, a crucial step in the path forward toward the application of the QAOA to more general problem instances.

A promising near-term application of quantum devices is the production of highly entangled states with metrological advantage or with properties of interest for many-body physics and quantum information processing. One possible approach to produce useful quantum states is to use quantum devices to perform adiabatic quantum computing (1, 2), which, in some cases, may provide an advantage over classical approaches (3). However, adiabatic quantum computing has stringent adiabaticity requirements that hinder its applicability on existing quantum platforms that have finite coherence times (4).

Alternatively, hybrid quantum–classical variational algorithms may approximately solve hard problems in realms such as quantum magnetism, quantum chemistry (5), and high-energy physics (6). This is because the key resource of quantum computers and simulators is quantum entanglement, which is exactly what makes these many-body quantum problems hard. In a hybrid variational algorithm, entangled states are functions of variational parameters that are iteratively optimized by a classical algorithm. One example is the Quantum Approximate Optimization Algorithm (QAOA) (7), which consists of a “bang-bang” protocol that can provide approximate answers in a time-efficient way, using devices with finite coherence times and without the use of error correction (8–12).

Similarly to adiabatic quantum computing, the QAOA protocol encodes the objective function of the optimization problem in a target spin Hamiltonian. The optimization steps of the QAOA are based on unitary evolution under the target Hamiltonian and a noncommuting “mixing” operator. In general, the QAOA relies on a classical outer loop to optimize the quantum circuit, aided by physical intuition (13–16) or observed structure of the variational parameters (11, 17, 18), producing fast, low-depth circuits for approximate solutions. The QAOA has also been proposed as an efficient way to produce entangled quantum states, such as the ground states of critical Hamiltonians, which gives access to their corresponding energies (19, 20).

In this work, we employ a collection of interacting trapped-ion qubits to experimentally implement a specific instance of the QAOA, which is native to our quantum hardware. We focus on both the energy minimization of the quantum Hamiltonian and the combinatorial optimization of the corresponding classical problem. Both problems are encoded in the transverse-field antiferromagnetic Ising Hamiltonian with long-range interactions:

$$H=\underset{H_A}{\underbrace{\sum _{i<j}{J}_{ij}{\sigma }_i^x{\sigma }_j^x}}+\underset{H_B}{\underbrace{B\sum _i{\sigma }_i^y}}.$$ [1]

Here, we set the reduced Planck’s constant $\hslash =1$; ${\sigma }_i^{\gamma }$ ($\gamma =x,y,z$) is the Pauli matrix acting on the $i^{\text{th}}$ spin along the $\gamma$ direction of the Bloch sphere; $J_{ij}>0$ is the Ising coupling between spins $i$ and $j$, which, in our case, falls off as a power law in the distance between the spins; and $B$ denotes the transverse magnetic field. It is well known (21) that the Hamiltonian (Eq. 1) exhibits a quantum-phase transition for antiferromagnetic interactions with power-law decay. One of the goals of this work is to find an approximation of the ground-state energy both at the critical point ${\left(B/J_0\right)}_c$, where $J_0$ is the average nearest-neighbor coupling, and in the case of $B=0$, optimizing the QAOA output for the classical Hamiltonian $H_A$. The realization of the QAOA entails a series of unitary quantum evolutions (Fig. 1) under the noncommuting Hamiltonians $H_A$ and $H_B$ (defined under Eq. 1) that are applied to a known initial state $\left|{\psi }_0\right.⟩$. The state obtained after $p$ layers of the QAOA is:

$$\left|\overrightarrow{\beta },\overrightarrow{\gamma }\right.⟩=\prod _{k=1}^p{e}^{-i{\beta }_k\left(H_B/J_0\right)}{e}^{-i{\gamma }_k\left(H_A/J_0\right)}\left|{\psi }_0\right.⟩,$$ [2]

where the evolution times (or, henceforth, “angles”) ${\beta }_k$ and ${\gamma }_k$ are variational parameters used in the $k$-th QAOA layer to minimize the final energy $E\left(\overrightarrow{\beta },\overrightarrow{\gamma }\right)=\left.⟨\overrightarrow{\beta },\overrightarrow{\gamma }\right|H\left|\overrightarrow{\beta },\overrightarrow{\gamma }\right.⟩$.

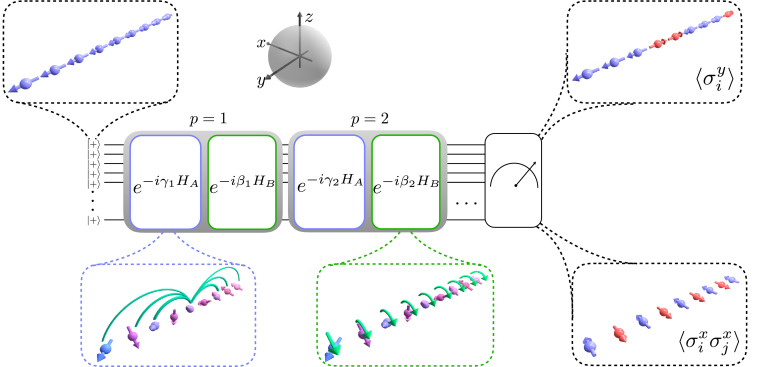
Fig. 1.

QAOA protocol. The system is initialized along the $y$ direction in the Bloch sphere in the ${\left|+\right.⟩}^{\otimes N}$ state. The unitary evolution under $H_{A\left(B\right)}$ is implemented for angles ${\gamma }_i\left({\beta }_i\right)$ for $p$ times. At the end of the algorithm, global measurements in the $x$ and the $y$ basis are performed to compute the average energy $⟨H⟩=E\left(\overrightarrow{\beta },\overrightarrow{\gamma }\right)$, which is compared to the theoretical ground-state energy $E_{gs}$.

In order to implement the quantum-optimization algorithm, each spin in the chain is encoded in the $2_{\mathrm{S}}^{1/2}\hspace{0.17em}\left|F=0,m_F=0\right.⟩\equiv {\left|\downarrow \right.⟩}_z$ and $\left|F=1,m_F=0\right.⟩\equiv {\left|\uparrow \right.⟩}_z$ hyperfine “clock” states of a ¹⁷¹Yb⁺ ion (SI Appendix). In this work, depending on the number of qubits and measurements required, we employ two different quantum-simulation apparatus to run the QAOA, which will herein be referred to as system 1 (22) and system 2 (23) (SI Appendix). Both systems are based on a linear radiofrequency Paul trap, where we store chains of up to $N=40$ ions and initialize the qubits in the ground state of $H_B$, namely, the product state ${\left|\uparrow \uparrow \cdots \uparrow \right.⟩}_y\equiv {\left|+\right.⟩}^{\otimes N}=\left|{\psi }_0\right.⟩$, where ${\left|\uparrow \right.⟩}_y\equiv \left({\left|\uparrow \right.⟩}_z+i{\left|\downarrow \right.⟩}_z\right)/\sqrt{2}$, and $B$ is assumed to be negative. The unitary evolution under $H_A$ is realized by generating spin–spin interactions through spin-dependent optical dipole forces implemented by an applied laser field. This gives rise to effective long-range Ising couplings that fall off approximately as $J_{ij}\approx J_{\mathrm{0}}/|i-j{|}^{\alpha }$ (24). The power-law exponent $\alpha \sim 1$ and the interaction strengths vary in the range $J_0/2\pi =$ (0.3–0.57) kHz, depending on the system size and the experimental realization (see SI Appendix for details). The unitary evolution under $H_B$ is generated by applying a global rotation around the $y$ axis of the Bloch sphere.

After each run of the algorithm, we performed a projective measurement of each spin in the $x\hspace{0.17em}\left(y\right)$ basis to measure $⟨H_A⟩$ ($⟨H_B⟩$) (Fig. 1). Measurements in the $x$ and $y$ bases were carried out by performing a $\pi /2$ rotation about the $y$ ($x$) axis of the Bloch sphere, illuminating the ions with resonant laser light, and collecting the ${\sigma }_i^z$-dependent fluorescence on a camera with site-resolved imaging. The energy was calculated by combining the measurements of the two-body correlators $⟨{\sigma }_i^x{\sigma }_j^x⟩$ and the total magnetization along the $y$ axis ${\sum }_i⟨{\sigma }_i^y⟩$, where the indices $i,j$ ranged from one to $N$. We benchmarked the experimental outcome $E\left(\overrightarrow{\beta },\overrightarrow{\gamma }\right)$ with the ground-state $E_{gs}$ of the target Hamiltonian (Eq. 1), calculated numerically with exact diagonalization or Density Matrix Renormalization Group (DMRG) (25). In order to quantify the performance of the QAOA, we used the dimensionless quantity

$$\eta \equiv \frac{E\left(\overrightarrow{\beta },\overrightarrow{\gamma }\right)-E_{max}}{E_{gs}-E_{max}},$$ [3]

where $E_{max}$ is the energy of the highest excited state. This choice maps the entire many-body spectrum to the $\left[\mathrm{0,1}\right]$ interval. In the following, we show that the best experimental performance ${\eta }^{*}$ is close to the theoretical performance ${\eta }_{th}$, which itself is less than unity for a finite number $p$ of QAOA layers.

Quantum Hamiltonian Optimization

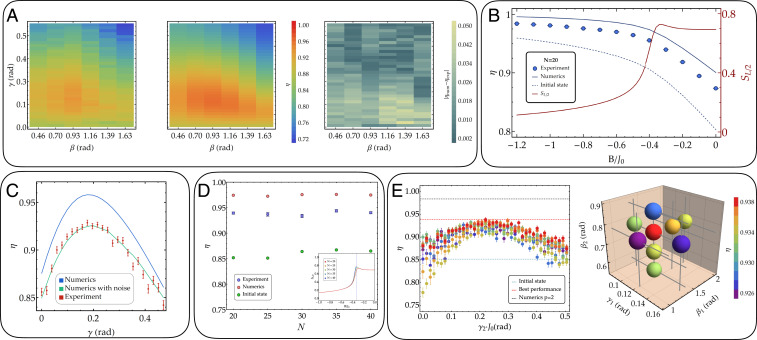
We first focused on the $p=1$ optimization of the full quantum problem, where two variational parameters ($\gamma$ and $\beta$) are used to minimize the energy of the Hamiltonian (Eq. 1). In this case, the time-evolved one- and two-point correlation functions can be efficiently computed (26, 27). This leads to a general formula for the energy expectation under a state produced by the $p=1$ QAOA that is used to compute the theoretical performance of the algorithm (SI Appendix). In Fig. 2A, we show an experimental exhaustive search over the parameter space $\left\{\gamma ,\beta \right\}$ and compare it to the theoretical performance of the algorithm, showing good agreement for $N=20$ qubits. We also compare the performance of our algorithm as a function of $B/J_0$ with the expected QAOA performance ${\eta }_{th}$ (Fig. 2B).

Fig. 2.

Exhaustive search for optimal performance. (A) Experimental (Left) and theoretical (Center) performance landscape and their absolute difference (Right) as a function of the variational parameters $\beta$ and $\gamma$ for $N=20$ qubits ($J_0/2\pi =0.57$ kHz, $B/J_0\sim -0.3$), displaying an average absolute difference of 1.9% over 210 different $\left\{\beta ,\gamma \right\}$ pairs. The optimal performance is ${\eta }^{*}=\left(93.8\pm 0.4\right)\%$, whereas the theoretical performance is ${\eta }_{th}=96.1\%$. Each data point is the result of 1,100 (800) experimental repetitions to measure in the $x\hspace{0.17em}\left(y\right)$ basis (data taken on system 1). (B) Exhaustive search optimization as a function of $B/J_0$ (Eq. 1) (data taken on system 1). The dark red solid line is the half-chain entanglement entropy $S_{L/2}$ computed numerically with DMRG. The dashed blue line represents the performance of the initial product state $\left|{\psi }_0\right.⟩$. (C) Comparison between experimental performances and numerics for $B/J_0=-0.25$ and $N=12$ as a function of $\gamma$ and ${\beta }^{*}=1.12$. Taking into account bit-flip errors and slow drifts in the experimental parameters explains well the discrepancy between experimental and ideal performance (see SI Appendix for details). (D) The $p=1$ QAOA performance as a function of system size $N$ up to 40 qubits (data taken on system 2). Comparison between QAOA experimental and theoretical performance for $B/J_0\sim -0.3$ is shown. Green points show the baseline performance of the initial state $\left|{\psi }_0\right.⟩$. (D, Inset) Convergence of the entanglement entropy peak as a function of number of qubits (SI Appendix). (E) $p=2$ exhaustive search for $N=20$ and $B/J_0\sim -0.3$. (E, Left) Every color corresponds to a fine scan of ${\gamma }_2$ with a different set of variational parameters ${\beta }_1,{\beta }_2$ and ${\gamma }_1$ (data taken on system 2). (E, Right) The three-dimensional color plot of the performance $\eta$, optimized over ${\gamma }_2$, as a function of the parameters ${\beta }_1,{\beta }_2$ and ${\gamma }_1$. The best outcome is ${\eta }^{*}=\left(93.9\pm 0.3\right)\%$ (colored red), whereas the theoretical performance is ${\eta }_{th}=98.4\%$ (see Quantum Hamiltonian Optimization for details). In B–E, the error bars are calculated by using the SD from the mean of the measured performance.

As shown in ref. 21, for transverse field greater than the critical value, the ground state is a low-entanglement paramagnet, whereas below the critical point, the ground state is an entangled superposition of antiferromagnetic states. We located this critical point at $|B/J_0|=0.31$ for 20 qubits by computing the half-chain entanglement entropy $S_{L/2}=-\text{Tr}\left({\rho }_{L/2}\log {\rho }_{L/2}\right)$ of the ground state numerically, where ${\rho }_{L/2}$ is the half-chain reduced density matrix. As shown in Fig. 2B, while the experimental performance was $\eta >94\%$ when $|B/J_0|$ is above the critical point, the gain relative to the initial state $\left|{\psi }_0\right.⟩$ was modest. On the other hand, below the critical point, the target state is more entangled, which allows for a larger experimental performance gain, at the expense of a reduced absolute performance. In order to quantitatively assess the gain over the finite initial-state performance, we introduced a performance natural scale based on the quantity ${\sigma }_{\eta }\left(J_0,B,N\right)$—namely, the SD around the mean performance achieved implementing a QAOA algorithm with random angles (see SI Appendix for details). For $N=20$ and $B/J_0\sim -0.3$, ${\sigma }_{\eta }\sim 2\times 10^{-3}$. Our experimental performance at the critical point ${\eta }^{*}$ is more than 20${\sigma }_{\eta }$ away from the initial state. On the other hand, the discrepancy between the ideal and experimental performance can be explained by taking into account our noise sources in the numerics (Fig. 2C and Combinatorial Optimization).

We investigated the performance of the $p=1$ QAOA algorithm as a function of the number of qubits. For each system size, we ensured that the spin–spin couplings $J_{ij}$ had the same dependence on the qubit distance $|i-j|$ by varying the trap parameters (SI Appendix). As shown in Fig. 2 D, Inset, the half-chain entanglement entropy as a function of system size $N$ exhibited a peak located at $B/J_0\sim -0.33$, displaying the onset of the phase transition as $N$ tended to infinity. For all system sizes, we optimized the algorithm by performing a scan of the interaction angle $\gamma$ and applying discrete variations of the mixing angle $\beta$ around the optimal value predicted by the theory. In Fig. 2D, we compare the optimal experimental and theoretical performances $\eta$ for different system sizes from 20 up to 40 qubits for fixed $B/J_0\sim -0.3$. We observed experimentally that the QAOA yielded a similar performance as a function of number of qubits, even if the algorithm runtime stayed approximately constant as the number of qubits increased. Numerically, we found that the performance $\eta$ scaled polynomially with $N$ and with the number of layers $p$ (28) (SI Appendix). Assuming that extrapolation to higher numbers of qubits holds, this scaling, combined with a polynomial-time search heuristic, suggests that for any desired energy threshold $ϵ$, our approach allows us to approximate the energy to a degree $\eta >1-ϵ$ in time and number of layers that scale as $\text{poly}\left(N,1/ϵ\right)$.

We experimentally performed a search for the optimal $p=2$ QAOA performance using 20 qubits. Unlike the $p=1$ case, there is no known analytic formula to efficiently compute the energy. However, exploiting relationships between optimal angles as a function of increasing $p$, we used a bootstrapping heuristic (see SI Appendix for details) that allows the experiment to identify a set of optimal angles faster than a global parameter search. The bootstrapping heuristic computes a guess for optimal angles at $p$ given optimal angles at lower $p$. A local optimizer, such as the greedy gradient descent described below, is then needed to take this guess to the true optimum. Our heuristic method allows us to find variational parameters in time that scale polynomially with the number of layers and sublinearly in the number of qubits (when used in conjunction with the quantum device).

We started from the optimal guess and performed a fine scan of ${\gamma }_2$, while varying ${\gamma }_1,{\beta }_1$ and ${\beta }_2$ in larger steps. The result is shown in Fig. 2D, where we plot the performances $\eta$ as a function of ${\gamma }_2$ for every set of parameters used in the experiment. Fig. 2D also shows a color plot of all of the optimal energies found as a function of the other three parameters ${\gamma }_1,{\beta }_1$, and ${\beta }_2$. The $p=2$ QAOA performance with 20 qubits ${\eta }^{*}=\left(93.9\pm 0.3\right)\%$ is in agreement with the $p=1$ performance in system 2, taken with the same parameters (Fig. 2C). This indicates that decoherence and bit-flip errors (SI Appendix) accumulated during longer evolution times were already balancing out the $2\%$ expected performance gain of one additional optimization layer.

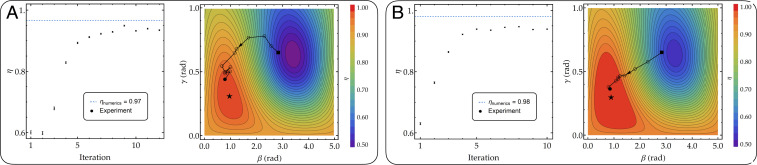
As a brute-force approach is inefficient, we implemented a closed-loop QAOA by interfacing the analog trapped-ion quantum simulator with a greedy gradient-descent algorithm to optimize the measured energy. In the $p=1$ QAOA, we can visualize the optimization trajectory on the theoretical performance surface, as shown in Fig. 3. Starting from a guess $\left({\beta }^{\left(0\right)},{\gamma }^{\left(0\right)}\right)$, we measured the approximate local gradient by performing the energy measurements in two orthogonal directions ${\beta }^{\left(0\right)}+\delta \beta$ and ${\gamma }^{\left(0\right)}+\delta \gamma$ to compute the new guess $\left({\beta }^{\left(1\right)},{\gamma }^{\left(1\right)}\right)$, where we measured the new energy on the quantum simulator. As shown in Fig. 3, the algorithm converged after about 10 iterations. Compared to an exhaustive search, the gradient descent used fewer queries to the quantum simulator and was therefore more robust to slow drifts in the experimental system. For this reason, we were able to achieve a better performance compared to the exhaustive search method.

Fig. 3.

Gradient descent search for P = 1 QAOA. $N=12$ (A) and $N=20$ (B). (A, Left and B, Left) Performance $\eta$ convergence as a function of iterations of the classical-quantum hybrid algorithm with $N=12$ ($J_0/2\pi =0.57$ kHz, $B/J_0=-0.3$) with a measured ${\eta }^{*}=\left(94.9\pm 0.2\right)\%$ (A) and $N=20$ qubits ($J_0/2\pi =0.55$ kHz, $B/J_0=-0.3$) with a measured ${\eta }^{*}=\left(94.7\pm 0.1\right)\%$ (B). (A, Right and B, Right) The algorithm trajectory on the theoretical performance landscape plotted as a function of $\gamma$ and $\beta$. Each energy evaluation takes 4,000 (6,000) shots for 12 (20) qubits. The error bars are SD from the mean of the measured performance (data taken on system 1).

Combinatorial Optimization

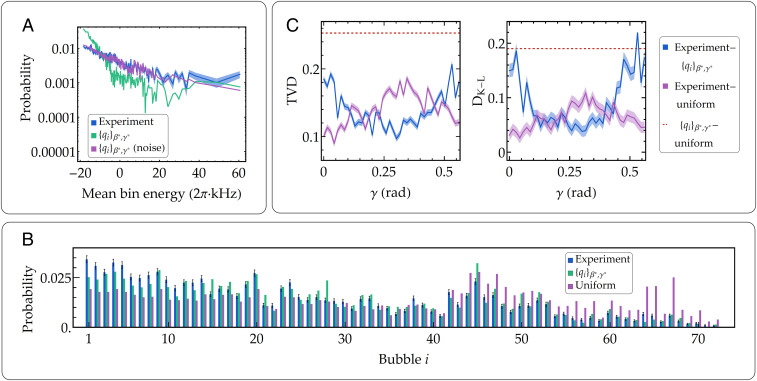
We further explored the performance of the trapped-ion system by investigating the combinatorial optimization of the classical Hamiltonian $H_A$ (Eq. 1 with $B=0$) approximately sampling the output of the $p=1$ QAOA, using high-fidelity, single-shot measurement of all of the qubits. It has been proven, under reasonable complexity-theoretic assumptions, that no classical algorithm can efficiently sample exactly from a sufficiently general class of $p=1$ QAOA circuits (8). Recent results (29, 30) suggest that this could also hold in the case of approximate sampling (SI Appendix). In this case, by measuring in the $x$ basis, it is possible to sample the probability distribution of all of the $2^N$ eigenstates $\left|x_i\right.⟩$ of the Hamiltonian $H_A$. We performed the experiment with 12 qubits so that we could both compute the expected QAOA theoretical output and also experimentally oversample the Hilbert space of all of the possible 2¹² = 4,096 possible outcomes. In Fig. 4A, we show on a log scale the QAOA eigenstates probability distribution using the optimal variational parameters ${\beta }^{*},{\gamma }^{*}$ and compare the experimental eigenstate histogram with the exact diagonalization prediction of the QAOA output state, sorting the eigenstates according to their energies.

Fig. 4.

Sampling from $p=1$ QAOA. (A) Eigenstate probability histogram for 12 qubits with $B=0$. The numerical histogram is computed by decomposing the ideal QAOA output state on the $\left\{\left|x_i\right.⟩\right\}$ basis. We performed 10,800 measurements to oversample the Hilbert space of dimension 2^N = 4,096 at the optimal parameters ${\beta }^{*}=0.25$ and ${\gamma }^{*}=0.31$. The 4,096 eigenstates are grouped in bins of 20 for clarity purposes. The uncertainty bands follow the multinomial distribution SD. Here, $J_0/2\pi =0.33$ kHz (see SI Appendix, Noise Sources for details). (B) Histogram of coarse-grained distributions (see Combinatorial Optimization for details) comparing data, theory, and the uniform distribution. The error bars here also represent the SD of the multinomial distribution. (C) TVD and Kullback–Leibler divergence as a function of $\gamma$, keeping $\beta$ fixed at the optimal value (1,350 shots per time step). The nonzero TVD value of the violet curve at $\gamma =0$ is due to state preparation and detection errors, as well as undersampling (SI Appendix). The distance from the uniform distribution increases as the $\gamma$ parameter reaches the optimal point ${\gamma }^{*}$. Dashed lines are the comparison between the ideal QAOA distribution ${\left\{q_i\right\}}_{{\beta }^{*},{\gamma }^{*}}$ and the uniform distribution. The uncertainty bands are based on the aforementioned error in the probability of each state bubble for the experimental distribution, propagated to the TVD and the ${\mathrm{D}}_{\mathrm{K}-\mathrm{L}}$, according to Eq. 4 (data taken on system 2)..

However, sampling from the full QAOA output distribution is a daunting task, since the experimental outcome is extremely sensitive to fluctuations in the Hamiltonian parameters and to experimental errors caused by detection and phonon-assisted bit-flip events and unwanted effective magnetic fields along the $z$ direction of the Bloch sphere caused by uncompensated light shift (see also SI Appendix). Given our measured experimental parameters, we can calculate the effect of these errors on the quantum evolution, resulting in a good agreement with the experimental outcome, as shown in Fig. 4A.

Another useful way to compare numerics and experimental data is to implement the coarse-graining procedure of the Hilbert space proposed in ref. 31. After sorting in decreasing order the observed states according to their experimental probability, we iteratively grouped the states into “bubbles” of Hamming distance $L$ around the most probable state, producing a coarse-grained dataset. We then applied the same coarse-graining to the theoretical probability distribution and plotted the comparison in Fig. 4B. In this procedure, the Hamming-distance radius was varied to ensure that each bubble contained a comparable number of experimental shots, leading to bubbles of average Hamming distance $\overline{L}=2.5$. In order to quantitatively compare the coarse-grained experiment and the theory, we used two different metrics, namely, the total variation distance (TVD) and the Kullback–Leibler divergence (${\mathrm{D}}_{K-\mathrm{L}}$), defined as:

$$\mathrm{T}\mathrm{V}\mathrm{D}=\frac{1}{2}\sum _i|p_i-q_i|,$$ [4]

$${\mathrm{D}}_{\mathrm{K}-\mathrm{L}}=-\sum _i{p}_i\log \left(\frac{q_i}{p_i}\right),$$ [5]

where $p_i\left(q_i\right)$ is the experimental (theoretical) probability of observing the $i$-th outcome. As shown in Fig. 4C, when the system is in the initial state, it is closer to a uniform probability distribution since $\left|{\psi }_0\right.⟩$ is an equal superposition of all of the eigenstates of $H_A$. Indeed, at $\gamma =0$, the TVD between the data $\left\{p_i\right\}$ and the uniform distribution is smaller than the one comparing the data and the ideal QAOA distribution ${\left\{q_i\right\}}_{{\beta }^{*},{\gamma }^{*}}$. On the other hand, as the $\gamma$ parameter was scanned, we observed a net decrease of both TVD and ${\mathrm{D}}_{\mathrm{K}-\mathrm{L}}$ between the experiment $\left\{p_i\right\}$ and the QAOA ideal distribution ${\left\{q_i\right\}}_{{\beta }^{*},{\gamma }^{*}}$, in agreement with the decrease in energy, computed by measuring one- and two-body correlators.

The variational quantum algorithm reported here, with up to 40 trapped-ion qubits, is the largest ever realized on a quantum device. We approximated the ground-state energy of a nontrivial quantum Hamiltonian, showing almost constant time scaling with the system size. Single-shot, high-efficiency qubit measurements in different bases gave access to the full distribution of bit-strings that is difficult or potentially impossible to model classically. With the addition of individual control over the interactions between qubits, as well as improvements to fidelity and system size, the variational quantum-classical hybrid approach can be employed in this experimental platform to give insight into quantum chemistry (32–34) and hard optimization problems (35), such as maximum-satisfiability or exact cover (36), or be used for the production of highly entangled states of metrological interest (37).

Data and Code Availability.

All study data are included in the article and SI Appendix.

Change History

August 16, 2021: The SI Appendix has been updated to coincide with a formal Correction.