Roboticizing fabric by integrating functional fibers

Significance

Fabrics are key materials for a variety of applications that require flexibility, breathability, small storage footprint, and low weight. While fabrics are conventionally passive materials with static properties, emerging technologies have provided many flexible materials that can respond to external stimuli for actuation, structural control, and sensing. Here, we improve upon and process these responsive materials into functional fibers that we integrate into everyday fabrics and demonstrate as fabric-based robots that move, support loads, and allow closed-loop controls, all while retaining the desirable qualities of fabric. Robotic fabrics present a means to create smart adaptable clothing, self-deployable shelters, and lightweight shape-changing machinery.

Abstract

Fabrics are ubiquitous materials that have conventionally been passive assemblies of interlacing, inactive fibers. However, the recent emergence of active fibers with actuation, sensing, and structural capabilities provides the opportunity to impart robotic function into fabric substrates. Here we present an implementation of robotic fabrics by integrating functional fibers into conventional fabrics using typical textile manufacturing techniques. We introduce a set of actuating and variable-stiffness fibers, as well as printable in-fabric sensors, which allows for robotic closed-loop control of everyday fabrics while remaining lightweight and maintaining breathability. Finally, we demonstrate the utility of robotic fabrics through their application to an active wearable tourniquet, a transforming and load-bearing deployable structure, and an untethered, self-stowing airfoil.

From natural plant fibers and animal wool to modern glass filaments and synthetic polymer thread, fabrics are among the most ubiquitous and adaptable materials in history. By nature of their interlaced fiber structure, fabrics are breathable, conformable, and highly compactible. Further, their general resiliency to crushing, tearing, and bending positions fabrics as the perfect class of material for wearables and other conformable applications, including specialized products such as extreme-weather-protective garments, rugged ripstop nylon in parachutes, and bullet-resistant vests. Given these versatile characteristics and unique application design space, the possibility of roboticizing fabrics could lead to smart adaptive clothing, self-deploying shelters, and lightweight, stowable, shape-changing machines.

Preliminary related works introduced the terms “smart textiles” and “e-textiles” (1–3) to designate fabrics enhanced with electrical circuitry via the development of flexible (4–6) or miniaturized (7, 8) versions of traditional electrical components. In particular, flexible sensors (1, 9–12), electrically conductive threads (3, 9), and energy collection devices (13–15) have come forth as potential building blocks for robotic fabrics. There have even been rare demonstrations of wearable fabric devices that use responsive materials for embedded actuation, including self-rolling temperature-sensitive sleeves (16), an orthotic limb support (17), and dynamic compression stockings (18). While the vast majority of these works showcase the success of individual robotic components, they are generally passive or uncontrolled, and the actuators rely on external actors to “reset” them after a single use or actuation cycle. As many of these concepts rely upon the presence of a host structure, such as the user of a wearable device, the notion of independently functioning fabric machines has also been little explored (19).

We demonstrate an expanded scope of fabric functionalization that, through controlled closed-loop behavior and autonomous task execution, becomes a complete stand-alone robotic platform (Fig. 1A). Our work addresses several gaps in the literature by introducing a set of functional fibers that unify actuation, structural control, and sensing functions into a cohesive robotic fabric unit (Fig. 1 B and C). By using fiber-like components as the active elements (Fig. 1D), we retain the desirable qualities of fabric, which opens the way for machines that are not only thin, lightweight, and breathable but which harness complex curvature and limitless surface configurations as key functions.

Fig. 1.

Robotic fabrics. (A) Rendering of a potential robotic fabric capable of locomotion. (B) Actualized robotic fabric demonstration. (C) Current robotic fabric vs. rendering of potential fully woven robot. (D) Fiber-form robotic components (from the left: sensors, actuators, and structural supports) can be combined in a variety of ways to create thin fabric-based machines.

Below, we detail the design and optimization of functional fibers as actuators, variable-stiffness (VS) components, and sensors. We then describe the integration of these functional fibers into robotic fabrics that enable new capabilities, such as reactive wearables and deployable fabric structures.

Results

Actuation.

As of this writing, motion-generating fabrics have made only rare appearances in end-user products (20). However, as efforts are made to mimic the stranded muscular tissue in living animals, several different fiber-like actuators of varying utility have come to light (19, 21). Some of the more promising examples include shape-memory polymers (22), shape-memory alloys (SMAs) (23), conductive polymers (24), electromechanical twisted carbon nanotube yarns (25, 26), and supercoiled nylon strands (27).

We selected Nitinol SMA wire as our actuating fiber. SMA is electrically conductive and, when programmed to remember a shape, activates with heat. These two traits make electrical control via joule heating a simple process. SMA wire is usually shaped into a coil or mesh to allow for high-strain linear contraction (23, 28, 29). We instead utilize SMA wire to generate bending motion (Fig. 2A and SI Appendix, Fig. S1), which has typically only been demonstrated using large SMA panels bent into “hinges” (30, 31). Bending allows the SMA wire to actuate “in-plane” with the fabric substrate (Fig. 2B) and facilitates reversible antagonistic motion when paired with an actuator on the opposite side of the fabric. Bending wire actuators can also be easily anchored to fabric by couching (Fig. 2C)—a well-established sewing technique.

Fig. 2.

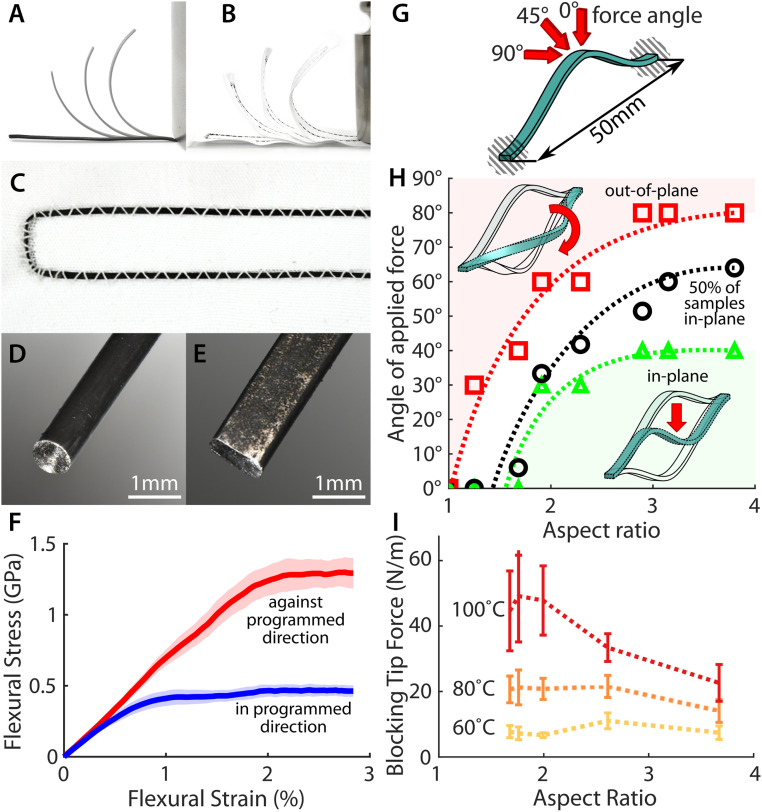
SMA actuators. (A) SMA ribbon programmed to exhibit bending motion. (B) Sewn SMA ribbon used to actuate fabric body. (C) Couching method to affix SMA ribbon to a fabric substrate. (D) Initial round SMA wire. (E) Flattened SMA ribbon. (F) Bending an SMA against its programmed direction induces higher flexural stress and encourages the wire to twist instead. Error cloud is 95% confidence interval. (G) Round and flattened wires were subjected to forces at increasing out-of-plane angles to determine bending response. (H) A flattened ribbon will tend to bend and buckle in plane (green) and a round wire will tend to twist and bend out of plane (red). (I) Round SMA actuators tend to generate higher bending force than flattened actuators of comparable cross-section. Error bars are one SD.

One challenge when integrating antagonistic wire bending actuators into a highly flexible fabric is that any off-center forces encourage the wire to twist the fabric rather than purely bend. This contortion can introduce chaotic actuation or even bending opposite the intended direction if the wire turns over within its couching. We overcame this challenge by flattening the round SMA wires (Fig. 2D) into ribbons (Fig. 2E), modifying the area moment of inertia such that bending is favored over twisting. Additionally, the couching is able to hold a flattened ribbon tighter to a fabric base, preventing the actuator from overturning.

To elucidate the cause of twisting we studied bidirectional actuation of fabric, where SMA ribbons are used in antagonistic pairs. When its opposing actuator is active, an SMA ribbon is forced to bend backward against its programmed actuation trajectory, building up a spring response within the ribbon. Three-point bending tests revealed that the flexural modulus of our SMA ribbons is consistent regardless of bending direction (E ≈ 66 GPa); however, plastic deformation occurs at different stresses depending on the bending direction (Fig. 2F). We surmise that it is this difference in maximum stress that often encourages a wire to twist such that it is again bending “forward,” avoiding excessive buildup of elastic energy.

We characterized the effectiveness of the flattening treatment by measuring the tendency for SMA wires and ribbons of various aspect ratios to remain in the desired bending plane in response to an external force. We clamped the SMA specimens in a prebuckled configuration and applied a force to the center point at different incoming angles (Fig. 2G). At an applied force angle of 0°, the wire is expected to experience a snap-through, remaining fully in-plane as it deflects. Conversely, at an angle of 90°, the wire should twist out of plane about the fixed-fixed axis. After recording the dominant behavior (in-plane or out-of-plane motion) for intermediate force angles, the results confirm that by increasing the wire aspect ratio (flattening the wires) they become more resistant to out-of-plane forces and favor in-plane deflection (Fig. 2H).

“Activated” (heated) SMA generates force by building up internal material stresses as its crystalline structure transitions from martensite to austenite (23). Given that stresses in bending are greatest on the outer surface, we would expect that regions farthest from the neutral axis contribute most to the bending force. That is, thicker wires generally provide larger output forces than thin ribbons of similar cross-sectional area (Fig. 2I). Indeed, we see that for flattened wires the output force is linearly proportional to the area moment of inertia (SI Appendix, Fig. S2). However, round wires underperform in this regard, reaching a force-output plateau due to actuation forces being directed out of plane.

As mentioned, when bending in the direction of programmed actuation, plastic deformation occurs at a relatively low stress, which is mostly a result of reversible detwinning of the martensitic crystal lattice (23). In the reverse direction, it is possible to introduce permanent dislocations and microcracks into the ribbon that interfere with the austenite–martensite transition and adversely affect the programmed actuation (32, 33). The point at which this damage occurs is determined by the material flexural strength (SI Appendix, Fig. S3A), although measured strength seems to be influenced by the processing steps and was not constant across SMA aspect ratios (SI Appendix, Fig. S3B). We maximize the lifetime of our actuators by avoiding this overstrained regime except for the initial unwrapping and straightening of the ribbon in preparation for the sewing step. By also avoiding excessive temperatures, we have continuously used our antagonistic actuators for upwards of 1,000 cycles with no noticeable degradation.

Given this characterization, we selected an SMA ribbon aspect ratio of 2.5 for all further demonstrations, as it provided a reasonable balance of output bending force, system stiffness, and stable in-plane motion. At 100 °C, the blocked force of our selected SMA ribbon reaches ∼33.3 N/m, about 1/14 the average blocked bending force of a human index finger, ∼480 N/m (34).

VS Support Structure.

Although a fabric might be equipped with locally reliable actuators, its inherent lack of a supportive structure limits control of the overall robot configuration. By actively softening and stiffening our VS fibers, we can regulate the direction and degree of actuation with higher repeatability and fewer total actuators. In addition, an on-demand support structure allows a robotic fabric to perform move-and-hold operations to sustain loads which would otherwise collapse a typical fabric. VS is possible using many different techniques (35, 36), but expressions of this concept in fiber-like morphologies are limited. The most successful examples include silicone tubes filled with a low-melting-point material (37, 38), strands of glass-transition polymer (39, 40), segment jamming via tension in an axial wire (41, 42), and the use of antagonistic actuator pairings (43).

Our VS fibers (Fig. 3 A–C) are based upon a thermally responsive epoxy that softens significantly as it undergoes a glass transition over the range of 45 °C to ∼60 °C (44) (Fig. 3 D and E). We also incorporate a low-melting-point metallic alloy particulate filler (Field’s metal; FM) (45) at a volume ratio of ∼85:100 (46 vol % FM), which increases the rigidity of the VS fibers when cold yet melts at 62 °C to further soften the material when heated (Fig. 3 F and G). The fibers are joule-heated via an internal conductive stainless-steel thread (Fig. 3 E and F).

Fig. 3.

VS fibers. (A) A shaped VS fiber supports a 20-g load. (B) VS fiber sewn onto a fabric substrate. (C) A VS fiber tethered by fabric is prevented from buckling outward, increasing support up to 50 g before legs begin slipping. (D) Neat epoxy VS fiber. (E) Neat epoxy cross-section. (F) FM composite cross-section. (G) FM composite VS fiber. (H) Hot and cold flexural modulus for both the neat epoxy and FM composite (46 vol % FM), with and without stainless steel yarn core used for joule heating. Error bars are SD. (I) Ultimate flexural strength of the VS fibers. (J) Measured thermal conductivity of the composite vs. volume percent of FM, compared with Bruggeman effective medium theory. Error bars are 95% confidence interval. (K) Free convection cooling of VS fibers. Experimental data are for neat epoxy specimens. Numerical simulations for both neat epoxy and FM composite had negligible difference (error cloud represents 95% CI). (Inset) Computed cross-sectional thermal gradient for both 0 and 50 vol % FM fibers after 7 s of cooling from 65 °C. (L) Numerical simulation results for a “worst-case” heating scenario, with the heating core center offset to two-thirds of the VS fiber diameter. (Inset) Computed cross-sectional thermal gradient after 6 s of heating at 13 W/m.

We measured the flexural moduli of fibers made from both the neat epoxy matrix and the FM composite over a range of temperatures (Fig. 3H). The addition of FM raises the maximum rigid modulus while lowering the heated (i.e., soft) modulus (45). Even with the addition of the flexible stainless-steel core in the fiber, the lower stiffness bound remains below 25 MPa, which is slightly less flexible than latex rubber and, when in fiber form, is well matched to the output force capabilities of our SMA actuators. While the addition of FM enables an increased modulus range, the FM composite has a lower ultimate flexural strength than neat epoxy, which may be due to poor bonding at the interfaces between epoxy and FM particles (Fig. 3I and SI Appendix, Fig. S4).

Because the response of a thermally responsive fiber is time-dependent, characterizing the time to completely transition between rigid and soft states is crucial for effective control sequencing in robotic fabrics. We measured the thermal conductivity of the VS composite fiber, and as expected when compared to analytical models the increased volume fractions of FM lead to increased thermal conductivity (Fig. 3J). We then developed a numeric heating and cooling simulation of the VS fibers under a wide range of material conditions and compared it to experimental data (SI Appendix, Figs. S5–S9). Fully cooling to room temperature from a uniform 65 °C in free convection takes ∼70 s regardless of FM content (Fig. 3K), although after only 20 s the fiber reaches below 45 °C and the glass transition is safely complete. Attaching the fibers to fabric interferes with this cooling process, and VS fibers used in the demonstrations below were consequently allowed an additional 20 s to ensure complete glass transition (SI Appendix, Fig. S10). On the other hand, heating times varied slightly depending on the material composition and whether the steel heating yarn was properly centered in the fiber (Fig. 3L). Notably, the increased thermal conductivity from the FM inclusions smooths the thermal gradient in the fiber, reducing hot spots which could result in premature material degradation and cold spots with incomplete phase transitions (Fig. 3 K and L).

With these results, we selectively use both the neat and composite VS fiber formulations depending on the use case, favoring higher rigidity and reduced deflections with the FM composite or higher strength and robustness with the neat epoxy.

Sensing.

An important part of any robot is the ability to sense internal or environmental changes and respond appropriately. To create sensors, we used a self-coagulating, paintable conductive ink, which allows a region of fabric to become highly sensitive to small changes in strain while adding negligible stiffness to the fabric (46). Composed of a polydimethyl-siloxane (PDMS) precursor emulsified in a carbon black nanoparticle/ethanol suspension, this ink can easily permeate and bond to individual filaments of a fabric (Fig. 4 A and B). Penetration into the fiber weave itself maintains much of the porosity of the fabric (Fig. 4 C and D) and creates an electrically conductive pathway that changes in resistance as the fabric weave is stretched and the gaps present between fibers are enlarged (Fig. 4E).

Fig. 4.

Conductive ink sensors. (A) The carbon black/PDMS/ethanol emulsion is printed directly onto the fabric. The surface conductivity is sufficient such that printed sensor blocks can be electrically connected by sewing over them with conductive thread. (B) A microscope image of ink-coated knitted spandex fabric. (C) Porosity measurement of neat, unstrained fabric. (D) Porosity of inked fabric. (E) Porosity of inked fabric after stretching. (F) A simple actuator-sensor device curls up and down, generating a sensor signal dependent on device curvature. (G) The curling device follows the control signal by modulating the power output to the SMA actuators. Each sensor is actively used only when the corresponding fabric face is in extension.

By printing this ink on opposite faces of a fabric, sensors can be used to detect structural bending. Despite some permeation through the cloth, the printed face will have a higher density of conductive material, and this small offset from the neutral axis is enough to bias the sensor toward a compression response in one bending direction and extension in the other. The sensor signal is most consistent in extension, so querying the corresponding sensor depending on bend direction leads to repeatable sensor values.

In Fig. 4F we show a section of fabric with these printed sensors and two antagonistic bending SMA ribbon actuators attached via couching. The sensor feedback made it possible to control the fabric actuation and hold different curvatures (represented as target sensor signals; Fig. 4G and Movie S1). Without VS elements, the device naturally relaxes into a neutral center position when neither actuator is active due to a balance in opposing spring forces in the SMA ribbons.

Applications.

We present a series of demonstrations that utilize the SMA ribbon actuators, VS fibers, and in-fabric strain sensors, suggesting a range of possible applications for robotic fabric.

First, we showcase a robotic fabric tourniquet (Fig. 5A and Movie S2). This device comprises a breathable fabric sleeve with embedded rows of parallel ribbon actuators, VS fibers, and conductive carbon ink traces. When the fabric is severed along one of the conductive carbon ink traces, the damage is detected as a broken circuit and an emergency response is triggered at the damage site. The fabric will compress and then hold that position without further power expenditure (Fig. 5 B–D). The bending motion of the SMA ribbons is suited to compressive actuation by squeezing from a circle to a pinched, “clover-like” configuration (Fig. 5 B, Inset), rather than circumferential contraction. Each SMA ribbon was measured to contribute ∼1.6 ± 0.1 kPa, which approaches the recommended arm cuff pressure of ∼2 kPa to combat orthostatic hypotension (47). We expect that further developments and an increased actuator count may achieve the higher pressure of ∼26.6 kPa that is recommended to properly cut off blood flow (48). The current implementation is able to soften, constrict, and stiffen at one damage site over a course of 100 s, consuming ∼415 J in the process. This type of responsive sleeve could potentially be used as a smart garment in military or exploratory environments, where automatic emergency measures could counteract life-threatening situations if medical aid is not immediately available. By altering the arrangement of actuators, sensors, and VS fibers, it is conceivable that other types of assistive wear could also be created, such as clothing that augments muscular motion, provides dynamic orthostatic pressure, or even simply changes shape to fit different climate conditions.

Fig. 5.

Robotic fabric demonstrations. (A) Robotic fabric tourniquet. (B) Tourniquet is buttoned about a foam body. It reacts to a damaged circuit by contracting and holding a tightened “clover-shape” pose. (C) Thermal image of the tourniquet as VS fibers soften. (D) Thermal image of activated SMA actuators constricting. (E) Robotic fabric “pop-up” table. (F) From an initial flat state, the table is able to stand up, stiffen into a load-bearing platform, and then collapse under a load as it softens and actuates back into its initial flat configuration. (G) Fabric “pop-up” table is ∼2 mm thick. (H) Activation and softening of table “leg” VS fibers. (I) Activation of SMA actuator wire, causing table to stand up. (J) Robotic fabric wing in self-stowed position. (K) Robotic fabric wing curls and uncurls from deployed, open state into a compacted, stowed state. (L) Robotic fabric wing in deployed position. (M) Activation and softening of wing VS fibers. (N) Activation of curling SMA wires.

Second, we demonstrate a shape-changing robotic fabric sheet that functions independently from any host body (Fig. 5 E and F and Movie S3). The initial form of this device is a flat, square section of cloth (Fig. 5G). Upon activation, the device softens its VS frame and lifts itself up into a table-like platform structure. This new shape becomes rigid and load-bearing, supporting a 50-g weight on the platform with little deflection, while the legs begin to buckle apart somewhat under a 100-g weight. The shape is then softened and returned to its initial configuration via an antagonistic ribbon actuator, which flattens the device again (Fig. 5F). Each complete shape change (soften, actuate, and stiffen) takes 90 s to complete, consuming ∼830 J. Carrying its own 50-g battery (11.1 V, 650 mAh), this robotic fabric could theoretically perform ∼25 such shape changes on a single charge. By choosing not to soften certain VS fibers, such as the central VS ring (Fig. 5 H and I), the actuation motion and subsequent shape is influenced. This signifies that even complex transformations may be possible with reduced component counts by leveraging actuators and VS components in concert. Further, the continuous curvature displayed by this machine sets robotic fabrics apart from origami-inspired machines (49), as the range of transformation and conformability is not limited by discrete folds. While this demonstration could be a preliminary version of a self-deploying shelter or load-bearing furniture, the shape-change ability demonstrated is also an early indication of the potential for extremely adaptable, independent machines with on-demand tool generation.

Last, taking inspiration from the fabric wings of the 1903 Wright Flyer, we demonstrate a self-deploying airplane wing in a fully untethered system (Movie S4). The robotic fabric wings are seated into small slits in the side of the fuselage, wherein all additional circuitry, microcontrollers, and batteries are enclosed. The fabric wings curl to wrap around the fuselage for compact storage (Fig. 5J) and uncurl into a deployed, rigid state with wings extended (Fig. 5 K–N). Each complete shape change (soften, curl or uncurl both wings, and stiffen) takes 160 s to complete, consuming ∼2,550 J. The 11.1-V, 1,200-mAh rechargeable battery used supports up to 47 shape changes with these energetics on a single charge. This demonstration shows the ease of integrating robotic fabric with rigid machinery, allowing fabric-based components that can self-stow or move out of the way when not in use. This is a key functionality for use cases when light weight and low storage volumes are highly desired, as in transportation to and from remote locations or in space exploration.

System Design Considerations.

As a planar structure, the mass of a robotic fabric unit will scale linearly with its length and width, assuming uniform distribution of functional fiber components. This is not an issue for the SMA ribbon actuators, as they exhibit a constant bending force along the length of the actuator, meaning a long actuator ribbon can curl up just as easily as a short ribbon. However, the support structure provided by VS fibers will be limited in this regard. Following Euler–Bernoulli beam theory, a cantilevered section of fabric of length $L$ and weight $w$ will induce high bending moments at the fixed end proportional to $L^2$ following $M=w{L}^2/2$, while deflection at the tip will increase proportional to $L^4$. With a weight of 2.16 g/m, a single rigid epoxy fiber could only sustain its self-weight up to 2.29 m before surpassing its ultimate flexural strength. For reference, the self-deploying airplane wings above have a wing length (cantilever length) of 130 mm, which exhibits minimal deflection in the extended position. An FM–epoxy composite fiber with its higher weight of 8.01 g/m would only support itself for 1.55 m. It is more likely, however, that an unsupported cantilever structure would become unbalanced before that occurred. For these reasons, it is encouraged that robotic fabric structures have a firm support on both ends of large extended regions, which will increase the viable length by a factor of 6 $\left(M=w{L}^2/12\right)$. Of course, the weight of all other components must be included when considering this step (2.51 g/m for SMA ribbons and 0.073 g/m for 10-mm-wide strips of cotton fabric).

Increased fiber lengths also require more power for full activation. Both the SMA ribbons and VS fibers are driven by joule heating, which requires power that scales linearly with length. In our case, our selected SMA actuators were powered at a rate of 25 W/m, and VS fibers were powered at 8.2 W/m. In addition to consuming more power, the higher voltages needed to maintain the appropriate current might be difficult to reach without a larger power supply. For this reason, it may be useful to split long fibers into multiple shorter fibers that can act in parallel and are only as long as necessary to affect their local region before powering down.

As both the SMA actuators and VS fibers are thermally responsive, it is important to avoid any thermal cross-talk to prevent unwanted activations. Observation of powered SMA ribbons up to 120 °C reveals that the adjacent fabric region drops to below the glass transition threshold of VS fibers at a distance of ∼3 mm on either side (SI Appendix, Fig. S11). Maintaining this 3-mm separation between functional fibers prevents the VS fibers from prematurely softening, as shown in the parallel fiber arrangement of the tourniquet demonstration. When components must cross, as in the shape-changing table demonstration, we have found that placing them on opposing faces of the fabric, or inserting a small snip of painter’s tape at the junction, is enough to thermally isolate the fibers. Our selected sensor material is also susceptible to temperature effects, exhibiting an increase in resistance approaching 5% at 125 °C (SI Appendix, Fig. S12A), although in practice, as in the controlled bending fabric example (Fig. 4F), if the sensor is placed at least 3 mm from any heated fibers the sensor temperature will not exceed ∼36 °C, which corresponds to a resistance change of only ∼0.9% (SI Appendix, Fig. S12B). Further, full enclosure of thermally responsive fibers inside the fabric should also be avoided to minimize cooling times.

Discussion

By treating fabric as the foundation of a robot, it can be enhanced from a passive material to smart adaptive clothing, self-deploying structures, or lightweight shape-changing machinery. We expect that with time scientific advances will unveil improved actuation, VS, and sensory technologies that are ideal for future robotic fabric developments. By leveraging well-established textile manufacturing process, we envision that the future will bring mass-produced rolls of robotic fabric, available for purchase, and programmable as-required to fit varied tasks. Self-reconfiguring machinery made from this material could bend and twist into new and complex shapes as needed and then collapse for compact storage.

Of course, there are still many hurdles to overcome before robotic fabrics reach their full potential. For wearables, washability and heat dissipation will be important. The added rigidity and bulk of specialized fibers could also make wearable robotic fabrics uncomfortable or difficult to don and doff. Additionally, thermally controlled materials typically have slow cycle times and are power-inefficient, which leads to increased battery size. Future work will also require advancements in other areas, such as the development of practical simulation and design tools for fiber placement optimization, robust thin-body controls, and even lightweight embedded power supplies. With this in mind, we hope that our early step toward robotic fabrics can inspire many more future advances in a field with so much potential.

Materials

Antagonistic Actuating Fiber Manufacture.

Flattening shape memory wire.

After annealing Nitinol wire (McMaster-Carr) at ∼500 °C and allowing it to air-cool it becomes ductile enough to allow incremental flattening via a simple manual rolling mill machine. The wire undergoes significant stress hardening during this step, so the annealing and pressing process is repeated as often as necessary until a wire of the desired thinness is obtained. A final annealing and pressing step is performed at the same thickness to firmly lock in the new cross-section by counteracting any shape loss that may occur due to residual shape-memory effect. The wire will experience some amount of elongation as it is flattened, and consequently the total wire cross section area is reduced slightly. All plotted data involving the Nitinol wires is normalized to account for this change in cross-section area.

Programming shape memory wire.

SMA wire is first annealed at 500 °C for 15 min and allowed to air-cool, making the wire malleable and easy to form into the desired shape. The wire is then tightly wrapped about a 3.175-mm (1/4 in)-diameter 316 stainless steel rod, with the ends clamped using split shaft collars (McMaster-Carr). The entire fixture is then heated to 390 °C for 15 min (50) and then quenched in room-temperature water. The heating and quenching process is repeated three times. At this stage, the wire is unclamped and unwrapped from its coiled shape and straightened. Application of heat to this wire will cause it to return to its tightly coiled programmed shape (SI Appendix, Fig. S1).

VS Fiber Manufacture.

FM particle preparation.

FM particles are created by melting the metal in warm water and agitating vigorously. A block of FM (Roto144F; RotoMetals) is weighed out to 60 g; 150 mL of deionized water is added to a 500-mL beaker and the FM is placed inside. A silicone oil bath is heated on a hot plate with a magnetic stirring rod up to 90 °C, and the 500-mL beaker is supported inside the silicone oil bath such that the water level is below the surface of the oil. The water is allowed to warm for ∼15 min until it settles at ∼70 °C and the metal is fully melted. At this stage, a mechanical homogenizer (VDI25; VWR) with a 20-mm-diameter attachment and a vortex generator (RW16; IKA-werke) with a 42-mm-diameter turbine attachment are placed into the water on opposite sides of the beaker. The beaker is tilted slightly such that the heavy metal will flow downward toward the homogenizer rather than gathering at the edges of the beaker. At this point, the homogenizer is turned on to a speed of 24,000 rpm and manually swept through the mixture for several seconds so as to initially break up the mass of metal which is held together by surface tension, dispersing it into the water. The homogenizer is turned off and then fixed in place. With both instruments in position, the homogenizer is again turned on to a speed of 24,000 rpm to further break up the melted particles, and the vortex generator is turned on to a speed of 1,200 rpm, which keeps the metal in motion and prevents it from settling and agglomerating. This agitation is applied for 10 min.

Next, the beaker is quickly raised out of the hot silicone oil bath to cool. The vortex generator remains on to keep particles in motion until they have cooled solid, but the homogenizer is turned off so as not to shatter the solidified particles, creating unpredictable particle geometries and sizes. The mixture is allowed to cool for ∼15 min until its temperature is well below the freezing point of FM (<∼50 °C), at which point the vortex generator is turned off and the mixture is allowed to settle. After several hours, the majority of the particles will have settled to the bottom of the beaker, and the supernatant is extracted via syringe (rather than pouring) so as not to disturb the small particles. The remaining particle sediment is then stirred and “fluffed” to minimize any cementing during the drying process. The particles are dried in a vacuum oven at 60 °C to remove as much of the remaining moisture as possible. The resulting dry material may clump together like sandstone and need to be shaken apart. The resulting material has a fine, sand-like appearance.

Epoxy preparation.

The stiffness-changing epoxy is created by combining an epoxy curing agent, Jeffamine D400 (Huntsman International, LLC), with a standard epoxy resin, EPON 828 (Momentive Performance Materials Inc.) at the stoichiometric ratio of 58:100 by weight, which maximizes the rigidity of the resulting cured epoxy when in the solid state. After stirring lightly by hand, the epoxy mixture is placed in a vacuum chamber for 15 min to remove any trapped air. The epoxy can then be used as is or mixed with particles of FM for an amplified stiffness-change behavior. The desired amount of FM is measured out by weight then poured into the epoxy and stirred by hand until thoroughly dispersed.

Fiber preparation.

The VS fibers are formed by first threading a strand of conductive steel yarn (Adafruit Industries) through a section of silicone tubing (McMaster-Carr) cut to the desired fiber length, with an inner diameter of 1.58 mm (1/16 in). This can be eased by first lubricating the tube with isopropyl alcohol and feeding in a long segment of rigid wire such as copper or nickel and then pulling the yarn through behind it. Both ends of the steel yarn are crimped with 1.5-mm-diameter noninsulated ferrules (McMaster-Carr) in such a way that the ferrules are recessed slightly inside the silicone tubing, keeping the steel yarn taut and discouraging leaking in the next step. This also provides a reliable electrical access point, since liquid epoxy will tend to wick up the steel thread, creating insulating surface that would otherwise make the steel thread inaccessible.

If no FM is used, the prepared epoxy can be injected directly into one end of the tubing using a syringe with an 18-gauge needle tip until the entire tube is filled. Otherwise, the epoxy–FM mixture will need to be continuously heated to melt the metal particles and allow it to flow through the tubing. This can be done by filling a large glass beaker (500 mL) with boiling water. A syringe is filled with the epoxy–FM mixture and affixed with an 18-gauge needle. After holding it under the hot water for several seconds until the mixture begins to flow inside, any excess air is expelled. The syringe can then be removed from the water and the needle is inserted into one end of the tubing. The steel yarn and crimp can be pulled out slightly on that end to allow the needle to fit and gain an airtight seal. The entire tubing and syringe assembly is then placed inside the hot water and allowed several seconds for the metal to melt again. At that point, the syringe is held with the nozzle pointing down and the material is injected until the entire tube is filled. If the syringe is held upright, the metal particles will settle to the back of the syringe and will not be expelled into the tube. The steel yarn and crimp are then reseated as needed in each end.

The filled tubes are placed into an incubator at 60 °C for 12 h for final curing. It should be noted that the working time of the epoxy can be up to a full day at room temperature, but only 30 min when submerged in boiling water. Finally, the silicone tubing can be cut away and the individual 1.59 mm (1/16 inch) diameter VS fibers can be removed. The conductive crimps can then be soldered to or inserted into a second crimp for electrical connection to the robotic fabric circuitry.

Conductive Strain-Sensory Ink Manufacture.

The conductive ink exploits conductive nanoparticles to stabilize a PDMS/ethanol emulsion. The conductive ink is made by first adding 0.705 g carbon black (Blackpearl 2000; Cabot) in 100 mL ethanol (15% by weight). The mixture is sonicated at 70% amplitude for 3 min, with a 1-s on/1-s off pulse using a tip sonicator (QSonica Q700) to break up carbon black aggregates. After sonication, 4 g of PDMS precursor (SEMICOSIL 964; Wacker) is added to the carbon black/ethanol mixture, and an identical sonication pulse is applied to emulsify the resin, creating a Pickering emulsion with precure PDMS particles stabilized by a carbon black particle “shell” at the surface. Upon completion, the emulsion is moved into a syringe where it can be expelled by hand or inserted into an extrusion printer for sensor fabrication.

This Pickering emulsion-based ink contains ∼2-µm droplets suspended in a nonviscous carrier solvent that evaporates upon deposition. The small droplets (which form the conductive composite) penetrate the fabric via the fiber-interstitial spaces, but some are also filtered by the fibers. As a result, the printed ink is thicker on the receiving side, while droplets that penetrated into the fabric enhance sensor-to-fabric adhesion and promote coating of individual fibers. We repeated the printing process three or four times on the same side of the fabric, further increasing the sensor thickness on that side and ensuring it is biased toward one bending direction. The applied ink cures in ∼1 h.

Methods

SMA Twist Vs. Bend Behavior Testing.

We characterized the tendency for SMA wires and ribbons to bend or twist out of plane in the presence of opposing forces. This is particularly useful data for the case where opposing antagonistic actuators are affixed to the fabric on opposite faces of the same cloth region. When the wires are round, the actuating wire will tend to force the opposing wire to flip over in its couching and bend in the same direction, which generally ruins subsequent actuation cycles and can even tangle nearby fiber components in the resulting chaotic fabric warping. For the remainder of this section, we refer to both round SMA wires and flattened SMA ribbons as simply “wires” with varying aspect ratio.

In this test, we clamped both ends of the SMA wires in a custom fixture, with clamps spaced 50 mm apart and the wire length at 52 mm. This placed the wires into a prebuckled configuration, as in Fig. 2G. All wires were clamped tightly enough that they could not rotate. Next, force was applied at a constant rate of 0.5 mm/s to the wire center point using a materials tester (Instron 3345). The bending state of the wires was observed by eye to determine whether snap-through had occurred by the time the testing tip had reached the midway point, in line with the fixed wire ends. If so, the specimen was marked as ultimately bending “in plane,” and if not, the wire had instead twisted a full 90° and was marked as “out of plane.” The fixture was designed to be attached to the Instron at different angles, allowing the force to be applied at differing angles relative to the snap-through direction of the wire. At an angle of 0°, parallel with the bending direction, the wire is expected to experience a snap-through as the beam is deflected (Fig. 2H, green region). Conversely, at an applied force angle of 90°, the wire should only twist about the fixed-fixed axis (Fig. 2H, red region). As the wire buckles in plane, the moment arm for twisting becomes smaller, while similarly as the wire twists out of plane the angle of force becomes aligned more directly toward further twist. Eventually, one of these two cases dominates. With increasing aspect ratio, the maximum angle of applied force where the in-plane snap-through still dominates also becomes larger, while smaller aspect ratios can occasionally twist even at very low angles of force (Fig. 2H). Therefore, with higher aspect ratio, an actuating ribbon will be more resistant to out-of-plane forces or slight misalignments, and will more consistently bend in plane with its paired antagonistic actuator rather than twisting around into a more favorable low-energy configuration.

SMA Bending Stiffness Testing.

Specimens of SMA ribbon of varying aspect ratio were measured in a 30-mm three-point bending setup on a materials tester (Instron 3345). The test provided bending stiffnesses of the ribbon through the equation $F=48dEI/L^3$ for an applied force $F$, deflection $d$, three-point support spacing $L$, flexural modulus $E$, and area moment of inertia $I$. The bending modulus was measured for ribbons in both the “forward” bending direction (in the direction of programmed curling actuation) and in the “reverse” direction (against the programmed actuation) by orienting each ribbon face up or face down as required. It was found that regardless of bend direction or ribbon aspect ratio, the flexural modulus was approximately equal at ∼66 GPa.

Each test was allowed to continue until plastic deformation was reached, detected by a plateau in the force-displacement curve. The yield stress determines the point of plastic deformation onset, and follows the formula ${\sigma }_{\text{flex}}=\left(F_{yield}L/8\right)\left(t/I\right)$ for yield force $F_{yield}$, three-point support spacing $L$, wire thickness t, and area moment of inertia I. Interestingly, while the flexural strength is nearly constant in the forward direction across SMA aspect ratios, the antagonistic flexural strength is not (SI Appendix, Fig. S3A). Additionally, since the bending moment of inertia is related to the flexural strength by ${\sigma }_{\text{flex}}=Mt/2I$, and the wire radius of curvature $R=EI/M$, we find the minimum radius of curvature before failure to be $R=Et/2{\sigma }_{\text{flex}}$. Notably, when using our experimental values for antagonistic flexural strength and wire thickness in this equation, we find that when forced to bend against their programmed curling direction, SMA actuators of all aspect ratios undergo plastic deformation at the about same radius of curvature, ∼12 mm (SI Appendix, Fig. S3B). This may indicate some atypical response due to stress-induced austenite–martensite phase transition behavior (51) that is dependent on the programmed shape, as each SMA ribbon was programmed to the same initial radius of 3.175 mm.

SMA Blocked Bending Force Testing.

To characterize the effect of SMA wire/ribbon cross-section on actuation force, we measured the blocked bending tip forces of several simple actuating fabric specimens on a materials tester (Instron 3345). Each fabric specimen consisted of a long SMA wire/ribbon of the aspect ratio to be tested, bent into a U-shape and sewn into a section of muslin fabric (Fig. 2C). This U-shaped wire was programmed such that the two parallel legs of the wire/ribbon bend in the same direction, lending the actuator some stability. The specimens were clamped on the end to provide an 8cm actuator arm, with the bend of the “U” positioned beneath the Instron probe. Specimens were supplied with increasing steps of electrical power, and the steady-state blocked force was recorded at each level. SMA temperature was also recorded after each plateau using a thermal camera (Fluke TiX 580). The data displayed in Fig. 2I and SI Appendix, Fig. S2 were normalized to account for any reduction in cross-sectional area that arose due to wire elongation in the flattening process.

Operating within the linear elastic region during antagonistic actuation, the remaining force $F_{rem}$ available to perform work on the environment will be the difference between actuating force $F_{act}$ and the force required to bend the antagonistic wire $F_{ant}$. Because both actuation force and antagonistic bending stiffness are linearly proportional to the wire’s area moment of inertia (i.e., $F_{act}=\alpha I$ and $F_{ant}=\beta I$ for some constant values $\alpha$, $\beta$ and moment of inertia $I$), we find that $F_{rem}=F_{act}-F_{ant}=\alpha I-\beta I=\left(\alpha -\beta \right)I$. Therefore, increasing the area moment of inertia should lead to a higher residual force to perform work. On the other hand, the bending stiffness of the system will depend on the rigidity of individual wires $\left(EI\right)$. For a robotic fabric, it is somewhat desirable to retain a measure of flexibility, meaning that there is a trade-off that must be made between working force and system softness.

VS Flexural Modulus Measurement.

The flexural moduli of VS fibers made from both neat epoxy and the FM composite were measured using a dynamic mechanical analyzer (DMA Q800; TA Instruments). Specimens were cut from lengths of VS fiber to dimensions of 1.5875-mm diameter × 10 mm. Specimens were placed in a single‐cantilever clamp with a clamp separation of 4 mm. Assuming the two ends of the specimen are clamped and do not rotate, the specimen flexural modulus $E_f$ can be calculated from the measured force: $E_f=F{L}^3/12\text{δI}$, where $L$ is the length of the beam, $I$ is the area moment of inertia of its cross‐section, and $F$ is the force needed to deflect the beam a distance $\delta$. All specimens were applied a temperature sweep from 25 °C to 85 °C at a rate of 1.5 °C/min around the glass and melting transitions from 50 to 70 °C, and 3 °C/min everywhere else. Specimens were applied a sinusoidal force on the end of the cantilever at a rate of 1.0 Hz and a maximum deflection of 150.0 μm. Specimens were clamped with a torque of 1 in-pounds.

VS Ultimate Strength and Failure Strain Measurements.

The ultimate flexural strength of VS fibers was calculated from the stress-strain curves of both neat epoxy and the FM composite, as measured in a three-point bending setup on a materials tester (Instron 3345). “Cold” specimens were tested at room temperature with a span length of 130 mm, while “hot” specimens were tested after heating with a heat gun to an approximately uniform temperature of 70 °C with a span length of 70 mm. Each test was allowed to continue beyond plastic deformation until total material failure, and each parameter combination was tested at least five times. The average stress and strain values for each specimen set are plotted in SI Appendix, Fig. S4, and the average ultimate stress and ultimate strain values are plotted in Fig. 3I.

VS Thermal Conductivity Measurement.

The thermal conductivity of the VS materials was measured using the transient hotwire method as in ref. 52, in which an embedded wire acts as both a resistive heat source and temperature sensor. Under a brief application of current, the wire measurably increases in resistivity as its temperature rises, with the magnitude of change dependent on the thermal conductivity of the surrounding material. Because of the high density of FM, the particles tend to settle while the epoxy cures over a 12-h period. To promote composite homogeneity, experimental samples were cured on a rotating fixture. These measurements appear to track the prediction supplied by the Bruggeman effective medium theory (Fig. 3J), using the thermal conductivities of FM ($k=19\hspace{0.17em}W\cdot m^{-1}\cdot K^{-1}$, approximated from ref. 53) and our own measured value for neat epoxy $\left(k=0.21\hspace{0.17em}W\cdot m^{-1}\cdot K^{-1}\right)$. Discrepancies between the experimental and analytical values here may be due to small amounts of residual particle settling or clustering around the platinum wire resulting in a higher local density of FM than calculated.

VS Heating and Cooling Measurement and Modeling.

To validate the numerical simulation of the heating and cooling of the VS fibers, a physical experiment was set up with a representative fiber suspended between two clamps. This fiber, composed of neat epoxy and a core stainless-steel yarn was joule-heated, with an infrared (IR) camera (Fluke TiX 580) recording a video of the external temperature across the suspended fiber. The fiber was heated using a range of powers (4.6 to 32.8 W/m, equivalent to 0.3 to 0.8 A of current from the power supply) and was allowed to cool down to room temperature between each heating test (SI Appendix, Fig. S5). Each heating rate was run four times to provide error data.

Heating and cooling data were extracted from the captured IR video using a native pixel-to-data exporter built into the IR camera processing software (Fluke SmartView), for each frame of the video. Data were analyzed only around the midsection of the fiber (see boxed region in SI Appendix, Fig. S5) to reduce the error introduced by conduction cooling through the clamps on the fiber ends. From the region of interest, the data for each frame was recorded with a timestamp, maximum temperature, minimum temperature, and average temperature down the center of the fiber across the whole region of interest. It is important to note that because the steel yarn sometimes did not remain fully centered within the VS fiber during manufacturing, the whole fiber did not heat evenly, but instead had warmer and cooler sections. However, during cooling, these warm/cold spots rapidly smoothed out until the maximum and minimums were equivalent to the average temperature on the fiber.

SI Appendix, Fig. S6 shows the average temperature across the region of interest of the fiber as it increased over time during the heating of the fiber. Each of the curves is the average of all tests run at each of the power inputs. For the most part, the data follow the logical conclusion that higher power inputs resulted in faster heating times. However, near the highest power inputs the data begin to run together. Additionally, all curves appear jagged and irregular, with the error bounds on the higher power inputs being much higher. Both of these oddities are artifacts of the IR camera’s limitations: The camera could only accurately record at a rate of nine frames per second of data, and this could occasionally be interrupted as the temperature rose beyond the current temperature scale and the camera performed an automatic recalibration on the temperature range. This resulted in the higher power regions sometimes having clipped initial data (they appear to start at higher temperatures; see SI Appendix, Fig. S6, Inset) and the more jagged averages. Regardless, the averages of the lower temperatures provided a large pool of data from which to evaluate the quality of the numeric simulation.

SI Appendix, Figs. S7–S9 show the time for the fiber to reach a specific temperature, at different power inputs, compared with the numerically computed time. The maximum and minimum temperatures were computed numerically by assuming the joule heating conduit is offset at two-thirds of the total fiber cross diameter to represent the steel thread being manufactured off-center. To compensate for calibration delays in the thermal camera when starting the heating cycle in the experimental data, the numerical data curves were truncated to start at the same temperature as the first recorded temperature of the experimental data. There is typically very good agreement between the numerical data and the experimental data for the average, maximum, and minimum values. Notable exceptions to this agreement occurred at in the observations of the maximum temperature at the highest power inputs—in which the temperature values changed so quickly that the data from the thermal camera are suspected to be a significant factor in this error. With this strong agreement spanning such a large range of power inputs and geometric constraints, we then moved on to observing the quality of the numerical model for predicting the cooling time.

As demonstrated in Fig. 3K, the cooling data for all of the different heating rates averaged out to nearly identical sets of curves, as recorded experimentally, regardless of heating rate or maximum temperature achieved. To compare the experimental data, we truncated the cooling temperature data sets to start at 70 °C, setting that time to t = 0 s and plotted the time for the fiber to cool down to 27 °C where the fiber would be fully solidified. This was sufficient for our purposed of confirming the validity of the numerical model, as it was close enough to room temperature that additional cooling required significantly longer times (due to the asymptotic nature of free convection heat transfer). To develop the numerical solution, we used the same material parameters used in the heating study and altered the geometry only in that we removed the “heating core” and simply treated the fiber as a single homogenous material. On doing this, the experimental data lined up neatly with the numerical data, validating the quality of our model (Fig. 3K). We note that Fig. 3K only showed the graphs starting from 65 °C as this is the temperature of interest for obtaining complete softening in the VS fibers, but the data starting at 70 °C still showed the same trend and agreement as is shown.

Further, we further tested the effect on cooling and heating times of integrating the VS fibers into cotton fabric, focusing on the transition from 27 °C to 70 °C in both directions. The addition of fabric on one side of a VS fiber hampers the effectiveness of free convection such that the cooling time is nearly doubled (SI Appendix, Fig. S10), but heating time is reduced somewhat except at low power inputs, where the fabric appears to wick away the heat. This behavior must be taken into account when determining actuation sequences to ensure the fiber can fully stiffen as needed.

Thermal Cross-Talk.

An unprogrammed, U-shaped SMA ribbon was couched into a section of fabric and suspended in the air at either end, such that the SMA was not touching any thermally conductive surface. The SMA was then joule-heated to 120 °C and held at that temperature for 2 min to reach a steady-state temperature profile in the adjacent fabric. The temperature was monitored with an IR camera (Fluke TiX 580). A temperature profile was generated using the IR analysis software (Fluke SmartView) showing that the temperature drops off to below 45 °C, the glass-transition onset point of the VS material, at a distance of ∼3 mm from the SMA ribbon center line (SI Appendix, Fig. S11), or about 2.5 mm from the ribbon edge. Thermally responsive fibers can be spaced at least 3 mm apart to avoid thermal cross-talk.

Sensor Response to Temperature.

A section of fabric prepared with a printed ink sensor was placed on a hotplate and heated to 125 °C. Resistance of the sensor was measured during this time while temperature was monitored with an IR camera (Fluke TiX 580). Within the operating temperature range of our SMA ribbons (100 °C), the maximum increase of the sensor resistance approaches 5% (SI Appendix, Fig. S12A), which can negatively impact sensor readings. In practice, if the sensor is placed at least 3 mm from any heated fibers the sensor temperature will not exceed ∼36 °C, which correlates with a ∼0.9% resistance change (SI Appendix, Fig. S12B).

Sensor Response to Curvature.

A section of fabric prepared with a printed ink sensor was wrapped about insulated tubing of various radii while the resistance was measured relative to the initial value. Around the tightest curve of radius 3/4 in, the sensor exhibited a maximal increase in resistance of 28% (SI Appendix, Fig. S12B). Measurements were repeated three times for each radius.

Sensor Controls.

In Fig. 4C we show a section of cloth with antagonistic bending SMA actuators attached, in conjunction with two small conductive ink traces printed on opposite faces. With the fabric device fixed at one end, it was able to curl up and down by cycling between the opposing actuators. The device naturally relaxed into a neutral center position when neither actuator was active due to a balance in opposing spring forces in the SMA wires. The bending motion was detected and measured by monitoring the resistance change in the sensor traces. Data were gathered after cycling the system through over 1,000 up-and-down curling cycles to remove any hysteresis in the sensors and fabric.

Tourniquet Cuff Pressure Measurement.

The SMA ribbons on the tourniquet were designed to pinch into a “clover” shape as seen in Fig. 5B, Inset, which allows compression actuation that is pure bending, rather than requiring linear contraction. As this type of actuation is nonuniform around the circumference of the tourniquet, we elected to measure the tourniquet cuff pressure using a dynamometer consisting of a soft rubber squeeze bulb affixed to a digital pressure sensor. This provides an approximate “average” pressure, as opposed to a local maximum at the points where the ribbon pinches inward. The tourniquet was positioned such that a single SMA ribbon was centered around the squeeze bulb, after which that single SMA ribbon was activated and allowed to constrict, producing sufficient force to significantly deform the bulb. Pressure measurements were repeated three times for each of the three wires, resulting in an average pressure of 1.6 kPa with an SD of 0.08 kPa.

Data Availability.

All data are included in the paper and SI Appendix.