Chaotic time series prediction using phase space reconstruction based conceptor network

Abstract

The Conceptor network is a new framework of reservoir computing (RC), in addition to the features of easy training, global convergence, it can online learn new classes of input patterns without complete re-learning from all the training data. The conventional connection topology and weights of the hidden layer (reservoir) of RC are initialized randomly, and are fixed to be no longer fine-tuned after initialization. However, it has been demonstrated that the reservoir connection of RC plays an important role in the computational performance of RC. Therefore, in this paper, we optimize the Conceptor’s reservoir connection and propose a phase space reconstruction (PSR) -based reservoir generation method. We tested the generation method on time series prediction task, and the experiment results showed that the proposed PSR-based method can improve the prediction accuracy of Conceptor networks. Further, we compared the PSR-based Conceptor with two Conceptor networks of other typical reservoir topologies (random connected, cortex-like connected), and found that all of their prediction accuracy showed a nonlinear decline trend with increasing storage load, but in comparison, our proposed PSR-based method has the best accuracy under different storage loads.

Introduction

Unlike traditional recurrent neural networks (RNNs), such as Long Short-Term Memory (LSTM), that use error backpropagation through time (BPTT) algorithm to train the network, reservoir computing (RC), another type of RNN, only uses the simple linear regression meethod to train its output weights, while other connection weights (like input weights, hidden weights) are fixed once initialized. Due to the advantages of high accuracy, fast training, and global convergence (Ding et al. 2005), some typical RC models, such as echo state network (ESN) (Jaeger and Haas 2004) and liquid state machine (LSM) (Maass et al. 2002), have been widely applied to time series prediction (Li et al. 2015; Ma et al. 2009; Jaeger et al. 2007; Li et al. 2016; Wang et al. 2019; Hu et al. 2020), pattern classification (Skowronski and Harris 2007; M E et al. 2009; Hu et al. 2015; Zhang et al. 2019), and anomaly detection (Chen et al. 2018; Mohammadpoory et al. 2019), and so on.

The core component of RC framework, the reservoir layer, which is generally initialized to be sparse-connected, large-scale and fixed-weight, plays the crucial role in the performance of RC. Jaeger et al. (2007) demonstrated that besides the connection weights, the structures of the reservoir also has a non-negligible influence on the computational performance of RC. Thus, RC models with differently-designed reservoir topologies have been proposed in these years, such as the reservoir with small-world topology (Deng and Zhang 2007), multi-clustered topology (Zhang et al. 2017), cortex-like topology (Li et al. 2015; Malagarriga et al. 2019) and the modular topology (Ma and Chen 2013). On the other hand, Zhang and Small (2006) proposed a transformation method from a pseudoperiodic time series to complex networks, by representing each cycle of the pseudoperiodic series as a basic node. Yang and Yang (2008) built RC networks by using the correlation matrices of time series input. Gao and Jin (2009) proposed a method for generating the RC networks from time series based on phase space reconstruction.

Recently, another computing framework of RC, namely Conceptor network, has been proposed by Jaeger (2014) in 2015. Conceptor networks can store multiple patterns of inputs into a reservoir layer, filter the corresponding states using a “Conceptor” module, and finally reconstruct the input signals to achieve high classification accuracy. Conceptor network has a significant advantage that it is able to online load new classes of input patterns, which is a tough challenge for most other conventional supervised training-based classifiers. Due to such an attractive feature, Conceptor networks have been researched to solve the problems such as image classification (Hu et al. 2015; Qian and Zhang 2018; Qian et al. 2018), natural language processing (Liu et al. 2018), time series classification (Wang et al. 2016; Xu et al. 2019).

In this paper, we proposed a novel Conceptor network whose reservoir component is generated by using time series phase space reconstruction (PSR) method. Signal reconstruction of a mix of two irrational-period sines was employed as the network performance-testing model. After obtaining the appropriate values of threshold of the PSR method, an experiment comparing the network performance using this model confirmed the advantages of the proposed reservoir over an ordinary random reservoir. The experimental results demonstrated the effectiveness of our proposed reservoir generation method. Furthermore, for deep understanding the PSR method, the effects of memory load on Conceptor network performance are discussed.

The rest of this paper is organized as follows: In “Basic principles of conceptor network” section, we briefly introduce some basic preliminaries of Conceptor network. “Proposed method” section presents our proposed reservoir generation method based on phase space reconstruction. In “Experimental design and results” section, we first initialized the reservoir of Conceptor by using four chaotic time series datasets, and then examines the reconstruction effects of the mix of two irrational-period sines to analyze the performance of the generated Conceptor network. Section “Conclusions” section concludes this paper as the end.

Basic principles of conceptor network

The Conceptor network is a type of recurrent neural network (RNN) as shown in Fig. 1, which is driven by several dynamic input patterns $p^1,p^2,\dots$. Suppose the hidden layer (reservoir) of Conceptor consists of N recurrent-connected neurons, if the network is driven by a pattern $p^i$, the reservoir activation constitutes a high-dimensional state space of $x^i={[x_1^i,x_2^i,\dots ,x_N^i]}^T$. Let ${\mathbf{W}}_{\mathit{in}}\in {\mathbb{R}}^{N\times x1}$ and ${\mathbf{W}}_{\mathit{out}}\in {\mathbb{R}}^{1\times N}$ be the input weights and output weights, respectively. And let $\mathbf{W}\in {\mathbb{R}}^{N\times N}$ be the hidden weights. Thus update rule at time step $k+1$ for the reservoir state can be given by

$$\begin{array}{cc}\hfill x^i(k+1)& =f(\mathbf{W}{x}^i(k)+{\mathbf{W}}_{\mathit{in}}{p}^i(k+1)+b)\hfill \\ \hfill y^i(k+1)& ={\mathbf{W}}_{\mathit{out}}{x}^i(k+1)\hfill \end{array}$$ 1

where $f(·)$ is a nonlinear activation function, and is usually selected as Tanh function. b is a random initialized bias. Similar to other reservoir computing models, such as ESN and LSM, once the input weights ${\mathbf{W}}_{\mathit{in}}$ and hidden weights $\mathbf{W}$, as well as the bias b are random initialized, they are keep fixed. Only the output weights ${\mathbf{W}}_{\mathit{out}}$ will be trained to reconstruct the input $p^i$ by using linear regression method.

Fig. 1.

Conceptor network structure

Denote the Conceptor matrix $\mathbf{C}\in {\mathbf{R}}^{N\times N}$, its diagonal elements are the principal components of the reservoir state x of an input pattern p. For a set of reservoir states $x(1),\dots ,x(K)$, design the loss function

$$\begin{array}{c}\hfill L=\sum _{j=1,\dots ,K}(\frac{\Vert x(j)-\mathbf{C}x(j){\Vert }^2}{K})+{\alpha }^{-2}\Vert \mathbf{C}{\Vert }^2\end{array}$$ 2

where $\alpha >0$ is a regularization term.

We can apply the stochastic gradient descent (SGD) algorithm to obtain the optimal $\mathbf{C}$ to minimize the value of (2):

$$\begin{array}{c}\hfill \frac{\partial L}{\partial \mathbf{C}}=\mathbf{I}-\mathbf{C}x{x}^T-{\alpha }^{-2}\mathbf{C}\end{array}$$ 3

Thus, we can update the Conceptor core $\mathbf{C}$ with an online fashion

$$\begin{array}{cc}\hfill \mathbf{C}(k+1)& =\mathbf{C}(k)\hfill \\ \hfill & +\lambda ((x(k)-\mathbf{C}(k)x(k))x^T(k)-{\alpha }^{-2}\mathbf{C}(k))\hfill \end{array}$$ 4

where $\lambda$ denotes the update rate.

Proposed method

PSR-based conceptor reservoir generation

In this paper, we proposed a time series prediction method based PSR of complex network. The time series is divided into fixed-length sequences and mapped to reservoir nodes. According to the correlation coefficient between the nodes to determine whether there is a connection between the nodes, when the coefficient is greater than a certain threshold, the connection between these two nodes is established, otherwise not established. For a time series $z(it),i=1,2,\dots ,M$, with t being the sampling interval, and M being the sample length, its phase space vector can be calculated by using the coordinate delay embedding algorithm:

$$\begin{array}{cc}\hfill \overrightarrow{{\mathbf{x}}_j}& ={\mathbf{x}}_j(1),{\mathbf{x}}_j(2),\dots ,{\mathbf{x}}_j(N)\hfill \\ \hfill & =\mathbf{z}(jt),\mathbf{z}(jt+\tau ),\dots ,\mathbf{z}(jt+(N-1)\tau )\hfill \end{array}$$ 5

where N is the reservoir dimension, i.e. the number of recurrent-connected neurons, as defined before. $\tau$ is the time delay, $j=1,2,\dots ,H$. H is the number of total time series vectors to be reconstructed, $H=M-(m-1)\tau /t$.

We use C-C method to determine the time delay $\tau$, its general idea is to subdivide a single time series $z_1,z_2,\dots ,z_M$ into t sequences, and then calculate S(m, M, r, t)

$$\begin{array}{cc}& S(m,M,r,t)=\frac{1}{t}\sum _{s=1}^t[{\mathbf{C}}_s(m,\frac{M}{t},r,t)]-{\mathbf{C}}_s^m(1,\frac{M}{t},r,t)\hfill \\ \hfill & \mathrm{\nabla }S(m,t)=max(S(m,M,r_j,t))-min(S(m,M,r_j,t))\hfill \end{array}$$ 6

where

$$\begin{array}{c}\hfill C\left(m,,,M,,,r,,,\tau \right)=\frac{2}{N(N-1)}\sum _{1\le i<j\le N}^{}\theta (r-\left|x_i,-,x_j\right|)\end{array}$$

, $r>0$, $\theta (·)$ denotes Heaviside function. The common setting of m and r are $2\le m\le 5$, and $\sigma /2\le r\le 2\sigma$ where $\sigma$ is the standard variance of the time series. The time series’ embedding dimension m is determined by using the false nearest neighbors method.

After reconstructing the phase space of time series, in order to build the corresponding network model, each vector element in the phase space can be regarded as a node, and their mutual distance in the phase space can be used to determine whether there is a connection between the nodes. Given two vector points $\overrightarrow{X_i}$ and $\overrightarrow{X_j}$, the phase space distance is defined as

$$\begin{array}{c}\hfill d_{\mathit{ij}}=\sum _{n=1}^m∥X_i,(n),-,X_j,(n)∥\end{array}$$ 7

where $X_i=z(it+(n-1)\tau )$ is the nth element of $\overrightarrow{X_i}$.

Thus, We can establish the network using the following approach: the connection between node i and j exists if $\mid {\mathbf{d}}_{\mathit{ij}}\mid \le {\mathbf{r}}_c$, and it keeps as a directed connection (from i to j), the connection weight is set as $w_{\mathit{ij}}=d_{\mathit{ij}}$. If $\mid {\mathbf{d}}_{\mathit{ij}}\mid >{\mathbf{r}}_c$, the nodes are not connected, which means $w_{\mathit{ij}}=0$.

Memory management

Once the Conceptor reservoir is generated, we should finetune its reservoir memory state to store the pattern features of input data. the memory management mechanism of Conceptor reservoir is as follows:

1. Gradually input data to the Conceptor: If the patterns $p^1,p^2,\cdots ,p^K$ have been already stored in the reservoir, the new model $p^{K+1}$ can be stored without disturbing the previously stored patterns, even without knowing what patterns are previously stored.

2. Measure the remaining memory capacity of the reservoir, which means to measure the capability of the Conceptor reservoir to store another new patterns.

3. Reduce redundancy: If a new data pattern has some similarity to a already stored pattern, load its completely different characteristics from other existing patterns into the reservoir memory. Then update the reservoir state set by

   $$\begin{array}{cc}\hfill X^i(k+1)& =f(\mathbf{W}{x}^i(k)+{\mathbf{W}}_{\mathit{in}}{p}^i(k+1))\hfill \\ \hfill & \approx f(\mathbf{W}{x}^i(k)+\mathbf{D}{x}^i(k))\hfill \end{array}$$ 8

   where $\mathbf{D}=d_{\mathit{ij}}$ denotes the distance matrix of reservoir weights. In a non-progressive training model, regularized linear regression can be used to calculate $\mathbf{D}$ by minimizing:

   $$\begin{array}{c}\hfill \mathbf{D}={\text{argmin}}_{\tilde{\mathbf{D}}}\sum _{i=1,\cdots ,K}\sum _{k=1,\cdots ,L}\Vert {\mathbf{W}}_{\mathit{in}}{p}^i(k)-\tilde{\mathbf{D}}{x}^i(k+1){\Vert }^2\end{array}$$ 9

   where K is the number of stored patterns and L is the length of the training samples. Then update the reservoir by $\mathbf{W}\leftarrow \mathbf{W}+\mathbf{D}$.

4. Combine the distance matrix ${\mathbf{D}}_i$ with ${\mathbf{C}}_i$ corresponding to the stored pattern $p^i$, and reconstruct the reservoir state $x(k+1)={\mathbf{C}}^{i}f(\mathbf{W}{x}^i(k)+{\mathbf{D}}^i{x}^i(k)+b)$ by the ith pattern.

5. Input training data of new pattern to Conceptor, and then calculate ${\mathbf{D}}^{i+1}$.

6. If there exists two training patterns are the same, i.e., $p^i=p^i,(i>j)$, then let ${\mathbf{D}}^j\leftarrow {\mathbf{D}}^{j+1}$, which means the Conceptor reservoir need not to update to store the duplicate one. If $p^i$ is similar to but not equal to $p^j,(i>j)$, the reservoir can reduce its information redundancy.

The key to the memory management of Conceptor reservoir is to track the memory storage space has whether be occupied or not by an input pattern. If the patterns $p^1,\dots ,p^i$ have been stored, the occupied memory storage space is remarked by $A^i=\vee ({\mathbf{C}}^1,\cdots ,{\mathbf{C}}^i)$, while the unoccupied space is denoted by the complement $⌝A^i$.

Let the training data of input pattern be $p^i(n)i=1,\cdots ,K;n=1,\cdots ,L$. The incremental memory storing algorithm is as shown in Algorithm 1.

Experimental design and results

Conceptor network generation

We use four different types of time series to generate the reservoir of Conceptor network by using PSR method. The four time series are:

1. Lorenz chaotic system:

   $$\begin{array}{cc}\hfill {\mathbf{d}}_x/{\mathbf{d}}_t& =\sigma (y-x),\hfill \\ \hfill {\mathbf{d}}_y/{\mathbf{d}}_t& =x(\rho -z)-y,\hfill \\ \hfill {\mathbf{d}}_z/{\mathbf{d}}_t& =xy-\beta z,\hfill \end{array}$$ 10

   where $\sigma =16,\rho =45.92$, and $\beta =4$.
2. Mackey-Glass chaotic system:

   $$\begin{array}{c}\hfill y[k+1]=y[k]+\delta (\frac{0.2y[k-\frac{\tau }{\delta }]}{1+y{[k-\frac{\tau }{\delta }]}^{10}}-0.1y[k]),\end{array}$$ 11

   where $\delta =0.1,\tau =17$ produces a mildly chaotic behavior.

3. Brownian motion system, representing a self-similar system model.

4. Gaussian white noise.

Figure 2 shows some samples of the four time series. By using the PSR method, we can build the Conceptor reservoir network based on these four datasets.

Fig. 2.

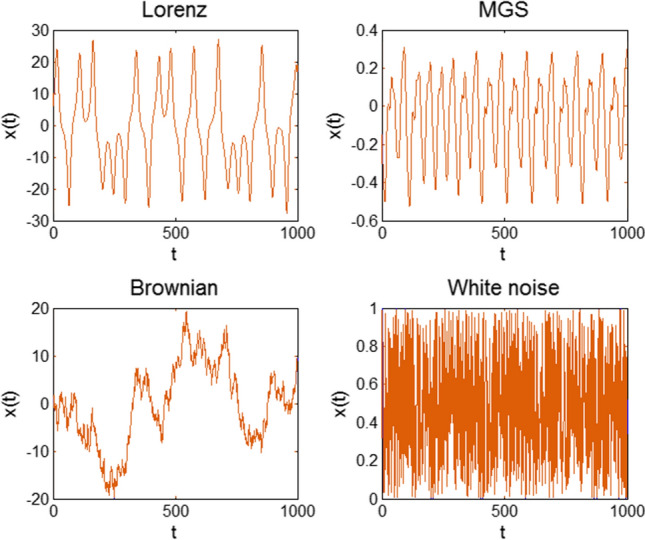
The four types of time series used for phase space reconstruction

Figure 3 presents the scatter diagram of the adjacency matrix of Conceptor reservoir. The black points indicate that there is a connection between the nodes whose X and Y coordinates are their index number. It can be seen that the reservoir network obtained from the chaotic system (Lorenz and Mackey Glass Series) and the affine system (Brownian motion) both exhibit clustering structure, while the network obtained from the White Noise sequence does not form a cluster structure. Observing the node degree distribution (Fig. 4), it is found that the network constructed by the White Noise has a Gaussian distribution, and the network constructed by the chaotic system presents Weibull distribution (like exponential distribution, which has a large value of information entropy). The affine system exhibits a multi-spike distribution. The network obtained from Lorentz system has a more obvious clustering structure, and its degree distribution also shows a Weibull-like distribution.

Fig. 3.

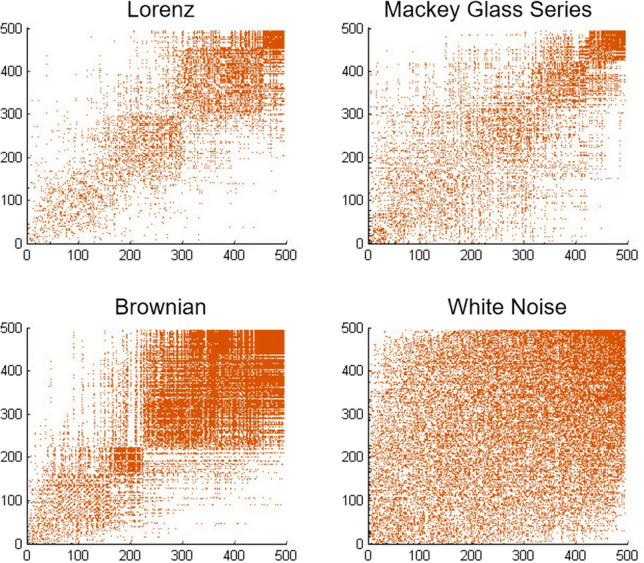
The reservoir connection topologies of Conceptor generated by the four time series according to phase space reconstruction

Fig. 4.

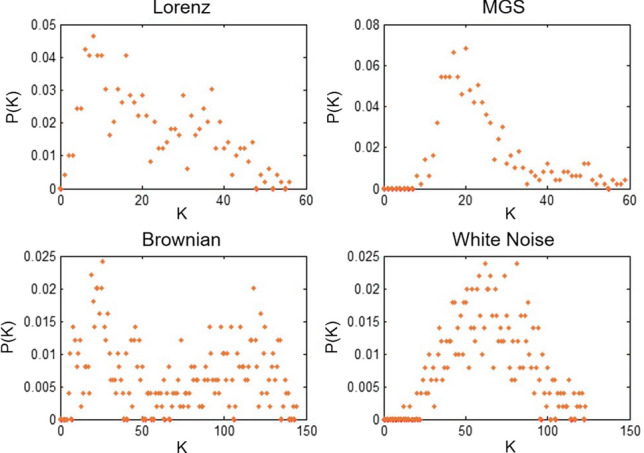
The neuronal degree distributions of the generated Conceptor reservoirs

Taking the Lorenz chaotic system as an example, we calculate the parameters of the reconstructed phase space. Construct a Lorentz PSR network with a scale of $N=200$, and its time delay $\tau$ can be obtained according to the C-C method. As shown in Fig. 5, $\tau$ is the value of X axis corresponding to the thick blue line when it reaches the local minimum, $\tau =10$. Figure 6 describes the response curve of the connection density of the reservoir network to the threshold $r_c$. When the network density growth rate is the maximum, the corresponding threshold $r_c$ is taken as the ideal value, where $r_c=11.2$.

Fig. 5.

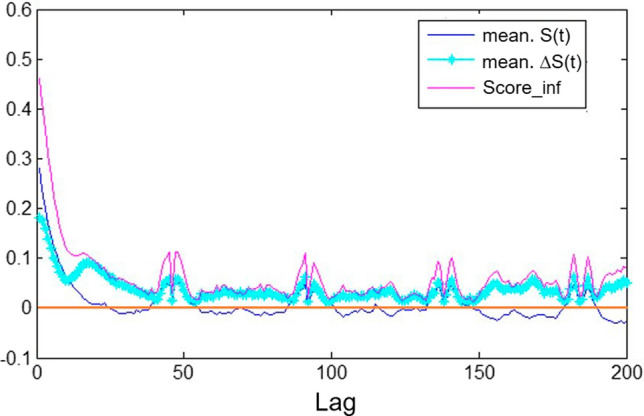
The latency calculated according to the C-C method. (Color figure online)

Fig. 6.

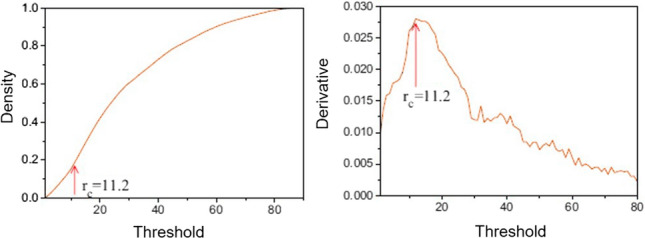
The network density responded on the threshold $r_c$

Performance comparison with other conceptors

To verify the effectiveness of out proposed PSR-based Conceptor, we compare the PSR-based Conceptor with other two typical networks, i.e. random Conceptor network and cortex Conceptor network. We use a time series composed of two sinusoids with different periods as the input pattern to test the performance of the Conceptor network. The periods of these two different sine sequences are $\sqrt{30}$ and $\sqrt{30}/2$, respectively, and their phase angles and amplitudes are random, but the sum of their amplitudes is fixed at 1. In Fig. 7, we show nine different randomly generated test time series. Table 1 shows the Conceptor parameters used in experiment.

Fig. 7.

Mixed irrational periodic sine signal

Table 1.

Parameter settings in the experiments

Parameter	Value	Parameter	Value
K	20	N	200
$\alpha$	100	$n_{\mathit{washout}}$	100
$n_{\mathit{cue}}$	30	$n_{\mathit{recall}}$	10000
${\lambda }_{\mathit{cue}}$	0.01	${\lambda }_{\mathit{recall}}$	0.01

Figure 11 shows the prediction accuracy (indicated by NRMSE, as defined by (12)) comparison between these three Conceptors.

$$\begin{array}{c}\hfill NRMSE=\sqrt{\frac{\sum _{i=1}({\mathbf{l}}_{\mathit{test}}{\mathbf{y}}_{\mathit{test}}[i]-{\mathbf{d}}_{\mathit{test}}[i]{)}^2}{{\mathbf{l}}_{\mathit{test}}{\sigma }^2}}\end{array}$$ 12

where ${\mathbf{y}}_{\mathit{test}}[n]$ is the network output during the testing phase; ${\mathbf{d}}_{\mathit{test}}[n]$ is the desired output during the testing phase and ${\sigma }^2$ is the variance of the desired output. The standard deviation of NRMSE ($\delta$) is defined as follows:

$$\begin{array}{c}\hfill \delta =\sqrt{\sum _{i=1}^T\frac{{(NRMSE(i)-NRMS{E}_{\mathit{av}})}^2}{T}},\end{array}$$ 13

where $NRMS{E}_{\mathit{av}}$ denotes the NRMSE average of the T independent trials.

Fig. 11.

The reconstruction NRMSE with ${\mathbf{C}}_{\mathit{cue}}$ and ${\mathbf{C}}_{\mathit{recall}}$ of PSR-based Conceptor

Prediction accuracy

As the prediction accuracy comparison that presented in Fig. 8, Conceptors with different reservoir structures exhibit different computational performance.

Fig. 8.

Effects of threshold $r_c$ on reconstruction accuracy for all reservoirs

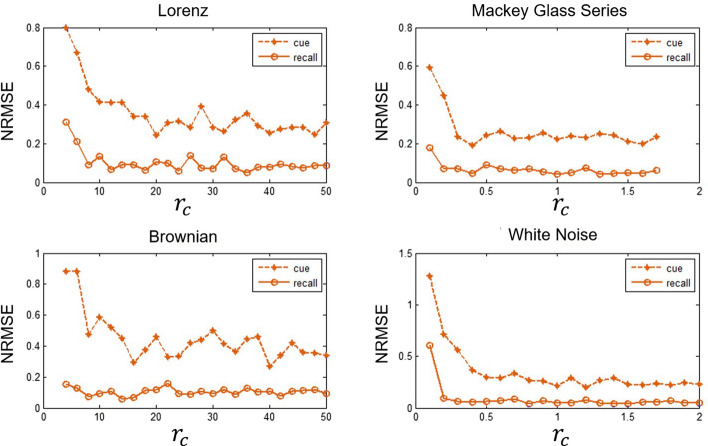
Figure 6 shows the effects of PSR threshold $r_c$ on the connection density of Conceptor reservoir. For further study, in Fig. 8, we present the NRMSE comparison between the four types of time series reconstructed Conceptors with different $r_c$. We can see that the NRMSEs are stable when $r_c$ is larger than 15 for Lorenz time series, 0.3 for Mackey Glass Series, 12 for Brownian time series and 0.5 for White Noise.

In Fig. 9 we show the reconstruction results ${\mathbf{C}}_{\mathit{recall}}$ of the first three input patterns of our proposed PSR-based Conceptor and other two networks to be compared.

Fig. 9.

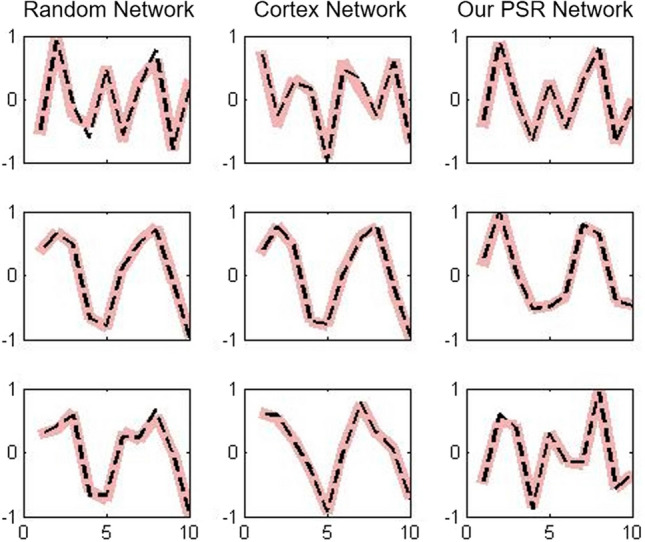
The reconstruction results of time series by Conceptor ${\mathbf{C}}_{\mathit{recall}}$

The black dotted line represents the input training pattern and pink bold line is the reconstructed pattern. Intuitively, we can see that the proposed PSR-based, the compared random and cortex Conceptor networks are all able to reconstruct the input patterns well.

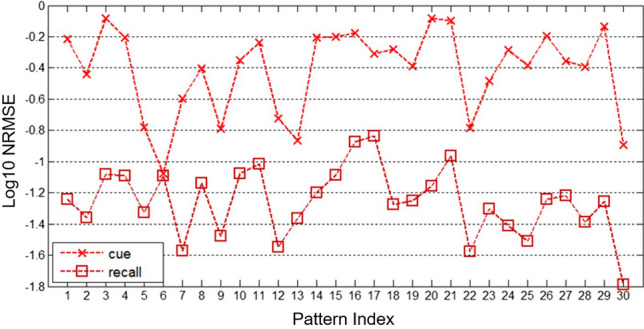
In order to deep understand the reconstruction ability of ${\mathbf{C}}_{\mathit{recall}}$, we calculate the reconstruction NRMSE of 30 input patterns for each Conceptor reservoir, result is given in Fig. 10. It can be seen that the reconstruction errors (NRMSE) of the cortex network (green line) and our PSR-based network (red line) are generally smaller than the random network (blue line), that is, the error distribution is more concentrated in the position where the NRMSE is smaller. Further, the error distribution of the our PSR-based network is the best. Table 2 specifically gives the mean and variance of NRMSE of the three networks. It shows that the average NRMSE of the random network is the largest and the error fluctuation is also the largest, while the average NRMSE of PSR-based network is the smallest and the error fluctuation is also the smallest. It demonstrates that our proposed PSR-based Conceptor network has the strongest reconstruction capability than other two models.

Fig. 10.

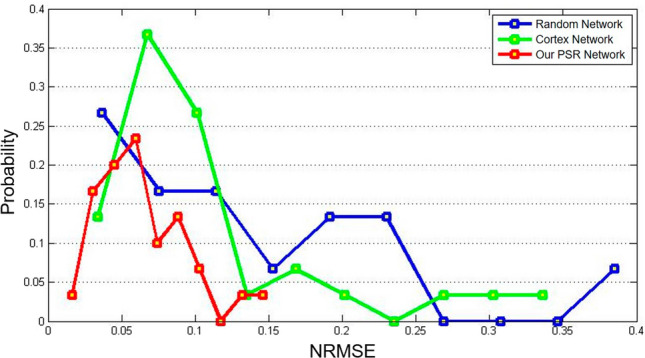
The NRMSE distribution of our PSR-based and other two Conceptor networks. (Color figure online)

Table 2.

Mean and standard deviation of NRMSE for the three types of Conceptors

Network	Avg. NRMSE	Std.
Random Net.	0.130	0.0934
Corte Net.	0.110	0.0776
PSR-based Net.	0.062	0.0309

Memory load effects on recall ccuracy

The prediction accuracy of time series reflects the computing performance of Conceptor, and is affected by the memory load of reservoir (Figs. 11, 12).

Fig. 12.

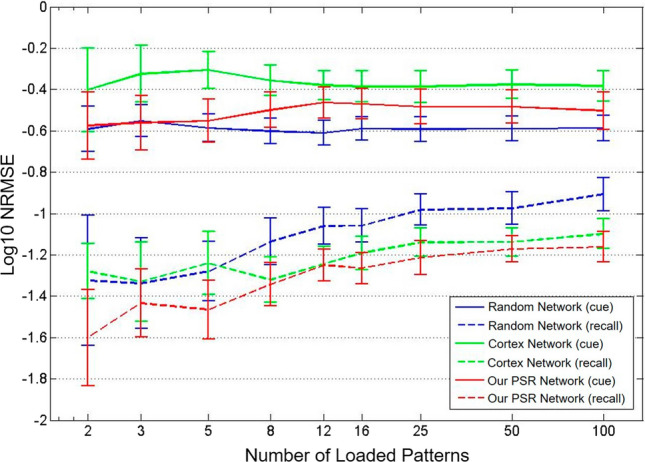
Effects of memory load on recall accuracy

In order to further study the relationship between the recall accuracy with memory load, and to know the reservoir memory capacity, we gradually increased the number of input patterns, and observed the change in the prediction error of the continuous memory load. Experiment is done as follows:

1. Build a Conceptor reservoir model;

2. In each independent trial, first load K input patterns to the Conceptor reservoir. Note that the K is gradually increasing by trial (from $K=2$ to $K=100$). Considering that the change trend is obvious when the number of input pattern is small, if the number is large, the memory storage space is close to saturation, and its change trend is weak, so let $K=[2,3,5,8,12,16,25,50,$ 100], respectively.

3. After the data pattern is loaded, repeat the above reconstruction step. Calculate the reconstruction error NRMSE for the first 10 loaded patterns.

4. Repeat step 2) and 3) five times, with newly created patterns, using the same reservoir.

The results are shown in Fig. 10, we can get that:

1. For all memory load situations and Conceptor networks, the reconstruction error (NRMSE) obtained by ${\mathbf{C}}_{\mathit{recall}}$ is smaller than that by ${\mathbf{C}}_{\mathit{cue}}$, which means from ${\mathbf{C}}_{\mathit{cue}}$ to ${\mathbf{C}}_{\mathit{recall}}$, the reconstruction accuracy of all Conceptors is improved.

2. The reconstruction error of all reservoir ${\mathbf{C}}_{\mathit{recall}}$ shows an upward trend. The more data patterns loaded into the reservoir, the greater the memory load and the worse the reconstruction accuracy.

3. Compared between the random network, cortex network and our PSR-based network, it is found that when K is small, the accuracy of the cortex network is similar to that of the random network, but it is better than the random network when the memory load is relative large. The PSR-based network has the highest reconstruction accuracy compared to both the convetional random network and cortex network.

Conclusions

This paper proposed a Conceptor reservoir method based on phase space reconstruction (PSR), which was investigated using a test involving the reconstruction of a mix of two irrational-period sines. Four PSR reservoirs had improved computational capability over the conventional random reservoir, and the improvement in the reconstruction precision of the Lorenz PSR reservoir and its standard deviation was largest. Experiments also revealed that reconstruction precision showed a nonlinear decline with increase in memory load, and the proposed Lorenz PSR-based reservoir maintained its advantages for different amounts of memory load. The generated reservoir can improve the computational accuracy of Conceptor networks, and experimental results proved the effectiveness of our proposed PSR-based Conceptor generation algorithm. By the deep analysis, we found that the precision of PSR-based reservoirs improves with the increase in threshold $r_c$, which is for the reason of the increase in reservoir network density. Due to the neuronal connection of our PSR-based Conceptor reservoir was dynamically updated if new data pattern was input into, the computational complexity had important impact on the reservoir generation, thus the further work can be focused to address the complexity of our PSR-based method.

Compliance with ethical standards

Conflict of interest

The authors declare that they have no conflict of interest.