Abstract
As SARS-CoV-2 continues to propagate around the world, it is becoming increasingly important to scale up testing. This is necessary both at the individual level, to inform diagnosis, treatment and contract tracing, as well as at the population level to inform policies to control spread of the infection. The gold-standard RT-qPCR test for the virus is relatively expensive and takes time, so combining multiple samples into “pools” that are tested together has emerged as a useful way to test many individuals with less than one test per person. Here, we describe the basic idea behind pooling of samples and different methods for reconstructing the result for each individual from the test of pooled samples. The methods range from simple pooling, where each pool is disjoint from the other, to more complex combinatorial pooling where each sample is split into multiple pools and each pool has a specified combination of samples. We describe efforts to validate these testing methods clinically and the potential advantages of the combinatorial pooling method named Tapestry Pooling that relies on compressed sensing techniques.
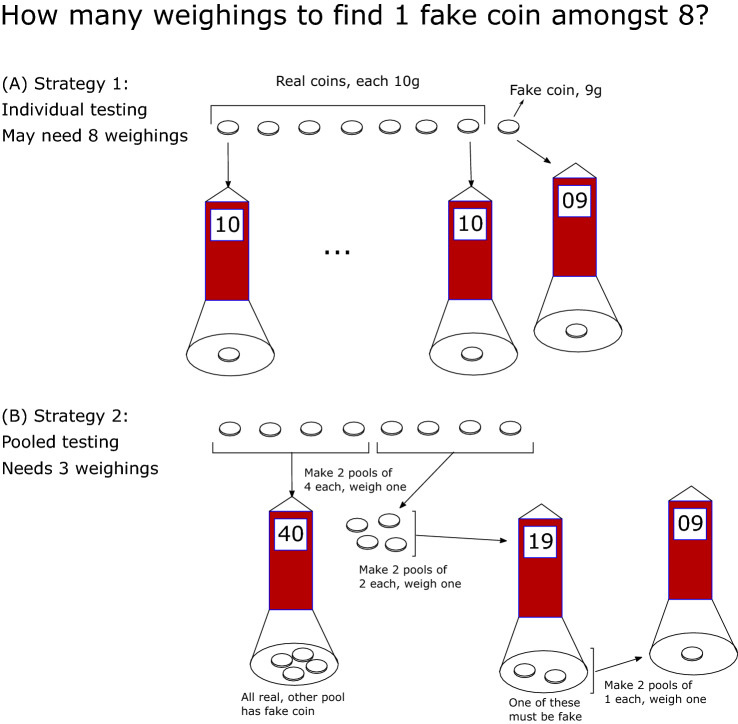
You may have heard of this puzzle about identifying a fake coin: You have eight Rs. 1 coins. Real coins weigh 10 g each, but you are told that one of the coins is fake and weighs less than the others. Using a simple weighing machine, on which you can place some coins and read out their total weight, what is the least number of weighings in which you can locate the fake coin?
You could check each coin one by one, which could need upto seven weighings if you’re unlucky (see Fig. 1a). Another way would be to ‘pool’ the coins into two sets of four coins and then weigh one pool and then the next. One of these pools will weigh 40 g and the other less, so you will already know that four coins are real. Then you could split the coins in the second pool into two each and weigh them, and then finally test each coin from the group of 2 that weighed less than 20 g. This would take three weighings to identify the fake coin (see Fig. 1b).
Figure 1:
Find the fake coin puzzle. We have eight coins of which one is fake. The real coins weigh 10 g and the fake coin 9 g. We have a weighing machine which can weigh one or more coins. a The simplest strategy is to weigh each coin one by one. This may need upto seven weighings to find the fake coin. b A binary search pooling strategy that iteratively splits the pool that is known to have the fake coin into two smaller pools, and so on, can find the fake coin in three weighings.
A similar idea can be used to pool samples to test for the virus SARS-CoV-2 which causes Covid-19. Instead of coins, we have samples taken from the nose, throat or saliva of people we are testing. Instead of weighing them, we use an RT-qPCR assay to test for the presence of the virus.
Suppose we had samples from eight people of whom one was infected. We could have tested each sample individually. In the worst case we need seven tests to identify the infected person. But if we pooled the samples into sets of four, and then sets of two, as with the coins, then we would need a mere three tests! Pooling samples can thus save tests. This can save time, reagents and plastics, manpower, money, and most importantly—by enabling more testing—lives.
Testing for SARS-CoV-2 is more involved than the setting of this puzzle. For starters, we do not know how many people are infected. We could modify the coin puzzle so that we do not know how many coins are fake either. In that case too, pooling coins reduces the number of weighings needed as long as the number of fake coins is much smaller than the number of real coins. Therefore, pooled testing of SARS-CoV-2 should help even if we do not know beforehand how many people are infected.
Another difference is that the RT-qPCR assay has a limit to its sensitivity. Though this is one of the most remarkable assays known to man—it can reliably catch a single molecule present in the test tube—it can still fail to detect very small amounts of the virus. This is because the RT-qPCR machine works with a fixed volume of sample. It might happen that the virus is so dilute in the sample that the volume of sample that found its way into the assay had no virus molecules. Then the assay has correctly reported that there were no virus molecules found in the tube. However the implication that the patient is not infected turns out to be incorrect.
This happens rarely enough when a single sample is tested at a time. But the problem can get amplified when multiple samples have to be pooled. This is because we take less amounts of each sample, leading to further effective dilution of a sample that might have had molecules from the virus.
Therefore, pooling samples dilutes them and a sample with a low viral load may fall below the level detectable by the machine. It is as if the coin weighing machine could fit only one coin. So to weigh a set of four we would have to cut out a quarter piece of each coin and weigh the four pieces, rather than four full coins. For a large pool, say ten coins, perhaps a weighing machine with limited sensitivity may not be able to tell the difference between all pieces being real and one piece being fake.
With clinical, it is quite possible for a sample to have very few virus particles, close to the limit of the detection by RT-qPCR. This depends on many things that are impossible to control, like how sick the person was from whom the sample was taken, or precisely how much material was taken from the nose, throat or saliva of the person, or how long the sample was stored before testing. From more than 30,000 samples that were tested positive at the testing centre at InStem and NCBS, Bangalore, we found that the viral load ranged across 5–6 orders of magnitude.
Another difference works to the advantage of virus testing. A single RT-qPCR machine can test a little under 100 pools simultaneously in one “round” of testing—it is as if we had 100 weighing machines that we could load with coins.
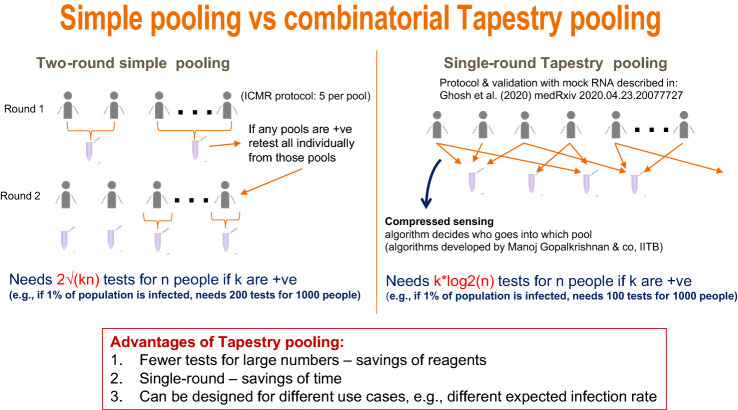
A simple pooling strategy known as Dorfman pooling has been widely deployed to test for SARS-CoV-2 using the RT-qPCR test in India and other parts of the world. In this method, one pools groups of five samples each. For this size of pool, with well-designed assays, one is reasonably confident of detecting even small viral loads. Each pool is tested in the RT-qPCR machine. All samples in a pool that tested negative are declared free of the virus. All samples in a pool that tested positive are then tested individually one more time, to determine if they are positive or negative (see the left side of Fig. 2).
Figure 2:
Comparison of two sample pooling strategies for testing SARS-CoV-2. On the left is depicted the “simple pooling” scheme. Samples are grouped into ‘pools’ of a specified size, and in the first round each pool is tested using RT-qPCR. In the second round, each sample from every pool that tested positive is retested individually. If the only consideration is to reduce the number of tests, then the best pool size to choose, for n people of whom k are infected, is 1. For this choice, the number of tests needed would be 1. However, large pool sizes do result in samples being more diluted so one may want to limit the pool size. ICMR has approved a scheme which limits the pool sizes to five samples, and this has been used in testing centres across India. On the right is an alternative scheme for pooling called Tapestry pooling. Here, unlike simple pooling, each sample goes into multiple pools. These pools are then tested on a single round of RT-qPCR. Which sample goes into which pool is specified by a carefully chosen matrix (see Eq. 1; Fig. 3) which allows the use of compressed sensing techniques to reconstruct precisely which individual samples are positive or negative from knowledge of which pools are positive or negative. With n people of whom k are positive, this can be done in as few as tests2. Both pooling schemes work best when the prevalence rate, k/n, is small. Simple pooling works upto 5% prevalence, while Tapestry pooling can work upto 15–20%2.
Dorfman pooling1 is a variant of the coin weighing strategy described above. It has one advantage that it works in just two rounds. So if there were ten infected people amongst 200, we would need at most 90 tests done in two rounds, which would take one day. If instead we split 200 into two pools of 100 each, then we would need pools of 50 each and so on. We would need fewer tests but it could take eight rounds, which could take several days.
Is it better to save on tests at the cost of time, or save on time at the cost of more tests? There is no one correct answer to this question. Covid19 treatment of a person is often based only on the symptoms they exhibit. So the real importance of testing is for contact tracing and quarantining and thereby limiting the spread of the infection. One advantage of getting test results quickly is that an infected person will spend less time unknowingly meeting others. Contact tracing effort will identify the people who might have come into contact with the infected person faster. In addition, uninfected persons will more quickly have their anxiety lifted and can get back to their life without fear of infecting others.
Simple pooling saves substantially only when relatively few people are infected. Taking the example of 200 people as above, suppose now 30 people were infected instead of 10 (15% instead of 5% prevalence). In that case, simple pooling could need as many as 190 tests. One might as well test all 200 individually! In the NCBS-InStem testing centre, we reached this situation in July and therefore stopped doing simple pooling. Many hospitals are reporting that 15–20% of their suspected Covid patients are testing positive. Similarly, amongst health care workers the prevalence of infection is reaching similar levels. Even large scale surveys of several cities, such as Delhi, Mumbai, Pune, are reporting that 20–40% of people tested (using a different type of test) have had SARS-CoV-2. In such a scenario, are there cleverer ways of using pooled testing successfully?
Tapestry Pooling2, a pooling scheme invented at IIT Bombay and validated at NCBS-InStem3, is such a scheme. It can work even when upto 20% of a population is infected and give results in a single round, leading to even faster detection of positives and negatives. At the same time, when less than 1% of the population is infected, it can save more than 90% of the tests required.
Unlike the simple pooling strategy described before, in Tapestry Pooling each sample goes into more than one pool, and each pool has a different combination of samples within it. Specifically, each sample is split into three different pools, each pool can have anywhere from 4 to 32 samples combined in it, and no two samples occur together in more than one pool. We use data science algorithms from the field of compressed sensing4–6 to reconstruct which individuals are positive and which are negative directly from the results of a single round of RT-PCR tests of each pool.
We use not just the positive or negative result of each test, but also the estimate of the total viral load of each pool that the RT-PCR provides. The RT-qPCR machine puts a sample through multiple cycles of high and low temperature. Every copy of a specified DNA or RNA sequence replicates every cycle. Thus, if the sample initially has a viral load of R(0) virus RNAs, then after n cycles of RT-qPCR, there will be copies of the viral RNA. The Ct value is the cycle number at which the number of copies of viral RNA crosses a certain threshold value. Thus, the higher the Ct value, the smaller the viral load. In practice, if the copy number does not cross the threshold in 40 cycles, the sample is considered negative. This test can detect viral loads as low as 1000 copies/ml of SARS-Cov-2 RNA.
Using the analogy to the coin puzzle, the weighing machine does not just tell you which pool of coins is lighter than expected but gives you the actual weight of the pool. If the weight of one of the faulty coins in that pool is determined by other measurements, we can estimate whether one more coin in this pool is faulty. Similarly, the RT-PCR machine reports not just whether the sample or pool tested was positive or negative, it gives an estimate for the viral load in that test. This is additional information we can use to reconstruct which individual is positive or negative with more accuracy. We are able to squeeze out more than 1 bit of information per pool tested, allowing us to obtain accurate results with a smaller number of tests, as well as making our scheme viable for high prevalence scenarios where simple pooling would be unviable, such as when the prevalence rate rises beyond 5%.
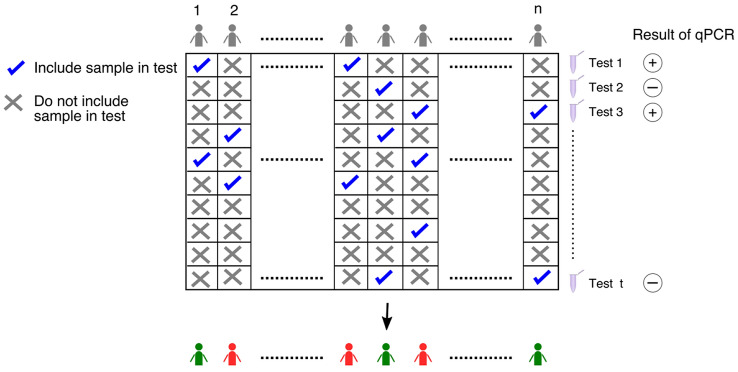
A pooling matrix, such as the one shown in Fig. 3 specifies which sample goes into which pool. The rows correspond to pools, and the columns to samples. All entries are either 0 or 1. A 1 entry in row j and column i indicates that sample i participates in pool j.
Figure 3:
Schematic of the pooling matrix used in Tapestry pooling. The matrix shows which samples go into which pools, and corresponds to the matrix in Eq. (1). In total t pools are formed from n samples. Typically, each sample is used in no more than three pools, and no two samples occur together in more than one pool. These properties, along with the sparsity assumption—that very few samples are positive—allows one to reconstruct which samples are positive (red) and which negative (green), given the results of testing each of the t pools. This scheme can work for prevalence rates as high as 15% where simple pooling will not work2.
Pooling matrices are chosen so that each sample is split into exactly three different pools, each pool can have anywhere from 4 to 32 samples combined in it, and most importantly no two samples occur together in more than one pool. This ensures that information obtained from one pool is maximized.
The viral load of each pool must be the sum of the viral loads of the samples participating in it. Thus each pool yields a linear equation with the pool viral load determined by the experiment, and the sample viral loads as the unknowns. The reconstruction problem can be written as a linear system of equations. Let be an N-element vector of 0s and 1s specifying which individuals are positive or negative, be an M-element vector of 0s and 1s specifying which pools tested positive or negative, and be an matrix whose th element is 1 if pool i contains sample j, and 0 otherwise. Then
| 1 |
is a linear system of equations where is specified, is measured experimentally, is unknown. Our task is to reconstruct , given and , and possibly some multiplicative noise. Since , Eq. (1) is an underdetermined system without a unique solution. However, if we assume that is sparse, then we can use compressed sensing techniques to estimate it. Compressed sensing estimates the sparsest that satisfies the constraint in Eq. (1)4–6. This allows us to reconstruct which individual sample is positive or negative with more accuracy, and with a smaller number of tests. The method remains viable even for scenarios where simple pooling would not work, such as when the prevalence rate is larger than 5%2.
Tapestry pooling assumes a certain prevalence rate. This assumption may occasionally be violated in practice if a batch of samples arrives that has an unexpectedly large number of positives. In such cases, the algorithm can no longer identify all the positives and negatives. However, we ensure that even in this setting, the algorithm avoids false negatives and false positives. Instead it identifies the samples whose results it is umsure about, and returns them as a small list of “undetermined” samples that need to be retested in a second round. We call this graceful failure of the algorithm, which needs to kick in only very rarely. The mathematical idea behind this behaviour is known in coding theory as “list decoding.”
A team at NCBS-TIFR and InStem, Bangalore, has extensively tested this combinatorial Tapestry pooling strategy using real SARS-CoV-2 samples. The method worked successfully for many different cases, which can be broadly classified into two categories: First, for identifying upto 15–20% positives amongst 100 or less individuals, in about half that number of tests. This would be useful for testing and diagnosis centres that are seeing such high levels of prevalence, where simple pooling does not work. Several testing centres and hospitals, such as the Tata Memorial Hospital, the Malabar Cancer Centre, and the Bangalore Medical College and Research Institute, are now testing this method to see if it works for the samples they receive. Second, for testing many hundreds to a thousand samples in less than 100 tests, but where the number of positives is not more than a few percent. Such large scale screening of populations could be used, for example, in campuses, factories or offices that want to re-open safely. The savings could potentially be huge because the method needs a very small number of tests, even compared with simple pooling. For this, it is important to build automated devices that can split the samples and pool them in the correct combinations because doing this manually for so many samples without error is very tedious. Setting up such devices and making them available across the country is the next challenge in deploying this method for Covid testing.
Biographies
Manoj Gopalkrishnan
is a faculty member in electrical engineering at IIT Bombay.
Sandeep Krishna
is a faculty member at the Simons center for living machines at NCBS Bangalore.
Footnotes
This article is an expanded version of an essay with the same title and authors, published on the Covid Gyan website: https://covid-gyan.in/. Figures and text have been reproduced with permission from Covid Gyan.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Dorfman R. The detection of defective members of large populations. Ann Math Stat. 1943;14(4):436–440. doi: 10.1214/aoms/1177731363. [DOI] [Google Scholar]
- 2.Ghosh S et al (2020) A compressed sensing approach to group-testing for COVID-19 detection. In: arXiv:2005.07895
- 3.Ghosh S et al (2020) Tapestry: a single-round smart pooling technique for COVID-19 testing. In: medRxiv. 10.1101/2020.04.23.20077727
- 4.Tibshirani R. Regression shrinkage and selection via the lasso. Commun Pure Appl Math. 1996;58(1):267–288. [Google Scholar]
- 5.Donoho DL. For most large underdetermined systems of linear equations the minimal norm solution is also the sparsest solution. Commun Pure Appl Math. 2006;59(6):797–829. doi: 10.1002/cpa.20132. [DOI] [Google Scholar]
- 6.Candès Emmanuel J, Romberg Justin K, Terence Tao. Stable signal recovery from incomplete and inaccurate measurement. Commun Pure Appl Math. 2006;59(8):1207–1223. doi: 10.1002/cpa.20124. [DOI] [Google Scholar]