Full three-dimensional segmentation and quantification of tumor vessels for photoacoustic images

Abstract

Quantitative analysis of tumor vessels is of great significance for tumor staging and diagnosis. Photoacoustic imaging (PAI) has been proven to be an effective way to visualize comprehensive tumor vascular networks in three-dimensional (3D) volume, while previous studies only quantified the vessels projected in one plane. In this study, tumor vessels were segmented and quantified in a full 3D framework. It had been verified in the phantom experiments that the 3D quantification results have better accuracy than 2D. Furthermore, in vivo vessel images were quantified by 2D and 3D quantification methods respectively. And the difference between these two results is significant. In this study, complete vessel segmentation and quantification method within a 3D framework was implemented, which showed obvious advantage in the analysis accuracy of 3D photoacoustic images, and potentially improve tumor study and diagnosis.

1. Introduction

The excessive growth of tumor vessel helps tumor cells obtain nutrients and oxygen more easily [1]. The tumor vessel has distinguishing characteristics including high curvature, low blood vessel density, reflux and intermittent flow, the structure and functions of tumor are abnormal [2,3]. They are usually with loose and irregular connection, wide joints and uneven distribution [4,5]. Vessel density and curvature are commonly used indicators to measure the degree of abnormality of vascular structure. The vessel curvature and vessel density of tumor vessels are significantly higher than those of normal vessels. The average difference in vessel density between normal tissues and tumor tissues is 24.6 and the difference in vessel curvature is high as 60 % [6,7]. A linear relationship between perfused tumor vessel (greater than 30 μm in diameter) and tumor cell clumps was discovered in previous study [8]. Besides, tumor cells metastasis can only be detected after the density of perfused tumor vessel have increased to a certain extent [9]. Nourishing blood vessels, especially the morphological characters, play an important role in judging the growth status of tumors. Thus, accurate quantification of vascular structure parameters is of great significance for evaluating tumor growth status.

Conventional imaging techniques, such as MR, CT, ultrasound, and optical imaging, have been applied to track changes of blood vessel. However, these conventional techniques cannot effectively visualize tumor vessel due to poor resolution [10], sensitivity [11], and imaging depth [12]. Photoacoustic tomography (PAT) is an emerging technology that uses hemoglobin as endogenous contrast agent to perform deep and high-resolution detection of blood vessel morphology with high sensitivity [[13], [14], [15], [16]]. Vascular volume network can be visualized at optical resolution, about 1−10 μm, by photoacoustic microscope [17]. The 3D high-resolution images obtained by OR-PAM present a complete and detailed network of blood vessels. Jeon et al. used PAM to obtain 3D photoacoustic images of the blood vessels in the mouse eyes, and then combined with machine learning algorithm to evaluate blood circulation in the eye [18]. Nie et al. developed a sensitive and resolution-scalable PAM to noninvasively monitor tumor therapy response in a timely manner. Compared with morphological measurement by standard imaging techniques, Nie's method can detect changes in tumor status earlier [19]. The quantification results for such images are expected to obtain more accurate vascular morphological information, which is expected to improve the accuracy of tumor diagnosis.

In the past, the quantification of microvascular was mainly based on conventional optical imaging technology. For example, Yousefi et al. developed a hybrid method based on Hessian / intensity for segmenting and quantifying capillaries in optical coherence tomography (OCT) images [20]. Nesper et al. quantified retinal capillary changes in diabetic patients based on OCT images [21]. Due to limited imaging depth, the above vessel segmentation and quantification methods were all performed in a 2D frame, which loses depth information and makes the blood vessel network information incomplete. Aiming at the photoacoustic imaging technology, Meiburger et al. proposed a skeleton extraction technology based on vascular filtering and central axis extraction, and used this algorithm to calculate vascular quantitative parameters to distinguish the vascular network of healthy tissue and burn tissue [22]. Zhang et al. extracted blood vessel density from photoacoustic images of mouse skin, and quantitatively measured the microvascular system [23]. Chen et al. have previously reported a quantitative algorithm based on a 2D Hessian matrix, however, it can only be applied to planar objects, and the shape of tumor has limited its application [24]. Zhao et al. have used 2D quantification methods to study tumor vessel, and quantify the growth process of tumor vessel by the diameter, microvascular density, vessel curvature and fractal dimension [25]. Liu and Zhao respectively used the 3D Hessian matrix to enhance the blood vessels in the 3D photoacoustic image, and obtained the quantified results of the vessel structure parameters based on the 2D MAP image [26,27]. However, the MAP image without depth information has a negative impact on the accuracy of quantization. To the best of our knowledge, photoacoustic imaging provides 3D information, while the previous photoacoustic image vessel quantification studies are still mostly based on 2D MAP images. The projection makes the 3D blood vessel network to be compressed or overlapped, which affects quantification accuracy. Thus, developing full 3D segmentation and quantification of blood vessels is critical for their potential application of accurate diagnosis of tumors.

In the 3D framework, we realized the complete process from vessel segmentation to quantification. For the first time, we obtained quantitative information such as vessel diameter, density and curvature based on 3D photoacoustic images. We verified the accuracy of this method through phantom experiments. Further, we compared the 2D and 3D quantification results of tumor vessel photoacoustic images and found that the 2D and 3D results of each parameters have significant differences. In order to obtain more accurate morphological information, blood vessels should be quantified within the 3D framework, which is of great significance for the accurate diagnosis of tumors.

2. Materials and methods

2.1. Photoacoustic imaging of tumor vessel

A custom-built OR-PAM system was applied to acquire all the imaging data in this manuscript, which we have reported in previous publications [26,28]. The excitation and detection devices were integrated on a 3-axis motorized translation stage. The lateral resolution and axial resolution is ∼3.8 μm and 27 μm respectively, which had been measured before [28].The scanning was performed at a 5 μm step size between adjacent B-Scans. The signal of each A-Line is acquired by a high-speed acquisition board with an acquisition frequency of 200 MHz.

Male BALB/c nude mice (4–6 weeks old and weighing 18–20 g) were used as animal models in this study. The human prostate cancer cells, C4-2, were suspended in 15 μl PBS and then inoculated into the ears of the mice. The ears of tumor-bearing mice were imaged on the 5th day after tumor implantation and the tumor size was about 6 × 4 mm.

2.2. 3D hybrid tumor vessel segmentation method

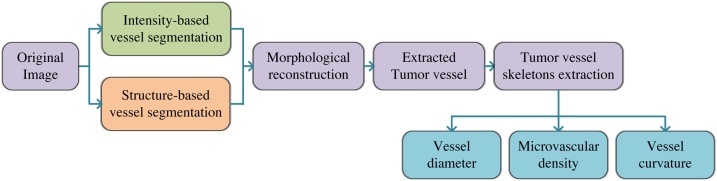
The 3D hybrid segmentation method (3D-HSM) includes two parts: tumor vessel segmentation and quantification, and the flow chart is shown as Fig. 1. In the vessel segmentation section, we merged the intensity-based segmentation images and structure-based segmentation images, and then used the morphological reconstruction method to obtain the fusion image of the two segmentation images. Based on the blood vessel skeletons, vessel diameter, microvascular density and vessel curvature were quantified. Due to the unique depth detection capabilities of photoacoustic imaging, we use 3D quantification method to obtain quantification results of vascular parameters, and compared the differences between 2D quantification and 3D quantification.

Fig. 1.

Flow chart of 3D hybrid segmentation method.

First, the original image was segmented based on intensity information, which includes three steps. First, a 3 × 3×3 Gaussian filter was applied to smooth and denoise original image, and then the top-hat operation was used to enhance the discrimination between the background and the segmentation target (tumor vessel). In particular, considering the tubular structure of the blood vessel, we choose a set of linear structural elements, each of which is set to a length of 5 pixels and an angle ranging from 0° to 180° with 15° interval. Due to the different directions of vessels, a group of structural elements with short lengths and different angles were selected. Histogram equalization was performed on the image after the top-hat operation, this step will minimize the effect of noise and inhomogeneity [29]. Secondly, the local Otsu method was used for image segmentation, steps in three dimensions are 80, 80, and 10, respectively. The steps were manually selected through experiments. The Otsu method is a method to adaptively obtain the image segmentation threshold through the histogram of the statistical image [30], and the local Otsu method divides the three-dimensional data into multiple sub-parts to realize the segmentation separately. Finally, connected components statistics and region growth were used to eliminate redundant details. A threshold was set to remove connected components with few pixels. Here we used the 26-connected rule to detect connected components and removed connected components with few pixels. Through multiple sets of parameter tests, the connected components with less than 60 pixels were removed.

Although the blood vessel segmentation based on the intensity information was simple and effective, due to the inevitable noise interference, it contained pixels that were erroneously segmented. Vessel segmentation based on structural information can effectively avoid noise interference. In this paper, this processing was mainly based on 3D Hessian matrix, which includes three steps. First, in order to highlight the vascular pixels and suppress the background noise, an open operator was applied to the original image. As for 3D volume, we performed open operation layer-by-layer. The second step was vessel segmentation based on 3D Hessian matrix. Finally, two-step transform was used to achieve contrast enhancement. We used high-frequency enhancement filtering to highlight the details in the image, and then used intensity transformation to further distinguish between blood vessels and background. In the photoacoustic images of mouse ear tumors, the distribution characteristics of blood vessels are significantly different with depth changes. The small blood vessels are densely distributed in the superficial layer, while the number of blood vessels with large diameter in the deep layer increases. Based on this fact, we selected two scale ranges for vessel segmentation, namely 1 ≤ s ≤ 5 and 3 ≤ s ≤ 9.

The last step of the vessel segmentation section is to reconstruct the vessels using the intensity-based segmentation image and structure-based segmentation image. The morphological reconstruction iterates elementary geodesic dilations of the marker-image and mask-image until it reaches a stable state. A series of images are generated during the iterative process, which can be expressed as Ik Rec, k = 0, 1, …, n. The marker image is the initial image of the iteration, which is I0 Rec. Mask image limits the scope of iterations, and the images in all iterations (Ik Rec) are a subset of mask image [31]. In our algorithm, we used morphological reconstruction to complete the reconstruction step, the structure-based segmentation image and the intersection of the structure-based segmentation image and the intensity-based segmentation image were selected as the mask-image and the marker-image, respectively.

2.3. Vessel skeletons extraction and parameters quantification

We used the Multi-Stencils Fast Marching Methods (MSFM) to extract the skeletons of tumor vessel. First, we divided the blood vessel into different connected components, and initialized the velocity map inside the blood vessel to 1, and the velocity map outside the blood vessel to 0, the boundaries of blood vessel are obtained by morphological boundary extraction operator. Secondly, we used the speed map from the previous step to calculate the distance from each point in the blood vessel to the blood vessel boundary using the MSFM method and mark the furthest point as the source point. The distance information was used to update the speed map. After that, we input the updated source point and velocity map into the MSFM method, calculated the new flight time, and obtain the farthest point and the gradient image. For a specific connected component, we connect the fastest gradient descent path between the source point and the furthest point. Finally, the skeletons of each connected component can be connected to obtain the skeletons of the whole vascular network, which is the tumor vessel skeleton. More details about the vessel skeletons extraction have been reported in the Ref. [25].

The tumor vessel in two different mice were used for imaging and quantification. The quantification parameters included blood vessel diameter, microvascular density (MVD), and three parameters related to blood vessel curvature, respectively the distance metric (DM), the inflection count metric (ICM), and the sum of angles metric (SOAM) [32].

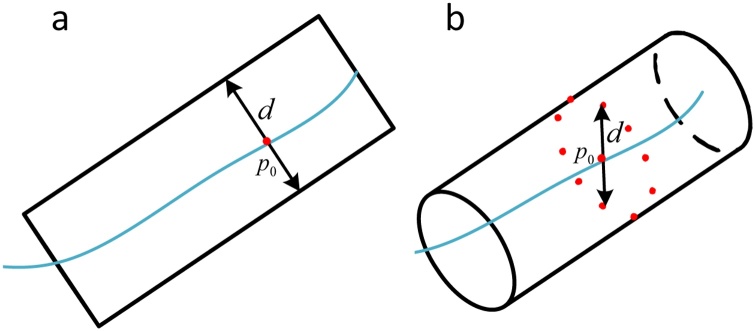
For vessel diameter, boundary intersection method is a commonly used quantitative method [33]. This method defines the distance between two blood vessel boundaries as the blood vessel diameter, as shown in Fig. 2a. However, the blood vessel boundary in the 3D image is a cylindrical structure, so it is difficult to use the distance between the boundary points to define the diameter of the cylinder. This results in this method being only suitable for 2D images. In this paper, we draw on the ideas of the above methods to quantify the vessel diameter in 3D framework, as shown in Fig. 2b. First, obtain the blood vessel boundary and the vessel skeleton in the 3D space. Secondly, fit a circle with p₀ as center and radius of D with the finite data points in the plane taking the vessel skeleton as the normal vector. In actual operation, the radius D increases by a certain step, and the number of data points are usually taken as 2ⁿ. Thirdly, traverse different radius until enough data points intersect the vessel boundary, such as the radius d_m satisfies the termination condition. Finally, calculate the average distance between all intersecting data points and p₀, then the average distance is the blood vessel diameter.

Fig. 2.

Quantification of vessel diameter in 2D and 3D framework: (a) boundary intersection method. (b) modified boundary intersection method in 3D framework.

MVD is defined as the ratio of the total vessel length to the total pixel number of observed volumes. For a specific vascular volume, a greater MVD will be obtained due to longer length of blood vessel. The definition of MVD can be described as follow formula:

$$MVD=\frac{\text{Total}\text{Vessel}\text{Length}}{\text{Number}\text{of}\text{Pixels}\text{in}\text{Volume}}$$ (1)

DM is defined as the ratio of the actual path length of the blood vessel (AL) segment in each subdomain to the linear distance between the two ends of the blood vessel (SL). The parameter ICM is used to overcome the deficiency of DM when dealing with “S”-shaped and “C”-shaped blood vessel. In extreme cases, the DM of the “C”-shaped blood vessel will be larger than that of the “S”-shaped blood vessel, however, this result is exactly the opposite of the actual curvature. ICM is defined as the product of DM and the number of inflection points of the blood vessel (N):

$$DM=\frac{AL}{SL}$$ (2)

$$ICM=DM\times N$$ (3)

SOAM is defined as the sum of the curvatures of all voxels along the skeletons of the blood vessel and normalized by the actual path length of the vessel. For each connected component, we calculate SOAM based on Ref. [32]:

$$SOAM=\frac{\sum _{k=1}^{n-3}C{P}_k}{\sum _{k=1}^{n-1}\left|P_k-P_{k-1}\right|}$$ (4)

where n is the number of pixels in the vascular skeleton of the connected component, P_k is the k-th point in the vascular skeleton, and CP_k is the total angles at the point P_k.

2.4. Phantom and animal experiments

For the 3D vessel parameters quantification, an authoritative public data set has not been established for algorithm verification, and the data used in this paper were obtained using a self-developed system. The blood vessels have not been manually marked by doctors or experts. In order to evaluate the accuracy of the algorithm in this paper, we first carried out the phantom experiment.

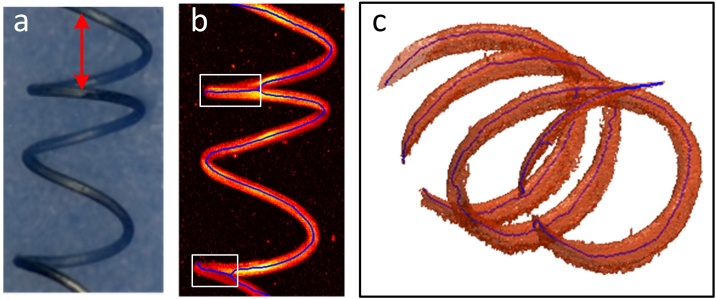
We designed two structures of the phantoms corresponding to the situations that may occur in actual imaging, respectively: blood vessels at different depths overlaying vertical and blood vessels extend in-depth direction. We used 80-microns tungsten wire, 150-microns tungsten wire and 350-microns pencil lead to simulate blood vessel of different diameters. The 80-microns tungsten wire and the 350-microns pencil lead were used to make the phantom-1, the two were placed up and down with an interval of about 450 microns (the pencil lead is located in the lower layer). In addition, the phantom-2 was made of a tungsten wire with a diameter of 150 μm. The 150-micron tungsten wire was made into a spring-like shape with a diameter of about 1.5 mm to simulate vessels that extend in the depth direction. We used the previously mentioned system to image the phantoms, image segmentation and parameter quantification were completed using the 3D-HSM.

For animal experiment data, the pixel pitch matches in three dimensions was unified to 10 μm in three dimensions. After that, the 3D-HSM was used to segment blood vessel, and then the vascular structure parameters were all quantified in the 3D framework. And the method, proposed in Ref. [23] for 2D vessel segmentation and vascular parameters quantification based on MAP, was applied to compare the difference between 2D and 3D quantification.

3. Results

3.1. OR-PAM image tumor vessel segmentation

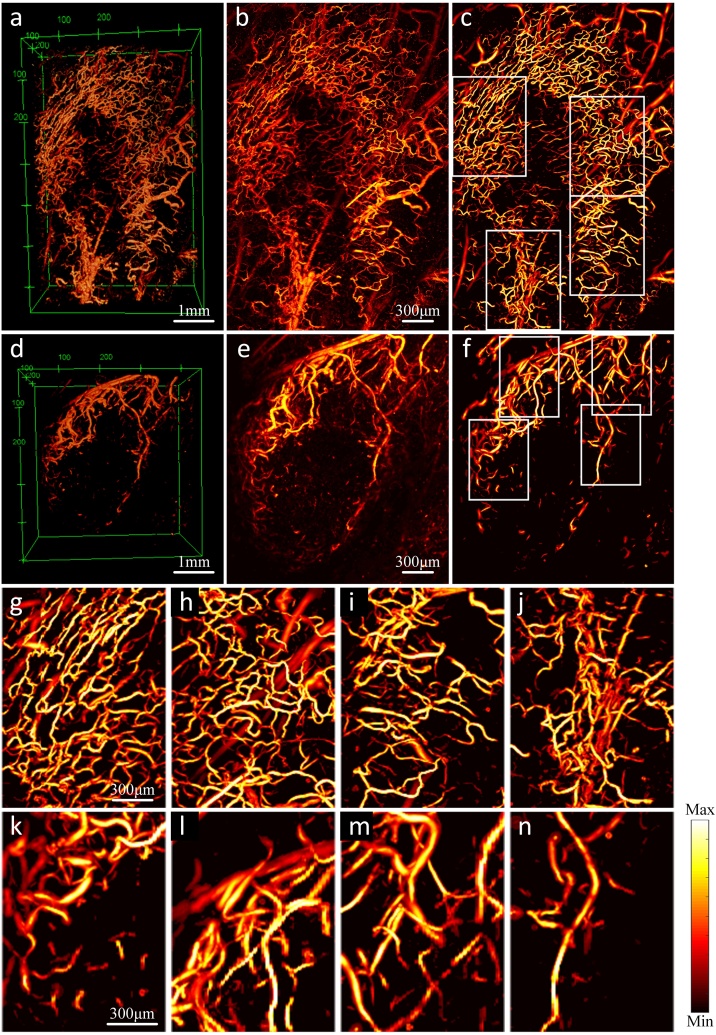
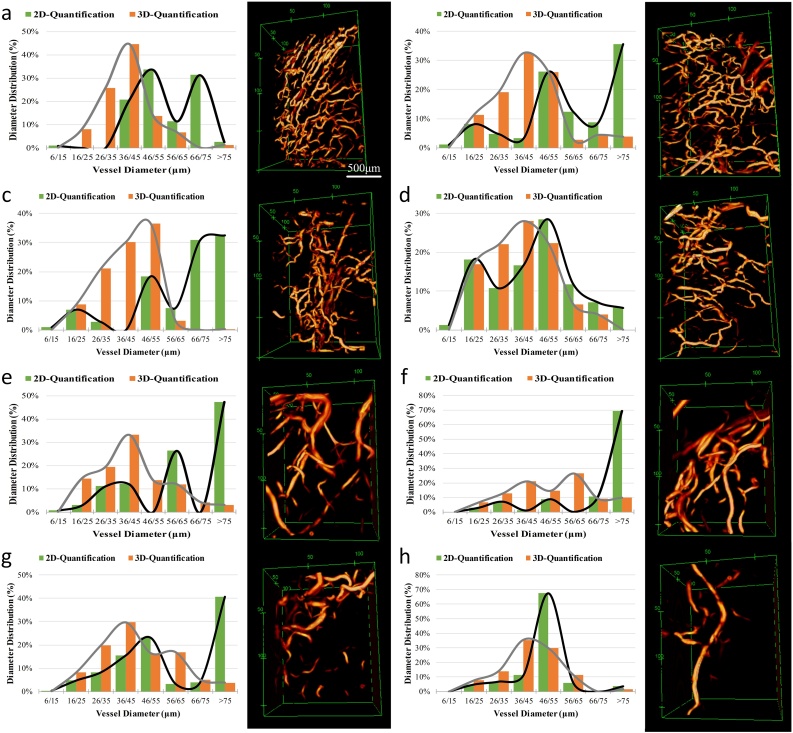
We imaged vessels surrounding C4-2 tumors and segmented the images using the 3D-HSM. In order to ensure that the size represented by the pixel pitch matches in three dimensions, and considering the amount of calculation, we unified this size to 10 μm. The segmented images are shown in Fig. 3. Except for two 3D sub-pictures (Fig. 3a and d), every other sub-picture in Fig. 3 is a MAP image, and the intensity is normalized to the range of 0∼1 by its own maximum value. Fig. 3a–c are the images of mouse-1, Fig.3d–f are the images of mouse-2. The field of view of Fig. 3a is 6.6 mm × 4.5 mm × 0.8 mm, and that of Fig. 3d is 4.5 mm × 4.5 mm × 0.8 mm. Comparing the original image and segmentation image in Fig. 3c, it can be found that the region with weak signal has been significantly enhanced by our algorithm, and the small scattered points in the image are also eliminated. Comparing the original image and segmentation image in Fig. 3f, some cluttered areas in original image are clearly distinguished in the segmentation image. In addition, the blood vessel in the segmentation images reduce a lot of burrs on the border. Fig. 3g–j are the enlarged pictures of the four white-framed areas in Fig. 3c. The field of view is 2.0 mm × 1.5 mm × 0.8 mm. Correspondingly, Fig. 3k–n are the enlarged pictures of the four white-framed areas in Fig. 3f. The field of view is 1.6 mm × 1.2 mm × 0.8 mm. We selected these eight regions for quantification to verify the difference between 2D and 3D quantification. Compare these eight enlarged images with their corresponding positions in the original image. It can be found that the signal-to-noise ratio has been significantly improved, and in addition, some connections and glitches that should not exist have been eliminated.

Fig. 3.

Segmentation of tumor vessel using 3D-HSM. (a–c) The 3D images, MAP images of the original images, and MAP images of the enhanced images using 3D-HSM of the mice-1. (d–f) The 3D images, MAP images of the original images, and MAP images of the enhanced images using 3D-HSM of the mice-2. (g–n) Eight quantized regions correspond to the white boxes in (a) and (d).

3.2. Structural parameters quantification of phantom

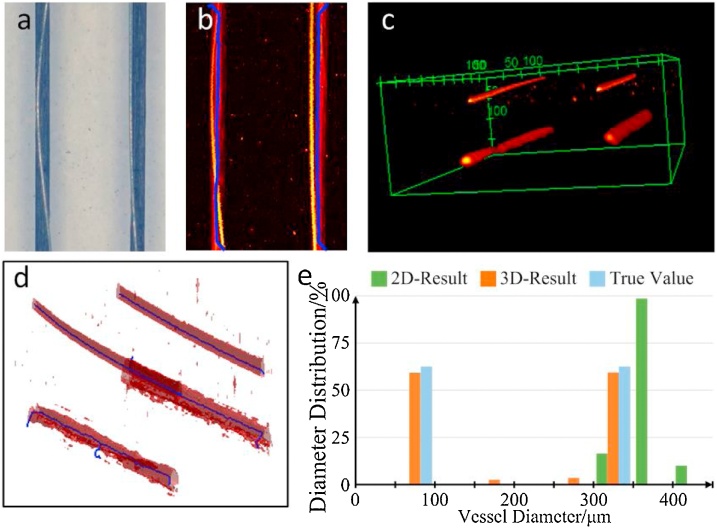
The quantification results of the phantom-1 are shown in Fig. 4. Fig. 4a is the top view of the phantom-1. The tungsten wire on the left side and the pencil lead completely overlap in the vertical direction, and the tungsten wire on the right side only partially overlaps the pencil lead. Similar result can also be found in the MAP image (Fig. 4b). The solid blue line represents the skeleton, and only two solid blue lines indicate that the four imaging objects are recognized as two in the MAP image. Fig. 4c and d are 3D photoacoustic images and 3D skeletons, the structure of the four imaging targets is completely preserved in 3D framework. According to the quantification results shown in Fig. 4e, the 3D quantification results have two obvious peaks, respectively 80 μm and 350 μm, which is consistent with the real diameter of phantom. However, the 2D quantification result shows obvious deviation, it only has a peak around 350 μm.

Fig. 4.

Skeletons and quantification results of phantom-1. (a) Physical picture of phantom-1. (b) MAP image of the original image, the blue line indicates the skeletons obtained by the 2D method. (c) 3D structure of phantom-1. (d) Skeletons obtained by the 3D method. (e) vessel diameter distribution obtained by 2D and 3D method.

Fig. 5a is a top view of the phantom-2. Fig. 5b is a MAP image, where the solid blue line represents the skeleton. Fig. 5c is 3D photoacoustic images and 3D skeletons. Comparing the skeletons shown in Fig. 5b and c, the skeletons obtained by the 3D method in Fig. 5c almost maintain the complete spring shape, which is consistent with the phantom setting, while the 2D skeleton in Fig. 5b shows a wave shape. The MVD obtained using 3D and 2D methods are 0.0218 and 0.0127, respectively. According to the definition of MVD, the true value of MVD is 0.0213, based on the length of the tungsten wire and the size of the imaging area. The MVD obtained from the 3D quantification is very close to it, while the 2D quantification result is much less than it. For the single ring indicated by the red arrow in Fig. 5a, the upper half arc and the lower half arc should not overlap during the projection, so the theoretical length of the skeleton in the MAP image is twice the diameter, while actually length will be the circumference of the ring in three dimensions.

Fig. 5.

Skeletons of phantom-2. (a) Physical picture of phantom-2. (b) MAP image of the original image, the blue line indicates the skeletons obtained by the 2D method. (c) Skeletons obtained by the 3D method.

3.3. Quantification of vascular parameters

3.3.1. Quantification of tumor vessel diameter

Fig. 6 is the quantification results of the blood vessel diameter of the eight enlarged regions in Fig. 3. Fig. 6a–h correspond to the Fig. 3g–n. Comparing the 2D and 3D quantitative results, three results can be clearly found. First, the range of vessel diameter distribution quantified by 3D method is wider than that obtained by 2D quantification method. Second, the blood vessel diameter distribution curves show that the peak position of the diameter distribution curve obtained by the 2D quantification method is different from the peak position obtained by the 3D quantification method. Third, compared with the 3D quantification result, the blood vessel diameter distribution curves obtained by 2D quantification method exhibit multiple peaks.

Fig. 6.

Vessel diameter distribution and 3D structure. (a–d) Regions correspond to the white boxes in Fig.3a, field of view is 2.0 × 1.5 × 0.8 mm³. (e–h) Regions correspond to the white boxes in Fig. 3b, field of view is 1.6 × 1.2 × 0.8 mm³.

3.3.2. Quantification of tumor vessel curvature

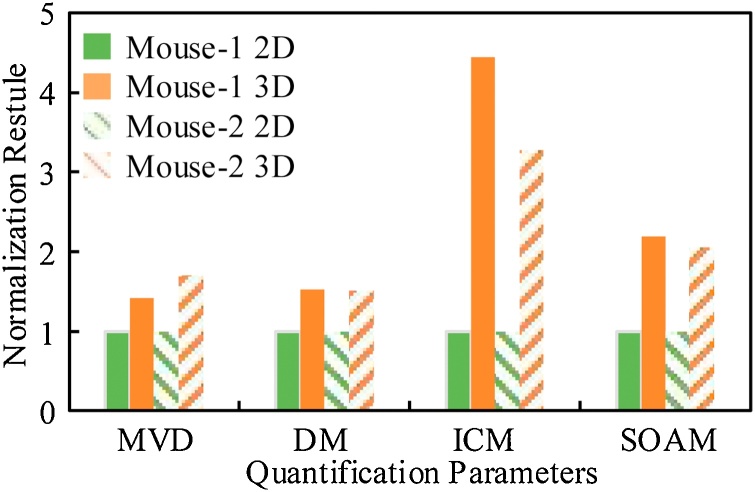
Fig. 7 shows the statistical results of MVD, DM, ICM, and SOAM. The solid bar indicates the quantitative result of mouse-1, the bar with the oblique line indicates the quantitative result of mouse-2, green indicates the 2D quantification results, and orange indicates the 3D quantification results. Each parameter is the mean of the quantification results of the four regions. In order to show the difference between the 2D and 3D quantification results, the 2D quantification results were normalized to 1. For MVD, since the units of the 3D quantification result and the 2D quantification result are inconsistent, 1/pixel³ and1/pixel², respectively, we multiply the 3D quantification result by the number of layers corresponding to the data. The 3D quantification results show higher MVD, the average difference between the results obtained by the two quantification methods are 42 % (mouse-1) and 71 % (mouse-2). Comparing the three parameters of the vessel curvature, it can be seen that the 3D quantification results all show greater curvature. The DM quantified by the 3D method is about 1.52 times that quantified by the 2D method on average. Because the number and angle of vascular inflection points are considered, ICM and SOAM show greater differences. The average difference of ICM obtained by different methods is 3.87 times, while the average difference of SOAM is 2.12 times. We listed the MVD and vessel curvature parameters of the eight regions used for quantification in Table 1.

Fig. 7.

Comparison of 2D and 3D quantification results. MVD and three different definitions (DM, ICM, and SOAM) of vascular tortuosity.

Table 1.

Quantified vascular parameters of the two mice.

		Mouse-1				Mouse-2
		MVD	DM	ICM	SOAM	MVD	DM	ICM	SOAM
Region 1	2D	0.0563	0.1093	0.5255	0.0039	0.0390	0.2139	0.6614	0.0107
	3D	0.0967	0.3026	2.6325	0.0170	0.0621	0.2373	1.7590	0.0144
Region 2	2D	0.0348	0.3842	1.0332	0.0114	0.0479	0.1581	0.6118	0.0079
	3D	0.0593	0.3868	3.3199	0.0173	0.0980	0.3759	1.8218	0.0300
Region 3	2D	0.0420	0.1978	0.8974	0.0049	0.0577	0.1644	0.3317	0.0092
	3D	0.0577	0.3521	4.2914	0.0124	0.0994	0.2447	2.2219	0.0156
Region 4	2D	0.0642	0.0882	0.5293	0.0046	0.0259	0.3102	0.9909	0.0137
	3D	0.0662	0.1453	3.0426	0.0075	0.0314	0.4182	2.7098	0.0249
Mean	2D	0.0493	0.1949	0.7464	0.0062	0.0426	0.2116	0.6490	0.0104
	3D	0.0700	0.2967	3.3216	0.0136	0.0727	0.3190	2.1281	0.0212

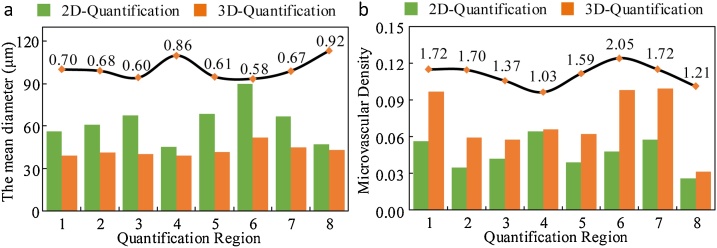
We calculated the mean diameter of blood vessel in eight quantized regions, as shown in Fig. 8a. For comparison, we used a curve to represent the ratio of mean diameters obtained by 2D quantification method to 3D. This confirms that the blood vessel diameter obtained by the 2D method will be larger than that obtained by the 3D method, and the average difference reaches 29.75 %. Besides, we compared the MVD of eight regions separately, as shown in Fig. 8b. It can be seen that in the eight quantification regions, the MVD obtained by the 3D method will be greater than that obtained by 2D quantification method, and the average difference reaches 54.87 %.

Fig. 8.

Comparison of the mean vessel diameter and MVD obtained by 2D and 3D methods. (a) Comparison of the mean diameters of eight quantized regions. (b) Comparison of MVD of eight quantized regions. The black line indicates the ratio of the 3D method results to the 2D method results.

4. Discussion and conclusion

At present, there is no 3D quantification for blood vessel photoacoustic images. For the first time, we have implemented a complete vessel segmentation and quantification method within the 3D framework. The original images were segmented using the 3D hybrid segmentation method, and the blood vessel skeletons were obtained based on Multi-Stencils Fast Marching Methods. Then the vessel structure parameters were quantified in 3D framework. Compared with the 2D quantization results, the structural parameters obtained by the 3D method are significantly different. The difference in the mean diameter is 29.75 %, the difference in MVD is 54.87 %, and the difference in vascular curvature is 250 %.

In this paper, we used the intensity (Local Otsu method) and structural information (Hessian matrix based) of images for 3D vessel segmentation. Zhao only uses structural information to segment blood vessels in 3D photoacoustic images [26]. In fact, the abnormal structure of deep blood vessels will affect the performance of Zhao's algorithm. The structure of the bottom blood vessel is a rectangle in B-Scan image, and it will become a plate-like structure in 3D space. This kind of blood vessel is difficult to be effectively segmented by a segmentation algorithm based on Hessian matrix. Liu's paper combined the Hessian matrix and the Otsu algorithm to reduce the dependence of the vessel segmentation algorithm on parameter selection [27]. We introduced the intensity information to overcome the problem of inaccurate segmentation of deep blood vessels.

In terms of quantification methods, Yang et al. once reported a similar quantification strategy. They used augmented fast marching method (AFMM) to obtain tumor vascular skeletons in photoacoustic images and quantified vascular parameters [34]. However, there are two main differences between our research and Yang's work. First, the method of obtaining the blood vessel skeleton is different. The AFMM used by Yang extracts blood vessel skeletons based on 6-neighbors, and the MSFM method we use extracts blood vessel skeletons based on 26-neighbors, which can obtain more accurate diagonal skeletons. Secondly, for the quantification parameter with the same name, the calculation process in 2D and 3D is different, as discussed in Section 2.3. For the blood vessel diameter, we improved the classic algorithm to make it suitable for 3D blood vessel quantification.

Because of the maximum amplitude projection, the overlapping blood vessels are severely compressed, even different imaging targets are embodied as the same one. Thus, when the blood vessels overlap, the 3D quantitative results are closer to the real situation Due to lack of a publicly recognized data set that used for verification of the accuracy of vascular quantification of 3D photoacoustic images, and the data used in this manuscript has not been manually marked by doctors or other professionals. We can only use the phantom experiment to verify the accuracy of the algorithm. Fortunately, the true value for quantification of vascular mimics can be accurately measured and calculated. Since blood vessels cannot be completely distributed in the horizontal plane (or imaging plane), we found there are two structures that are most likely to cause interference to quantification accuracy. The phantoms we designed represents the above two typical structures. Furthermore, we verified the advantages of the 3D algorithm in quantifying the above two types of structures ensure that it has higher accuracy than the 2D method. For the phantom-2, the MVD obtained by 3D quantification method is 0.0218, which is closed to the true value 0.0213. Due to the large diameter of the tungsten wire, the tungsten wire distributed up and down is shown as a thick tungsten wire in the process of maximum projection, as shown by the white frame position in Fig. 5b, so the quantification of MVD shows a greater deviation.

For the quantification results of in vivo data, the 2D and 3D quantification results of vessel diameter, MVD, and vessel curvature all show significant differences. For the quantification of vessel diameter, the range of blood vessel diameter distribution quantified by 3D method will be bigger than the 2D quantification method, and the vessel diameter obtained by 2D method tends to be larger than the diameter obtained by 3D method. This result occurs because during the maximum amplitude projection, some of the vessels distributed along the depth direction were compressed, and vessels of different depths overlapped, so that the blood vessel diameter obtained by the 2D quantification method tend to be larger. We also found that the blood vessel diameter distribution curves obtained by 2D quantification method exhibit multiple peaks, which may also be caused by spatial overlap. Due to the overlapping of tumor vessel, some tumor vessel with small diameter differences were quantified as blood vessel with the same diameter. The MVD obtained by the 3D quantification method is larger than that obtained by 2D quantification method, and the difference between the two reaches 54.87 %, which also proves that the maximum amplitude projection will obscure some useful information. If the blood vessel diameter and cross-sectional area are taken into account, the blood vessel density will show a greater difference. The three parameters related to the vessel curvature all exhibit the same trend, that is, the 3D quantification method obtains larger quantification results than the 2D method, and the differences between DM, ICM, and SOAM were 1.52, 3.87, and 2.12 times, respectively. The single most striking observation to emerge from the data comparison is that there is a clear difference between 3D and 2D quantification results. Such a huge difference may have a huge impact on the judgment of tumor growth status.

High-resolution vessel imaging can provide a powerful help for the quantification of vascular structure parameters, which is very significant. Photoacoustic imaging has unique advantages in blood vessel imaging, and can conveniently provide a high-resolution 3D vessel network structure. However, the blood vessels underneath some upper ones may have reduced PA signal intensity cause the upper vessels may absorb most of the laser energy. The problem of imaging of the underlying blood vessels can be divided into two categories. Firstly, the PA signal of the deeper layer blood vessels is submerged in noise (SNR is close to 1), and it is difficult to perform further segmentation and quantification operations on such blood vessels. For this situation, the necessary system improvements may need to be studied to further increase the PA signal intensity of the underlying blood vessels. Secondly, the PA signal intensity of deeper layer blood vessels are weak, but it still shows contrast to the background noise. For this situation, the blood vessel can be enhanced by segmentation algorithm.

In summary, based on the 3D photoacoustic image, we have implemented a complete vessel segmentation and quantification method within the 3D framework for the first time. Phantom experiments verified the 3D quantification methods based on 3D volume images can bring much more accurate results than 2D quantification methods based on MAP images. And each parameter of tumor vessels quantitated by 2D and 3D methods, based on in vivo photoacoustic imaging, shows significant differences. The obvious advantages of 3D quantification prove its great potential in the early diagnosis of tumors, disease evaluation, and treatment effect monitoring.

Funding

This work was supported by grants from the National Natural Science Foundation of China [61975226, 11874133]; from National Key R&D Program of China grant [2017YFE0121000, 2018YFC0114800]; from Guangdong Provincial Key Laboratory of Biomedical Optical Imaging Technology [2020B121201010]; from Shandong Natural Science Foundation grant [ZR2017MF041]; from Shandong Science and Technology Development Plan [2018GGX103047]; from Shenzhen Science and Technology Innovation Program [JCYJ20160608214524052, JCYJ20170818163841756, ZDSY20130401165820357].

Declaration of Competing Interest

The authors declare that there are no conflicts of interest.

Biographies

Mingjian Sun is an associate professor at Harbin Institute of Technology, Weihai, China. He received B.E. degree from Harbin Institute of Technology in 2003, and Ph.D degree from Harbin Institute of Technology in 2011, respectively. His main research interests include photoacoustic imaging technology, artificial intelligence medicine and its clinical translation

Chao Li is currently pursuing his Master's degree in the School of School of Information Science and Engineering, Harbin Institute of Technology, Weihai, China. His research interests include photoacoustic endoscopy imaging and medical image processing.

Ningbo Chen is a research assistant at Shenzhen Institutes of Advanced Technology Chinese Academy of Sciences, Chinese Academy of Sciences. He received his Master's degree in Mechanical Engineering from Guangzhou University in 2019. His research interests include developing novel biomedical imaging tools based on photoacoustic imaging for preclinical and clinical applications.

Huangxuan Zhao received his bachelor’s degree in mechanical engineering from Wuhan University of Technology in 2013, and PhD degree in the Department of Biomedical Engineering at Capital Medical University in China. His research interests include utilizing photoacoustic imaging for the detection of diseases and developing new surgical guidance methods for clinical applications.

Liyong Ma is an associate professor at Harbin Institute of Technology, Weihai, China. He received B.E. degree from Harbin Institute of Technology in 1993, and Ph.D degree from Harbin Institute of Technology in 2007, respectively. His main research interests include medical imaging and artificial intelligence.

Chengbo Liu is an Associate Professor at Shenzhen Institutes of Advanced Technology Chinese Academy of Sciences, Chinese Academy of Sciences. He received both his Ph.D and Bachelor degree from Xi'an Jiaotong University, each in 2012 in Biophysics and 2007 in Biomedical Engineering. During his Ph.D. training, he spent two years doing tissue spectroscopy research at Duke University as a visiting scholar. Now he is an associate professor at SIAT, working on multi-scale photoacoustic imaging and its translational research.

Yi Shen is a professor and a PhD candidate supervisor at Harbin Institute of Technology, China. His interest includes automatic control technology and ultrasound imaging technology, such as intelligent detection, ultrasonic beam forming and ultrasound image processing.

Riqiang Lin, senior engineer, received his MA.Sc and B.S. degree in Shenzhen University. Since joined the Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences in 2011, Riqiang Lin focuses in the research of Photoacoustic Imaging, has developed a series of novel photoacoustic system, including optical resolution (OR) and acoustic resolution (AR) photoacoustic microscopy, full field-of-view photoacoustic endoscopy.

Xiaojing Gong is an associate professor at Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences. He received B.S. degree in Mechatronics from the Southeast University in 2000, and Ph.D. degree in Fine Instruments and Mechanics from the University of Science and Technology of China in 2007. His interest includes endoscopic optical/acoustic imaging research and its clinical translation, such as intravascular photoacoustic imaging, photoacoustic endoscopy, multi-modality endoscopic imaging.