Impact assessment of full and partial stay-at-home orders, face mask usage, and contact tracing: An agent-based simulation study of COVID-19 for an urban region

Abstract

Purpose

Social intervention strategies to mitigate COVID-19 are examined using an agent-based simulation model. Outbreak in a large urban region, Miami-Dade County, Florida, USA is used as a case study. Results are intended to serve as a planning guide for decision makers.

Methods

The simulation model mimics daily social mixing behavior of the susceptible and infected generating the spread. Data representing demographics of the region, virus epidemiology, and social interventions shapes model behavior. Results include daily values of infected, reported, hospitalized, and dead.

Results

Results show that early implementation of complete stay-at-home order is effective in flattening and reversing the infection growth curve in a short period of time. Whereas, using Florida's Phase II plan alone could result in 75% infected and end of pandemic via herd immunity. Universal use of face masks reduced infected by 20%. A further reduction of 66% was achieved by adding contact tracing with a target of identifying 50% of the asymptomatic and pre-symptomatic.

Conclusions

In the absence of a vaccine, the strict stay-at-home order, though effective in curbing a pandemic outbreak, leaves a large proportion of the population susceptible. Hence, there should be a strong follow up plan of social distancing, use of face mask, contact tracing, testing, and isolation of infected to minimize the chances of large-scale resurgence of the disease. However, as the economic cost of the complete stay-at-home-order is very high, it can perhaps be used only as an emergency first response, and the authorities should be prepared to activate a strong follow up plan as soon as possible. The target level for contact tracing was shown to have a nonlinear impact on the reduction of the percentage of population infected. Increase in contact tracing target from 20% to 30% appeared to provide the largest incremental benefit.

List of abbreviations and acronyms

WHO	World Health Organization
AB	Agent-based
CI	Confidence interval
aOR	Adjusted odds ratio
SEIR	Susceptible exposed infected recovered/removed
GB	Giga bytes
SARS-CoV-2	Severe acute respiratory syndrome coronavirus 2
COVID-19	Coronavirus Disease 2019.

Introduction

Emergence of the severe acute respiratory syndrome coronavirus type 2 (SARS-CoV-2) was first reported on December 31, 2019 in Wuhan, China and subsequently declared a global pandemic on March 11 by the World Health Organization (WHO) [3,52]. As of Sept. 9, 2020, the number of reported cases worldwide has reached over 27.5 million causing 897,789 deaths. The number of infected cases continues to rise quite significantly [2]. The U.S. has been among the hardest hit by the coronavirus pandemic with 6.3+ million reported infections and 189,538 reported deaths (>21% of the total reported deaths worldwide) so far. However, as the daily new cases, hospital admissions, and deaths began to decline in mid-May, most States in the U.S. began phased lifting of their social intervention measures. For example, Florida adopted a three phased approach: Phase I (which began in May 18, 2020) allowed most businesses and workplaces to reopen with up to 50% of their building capacities and with large events constrained to 25%; Phase II (began in June 5, 2020) allowed all businesses to reopen for up to 50–75% of their capacities and also permitted events in large venues with no more than 50% of their capacities; Phase III will be akin to a complete reopening for which neither a date nor the criteria have been declared. A summary of Florida's phased intervention plan can be seen in Figure A1 (in the Appendix). As the reopening entered Phase II, Florida, along with many other states, began to see sharp increases in daily new infections (e.g., Florida reported over 15,000 new cases on July 11, 2020 along with a test positivity rate reaching over 15%).

In this paper, we investigate a few ‘what-if’ scenarios for social intervention policies including if the stay-at-home order were not lifted, if the Phase II order continues unaltered, what impact will the universal face mask usage have on the infections and deaths, and finally, how do the benefits of contact tracing vary with various target levels for identifying asymptomatic and pre-symptomatic. We conduct our investigation by first developing a comprehensive agent-based simulation model for COVID-19, and then using a major urban outbreak region (Miami-Dade County of Florida, USA with 2.8 million population) as the case study for the model.

Methodology

Agent-based (AB) simulation models have been widely used to mimic complex social contact processes and transmission dynamics of influenza and respiratory type viruses. One of the early applications of AB simulation model for influenza can be found in [16]. The authors examined flexible immunization routines and variable vaccine response patterns on 1957 Asian and 1968 Hong Kong pandemic strains of influenza A. In [18,19,24], authors presented AB simulation models with a detailed approach to generate new infections using calculation of force of infection received by susceptible from infected for potential pandemic outbreaks of A(H5N1) influenza virus in Southeast Asia and U.S./U.K. Assessment of disease burden from a potential A(H7N9) outbreak in the U.S. was studied using an AB simulation model in [43]. AB models have been used for examining both pharmaceutical and non-pharmaceutical intervention strategies, for example, mass vaccination for smallpox outbreak [26], effectiveness of targeted antiviral prophylaxis to contain influenza before widespread availability of a vaccine [33], development of mitigation strategies for a potential A(H5N1) outbreak using a design of experiment approach [35], optimal resource allocation among multiple regions of a country during an influenza pandemic [51], and simulation-based reinforcement learning framework for dynamic mitigation of influenza [14].

A number of papers have appeared in recent literature using AB models to examine COVID-19 outbreak. The papers include: an AB model integrated with mobility data to evaluate intervention measures such as testing, social distancing, contact tracing and quarantine for a potential second wave of the COVID-19 pandemic in the Boston metropolitan area [1]; a general framework of an AB simulator for COVID-19 using geo-spatial data to evaluate intervention measures such as closure of community locations, shops, social distancing, face mask, isolation, among others [34]; health and economic impacts of social interventions for COVID-19 [42]; a probabilistic approach using an AB model to simulate COVID-19 transmission and evaluate mitigation strategies in a closed built environment [15]; and a granular AB model of COVID-19 in Australia to compare school closures and varying levels of intervention strategies such as air travel, case isolation, quarantine, and social distancing [9].

COVID-19 in the U.S. has been handled in a very decentralized manner, where mitigation policies were developed and adopted at municipality/county levels. For example, several counties within the State of Florida, U.S.A. adopted the universal facemask policy while others didn't. As a result, spread of SARS-CoV-2 has not been uniform. Hence, we focused on developing a granular model that can be region-specific and can yield outcomes to guide regional decision makers. While we have presented the model development in the main body of the paper using Miami-Dade County (a county of Florida with 2.8 million population) as a case study region, we have also presented a step-by-step approach (in the Appendix) on how the model can be implemented for other regions. The virus transmission model that is embedded within our AB model follows closely the approach used in [18] that modeled a potential A(H5N1) pandemic. Instead of using real-time mobility data, access to which is limited in the U.S. for privacy reasons, we used detailed census data for generating both population and establishments in the region. This information together with people's daily schedules, guided by the prevailing social-behavioral norms, were used to generate social mixing process for the COVID-19 pandemic. The model is first calibrated and validated with evolving daily age-specific reported data on infection, hospitalization, and deaths. We then extended the model into future months to forecast pandemic impact under various intervention conditions.

Models for COVID-19 in literature are either data-driven (e.g., [4,5,11,17,53]) or compartmental like SEIR (susceptible, exposed, infected, and recovered) or their variants (e.g. [1,28,41,54,55]). Observation data driven models are well suited for understanding the past progression of a pandemic and also for estimating parameters characterizing virus epidemiology. However, they offer limited prediction ability for the future, especially in situations where conditions are changing (e.g., testing and treatment ability, social interventions, people's behavior, and response). SEIR type compartmental models guided by differential equations have been most widely used for communicable diseases, some early examples are [13,29,30]. Such models are aggregate in nature and assume uniform behavior of the population over time. Hence, these models also do not adapt well to changing pace of disease transmission. As stated in [10], an agent-based modeling approach is more suitable for a detailed consideration of individual attributes, specific disease natural history, and complex societal interventions that change over time.

The AB simulation model replicates the dynamics of the pandemic outbreak by incorporating: 1) population demography of the outbreak region for all age groups and their employment categories, 2) establishment information concerning numbers, sizes, and compositions of households, schools, workplaces, and community places, 3) daily schedules for people of all age groups before and during the intervention orders (e.g., stay-at-home), 4) isolation of infected and quarantine of household members, 5) closure of schools, workplaces, and community places, 6) compliance to isolation and quarantine requirements, and 7) epidemiological parameters of the virus. The key epidemiological parameters include: disease natural history with average lengths of latent, incubation, symptomatic, and recovery periods; distribution of infectiousness; percent asymptomatic; and fatality rate.

Each day, the AB model tracks the following for each person: 1) hourly movements and locations based on their daily schedules that depend on age, employment status, prevailing intervention orders, and quarantine/isolation status; 2) hourly contacts with other susceptible and infected; 3) force of infection accumulation; 4) start of infection; 5) visit/consult with a doctor (if symptomatic and insured); 6) testing (if infected and visited/consulted a doctor or asymptomatic chosen for testing either randomly or via contact tracing); 7) test reporting delay; 8) disease progression of infected; 9) hospitalization (if infected with acute illness); and 10) recovery or death. The AB model reports daily and cumulative values of actual infected, doctor visits, tested, reported cases, hospitalized, recovered, and deaths, for each age category. A schematic diagram depicting the algorithmic sequence and parameter inputs for the AB simulation model is presented in Fig. 1 .

Fig. 1.

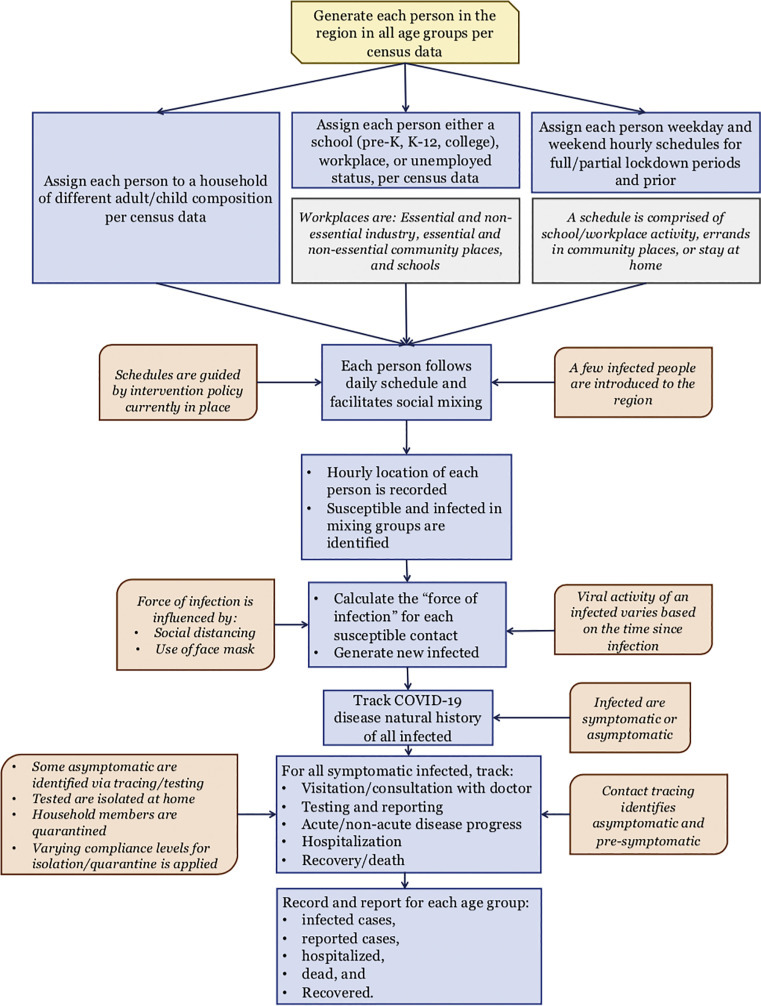
A schematic of agent-based simulation model for COVID-19.

Our AB simulation model works as follows. It begins by generating the individual people according to the U.S. census data that gives population attributes including age (see Table A1) and occupational distribution (see Table A4). Thereafter, it generates the households based on their composition characterized by the number of adults and children (see Table A2). The model also generates, per census data, schools (see Table A3) and the workplaces and other community locations (see Table A4). Each individual is assigned a household, while maintaining the average household composition, and, depending on the age, either a school or a workplace (considering employment levels). A daily (hour by hour) schedule is assigned to every individual, chosen from a set of alternative schedules, based on their attributes. The schedules vary between weekdays and weekends and also depend on the prevailing social intervention orders (see Table A5).

Simulation begins on the day when one or more infected people are introduced to the region (referred to as simulation day 1). Simulation model tracks hourly movements of each individual (susceptible and infected) every day, and records for each susceptible the number of infected contacts and their identification at each location. Based on the level of infectiousness of each infected contact (which depends on the day of his/her infectiousness period), the model calculates the daily force of infection received by each susceptible from all infected contacts at all hours of the day [18]. Daily force of infection is considered to accumulate. However, it is assumed that if a susceptible does not gather any additional force of infection (i.e., does not come in contact with any infected) for two consecutive days, the cumulative force of infection for the susceptible reduces to zero. At the end of each day, the model uses cumulative force of infection to calculate the probability of infection for each susceptible. The model updates the infection status of all individuals to account for new infections as well as disease progression of infected individuals. A pseudo-code in Fig. 2 depicts the major elements and structure of the agent-based simulation program.

Fig. 2.

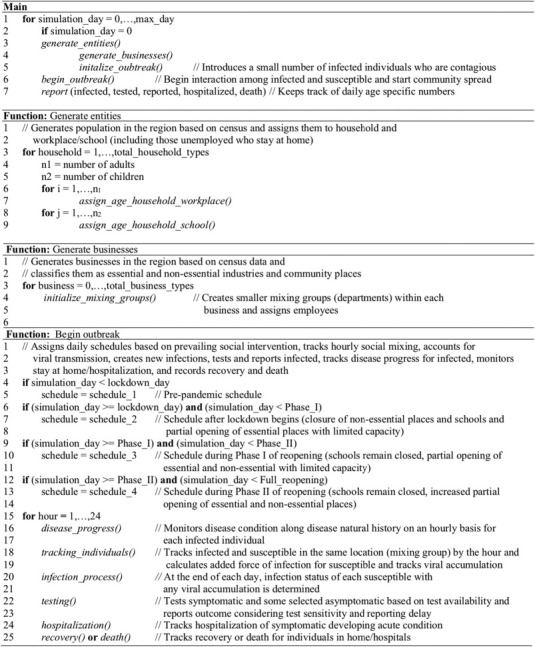
Pseudo-code for agent-based simulation model of COVID-19.

Epidemiological models and other parameters that guide the AB model are described next. Fig. 3 presents a schematic of the disease natural history of COVID-19, parameters of which are given in Table A6. Once infected, an individual simultaneously begins the latency and the incubation periods. The individual becomes infectious after the latent period is complete but displays symptoms (unless asymptomatic) at the end of the incubation period. The period between end of latency and end of incubation is referred to as pre-symptomatic, a time when the infectiousness grows rapidly and almost reaches its peak. Symptomatic cases either follow a non-acute progression (majority of cases, not requiring hospitalization) or acute progression (requiring hospitalization). Cases for whom disease does not become acute, enter a recovery period after infectiousness ends. Those with acute disease progression (generally toward the end of the infectious period) are hospitalized. After the hospital stay period, cases either recover or die. For average lengths of recovery and hospitalized periods that are used in the AB model, see Table A6. There is some evidence based on animal experimentation that recovered individuals may become immune to reinfection [31,40]. But other studies remain inconclusive [32]. Hence, due to lack of established data on this matter, our model considers the recovered cases to be immune to further COVID-19 infections.

Fig. 3.

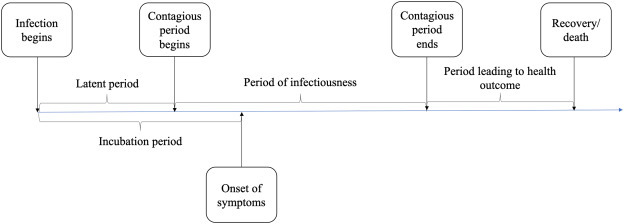
Disease natural history of COVID-19 (see Table A6 for average lengths of the periods).

The duration and intensity of infectiousness is considered to be guided by a lognormal density function (see Fig. 4 ). The function is truncated at the average length of the infectiousness period (which is considered to be 9.5 days). Asymptomatic cases are assumed to follow a similar infectiousness intensity profile but scaled by a factor (C _k in the force of infection calculation (1), see Table A7).

Fig. 4.

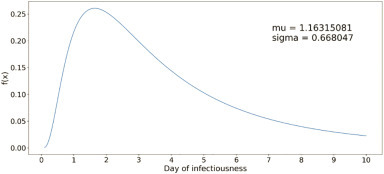
Lognormal distribution function for infectiousness profile of a COVID-19 case.

The AB model estimates the probability of infection for a susceptible i using the accumulated value of daily force of infection (λ _i), which is calculated as follows.

$${\lambda }_i={\sum }_{k\mid h_k=h_i}\frac{I_k{\beta }_h\kappa \left(t-{\tau }_k\right){\rho }_k\left[1+C_k\left(\omega -1\right)\right]}{n_i^{\alpha }}+\sum _{j,k\mid l_k^j=l_i^j}\frac{I_k{\beta }_p^j\kappa \left(t-{\tau }_k\right){\rho }_k\left[1+C_k\left(\omega -1\right)\right]}{m_i^j}.$$ (1)

The first component in (1) accounts for the force experienced by susceptible individual i at home from other infected household members k. The second component captures the force experienced at schools/workplaces/community places for work and also at community places visited for daily errands; this happens when a susceptible i is in the same location type j where infected k is at hour t. The definition and values of the parameters of (1) are given in Table A7. Eq. (1) is a modified version of the force of infection equation given in [18], which has three components that separately calculate force of infection received at home, at indoor workplaces, and at outdoor community. For the sake of simplicity, we have considered only the first two components, home and indoor workplaces, where most of the COVID-19 transmission is assumed to be taking place. We have assumed that the mode of virus transmission at indoor community places that are routinely visited by people as part of their daily errands (like grocery stores, home goods stores, dine-in/take-out restaurants, etc.) is similar to that of indoor workplace transmission.

The force of infection is gathered by a susceptible individual each day from all infected contacts in his/her mixing groups (home, school/workplace, and community places). The cumulative value of λ _i is used at the end of each day to calculate the probability of infection as 1 − exp ^−λ_i.

The AB model incorporates all applicable intervention orders like stay-at-home, school and workplace closure, isolation of symptomatic cases at home, and quarantine of household members of those who are infected. The model also considers: varying levels of compliances for isolation and quarantine, lower on-site staffing levels of essential work and community places during stay-at-home order, restricted daily schedule of people during various social intervention periods, phased lifting of interventions, use of face masks in workplaces, schools and community places with varying compliance levels, and contact tracing with different target levels to identify asymptomatic and pre-symptomatic cases. The timeline for social interventions implemented in the model are summarized in Table A8.

Other salient considerations in the implementation of our AB model are as follows. Across all age groups, 35% of the infected cases were considered asymptomatic [7]. Approximately, 20% (20%) of Florida residents are reported as uninsured and do not have access to a primary care physician [49]. Uninsured people thus considered not to have the doctor referral required for most of the testing facilities in Miami-Dade County, and hence not tested. All symptomatic cases with health insurance were assumed to visit/consult with a doctor. Depending on their symptoms, travel history, and contact history, some of them were given referrals for testing. We considered that only a small percentage of cases visiting/consulting a doctor were given referrals in the early months of the pandemic (until the middle of April 2020), due to the shortage of testing and restrictive CDC guidelines on who could be tested [6]. However, as CDC relaxed its test eligibility guidelines [39] and the capacity to test increased in Florida, we gradually increased the probability of getting a test referral from a doctor closer to 100% by early June 2020 for symptomatic cases (see Table A9). We also considered in our model that a small fraction (reaching only up to 10% over time) of the asymptomatic cases are randomly tested through various community testing protocols, e.g., at elderly care facilities, healthcare facilities, workplaces, etc. Note that we did not consider co-infection, and therefore all cases that were tested in our simulation model had COVID-19. Hence, each test yielded a positive outcome with a probability equal to the test sensitivity (see Table A9). Based on the data reported on Florida COVID-19 dashboard, a test result reporting delay of up to 10 days on average was considered at the start of the pandemic, which was progressively reduced (see Table A9). All symptomatic cases with or without testing were considered to isolate at home with a given probability of compliance. The probability of compliance was considered to vary during the length of the symptomatic period of infection. For this purpose, we divided the symptomatic period into three parts: I, II, and III, and assumed a lower isolation compliance in parts I and III and higher in part II, when the illness is more apparent. See Table A10 for the isolation compliance probabilities. Susceptible members of the households with one or more infected cases are considered to quarantine themselves. We also assumed a level of compliance for quarantine (see Table A10). We used hospitalization and death data reported for Miami-Dade County [20] for each age group to obtain probabilities of hospitalization of the reported cases, and probabilities of death for those who are hospitalized (see Table A11).

Though we have implemented our AB simulation model for a specific region, it is quite general in its usability for other urban regions with similar demography, societal characteristics, and intervention measures. In our model, Table A1, Table A2, Table A3, Table A4 summarize the demographic inputs (age and household distribution, number of schools for various age groups, and number of workplaces of various types and sizes). These data will need to be curated from both national and local census records. Social interventions vary from region to region and hence the data in Table A8 will need to be updated. Similarly, testing availability, test sensitivity, and test outcome reporting delay may also vary significantly from region to region, and thus Table A9 will also need to be updated. The rest of the data (in Table A5, Table A6, Table A7, Table A10, Table A11) are related to epidemiology of COVID-19. These are unlikely to be significantly different, though some adjustments of these based on population demographics may be needed.

Model calibration

The AB model utilizes a large number of parameters, which are demographic parameters, epidemiological parameters, and social intervention parameters. We kept almost all of the above parameters fixed at their respective chosen values and calibrated the model by changing values for only a few. The calibrated parameters include the transmission coefficients used in calculating force of infection at home, work, school, and community places (β _h and β _p ^j). The choice of the values of transmission coefficients was initially guided by [18] and the prevailing estimates of R0, and thereafter adjusted at different points in time during the calibration period (first 127 days of the simulation starting on February 12 until the start of Phase II reopening order on June 5, 2020). The transmission coefficient for school was only applicable for the first 35 days of the simulation period until the beginning of the stay-at-home order on March 17, 2020. The only other parameters that were calibrated are the number of errands in the daily schedules under various intervention conditions and the percentage of workers in essential (e.g., utility services and grocery stores) and non-essential (e.g., offices and restaurants) workplaces who physically reported to work during different intervention periods. Calibration of the above parameters was done so that the daily cumulative numbers of reported infected cases and deaths from the AB simulation model closely match the values published in the Florida COVID-19 dashboard until June 17, 2020. Fig. 5 (a) and (b) show the daily cumulative mean values (with 95% confidence intervals) for the reported infected cases and deaths as obtained from the simulation model. The dotted lines represent the actual numbers reported in the Florida COVID-19 dashboard for Miami-Dade County [22]. Fig. 5 (c) depicts the difference of the 7-day moving average values of simulated and actual reported number of cases.

Fig. 5.

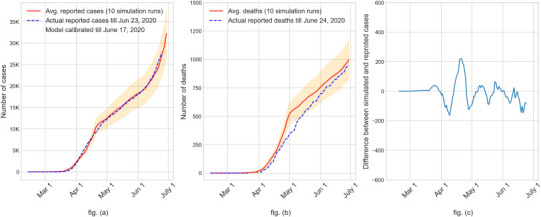
Validation of AB simulation model results using the State reported numbers of ‘cumulative infected cases’ in fig. (a) and ‘cumulative deaths’ in fig. (b) for Miami-Dade County, Florida, USA. Fig. (c) difference of the 7-day moving average between cumulative reported cases from simulation and surveillance (mean difference − 8 and 95% CI (−145 to 130)).

Once the model is calibrated and validated with available reported data on infected and dead, we extended the model into the future to predict outcomes. The only parameters that were altered after the calibration period are to reflect the expected changes in social interventions, e.g., order mandating use of face mask, re-closing some community places, expected increase in contact tracing, and changes in community response via daily schedule restrictions. Hence, the parameters that were changed after the calibration period included those for daily schedules, transmission coefficients, testing and contact tracing rates, and compliance to isolation and quarantine. Most of the parameter values used in the AB model were obtained from government archives and research literature, for which references are provided (see Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11). For some of the parameters for which we could not find an archived data source, we used expert opinion and current media reports.

Results

We used our model to predict the rate of growth of infected cases, reported cases, hospitalizations, and deaths for the case study region (Miami-Dade County, Florida, USA) under various social intervention scenarios. First, we allowed the model to mimic retrospectively the progress of the pandemic under three separate intervention scenarios for a large number of days. The scenarios are: stay-at-home order continued without reopening until pandemic subsides, Phase I of reopening continued without moving into Phase II, and Phase II of reopening continued without the use of face mask or any other changes. Thereafter, we conducted a prospective examination of the impact we are likely to see in coming days from the use of face masks and contact tracing.

We first present a summary of the key results of our study (see Table 1 ), from which a number of key insights can be derived that may apply to other similar urban regions experiencing respiratory/influenza type virus outbreaks. Early imposition of stay-at-home order appears to have been quite effective in first flattening and then reversing the growth curve. Per our model, if the stay-at-home order was allowed to remain enforced, the pandemic would have subsided with a relatively low percentage of the population (5.8%) infected and approximately 0.04% dead within six months of inception; 50 or below daily new infections was used as the criterion to consider that pandemic has subsided in Miami-Dade County. If the extent of social mixing akin to Phase II reopening of Florida is in place for an urban region (without the use of face mask and contact tracing), the pandemic would likely have raged for 8–9 months and subside only after reaching herd immunity with over 75% of the population infected and 1.3% of the population dead. Universal use of face masks of surgical variety was shown by the model to reduce average total infected, hospitalized, and dead by 20%, 19%, and 15%, respectively. Aggressive contact tracing with a goal to identify 50% of the asymptomatic and pre-symptomatic was also projected to have a very significant positive impact with an average reduction of 66% of total infected. The average reductions in total infected with 40%, 30%, and 20% contact tracing targets were found to be 58%, 41%, and 14%, respectively.

Table 1.

Summary of the key results from the AB simulation model implemented on a sample urban outbreak region (Miami-Dade County of Florida, USA) with population of 2.8 million.

Interventions ➞ Outcomes ⬇	If Stay-At-Home order were not lifted (started March 17, 2020)	If Phase I reopening continued (started May 18, 2020)	If Phase II reopening continues without alterations (started June 5, 2020)	If Phase II reopening continues with mandatory use of face masks (started June 25, 2020)	If Phase II reopening continues with use of face masks and contact tracing with 50% target (starting June 30, 2020)
Time when pandemic subsides below a threshold	Early Aug. 2020	July 2021	End-Oct. 2020	End-Nov. 2020	End-Sept. 2020
Total number of infections (95% C.I.)	162K (136K – 188K)	600K (530K – 670K)	2.17M (2.16M – 2.18M)	1.74M (1.73M – 1.75M)	581K (447K – 716K)
Total number of reported cases (95% C.I.)	23K (19K – 27K)	220K (186K – 254K)	866K (854K – 877K)	714K (702K – 726K)	247K (178K – 316K)
Total number of hospitalizations (95% C.I.)	4.1K* (3.5K – 4.8K)	37.5K* (31.7K – 43.4K)	149K* (147K – 151K)	120K* (119K – 122K)	35.2K* (25.6K – 44.8K)
Total number of deaths (95% C.I.)	1K** (0.9K – 1.2K)	9.4K** (7.9K – 10.8K)	36.4K** (35.8K – 36.9K)	29.7K** (29.3K – 30.2K)	8.8K** (6.5K – 11.1K)

*The numbers presented in the table were computed in mid-late June. Per State reported data, in the months of July and August, the probability of hospitalization reduced significantly across all age groups by over 80%. Hence, our estimates for total number of hospitalizations are much higher than the expected outcome.

**Since the deaths are simulated by applying a probability on those hospitalized, estimates of the number of deaths from our model are much higher than the expected outcome.

In what follows, we expound the results from our study. Fig. 6, Fig. 7 show the simulation results for the retrospective examination scenarios with average values (with 95% CIs in shade) of daily cumulative cases of actual infected, reported, hospitalized, and dead. The blue dotted lines represent the actual numbers of infected and dead as reported in the Florida COVID-19 dashboard till June 24 (our calibration period was till June 17).

Fig. 6.

Growth of actual and reported infected cases (fig. (a)) and hospitalizations and deaths (fig. (b)) if stay-at-home order were not lifted.

Fig. 7.

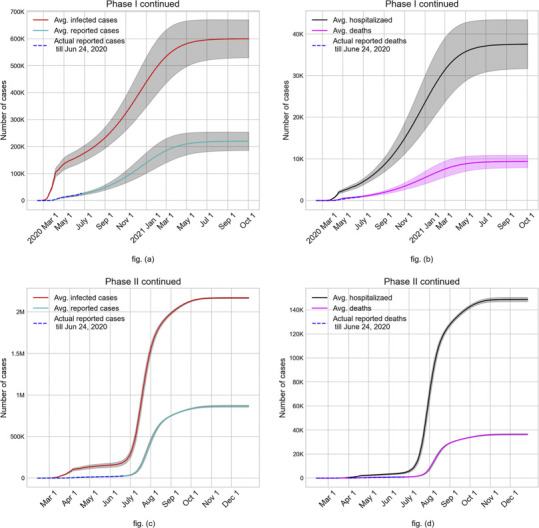
Case study outcomes (average values with 95% C.I.) of continuing with Phase I reopening (fig. (a) and fig. (b)) and Phase II reopening without face mask and contact tracing (fig. (c) and fig. (d)).

Fig. 6 shows a strong influence of continuing with the stay-at-home order in curbing the COVID-19 growth within approximately 6 months from its inception with on average less than 5.8% of the population infected, 0.15% hospitalized, and 0.037% dead; 50 or below daily new infections was used as the criterion to consider that pandemic has subsided in Miami-Dade County. Such a quick suppression of a virus outbreak always leaves the possibility of resurgence, for which an effective plan of contact tracing, testing, isolation, and support for those isolated (when needed) should be in place.

Fig. 7 shows the expected outcomes of continuing with the Phase I order and the Phase II order. Fig. 7(a) demonstrates a clear upward swing of the number of infected by the end of May as a result of Phase I reopening, in contrast to stay-at-home scenario where the numbers actually begin to drop at the end of May. The upward trajectory continues for nearly 12 months after reopening before curving down and subsiding the pandemic in July 2021. This scenario would have resulted in on average approximately 21% of the population infected (see fig. (a)), 1.3% hospitalized, and 0.34% dead (see fig. (b)). Figs. 7(c) and 7(d) depict the rather grim outcome of continuing with Phase II order without face mask where over 75% of the population gets infected, 5.5% of the population hospitalized, and 1.3% dead. The steep multi-fold increase in the number of infected in late June after the Phase II reopening in June 5 results in an expected end of the pandemic via herd immunity by late October 2020. We note that at the time of implementing the simulation model (late June 2020) to obtain the above results, the percentage of hospitalized people that died was quite high, especially at the higher age groups. However, by the time of revising the manuscript per reviewer comments and resubmission (early September 2020), the death rate of hospitalized COVID-19 cases has dropped significantly. Hence our model's predictions for the number of deaths are much higher than what is expected.

Hereafter, we used our model in a prospective examination of the pandemic progression under Phase II with the use of face mask and contact tracing. Universal use of face mask in workplaces, schools and community places, where maintaining social distancing is not always feasible, was added to the Phase II guidelines starting June 25, 2020 in Miami-Dade County. In an article that analyzed data from the literature for SARS, MERS, and COVID-19 outbreaks, it is shown that the average value of the adjusted odds ratio (aOR) of getting an infection after wearing surgical variety face masks versus without wearing face mask is 0.33 [12]. This can be interpreted as the likelihood of getting infected if wearing a surgical variety face mask is one third of what it would be for not wearing a mask. Hence, we considered a 67% reduction in the transmission coefficient (β _p ^j) used in calculating the force of infection (see eq. (1)), assuming a 100% compliance in the use of surgical variety masks at workplaces, schools and community places. We also tested the impact of 30% and 45% reductions in the transmission coefficient value (β _p ^j), which translate to approximately 50% and 70% compliance for face mask usage, respectively. The anticipated impact of face mask usage together with Phase II order on the average cumulative numbers of infected are shown in Fig. 8(a). It also depicts the risk difference between the average values of cumulative infected without and with the universal use of face mask. It may be noted that since the infections grow slower with the use of face mask, the cumulative risk difference rises to almost 875 K in the middle of August and then settles down close to 430 K, when pandemic is predicted to subside by the end of November 2020. Fig. 8(b) depicts the daily values of the average infected for Phase II without and with the universal face mask policy. As expected, the peak of daily infections with face mask usage shifted to a slightly later date and the downward trend began after a smaller percentage (31%) of the total population are infected compared to 36% without the use of face mask.

Fig. 8.

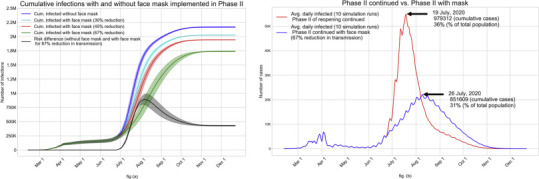
(a): Impact of face mask usage starting June 25 (together with Phase II order) on the average cumulative infected for all compliance levels; fig. (b): Impact of universal use of face mask on the average daily infected.

Though the universal use of face mask together with the Phase II order is likely to reduce a large number of infections (an estimated 430 K), this strategy still leaves a high percentage (63%) of the total population infected before the pandemic is predicted to subside, likely after reaching herd immunity. While a vaccine is still unavailable, perhaps the only other way to reduce the size of this impacted population is through contact tracing. We used our model to examine a number of different contact tracing strategies by adding them to the scenario of Phase II with universal face mask usage. We implemented contact tracing starting June 30 with a number of different targets (20%, 30%, 40%, and 50%) of identifying asymptomatic and pre-symptomatic cases. The impact on the average cumulative values of actual infected and the reported cases are shown in Figs. 9(a) and 9(b). It can be observed that contact tracing can significantly reduce the number of people infected. With the 50% target for contact tracing (which is an aggressive goal), the average cumulative number of infected by the time the daily number of new infections falls below a threshold (possibly by the end of September 2020) would reduce to 581 K from over 1.73 million with Phase II and face mask alone (a 66% reduction). The corresponding reductions in cumulative infections and the associated times for pandemic to subside that can be expected from contact tracing targets of 40%, 30%, and 20% are 58% (mid-October), 41% (mid-November), and 14% (mid-December). It may also be noted that the impact of contact tracing target on the reduction of cumulative infected is nonlinear. Figs. 9(c) and 9(d) show the average cumulative numbers of hospitalizations and deaths. Expected reductions in hospitalization achieved from contact tracing targets of 50%, 40%, 30%, and 20% compared to the use of face mask alone (during Phase II) are 71%, 62%, 43%, and 14%, respectively. The corresponding expected reductions in the number of deaths are 70%, 62%, 43%, and 14%, respectively. We note again that since we completed our simulations runs in late June, the death rates of those hospitalized for all ages have dropped multi-fold during the months of July and August. Thus, our predicted numbers of deaths as depicted in Fig. 9(d) are much higher than what is expected.

Fig. 9.

Impact of contact tracing, starting on June 30, during Phase II with universal face mask usage.

Fig. 9(e) shows the impact of contact tracing starting on June 30, 2020 on the average daily infected values. It is interesting to note from the figure that an aggressive contact tracing/testing and isolation of those found infected appears to be capable of quickly turning the tide on new infections. Various COVID-19 dashboards maintained by government and private agencies have been reporting data including numbers of infected (tested positive), hospitalized, and dead. But the actual numbers of infected people in the outbreak regions remain a subject of expert opinion. Speculations abound place the ratio of actual to reported numbers of infected to as high as 10. As our simulation model yields estimates of the actual number of infected, we calculated the daily values of the ratio of average actual infected to average reported for a few scenarios: Phase II continued, Phase II with universal face mask usage, and Phase II with universal face mask usage and contact tracing with a 30% target. Values of these ratios are shown in Fig. 9(f). It can be seen that in the initial days of the pandemic, the ratios are very high (close to 30), which we believe is due to under testing together with long reporting delay. However, as the testing of the symptomatic increased and reporting delay decreased over time, the ratios came down sharply to 10 and continued to fall to near 7. The ratios are expected to further decrease gradually to about 2.5 as the predicted values of daily new infections begin to fall starting late July and early August.

Discussion

We have presented in this paper an agent-based simulation model for COVID-19 pandemic to serve as a policy evaluation tool for public health decision makers. We have implemented the model on one of the epicenters of COVID-19 outbreak in the U.S. (Miami-Dade County of Florida, an urban metropolitan region with 2.8 million population). The model implementation demonstrates the efficacy of our model in both retrospective and prospective assessment of a number of social intervention strategies via their impact on the numbers of infected, hospitalized, and deaths. We have analyzed sensitivity of a number of intervention parameters (partial closures, compliance of face mask usage, and contact tracing targets) in order to support the task of decision making by our public health policy makers.

Our simulation model is written in C/C++ and implemented using GNU General Public License [25].

Our model offers the flexibility to implement a variety of societal conditions including test availability, test reporting delay, stay-at-home order, partial reopening, selective closures of schools and workplaces when infections reappear, use of face mask with various levels of compliance, contact tracing, vaccinations, and use of antivirals. Only a subset of these conditions has been examined and reported in this paper. At the time of revising the manuscript for resubmission for publication, in order to retool the model to reflect changing conditions, we further calibrated our model until July 15, 2020. The recalibrated model was validated by comparing age-specific values of average number of cases reported, hospitalized, and dead for months March to September with the data published in the Florida COVID-19 dashboard for Miami-Dade County until September 30, 2020 [22]. See Fig. A2 in Appendix for monthly comparisons. Fig. 10 (a) shows the cumulative values (with 95% confidence interval) of the average reported cases as obtained from the recalibrated simulation model. The dotted line represents the actual numbers of reported cases from the Florida COVID-19 dashboard. Fig. 10 (b) shows the error between simulated and surveillance values for the cumulative number of reported cases.

Fig. 10.

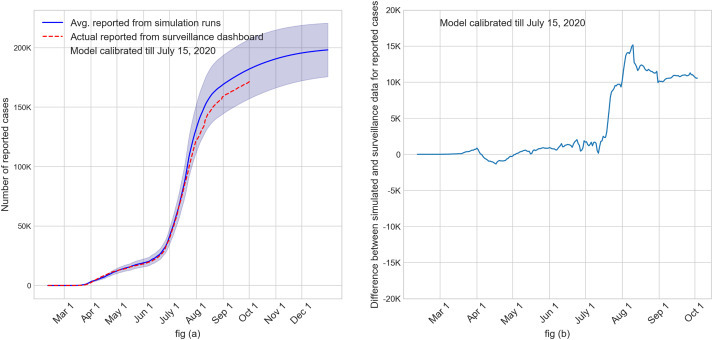
Validation of calibrated simulation model using state reported surveillance numbers for cumulative reported cases. Fig. (a): Cumulative plot of the average reported cases from simulation (with 95% CI) along with surveillance data. Fig (b): Plot of the difference between cumulative values of average reported cases from simulation and surveillance.

Our agent-based model has several limitations. First and foremost, the simulation model is an abstraction of how a pandemic impacts a large and complex society. Though our model deliberately introduces some variabilities, somewhat pre-defined daily schedules are used to approximate a highly dynamic contact process of an urban region. Also, the contact process does not account for significant variabilities in the types and lengths of interactions even within each mixing groups. We did not assign geographic locations (latitude and longitude) for households, businesses, schools, and community places, and assumed them to be uniformly distributed over the region. It is common for urban population centers and associated establishments to grow in clusters, for which the contact patterns are expected to be different from those in uniformly dispersed regions. We did not consider special events like parties, games, and street protests, some of which are known to have caused superspreading of the virus and case increases. Finally, and perhaps most importantly, the model uses a large number of parameters (listed in Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11 in the Appendix), and hence the model predictions are influenced by the choice of those values. We have used published data from the government archives and research literature for most of the parameters. In absence of established data source, we have used expert opinion and media reports. Hence, the model results, as presented in this paper, are only expected outcomes based on currently available information.

Each scenario of our case study with 10 replicates (with different seeds) takes approximately 8–12 h to run in a standard desktop computer with Intel Core i7 with 16GB memory. In the interest of presenting our observations quickly to the public health decision makers, while COVID-19 is still rampant in the region, we chose to use a limited number (10) of replicates. As the main purpose of this paper is to conduct a broad what-if analysis, we do not believe that use of a small number of replicates has negatively influenced our observations. The trends and observations derived from our results are only intended to be used for planning and guidance of public health decision makers.

As part of our continuing (future) work, we plan to use our model to examine the impact of reopening of K-12 schools and colleges/universities for the new academic year, which began at the end of August and early September. We also plan to use our AB model to assess efficacy of various prioritization strategies (based on age, risk, and work groups) for the vaccines that are anticipated to be available in limited quantities by the beginning of 2021.

Declaration of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix

Step-by-step approach for implementing the AB simulation model for a pandemic outbreak region.

In what follows, we present a detailed outline of a step-by-step approach for implementing our AB simulation model for a pandemic outbreak in a region caused by influenza or respiratory viruses, as in COVID-19 that is affecting the world. The main body of the paper uses Miami Dade County of Florida, USA as the case study region. Here we use another region, Boston city/Suffolk County, as an example.

Step 1: Model input data gathering.

The following data must be gathered as the first step for applying our AB simulation model to another region like Boston city/Suffolk County.

• 1) Population distribution by age: U.S. census bureau provides county specific age distribution data. For the chosen region, e.g., Boston city/Suffolk county, this information can be found in [A1].
• 2) Household composition of adults and children: Family compsition with sizes of adults and children may not be directly available for all regions, it can be calculated using other sources, like [A2], which provides Boston's households by type and size. Composition of adult and children in these households can be assumed to be similar to another comparable city/county region in the U.S for which data is available.
• 3) Distribution of categories of workplaces: U.S. Census bureau provides, for various industry types, the number of establishments and the corresponding size of employment[A3]. This national data can be proportioned for the specific region if county data is not avaialble.
• 4) Characterization of workplaces (essential or non-essential): Essential and non-essential workplace characterization can be gathered from state level data, if available. In most regions within the U.S., this characterization can be assumed to be similar. A list of essential and non-essential characterization for the state of Massachusetts can be found in [A4].
• 5) Employment levels at various workplace categories, and unemployment: This data is provided by U.S. Census for some counties and states. Refer to [A3] for data for Boston. When this data is unavailable, national estimates can be used in proportion to the population of the region.
• 6) Percentage uninsured: U.S. Census data's quick facts provides this information [A5].
• 7) Distribution of schools (K-12, colleges and universities): Total number of schools and staffing levels are categorized as public and private. For information on public schools, see [A7], and for private schools, see [A8].
• 8) Distribution of school attendance (K-12, colleges and universities): Enrollment levels in public and private schools for K-12 and universities can be found in [A6].
• 9)
  Social intervention policies: Multi-phased policies are commonly used in most regions in the U.S. However, the dates and the nature of these intervention policies vary widely from region to region. For example, Alaska, Arizona and Georgia, among others, didn't have a mandatory face mask policy, while other states did. Some states did not have a statewide policy, but each municipality adopted their own.

  • a)
    Lockdown policy: Time-varying policy applicable for Boston city/Suffolk County can be found in [A11].
  • b)
    Policies for phased lifting of social interventions: Time-varying policy applicable for Boston city/Suffolk County can be found in [A11].
  • c)
    Use of face mask: Boston implemented a facemask policy in early May in an executive order by the State [A9].
  • d)
    Implementation of contact tracing: Massachusetts state government provides a dashboard on the community health outcomes for COVID-19. Details on the success of contact tracing in the communities along with the outcome measures varying over time can be found in [A10].
  • e)
    Policy for returning to school: School reopening policies also widely vary from state to state and also among counties within a state. Information on Boston's public school reopening policy can be found in [A12]. It is important to frequently check sources on school policy as they are transient. For example, Boston planned to reopen on October 15, but shifted to October 22 after seeing an increase in the number of cases.
• 10) Time varying testing of symptomatic and asymptomatic: Limited testing availability has been a serious concern in many U.S. regions that suffered from a high level of disease spread. Time varying data on test availability and test outcome reporting delay are difficult to find in indexed literature during a pandemic. Hence, these can be assumed from regional news reports, test reporting data, and/or other grey literature.
• 11) Number of reported, hospitalized and deaths: Daily data and archived data on the number of people reported positive, hospitalized and dead can be found from dashboard in [A10].
• 12) Probability of hospitalization for reported cases and probability of death for hospitalized: This can be calculated from [A10] based on age specific reporting.

The information contained in the following tables for Miami Dade County are likely to be same for other regions like Boston city/Suffolk County.

• 13)Daily schedules for people can be assumed to be same as in Table A5.
• 14)Disease natural history parameters for COVID-19 can be assumed to be same across regions within a country, see Table A6.
• 15)Some of the parameters in Table A7 for calculating the force of infection need to be calibrated (see Step 3). However, the remaining parameters in Table A7 can be assumed to be same.
• 16)Self-isolation compliance for symptomatic cases, and quarantine compliance for household members can be assumed to be same for different urban regions within a country, as in Table A10.

Step 2: Updating the simulation model.

Once the input data collection is complete, the next step is to update the model parameters as follows.

• 1) Update the simulation model with all gathered input data from step 1: After gathering data, it needs to be curated and transformed into .txt files to be read by the simulation model. Some of the data are directly coded in the model, where applicable.
• 2) Decide simulation begin date: Simulation begin date depends on the outbreak region and is based on the date of the first reported case. Up to 14 days before the first reported case can be used as a potential date for simulation model to begin.
• 3) Decide simulation end date: Simulation end date is chosen as desired by the modeler.
• 4)Number of initial infected cases: Most Departments of Health (DOH) provide a count and characterization of the number of initial infected cases with travel histories. One can identify these initial infected cases during the first month of the outbreak and use those cases to initiate social mixing and community spread.

Step 3: Calibrate and validate simulation model.

Once the simulation model is updated with the input data for the region, the model is calibrated using a small applicable subset of input data and the model output is validated with actual surveillance data from the region, as follows.

• 1)Generate multiple seeds for the uniform random variables that are used to calculate the probabilities of infection, hospitalization, death, testing, symptomatic, disease severity, test sensitivity, compliance for isolation and quarantine, among others. Simulation output from each seed is considered a replicate. Using output data from all replicates, an average value and a corresponding confidence interval for each output measure are calculated.
• 2)A set of initial values of the transmission coefficients for home, school, work, and community places are assumed (based on current literature and published models for outbreaks of similar diseases). These transmission coefficients (along with other parameters, see Table A7) are used for calculating force of infection, which is then used to calculate the probability of infection. Different sets of transmission coefficient values are selected for different reference points in time in the simulation, depending on changes in social intervention status and significant current events. For example, the transmission coefficients are appropriately calibrated (reduced) on the day universal use of facemask is announced. Also, percentage testing of asymptomatic and pre-symptomatic are increased when contact tracing begins. Street protests combined with Independence Day holiday in early July 2020 are examples of current events that may require adjustment of transmission coefficient values.
• 3)Other parameters that are considered suitable for the AB model calibration are probability of running errand that guides daily schedule and probability of employees reporting to work for essential and non-essential businesses. These values can also be assumed to change over time during a pandemic depending on the phased intervention policies implemented by the government in the outbreak region.
• 4)The simulation is calibrated for a chosen period. In this study, the model was calibrated up to July 15th, as reported data was available until that date for validation purposes at the time of model calibration.
• 5)Results for reported cases, hospitalized, and dead for all age groups are gathered from the simulation model for each seed.
• 6)Average values (with confidence interval) are computed for the numbers of reported, hospitalized and dead.
• 7)For model validation, the simulated average values for the reported, hospitalized, and dead and compared with actual surveillance data.
• 8)Alter calibration parameters as needed to obtain desired level of validation accuracy. Measure validation accuracy is calculated as the difference in the seven-day moving average between simulated and surveillance data.

Step 4: Implement calibrated model for prediction

• 1)Run calibrated simulation model for all seeds for a desired prediction period beyond the calibration/validation time.
• 2)Extract age specific data for total infected, reported cases, hospitalized, and dead from simulation for each seed.
• 3)Report mean and confidence interval.

References for step by step approach

[A1] United Census Bureau. ACS Demographic And Housing Estimates: 2019, https://data.census.gov/cedsci/table?q=Boston%20city,%20Suffolk%20County,%20Massachusetts&tid = ACSDP1Y2019.DP05&hidePreview = false; [accessed 10.06.2020].

[A2] The Boston Planning and Development Agency. Boston by the numbers 2018, http://www.bostonplans.org/getattachment/3e8bfacf-27c1-4b55-adee-29c5d79f4a38; [accessed 10.06.2020].

[A3] United Census Bureau. Annual Business Survey: Statistics for Employer Firms by Industry, Sex, Ethnicity, Race, and Veteran Status for the U.S., States, Metro Areas, Counties, and Places: 2017, https://data.census.gov/cedsci/table?q=employment%20size%20boston%20&t=Employment&tid=ABSCS2017.AB1700CSA01&hidePreview=false; [accessed 10.06.2020].

[A4]  Mass.gov. COVID-19 Essential Services, https://www.mass.gov/info-details/covid-19-essential-services; [accessed 10.06.2020].

[A5] United Census Bureau. QuickFacts Boston City, Massachusetts, https://www.census.gov/quickfacts/bostoncitymassachusetts#qf-flag-X; [accessed 10.06.2020].

[A6] United Census Bureau. School Enrollment, https://data.census.gov/cedsci/table?q=Boston%20city,%20Suffolk%20County,%20Massachusetts&t = Education&tid = ACSST1Y2019.S1401&hidePreview = false; [accessed 10.06.2020].

[A7] BPS Communications Office. Boston Public Schools At A Glance 2019–2020, https://www.bostonpublicschools.org/cms/lib/MA01906464/Centricity/Domain/187/BPS%20at%20a%20Glance%202019-20_FINAL.pdf; [accessed 10.06.2020].

[A8] Private School Review. Largest Massachusetts Private Schools, https://www.privateschoolreview.com/school-size-stats/massachusetts; [accessed 10.06.2020].

[A9]  AARP.org. State-by-State Guide to Face Mask Requirements, https://www.aarp.org/health/healthy-living/info-2020/states-mask-mandates-coronavirus.html; [accessed 10.06.2020].

[A10]  Mass.gov. COVID-19 Response Reporting, https://www.mass.gov/info-details/covid-19-response-reporting; [accessed 10.06.2020].

[A11]  Mass.gov. COVID-19 State of Emergency, https://www.mass.gov/info-details/covid-19-state-of-emergency; [accessed 10.06.2020].

[A12] Boston Public Schools. Important Information About School Reopening, https://www.bostonpublicschools.org/reopening2020; [accessed 10.06.2020].

Fig. A1.

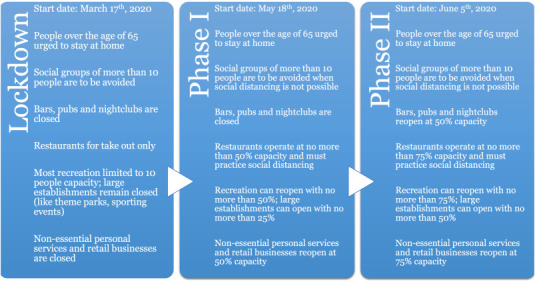
Florida's phased social intervention plan for COVID-19 pandemic [44].

Fig. A2.

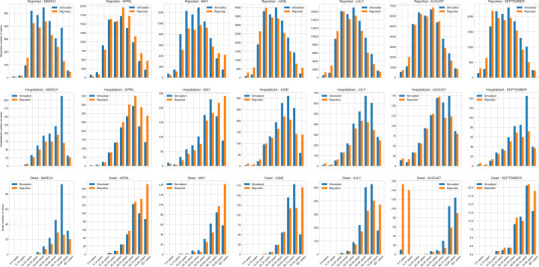
Validation of simulation model by comparing monthly average values of reported cases, hospitalized, and deaths (in orange) with the corresponding reported values from Florida COVID-19 Dashboard (in blue). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Table A1.

Age distribution of Miami-Dade population [47].

Age range	Percentage
0–5	6.9
6–9	4.2
10–14	5.8
15–17	3.5
18–22	6.1
23–29	9.5
30–64	47.8
65–99	16.2

Table A2.

Household composition of adults and children in Miami-Dade County of Florida, USA [37].

Household type	Percentage
1 adult 0 children	23
1 adult 1 children	1
2 adults 0 children	26
1 adult 2 children	3
2 adults 1 children	6
3 adults 0 children	10
1 adult 3 children	1
2 adults 2 children	6
4 adults 0 children	8
1 adult 4 children	1
2 adults 3 children	8
3 adults 3 children	4
4 adults 3 children	3

Table A3.

Distribution of educational institutions in Miami-Dade County; all children ages 6–22 are assumed to attend school; among all children in ages 0–5, only 50,540 are assumed to attend school; the remaining children stay at home [[36], [50]].

Age range	School type	Percentage	Number of schools	Number of classes in each school	Average number of students in each class	Average number of students in attending each school
0–5	Pre-K	26	190	14	19	266
6–9	Elementary	16	323	20	19	380
10–14	Junior	22	147	44	25	1100
15–17	Senior	13	232	22	19	418
18–22	College/University	23	9	375	50	18,750

Table A4.

Distribution of different types of workplaces in Miami-Dade County. All industries and community places are classified into essential or non-essential. Essential industries remain functional with a percentage of their workforce reporting during interventions like stay-at-home or phased reopening. Non-essential industries are considered to operate remotely. Essential industries include wholesale trade, waste management and remediation services, agriculture, forestry, fishing and hunting, mining, quarrying, oil and gas extraction, utilities, construction, manufacturing, transportation and warehousing. Non-essential industry includes finance and insurance, real estate and rental and leasing, professional, scientific and technical services, management of companies and enterprises, administrative and support for waste management and remediation services, educational services, other services except public administration. Essential community includes grocery stores, convenience stores, pharmacies and drug stores, home centers, health care and social assistance. Non-essential community includes retail, arts, entertainment and recreation and accommodation and food services. For details on education institutions, see Table A3. The total employed population in Miami-Dade County is 1,171,404 [[45], [46], [48]].

Category of workplaces	Number of establishments	Average number of people working in each	Number of mixing groups in each establishment	Average number of people in each mixing group
Essential industry	19,378	6	1	6
Essential industry	356	100	2	50
Essential industry	205	200	4	50
Essential industry	81	400	8	50
Essential industry	12	600	12	50
Essential industry	6	1000	20	50
Non-essential industry	37,002	6	1	6
Non-essential industry	546	100	2	50
Non-essential industry	346	200	4	50
Non-essential industry	100	400	8	50
Non-essential industry	26	600	12	50
Non-essential industry	8	1000	20	50
Essential community	10,709	6	1	6
Essential community	237	100	2	50
Essential community	236	200	4	50
Essential community	41	400	8	50
Essential community	17	600	12	50
Essential community	19	1000	20	50
Non-essential community	14,571	6	1	6
Non-essential community	601	100	2	50
Non-essential community	296	200	4	50
Non-essential community	87	400	8	50
Non-essential community	32	600	12	50
Educational institution	190	42	14	3
Educational institution	323	60	20	3
Educational institution	147	176	44	4
Educational institution	232	66	22	3
Educational institution	9	1500	375	4

Table A5.

Daily schedules for adults and children.

	Employed Adults	Unemployed Adults	Children
Weekday (regular schedule before social intervention)	•At work from 8 AM – 4 PM •One errand (for one hour) between 5 and 7 PM •Home from 7 PM – 8 AM	•Runs 3 errands during three randomly selected hours between 8 AM and 7 PM •Home from 7 PM – 8 AM	•At school from 8 AM – 3 PM •Home 4 PM – 8 AM
Weekend (regular schedule before social intervention)	•Runs 3 errands during three randomly selected hours between 8 AM and 7 PM	•Runs 3 errands during three randomly selected hours between 8 AM and 7 PM	•Engages in 3 activities from 8 AM - 7 PM
If isolated or Quarantined or under stay-at-home order	•Runs one errands during a randomly selected hour between 8 AM and 7 PM with probability 0.2 (and applicable compliance probability)	•Runs one errands during a randomly selected hour between 8 AM and 7 PM with probability 0.2 (and applicable compliance probability)	•Stay at home
If isolated or Quarantined or otherwise under Phase I or Phase II order	•Runs 2 errands during two randomly selected hours between 8 AM and 7 PM with probability 0.4 in Phase I and 0.8 in Phase II (and applicable compliance probabilities for isolated and quarantined)	•Runs 2 errands during two randomly selected hours between 8 AM and 7 PM with probability 0.4 in Phase I and 0.8 in Phase II (and applicable compliance probabilities for isolated and quarantined)	•Stay at home

Table A6.

Disease natural history parameters of COVID-19.

Disease natural history parameters	Average value
Latent period	3 days [27]
Incubation period	5.5 days [38]
Contagious period	9.5 days [27]
Asymptomatic percentage	35% [7]
Health outcome parameters	Average value
Percent of Florida residents without health insurance	20% [49]
Time to visit doctor for symptomatic	1–2 days after onset of symptoms
Symptomatic (who visits/consults doctor) not hospitalized assumed to be recovered for normal activity	14 days from after doctor visit
Symptomatic who do not visit/consult doctor assumed to resume normal activity	8.5 days after onset of symptoms
Time to hospitalization	5–9 days after onset of symptoms [23]
Hospitalized period / time to recovery/death for hospitalized	9–12 days after hospitalization [8]

Table A7.

Parameters of the force of infection (eq. (1)).

Parameter	Description	Value
Ik	Infected status of an individual k	1 if infected and 0 otherwise
βh	Transmission coefficient at homea		Period
		0.7	Before stay-at-home orders
		0.015	During stay-at-home orders
		0.5	During Phase I
		0.5	During Phase II
βpj	Transmission coefficient at school, work, and community placesa	School	Work	Community	Period
		0.7	0.8	0.18	Before stay-at- home order
		0.0	0.025	0.0065	During stay-at- home order
		0.0	0.5	0.057	During Phase I
		0.0	0.5	0.22	During Phase II
κ(t)	Infectiousness at time t (t denotes the elapsed time after completion of latency)b	Lognormal function value at t with μ = 1.16315081 and σ = 0.668047
ρk	Relative infectiousness of individual kc	1
Ck	Scaling factor for mild/asymptomatic vs severe infectionc	1 if severe/symptomatic, 0 for mild/asymptomatic
ω	Scaling factor for infectiousness for a mild vs severe infectionc	2 for severe infection relative to a mild one
α	Scaling factor for household sizec	0.8
ni	Number of people in the household of individual i	Calculated from simulation
mij	Number of people in the place type j where individual i is	Calculated from simulation

^aChoice of these parameters were guided by Ferguson [18], literature estimates of R0 for SARS-CoV-2, and prevailing interventions. Transmission coefficients were subsequently calibrated to arrive at the values given here.

^bParameters of the lognormal distribution function were selected to have the mean length of infection as 4 days and a standard deviation of 3 days [27].

^cSelected from Ferguson [18].

Table A8.

Social intervention order timeline for Miami-Dade County [44].

Intervention policy implemented at Miami-Dade County, Florida, U.S.	Date of implementation	Day of Simulation
Stay at home policy	March 172,020	35
Phase I reopening	May 182,020	97
Phase II reopening	June 52,020	115
Mandatory usage of Face mask	June 252,020	135
Contact tracing (assumed to begin)	June 302,020	140

Table A9.

Time varying data of testing rate, test sensitivity, and test result reporting delay. (values are based on expert opinion, news reports, and Florida COVID-19 Dashboard data [22])

Date range	Proportion of asymptomatic cases randomly tested (before contact tracing)	Proportion of symptomatic cases who are tested⁎	Test sensitivity	Test result reporting delay
Feb 12, 2020 – March 12, 2020	0.05	0.2	0.8	10
March 13, 2020 – April 11, 2020	0.05	0.2	0.8	7
April 12, 2020 – May 11, 2020	0.06	0.3	0.8	7
May 12, 2020 – June 5, 2020	0.07	0.6	0.8	6
June 6, 2020 – July 10, 2020	0.1	0.85	0.8	2
July 11, 2020 onwards	0.1	0.9	0.9	2⁎

^⁎Test result reporting delay appeared to have increased again to up to a week or more in Florida, but not implemented in the model.

Table A10.

Self-isolation compliance for symptomatic cases and quarantine compliance for household members.

Parameter	Value⁎
Isolation compliance of adults in Part I of symptomatic period	75%
Isolation compliance of adults in Part II of symptomatic period	95%
Isolation compliance of adults in Part III of symptomatic period	90%
Isolation compliance of children in Part I of symptomatic period	80%
Isolation compliance of children in Part II of symptomatic period	99%
Isolation compliance of children in Part III of symptomatic period	95%
Duration of Part I of symptomatic period	1.5 days
Duration of Part II of symptomatic period	3.5 days
Duration of Part III of symptomatic period	2 days
Quarantine compliance of susceptible in households with infected	75%

^⁎Values are assumed based on expert opinion.

Table A11.

Probability of hospitalization for reported cases and probability of death for hospitalized [21].

Age range	Probability of hospitalization among those reported	Probability of death among those hospitalized
0–4	0.08	0.00
5–14	0.03	0.00
15–24	0.04	0.01
25–34	0.06	0.03
35–44	0.10	0.05
45–54	0.14	0.07
55–64	0.20	0.13
65–74	0.34	0.25
75–84	0.46	0.37
85–100	0.49	0.57