Abstract
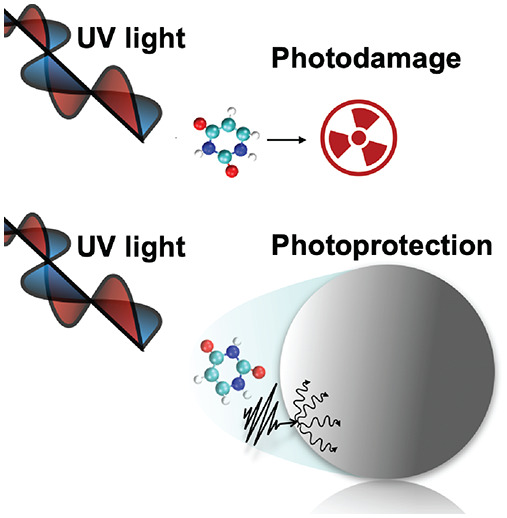
We analyze how the photorelaxation dynamics of a molecule can be controlled by modifying its electromagnetic environment using a nanocavity mode. In particular, we consider the photorelaxation of the RNA nucleobase uracil, which is the natural mechanism to prevent photodamage. In our theoretical work, we identify the operative conditions in which strong coupling with the cavity mode can open an efficient photoprotective channel, resulting in a relaxation dynamics twice as fast as the natural one. We rely on a state-of-the-art chemically detailed molecular model and a non-Hermitian Hamiltonian propagation approach to perform full-quantum simulations of the system dissipative dynamics. By focusing on the photon decay, our analysis unveils the active role played by cavity-induced dissipative processes in modifying chemical reaction rates, in the context of molecular polaritonics. Remarkably, we find that the photorelaxation efficiency is maximized when an optimal trade-off between light–matter coupling strength and photon decay rate is satisfied. This result is in contrast with the common intuition that increasing the quality factor of nanocavities and plasmonic devices improves their performance. Finally, we use a detailed model of a metal nanoparticle to show that the speedup of the uracil relaxation could be observed via coupling with a nanosphere pseudomode, without requiring the implementation of complex nanophotonic structures.
The functionalization of nanoparticles with macromolecular structures like DNA and RNA is quickly gathering interest as a tool for sensing applications and drug-delivery in medicine and biology.1−4 When functionalized, the nanoparticles can travel within the biological system and be transported to a target region. Upon irradiation, the functionalized nanoparticles boost the optical response of the surrounding molecules. However, such enhancement does not come without risk: as a result of the electromagnetic field enhancement effect induced by the nanoparticle, the nucleobases in DNA and RNA are more prone to absorb radiation. In turn, the enhanced light absorption can potentially drive the nucleobases to trigger photodamaging chain events,5−7 resulting in dangerous mutations of the DNA/RNA macrostructure. Although characterized by an intrinsically low quantum yield, the pathway associated with photodamage occurs as a side intersystem crossing reaction starting from the S2 bright excited states of nucleobases.7−9 Under ambient conditions of irradiation, this low quantum yield is mostly due to the quick de-excitation mechanism of the nucleobases. This mechanism then prevents dangerous reactions,10 with an estimated permanence on the S2 excited state of ∼0.5 ps for both DNA9−11 and RNA.12−14 However, this self-preservation mechanism fails under high-intensity irradiation, like in fluorescence imaging techniques or in vitro preparations.15−18 It then becomes natural to look for new pathways to improve the photoprotection mechanism, already at the single-molecule level.
A compelling strategy to control the chemical and dynamical properties of molecules relies on the modulation of their electromagnetic environment via cavity quantum electrodynamics (cQED) devices. The collection of models and experimental techniques aiming at controlling chemistry via coupling to quantum light goes by the name of polaritonic chemistry or molecular polaritonics.19−24 In this framework the molecules are confined in optical cavities and are resonantly coupled to localized modes of the electromagnetic field.25−28 Whether this coupling is strong enough to drive substantial chemical modifications depends on the specifics of the system:29 the oscillator strength of the molecular excitation, the volume of the mode in the nanocavity, the number of molecular emitters, together with the lifetimes of the exciton and nanocavity mode. When the coupling strength exceeds the decay rates of both the cavity mode and the exciton (strong-coupling regime), the states of the system can be suitably described as hybrids between light and matter: the polaritons.24 Very recent theoretical works and experiments have proven that reaching the strong coupling regime is a useful way to catalyze photochemical reactions,30−34 to modify the relaxation pathways of molecules,35−37 and to mediate energy transport phenomena,38−40 as well as to enhance the molecular optical response.41−44 In the same fashion, Shegai and collaborators have shown that strong coupling to plasmonic nanoantennas can significantly increase the photostability of chromophores.45 Promising experimental setups exploited in molecular polaritonics rely on nanocavities coupled to organic molecules.46 This kind of setup is beneficial as it guarantees high oscillator strengths on the molecular side and a nanometric mode volume on the nanocavity side,47−49 carrying the possibility to observe molecular strong coupling down to the single-molecule level at room temperature.50,51 However, it comes with the drawback of the modes living for only a few tens of femtoseconds.52,53 It is then a common aim in the field to work toward extending the cavity lifetimes, guided by the intuitive idea that a larger coupling/dissipation ratio would correspond to more exotic properties. While this may be desirable in light-harvesting41−44 and energy transport applications,38−40 we show here that increasing the mode lifetime is not necessarily the best approach to pursue for opening up efficient relaxation pathways.
In the present work, we show how the uracil photorelaxation mechanism can be improved by coupling with a lossy nanocavity mode. As a starting point, we analyze the photorelaxation dynamics of the isolated uracil molecule. This first step lets us identify how to act with the nanocavity mode on the photoprotection mechanism. By making use of a non-Hermitian formalism to include cavity losses, we perform quantum dynamics simulations and look for the cavity parameters that optimize the photorelaxation mechanism of the isolated nucleobase. Indeed, we identify such conditions between coupling strength and mode lifetime and we characterize the mechanism leading to the improved photoprotection. Our simulations also reveal that the best efficiency is obtained when the ratio between coupling strength and mode lifetime is at the crossover between weak and strong coupling. We then show that these coupling conditions can be met by coupling the uracil with a spherical silver nanoparticle, surrounded by a dielectric with properties reflecting those of a nanoparticle functionalized with DNA.49 We also show that, for the case of a silver nanosphere coupled to uracil, no field enhancement in the nucleobase excitation window is present. Thus, the photoprotection is not compromised by an improved absorption of dangerous radiation. The results presented in the current work are doubly beneficial: on one front, we show how to substantially speed-up the photorelaxation of DNA-like structures with simple nanospheres, without relying on complex nanophotonics setups. In a more general perspective, we demonstrate that better cavities do not necessarily correspond to improved photochemistry. Similar non-Hermitian schemes to investigate cavity losses in polaritonic chemistry have been independently developed by Foley and collaborators54 for the azobenzene molecule and by Ulusoya and Vendrell55 for NaI and pyrazine molecules.
Let us first briefly
review the relaxation dynamics of the isolated
uracil molecule.13,14 Uracil, as the other nucleobases,
is characterized by a dark n–π* transition
(S0 → S1) in the visible and a bright π–π* (S0 → S2) transition
occurring by absorption of UV light. The dynamics taking place in
the S2 state determines whether the molecule
relaxes through internal conversion (photoprotection mechanism) or
whether it incurs photodamage.10,13 The degrees of freedom
responsible for the internal conversion from the S2 excited state involve a collective deformation of the
ring-like structure. On the other hand, a well-known photodamaging
reaction pathway like the formation of cyclobutane pyridine dimers
starts with an intersystem crossing side-reaction, occurring from
a local minimum on the S2 state. Indeed,
although it is known10,56,57 that an S2/S1 conical intersection (CoIn) rules the photoprotection mechanism,
two more configurations are particularly relevant to properly describe13 the processes occurring in the S2 state: the Franck–Condon point (FC) and the left-hand
minimum of S2 (S2min). The S2 potential energy surface (PES) along the vectors
(qFC→CoIn, 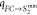 ) respectively
connecting the FC to CoIn
and to S2 is displayed in Figure 1a. The potential energy landscape presents
a double-well structure, with a potential energy barrier hindering
the pathway between S2min and the CoIn seam. We label such a
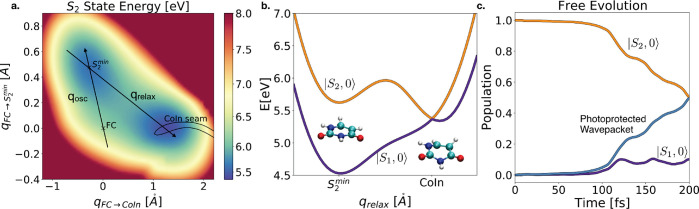
pathway as qrelax and plot it in Figure 1b. We compute the
PESs on a finite-element discrete-variable (FEDVR)58 spatial grid as described in Methods to represent the nuclear wave function. Upon UV photoexcitation
of uracil, the nuclear wavepacket (WP) is transferred from the ground
state to the FC point on the S2 state.
Following the shape of the PESs, it then evolves toward S2 and starts
to oscillate between FC and S2min along the coordinate labeled
as qosc. As enough kinetic energy is redistributed
during the oscillation to the other coordinate, the WP overcomes the
barrier along qrelax and it reaches the
CoIn seam, finally relaxing to the S1 state.
The height of the barrier along qrelax is then what determines the permanence time of the wavepacket on
the S2 state. Overcoming this barrier
and reaching the conical intersection is vital to trigger the photoprotection
mechanism, as the probability to incur photodamage is directly related
to the permanence time in the S2 basin. Indeed, from S2min an intersystem crossing reaction can occur, potentially resulting
in photodamage.59 A previous work14 also shows how the RNA environment of uracil
further hinders the relaxation by stabilizing the S2, resulting
in a higher barrier to overcome and a substantially longer permanence
time in S2. In the most optimistic prevision,
namely for the isolated molecule, the time needed by the WP to start
overcoming the barrier is about 120 fs, as shown in the population
plot (Figure 1c).
) respectively
connecting the FC to CoIn
and to S2 is displayed in Figure 1a. The potential energy landscape presents
a double-well structure, with a potential energy barrier hindering
the pathway between S2min and the CoIn seam. We label such a
pathway as qrelax and plot it in Figure 1b. We compute the
PESs on a finite-element discrete-variable (FEDVR)58 spatial grid as described in Methods to represent the nuclear wave function. Upon UV photoexcitation
of uracil, the nuclear wavepacket (WP) is transferred from the ground
state to the FC point on the S2 state.
Following the shape of the PESs, it then evolves toward S2 and starts
to oscillate between FC and S2min along the coordinate labeled
as qosc. As enough kinetic energy is redistributed
during the oscillation to the other coordinate, the WP overcomes the
barrier along qrelax and it reaches the
CoIn seam, finally relaxing to the S1 state.
The height of the barrier along qrelax is then what determines the permanence time of the wavepacket on
the S2 state. Overcoming this barrier
and reaching the conical intersection is vital to trigger the photoprotection
mechanism, as the probability to incur photodamage is directly related
to the permanence time in the S2 basin. Indeed, from S2min an intersystem crossing reaction can occur, potentially resulting
in photodamage.59 A previous work14 also shows how the RNA environment of uracil
further hinders the relaxation by stabilizing the S2, resulting
in a higher barrier to overcome and a substantially longer permanence
time in S2. In the most optimistic prevision,
namely for the isolated molecule, the time needed by the WP to start
overcoming the barrier is about 120 fs, as shown in the population
plot (Figure 1c).
Figure 1.
Uracil photorelaxation dynamics under free evolution. (a) Main coordinates dominating the photorelaxation in uracil from the S2 state. Absent cavity, the WP oscillates for more than 100 fs along the qosc coordinate, until it manages to overcome the barrier (panel b) along qrelax. (c) State populations over evolution time. The light blue line shows the total population of the protected wavepacket. Once the WP starts overcoming the barrier, it can reach the S2/S1 conical intersection, and it is quickly transferred to the |S1, 0⟩ state (where S1 denotes the excitonic state, while the second index gives the photon number).
As the early stages of the relaxation dynamics occur between FC and S2min, an effective way to speed up the dynamics would be to open an alternative relaxation pathway along qosc. The new relaxation channel would be independent both from the height of the barrier and from the environment affecting the depth of S2. In the course of the present work, we show that such an additional relaxation pathway can be introduced by coupling the molecule with a localized photonic mode. In particular, we consider a single-mode nanocavity whose frequency Ωc is set in the near-UV to be resonant with the S0 → S2 molecular transition. The cavity–molecule coupling takes advantage of the high transition dipole moment between S0 and S2, resulting in the opening of a direct channel to the ground state. The efficiency of this new channel is strongly affected by photon decay, as discussed later in the Letter. In this regard, let us briefly describe how these photon losses can be included in our model. Quantum systems weakly coupled to dissipative Markovian environments are commonly treated by a Lindblad master equation approach. There, the density matrix of the quantum system is propagated in time, according to eq 5 in Methods. In the single-photon subspace, an equivalent method consists of adopting a non-Hermitian formalism, where dissipative effects are implicitly included by adding a complex energy contribution to the lossy states in the effective non-Hermitian Hamiltonian (see Methods). The photon decay is then accounted for by a loss of norm of the WP during the propagation. For the present case, we include the cavity losses with a non-Hermitian term proportional to the cavity decay rate γ. Resorting to the non-Hermitian framework carries two main advantages: First, the photon decay enters the photorelaxation mechanism also at the PESs level via the complex contribution to the energy of lossy states, providing an intuitive picture. Second, it reduces the computational complexity. Indeed, the non-Hermitian formalism allows us to propagate states instead of the full density matrix and to restrict the state space to the three relevant PESs directly involved in the cavity-assisted photorelaxation. More details are provided in Methods.
Before moving to the description
of the dynamics, we introduce
the polaritonic formalism and the relevant states involved in the
cavity-assisted photorelaxation mechanism. In the presence of the
cavity, the states associated with the PESs correspond to the tensor
product between the electronic states (|Si⟩) and the cavity mode number states (|p⟩). We label the resulting states as |Si, p⟩, where i is the electronic state index and p is
the cavity-mode occupation number, safely assumed to be either zero
or one as the cavity is not externally driven. The energy of the zero-photon
states |Si, 0⟩
is purely electronic. Conversely, when the photon mode is excited,
the energy of the states |Si, 1⟩ is the Si PES lifted by the single-photon energy Ωc. The PESs involved in the dynamics are associated with the states
|S2, 0⟩, |S1, 0⟩ and |S0, 1⟩.
In Methods, we give the detailed derivation
of the model and of the space reduction. To visualize the effects
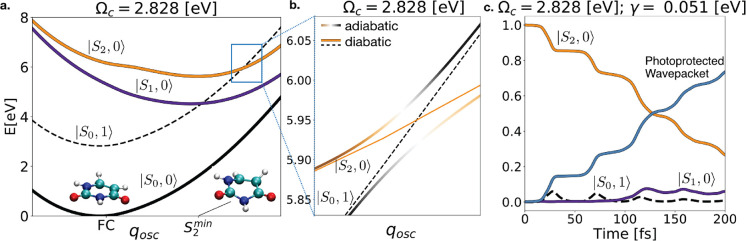
of the cavity on the energy landscape, in Figure 2a we examine the section of the PESs involved
in the relaxation along qosc. The full
lines represent the bare electronic states of the isolated molecule,
namely |S0, 0⟩ (black), |S1, 0⟩ (purple), and |S2, 0⟩ (orange). The dashed black line corresponds
to the molecule in the ground state and a single photonic excitation,
that is |S0, 1⟩. By the effect
of the strong light–molecule coupling, the bare states |S2, 0⟩ and |S0, 1⟩ hybridize into polaritons, depicted as full shaded lines
in Figure 2b. There,
the strength g of the coupling term (defined in eq 4 in Methods) is given by the product between the molecular transition moment
μ(R) and the single-photon electric field E1ph, which depends on the nanocavity design.
The polaritonic states are obtained by diagonalization of the non-Hermitian
Hamiltonian, where the energy splitting at the avoided crossings is
given by  . The splitting is opened for g ≥ γ/4;
this condition is often used to define the onset
of the strong coupling regime. Following the initial oscillation along qosc on the upper polaritonic surface, the composition
of the state gradually changes from purely excitonic (|S2, 0⟩) to purely photonic (|S0, 1⟩). The region of the polaritonic PESs characterized
by a major |S0, 1⟩ component (displayed
with the color black) is exposed to photon losses. As a consequence,
a WP traveling the black region can incur an ultrafast radiative de-excitation
from |S0, 1⟩ to the |S0, 0⟩ state. The velocity of such de-excitation
processes is ruled by the cavity decay rate γ. We note for later
discussion that the propagation of a nuclear wavepacket following
the polaritonic states (shaded lines) is adiabatic. Conversely, we
define the motion as diabatic if the wavepacket propagates following
the |S2, 0⟩ and |S0, 1⟩ PESs.
. The splitting is opened for g ≥ γ/4;
this condition is often used to define the onset
of the strong coupling regime. Following the initial oscillation along qosc on the upper polaritonic surface, the composition
of the state gradually changes from purely excitonic (|S2, 0⟩) to purely photonic (|S0, 1⟩). The region of the polaritonic PESs characterized
by a major |S0, 1⟩ component (displayed
with the color black) is exposed to photon losses. As a consequence,
a WP traveling the black region can incur an ultrafast radiative de-excitation
from |S0, 1⟩ to the |S0, 0⟩ state. The velocity of such de-excitation
processes is ruled by the cavity decay rate γ. We note for later
discussion that the propagation of a nuclear wavepacket following
the polaritonic states (shaded lines) is adiabatic. Conversely, we
define the motion as diabatic if the wavepacket propagates following
the |S2, 0⟩ and |S0, 1⟩ PESs.
Figure 2.
Cavity-assisted uracil photorelaxation. (a) Uracil potential energy curves along the qosc coordinate. The full lines represent the isolated molecules potential energy curves, namely |S2, 0)⟩ (orange), |S1, 0⟩ (purple), and |S0, 0⟩ (black). The dashed black line represents the ground state shifted by the cavity mode frequency (|S0, 1⟩). (b) Detail of the polaritonic avoided crossing. The diabatic states |S2, 0⟩ and |S0, 1⟩ are split in polaritonic adiabatic states, represented by the shaded lines. (c) Population dynamics of uracil excited states in the presence of a cavity mode set at Ωcav = 2.8 eV, e1ph = 0.001 au and τcav = 12 fs. The light blue line shows the total population of the protected WP, that is the |S0, 1⟩ and |S1, 0⟩ occupation plus incoherent losses. Here, the earlier stage of the dynamics is governed by the new relaxation pathway opened by the presence of the cavity.
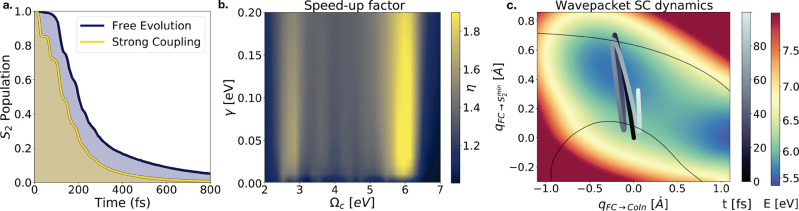
Let us move to the description of the dynamics in the presence of the cavity. To this aim, we display the populations for the cavity-assisted dynamics in Figure 2c. Immediately we note that the early dynamics is ruled by the transfer of the WP from |S2, 0⟩ (full orange line) to |S0, 1⟩ (black dashed line), which is active along the qosc coordinate. Here, the state |S0, 1⟩ is only transiently populated, as the WP is quickly lost by the effect of photon leakage, which transfers the WP to the |S0, 0⟩ state. The light blue line shows the total population of the protected WP, which amounts to the sum of the |S0, 1⟩ and |S1, 0⟩ state occupations, plus the population lost through the photonic or nuclear dissipation channels (accounted for by norm loss in the non-Hermitian formalism). The comparison of the cavity-assisted case to the first 120 fs of the free evolution dynamics (Figure 1c) reveals that the cavity opens a faster and alternative relaxation pathway. Indeed, in the free-evolution case, the WP is still confined at 120 fs by the barrier along qrelax. The norm of the WP transferred from the |S2, 0⟩ to the |S0, 1⟩ strongly depends on how adiabatic the WP moves on the polaritonic surface, namely on how much it follows the upper polaritonic state of Figure 2b. Indeed, it has recently been noted60 that the WP is efficiently transferred with an optimal trade-off between the time it spends in the coupled region (WP velocity), the speed of the photon leakage (decay rate γ or cavity lifetime τcav = 1/γ), and how much the states shall be coupled to guarantee an adiabatic motion of the WP from |S2, 0⟩ to |S0, 1⟩ (splitting). Aiming to quantify the effective improvement of this new relaxation channel with respect to the different conditions, we adopt as a figure of merit the relaxation speed-up η. We compute η as the ratio between the |S2, 0⟩ population integrated over time for two cases, separately in the presence of the cavity and for the free evolution (Figure 3a). The reason is twofold: First, it is directly related to the probability to incur photodamage. Second, it provides a good insight of the overall relaxation process in the presence of multiple decay channels acting on different time scales, namely, the photon loss and the relaxation through the CoIn seam for the present case. The coupling conditions adopted for the long-time dynamics shown in Figure 3a are the same as in Figure 2c, i.e., a cavity of Ωc = 2.8 eV with an associated single-photon electric field of e1ph = 0.001 au and a decay rate of about γ = 0.05 eV (lifetime of 12 fs). Under such conditions, the |S2, 0⟩ state is depleted ∼1.6 times quicker than for the free evolution case.
Figure 3.
Cavity-enhanced photorelaxation mechanism of uracil. (a) Integrated S2 population during the uracil photorelaxation in the presence (yellow) and absence (blue) of a cavity. The total area estimates the probability to incur photodamage. (b) Best cavity conditions to optimize the speed-up η of the uracil photorelaxation, resulting in a more efficient photoprotection. (c) Motion of the WP center of mass. The background shows the S2 PES, while the black lines identify the seams of intersection between the states |S2, 0⟩ and |S0, 1⟩, for the optimal values Ωc = 2.8 eV and Ωc = 6.2 eV of the cavity frequencies. Transfer is maximized if the two states are resonant in the regions where the WP is slower. In general, the conditions leading to the most efficient photoprotection are given by a delicate interplay between cavity frequency, wavepacket velocity, and cavity lifetime.
We now discuss the effect of the coupling conditions on the relaxation dynamics. To this aim, we set the single-photon energy at 0.001 au and consider the speed-up factor for different cavity frequencies and lifetimes. The results are reported in Figure 3b. Overall, we obtain a global speed-up factor η > 1.2 for all the range of cavity frequencies between Ωcav = 2.3 and 6.5 eV. We identify two regions characterized by a major speed-up factor around two values of the cavity frequency, Ωcav ≈ 2.8 eV and Ωcav ≈ 6 eV. The cavity frequency rules the position of the polaritonic avoided crossing and hence the conditions to transfer the WP from |S2, 0⟩ and |S0, 1⟩. By tuning Ωcav, the position of the polaritonic avoided crossing is adjusted along the qosc coordinate. The coupling strength g at the polaritonic avoided crossing (Figure 2b) is consequently affected because of the dependence of the S0 → S2 transition dipole on the nuclear coordinates. However, for the present case, the S0 → S2 transition dipole moment is approximatively constant in all the region corresponding to the S2 left minimum.13 Hence, the |S0, 1⟩ state ends up efficiently coupling to |S2, 0⟩ for any Ωcav in the range between 2.3 and 6.5 eV. While this effect explains the overall speed-up of the reaction, it does not account for the maximum speed-up regions at the edges of the frequency range. To understand the optimal speed-up at 2.8 and 6.2 eV, we consider the WP oscillation along qosc in Figure 3c. Here, we represent the polaritonic avoided crossing in the two cases as black lines labeled by their respective cavity frequencies. We observe that the avoided crossings are located at the edges of the oscillation coordinate qosc, where the WP velocity approaches zero as it reverts its motion. Coherently with the study by Silva et al.,60 we then see that a more efficient transfer to |S0, 1⟩ is obtained when the WP moves slowly and spends more time in the coupled region; that is, its motion tends to follow the adiabatic behavior introduced above. The pseudoharmonic oscillation around the S2min is also responsible for the stair-like population dynamics of the |S2, 0⟩ state, presented in Figure 2c. In particular, the transfer occurs only when the WP hits the resonant region sitting at the limit of qosc. Considering the WP velocity as a factor affecting the transfer also allows us to understand the dependence of the speed-up factor on the cavity lifetime. Too small a decay rate γ with respect to the WP permanence time in the coupled region would result in a coherent exchange of the WP back and forth between |S2, 0⟩ and |S0, 1⟩. The coherent exchange continues until the WP exits the coupled region, resulting in an overall minor transfer. On the other hand, a cavity decay rate which is too large with respect to the coupling strength g, would result in an effective decoupling of the polaritonic PESs. While it is indeed possible to find an optimal γ at each cavity frequency, we stress that the effect of γ on the speed-up is very dependent on two factors: the coupling strength g and the velocity of the WP when it crosses the polaritonic avoided crossing region. This point will be further discussed later for the specific case presented. Notice that, as shown in Figure 3b, in the presence of the cavity the photoprotection mechanism can be up to twice as efficient (η ≈ 2) as for the isolated molecule. This improvement is already a compelling result, also considering that photoprotection in uracil can be only slightly improved using alternative techniques such as optical pulse shaping.13 Furthermore, we are considering conservative values for the light–matter coupling strength that can be achieved with simple photonic structures, and the speed-up factor could be further improved by increasing the coupling strength using more complex structure.61 The light–matter interaction strength could also be enhanced by the collective nature of the coupling in the many-molecule case. However, a specific analysis should be performed to assess whether the cavity-induced photoprotection mechanism could benefit from collective phenomena, and to understand the role of dark states55 in this context.
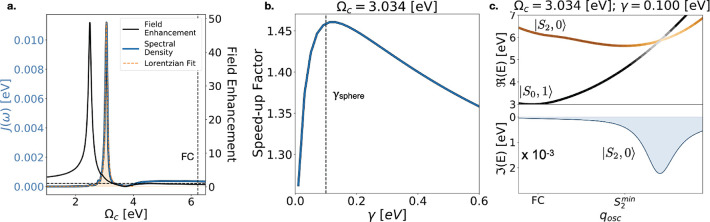
So far, the photonic part of our system has been described with a single-mode cavity coupled to a Markovian dissipation bath. Let us now introduce a more detailed physical model of a nanophotonic structure that reproduces the considered model to a very good degree of approximation. We consider a silver nanoparticle embedded in a nondispersive dielectric medium, and we show that even such a simple structure makes it possible to obtain a significant photorelaxation speed-up with realistic physical parameters. The nanoparticle dielectric response is fitted from the experimental data,62 and it is used in a semianalytic approach63 to evaluate its spectral properties. In particular, we consider a silver nanosphere of radius a = 15 nm, embedded in a high-refractive-index continuous dielectric. We take a value of the background dielectric constant of ϵd = 4.41, which has been experimentally observed by Baumberg and collaborators49 using DNA-origami. We place the molecule at a distance of 1 nm from the nanoparticle surface. The molecule–nanoparticle interaction can be described in terms of a pseudomode, which is an effective representation of an ensemble of independent harmonic oscillators.64 For the present case, the pseudomode represents a manifold of plasmonic quasi-degenerate multipole modes embedded in a dielectric environment,65 which are coupled to the S0 → S2 transition. In Figure 4a we report the computed spectral density (blue continuous line) and the corresponding Lorentzian fit (orange dashed line). The good agreement between the spectral density and the fit shows that the nanoparticle is well approximated by a single pseudomode with resonance frequency Ωc = 3.0 eV and decay rate γ = 0.1 eV (∼6–7 fs lifetime). We note that because of the proximity of the molecule to the sphere, this dominant mode corresponds to a combination of high-order multipole modes in the sphere,63 and not the dipole resonance of the sphere at Ω ≈ 2.5 eV (which is the only efficiently coupled to free-space radiation, as seen in the field enhancement in Figure 4a). We set the dipole moment to μ = 4.2 D, which is the value of the uracil model at the relevant crossing point (see Figure 3c).13 The light–matter coupling strength g with such parameters measures 0.042 eV, which is consistent with the value of e1ph = 0.001 au considered in the numerical simulations throughout this Letter. In Figure 4a we also show the enhancement of the field (full black line) intensity experienced by the molecule due to the nanoparticle, considering an incident plane wave. It is important to remark that at the FC frequency (ΩFC ≈ 6.2 eV) the field enhancement is slightly less than 1, implying that the presence of the cavity does not improve the absorption efficiency. By reaching strong coupling with a localized photonic mode (Figure 4a), we are able to meet two apparently contradictory requirements to improve the uracil photoprotection mechanism: the introduction of an efficient photorelaxation channel and the absence of enhancement of the photoexcitation rate. In Figure 4b, we extract the section of the speed-up factor map (Figure 3b) at the pseudomode frequency, namely Ωcav = 3.0 eV. Notice that there exists an optimal value of the decay rate which maximizes the speed-up factor. The optimal condition depends on the photon mode frequency, as it is given by a complex interplay between different factors such as the detuning from the optimal frequency, the speed of the wavepacket, and the strength of the light–matter interaction. For example, the optimal decay rate γ = 0.1 eV (6–7 fs lifetime) observed for Ωcav = 3.0 eV is larger than the one estimated to be the best for Ωcav = 2.8 eV, i.e., γ = 0.05 eV (∼12 fs). Notice that for the considered silver nanoparticle, the decay rate associated with the pseudomode γsphere = 0.1 eV is very close to the maximum speed-up value, showing that optimal enhancement of the photorelaxation efficiency can be obtained with standard nanophotonic structures. Notice that the speed-up factor drops abruptly in the low-γ region in Figure 4b, because of the slower decay of the wavepacket when passing through the crossing region. Furthermore, in the limit of a lossless optical mode, the WP could indefinitely occupy the |S0, 1⟩ state without decaying, which can result in late population transfer back to |S2, 0⟩. In this case, vibrational dissipation on the |S0, 1⟩ state could play a role by damping the nuclear oscillation amplitude and preventing the WP to access the strong-coupling region after few oscillations. In our model, vibrational dissipation has not been included, as it has a negligible effect on the dynamics for loss rates relevant for realistic nanophotonic structures. Finally, in Figure 4c we show the real and imaginary parts of the non-Hermitian polaritonic states obtained with the physical parameters of the silver nanosphere pseudomode. As the coupling strength is smaller than the exceptional point value g < γ/2, there is no splitting in the real part of the polaritonic energies. Accordingly, no avoided crossing is observed and the polaritonic energies overlap with the bare PESs. In this case the system is said to be in the weak-coupling regime, and it is not possible to observe a coherent excitation transfer between the states |S2, 0⟩ and |S0, 1⟩ within the cavity lifetime. However, the coupling with the pseudomode introduces a decay mechanism that is described in the non-Hermitian formalism by a localized complex potential, which is shown in the lower panel of Figure 4c. Accordingly, the nanoparticle mediates an efficient channel that can speed up the photorelaxation process by ∼1.45 times (as shown in Figure 4b) even in the weak-coupling regime.
Figure 4.
Plasmonic pseudomode of a silver nanosphere of 30 nm diameter. (a) Lorentzian fit (dashed orange line) of the plasmonic pseudomode (full blue line) in a silver nanosphere, located centered at 3.0 eV. The agreement with the Lorentzian shows that the nanoparticle can be well-approximated by a single-mode cavity. The full black line in panel a shows the field enhancement. The absence of field enhancement at FC (6.2 eV, vertical dashed line) guarantees that the presence of the nanoparticle does not enhance the absorption of the sample, which could potentially result in an augmented photodamage probability. (b) The cavity decay rate associated with the silver nanosphere pseudomode (γ = 0.1 eV) also yields the maximum speed-up factor for the uracil photorelaxation when Ωcav = 3.0 eV. (c) Real and imaginary parts of the polaritonic energy close to resonance. The splitting in the real part is zero; hence, no transfer to the |S0, 1⟩ state should be observed because of the coupling. Yet, a ∼1.5 speed-up of the reaction is still observed by effect of the imaginary contribution to the coupling on |S2, 0⟩.
In the present work, using 2D wavepacket dynamics calculations on lossy polaritonic PESs, we have shown how the coupling of uracil molecules with localized electromagnetic modes can be used to open an additional relaxation pathway, which is up to twice as efficient as the natural photoprotection mechanism hard-wired in the molecular structure. We have characterized the physical properties of the photonic device that optimizes the photorelaxation mechanism, and we have identified optimal conditions which do not require the implementation of complex nanophotonic structures. The highest efficiency is obtained at the limit between the weak and the strong coupling regimes. An important consequence emerges from these results: improving the nanocavity lifetime does not necessarily enhance the photoprotection efficiency. Even more, the new relaxation pathway is already efficient when coupling simple metallic nanoparticles to the uracil molecule in the weak coupling regime. We show that a simple silver nanosphere embedded in a dielectric background can lead to a speed-up of about 50% of the relaxation dynamics. Although a coherent transfer of population does not occur in the weak coupling regime, the photon mode introduces an effective complex potential which is sufficient to significantly improve the photorelaxation. Through the description of the nanophotonic structure, we show that the mode under study does not enhance the absorption of the molecule in the photodamaging UVB excitation window for uracil. Consequently, the coupling introduces an additional photorelaxation channel without enhancing the photoexcitation efficiency, resulting in a purely photoprotective effect. In conclusion, by merging chemically and physically accurate descriptions of molecules and nanoparticles, we have shown that photon decay can play an active role in the modification of chemical reaction rates induced by nanophotonics structures, in the context of molecular polaritonics. Our study paves the way to the use of lossy photonic devices as a tool to tailor photorelaxation channels and to selectively inhibit reaction pathways. Because of its simplicity, the setup proposed for the silver nanosphere and uracil can be feasibly implemented experimentally with current nanophotonic technology.
Methods
Molecular Calculation. The isolated uracil potential energy surfaces are computed at the MRCI(12,9)/cc-pVDZ level13 with an active space of 12 electrons in 9 orbitals, with single excitations allowed out of the active space into the virtual space. The propagation was performed by relying on a finite elements discrete variable representation (FEDVR58) spatial grid, including 11 spline basis functions for each grid point to represent the nuclear wave function. In the propagation, the nonadiabatic coupling vectors are evaluated at SA-CASSCF level within the same active space on the same FEDVR grid.14 As the WP reaches S1 from S2 through the conical intersection, an absorbing potential gradually set along the slopes of the S1 state acts to decrease the WP norm. By these means, we mimic the fast internal conversion from the S1 state, together with avoiding unphysical behaviors due to the WP traveling back to S2.
Light–Matter Hamiltonian. We consider a model composed of a uracil nucleobase individually coupled to a single quantum optical mode, of frequency Ωc and decay rate γ. Let us first describe the system full Hamiltonian, we will discuss later how the dissipation is included in our model. The total Hamiltonian is given by three main components Ĥ = Ĥmol+Ĥcav+Ĥint. The bare molecular energy can be written as
| 1 |
where T̂nuc is the nuclear kinetic energy operator; i and j denote the bare molecule electronic states in the adiabatic representation. Vi(R) are the potential energy surfaces (PESs), and the term Gij(R) gathers the nonadiabatic couplings vectors which correct the Born–Oppenheimer approximation. The photonic contribution to the Hamiltonian is written as the quantized electromagnetic field Hamiltonian:
| 2 |
in terms of creation ↠and annihilation â operators, where Ωc is the cavity frequency. Finally, the light–matter interaction term is given by
| 3 |
where the interaction strength gij(R) = μij(R)·E1ph is given by the scalar product of the dipole transition moments μij(R) with the electric field generated by a single photon and polarized along λ, that is E1ph = λe1ph. The full space to propagate for the cavity–molecule system is composed by the manifold of the |Si, p⟩ states, where i is the electronic state index and p is the cavity occupation number. For the molecule, we restrict to the three electronic states directly involved in the free evolution dynamics, namely |S2, 0⟩, |S1, 0⟩, and |S0, 0⟩. We shall now discuss some reasonable approximations for the cavity–molecule coupling to reduce the complexity of the model and to cut the computational cost. First, we perform the rotating-wave approximation and hence neglect the far off-resonant terms, namely, the coupling to the states |Si, p ≥ 1⟩. Among the off-resonant states, the lowest in energy is |S1, 1⟩, which sits at least 2 eV above the |S2, 0⟩. This difference is well beyond the relevant window for the dynamics occurring on |S2, 0⟩. Second, we assume that the cavity mode is occupied by at most one photon, which is always the case under rotating-wave approximation if the cavity mode itself is not externally driven. Accordingly, in the reduced model the potential energy landscape is composed of four relevant PESs, corresponding to the states |S0, 0⟩, |S1, 0⟩, |S2, 0⟩, and |S0, 1⟩. In the absence of any light–matter interaction, the states |Si, 0⟩ correspond to the potentials Vi(R), while the state |S0, 1⟩ has the energy V0(R) + Ωc, that is, the S0 PES lifted by the cavity frequency (Figure 2a,b). The light–matter interaction for the present case is given by the Hamiltonian
| 4 |
and so it can induce transitions between the states |S2, 0⟩ and |S0, 1⟩. Let us now discuss how dissipative effects are included in our formalism.
Non-Hermitian propagation cavity losses can be formally taken into account using the Lindblad master equation, which is based on the assumption that the cavity mode is weakly coupled to a Markovian bath. At zero temperature, the evolution of the system density matrix is given by
| 5 |
where γ is the photon decay
rate. Notice
that the term aρ̂↠induces incoherent transitions |Si, p⟩ → |Si, p – 1⟩,
which in our reduced subspace corresponds only to the transition |S0, 1⟩ → |S0, 0⟩. Given that we want to focus on the population
that is leaking out from the S2 electronic
state, we can reduce further the computational space, keeping into
account only the states |S1, 0⟩,
|S2, 0⟩, and |S0, 1⟩. In this subspace, the term aρ̂↠vanishes and can be dropped. We can then rewrite
the master equation (eq 5) in terms of a non-Hermitian Hamiltonian,66 ρ̇ = −i(ĤNHρ – ρĤNH†) where 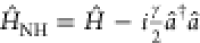 . In this non-Hermitian formalism, photon
losses are then kept into account by the loss of norm of the system
state during the time-evolution. The system evolution can be then
calculated solving the non-Hermitian Schroedinger equation for state vectors, instead of using the full Lindblad master
equation for density matrices.
. In this non-Hermitian formalism, photon
losses are then kept into account by the loss of norm of the system
state during the time-evolution. The system evolution can be then
calculated solving the non-Hermitian Schroedinger equation for state vectors, instead of using the full Lindblad master
equation for density matrices.
Acknowledgments
The authors thank Stefano Corni (University of Padova) for fruitful scientific discussion. This work has been funded by the European Research Council through Grants ERC-2016-StG-714870 (S. Felicetti, J. Feist, and J. Fregoni) and ERC-2015-CoG-681285 (J. Fregoni, PI Stefano Corni) and by the Spanish Ministry for Science, Innovation, and Universities—Agencia Estatal de Investigación through Grants RTI2018-099737-B-I00, PCI2018-093145 (through the QuantERA program of the European Commission), and MDM-2014-0377 (through the María de Maeztu program for Units of Excellence in R&D). T. Schnappinger and R. de Vivie-Riedle gratefully acknowledge the DFG Normalverfahren. S. Reiter gratefully acknowledges financial support by the International Max Planck Research School of Advanced Photon Science (IMPRS-APS).
Author Contributions
⊥ S. Felicetti and J. Fregoni contributed equally to this work
The authors declare no competing financial interest.
References
- Wang E. C.; Wang A. Z. Nanoparticles and their applications in cell and molecular biology. Integr. Biol. 2014, 6, 9–26. 10.1039/c3ib40165k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S.; Kim J. H.; Kwon W. Y.; Hwang S. H.; Cha B. S.; Kim J. M.; Oh S. S.; Park K. S. Synthesis of DNA-templated copper nanoparticles with enhanced fluorescence stability for cellular imaging. Microchim. Acta 2019, 186, 479. 10.1007/s00604-019-3620-5. [DOI] [PubMed] [Google Scholar]
- Aslan K.; Huang J.; Wilson G. M.; Geddes C. D. Metal-Enhanced Fluorescence-Based RNA Sensing. J. Am. Chem. Soc. 2006, 128, 4206–4207. 10.1021/ja0601179. [DOI] [PubMed] [Google Scholar]
- Jasinski D.; Haque F.; Binzel D. W.; Guo P. Advancement of the Emerging Field of RNA Nanotechnology. ACS Nano 2017, 11, 1142–1164. 10.1021/acsnano.6b05737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y.; Ye Y.; Zhou X.; Chen J.; Jin Y.; Hanson A.; Zhao J. X.; Wu M. Photosensitive fluorescent dye contributes to phototoxicity and inflammatory responses of dye-doped silica NPs in cells and mice. Theranostics 2014, 4, 445–459. 10.7150/thno.7653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng Y.; Sanche L. Gold Nanoparticles Enhance DNA Damage Induced by Anti-cancer Drugs and Radiation. Radiat. Res. 2009, 172, 114–119. 10.1667/RR1689.1. [DOI] [PubMed] [Google Scholar]
- Mroz R. M.; Schins R. P. F.; Li H.; Jimenez L. A.; Drost E. M.; Holownia A.; MacNee W.; Donaldson K. Nanoparticle-driven DNA damage mimics irradiation-related carcinogenesis pathways. Eur. Respir. J. 2008, 31, 241–251. 10.1183/09031936.00006707. [DOI] [PubMed] [Google Scholar]
- Rössle S.; Friedrichs J.; Frank I. The Formation of DNA Photodamage: The Role of Exciton Localization. ChemPhysChem 2010, 11, 2011–2015. 10.1002/cphc.201000081. [DOI] [PubMed] [Google Scholar]
- Kwok W.-M.; Ma C.; Phillips D. L. A Doorway State Leads to Photostability or Triplet Photodamage in Thymine DNA. J. Am. Chem. Soc. 2008, 130, 5131–5139. 10.1021/ja077831q. [DOI] [PubMed] [Google Scholar]
- Barbatti M.; Aquino A. J. A.; Szymczak J. J.; Nachtigallová D.; Hobza P.; Lischka H. Relaxation mechanisms of UV-photoexcited DNA and RNA nucleobases. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 21453–21458. 10.1073/pnas.1014982107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crespo-Hernández C. E.; Cohen B.; Kohler B. Base stacking controls excited-state dynamics in A·T DNA. Nature 2005, 436, 1141–1144. 10.1038/nature03933. [DOI] [PubMed] [Google Scholar]
- Richter M.; Mai S.; Marquetand P.; González L. Ultrafast intersystem crossing dynamics in uracil unravelled by ab initio molecular dynamics. Phys. Chem. Chem. Phys. 2014, 16, 24423–24436. 10.1039/C4CP04158E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keefer D.; Thallmair S.; Matsika S.; de Vivie-Riedle R. Controlling Photorelaxation in Uracil with Shaped Laser Pulses: A Theoretical Assessment. J. Am. Chem. Soc. 2017, 139, 5061–5066. 10.1021/jacs.6b12033. [DOI] [PubMed] [Google Scholar]
- Reiter S.; Keefer D.; de Vivie-Riedle R. RNA Environment Is Responsible for Decreased Photostability of Uracil. J. Am. Chem. Soc. 2018, 140, 8714–8720. 10.1021/jacs.8b02962. [DOI] [PubMed] [Google Scholar]
- Schilling Z.; Frank E.; Magidson V.; Wason J.; Lončarek J.; Boyer K.; Wen J.; Khodjakov A. Predictive-focus illumination for reducing photodamage in live-cell microscopy. J. Microsc. 2012, 246, 160–167. 10.1111/j.1365-2818.2012.03605.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinterdorfer P.; Van Oijen A.. Handbook of single-molecule biophysics; Springer Science & Business Media, 2009; p 71. [Google Scholar]
- Wurtmann E. J.; Wolin S. L. RNA under attack: Cellular handling of RNA damage. Crit. Rev. Biochem. Mol. Biol. 2009, 44, 34–49. 10.1080/10409230802594043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kladwang W.; Hum J.; Das R. Ultraviolet Shadowing of RNA Can Cause Significant Chemical Damage in Seconds. Sci. Rep. 2012, 2, 517. 10.1038/srep00517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feist J.; Galego J.; Garcia-Vidal F. J. Polaritonic Chemistry with Organic Molecules. ACS Photonics 2018, 5, 205. 10.1021/acsphotonics.7b00680. [DOI] [Google Scholar]
- Ebbesen T. W. Hybrid Light-Matter States in a Molecular and Material Science Perspective. Acc. Chem. Res. 2016, 49, 2403–2412. 10.1021/acs.accounts.6b00295. [DOI] [PubMed] [Google Scholar]
- Ruggenthaler M.; Tancogne-Dejean N.; Flick J.; Appel H.; Rubio A. From a quantum-electrodynamical light–matter description to novel spectroscopies. Nat. Rev. Chem. 2018, 2, 0118. 10.1038/s41570-018-0118. [DOI] [Google Scholar]
- Ribeiro R. F.; Martínez-Martínez L. A.; Du M.; Campos-Gonzalez-Angulo J.; Yuen-Zhou J. Polariton chemistry: controlling molecular dynamics with optical cavities. Chem. Sci. 2018, 9, 6325–6339. 10.1039/C8SC01043A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hertzog M.; Wang M.; Mony J.; Börjesson K. Strong light-matter interactions: a new direction within chemistry. Chem. Soc. Rev. 2019, 48, 937–961. 10.1039/C8CS00193F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrera F.; Owrutsky J. Molecular polaritons for controlling chemistry with quantum optics. J. Chem. Phys. 2020, 152, 100902. 10.1063/1.5136320. [DOI] [PubMed] [Google Scholar]
- Kowalewski M.; Bennett K.; Mukamel S. Cavity Femtochemistry: Manipulating Nonadiabatic Dynamics at Avoided Crossings. J. Phys. Chem. Lett. 2016, 7, 2050. 10.1021/acs.jpclett.6b00864. [DOI] [PubMed] [Google Scholar]
- Herrera F.; Spano F. C. Cavity-Controlled Chemistry in Molecular Ensembles. Phys. Rev. Lett. 2016, 116, 238301. 10.1103/PhysRevLett.116.238301. [DOI] [PubMed] [Google Scholar]
- Galego J.; Garcia-Vidal F. J.; Feist J. Cavity-Induced Modifications of Molecular Structure in the Strong-Coupling Regime. Phys. Rev. X 2015, 5, 041022. 10.1103/PhysRevX.5.041022. [DOI] [Google Scholar]
- Schwartz T.; Hutchison J. A.; Léonard J.; Genet C.; Haacke S.; Ebbesen T. W. Polariton Dynamics under Strong Light-Molecule Coupling. ChemPhysChem 2013, 14, 125–131. 10.1002/cphc.201200734. [DOI] [PubMed] [Google Scholar]
- Flick J.; Ruggenthaler M.; Appel H.; Rubio A. Atoms and molecules in cavities, from weak to strong coupling in quantum-electrodynamics (QED) chemistry. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 3026–3034. 10.1073/pnas.1615509114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennett K.; Kowalewski M.; Mukamel S. Novel photochemistry of molecular polaritons in optical cavities. Faraday Discuss. 2016, 194, 259. 10.1039/C6FD00095A. [DOI] [PubMed] [Google Scholar]
- Schwartz T.; Hutchison J. A.; Genet C.; Ebbesen T. W. Reversible Switching of Ultrastrong Light-Molecule Coupling. Phys. Rev. Lett. 2011, 106, 196405. 10.1103/PhysRevLett.106.196405. [DOI] [PubMed] [Google Scholar]
- Galego J.; Garcia-Vidal F. J.; Feist J. Many-Molecule Reaction Triggered by a Single Photon in Polaritonic Chemistry. Phys. Rev. Lett. 2017, 119, 136001. 10.1103/PhysRevLett.119.136001. [DOI] [PubMed] [Google Scholar]
- Fregoni J.; Granucci G.; Persico M.; Corni S. Strong Coupling with Light Enhances the Photoisomerization Quantum Yield of Azobenzene. Chem. 2020, 6, 250. 10.1016/j.chempr.2019.11.001. [DOI] [Google Scholar]
- Martínez-Martínez L. A.; Du M.; Ribeiro R. F.; Kéna-Cohen S.; Yuen-Zhou J. Polariton-Assisted Singlet Fission in Acene Aggregates. J. Phys. Chem. Lett. 2018, 9, 1951–195u. 10.1021/acs.jpclett.8b00008. [DOI] [PubMed] [Google Scholar]
- Dunkelberger A. D.; Spann B. T.; Fears K. P.; Simpkins B. S.; Owrutsky J. C. Modified relaxation dynamics and coherent energy exchange in coupled vibration-cavity polaritons. Nat. Commun. 2016, 7, 13504. 10.1038/ncomms13504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ulusoy I. S.; Gomez J. A.; Vendrell O. Modifying the Nonradiative Decay Dynamics through Conical Intersections via Collective Coupling to a Cavity Mode. J. Phys. Chem. A 2019, 123, 8832–8844. 10.1021/acs.jpca.9b07404. [DOI] [PubMed] [Google Scholar]
- Groenhof G.; Climent C.; Feist J.; Morozov D.; Toppari J. J. Tracking Polariton Relaxation with Multiscale Molecular Dynamics Simulations. J. Phys. Chem. Lett. 2019, 10, 5476–5483. 10.1021/acs.jpclett.9b02192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong X.; Chervy T.; Zhang L.; Thomas A.; George J.; Genet C.; Hutchison J. A.; Ebbesen T. W. Energy Transfer between Spatially Separated Entangled Molecules. Angew. Chem. 2017, 129, 9162–9166. 10.1002/ange.201703539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schachenmayer J.; Genes C.; Tignone E.; Pupillo G. Cavity-Enhanced Transport of Excitons. Phys. Rev. Lett. 2015, 114, 196403. 10.1103/PhysRevLett.114.196403. [DOI] [PubMed] [Google Scholar]
- Sáez-Blázquez R.; Feist J.; Fernández-Domínguez A. I.; García-Vidal F. J. Organic polaritons enable local vibrations to drive long-range energy transfer. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 97, 241407. 10.1103/PhysRevB.97.241407. [DOI] [Google Scholar]
- Tsargorodska A.; Cartron M. L.; Vasilev C.; Kodali G.; Mass O. A.; Baumberg J. J.; Dutton P. L.; Hunter C. N.; Törmä P.; Leggett G. J. Strong Coupling of Localized Surface Plasmons to Excitons in Light-Harvesting Complexes. Nano Lett. 2016, 16, 6850–6856. 10.1021/acs.nanolett.6b02661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coles D. M.; Yang Y.; Wang Y.; Grant R. T.; Taylor R. A.; Saikin S. K.; Aspuru-Guzik A.; Lidzey D. G.; Tang J. K.-H.; Smith J. M. Strong coupling between chlorosomes of photosynthetic bacteria and a confined optical cavity mode. Nat. Commun. 2014, 5, 5561. 10.1038/ncomms6561. [DOI] [PubMed] [Google Scholar]
- Groenhof G.; Toppari J. J. Coherent Light Harvesting through Strong Coupling to Confined Light. J. Phys. Chem. Lett. 2018, 9, 4848–4851. 10.1021/acs.jpclett.8b02032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martínez-Martínez L. A.; Eizner E.; Kéna-Cohen S.; Yuen-Zhou J. Triplet harvesting in the polaritonic regime: A variational polaron approach. J. Chem. Phys. 2019, 151, 054106. 10.1063/1.5100192. [DOI] [Google Scholar]
- Munkhbat B.; Wersäll M.; Baranov D. G.; Antosiewicz T. J.; Shegai T. Suppression of photo-oxidation of organic chromophores by strong coupling to plasmonic nanoantennas. Sci. Adv. 2018, 4, eaas9552. 10.1126/sciadv.aas9552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barnes B.; García Vidal F.; Aizpurua J. Special Issue on “Strong Coupling of Molecules to Cavities. ACS Photonics 2018, 5, 1. 10.1021/acsphotonics.7b01609. [DOI] [Google Scholar]
- Hugall J. T.; Singh A.; van Hulst N. F. Plasmonic Cavity Coupling. ACS Photonics 2018, 5, 43. 10.1021/acsphotonics.7b01139. [DOI] [Google Scholar]
- Baranov D. G.; Wersäll M.; Cuadra J.; Antosiewicz T. J.; Shegai T. Novel Nanostructures and Materials for Strong Light-Matter Interactions. ACS Photonics 2018, 5, 24–42. 10.1021/acsphotonics.7b00674. [DOI] [Google Scholar]
- Chikkaraddy R.; Turek V. A.; Kongsuwan N.; Benz F.; Carnegie C.; van de Goor T.; de Nijs B.; Demetriadou A.; Hess O.; Keyser U. F.; et al. Mapping Nanoscale Hotspots with Single-Molecule Emitters Assembled into Plasmonic Nanocavities Using DNA Origami. Nano Lett. 2018, 18, 405–411. 10.1021/acs.nanolett.7b04283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chikkaraddy R.; de Nijs B.; Benz F.; Barrow S. J.; Scherman O. A.; Rosta E.; Demetriadou A.; Fox P.; Hess O.; Baumberg J. J. Single-molecule strong coupling at room temperature in plasmonic nanocavities. Nature 2016, 535, 127. 10.1038/nature17974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ojambati O. S.; Chikkaraddy R.; Deacon W. D.; Horton M.; Kos D.; Turek V. A.; Keyser U. F.; Baumberg J. J. Quantum electrodynamics at room temperature coupling a single vibrating molecule with a plasmonic nanocavity. Nat. Commun. 2019, 10, 1049. 10.1038/s41467-019-08611-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kongsuwan N.; Demetriadou A.; Chikkaraddy R.; Benz F.; Turek V. A.; Keyser U. F.; Baumberg J. J.; Hess O. Suppressed Quenching and Strong-Coupling of Purcell-Enhanced Single-Molecule Emission in Plasmonic Nanocavities. ACS Photonics 2018, 5, 186. 10.1021/acsphotonics.7b00668. [DOI] [Google Scholar]
- Zhang Y.; Meng Q.-S.; Zhang L.; Luo Y.; Yu Y.-J.; Yang B.; Zhang Y.; Esteban R.; Aizpurua J.; Luo Y.; et al. Sub-nanometre control of the coherent interaction between a single molecule and a plasmonic nanocavity. Nat. Commun. 2017, 8, 15225. 10.1038/ncomms15225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Antoniou P.; Suchanek F.; Varner J. F.; Foley J.. The Role of Cavity Losses in Polaritonic Chemistry. ChemRxiv 2020. 10.26434/chemrxiv.12673259.v2 [DOI] [PubMed] [Google Scholar]
- Ulusoy I. S.; Vendrell O. Dynamics and spectroscopy of molecular ensembles in a lossy microcavity. J. Chem. Phys. 2020, 153, 044108. 10.1063/5.0011556. [DOI] [PubMed] [Google Scholar]
- Nachtigallová D.; Aquino A. J. A.; Szymczak J. J.; Barbatti M.; Hobza P.; Lischka H. Nonadiabatic Dynamics of Uracil: Population Split among Different Decay Mechanisms. J. Phys. Chem. A 2011, 115, 5247–5255. 10.1021/jp201327w. [DOI] [PubMed] [Google Scholar]
- Mai S.; Richter M.; Marquetand P.; González L. In Photoinduced Phenomena in Nucleic Acids I: Nucleobases in the Gas Phase and in Solvents; Barbatti M., Borin A. C., Ullrich S., Eds.; Springer International Publishing: Cham, 2015; pp 99–153. [Google Scholar]
- Bandrauk A.; Ivanov M.. Quantum Dynamic Imaging: Theoretical and Numerical Methods; 2011. [Google Scholar]
- Friedel M. G.; Gierlich J.; Carell T.. PATAI’S Chemistry of Functional Groups; American Cancer Society, 2009. [Google Scholar]
- Silva R. E. F.; Pino J. d.; García-Vidal F. J.; Feist J. Polaritonic molecular clock for all-optical ultrafast imaging of wavepacket dynamics without probe pulses. Nat. Commun. 2020, 11, 1423. 10.1038/s41467-020-15196-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baumberg J. J.; Aizpurua J.; Mikkelsen M. H.; Smith D. R. Extreme nanophotonics from ultrathin metallic gaps. Nat. Mater. 2019, 18, 668–678. 10.1038/s41563-019-0290-y. [DOI] [PubMed] [Google Scholar]
- Johnson P. B.; Christy R. W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370–4379. 10.1103/PhysRevB.6.4370. [DOI] [Google Scholar]
- Delga A.; Feist J.; Bravo-Abad J.; Garcia-Vidal F. J. Quantum Emitters Near a Metal Nanoparticle: Strong Coupling and Quenching. Phys. Rev. Lett. 2014, 112, 253601. 10.1103/PhysRevLett.112.253601. [DOI] [PubMed] [Google Scholar]
- Mazzola L.; Maniscalco S.; Piilo J.; Suominen K.-A.; Garraway B. M. Pseudomodes as an effective description of memory: Non-Markovian dynamics of two-state systems in structured reservoirs. Phys. Rev. A: At., Mol., Opt. Phys. 2009, 80, 012104. 10.1103/PhysRevA.80.012104. [DOI] [Google Scholar]
- Delga A.; Feist J.; Bravo-Abad J.; Garcia-Vidal F. J. Theory of strong coupling between quantum emitters and localized surface plasmons. J. Opt. 2014, 16, 114018. 10.1088/2040-8978/16/11/114018. [DOI] [Google Scholar]
- Visser P. M.; Nienhuis G. Solution of quantum master equations in terms of a non-Hermitian Hamiltonian. Phys. Rev. A: At., Mol., Opt. Phys. 1995, 52, 4727–4736. 10.1103/PhysRevA.52.4727. [DOI] [PubMed] [Google Scholar]