Entry Modes of Ellipsoidal Nanoparticle by Membrane during Clathrin-mediated Endocytosis

Abstract

The membrane wrapping and internalization of nanoparticles, such as viruses and drug nanocarriers, through clathrin-mediated endocytosis (CME) are vitally important for intracellular transport. During CME, the shape of the particle plays crucial roles in determination of particle-membrane interactions, but much of the previous work has been focused on spherical particles. In this work, we develop a stochastic model to study the CME of ellipsoidal particles. In our model, the deformation of the membrane and wrapping of the nanoparticles are driven by the accumulation of clathrin lattices, which is stimulated by the ligand-receptor interactions. Using our model, we systematically investigate effect of particle shape (ellipsoid with different aspect ratios) on the CME. Our results show three entry modes: tip-first, tilted, and laying-down mode, used by ellipsoidal nanoparticles for internalization depending on the aspect ratio. Certain ellipsoids are able to take multiple entry modes for internalization. Interestingly, the prolate ellipsoid with aspect ratio of 0.45 can get internalized with significantly reduced number of ligand-receptor bonds. Particles which can be internalized with less bonds are excellent candidates for transcellular drug delivery. Moreover, our results demonstrate that internalization of ellipsoids with intermediate aspect ratios is easier than particles with low and high aspect ratios. Our model and simulations provide critical mechanistic insights on CME of ellipsoidal particles, and represents a viable platform for optimal design of nanoparticles for targeted drug delivery applications.

1. Introduction

The clathrin-mediated endocytosis (CME) is an important route for the intracellular transport of nanoparticles such as viruses and drug agents. Many physical and chemical parameters of the nanoparticle such as size, shape and surface functionality etc. potentially impact the membrane wrapping and particle uptake. Most current nanoparticles designed in lab or clinical trials has been spherical because of fabrication easiness. However, viruses and bacteria in nature are often in non-spherical shapes ^{1, 2}. The human cells are also capable of recognizing and ingesting non-spherical particles ³. The recent advancement of nanofabrication techniques makes the manufacturing of various non-spherical particles possible for drug delivery and medical diagnosis ^{4, 5}. Therefore studying the impact of the shape of nanoparticle on the membrane wrapping is of great significance for the future biomedical applications. Recent experimental and theoretical studies on the nanoparticle shapes have shown scattered results. The interactions between the non-spherical nanoparticles and the membrane during CME are still illusive.

Experimental studies have uncovered the existence of different uptake behaviors between non-spherical and traditional spherical particles through endocytosis. Some of the studies proposed higher internalization efficiency of spherical nanoparticle than the anisotropy counterparts. For example, Chithrani et al. ⁶ have found less nonspecific uptake of rod-shaped gold nanoparticles (AuNR) compared to gold nanospheres (AuNS) in HeLa cells. A follow up study demonstrated suppressed CME of transferrin-coated nanorods in comparison to spheres with STO, HeLa and SNB19 cells ⁷. The ellipsoidal polymeric nanoparticles and polystyrene nanodisks are also found less internalized than the spherical counterparts ^{8, 9}. In contrast, Barua et al. observed higher specific uptake of ligand-coated nanorods than nanospheres and nanodisks in breast cancer cell lines ¹⁰. Huang et al. ¹¹ also proposed higher and faster internalization of larger aspect ratio silica rod-shaped nanoparticles into A375 human melanoma cells. These controversial results illustrate the fact that the uptake of nanoparticle is highly shape, size and cell type dependent.

For nonspherical nanoparticles, the interplay between aspect ratio (AR), shape and size are complicated. The intermediate AR are found to facilitate the internalization while high AR may suppress the uptake ^{8, 12}. In contrast, it is found that higher internalization rate of high AR rod-like nanohydrogels than lower AR ones in HeLa cells ¹³. Besides, it is also found that the optimal AR and shape for uptake are varying in different mammalian cells ¹⁴. They observed higher uptake of nanodiscs with intermediate aspect ratio than nanorods in the endothelia cells, while high aspect ratio nanodiscs are preferred by epithelial and immune cells. The shape of nanoparticle also determines the optimal uptake size. For example, the disk-like nanoparticles may have a larger optimal size than spherical particles ¹⁵. Understanding the relationship between AR and nanoparticle uptake provides important insights for rational design of future drug carriers.

Continuum and coarse-grained molecular dynamics (CGMD) models have been developed to understand both the passive penetration and active endocytosis for spherical and nonspherical nanoparticles.^16–21 The studies have demonstrated the importance of shape in determining the nanoparticle uptake mechanisms ^21–25. Moreover, the rotation of anisotropic particle is found to play crucial roles during the membrane wrapping ^26–29. The internalization efficiency is compared between spherical and nonspherical nanoparticles. Some studies suggest higher endocytosis rate of spherical particles than ellipsoidal, rod-like and disk-shape counterparts ^{26, 30}. In contrast, Vácha et al. ²³ found that the internalization rate is higher for spherocylindrical particles than spheres. The influence of aspect ratio on the endocytosis is also studied but still under debate. Recent studies illustrated faster internalization of solid oblate ellipsoid than prolate-shape particle ²⁵, while other studies showed opposite trend ^{30, 31}.

In this work, we systematically investigate the CME of spherical and ellipsoidal nanoparticles through stochastic modeling and simulations. This model is based on our previously proved stochastic model for CME ³². Different from previous theoretical models, in our current model the deformation of the membrane and the wrapping of the nanoparticles are driven by the accumulation of the clathrin lattices, which is triggered by the ligand-receptor interactions. Using this model we explore the effects of nanoparticle AR and rotation on the overall process of endocytosis. Our results demonstrate three entry modes of the ellipsoidal nanoparticles with distinct patterns of bond formation. The particle entry mode is highly dependent on the particle shape. The simulations show consistent results with various experimental measurements and help to uncover fundamental mechanisms involved in this complex process. The model and simulations presented in this paper may provide theoretical guidelines for optimal design of nanoparticles for targeted drug delivery.

2. Model and Methods

2.1. Ellipsoidal Nanoparticle

In a Cartesian coordinate system, the standard form for an ellipsoid with center located at the origin can be expressed as:

$$\frac{x^2+y^2}{a^2}+\frac{z^2}{b^2}=1$$ (1)

The aspect ratio is (AR) defined by AR = a/b. Then we could define different nanoparticle shapes with various AR s (Figure 1). If AR > 1, the ellipsoid is oblate-shaped, and if AR < 1, the ellipsoid is prolate-shaped. If AR = 1 then the nanoparticle is a sphere.

Figure 1.

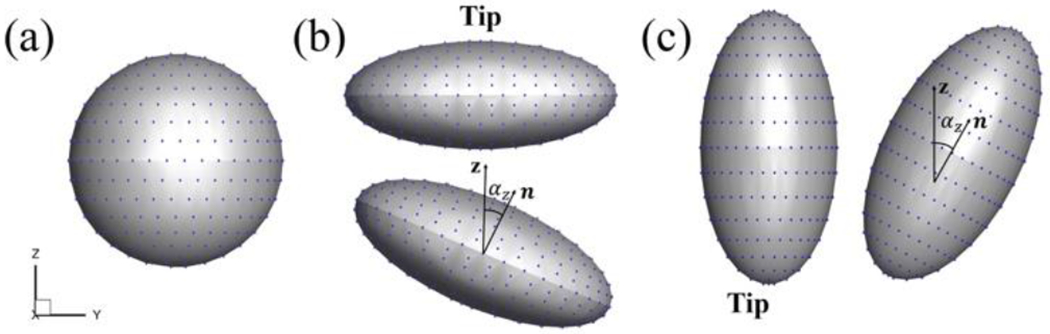
Shapes of sphere, oblate-shaped and prolate-shaped ellipsoids with ligands. Blue dots are the positions for coated ligands. Unit vector n indicates the direction of the ellipsoidal nanoparticle. α_z is the angle between vector n and the z-axis. (a) Spherical nanoparticle AR = 1. (b) Oblate-shaped ellipsoid with AR = 2.5. (c) Prolate-shaped nanoparticle with AR = 0.5.

The tip orientation is defined along the major and minor axes of the prolate and oblate-shaped ellipsoids, respectively. Thus, the oblate-shaped ellipsoid has a flat tip while prolate-shaped ellipsoid has a highly curved tip. The unit vector n defines the orientation of the nanoparticle. It rotates together with the rotation of the nanoparticle during the simulations such that we can trace the orientation of the nanoparticle. α_z defines the angle between vector n and the z-axis of the coordinate system. The nanoparticle is not allowed to rotate before having at least two ligand-receptor bonds in order to precisely control the initial attack angle of the nanoparticle to the membrane surface. After that, the nanoparticle is able to freely rotate.

2.2. Clathrin-mediated Endocytosis Model

In our model, the ligands are approximated as cylinders and uniformly distributed on the surface of the rigid nanoparticle (Figure 1). The nanoparticle is able to translate and rotate. The ligands and receptors are modeled as cylinders with one end attached to the particle/membrane surface and the other free end as binding tip. The receptors are placed normal to the local surface and can freely diffusion on the membrane. The membrane surface is modeled with Helfrich Hamiltonian. ^{33, 34} The total energy E of membrane is:

$$E=\iint \left[\frac{\kappa }{2}{(2H-H_0)}^2+\overline{\kappa }K+\sigma \right]dA$$ (2)

where κ and $\overline{\kappa }$ are the bending rigidity and Gaussian rigidity of the membrane, and σ represents the membrane tension. H = (c₁ + c₂)/2 is the mean curvature and K = c₁c₂, is the Gaussian curvature of the surface, c₁ and c₂ are the principal radii of curvatures. H₀ is the intrinsic or spontaneous mean curvature of the membrane. Recent works have demonstrated the critical roles of intrinsic curvature on selection of particle size and shape during the endocytosis. ^{35, 36} The Gaussian rigidity term remains a constant and is hence not included in the model, because of fixed topological of membrane during simulation. The parameters in Eq. (2) depend on the properties of the membrane bilayer, local protein expressions and cytoskeleton networks etc.^37–39 In this work the membrane properties (κ and σ) are fixed (see Table A1). In our model as illustrated in Figure 2, the membrane surface is discretised in a triangulate system, ^{40, 41} which is consist of a number of vertices connected by links. The deformation is through the displacement of vertices and flipping of links,⁴² each movement of affect the membrane energy in Eq. (2).

Figure 2.

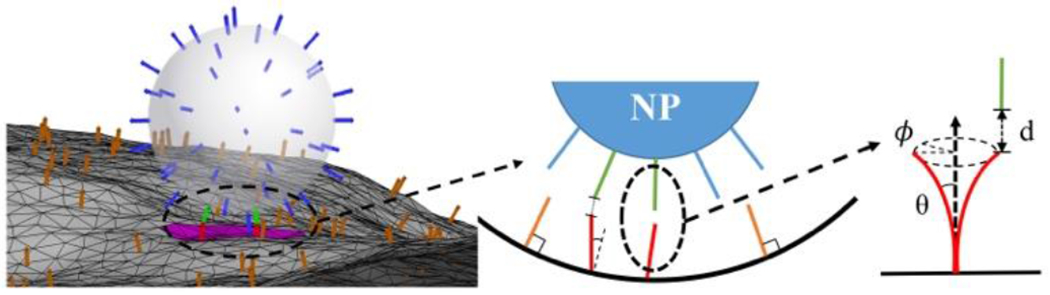
Schematic of the binding of the ligand (blue) coating nanoparticle (NP) to the cell membrane. The membrane is discretised by triangulate system containing vertices and links. The binding is mediated by the interactions between the bonded ligands (green) and receptors (red) when the corresponding tip distances d are within the reaction cut-off range. The bonded receptors are allowed to bend and rotate in θ and ϕ. The ligand-receptor bindings introduce the clathrin-coated pit (pink) on the membrane. The unbonded receptors (orange) can freely diffuse on the membrane.

During CME, the accumulation of clathrin-coated pit (CCP) plays key roles in driving the deformation of membrane. Experiments have shown that the energetically favorable shape of CCP is the spherical-shaped structure ^{43, 44}. The indispensable role of CCP for driving the deformation is also observed ⁴⁵. In addition, it has been shown that CCP alone provides sufficient curvature to bend the membrane for budding. The underling mechanism of CCP transformation from flat to curved shape is extremely complicated involving the coordination of many factors, such as the APs, topological disclinations and clathrin network elasticity.^46–49 In our model, the effect of CCP is simplified and modeled as additional intrinsic curvature H_cla with higher bending rigidity κ_cla. Therefore, the total energy of the membrane with clathrin can be expressed as:

$$E=\iint \left[\frac{\kappa }{2}{\left(2H\right)}^2+\sigma \right]dA+\iint \left[\frac{{\kappa }_{cla}}{2}{(2H-H_{cla})}^2\right]dA$$ (3)

where κ_cla = 200 k_B T ⁵⁰ and H_cla = 0.036 nm^{−1 51, 52} are the bending rigidity and intrinsic curvature of the clathrin coat. The first and second terms on the right-hand side of Eq. (3) account for the regions without and with clathrin respectively.

The cytoplasmic domain of the receptor has specific signal sequences that are able to bind with adaptor proteins (APs) promoting the accumulation of clathrin units.⁵³ With the presence of receptors, the binding affinity between AP and membrane has shown to be greatly increased in experiments.⁵⁴ The ligand-receptor interactions help stabilize the receptor molecules and may further assist the recruitment of Aps. This act as the bridge between the receptor and clathrin lattices on the membrane, and facilitate clathrin accumulation ^{55, 56}. In addition, studies have also observed continuous growing of CCP during the CME, indicating the continuous accumulation of clathrin units and a steady increase of CCP area during the internalization. ⁵⁷ Base on those facts, we model the accumulation of clathrin lattices as a ligand-receptor dependent process. Each time when a new ligand-receptor bond is formed, a clathrin lattice appears at the new binding site and the effect is represented as a clathrin induced intrinsic curvature field. The affected field will cover a circular areas with radius of 14 nm on the membrane surface according to experiments ⁵⁸. Moreover, the local clathrin coats will be dissembled when the nanoparticle completely detached from the membrane.

We assume monovalent and stochastic binding between ligand and receptor. The ligand-receptor interactions are modeled by the Bell model ⁵⁹ :

$$\Delta G_r\left(d\right)=\Delta G_0+\frac{1}{2}k{d}^2$$ (4)

Here d is the distance between the binding tips of the interacting ligand and receptor (see Figure 2), ΔG₀ is the equilibrium free energy change at d = 0, and k is the interaction bond force constant. ΔG₀ is obtained from the dissociation constant K_d via ΔG₀ = −k_B TlnK_d, where k_B is the Boltzmann constant and T is the thermodynamic temperature. We also account for the flexural movement of the receptors during ligand-receptor binding since it is directly related to the entropy change. For a bonded receptor, it is allowed to bend and rotate (Figure 2). Under the assumption of small deformations, we model the flexure of a receptor as bending a beam from equilibrium (normal to membrane surface) position, and the bending energy is calculated as:

$$\Delta G_f\left(\theta \right)=(2EI/L){\theta }^2$$ (5)

where EI is the receptor flexural rigidity, L is the receptor length and θ represents the bending angle from the normal direction of the local membrane. When the binding tips between a ligand-receptor pair are close, the bond formation is possible. An arbitrary flexural bending angle θ is selected, and then the distance between the tips (d) is measured. When d is less than the reaction cut-off range (Table A1), the total energy change, including the reaction energy from Eq. (4) and receptor bending energy from Eq. (5), is calculated and then is used to determine whether the bond formation is accepted or rejected. The existing ligand-receptor bonds may also break according to the energy change (Eq. (4) and Eq. (5)) during breakage. Once the bond breaks, the receptor returns to the normal direction. More details regarding the clathrin-mediated endocytosis model can be found from our previous publication³².

The simulations contain four types of Monte Carlo (MC) steps: receptor diffusion, particle translation or rotation, bond formation or breakage, and membrane surface evolution. In each MC step, one of the movements will be randomly selected and the system energy (U) is calculated for the new configuration. The U_new includes the membrane elastic energy E, ligand-receptor interaction energy ΔG_r, and receptor flexural energy ΔG_f. The new configuration is accepted with the following probability: min{1, exp [−(U_new − U_old) / k_B T]}.

3. Results and Discussion

In our simulations we adopt the transferrin (Tf)-transferrin receptor (TfR) parameters for ligand-receptor interactions, since they are well known for triggering the CME and have been extensively studied for the drug delivery across the blood-brain barrier (BBB) ^60–64. We focus on the ellipsoidal nanoparticles because they have been used for the drug delivery purpose ⁴. However, this model can be easily extended to study other nonspherical nanoparticles. The ellipsoidal nanoparticles in our study have the same volumes as the 80 nm-diameter spherical particles. Based on our previous studies ³², 80 nm-diameter ligand-coated spherical particles are highly likely to be internalized during CME. The ligand density for all various shaped particles is set to be 5300 / μm^{2 65}. The initial attack angles are set at α_z = 0, which means the vector n is parallel to the z-axis at the beginning of the simulations (Figure 1). For each case, we run at least 5 independent simulations for statistical consistency. Some of the other parameters used in the simulation are shown in Appendix A.

3.1. Endocytosis of Oblate-shaped Ellipsoid

We first consider the CME of oblate-shaped nanoparticles with 1 < AR < 3. Table 1 shows the aspect ratio and size parameters used for the simulations. The number of ligands coated on particle surface is calculated based on the surface area of the particle and the ligand density. The a- and b- axes are the major and minor axes in Eq. (1).

Table 1:

Shape and size parameters for oblate ellipsoids

Aspect Ratio (AR)	a-axis Radius (nm)	b-axis Radius (nm)	Number of Ligands
1	40	40	106
1.17	42	36	106
1.47	45.5	31	110
2.08	51	24.5	118
2.62	55	21	126

The CME of oblate ellipsoid shows two entry modes: tip-first mode with minimal rotation (< 15 degrees) and tilted entry mode with a moderate rotation (15 – 45 degrees) as shown in Figure 3a. But no laying-down (> 45 degrees) pattern has been observed in this study. Both the sphere and high AR oblate ellipsoids (AR = 2.08 and AR = 2.62) rotate less than 10 degrees throughout the simulations. Sphere has less rotation due to the homogenous distributed curvatures. For high AR oblate ellipsoids, the flat tip with low curvature helps stabilize the nanoparticle on the membrane with less rotation. Small to intermediate AR oblate ellipsoids (AR = 1.17 and AR = 1.47) are capable of taking advantage of both tip-first and tilted entry modes.

Figure 3.

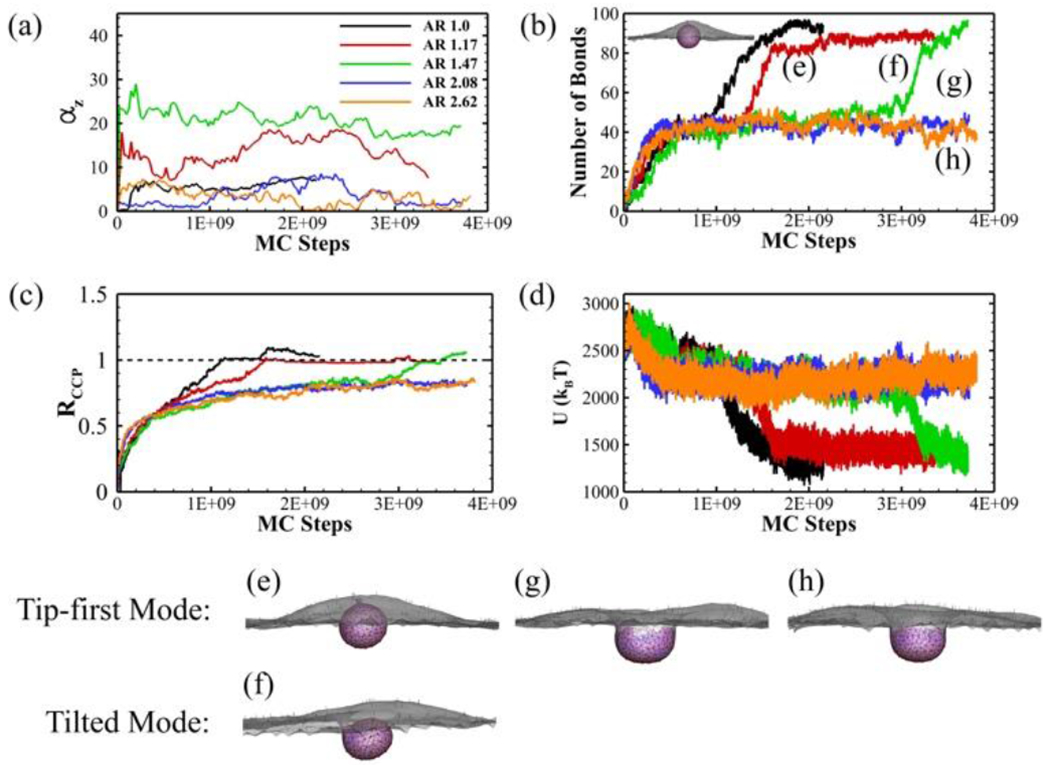
Endocytosis of sphere and oblate ellipsoids with various aspect ratios. (a) The rotation of the nanoparticle (α_z); (b) The number of ligand-receptor bonds (the equilibrium profile of spherical nanoparticle is also shown); (c) The normalized CCP area ratio R_CCP; and (d) The total energy of the system U as a function of MC steps during CME. The equilibrium particle-membrane profiles for ellipsoid with (e) AR = 1.17, (f) AR = 1.47, (g) AR = 2.08 and (h) AR = 2.62. The CCP (pink region), bonded TfR (red dots), free TfR (black dots), bonded Tf (green dots) and unbonded Tf (blue dots) are all shown in the profiles.

As shown in Figure 3b, the number of ligand-receptor bonds for spherical nanoparticle continuously increases without significant interruptions. The nanoparticle is fully endocytosed after 1.2e9 MC steps. For the tip-first and tilted entries of particles with AR = 1.17 and AR = 1.47, the number of bonds shows a two-step growth pattern with two major bond forming periods separated by a plateau in between. The oblate ellipsoid with AR = 1.17 has an initial rapid bond forming period because of the large contact area of the flat tip surface. But the number of bonds reaches the plateau when half of the coated ligands are bonded. This period ends with further growth of CCP and membrane deformation. The nanoparticle is quickly wrapped with number of bonds jumping from 40 to 80. The ellipsoid with AR = 1.47 follows a similar two-step bond formation pattern. The main difference is that the first plateau lasts for much more MC steps due to sharper edges. For the tip-first entry of high AR ellipsoids (AR = 2.08 and AR = 2.62), the number of bonds is saturated at around 40 after initial bond formation on the flat tip surface near the membrane.

The normalized CCP ratio, R_CCP, reflects similar trend as the number of bond formation (Figure 3c). R_CCP is defined as the area of CCP over the area of minimal ellipsoid that encapsulates the particle. For AR = 1.17 and AR = 1.47 oblate particle, the CCP growth rate significantly drops after R_CCP~0.5. The flat tip of oblate ellipsoid makes it easy to wrap half of the particle. The growth rate is reduced because of the highly curved edges. After overcoming the curved edge, the CCP growing is accelerated until full wrapping with R_CCP~1.0. For high aspect ratio ellipsoids, the CCP area also grows fast at beginning until R_CCP~0.5. It slowly reaches the maximum value of R_CCP~0.8 during the rest of the simulation. As shown in Figure 3d, the decrease of the total energy is mainly driven by the increase of existing bonds in the simulation. Therefore, the energy change follows a subsequent two-step decrease pattern for low to intermediate AR particles. In contrast, the system energy of high AR particles reaches equilibrium rapidly after initial decrease.

Figure 3e, g and h show the equilibrium profiles of particles with tip-first entry mode. The AR = 1.17 particle shows fully wrapped profile (Figure 3e) with symmetric vesicle at equilibrium. For high aspect ratio ellipsoids with AR = 2.08 and AR = 2.62, we observe firm attachment of the particle to the membrane but no internalization (Figure 3 g and h). The membrane partially wraps the oblate with R_CCP < 1.0 and further bending is suppressed by the highly curved edges. The ellipsoid shows minimal rotation (α_z < 10 degrees) and a symmetric wrapping. This is due to an initial large contact area respect to the membrane surface, which leads to higher adhesion stability and less rotation. The results are consistent with the theoretical work from Bahrami ⁶⁶, that higher adhesion strength is required for high aspect ratio ellipsoid to be internalized. Another theoretical study also proposed a similar prediction that increased aspect ratio makes it easier for attachment but more difficult to achieve completely wrapped state for the ellipsoidal nanoparticle ³⁰. The vesicle formed by the oblate ellipsoid with AR = 1.47 through tilted entry mode is shown in Figure 3f. In this situation, the nanoparticle adjusts itself to a tilted position around 20 – 25 degrees to help bond formation on one side of the edge. Similar rotation of oblate-shaped ellipsoid during RME has also been observed in Refs. ^{25, 29}. The tilting of the ellipsoid leads to an asymmetric wrapping of the membrane.

The internalization of the oblate ellipsoid with AR = 1.17 can take both tip-first and tilted entry modes. Figure 4 shows the detailed comparison between these two modes. As shown compared with the tip-first entry, a large degree of rotation (40 to 45 degree) during the early stage leads to the tilted entry. The rotation helps bond formation on one side of the curved edges but makes it more difficult for further bond formation on the flat surface. The bond formation reaches the plateau quickly with only ~ 10 bonds. The formation of plateau period is the result of inhomogeneous distributed curvatures on oblate nanoparticles. After a quick bond formation, the nanoparticle stays partially wrapped before the membrane could overcome the highly curved edges (Figure 4d(1)). Driven by the spontaneous deformation of the CCP, the membrane is further bended gradually near the edge (Figure 4d(2)). After overcoming the bending energy barrier introduced by the curved edges, the free receptors can bind with the ligands on the other side of the oblate ellipsoid (Figure 4d(3)). The total energy change of system indicates the energy reduction from the ligand-receptor bindings during the simulation (Figure 4c). The system energy decreases dramatically after the plateau period, showing the important role of the thermodynamic driving force in determining internalization. During the internalization, the oblate ellipsoid simultaneously adjusts its orientation with respect to the membrane to accommodate the wrapping. As shown in Figure 4d and e, the tilted nanoparticle forms an asymmetric mature vesicle due to extensive reorientation while the tip-first mode follows a more symmetric membrane wrapping.

Figure 4.

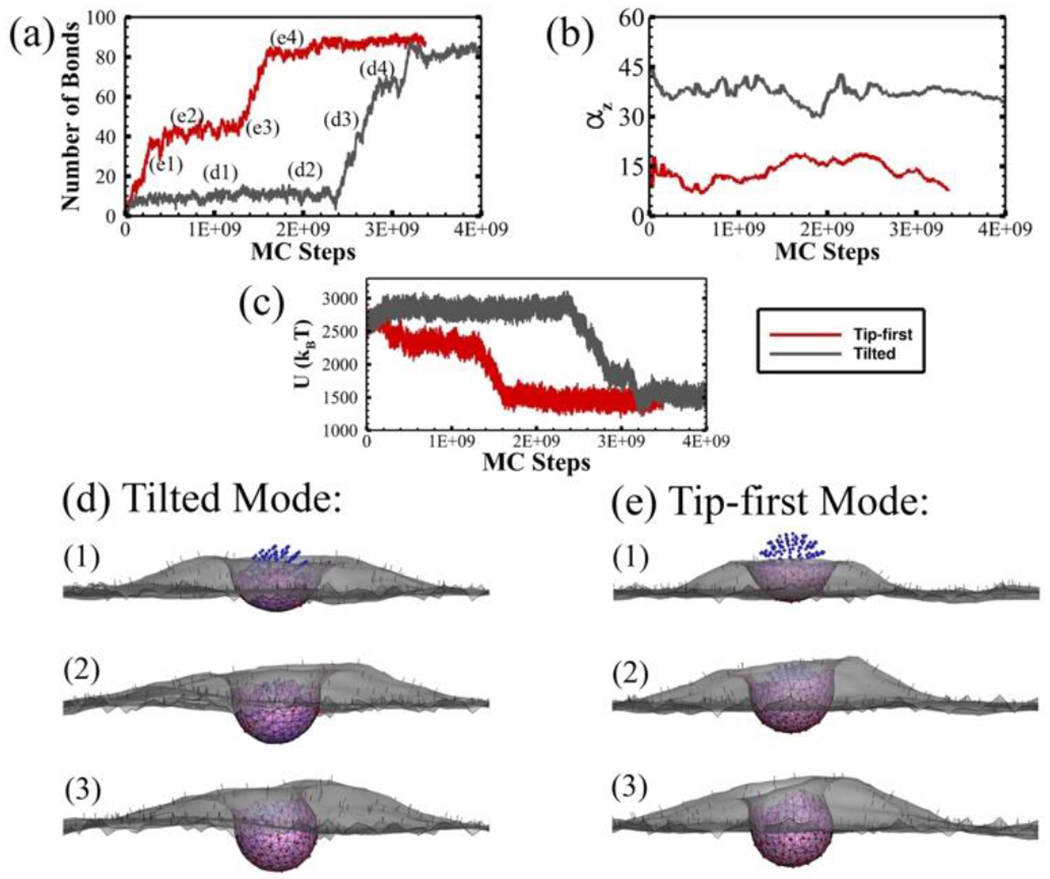
Two entry modes (tip-first and tilted) of the oblate ellipsoid with AR = 1.17. (a) The number of ligand-receptor bonds; (b) The rotation of the particle (α_z); (c) The total energy of the system U as a function of MC steps during CME. (d-e) The membrane-particle profiles at different stages identified in (a). The CCP (pink region), bonded TfR (red dots), free TfR (black dots), bonded Tf (green dots) and unbonded Tf (blue dots) are all shown in the profiles.

3.2. Endocytosis of Prolate-shaped Ellipsoid

In this section we investigate the CME of prolate-shaped nanoparticles with aspect ratio of 0.25 < AR < 1. The geometrical parameters of the particles are shown in Table 2.

Table 2:

Shape and size parameters for prolate ellipsoids

Aspect Ratio (AR)	a-axis Radius (nm)	b-axis Radius (nm)	Number of Ligands
1	40	40	106
0.9	38.5	43	106
0.67	35	52	108
0.42	30	71	118
0.25	25	102	136

As shown in Figure 5a, we also observe two entry modes for prolate-shaped nanoparticles: tip-first and laying-down modes. The tip-first mode is chosen by high to intermediate aspect ratio particles with AR = 0.9 and AR = 0.67, characterized by the two-step growth pattern of bonds (Figure 5b). Since the tip of the prolate particle is highly curved, the bond formation reaches the plateau quickly at ~ 2e8 MC steps with less than 20 ligand-receptor bonds. The periods of the plateau are similar for both AR = 0.9 and AR = 0.67 ellipsoids. This is quite different from the oblate-shaped cases where higher AR particle has a significantly longer plateau period than smaller AR one (see Figure 3b). After 2.0e9 MC steps, the number of bonds quickly increases to more than 80 for both cases due to the easiness of bond formation on the flat edges of the prolate ellipsoid. The R_CCP and system energy U also follow a similar step-wise change in the simulations (Figure 5c and d). During the wrapping, the ellipsoid keeps perpendicular to the membrane surface with little rotation. The vesicle formed by the nanoparticle with AR = 0.9 is still spherical shaped while it becomes ellipsoidal shape for ellipsoid with AR = 0.67 due to lower aspect ratio (Figure 5e and f).

Figure 5.

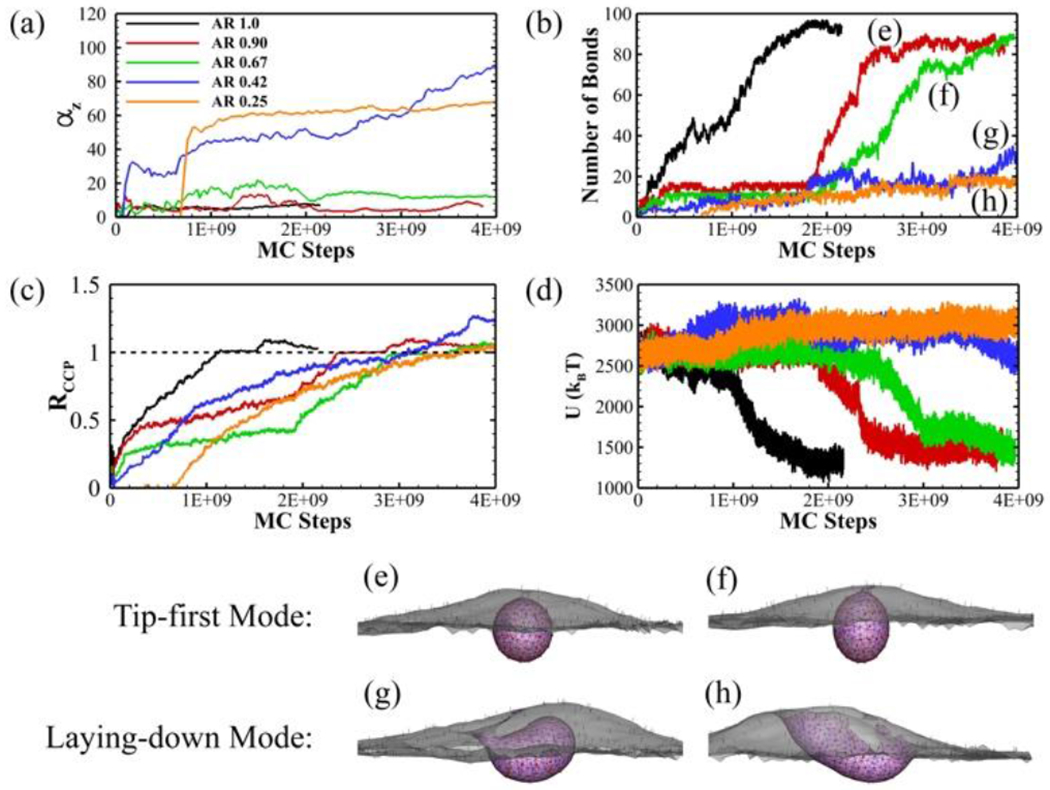
Endocytosis of sphere and prolate-shaped ellipsoids with different aspect ratios. (a) The rotation of the nanoparticle (α_z); (b) The number of ligand-receptor bonds; (c) The normalized CCP area ratio R_CCP; and (d) The total energy of the system U as a function of MC steps during CME. The equilibrium particle-membrane profiles for ellipsoid with (e) AR = 0.90, (f) AR = 0.67, (g) AR = 0.42 and (h) AR = 0.25. The CCP (pink region), bonded TfR (red dots), free TfR (black dots), bonded Tf (green dots) and unbonded Tf (blue dots) are all shown in the profiles.

On the other hand, the low aspect ratio nanoparticles with AR = 0.42 and AR = 0.25 use the laying-down entry mode during which the particles rotate to a nearly horizontal position (Figure 5a). The number of bonds during the uptake is much less than the tip-first mode (Figure 5b). As a result, the total energies of the systems U do not decrease (Figure 5d). However, the R_CCP still keeps growing during the simulation (Figure 5c). The AR = 0.42 ellipsoid is fully wrapped while the AR = 0.25 ellipsoid does not completely internalize (Figure 5g and h). Though the R_CCP of AR = 0.25 particle also reaches 1.0, the CCP cannot bend itself to fully wrap the particle because of the extremely high aspect ratio.

Our results indicate that prolate ellipsoids with low AR prefer to take the laying-down mode to enter cells. Experiments have observed both tip-first and laying-down entry modes for viruses with low AR ^{67, 68}. Coarse-grained molecular dynamics (CGMD) studies also showed a similar perpendicular to parallel reorientation of low AR spherocylinder in RME ⁶⁹. A more recent theoretical study also showed that the parallel orientation of ellipsoid is more energetic favorable than tip-first orientation because of higher bending energy cost per area at tip ²⁴. However, the theoretical work from Yi et al. ⁷⁰ and CGMD simulations from Shen et al. ²⁵ showed that the low AR ellipsoids preferred tip-first entry mode at low membrane tension. In Ref. ⁷⁰, the ligand-receptor interactions have been modeled as a direct adhesion within certain area and the membrane wrapping was driven by the energy reduction caused by the adhesion. In Ref. ²⁵, discrete ligand-receptor interactions have been considered with a relatively high binding strength (50 k_B T) and very long interaction cutoff (37.5 nm). In our model, the ligand-receptor interaction cutoff is much shorter, therefore it is much harder to continuously form bonds from a tip-oriented position with high curvatures. Laying-down helps bond formation on the flat side and further reduce the energy of the system.

Another interesting observation with AR = 0.42 and AR = 0.25 particles is that the R_CCP continuously increases while the number of ligand-receptor bonds keeps nearly constant at a relatively low value (less than 30) (Figure 5b and c). In our model, the recruitment and accumulation of clathrin are stimulated by the formation of new ligand-receptor bonds (see method section). Laying-down of the particle allows continuous new ligand-receptor bonds formation at the new binding sites. However, the existing bonds break more frequently at the same time. This is due to the fact that the radius of the curvature on membrane caused by the clathrin (H_cla) is ~ 30 nm, this is significantly smaller than the b-axis radii of the ellipsoids (71 nm and 102 nm for AR = 0.42 and AR = 0.25 particles). Therefore, the bending of the membrane caused by clathrin tends to break the existing ligand-receptor bonds. As a result, the prolate ellipsoid with AR = 0.42 is fully wrapped with only ~ 30 bonds, less than half of the spherical counterpart at equilibrium. As shown in Figure 5d, we do not observe significant total energy decrease, which is similar with the high AR oblate ellipsoid case in Figure 3d. The ability to get internalized with less number of ligand-receptor bonds is important to transcellular drug delivery. For transcellular drug delivery, the nanoparticle need to first enter the cell at one side and then release from the cell at the other side. Less number of ligand-receptor bonds during internalization facilities the particle release during expulsion. Indeed, experiments have demonstrated that spherical nanoparticles with lower avidity have better efficiency for transcytosis across blood-brain barriers ^{65, 71}. In addition, it has also been observed in in vivo experiments that it is easier for the Tf-coated nanorods to release from the cell than spherical ones ⁷.

Moreover, for ellipsoid with intermediate aspect ratio AR = 0.67, we find that the particle can be internalized by all three modes. Figure 6 presents the entry of tip-first and laying -down modes. Compared with the two-step growth of bonds in tip-first mode, the laying-down mode features a continuous increase of bonds until fully endocytosed. The internalization of laying-down ellipsoid takes less MC steps than the tip-first mode. This is because that the rotation of the particle allows the ligands on the flat side to interact with receptors on membrane. The equilibrium energy of the tip-first mode is lower than the laying-down mode, meaning that the tip-first mode is a more energetically favorable status for this ellipsoidal nanoparticle.

Figure 6.

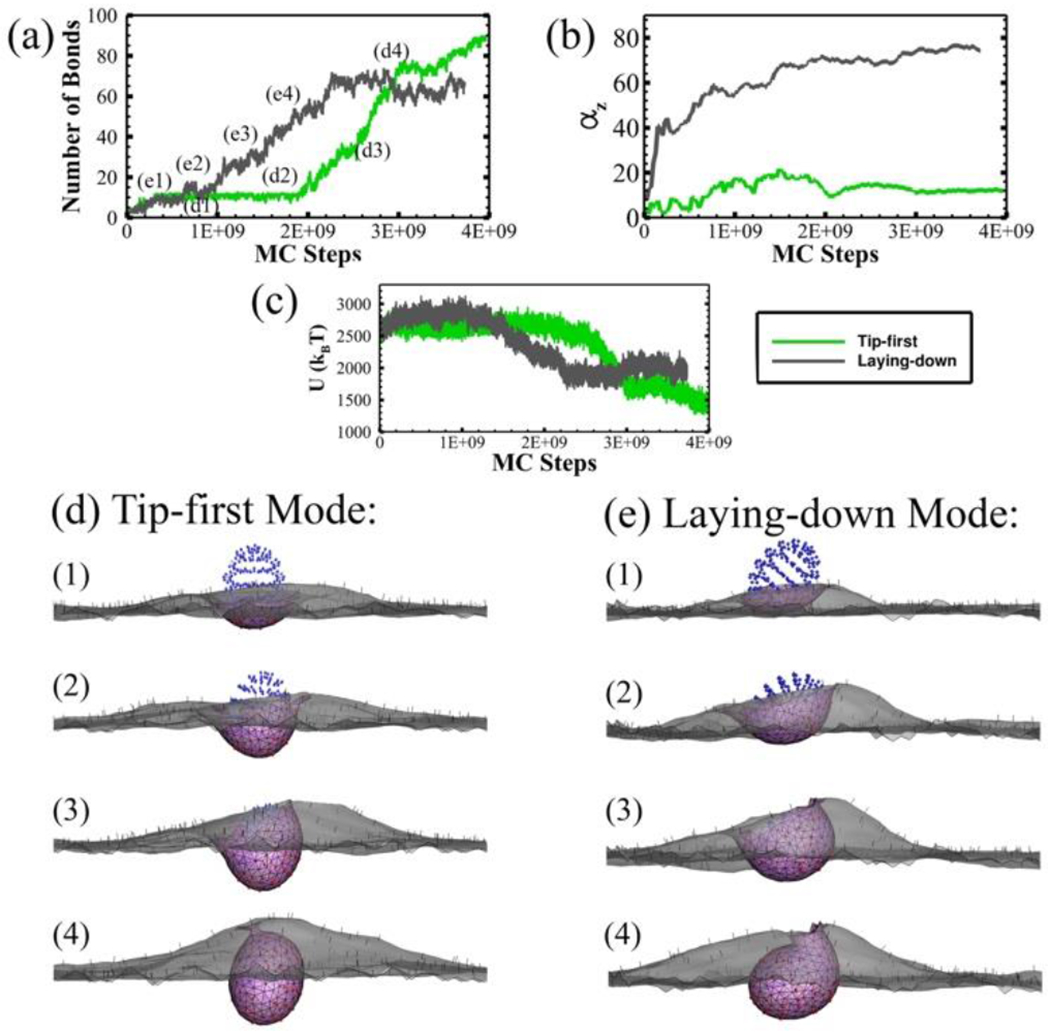
Two entry modes of the prolate ellipsoid with AR = 0.67. (a) The number of ligand-receptor bonds; (b) The rotation of the particle (α_z); (c) The total energy of the system U as a function of MC steps during CME. (d-e) The membrane-particle profiles at different stages identified in (a). The CCP (pink region), bonded TfR (red dots), free TfR (black dots), bonded Tf (green dots) and unbonded Tf (blue dots) are all shown in the profiles.

3.3. Overall Endocytosis Comparison

Figure 7 summarizes our findings of endocytosis for ellipsoid particles. As shown in Figure 7a, there are three major patterns for the entry of ellipsoids with different aspect ratios. Characterized by the degrees of rotation during the entry, we observe tip-first mode (< 15 degrees), tilted entry mode (15 – 45 degrees) and laying-down mode (> 45 degrees). The oblate ellipsoid with AR > 1.47 only take tip-first entry mode. On the other hand, the low aspect ratio prolate nanoparticles with AR = 0.25 and AR = 0.42 only use the laying-down entry mode. Intermediate aspect ratio ellipsoids with 0.67 ≤ AR ≤ 1.47 may choose either tip-first mode or tilted entry mode. Interestingly the prolate ellipsoid with AR = 0.67 shows the flexibility and may take any of the three entry modes for endocytosis. The capability of taking any entry mode is helpful for the drug delivery applications. In realistic biological scenarios, the initial contact direction between the particle and cell membrane is random. Therefore particles that can adopt all entry modes may have better opportunities to enter the cells. Overall the prolate nanoparticles rotate more to enter the cell compared with the sphere and oblate nanoparticles during the endocytosis, because of the highly curved tip of prolate ellipsoid.

Figure 7.

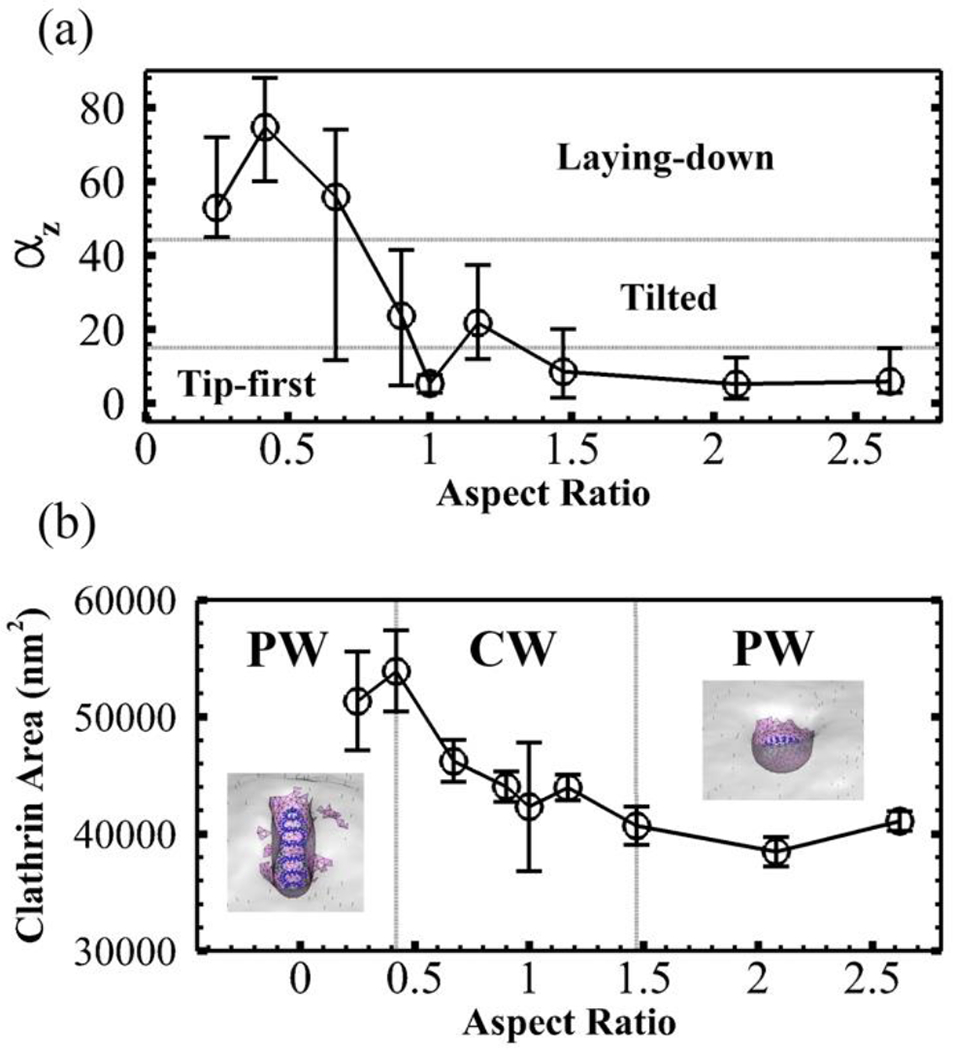
Equilibrium rotation angles and clathrin coated area for spherical and ellipsoidal nanoparticles. (a) The nanoparticles show three entry patterns: tip-first mode (<15 degrees), tilted entry mode (15 – 45 degrees) and laying-down mode (>45 degrees) depending on the degrees of rotation. The error bars represent the minimal and maximal degrees of rotation observed in 5 independent simulations. (b) The clathrin area plot shows the influence of the shape of nanoparticle on the internalization capability. The error bars are based on the standard deviation from 5 independent simulations. The nanoparticle is able to be completely wrapped (CW) within 0.42 ≤ AR ≤ 1.47 while only partially wrapped (PW) for AR < 0.42 or AR > 1.47. The equilibrium membrane profiles for nanoparticle with AR = 0.25 and 2.62 are shown respectively.

Figure 7b summarizes the internalization stages of all the particles with different shapes. We have observed complete wrapping (CW) for nanoparticles with aspect ratio 0.42 ≤ AR ≤ 1.47. The sphere nanoparticle can be internalized with the least MC steps indicating the highest efficiency. Although ellipsoidal particles are more difficult to enter the cell, in general they require less number of ligand-receptor bonds compared with spherical particles. Especially, the prolate ellipsoid with AR = 0.42 can have CW with significantly less number of bonds (~ 30). This is especially important for transcellular drug delivery since less number of bond during endocytosis may lead to a higher exocytosis efficiency. Overall, our results are consistent with the experimental observations ^{6, 7}, low AR prolate and high AR oblate nanoparticles, with AR < 0.42 or AR > 1.47 in our study, only show partial wrapping (PW) indicating a low internalization efficiency.

The rotation of the particles, different entry modes and wrapping states during endocytosis on fluid membranes have been studied through various analytical analysis and simulations. ^{24, 25, 29, 30, 66, 69, 72} The distinctive feature of our model is that the deformation of the membrane and wrapping of the particles are driven by the assembly of CCP. In our model, the accumulation of CCP is triggered by the ligand-receptor interactions, while the ligand-receptor binding is modeled as a stochastic process and the modelling parameters are directly obtained from experiments. Therefore, entire particle internalization process is stochastic and dictated by many inter-correlated events, such as ligand-receptor bond formation/breakage, particle translation/rotation, clathrin assembly/dissembly, membrane deformation, etc. As a result, our simulations provide additional information. For example, our results indicate that the internalization of particles may not always correlate with continuous increasing of bonds in CME (see Figure 3). The rotation (or entry mode) of the same nanoparticle may be different due to localized CCP recruitment. Indeed, our results indicate that multiple entry modes may be taken by specific nanoparticles. Due to the stochastic nature, the wrapping state of the certain particles may also become scattered.

4. Conclusions

CME is the fundamental biological mechanism for the cell metabolism and intracellular transport of nanoparticles. The advancement of nanotechnology makes the manufacturing of nanoparticles with different shapes possible for biomedical application. But how the different shaped nanoparticles interact with the cell membrane is complicated and still under debate. In this work, we systematically investigated the CME of transferrin-coated spherical and ellipsoidal nanoparticles through modeling and simulations. Our stochastic model takes into account the membrane deformation, clathrin lattices accumulation and transferrin-transferrin receptor interactions based on Monte Carlo simulations. In our model, the membrane deformation and particle internalization are primarily driven by the clathrin polymerization, which is stimulated from the ligand-receptor interactions.

Through our simulations, we found three entry modes for the CME of sphere and ellipsoid including tip-first, tilted entry and laying-down mode. Each mode is characterized by the distinctive degrees of rotation during the wrapping of the membrane. High aspect ratio oblate ellipsoids with AR > 2 use only tip-first entry mode. Small to Intermediate aspect ratio ellipsoids with 0.67 ≤ AR ≤ 1.47 are able to take tip-first and tilted entry modes. Low aspect ratio prolate nanoparticles with AR < 0.5 only internalize through the laying-down mode. Moreover, we have observed certain moderate aspect ratio prolate ellipsoid, such as AR = 0.67 in our study, is able to take advantage of all of the three modes for internalization.

The bond formation and CCP growth of both tip-first and tilted mode show a two-step wrapping pattern with a plateau in between. The plateau period dependents on the aspect ratio and rotation of the nanoparticle. The laying-down mode has a continuous CCP wrapping pattern, but the equilibrium number of bonds is highly dependent on the aspect ratio of the nanoparticle. The prolate ellipsoid with AR = 0.42 is internalized with more MC steps but much less ligand-receptor bonds than other shapes. Internalization of nanoparticles with less number of ligand-receptor bonds may significantly facilitate release of the particle during transcellular drug delivery. In addition, we have observed complete wrapping for particles with intermediate AR range of 0.42 ≤ AR ≤ 1.47 for. In general, the internalization of spherical nanoparticles is easier than ellipsoidal particles. In summary, our simulation results are consistent with a variety of experimental measurements and provide deeper understanding of the fundamental mechanisms involved in CME of nanoparticles with different shape. Our model represents a powerful and viable platform for facilitating the rational design of nanoparticles for targeted drug delivery.

Appendix A: Simulation parameters

The table below lists some of the simulation parameters used and the corresponding references:

Table A1.

Summary of some parameters used in the simulation

Parameters	Value	Ref
Size of membrane surface	910 nm × 910 nm
Membrane bending rigidity κ	20 kB T	73
Membrane characteristic tension σ	0.001 pN / nm	74
Clathrin bending rigidity κcla	200 kB T	75
Clathrin intrinsic curvature Hcla	0.036 nm−1	51
Transferrin receptor length	9.3 nm	76
Transferrin receptor radius	5 nm	76
Antibody length	9 nm	77
Antibody radius	2.5 nm	77
Number of transferrin receptors on luminal side	300	78
Equilibrium free energy change ΔG0	−8.64e−20 J	79
Reactive compliance (reaction cut-off distance)	0.9 nm	79
Receptor flexural rigidity EI	7000 pN · nm2	80
System temperature	298 K